Epsilon-Delta-Kriterium der Stetigkeit – Serlo „Mathe für Nicht-Freaks“
Das Epsilon-Delta-Kriterium ist neben dem Folgenkriterium eine weitere Variante, die Stetigkeit einer Funktion zu definieren. Sie umschreibt die charakteristische Eigenschaft stetiger Funktionen, dass hinreichend kleine Änderungen des Arguments beliebig kleine Änderungen im Funktionswert verursachen.
Motivation
[Bearbeiten]Zu Beginn des Kapitels haben wir gelernt, dass die Stetigkeit einer Funktion zumindest vereinfacht als Abwesenheit von Sprüngen interpretiert werden kann. An einer stetigen Stelle ändern sich die Funktionswerte also beliebig wenig, wenn nur das Argument hinreichend wenig geändert wird. Es gilt also , wenn hinreichend nah an liegt. Solche Funktionswerte können zur Annäherung von herangezogen werden.
Stetigkeit bei Approximation von Funktionswerten
[Bearbeiten]Hat eine Funktion keine Sprünge, kann man ihre Funktionswerte durch umliegende Werte approximieren. Für diese Annäherung und somit auch für den Beweis der Stetigkeit verwenden wir das Epsilon-Delta-Kriterium stetiger Funktionen. Doch was bedeutet das genau?
Nehmen wir an, wir führen ein Experiment durch, bei dem wir die Lufttemperatur messen wollen. Sei die Funktion für den Temperaturverlauf. ist also die Temperatur zum Zeitpunkt . Aufgrund eines technischen Fehlers fehlt uns ein bestimmter Wert , den wir nun möglichst genau approximieren wollen:

Durch den technischen Fehler war die direkte Messung von nicht möglich. Weil sich der Temperaturverlauf kontinuierlich ändert und es damit insbesondere zum Zeitpunkt keinen Sprung im Temperaturverlauf gibt, können wir ersatzweise die Temperatur zeitnah an bestimmen. Wir nähern also den Wert an, indem wir eine Temperatur bestimmen, bei der der Zeitpunkt nah an liegt. ist dann eine Annäherung von . Wie nah muss hierzu an liegen?
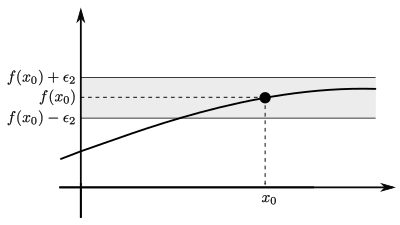
Nehmen wir an, dass sich für die spätere Auswertung die gemessene Temperatur maximal um den Fehler von der tatsächlichen Temperatur unterscheiden darf. Unser Messwert muss sich also im grau hinterlegten Bereich der folgenden Grafik befinden. Das sind alle Punkte, deren Funktionswerte zwischen und liegen, die sich also im offenen Intervall befinden:

In der Graphik sehen wir, dass es um einen Bereich gibt, in dem sich die Funktionswerte maximal um von unterscheiden. Es gibt also einen Zeitabstand , so dass alle Funktionswerte mit Argumenten im Intervall im grau hinterlegten Bereich liegen:

Es ist also möglich, unseren gesuchten Wert ausreichend gut (sprich mit einem Maximalfehler von ) zu approximieren. Wenn wir nämlich einen Zeitpunkt mit einem Abstand von kleiner als den Zeitabstand wählen, so ist der Abstand von zu kleiner als der geforderte Maximalabstand . Wir können so als Annäherung von wählen.
Zusammenfassung: Es gibt ein , so dass der Abstand kleiner als für kleiner als ist. Also:
Erhöhte Anforderungen an die Approximation
[Bearbeiten]Was passiert, wenn wir bei unserer Messung aufgrund erhöhter Anforderungen an die Auswertung den Temperaturwert besser kennen müssen? Was ist, wenn beispielsweise der geforderte Maximalfehler der Temperaturmessung nun und nicht mehr ist?
Auch in diesem Fall gibt es einen Bereich um , in dem sich die Funktionswerte weniger als von unterscheiden. Es gibt also ein , so dass sich um maximal von unterscheidet, wenn ist:

Egal wie klein gewählt wird, es kann wegen des kontinuierlichen Temperaturverlaufes immer ein gefunden werden, so dass sich um maximal von unterscheidet, wenn der Abstand von zu kleiner als ist. Es gilt:
Egal welchen Maximalfehler wir vorgeben, es gibt immer einen Bereich um in der Form mit , in der die Funktionswerte einen Abstand kleiner als von entfernt liegen.
Der obige Umstand ist deswegen erfüllt, weil die Funktion bei kontinuierlich verläuft und keinen Sprung macht oder – anders formuliert – weil die Funktion an der Stelle stetig ist. Es gilt sogar mehr: Dieser Umstand charakterisiert auf eine formale Art die Tatsache, dass es bei keinen Sprung im Funktionsgraphen von gibt. Wir können ihn also als formale Definition der Stetigkeit nutzen. Wegen der auftretenden Variablen und wird diese Definition das Epsilon-Delta-Kriterium der Stetigkeit genannt.
Epsilon-Delta-Kriterium der Stetigkeit
[Bearbeiten]Warum gilt das Epsilon-Delta-Kriterium genau dann, wenn der Funktionsgraph an der entsprechenden Stelle keinen Sprung macht (also an dieser Stelle stetig ist)? Am Beispiel des Temperaturverlaufs konnten wir intuitiv nachvollziehen, dass das Epsilon-Delta-Kriterium bei stetigen Funktionen erfüllt ist. Ist es auch so, dass bei Sprüngen an einer Stelle im Funktionsgraphen das Epsilon-Delta-Kriterium nicht erfüllt ist? Nehmen wir nun hypothetisch an, dass der Temperaturverlauf an der Stelle einen Sprung macht:

Sei nun ein Maximalfehler, der kleiner als die Sprungweite ist:

Dann können wir keinen -Bereich um finden, in dem alle Funktionswerte einen Abstand kleiner als von besitzen. Wenn wir beispielsweise das folgende wählen, dann gibt es ein zwischen und , welches einen Abstand größer als von besitzt:

Auch wenn wir ein kleineres wählen, findet sich ein mit :

Egal wie klein ist, es gibt immer mindestens ein Argument mit einen Abstand kleiner als von , dessen Funktionswert sich mehr als um unterscheidet. So sehen wir intuitiv, dass das Epsilon-Delta-Kriterium bei Sprüngen im Graphen nicht erfüllt ist. Damit charakterisiert das Epsilon-Delta-Kriterium die Tatsache, dass der Funktionsgraph an der betrachteten Stelle keinen Sprung macht. Es ist eine Definition der Stetigkeit. Da in diesem Kriterium nur bereits definierte mathematische Begriffe verwendet werden, genügt es den Anforderungen einer formalen Definition.
Definition
[Bearbeiten]Epsilon-Delta-Kriterium der Stetigkeit
[Bearbeiten]Die - Definition der Stetigkeit an einer Stelle im Definitionsbereich lautet:
Definition (Epsilon-Delta-Definition der Stetigkeit)
Eine Funktion mit ist genau dann stetig an der Stelle , wenn es zu jedem ein gibt, so dass für alle mit ist. ist also genau dann in stetig, wenn gilt
Erläuterung der Quantorenschreibweise:
Die obige Definition beschreibt die Stetigkeit an einem Punkt. Eine Funktion nennt man stetig, wenn sie an jedem Punkt in ihrem Definitionsbereich nach dem Epsilon-Delta-Kriterium stetig ist.
Herleitung des Epsilon-Delta-Kriterium für Unstetigkeit
[Bearbeiten]Durch Negation der obigen Definition erhalten wir das Epsilon-Delta-Kriterium der Unstetigkeit. Im Kapitel „Aussagen negieren“ haben wir besprochen, wie mathematische Aussagen negiert werden können. Dabei wird aus dem Allquantor ein Existenzquantor und umgekehrt. Bei der inneren Implikation müssen wir beachten, dass die Negation von äquivalent zur Aussage ist. Wenn wir das Epsilon-Delta-Kriterium der Stetigkeit negieren, erhalten wir:
Damit erhalten wir als Negation der Stetigkeit:
Epsilon-Delta-Kriterium für Unstetigkeit
[Bearbeiten]Definition (Epsilon-Delta-Definition der Unstetigkeit)
Eine Funktion mit ist genau dann unstetig an der Stelle , wenn es ein gibt, so dass es für alle ein mit und gibt. ist also genau dann in unstetig, wenn gilt
Erläuterung der Quantorenschreibweise:
Erklärungen zum Epsilon-Delta-Kriterium
[Bearbeiten]Die Ungleichung bedeutet, dass der Abstand zwischen und kleiner als ist. Analog ist gleichbedeutend damit, dass der Abstand zwischen und kleiner als ist. Aus der Implikation folgt damit, dass der Abstand zwischen und garantiert kleiner als ist, wenn der Abstand zwischen und kleiner als ist. Die Epsilon-Delta-Definition der Stetigkeit kann somit auch folgendermaßen interpretiert werden:
Egal wie klein man den Maximalabstand bezüglich des Funktionswertes vorgibt, gibt es ein , so dass der Abstand von zu garantiert kleiner als ist, wenn einen Abstand kleiner als zu besitzt.
Bei stetigen Funktionen kann man also den Fehler – sprich den Abstand – in den Funktionswerten kontrollieren, indem man den Abstand in den Argumenten hinreichend klein hält. Die Suche nach dem entspricht der Beantwortung der Frage: Wie klein muss ich den Abstand im Argument wählen, damit der Abstand im Funktionswert maximal ist? Diese Frage ist durchaus relevant. Stell dir vor, du erhebst einen Messwert und berechnest damit einen Wert über eine stetige Funktion . Dann kannst du einen Argumentenfehler bestimmen, der dir garantiert, dass der Endfehler der Berechnung garantiert kleiner als ist, wenn der Fehler im Argument kleiner als ist.
Ein kann nur dann gefunden werden, wenn kleine Änderungen des Arguments kleine Änderungen des Funktionswertes verursachen. Bei stetigen Funktionen an der Stelle muss also gelten:
Diese Implikation muss man so lesen: Wenn hinreichend nah an liegt, dann ist ungefähr . Diese Tatsache kann auch mit dem Begriff der -Umgebung beschrieben werden:
Zu jeder noch so kleinen -Umgebung um gibt es eine -Umgebung um , deren Funktionswerte alle in der -Umgebung liegen.
Diese Beschreibung wird in der Topologie weiter verallgemeinert und führt zur topologischen Definition der Stetigkeit.
Visuelle Interpretation des Epsilon-Delta-Kriteriums
[Bearbeiten]Beschreibung der Stetigkeit im Graphen
[Bearbeiten]Das Epsilon-Delta-Kriterium kann gut im Graphen visualisiert werden. Wir starten hier mit der Implikation . Nach ihr ist der Abstand von zu kleiner als Epsilon, wenn der Abstand von zu kleiner als ist. Sprich: Für ist . Dies kann dadurch illustriert werden, dass der Punkt im Inneren des Rechtecks liegt. Dabei ist das Innere des Rechtecks mit Breite und der Höhe um den Mittelpunkt :

Dieses Rechteck werden wir im Folgenden --Rechteck nennen. Der Rand des Rechtecks gehört dabei nicht dazu. Nach dem Epsilon-Delta-Kriterium ist die Implikation für alle Argumente erfüllt. Damit müssen alle Punkte des Graphen von eingeschränkt auf die Argumente im Intervall im Inneren des --Rechtecks liegen (grüner Bereich in der folgenden Zeichnung) und dürfen sich nicht oberhalb oder unterhalb des Rechtecks befinden (roter Bereich):

Insgesamt kann das Epsilon-Delta-Kriterium folgendermaßen beschrieben werden:
Zu jedem gibt es ein (hinreichend kleines) , so dass der Graph von eingeschränkt auf komplett im Inneren des --Rechtecks liegt.
Beispiel einer stetigen Funktion
[Bearbeiten]Schauen wir uns dies am Beispiel der Funktion an. Diese Funktion ist an jeder Stelle stetig und damit insbesondere auch im Punkt . Es ist . Betrachten wir zunächst den maximalen Fehler um . Wir finden mit ein , so dass der Graph von im Inneren des --Rechtecks verläuft:

Nicht nur für , sondern zu jedem können wir ein angeben, so dass im Inneren und nicht ober- bzw. unterhalb des --Rechtecks liegt:
-
Für kann man wählen und der Graph verläuft im Inneren des --Rechtecks.
-
Im Fall von ist die Wahl von ausreichend, damit der Graph sich im Inneren des --Rechtecks befindet.
Beispiel einer unstetigen Funktion
[Bearbeiten]Was passiert, wenn die Funktion unstetig ist? Nehmen wir die Vorzeichenfunktion , die im Nullpunkt unstetig ist:
So sieht der Graph der Vorzeichenfunktion aus:

Am Graphen kann man schon intuitiv erkennen, dass bei dem Argument eine Unstetigkeitsstelle vorliegt. Hier schlägt auch unsere Visualisierungsmöglichkeit der Stetigkeit fehl. Wählt man ein , welches kleiner als die Sprunghöhe ist (also ein ), dann gibt es kein , so dass der Graph vollständig im Inneren des --Rechtecks verläuft. Wenn wir beispielsweise wählen, dann gibt es für jedes noch so kleine mindestens einen Funktionswert, der oberhalb bzw. unterhalb des --Rechtecks liegt:
-
Für gibt es bei der Vorzeichenfunktion für Funktionswerte, die oberhalb bzw. unterhalb des --Rechtecks liegen (rot eingezeichnete Punkte).
-
Auch für gibt es Punkte im Graphen, die sich oberhalb bzw. unterhalb des --Rechtecks befinden.
Abhängigkeiten der Variablen
[Bearbeiten]Stetigkeit
[Bearbeiten]Wir betrachten die Stetigkeit einer Funktion am Punkt . Zunächst wird ein beliebiges vorgegeben. Nun muss ein gefunden werden, so dass der Graph von eingeschränkt auf Argumente im Intervall komplett im Epsilon-Schlauch liegt. Hierzu muss das hinreichend klein gewählt werden. Wenn zu groß ist, gibt es gegebenenfalls ein Argument in , bei dem einen Abstand größer als von aufweist:
-
Wenn bei einem vorgegebenen ein zu großes gewählt wird, können Funktionswerte ober- beziehungsweise unterhalb des --Rechtecks liegen (hier rot markiert).
-
Wenn hinreichend klein ist, verläuft der Graph der Funktion im Inneren des --Rechtecks.
Wie klein gewählt werden muss, hängt von vielen Faktoren ab: Der betrachteten Funktion , dem vorgegebenen und dem Argument . Je nach Funktionsverlauf muss ein anderes gewählt werden. Im Allgemeinen muss auch bei einem kleineren ein kleineres gewählt werden. Dies zeigen die folgenden Diagramme. Hier ist die Quadratfunktion abgebildet, welche bei stetig ist. Bei einem kleineren fällt die Wahl des kleiner aus:

Auch von der betrachteten Stelle hängt das ab. Je stärker sich eine Funktion in der Umgebung der betrachteten Stelle ändert, desto kleiner muss gewählt werden. In der folgenden Grafik ist der gefundene -Wert zwar für ausreichend klein, für ist er jedoch zu groß:
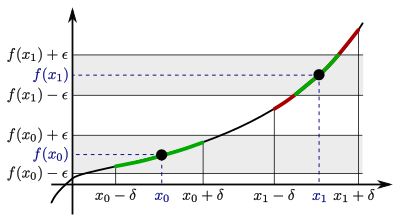
In der Umgebung von ändert sich die Funktion stärker als in der Umgebung um . Daher müssen wir das für kleiner wählen. Wir bezeichnen die -Werte an den Punkten und entsprechend mit und und wählen kleiner als vorher:

Wir haben gesehen, dass die Wahl von von der betrachteten Funktion , der betrachteten Stelle und dem vorgegebenen abhängt.
Unstetigkeit
[Bearbeiten]Im Fall der Unstetigkeit ändern sich die Zusammenhänge der Variablen untereinander. Dies liegt daran, dass bei der Negation die Quantoren vertauscht werden. Um die Unstetigkeit zu zeigen, muss zunächst ein gefunden werden, bei dem für kein der Graph von komplett im Inneren des --Rechtecks verläuft. Hierzu muss hinreichend klein sein. Wenn beispielsweise die Unstetigkeit durch einen Sprung hervorgerufen wird, sollte kleiner als die Sprunghöhe gewählt werden. Wenn zu groß ist, gibt es gegebenenfalls ein , so dass im Inneren des --Rechtecks liegt:
-
Wenn bei der Vorzeichenfunktion ein zu großes gewählt wird, gibt es ein , so dass die Vorzeichenfunktion komplett im Inneren des --Rechtecks verläuft.
-
Wenn klein genug ist, gibt es für alle Funktionswerte, die direkt ober- bzw. unterhalb des --Rechtecks liegen.
Welches gewählt werden muss, hängt vom Funktionsverlauf und der betrachteten Stelle ab. Nachdem gewählt wurde, wird beliebig vorgegeben. Nun muss es ein zwischen den Zahlen und geben, so dass einen Abstand größer gleich von aufweist. Der Punkt liegt also ober- bzw. unterhalb des --Rechtecks. Welches gewählt werden muss, hängt von vielen Parametern ab: Von dem und dem , dem Funktionsverlauf und der betrachteten Unstetigkeitsstelle.
Beispielaufgaben
[Bearbeiten]Stetigkeit
[Bearbeiten]Aufgabe (Stetigkeit einer linearen Funktion)
Beweise, dass die lineare Funktion mit stetig ist.
Wie kommt man auf den Beweis? (Stetigkeit einer linearen Funktion)

Um die Stetigkeit von zu beweisen, müssen wir die Stetigkeit an jedem Argument beweisen. Sei also eine beliebige reelle Zahl. Nun nehmen wir einen beliebigen Maximalfehler an. Unsere Aufgabe liegt jetzt darin, ein hinreichend kleines zu finden, so dass für alle Argumente mit ist. Schauen wir uns hierzu die Ungleichung genauer an:
Es muss also für alle mit gelten. Wie muss gewählt werden, so dass aus die Ungleichung folgt?
Nun können wir ausnutzen, dass in der Ungleichung der Betrag vorkommt. Wegen wissen wir, dass dieser Betrag kleiner als ist. Dies können wir in den Term einsetzen:
Wenn wir so geschickt wählen, dass ist, folgt aus die zu zeigende Ungleichung . Durch Äquivalenzumformungen von können wir ein hinreichend kleines finden:
Jedes mit ist für den Beweis ausreichend. Für den finalen Beweis wählen wir .
Beweis (Stetigkeit einer linearen Funktion)
Sei mit und sei beliebig. Sei weiterhin beliebig. Wir wählen . Sei mit . Es ist:
Damit ist , womit die Stetigkeit von an der Stelle bewiesen ist. Da beliebig gewählt wurde, ist stetig.
Unstetigkeit
[Bearbeiten]Aufgabe (Unstetigkeit der Vorzeichenfunktion)
Beweise, dass die Vorzeichenfunktion mit folgender Zuordnungsvorschrift unstetig ist:
Wie kommt man auf den Beweis? (Unstetigkeit der Vorzeichenfunktion)
Um die Unstetigkeit zu beweisen, müssen wir eine Unstetigkeitsstelle der Funktion finden. Schauen wir uns hierzu den Graphen der Funktion an:

Man sieht, dass die Funktion an der Nullstelle einen Sprung aufweist. Bei sollte sich also eine Unstetigkeitsstelle befinden. Nun müssen wir ein finden, für welches kein gefunden werden kann, so dass die Funktion komplett im --Rechteck liegt. Hier müssen wir kleiner als die Sprunghöhe wählen – zum Beispiel . Egal welches wir nun vorgeben, es muss Funktionswerte unter- oder oberhalb des --Rechtecks geben.
Sei also beliebig. Wir müssen nun zeigen, dass es ein mit und gibt. Schauen wir uns zunächst die Ungleichung an:
Bei der Ungleichung ergibt sich:
Das muss damit so gewählt werden, dass und ist. Beginnen wir mit der zweiten Ungleichung . Für ist entweder oder . Für gilt somit immer .
Blicken wir nun auf die Ungleichung . Wie wir gerade geschlossen haben, soll sein. Dies ist zum Beispiel für alle mit erfüllt. Wählen wir also für den Mittelwert zwischen und mit .
Dies sehen wir auch in folgender Grafik. Hier haben wir das --Rechteck mit und eingetragen. Alle Punkte, die unter- oder oberhalb des Rechtecks liegen, sind rot markiert. Dies sind alle im Intervall mit . Unsere Wahl ist gesondert markiert und liegt oberhalb des Rechtecks:
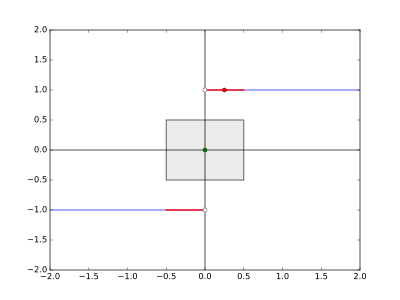
Die Wahl von reicht aus.
Beweis (Unstetigkeit der Vorzeichenfunktion)
Wir setzen . Außerdem wählen wir . Sei beliebig. Wählen wir . Zum einen ist:
Zum anderen ist
Damit ist an der Stelle unstetig und somit insgesamt unstetig.
Zusammenhang mit dem Folgenkriterium
[Bearbeiten]Es gibt zwei Definitionen der Stetigkeit: das Epsilon-Delta-Kriterium und das Folgenkriterium. Um zu zeigen, dass beide Definitionen das gleiche Konzept beschreiben, müssen wir beweisen, dass beide Kriterien äquivalent zueinander sind. Wenn das Folgenkriterium erfüllt ist, muss auch das Epsilon-Delta-Kriterium erfüllt sein und umgekehrt.
Epsilon-Delta-Kriterium impliziert Folgenkriterium
[Bearbeiten]Satz (Das Epsilon-Delta-Kriterium impliziert das Folgenkriterium)
Sei mit eine Funktion. Wenn diese Funktion an der Stelle das Epsilon-Delta-Kriterium erfüllt, dann ist auch das Folgenkriterium an der Stelle erfüllt.
Wie kommt man auf den Beweis? (Das Epsilon-Delta-Kriterium impliziert das Folgenkriterium)
Nehmen wir an, dass die Funktion an der Stelle das Epsilon-Delta-Kriterium erfüllt. Es gilt also:
Zu jedem gibt es ein , sodass für alle mit ist.
Wir wollen nun zeigen, dass auch das Folgenkriterium erfüllt ist. Für jede Argumentenfolge mit Grenzwert soll also gelten. Sei also eine Folge von Argumenten mit . Wir müssen nun zeigen, dass der Grenzwert der Funktionswertfolge gleich ist. Es soll also gelten:
Zu jedem gibt es ein mit für alle .
Sei beliebig. Wir müssen nun ein finden, so dass für alle erfüllt ist. Wir kennen die Ungleichung aus der Konklusion des Epsilon-Delta-Kriteriums. Der Unterschied liegt darin, dass wir anstelle des Arguments das Folgenglied haben. Wenden wir also das Epsilon-Delta-Kriterium auf unseren speziellen Fall mit dem vorgegebenen an. Wir erhalten:
Es gibt ein , so dass für alle Folgenglieder mit ist.
Wir kommen dem Ziel näher. Wenn ein Folgenglied die Ungleichung erfüllt, erfüllt es auch die Zielungleichung . Nun wissen wir wegen , dass beliebig klein wird. Damit gibt es ein , so dass für alle erfüllt ist. Dieses können wir als unser wählen. Ist nämlich , so ist und damit nach dem Epsilon-Delta-Kriterium.
Beweis (Das Epsilon-Delta-Kriterium impliziert das Folgenkriterium)
Sei eine Funktion, die an der Stelle das Epsilon-Delta-Kriterium erfüllt. Sei eine Folge mit für alle und . Wir wollen zeigen, dass für beliebiges ein existiert, sodass für alle gilt.
Sei beliebig. Nach dem Epsilon-Delta-Kriterium gibt es ein , sodass für alle mit ist. Wegen der Konvergenz von gegen können wir ein finden, sodass für alle ist.
Sei beliebig. Es ist damit . Nach dem Epsilon-Delta-Kriterium gilt damit . Dies beweist und damit das Folgenkriterium.
Folgenkriterium impliziert Epsilon-Delta-Kriterium
[Bearbeiten]Satz (Das Folgenkriterium impliziert das Epsilon-Delta-Kriterium)
Sei mit eine Funktion. Wenn an der Stelle das Folgenkriterium erfüllt, erfüllt sie auch das Epsilon-Delta-Kriterium.
Wie kommt man auf den Beweis? (Das Folgenkriterium impliziert das Epsilon-Delta-Kriterium)
Wir müssen folgende Implikation beweisen:
Wir beweisen diese Implikation über Kontraposition. Wir werden also zeigen, dass folgende Implikation gilt:
Also:
Sei also eine Funktion, die das Epsilon-Delta-Kriterium an der Stelle nicht erfüllt. Damit erfüllt die Unstetigkeitsversion des Epsilon-Delta-Kriteriums an der Stelle . Es existiert ein , so dass es für jedes ein mit und gibt. Wir müssen nun zeigen, dass das Folgenkriterium nicht erfüllt ist. Hierzu müssen wir eine Folge von Argumenten finden, so dass und ist.
Um die gesuchte Folge zu finden, müssen wir die Unstetigkeitsversion des Epsilon-Delta-Kriteriums geschickt nutzen. Hier wird uns ein vorgegeben, so dass für gewisse Argumente die Ungleichung gilt. Wenn wir als Folgenglieder nur solche Argumente verwenden, dann ist automatisch wegen dieser Ungleichung .
Nun brauchen wir eine Argumentenfolge , die gegen konvergiert. Hierzu suchen wir uns eine Nullfolge . Bespielsweise kann gewählt werden. Für jedes finden wir ein Argument mit und . Aus diesen bilden wir die gesuchte Argumentenfolge . Diese erfüllt zum einen und wegen damit . Zum anderen kann wegen die Funktionswertfolge nicht gegen konvergieren.
Beweis (Das Folgenkriterium impliziert das Epsilon-Delta-Kriterium)
Wir beweisen den Satz über Kontraposition. Hierzu müssen wir zeigen, dass eine Funktion , die das Epsilon-Delta-Kriterium an der Stelle nicht erfüllt, auch das Folgenkriterium an der Stelle nicht erfüllt. Sei also mit eine Funktion, die an der Stelle das Epsilon-Delta-Kriterium nicht erfüllt. Es gibt also ein , so dass für alle ein mit und existiert.
Für jedes gibt es damit ein mit und . Aus der Ungleichung folgt . Da ist, ist sowohl als auch . Nach dem Sandwichsatz konvergiert damit die Folge gegen .
Jedoch kann wegen für alle die Folge nicht gegen konvergieren. Damit ist das Folgenkriterium an der Stelle für die Funktion nicht erfüllt. Es gibt nämlich eine Argumentenfolge mit und .
Übungsaufgaben
[Bearbeiten]Quadratfunktion
[Bearbeiten]Aufgabe (Stetigkeit der Quadratfunktion)
Beweise, dass die Funktion mit stetig ist.
Wie kommt man auf den Beweis? (Stetigkeit der Quadratfunktion)
Für den Beweis müssen wir zeigen, dass die Quadratfunktion an jeder Stelle stetig ist. Nach der allgemeinen Beweisstruktur des Epsilon-Delta-Kriteriums wird ein beliebiges vorgegeben. Wir müssen dann ein geeignetes finden, sodass die Ungleichung für alle erfüllt ist.
Um ein geeignetes zu finden, setzen wir zunächst in den Term die bekannte Funktionszuordnung ein:
Den Term können wir kontrollieren. Daher ist es sinnvoll, den Term so umzuformen bzw. nach oben abzuschätzen, dass auftaucht. Hierzu bietet sich die dritte binomische Formel an:
Aus unserer Voraussetzung, dass gelten soll, können wir den Ausdruck nach oben abschätzen:
Da das , welches wir suchen, nur von und abhängen darf, stört uns die vorhandene Abhängigkeit von in . Um diese Abhängigkeit zu eliminieren, können wir den Faktor geschickt nach oben abschätzen. Dabei verwenden wir einen unscheinbaren – aber häufig verwendeten – "Trick": Wir subtrahieren an geeigneter Stelle ein und addieren es wieder, so dass der Term entsteht:
Damit wir den Betrag erhalten, nutzen wir die Dreiecksungleichung. Den Term können wir wieder nach oben durch abschätzen:
Durch geschicktes Umformen und Abschätzen haben wir so erhalten:
Mit dieser Ungleichung sind wir fast am Ziel. Wenn wir so geschickt wählen, dass ist, wird unsere Zielungleichung erfüllt. So könnten wir die "Mitternachtsformel" bei der quadratischen Gleichung anwenden, um eine passende Wahl von zu finden. Der Term kann durch eine weitere Abschätzung jedoch vereinfacht werden. Hierzu können wir ausnutzen, dass wir beliebige Bedingungen an das stellen können. So folgt aus der Bedingung , dass ist und damit gilt:
Somit führt auch zum Ziel. Diese Ungleichung können wir umstellen, um eine zweite Bedingung für zu finden (unsere erste Bedingung lautet ):
Wir haben zwei Bedingungen für gefunden: und . Beide Bedingungen sind erfüllt für . Diese Wahl treffen wir im finalen Beweis und führen die Abschätzungen so, wie wir sie gerade gefunden haben.
Beweis (Stetigkeit der Quadratfunktion)
Sei beliebig und sei . Wenn erfüllt ist, dann folgt:
Damit haben wir gezeigt, dass die Quadratfunktion stetig ist.
Verkettete Betragfunktion
[Bearbeiten]Aufgabe (Beispiel für Stetigkeitsbeweise)
Zeige, dass folgende Funktion an der Stelle stetig ist:
Wie kommt man auf den Beweis? (Beispiel für Stetigkeitsbeweise)
Wir müssen zeigen, dass zu jedem ein existiert, so dass für alle mit die Ungleichung erfüllt ist. Dabei ist bei uns . Somit können wir über den Term kontrollieren. Zunächst können wir den Term der Zielungleichung vereinfachen:
Unser Ziel ist es, durch Abschätzungen nach oben und Umformungen möglichst viele Ausdrücke „herzustellen“, da wir diese wegen abschätzen können. Die nächsten Schritte erfordern ein wenig Erfahrung mit Epsilon-Delta-Beweisen um „zu sehen“, wie man vorgehen sollte. Um die Betragsstriche innerhalb der äußeren Betrags loszuwerden, können wir die Ungleichung benutzen. Eine Möglichkeit ist folgende:
Nun wird der Term für nicht mehr beliebig klein und somit ist unsere Abschätzung nicht zielführend. Besser ist es, wenn wir vor der Anwendung der Ungleichung die Gleichung verwenden:
Wir erkennen die dritte binomische Formel und können schreiben:
Und weiterhin wegen :
Da das , welches wir suchen, nur von und abhängen darf, stört uns die vorhandene Abhängigkeit von in . Dazu müssen wir den Ausdruck geschickt nach oben abschätzen. Da wir nur ein bestimmtes für unseren Beweis angeben müssen, um die Zielungleichung zu erhalten und beliebige Bedingungen an das stellen zu können, setzen wir . Dies ist eine willkürliche Wahl (analog funktioniert auch usw). Was ergibt sich nun aus dieser Festlegung?
Es muss weiterhin gelten: . Wegen folgt . Damit gilt durch Umstellen der Ungleichung: . Es folgt somit und damit :
Da wir zeigen wollen, dass wählen wir so, dass ist. Dadurch erhalten wir:
Wir haben auf unserem Rechenweg zwei Bedingungen für das gefunden ( und ). Diese fassen wir zusammen durch: . Damit können wir unseren Beweis aufschreiben.
Beweis (Beispiel für Stetigkeitsbeweise)
Sei beliebig und sei . Sei mit . Dann folgt:
Beweisschritt 1:
Wegen ist . Damit ist und somit . Es folgt und damit .
Beweisschritt 2:
Damit ist die Funktion an der Stelle stetig.
Hyperbel
[Bearbeiten]Aufgabe (Stetigkeit der Hyperbelfunktion)
Beweise, dass die Funktion mit stetig ist.
Wie kommt man auf den Beweis? (Stetigkeit der Hyperbelfunktion)
Das grundlegende Muster bei Epsilon-Delta-Beweisen bleibt erhalten. Wir wollen die Implikation zeigen. Als Erstes setzen wir das ein, was wir bereits wissen und formen etwas um:
Wir wissen, dass nach Voraussetzung gilt. Also:
Da die Wahl von unserem nur von und abhängen darf, müssen wir in diesem Fall geschickt abschätzen, um die Abhängigkeit von zu eliminieren. Hierzu betrachten wir .
Wie kommen wir auf die Bedingung ? Wir schieben an dieser Stelle eine kurze Erklärung ein, in der wir die Wahl erklären: Wir benötigen eine -Umgebung, die innerhalb des Defintionsbereichs unserer Funktion liegt. Hätten wir die Bedingung gewählt und dabei den Punkt betrachtet, so würden wir auf folgendes Problem stoßen:
Der größte -Wert mit ist und der kleinste ist . Jedoch liegt nicht im Definitionsbereich der Funktion . Vor allem liegt in diesem Bereich, wo nicht definiert ist.
Eine geschickte Wahl des , so dass die -Umgebung die -Achse nicht berührt, ist . Denkbar sind auch: , oder .
Wegen und unserer Voraussetzung, dass ist . Darüber kommen wir zur Abschätzung: . Wir können nun schreiben:
Somit erhalten wir den Zusammenhang:
Da wir zeigen wollen, wählen wir . Einsetzen zeigt, dass wir dadurch die Zielungleichung zeigen können.
In der ganzen Herleitung haben wir zwei Bedingungen für gefunden: und . Im Beweis setzen wir deswegen , um beide Bedingungen zu erfüllen.
Beweis (Stetigkeit der Hyperbelfunktion)
Sei mit und sei beliebig. Sei außerdem beliebig. Wähle . Für alle mit gilt:
Damit ist die Funktion an der Stelle stetig. Da beliebig gewählt wurde, ist stetig.
Verkettete Wurzelfunktion
[Bearbeiten]Aufgabe (Epsilon-Delta-Beweis für Stetigkeit einer Wurzelfunktion)
Beweise mit der Epsilon-Delta-Definition der Stetigkeit, dass folgende Funktion stetig ist:
Wie kommt man auf den Beweis? (Epsilon-Delta-Beweis für Stetigkeit einer Wurzelfunktion)
Wir müssen zeigen, dass für jedes ein existiert, so dass alle mit die Ungleichung erfüllen. Hierzu betrachten wir zunächst die Zielungleichung und schätzen den Betrag geschickt nach oben ab. Da wir den Term kontrollieren können, schätzen wir so nach oben ab, dass wir den Betrag erhalten. Wir suchen also eine Ungleichung der Form
Dabei ist irgendein von und abhängiger Term. Der zweite Faktor ist kleiner als und kann damit durch eine geschickte Wahl von beliebig klein gemacht werden. Eine solche Abschätzung ist folgende:
Wegen ist:
Wenn wir so klein wählen, dass ist, folgt die Zielungleichung . Jedoch hängt von ab und diese Abhängigkeit würde sich auf vererben und wir dürfen nicht in Abhängigkeit von wählen. Deswegen müssen wir die Abhängigkeit des ersten Faktors von eliminieren. Dies erreichen wir, indem wir den ersten Faktor nach oben so abschätzen, dass wir eine Ungleichung der Form erreichen. Eine solche Umformung ist:
Wir haben sogar unabhängig von gemacht, was nicht nötig gewesen wäre. Somit haben wir die Ungleichung
Wir brauchen nun die Abschätzung , damit die Zielungleichung erfüllt ist. Die Wahl von ist hierfür ausreichend.
Beweis (Epsilon-Delta-Beweis für Stetigkeit einer Wurzelfunktion)
Sei mit . Sei und beliebig. Wir wählen . Für alle mit gilt:
Damit ist eine stetige Funktion.
Unstetigkeit der topologischen Sinusfunktion
[Bearbeiten]Aufgabe (Unstetigkeit der topologischen Sinusfunktion)
Beweise die Unstetigkeit der folgenden Funktion an der Stelle :
Wie kommt man auf den Beweis? (Unstetigkeit der topologischen Sinusfunktion)
Bei dieser Aufgabe soll die Unstetigkeit einer Funktion gezeigt werden. Wir betrachten hierzu die Negation des Epsilon-Delta-Kriteriums. Unser Ziel ist es sowohl ein , als auch ein so zu wählen, dass und ist. Dabei darf in Abhänigigkeit von gewählt werden, während unabhängig für alle sein muss. Für eine Lösung können wir folgendermaßen vorgehen:
Schritt 1: Zielungleichungen vereinfachen
Zunächst können wir beide Ungleichungen, die erfüllt sein müssen, umschreiben, denn in unserem Fall ist und . Dadurch können wir schreiben: und .
Schritt 2: Wahl eines geeigneten
Wir betrachten nun den Graphen der Funktion – dieser hilft uns nämlich unsere „Beweisbausteine“ zu finden:
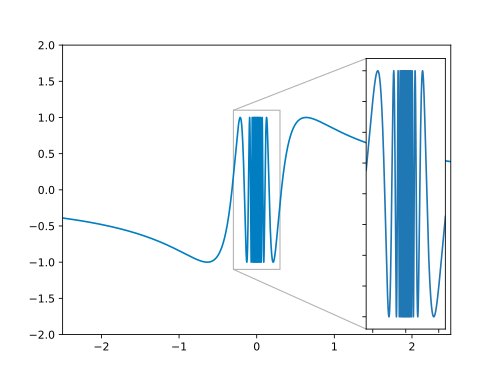
Wir müssen ein finden, so dass es stets Funktionswerte im Bereich gibt, die einen Abstand größer gleich von haben – egal wie klein ist. Sprich: Egal, welches wir wählen, es gibt immer Punkte die oberhalb oder unterhalb des --Rechtecks liegen.
In der Grafik erkennen wir, dass die Funktion in der Nähe des Nullpunkts unendlich oft zwischen und oszilliert. Damit bietet sich ein an. Dann gibt es nämlich immer Funktionswerte in jeder noch so kleinen Umgebung von der Null mit . Wir wählen . In der folgenden Grafik ist dies illustriert:
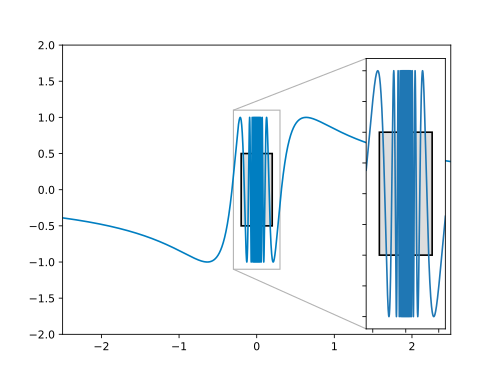
Im Beweis müssen wir nach der Wahl von das beliebig größer Null wählen. Das machen wir dann auch.
Schritt 3: Wahl eines geeigneten
Wir haben gesetzt. Es muss nun gelten . Damit diese Bedingung erfüllt ist, können wir solche mit wählen. Nun ist genau dann, wenn für ein ist. Für die gesuchten gilt also:
Damit haben wir verschiedene gefunden, für die gilt. Jetzt muss noch die erste Bedingung beachtet werden. Unsere hängen von ab. Wir müssen ein geeignetes mit finden, so dass erfüllt ist. Setzen wir also in diese Ungleichung die gefundene Gleichung ein und stellen sie nach um:
Dies liefert den Ausdruck . Wählen wir also eine natürliche Zahl , die größer als ist, so ist erfüllt. Ein solches muss nach dem archimedischen Axiom existieren. Wählen wir ein solches und definieren damit das über , haben wir sowohl als auch gegeben. Damit sind alle Bausteine für den Beweis gefunden und dieser muss nur noch sauber aufgeschrieben werden.
Beweis (Unstetigkeit der topologischen Sinusfunktion)
Wähle und sei beliebig. Wähle eine natürliche Zahl , so dass . Eine solche natürliche Zahl muss nach dem Archimedischen Axiom existieren. Weiter sei . So gilt:
Weiter ist:
Damit ist die Funktion unstetig an der Stelle .





































![{\displaystyle {\begin{aligned}{\begin{array}{l}\underbrace {{\underset {}{}}\forall \epsilon >0} _{{\text{Für alle }}\epsilon >0}\underbrace {{\underset {}{}}\exists \delta >0} _{{\text{ gibt es ein }}\delta >0}\underbrace {{\underset {}{}}\forall x\in D} _{{\text{, so dass für alle }}x\in D}\\[1em]\quad \underbrace {{\underset {}{}}|x-x_{0}|<\delta } _{{\text{ mit Abstand von }}x_{0}{\text{ kleiner }}\delta }\underbrace {{\underset {}{}}\implies } _{\text{ gilt}}\underbrace {{\underset {}{}}|f(x)-f(x_{0})|<\epsilon } _{{\text{, dass der Abstand von }}f(x){\text{ zu }}f(x_{0}){\text{ kleiner als }}\epsilon {\text{ ist}}}\end{array}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ae9e04d5fff99e6521ee1d4e11398dd561e29ca7)




![{\displaystyle {\begin{aligned}{\begin{array}{rrrrrcr}&\neg {\Big (}\forall \epsilon >0\,&\exists \delta >0\,&\forall x\in D:&|x-x_{0}|<\delta &\implies &|f(x)-f(x_{0})|<\epsilon {\Big )}\\[0.5em]\iff &\exists \epsilon >0\,&\neg {\Big (}\exists \delta >0\,&\forall x\in D:&|x-x_{0}|<\delta &\implies &|f(x)-f(x_{0})|<\epsilon {\Big )}\\[0.5em]\iff &\exists \epsilon >0\,&\forall \delta >0\,&\neg {\Big (}\forall x\in D:&|x-x_{0}|<\delta &\implies &|f(x)-f(x_{0})|<\epsilon {\Big )}\\[0.5em]\iff &\exists \epsilon >0\,&\forall \delta >0\,&\exists x\in D:&\neg {\Big (}|x-x_{0}|<\delta &\implies &|f(x)-f(x_{0})|<\epsilon {\Big )}\\[0.5em]\iff &\exists \epsilon >0\,&\forall \delta >0\,&\exists x\in D:&|x-x_{0}|<\delta &\land &\neg {\Big (}|f(x)-f(x_{0})|<\epsilon {\Big )}\\[0.5em]\iff &\exists \epsilon >0\,&\forall \delta >0\,&\exists x\in D:&|x-x_{0}|<\delta &\land &|f(x)-f(x_{0})|\geq \epsilon \end{array}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a4575e200c1888fae248ce7a97ec488df4013fd9)

![{\displaystyle {\begin{aligned}{\begin{array}{l}\underbrace {{\underset {}{}}\exists \epsilon >0} _{{\text{Es gibt ein }}\epsilon >0,}\underbrace {{\underset {}{}}\forall \delta >0} _{{\text{ so dass für alle }}\delta >0}\underbrace {{\underset {}{}}\exists x\in D} _{{\text{ ein }}x\in D{\text{ existiert}}}\\[1em]\quad \underbrace {{\underset {}{}}|x-x_{0}|<\delta } _{{\text{ mit Abstand von }}x_{0}{\text{ kleiner }}\delta }\underbrace {{\underset {}{}}\land } _{\text{ und}}\underbrace {{\underset {}{}}|f(x)-f(x_{0})|\geq \epsilon } _{{\text{der Abstand von }}f(x){\text{ zu }}f(x_{0}){\text{ ist größer gleich }}\epsilon }\end{array}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aef8f60bc0c23734c9204edb9a4f1fa1f1d322dd)



































![{\displaystyle {\begin{aligned}{\begin{array}{rrl}&|f(x)-f(x_{0})|&<\epsilon \\[0.5em]\iff &\left|{\frac {1}{3}}x-{\frac {1}{3}}x_{0}\right|&<\epsilon \\[0.5em]\iff &\left|{\frac {1}{3}}(x-x_{0})\right|&<\epsilon \\[0.5em]\iff &{\frac {1}{3}}|x-x_{0}|&<\epsilon \end{array}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5d31310b5d997a542e2d16535a112538e5d5bd35)









![{\displaystyle {\begin{aligned}|f(x)-f(x_{0})|&=\left|{\frac {1}{3}}x-{\frac {1}{3}}x_{0}\right|\\[0.5em]&=\left|{\frac {1}{3}}(x-x_{0})\right|\\[0.5em]&={\frac {1}{3}}|x-x_{0}|\\[0.5em]&\quad {\color {Gray}\left\downarrow \ |x-x_{0}|<\delta \right.}\\[0.5em]&<{\frac {1}{3}}\delta \\[0.5em]&\quad {\color {Gray}\left\downarrow \ \delta =3\epsilon \right.}\\[0.5em]&\leq {\frac {1}{3}}(3\epsilon )=\epsilon \end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4cc60cea8cdcb2598454593c6b521c7516e7f89c)





![{\displaystyle {\begin{aligned}{\begin{array}{rrl}&|f(x)-f(x_{0})|&\geq \epsilon \\[0.5em]\iff &|\operatorname {sgn}(x)-\operatorname {sgn}(x_{0})|&\geq {\frac {1}{2}}\\[0.5em]\iff &|\operatorname {sgn}(x)-\operatorname {sgn}(0)|&\geq {\frac {1}{2}}\\[0.5em]\iff &|\operatorname {sgn}(x)|&\geq {\frac {1}{2}}\end{array}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bcc44b40d90ac63c780e7d0dc1f8f767d68457c2)










![{\displaystyle {\begin{aligned}{\begin{array}{rrl}&{\frac {1}{2}}&<1\\[0.5em]\implies &{\frac {1}{2}}\delta &<\delta \\[0.5em]\implies &\left|{\frac {1}{2}}\delta \right|&<\delta \\[0.5em]\implies &\left|{\frac {1}{2}}\delta -0\right|&<\delta \\[0.5em]\implies &|x-x_{0}|&<\delta \end{array}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/57e7f87669f9fd77335e50cfd861641e94a2002b)
![{\displaystyle {\begin{aligned}|f(x)-f(x_{0})|&=|\operatorname {sgn}(x)-\operatorname {sgn}(x_{0})|\\[0.5em]&=\left|\operatorname {sgn} \left({\frac {\delta }{2}}\right)-\operatorname {sgn}(0)\right|\\[0.5em]&=\left|1-0\right|\\[0.5em]&=1\\[0.5em]&\geq {\frac {1}{2}}=\epsilon \end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e3167c8c11ff695bed71173f7068a3da353af4e5)



















































![{\displaystyle {\begin{aligned}|f(x)-f(x_{0})|&=|x^{2}-x_{0}^{2}|\\[0.5em]&=|x+x_{0}||x-x_{0}|\\[0.5em]&\quad {\color {OliveGreen}\left\downarrow \ |x-x_{0}|<\delta \right.}\\[0.5em]&<|x+x_{0}|\cdot \delta \\[0.5em]&=|x\underbrace {-x_{0}+x_{0}} _{=\ 0}+x_{0}|\cdot \delta \\[0.5em]&=|x-x_{0}+2x_{0}|\cdot \delta \\[0.5em]&\leq (|x-x_{0}|+2|x_{0}|)\cdot \delta \\[0.5em]&\quad {\color {OliveGreen}\left\downarrow \ |x-x_{0}|<\delta \right.}\\[0.5em]&<(\delta +2|x_{0}|)\cdot \delta \\[0.5em]&\quad {\color {OliveGreen}\left\downarrow \ \delta \leq 1\right.}\\[0.5em]&\leq (1+2|x_{0}|)\cdot \delta \\[0.5em]&\quad {\color {OliveGreen}\left\downarrow \ \delta ={\frac {\epsilon }{1+2|x_{0}|}}\right.}\\[0.5em]&=(1+2|x_{0}|)\cdot {\frac {\epsilon }{1+2|x_{0}|}}\\[0.5em]&=\epsilon \end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ebb3bb75ca3552607bc833f51fcbb75f3d72b660)



![{\displaystyle {\begin{aligned}|f(x)-f(x_{0})|&=|f(x)-f(1)|\\[0.5em]&=|5\cdot |x^{2}-2|+3-(5|1^{2}-2|+3)|\\[0.5em]&=|5\cdot |x^{2}-2|-5|\\[0.5em]&=5\cdot ||x^{2}-2|-1|\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/69d266482610f10dbbb503cde4f016731c087395)

![{\displaystyle {\begin{aligned}|f(x)-f(x_{0})|&=\ldots \\[0.3em]&=5\cdot ||x^{2}-2|-1|\\[0.3em]&=5\cdot ||x^{2}-2|-|1||\\[0.3em]&\ {\color {Gray}\left\downarrow \ ||a|-|b||\leq |a-b|\right.}\\[0.3em]&\leq 5\cdot |x^{2}-2-1|\\[0.3em]&=5\cdot |x^{2}-3|\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ad49ec4121be7ebbb9c70668503e553b2e8f40a8)



![{\displaystyle {\begin{aligned}|f(x)-f(x_{0})|&=\ldots \\[0.3em]&=5\cdot |x^{2}-2|-1|\\[0.3em]&=5\cdot |x^{2}-2|-|-1||\\[0.3em]&\quad {\color {Gray}\left\downarrow \ |a-b|\geq ||a|-|b||\right.}\\[0.3em]&\leq 5\cdot |x^{2}-2-(-1)|\\[0.3em]&=5\cdot |x^{2}-1|\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b95d37135edaa1cb43baadd154883fd2cbbaecf)
![{\displaystyle {\begin{aligned}|f(x)-f(x_{0})|&=\ldots \\[0.5em]&\leq 5\cdot |x^{2}-1|\\[0.5em]&=5\cdot |x+1||x-1|\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/354cef939486c44d804e4332f3c9b82b2167b60c)
![{\displaystyle {\begin{aligned}|f(x)-f(x_{0})|&=\ldots \\[0.5em]&\leq 5\cdot |x^{2}-1|\\[0.5em]&=5\cdot |x+1||x-1|\\[0.5em]&<5\cdot |x+1|\cdot \delta \end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ae97a41cdc436eb91a8d1f524c1c5b05f7aaa7bf)




![{\displaystyle x\in [1-1;1+1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/efd6f0b16fff92863add316a12def2b473ce7ef6)
![{\displaystyle 1+x\in [1;3]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0e1e41ddeb905578af9d8e17d3bd454394f356a3)

![{\displaystyle {\begin{aligned}|f(x)-f(x_{0})|&=\ldots \\[0.5em]&<5\cdot |x+1|\cdot \delta \\[0.5em]&\quad {\color {Gray}\left\downarrow \ |x+1|\leq 3\right.}\\[0.5em]&\leq 15\cdot \delta \end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/da02b2abe01990a7c8869caea17519cab0ed54cc)


![{\displaystyle {\begin{aligned}|f(x)-f(x_{0})|&=\ldots \\[0.5em]&<15\cdot \delta \\[0.5em]&\leq 15\cdot {\frac {\epsilon }{15}}\\[0.5em]&\leq \epsilon .\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/84d0b6afce1242e6ac5d9dc35dc5c1b094bd2f52)


![{\displaystyle {\begin{aligned}|f(x)-f(x_{0})|&=|f(x)-f(1)|\\[0.5em]&=|5\cdot |x^{2}-2|+3-(5|1^{2}-2|+3)|\\[0.5em]&=|5\cdot |x^{2}-2|-5|\\[0.5em]&=5\cdot ||x^{2}-2|-1|\\[0.5em]&\quad {\color {Gray}\left\downarrow \ 1\iff |-1|\right.}\\[0.5em]&=5\cdot ||x^{2}-2|-|-1||\\[0.5em]&\quad {\color {Gray}\left\downarrow \ |a-b|\geq ||a|-|b||\right.}\\[0.5em]&\leq 5\cdot |x^{2}-2-(-1)|\\[0.5em]&=5\cdot |x^{2}-1|\\[0.5em]&\quad {\color {Gray}\left\downarrow \ a^{2}-b^{2}=(a+b)(a-b)\right.}\\[0.5em]&=5\cdot (|x+1|\cdot \underbrace {|x-1|} _{<\delta })\\[0.5em]&<5\cdot |x+1|\cdot \delta \\[0.5em]&\quad {\color {Gray}\left\downarrow \ |x+1|\leq 3\right.}\\[0.5em]&\leq 15\delta \\[0.5em]&\quad {\color {Gray}\left\downarrow \ \delta \leq {\frac {\epsilon }{15}}\right.}\\[0.5em]&\leq 15\cdot {\frac {\epsilon }{15}}\\[0.5em]&\leq \epsilon \end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e3f079fd76948d55904bf52cbe54a2f329af8b71)


![{\displaystyle {\begin{aligned}|f(x)-f(x_{0})|&=\left|{\frac {1}{x}}-{\frac {1}{x_{0}}}\right|\\[0.5em]&=\left|{\frac {x-x_{0}}{x\cdot x_{0}}}\right|\\[0.5em]&={\frac {|x-x_{0}|}{|x||x_{0}|}}\\[0.5em]&={\frac {1}{|x||x_{0}|}}\cdot |x-x_{0}|\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/01ba499ec4117d2c9c4aaecaf73508b9e7e25786)














![{\displaystyle x\in \left[{\tfrac {x_{0}}{2}};{\tfrac {3x_{0}}{2}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d47a3aef04163c30d6cf6b0d2e661e3d0ca39a79)

![{\displaystyle {\begin{aligned}|f(x)-f(x_{0})|&=\ldots <{\frac {1}{|x||x_{0}|}}\cdot \delta \\[0.5em]&\quad {\color {Gray}\left\downarrow \ \delta ={\frac {\epsilon \cdot |x_{0}|^{2}}{2}}\right.}\\[0.5em]&\leq {\frac {2}{|x_{0}|^{2}}}\cdot \delta \end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/97179ce859e8df4cffeebc20e36e4fff137f8bbf)





![{\displaystyle {\begin{aligned}|f(x)-f(x_{0})|&=\left|{\frac {1}{x}}-{\frac {1}{x_{0}}}\right|\\[0.5em]&=\left|{\frac {x-x_{0}}{x\cdot x_{0}}}\right|\\[0.5em]&={\frac {|x-x_{0}|}{|x||x_{0}|}}\\[0.5em]&={\frac {1}{|x||x_{0}|}}|x-x_{0}|\\[0.5em]&\quad {\color {Gray}\left\downarrow \ {\frac {1}{|x|}}\leq {\frac {2}{|x_{0}|}}\right.}\\[0.5em]&\leq {\frac {2}{|x_{0}|^{2}}}|x-x_{0}|\\[0.5em]&\quad {\color {Gray}\left\downarrow \ |x-x_{0}|<\delta \right.}\\[0.5em]&<{\frac {2\delta }{|x_{0}|^{2}}}\\[0.5em]&\quad {\color {Gray}\left\downarrow \ \delta ={\frac {\epsilon \cdot |x_{0}|^{2}}{2}}\right.}\\[0.5em]&={\frac {2}{|x_{0}|^{2}}}\cdot {\frac {\epsilon \cdot |x_{0}|^{2}}{2}}\\[0.5em]&=\epsilon \end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ff8bd751a75cee3af77911fbab6f8d4abb0b9058)








![{\displaystyle {\begin{aligned}|f(x)-f(a)|&=\left|{\sqrt {5+x^{2}}}-{\sqrt {5+a^{2}}}\right|\\[0.3em]&\quad {\color {Gray}\left\downarrow \ {\text{Erweitere mit}}\left|{\sqrt {5+x^{2}}}+{\sqrt {5+a^{2}}}\right|\right.}\\[0.3em]&={\frac {\left|{\sqrt {5+x^{2}}}-{\sqrt {5+a^{2}}}\right|\cdot \left|{\sqrt {5+x^{2}}}+{\sqrt {5+a^{2}}}\right|}{\left|{\sqrt {5+x^{2}}}+{\sqrt {5+a^{2}}}\right|}}\\[0.3em]&\quad {\color {Gray}\left\downarrow \ {\sqrt {5+x^{2}}}+{\sqrt {5+a^{2}}}\geq 0\right.}\\[0.3em]&={\frac {\left|x^{2}-a^{2}\right|}{{\sqrt {5+x^{2}}}+{\sqrt {5+a^{2}}}}}\\[0.3em]&={\frac {\left|x+a\right|}{{\sqrt {5+x^{2}}}+{\sqrt {5+a^{2}}}}}\cdot |x-a|\\[0.3em]&\quad {\color {Gray}\left\downarrow \ K(x,a):={\frac {\left|x+a\right|}{{\sqrt {5+x^{2}}}+{\sqrt {5+a^{2}}}}}\right.}\\[0.3em]&=K(x,a)\cdot |x-a|\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ed645010661b6924eda61371b0925511d02a83a4)




![{\displaystyle {\begin{aligned}K(x,a)&={\frac {\left|x+a\right|}{{\sqrt {5+x^{2}}}+{\sqrt {5+a^{2}}}}}\\[0.3em]&\quad {\color {Gray}\left\downarrow \ {\text{Dreiecksungleichung}}\right.}\\[0.3em]&\leq {\frac {\left|x\right|}{{\sqrt {5+x^{2}}}+{\sqrt {5+a^{2}}}}}+{\frac {\left|a\right|}{{\sqrt {5+x^{2}}}+{\sqrt {5+a^{2}}}}}\\[0.3em]&\quad {\color {Gray}\left\downarrow \ {\frac {a}{b+c}}\leq {\frac {a}{b}}{\text{ für }}a,c\geq 0,b>0\right.}\\[0.3em]&\leq {\frac {\left|x\right|}{\sqrt {5+x^{2}}}}+{\frac {\left|a\right|}{\sqrt {5+a^{2}}}}\\[0.3em]&\quad {\color {Gray}\left\downarrow \ {\frac {|a|}{\sqrt {5+a^{2}}}}\leq 1{\text{, da }}{\sqrt {5+a^{2}}}\geq {\sqrt {a^{2}}}=|a|\right.}\\[0.3em]&\leq 2=:{\tilde {K}}(a)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1d19f12c33f51f6b090176ccb10abb3937672bfc)






![{\displaystyle {\begin{aligned}|f(x)-f(a)|&=\left|{\sqrt {5+x^{2}}}-{\sqrt {5+a^{2}}}\right|\\[0.3em]&={\frac {\left|{\sqrt {5+x^{2}}}-{\sqrt {5+a^{2}}}\right|\cdot \left|{\sqrt {5+x^{2}}}+{\sqrt {5+a^{2}}}\right|}{\left|{\sqrt {5+x^{2}}}+{\sqrt {5+a^{2}}}\right|}}\\[0.3em]&={\frac {\left|x^{2}-a^{2}\right|}{{\sqrt {5+x^{2}}}+{\sqrt {5+a^{2}}}}}\\[0.3em]&={\frac {\left|x+a\right|}{{\sqrt {5+x^{2}}}+{\sqrt {5+a^{2}}}}}\cdot |x-a|\\[0.3em]&\leq \left({\frac {\left|x\right|}{{\sqrt {5+x^{2}}}+{\sqrt {5+a^{2}}}}}+{\frac {\left|a\right|}{{\sqrt {5+x^{2}}}+{\sqrt {5+a^{2}}}}}\right)\cdot |x-a|\\[0.3em]&\leq \left({\frac {\left|x\right|}{\sqrt {5+x^{2}}}}+{\frac {\left|a\right|}{\sqrt {5+a^{2}}}}\right)\cdot |x-a|\\[0.3em]&\leq (1+1)\cdot |x-a|\\[0.3em]&\leq 2\cdot |x-a|\\[0.3em]&\quad {\color {Gray}\left\downarrow \ |x-a|<\delta ={\frac {\epsilon }{2}}\right.}\\[0.3em]&<2\cdot {\frac {\epsilon }{2}}=\epsilon \end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/12cd8aa90f8a0c4e92c8ba9955b4a65297f2b797)















![{\displaystyle {\begin{aligned}\left|x\right|<\delta &\iff \left|{\frac {1}{{\frac {\pi }{2}}+2k\pi }}\right|<\delta \\[0.5em]&\iff {\frac {1}{{\frac {\pi }{2}}+2k\pi }}<\delta \\[0.5em]&\iff 2k\pi +{\frac {\pi }{2}}>{\frac {1}{\delta }}\\[0.5em]&\iff 2k\pi >{\frac {1}{\delta }}-{\frac {\pi }{2}}\\[0.5em]&\iff k>{\frac {1}{2\pi }}\left({\frac {1}{\delta }}-{\frac {\pi }{2}}\right)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/25af20f89560c07b3820129dd8d10ce2b902d7e9)



![{\displaystyle {\begin{aligned}k>{\frac {1}{2\pi }}\left({\frac {1}{\delta }}-{\frac {\pi }{2}}\right)&\implies 2k\pi >{\frac {1}{\delta }}-{\frac {\pi }{2}}\\[0.5em]&\implies 2k\pi +{\frac {\pi }{2}}>{\frac {1}{\delta }}\\[0.5em]&\quad {\color {OliveGreen}\left\downarrow \ {\frac {1}{a}}>{\frac {1}{b}}>0\iff 0<a<b\right.}\\[0.5em]&\implies {\frac {1}{{\frac {\pi }{2}}+2k\pi }}<\delta \\[0.5em]&\quad {\color {OliveGreen}\left\downarrow \ {\frac {1}{{\frac {\pi }{2}}+2k\pi }}>0\right.}\\[0.5em]&\implies \left|{\frac {1}{{\frac {\pi }{2}}+2k\pi }}\right|<\delta \\[0.5em]&\quad {\color {OliveGreen}\left\downarrow \ x={\frac {1}{{\frac {\pi }{2}}+2k\pi }}\right.}\\[0.5em]&\implies \left|x\right|<\delta \end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ad7985a4bd1699ae43466813ef6cb9d56079acd3)
![{\displaystyle {\begin{aligned}\left|f(x)-f(0)\right|&=\left|\sin \left({\frac {1}{x}}\right)-0\right|\\[0.5em]&\quad {\color {OliveGreen}\left\downarrow \ x={\frac {1}{{\frac {\pi }{2}}+2k\pi }}\right.}\\[0.5em]&=\left|\sin \left({\frac {\pi }{2}}+2k\pi \right)\right|\\[0.5em]&\quad {\color {OliveGreen}\left\downarrow \ \sin \left({\frac {\pi }{2}}+2k\pi \right)=1\right.}\\[0.5em]&=\left|1\right|\geq {\frac {1}{2}}=\epsilon \end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3fa308896735c40f86148e2d6dfd09fa66590f03)
