Mengendiagramme: Euler- und Venn-Diagramm – Serlo „Mathe für Nicht-Freaks“

Mengendiagramme

Erklärungen zu Venn- und Euler-Diagrammen (Video vom Podcast The Wicked Mu)

Oft werden Flächen genutzt, um Mengen grafisch darzustellen. Jede dieser Flächen repräsentiert dabei eine Menge. Die Größe der Fläche spielt dabei keine Rolle und sie spiegelt in der Regel auch nicht die Mächtigkeit dieser Menge wider. Solche Darstellungen werden Mengendiagramme genannt. Sie werden insbesondere eingesetzt, um Beziehungen zwischen Mengen zu visualisieren. Schauen wir uns als Beispiel ein Mengendiagramm einer Menge von Polygonen an:

Beispielmenge mit Polygonen

Hier wird die Menge durch die Ellipse dargestellt. Außerdem wurden innerhalb der Ellipse alle Elemente der Menge eingezeichnet. Dies ist aber nicht immer so und ist auch nur bei endlichen Mengen mit wenigen Elementen möglich. Bei unendlichen oder sehr großen endlichen Mengen werden nur einige Elemente als repräsentative Beispiele aufgezählt. Oftmals werden die Elemente auch komplett weggelassen.

Mengendiagramme werden oft zusätzlich beschriftet. So werden die Mengenbezeichnungen oftmals innerhalb oder direkt neben der zur Menge gehörenden Fläche aufgeschrieben. Auch werden Farben eingesetzt, um entweder die einzelnen Flächen und ihre Überlappungen besser erkennen zu können oder um gewisse Bereiche hervorzuheben. Es gibt zwei Arten von Mengendiagrammen: Euler-Diagramme und Venn-Diagramme.

Euler-Diagramme

Leonhard Euler

Euler-Diagramme sind nach dem Mathematiker Leonhard Euler benannt. Dabei spiegeln die Beziehungen der Flächen untereinander die Beziehung der zu den Flächen korrespondierenden Mengen wider. Wenn sich zwei Flächen überlappen, dann besitzen die Mengen zu den Flächen auch gemeinsame Elemente. Wenn aber wiederum zwei Mengen keine gemeinsamen Elemente besitzen, dann überlappen sich auch ihre Flächen nicht. Betrachte hierzu das folgende Euler-Diagramm:

Beispiel für ein Euler-Diagramm

Du erkennst, dass alle Lebewesen mit vier Beinen Tiere sind, es aber auch Tiere ohne beziehungsweise mit mehr oder weniger als vier Beine gibt. Außerdem erkennst du, dass es kein Mineral gibt, welches gleichzeitig ein Tier ist. Weitere Beispiele sind

• 
  Euler-Diagramm der Zahlenbereiche
• 
  Zugehörigkeit der europäischen Staaten zu den europäischen Institutionen
• 
  Euler-Diagramm der britischen Inseln

Venn-Diagramme

Die lateinischen, griechischen und kyrillischen Buchstaben in einem Venn-Diagramm

Bleiverglastes Fenster mit einem Venn-Diagramm im britischen Cambridge, dem Studienort John Venns

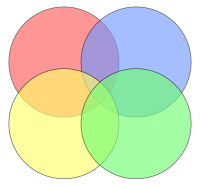
Venn-Diagramme sind nach dem englischen Mathematiker John Venn benannt, der diese Form der Mengendarstellung Ende des 19. Jahrhunderts entwickelte. Diese Diagramme zeichnen sich dadurch aus, dass stets alle Kombinationen von Flächenüberlappungen dargestellt werden. Insbesondere werden auch solche Kombinationen von Überlappungen eingezeichnet, für die es kein Objekt gibt, welches Element genau der überlappenden Mengen an dieser Stelle ist. Folgendes Diagramm zeigt beispielsweise ein Venn-Diagramm mit vier Flächen:

Venn-Diagramm mit vier Flächen

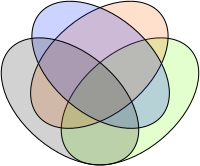
Demgegenüber ist das folgende Diagramm kein Venn-Diagramm:

Diagramm mit vier Flächen, welches kein Venn-Diagramm ist

Es gibt nämlich keinen Bereich, in dem sich nur die gelbe und die blaue beziehungsweise nur die rote und die grüne Fläche überschneiden.

Weil stets alle Kombinationen von Flächenüberlappungen dargestellt werden müssen, können Venn-Diagramme schnell komplex werden. So sieht beispielsweise Venns Vorschlag für ein Diagramm mit sechs Mengen folgendermaßen aus:

Venn-Diagramm mit 6 Mengen

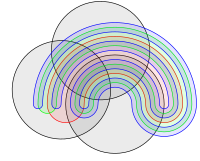
Unterschiede zwischen Euler- und Venn-Diagrammen

Den Unterschied beider Mengendiagrammarten wird insbesondere dann deutlich, wenn man sich beide Diagramme für ein konkretes Beispiel anschaut. Nimm hierzu die folgenden drei Mengen:

• $A=\{1,\,2,\,5\}$
• $B=\{1,\,6\}$
• $C=\{4,\,7\}$

Schauen wir uns diese drei Mengen jeweils in einem Euler- und in einem Venn-Diagramm an:

• 
  Euler-Diagramm
• 
  Venn-Diagramm

Du siehst hier sehr gut die Unterschiede zwischen den beiden Darstellungen. Während in Euler-Diagrammen nur die tatsächlichen Überschneidungen zwischen den Mengen zu sehen sind, werden in Venn-Diagrammen alle möglichen Überlappungen der Flächen dargestellt (auch wenn diese keine Objekte enthalten).

Verständnisfrage: Betrachte folgendes Diagramm:

Nach dem Lesen dieses Artikels solltest du zur Gruppe 3 gehören  

Handelt es sich hier um ein Euler- oder um ein Venn-Diagramm? (Hoffentlich gehörst du nach dem Lesen dieses Artikels zur dritten Gruppe  )

Es ist ein Euler- aber kein Venn-Diagramm. Es ist kein Venn-Diagramm, weil es beispielsweise keinen Bereich gibt, wo sich nur die erste und die dritte Menge schneiden. Nach dem Diagramm gibt es im Übrigen Leute, die zwar Euler- und Venn-Diagramme kennen, die aber nicht wissen, was der Unterschied zwischen den beiden Diagrammarten ist.