Vereinigung und Durchschnitt von Vektorräumen – Serlo „Mathe für Nicht-Freaks“
Motivation
[Bearbeiten]Wir kennen verschiedene Operationen, um aus gegebenen Mengen eine neue Menge zu konstruieren. Ist eine Familie von Mengen, so können wir zum Beispiel den Durchschnitt oder die Vereinigung bilden. Angenommen, die sind außerdem Untervektorräume eines größeren Vektorraums . Das heißt, die sind nichtleere Teilmengen von , die abgeschlossen unter Addition und skalarer Multiplikation sind. Sind der Durchschnitt und die Vereinigung der dann ebenfalls Untervektorräume von ?
Durchschnitt von Untervektorräumen
[Bearbeiten]Ist der Schnitt von Unterräumen eines Vektorraums wieder ein Unterraum? Um diese Frage zu beantworten betrachten wir zunächst den Fall von zwei Unterräumen und schauen uns Beispiele im an.
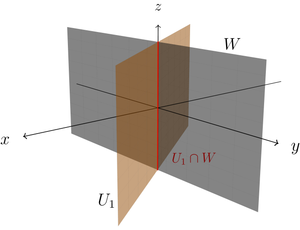
- Betrachten wir zunächst die beiden Ebenen und (die y-z-Ebene). Im Bild sehen wir, dass ihr Schnitt die z-Achse , also ein Unterraum von ist.
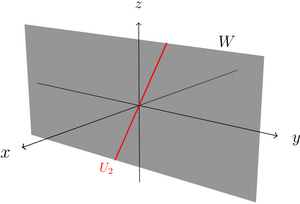
- Das zweite Bild zeigt, dass der Schnitt der Geraden mit der y-z-Ebene ebenfalls eine Gerade ist, und zwar .
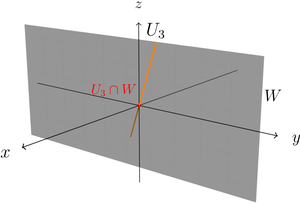
- Schneiden wir die y-z-Ebene stattdessen mit der Geraden , so sehen wir, dass der Durchschnitt nur die Null enthält. Auch das ist ein Unterraum von .
-
Schnitt zweier Ebenen
-
Schnitt einer Ebene mit einer Geraden
-
Schnitt einer Ebene mit einer Geraden
In den Beispielen ist der Durchschnitt der beiden Unterräume also stets wieder ein Unterraum von . Wir zeigen jetzt, dass das auch für allgemeine Unterräume eines beliebigen Vektorraums gilt.
Satz (Durchschnitt von Vektorräumen)
Seien und zwei Untervektorräume eines Vektorraums . Der Durchschnitt von und ist ein Untervektorraum von .
Beweis (Durchschnitt von Vektorräumen)
Zum Beweis müssen wir die drei Unterraumkriterien nachweisen:
Beweisschritt: ist nicht leer
Da und Unterräume sind, gilt und . Es folgt , also ist .
Beweisschritt: ist abgeschlossen unter Addition.
Seien nun beliebig. Dann gilt und . Da die Unterräume und abgeschlossen unter Addition sind, folgt und . Damit ist auch .
Beweisschritt: ist abgeschlossen unter Skalarmultiplikation.
Seien und beliebig. Dann gilt und . Da die Unterräume und abgeschlossen unter Skalarmultiplikation sind, folgt und . Damit ist auch .
Hinweis
Wir haben gesehen, dass ein Unterraum von ist. Wegen ist der Durchschnitt zudem ein Unterraum . Daraus folgt . Analog folgt aus . Das ergibt intuitiv Sinn: Wenn wir einen Unterraum mit einem anderen schneiden, kann seine Dimension unmöglich größer werden.
Wir haben gezeigt, dass der Schnitt von zwei Untervektorräumen wieder ein Untervektorraum ist. Im Beweis ist es aber an keiner Stelle relevant, dass es sich nur um zwei oder um endlich viele Unterräume handelt. In der Tat gilt die Aussage für beliebige Familien von Unterräumen.
Aufgabe (Beliebiger Durchschnitt von Vektorräumen)
Sei eine beliebige Indexmenge und eine Familie von Untervektorräumen eines Vektorraums . Dann ist der Durchschnitt ein Untervektorraum von .
Lösung (Beliebiger Durchschnitt von Vektorräumen)
Sei und seien Untervektorräume des -Vektorraums . Der Schnitt aller Vektorräume ist wieder ein Vektorraum.
Beweisschritt: ist nicht leer.
Da die Untervektorräume sind, ist für alle und damit ist . Somit ist nicht leer.
Beweisschritt: ist abgeschlossen unter Addition.
Seien . Dann gilt für alle . Weil alle Vektorräume sind, gilt die Abgeschlossenheit der Addition und es ist für alle . Damit ist .
Beweisschritt: ist abgeschlossen unter Skalarmultiplikation.
Seien und . Dann gilt für alle . Da alle Vektorräume sind, gilt die Abgeschlossenheit der Skalarmultiplikation und es ist für alle . Damit ist auch .
Vereinigung von Untervektorräumen
[Bearbeiten]Ist die Vereinigung von Unterräumen eines Vektorraums wieder ein Vektorraum? Betrachten wir zunächst ein Beispiel.
Beispiel (Koordinatenachsen sind kein Untervektorraum)
Sei . Als Unterräume wählen wir die Koordinatenachsen und . Ihre Vereinigung ist das Achsenkreuz in . Anhand des Bildes können wir schon vermuten, dass es sich dabei nicht um einen Untervektorraum von handelt: Es gibt zwei "Richtungen", gleichzeitig ist aber nicht die zwei-dimensionale Ebene. Und in der Tat sind die beiden Vektoren und in , aber ihre Summe liegt nicht in der Vereinigung. Also ist kein Unterraum.

Wir sehen also, dass die Vereinigung von zwei Unterräumen im Allgemeinen kein Unterraum ist. Ist das immer der Fall?
Beispiel (Vereinigung von Unterräumen ist Unterraum)
Wir betrachten die beiden Unterräume und von . Wegen ist . Also gilt und die Vereinigung der beiden Unterräume ist wieder ein Unterraum.

Die Vereinigung von zwei Unterräumen ist also in manchen Fällen, aber nicht immer, ein Unterraum. Im Beispiel war in enthalten, sodass ein Unterraum war. Das funktioniert immer: Sind zwei Unterräume gegeben und ist einer davon im anderen enthalten, dann ist die Vereinigung gleich dem größeren der beiden, also wieder ein Unterraum.
Das ist der einzige Fall, in dem die Vereinigung von zwei Unterräumen wieder ein Unterraum ist, wie anhand des ersten Beispiels mit den Koordinatenachsen anschaulich klar wird: Gilt und , dann wird die Vereinigung nicht abgeschlossen unter Addition sein. Denn es gibt dann zwei Vektoren mit und . Die Summe enthält dann einen Anteil, der nicht in liegt, und kann deshalb nicht in liegen: Andernfalls wäre auch . Ebenso begründet man .
Wir haben also folgendes Kriterium dafür, wann die Vereinigung von zwei Unterräumen ein Unterraum ist.
Satz (Bedingung dafür, dass die Vereinigung von zwei Vektorräumen wieder ein Vektorraum ist)
Sei ein Vektorraum über einem Körper und seien und zwei Untervektorräume von . Dann ist genau dann ein Untervektorraum von , wenn oder gilt.
Beweis (Bedingung dafür, dass die Vereinigung von zwei Vektorräumen wieder ein Vektorraum ist)
Beweisschritt: Ist ein Untervektorraum von , dann gilt oder .
Wir zeigen die Aussage per Kontraposition: Angenommen, es gilt weder noch . Wir zeigen, dass dann kein Unterraum von ist. Dafür finden wir zwei Elemente , sodass :
Wegen gibt es ein Element , das nicht in enthalten ist. Ebenso gibt es wegen ein , das nicht in enthalten ist.
Dann gilt . Aber die Summe liegt weder in noch in : Wäre , dann wäre auch , im Widerspruch zur Wahl von . Hierbei haben wir benutzt, dass wegen auch gilt und dass als Unterraum abgeschlossen unter Addition ist. Genauso sieht man ein, dass nicht in liegt.
Also gilt . Damit ist die Vereinigung nicht abgeschlossen unter Addition, also kein Unterraum.
Beweisschritt: Ist oder , so ist ein Vektorraum.
Gilt , so ist , also ist die Vereinigung ein Unterraum. Analog folgt aus , dass ein Unterraum ist.
Der Beweis des Satzes zeigt, dass die Eigenschaft, ein Unterraum zu sein, an der Addition scheitert. Die skalare Multiplikation auf war im Beweis nicht relevant. Tatsächlich ist stets unter skalarer Multiplikation abgeschlossen, selbst wenn sich bei der Vereinigung nicht um einen Untervektorraum handelt: Ist und , etwa , dann gilt , da als Unterraum abgeschlossen unter skalarer Multiplikation ist. Der Fall ist analog.
Da ein Vektorraum und Unterräume sind, bildet eine Gruppe und Untergruppen. Wir haben also effektiv gezeigt: ist genau dann eine Untergruppe von , wenn oder gilt. Es gibt eine allgemeinere Aussage über (nicht notwendigerweise kommutative) Gruppen. Der Beweis ist ganz analog zu dem Beweis für Unterräume, den wir oben geführt haben.
Satz (Vereinigung von Untergruppen)
Seien eine Gruppe und Untergruppen. Dann ist genau dann eine Untergruppe von , wenn oder gilt.
Die Vereinigung von Unterräumen und ist zwar im Allgemeinen kein Unterraum. Man kann aber den kleinsten Unterraum definieren, welcher enthält. Dieser Unterraum ist die Summe .