MathemaTriX ⋅ Theorie. Reifeniveau 6

Hoch

STOPP PUSHBACKS • FREE ASSANGE • FRIEDEN AUF DER WELT ${\color {grey}\mathbf {MATHE} \mu \alpha T\mathbb {R} ix}$ DEINE FESTE BEGLEITERIN FÜR DIE SCHULMATHEMATIK EINFACH UND VERSTÄNDLICH GRATIS!* MIT MEHR ALS 200 THEORIE- UND AUFGABEN-ERKLÄRUNGS VIDEOS! Mathe lernen ist wie Fahrradfahren lernen: Du kannst es dir stundenlang erklären lassen, du wirst nie fahren können, wenn du nicht selber zu fahren probierst.

AUFGABEN Niveaus: Grundniveau 1 Grundniveau 2 Grundniveau 3 Mitteniveau 1 Mitteniveau 2 Mitteniveau 3 Reifeniveau 1 Reifeniveau 2 Reifeniveau 3 Reifeniveau 4 Reifeniveau 5 Reifeniveau 6 Reifeniveau 7 Grundrechenarten und Bruchrechnungen Dieses Kapitel fängt im Grundniveau 1 an und wurde im mittleren Niveau 2 vervollständigt. Schluss und Prozentrechnung Dieses Kapitel fängt im Grundniveau 1 an und wurde im mittleren Niveau 3 vervollständigt. Exponential und Logarithmus Funktion Dieses Kapitel fängt im Grundniveau 3 an und wurde im Reifeniveau 5 vervollständigt. Arbeiten mit Termen Dieses Kapitel fängt im Grundniveau 1 an und wurde im Reifeniveau 3 vervollständigt. Zahlendarstellungen Mengentheorie und Aussagenlogik Aussagenlogik Logische Aussage Eine Aussage ist in der Logik ein Satz, der entweder wahr oder falsch sein kann. Was wahr oder nicht wahr ist, ist letztendlich eine tiefe philosophische Frage. Damit werden wir uns hier nicht beschäftigen. Wir werden an den Konventionen unserer Sprache verbleiben und verschieden Sätze, um ihre Möglichkeit wahr oder nicht wahr zu sein, untersuchen. Ein Auto ist ein Verkehrsmittel. So ein Satz kann war oder nicht wahr sein. Er ist also eine Aussage. In diesem Fall ist er wahr. Schreiben wir "Eine Orange ist ein Verkehrsmittel", haben wir wieder einen Satz der wahr oder nicht wahr sein kann. In diesem Fall ist er nicht wahr. Es gibt allerdings viele Sätze, die keine logische Aussage sind: Die Rose ist die schönste Blume. Dieser Satz ist grundsätzlich eine Meinung. Antworten zu ästhetischen Fragen (Fragen, die mit dem Schönen zu tun haben) sind nicht objektiv, besser gesagt nicht intersubjektiv. Man kann nicht sagen, ob sie wahr oder nicht wahr sind. Das ist eben eine Geschmackssache. Michael meint, dass die Rose die schönste Blume ist. Dieser Satz ist allerdings schon eine logische Aussage. Sie kann nur wahr oder nicht wahr sein. Ist die Rose die schönste Blume? Alle Fragen können keinen logische Aussage sein. Man kann sie logisch nicht als wahr oder falsch einschätzen. Schneide diese Rose Es sollte schon klar sein: Dieser Satz ist auch keine logische Aussage. Logische Aussageform Eine Aussage, in der zumindest ein geeigneter Teil durch eine Variable (einen "Platzhalter") ersetzt wird, ist eine Aussageform. Sobald der Platzhalter durch den geeigneter Wert ersetzt wird, entsteht eine Aussage, die wahr oder falsch sein kann. _________ hat vier Beine. Sobald wir in der Lücke ein Tier oder ein Gegenstand mit Beinen einsetzen, wird der Satz wahr oder nicht wahr sein. Schreiben wir in der Lücke "Huhn", ist er nicht wahr, schreiben wir "Tisch", kann er wahr sein, je nachdem, welches Tisch gemeint ist. Es geht also um eine Aussageform. Logische Verknüpfungen In der Aussagelogik wird die Kombination von Aussagen nach ihrem Wahrheitswert untersucht. Es gibt verschiedene Weise Aussagen zu Kombinieren (man sagt "zu verknüpfen"). Die Konjunktion. Das ist das logische "und". Die Konjunktion von zwei Aussagen ist nur dann wahr, wenn beide wahr sind. Das Symbol dafür ist $\land$. Beispiel: "44 hat zwei Ziffern" $\land$ "Ein Kugelschreiber ist eine Pflanze" ist nicht wahr, da der zweite Satz eindeutig nicht wahr ist. Die Disjunktion. Das ist das logische "oder". Die Disjunktion von zwei Aussagen ist nur dann wahr, wenn zumindest eine der beiden Aussagen wahr sind. Das Symbol dafür ist $\lor$. Beispiel: "44 hat zwei Ziffern" $\lor$ "Ein Kugelschreiber ist eine Pflanze" ist wahr, da zumindest ein Satz, hier der erste, wahr ist. "44 hat zwei Ziffern" $\lor$ "Ein Baum ist eine Pflanze" ist auch wahr, da zumindest ein Satz wahr ist, in diesem Fall allerdings beide. Die Adjunktion. Das ist das logische "entweder-oder". Die Disjunktion von zwei Aussagen ist nur dann wahr, wenn genau eine der beiden Aussagen wahr ist. Das Symbol dafür ist ${\dot {\lor }}$. Beispiel: "44 hat zwei Ziffern" ${\dot {\lor }}$ "Ein Kugelschreiber ist eine Pflanze" ist wahr, da genau ein Satz, hier der erste, wahr ist. "44 hat zwei Ziffern" ${\dot {\lor }}$ "Ein Baum ist eine Pflanze" ist allerdings hier doch nicht wahr, da nicht genau einer, sondern beide Sätze wahr sind, es gilt also das "entweder-oder" nicht. Die Negation. Die Negation eines Satzes ist dann wahr, wenn der anfängliche Satz nicht wahr ist und umgekehrt. Das Symbol dafür ist $\neg$. $\neg$"Ein Baum ist eine Pflanze" ist nicht wahr, da der Satz "Ein Baum ist eine Pflanze" schon wahr ist. Die Implikation. Oft benutzen wir in der Sprache Folgerungen. Das sind Sätze der Form "wenn-dann". Den "wenn"-Satz nennen wir oft "Voraussetzung", den "dann"-Satz "Konsequenz". Diese Art von "wenn-dann" Sätzen nennt man in Logik Implikation. Das Symbol dafür ist $\Rightarrow$. Dabei müssen sie in der Logik nicht unbedingt einen tatsächlichen Zusammenhang haben. Eine Implikation ist nur dann nicht wahr, wenn die "Voraussetzung" wahr und die "Folgerung" nicht wahr ist. Ein Beispiel: "44 hat zwei Ziffern" $\Rightarrow$ "Ein Kugelschreiber ist eine Pflanze" ist nicht wahr, da die "Voraussetzung" wahr, die "Konsequenz" allerdings nicht wahr ist. Die Äquivalenz. Sie ist ein Implikation in beiden Richtungen. Das Symbol dafür ist $\Leftrightarrow$. Eine Äquivalenz ist nur dann wahr, wenn beide Aussagen den gleichen Wahrheitswert haben, also wenn sei beide wahr oder beide nicht wahr sind. Beispiel: "44 hat zwei Ziffern" $\Leftrightarrow$ "Ein Kugelschreiber ist eine Pflanze" ist nicht wahr, weil ein Satz wahr (hier der erste) und ein Satz nicht wahr (hier der zweite) ist. "44 hat fünf Ziffern" $\Leftrightarrow$ "Ein Kugelschreiber ist eine Pflanze" ist allerdings wahr, weil beide Aussagen den gleichen Wahrheitswert haben (hier sind sie beide nicht wahr) Wahrheitstabellen Den Wahrheitswert der verschiedenen Verknüpfungen kann man auch in einer Tabelle darstellen: Belegung UND ODER ENTW. ODER WENN DANN WENN DANN GENAU DANN WENN $a$ $b$ $\ a\land b\$ $\ a\lor b\$ $\ a{\dot {\lor }}b\$ $\ a\Rightarrow b\$ $\ b\Rightarrow a\$ $\ a\Leftrightarrow b\$ w w w w f w w w w f f w w f w f f w f w w w f f f f f f f w w w Mit Hilfe einer solchen Tafel kann man den Wert von Kombinationen von Verknüpfungen herausfinden. Hier ein paar Beispiele: Belegung Untersuchung des Wahrheitswerts des Ausdrucks $\ ((\neg (a\land b)\Rightarrow c){\dot {\lor }}\neg a)\Leftrightarrow b\$ $a$ $b$ $c$ $\ a\land b\$ $\ \neg (a\land b)\$ $\ \neg (a\land b)\Rightarrow c\$ $\ \neg a$ $\ (\neg (a\land b)\Rightarrow c){\dot {\lor }}\neg a\$ $\ ((\neg (a\land b)\Rightarrow c){\dot {\lor }}\neg a)\Leftrightarrow b\$ w w w w f w f w w w w f w f w f w w w f w f w w f w f w f f f w f f f w f w w f w w w f f f w f f w f w w w f f w f w w w f f f f f f w f w w w Mit dem nächsten Beispiel wird es klar, dass manchmal Klammer notwendig sind, sonst hat der Ausdruck keinen klaren Wahrheitswert. Zwischen vorletzten und letzten Spalte ist die Klammersetzung der einzige Unterschied. Man merkt, dass die Wahrheitswerte für einige Kombinationen dann schon unterschiedlich sind. Belegung $a$ $b$ $c$ $\ a\land b\$ $\ b\Rightarrow c\$ $\ (a\land b)\Rightarrow c\$ $\ a\land (b\Rightarrow c)\$ w w w w w w w w w f w f f f w f w f w w w w f f f w w w f w w f w w f f w f f f w f f f w f w w f f f f f w w f Lass uns die letzte Tabelle ein bisschen erweitern: Belegung $a$ $b$ $c$ $\ a\land b\$ $\ b\Rightarrow c\$ $\ (a\land b)\Rightarrow c\$ $\ a\land (b\Rightarrow c)\$ $\ ((a\land b)\Rightarrow c)\lor (a\land (b\Rightarrow c))\$ $\ ((a\land b)\Rightarrow c){\dot {\lor }}(a\land (b\Rightarrow c))\$ $\ \neg a\$ w w w w w w w w f f w w f w f f f f f f w f w f w w w w f f w f f f w w w w f f f w w f w w f w w w f w f f f w f w w w f f w f w w f w w w f f f f w w f w w w Man merkt, dass die zwei letzten Spalten identisch sind. In diesem Fall spricht man von einer Tautologie. Die Ausdrücke $\ ((a\land b)\Rightarrow c){\dot {\lor }}(a\land (b\Rightarrow c))\$und$\ \neg a\$haben daher immer den gleichen Wert, egal was die Aussagen a, b und c besagen. Das gleiche gilt auch für die Ausdrücke $\ (a\land b)\Rightarrow c\$und$\ ((a\land b)\Rightarrow c)\lor (a\land (b\Rightarrow c))\$(6. und 8. Spalte) Symbole und Konventionen in Mathematik und Logik In Mathematik (und daher auch in der Logik als Teilgebiet der Mathematik) werden viele Symbole und viele Konventionen benutzt. Es muss klar sein: Es hat Jahrtausende gedauert, bis die Menschen diese Symbole erdacht haben und ihre internationale Anwendung ist eine Konvention, die oft erst vor kurzem vereinbart wurde. Für viele von diesen Symbolen gab es mehrere verschiedene Darstellungen und viele werden immer noch in verschiedenen Länder anders dargestellt. Zunächst einmal gibt es die Ziffern von 0 bis 9 und ihre Anwendung in den Zahlen im dekadischen (und nicht nur) System. Dass in der Zahl 783,94 mit 7 die Hunderte, mit 8 die "Zehner", mit 3 die "Einser", mit 9 die Zehntel und mit 4 die Hundertstel dargestellt werden ist wiederum eine Konvention des dekadischen Systems. Die einfachsten Symbole sind die vier Grundrechnungen + (plus), − (minus), ⋅ (oder ×) (mal), : (oder ÷ oder /) (durch) und dazu das Symbol für Gleichheit $=$, Ungleichheit $\neq$ und ungefähre Gleichheit $\approx \ \simeq$. Die Multiplikation ist eine Konvention, die das mehrfache Addieren der gleichen Zahl darstellt. Entsprechend gibt es die Darstellung der Potenzzahlen an, die eine Konvention für die mehrfache Multiplikation der gleichen Zahl ist. Dann gibt es auch Vergleichssymbole wie $<,>,\leq ,\geq$, was "kleiner als", "größer als", "kleiner oder gleich wie" bzw. "größer oder gleich wie" bedeuten (immer von links nach rechts gelesen). Eine Konvention ist auch die Darstellung der Funktionen in der Form f(x) (wobei jeder Buchstabe für f und irgendeiner anderer Buchstabe für x benutzt werden darf): In diese Darstellung steht f(x) für die abhängige Variable (die i. d. R. auf der y-Achse dargestellt wird) und x (also der Buchstabe in Klammern) für die unabhängige (die i. d. R. auf der x-Achse dargestellt wird). Eine Konvention ist auch, dass kleine Buchstaben (besonders die ersten) in der Geometrie für Seiten benutzt werden, große für (Eck-) Punkte und griechische für Winkel. In der Mengenlehre gibt es die Symbole $\bigcap \$für die "Schnittmenge", $\bigcup \$für die "Vereinigung", $\setminus \$für die "Differenz", $\subseteq \$für die "Teilmenge" und $\times \$für das "kartesische Produkt". In der Logik gibt es Symbole für die Verknüpfungen von Aussagen, wie $\land$ (logisches „und“), $\lor$ (logisches „oder“), ${\dot {\lor }}$ (logisches „entweder oder“), $\Leftarrow$ und $\Rightarrow$ (logisches „daraus folgt“, „wenn …, dann …“ in der Richtung des Pfeils), $\Leftrightarrow$ (logisches „genau dann, wenn“) und $\neg$ (logische "Negation"). Weitere Symbole, die in der Logik benutzt werden, sind: $\in \$: das bedeutet, dass ein Objekt Element einer Menge sein soll. Die Gegenaussage ist dann: $\notin \$also kein Element. $\forall \$: das bedeutet „für jedes“ (Element), „für alle“ (Elemente) $\exists \$: das bedeutet „es gibt“ („zumindest eins“), die Gegenaussage ist dann: $\nexists \$: „es gibt nicht“ oder „es gibt keine“. $:\$ bedeutet „so dass“. $|\$ bedeutet „gilt“. Mengenlehre und Aussagenlogik *$A\bigcap \ B=\{x|(x\in A)\land (x\in B)\}$ Das kann man so ablesen: Die Schnittmenge der Mengen A und B sind die Objekte x, für denen es gilt, dass sie sowohl Elemente der Menge A also auch Elemente der Menge B sind. $A\bigcup B=\{x|(x\in A)\lor (x\in B)\}$ Das kann man so ablesen: Die Vereinigungsmenge der Mengen A und B sind die Objekte x, für denen es gilt, dass sie Elemente zumindest einer der Mengen A und Menge B sind, also Elemente der Menge A, oder der Menge B oder der beiden Mengen A und B. $A\setminus B=\{x|(x\in A)\land (x\notin B)\}$ Das kann man so ablesen: Die Differenzmenge der Mengen A und B sind die Objekte x, für denen es gilt, dass sie zwar Elemente der Menge A sind aber nicht und Menge B. Wenn also die Menge A auch Elemente der Menge B beinhaltet, gehören letztere nicht zu dieser Differenzmenge. $A\subseteq B\Leftrightarrow (\forall x\in A|x\in B)$ Das kann man so ablesen: Die Menge A ist genau dann eine Teilmenge der Menge B, wenn für jedes Element der Menge A auch gilt, dass es ein Element der Menge B ist. $A\times B=\{(a|b)|a\in A\land b\in B)\}$ Das kann man so ablesen: Das kartesische Produkt der Mengen A und B sind alle geordneten Objektpaaren bei denen das erste Objekt des Paares ein Element der Menge A ist und das zweite ein Element der Menge B. Einheiten Dieses Kapitel fängt im Grundniveau 2 an und wurde im Reifeniveau 3 vervollständigt. Statistik und Wahrscheinlichkeitsrechnung Regression und Korrelation Regression Nehmen wir ein einfaches konkretes Beispiel: die Beziehung zwischen Gewicht und Größe einer Person. Je größer eine Person ist, desto mehr wiegt sie. Man kann sich fragen, ob es möglich ist, diesen Zusammenhang durch eine Funktion zu beschreiben. 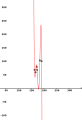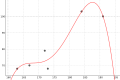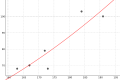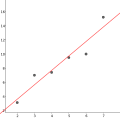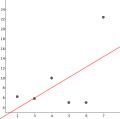cm kg 173 68 184 103 167 70 172 79 191 100 163 68 Machen wir das Beispiel noch konkreter: Nehmen wir an, dass wir das Gewicht und die Größe von 6 Personen gemessen und die Ergebnisse in der beiliegenden Tabelle dargestellt haben. Wir können verschiedenen Geraden, die irgendwie zwischen den Daten stehen, benutzten, um einen linearen Zusammenhang darzustellen (erstes Bild). Wie können wir eine Entscheidung über die geeignetste Gerade treffen? Unter anderen der berühmte Mathematiker Carl Friedrich Gauß hat eine Methode entwickelt, um die am besten angepassten Gerade zu finden: die Methode der kleinsten Quadrate. Im zweiten Bild sieht man zwischen jedem Punkt und Gerade eine Strecke, deren Länge die Differenz des y-Wertes des Punktes vom y-Wert der Gerade an dieser Stelle (x-Wert) ist. Nach der Methode der kleinsten Quadrate wird diejenige Gerade gewählt, für die es gilt, dass die Summe der Quadrate dieser Differenzen die kleinste ist. Für unsere Daten ist diese im dritten Bild dargestellt. Man kann allerdings ziemlich leicht feststellen, dass diese Gerade für unseren Zusammenhang nicht gerade die geeignetste ist. Wenn die Gerade verlängert wird (4. Bild), stellt man fest, dass für eine Größe kleiner als ca. 115 cm das Gewicht negativ wird! Das hat selbstverständlich keinen physikalischen Sinn. Ideal wäre die Gerade, wenn sie durch den Punkt (0,0) ginge und für die restlichen Werte die Regel der kleinsten Quadrate erfüllte. So eine Gerade zu finden ist auch möglich, wenn auch ziemlich komplexer und wird hier nicht weiter untersucht. Für die gegebenen Daten ist also die im dritten Bild dargestellte Gerade die nach dem Kriterium der kleinsten Quadrate die am besten angepasste. Es gibt aber keinen Grund zu denken, dass der Zusammenhang unbedingt linear sein sollte. Sehen noch drei andere Möglichkeiten für unsere Daten: Um zu entscheiden, ob eine Funktion zu den Daten gut passt, gibt es unterschiedliche Kriterien. Eines davon hat mit der Methode der kleinsten Quadrate zu tun und wird Bestimmtheitsmaß genannt. Das Symbol dafür ist R². Null ist dieses Maß, wenn die Kurve durch alle Datenpunkte geht. Im 1. Bild sehen wir eine Polynomfunktion, die durch alle Punkte geht. Das ist allerdings keine Überraschung. Für jede Anzahl von Punkte gibt es eine Polynomfunktion, die durch alle Punkte geht, nämlich eine Polynomfunktion, deren Grad um 1 kleiner als die Anzahl der Punkte ist. Wenn wir allerdings diese Funktion außerhalb des Bereichs der gegebenen Punkte betrachten, stellen wir fest, dass sie überhaupt nicht geeignet ist, um unseres Beispiel zu beschreiben, auch wenn das Bestimmtheitsmaß null ist. Im 2. und 3. Bild sehen wir noch eine Polynomfunktion, diesmal 4. Grades (also um 2 weniger als die Anzahl der Punkte). Wie leicht zu sehen ist, hat sie genau das gleiche Problem wie die Funktion 5. Grades. Im 4. und 5. Bild sehen wir eine quadratische Funktion, die nach der Methode der kleinsten Quadrate erzeugt wurde. Diese hat immer noch Nachteile, ihre Wert wird beispielsweise ca. unterhalb der Stelle 80 cm größer für fallende Größe, was nicht logisch ist (kleinere Personen und Kinder wiegen ja weniger als größere und nicht mehr). Allerdings ist dieses Modell doch besser als das lineare Modell. Die Werte werden für kleinere Stellen nicht mehr negativ. Es macht auch physikalisch Sinn, wegen der Konstruktion des menschlichen Körpers und die Art in der ein Mensch wächst, dass der Zusammenhang zwischen Gewicht und Größe nicht linear ist. Daher könnte man sich in diesem Fall doch für die quadratische Funktion entscheiden. Korrelation Nehmen wir ein einfaches konkretes Beispiel: die Beziehung zwischen Gewicht und Größe einer Person. Je größer eine Person ist, desto mehr wiegt sie. Dieser Zusammenhang lässt sich möglicherweise durch eine lineare Funktion beschreiben. Für die Erzeugung einer solchen linearen Funktion wird i. d. R. die Methode der kleinsten Quadrate angewendet (Regression). Die Frage ist allerdings, wie nah zu einer linearen Funktion die tatsächlichen Daten stehen. Der Korrelationskoeffizient ist ein Maß dieser "Nähe". Schauen wir uns folgende Bilder an: In allen drei Bildern lautet die lineare Funktion ungefähr $y=2\ x-0{,}4$. Wir können allerdings klar sehen, dass im ersten Bild alle Punkte ziemlich nah zur Gerade sind, im zweiten etwas weiter und im dritten ziemlich weit. Der Korrelationskoeffizient ist im ersten Fall fast 1, im zweiten ca. 0,9 und im dritten weniger als 0,7. Der Korrelationskoeffizient ist ein Maß der Nähe der Punkte der Datenpaare zur von denen mit Hilfe der Regression erzeugte linearen Funktion. Der Korrelationskoeffizient hat mit der Steigung der Regressionsgerade das gleiche Vorzeichen, allerdings hat er zur Steigung keinen (anderen) Zusammenhang. Betrachten wir folgende Bilder: Der Betrag der Korrelationskoeffizient ist in allen Fällen ca. 0,998. Der Koeffizient ist positiv im 1. Bild und negativ in den anderen 2. Die Steigung der Gerade ist im 1. Bild ca. 2, im 2. Bild ca. −0,7 und im 3. Bild ca. −2, obwohl der Korrelationskoeffizient gleich ist. Der Korrelationskoeffizient hat mit der Steigung der Regressionsgerade außer dem gleichen Vorzeichen gar nichts zu tun. Man könnte auch denken, dass es keinen Zusammenhang zwischen den dargestellten Größen gibt, wenn der Korrelationskoeffizient null ist. Das ist doch nicht der Fall. Betrachten wir folgende Bilder: In der dritten Bildreihe sehen wir Punktwolken, die doch einer Funktion entsprechen könnten. Das erste Bild der dritten Bildreihe könnte beispielsweise durch eine Sinusfunktion angenähert werden, das vierte durch eine quadratische, das fünfte durch eine hyperbolische, das sechste durch einen Kreis und das siebte durch vier Kategorien: Ein Korrelationskoeffizient gleich null schließt einen Zusammenhang der Daten überhaupt nicht aus. Er schließt dann höchstens nur einen linearen Zusammenhang aus. In der zweiten Bildreihe sehen wir, dass alle Punkte (alle Datenpaare) sich auf einer Gerade befinden. In allen diesen Fällen ist der Korrelationskoeffizient (selbstverständlich) 1 (für positiver Steigung) bzw. −1 (für negative Steigung), auch wenn die Steigung vom Fall zum Fall völlig unterschiedlich ist. In der ersten Bildreihe sehen wir noch eindeutlicher als vorher, dass je mehr die Datenpaaren in einer von einer Gerade entfernte "Punktwolke" dargestellt werden, desto näher zu null der Korrelationskoeffizient ist. Was könnte der Korrelationskoeffizient für den Zusammenhang zwischen den zwei Größen der Datenpaare bedeuten? Ein Korrelationskoeffizient könnte eine Kausalität bedeuten. Rauchen ist mit einigen Herzerkrankungen stark korreliert und gilt als begründete Ursache (wenn auch eine von mehreren). Rauchen allerdings kann auch zur gelber Färbung der Fingernägel führen. Es gibt daher eine Korrelation zwischen Fingernagelfärbung und Herzerkrankungen. Es gilt aber in diesem Fall eben nicht, dass die Fingernagelfärbung eine Ursache der Herzerkrankungen ist, noch das Gegenteil. In diesem Beispiel wird die Korrelation durch eine gemeinsame Ursache erzeugt. Es kann allerdings auch vorkommen, dass eine Korrelation völlig zufällig ist und dass es keinen Zusammenhang zwischen den korrelierten Größen besteht. Geometrische Konstruktionen Dieses Kapitel fängt im Grundniveau 2 an und wurde im mittleren Niveau 3 vervollständigt. Geometrie der Ebene Dieses Kapitel fängt im Grundniveau 2 an und wurde im mittleren Niveau 2 vervollständigt. Geometrie des Raums Dieses Kapitel ist nur im mittleren Niveau 3 behandelt. Diagramme Dieses Kapitel fängt im Grundniveau 2 an und wurde im Reifeniveau 5 vervollständigt.   Funktionen. Darstellungen der linearen Funktion Es gibt verschiedene Weisen eine lineare Funktion anzugeben. Hier werden nur manche davon angegeben. Die explizite Form Die Darstellung y=a⋅x+b der linearen Funktion nennt man explizite Form. In dieser Form steht die abhängige Variable y auf der rechten Seite und auf der linken die unabhängige Variable x - mit einer Konstante a (bzw. d, m usw.) vor ihr - plus eine zweite Konstante b (bzw. d, n usw.). Es gibt aber auch andere Darstellungen der linearen Funktion. Die implizite Form Die implizite Form ist: a⋅x+b⋅y+c=0   (oder   a⋅x+b⋅y=c) Die Parameterform (Vektorform) Die Parameterform wird durch zwei Gleichungen angegeben: $x=a_{1}\cdot t+b_{1}$ $y=a_{2}\cdot t+b_{2}$ Die Variable t nennt man Parameter Das gleich kann man in der sogenannten Vektorform darstellen: $\textstyle \mathbf {X} =\mathbf {A} \ \cdot t+\mathbf {B} \$ $\textstyle \mathbf {X} ,\ \mathbf {A} ,\$und $\ \mathbf {B} \$sind Vektoren, nämlich $\textstyle {\binom {x_{1}}{x_{2}}},\ {\binom {a_{1}}{a_{2}}},\ {\binom {b_{1}}{b_{2}}}$: $\textstyle {\binom {x_{1}}{x_{2}}}={\binom {a_{1}}{a_{2}}}\ \cdot t+{\binom {b_{1}}{b_{2}}}\$ Diese Darstellung ist gleichbedeutend mit den folgenden zwei Gleichungen: $x_{1}=a_{1}\cdot t+b_{1}$ $x_{2}=a_{2}\cdot t+b_{2}$ Es ist oft so in der Vektorrechnung, dass die Achsen des Koordinatensystems durchnummeriert werden. Hier steht $x_{1}\$an der Stelle von $x\$und $x_{2}\$an der Stelle von $y$. Graphische Darstellung Drei verschieden lineare Funktionen Wie schon beschrieben kann man Geometrie und Algebra kombinieren. Wir haben dort gesehen, dass die algebraische Form eines Kreises x2+y2=r2 ist. Die geometrische Form einer linearen Gleichung in einem kartesischen Koordinatensystem ist eine Gerade: In diesem Bild haben die rote und die grüne Gerade den gleichen y-Achsenabschnitt, die rote und die blaue die gleiche Steigung (sie sind parallel). Die blaue und die grüne haben einen gemeinsamen Punkt bei (-4/3|-5/3) Umwandeln von einer Form zu einer anderen Im folgenden werden die unterschiedlichen Symbole für die explizite Form benutzt, die in den verschiedenen deutschsprachigen Staaten benutzt werden. Nochmal: y=k⋅x+d     ist gleich wie     y=m⋅x+n     ist gleich wie     y=m⋅x+q Wichtig ist nur zu wissen: Die Konstante, die in der explizite Form mit x multipliziert wird, ist die Steigung. (in der Schweiz und in Deutschland m, in Österreich k - in der Regel!) Die Konstante, die zu diesem Produkt addiert wird, ist der y-Achsenabschnitt. (in der Schweiz q, in Deutschland n, in Österreich d - in der Regel!) Explizite zur impliziten Form y=k⋅x+d ⇔ -k⋅x+y-d=0 Das ist schon die implizite Form   a⋅x+b⋅y+c=0   mit -k statt a (Konstante vor x in der impliziten Form), 1 statt b (Konstante vor y in der impliziten Form) und -d statt c (Konstante ohne Variable in der impliziten Form). Explizite zur Parameterform y=m⋅x+n Wenn wir x=t stellen, dann haben wir schon die Parameterform: x=t y=m⋅t+n Vektorform:$\quad {\binom {x}{y}}={\binom {1}{m}}\cdot t+{\binom {0}{n}}$ Vergleichen wir das mit dem allgemeineren Parameterform (x=a1⋅t+b1  und  y=a2⋅t+b2), dann stellen wir fest, dass hier a1=1, b1=0, a2=m und b2=n ist. Implizite zur expliziten Form a⋅x+b⋅y+c=0 Mit unseren Kenntnissen können wir diese Gleichung auf y umformen: a⋅x+b⋅y+c=0   ⇔   b⋅y=-c-a⋅x und daher: $\mathbf {y={\frac {-a}{b}}\cdot x+{\frac {-c}{b}}}$ Das ist die explizite Form mit -a/b als Steigung (m, k usw.) und -c/b als y-Achsenabschnitt (n,p,d usw.). Implizite zur Parameterform Man nimmt das Ergebnis aus dem letzten Abschnitt und wandelt diese explizite in die Parameterform: $\mathbf {x=t}$ $\mathbf {y={\frac {-a}{b}}\cdot t+{\frac {-c}{b}}}$ Vektorform:$\quad {\binom {x}{y}}={\binom {1}{-{\frac {a}{b}}}}\cdot t+{\binom {0}{-{\frac {c}{b}}}}$ Parameter- zur expliziten Form x=a1⋅t+b1 y=a2⋅t+b2 Vektorform:$\quad {\binom {x}{y}}={\binom {a_{1}}{a_{2}}}\cdot t+{\binom {b_{1}}{b_{2}}}$ Man formt die erste Gleichung auf t um und setzt dieses t in die zweite Gleichung ein: $t={\frac {1}{a_{1}}}\cdot x-{\frac {b_{1}}{a_{1}}}\quad \Rightarrow \quad y=a_{2}\cdot \left({\frac {1}{a_{1}}}\cdot x-{\frac {b_{1}}{a_{1}}}\right)+b_{2}\quad \Rightarrow$ $\mathbf {y={\frac {a_{2}}{a_{1}}}\cdot x+{\frac {a_{1}\cdot b_{2}-a_{2}\cdot b_{1}}{a_{1}}}}$ Die Steigung in der Parameterform ist daher $\mathbf {\frac {a_{2}}{a_{1}}}$ und der y-Achsenabschnitt ist $\mathbf {\frac {a_{1}\cdot b_{2}-a_{2}\cdot b_{1}}{a_{1}}}$ Parameter- zur impliziten Form Man benutzt die Gleichung    $y=a_{2}\cdot \left({\frac {1}{a_{1}}}\cdot x-{\frac {b_{1}}{a_{1}}}\right)+b_{2}$    aus dem letzten Abschnitt und formt sie um: $\mathbf {a_{2}\cdot x-a_{1}\cdot y+(a_{1}\cdot b_{2}-a_{2}\cdot b_{1})=0}$ Das ist schon die implizite Form   a⋅x+b⋅y+c=0   mit $a_{2}$ statt a (Konstante vor x in der impliziten Form), $-a_{1}$ statt b (Konstante vor y in der impliziten Form) und $(a_{1}\cdot b_{2}-a_{2}\cdot b_{1})$ statt c (Konstante ohne Variable in der impliziten Form). Die lineare Funktion graphisch darstellen Durch die Definition der Gerade versteht man, dass zwei Punkte ausreichen, um eine Gerade eindeutig zu definieren. Ein Punkt ist durch zwei Werte bestimmt, die x-Koordinate und die entsprechende y-Koordinate. Um zwei Punkte einer linearen Funktion zu finden, reicht es daher aus, willkürlich zwei Werte für x in der Funktion einzugeben und die entsprechende Werte für y finden. Diese zwei Punkte zeichnet man dann im Koordinaten System. Die Gerade, die durch diese zwei Punkte läuft, entspricht der gegebenen linearen Funktion. Lineare Gleichungssysteme Dieses Kapitel fängt im Grundniveau 3 an und wurde im Reifeniveau 4 vervollständigt. Trigonometrische Funktionen Dieses Kapitel fängt im Reifeniveau 1 an und wurde im Reifeniveau 5 vervollständigt. Vektoren Dieses Kapitel ist nur im Reifeniveau 5 behandelt. Differentialrechnung Dieses Kapitel fängt im Reifeniveau 1 an und wird im Reifeniveau 7 weitergeführt. Integralrechnung Dieses Kapitel fängt im Reifeniveau 3 an und wird im Reifeniveau 7 weitergeführt. Folgen in Mathematik Eine Zahlenfolgelegende und die geometrische Summenformel Nach einer alten Legende schuf in Indien ein Brahmane (etwas wie Priester) das Schachspiel, um die Aufmerksamkeit seines grausamen Herrschers abzulenken. Der Herrscher war so begeistert, dass er dem Brahmanen belohnen wollte. Der Brahmane fragte dann als Belohnung die folgende Summe von Weizenkörnern. Auf das erste Feld des Schachbretts sollte ein Korn sein, am zweiten sollten doppelt so viele Körner sein usw. bis zum letzten Feld. Der Herrscher kannte keine Exponentialfunktionen und hat gedacht, dass diese Belohnung nicht so hoch wäre. Bald hat sich allerdings herausgestellt,dass er sich enorm geirrt hatte. Versuchen wir zu berechnen, wie viele Körner das wären. Jedes mal muss mit zwei multipliziert werden. Dadurch bekommen wir die Zahlen 1, 2, 4, 8, 16, 32, 64, 128... Mit 128 sind wir noch beim 8. Feld. Wie wird die Zahl am 64. Feld aussehen? Dafür müssen wir eine andere Darstellung dieser Zahlenreihe benutzen. Das erste Feld hat $2^{0}=1\$Korn, das zweite $2^{1}=2$, das dritte $2^{2}=4$, das vierte $2^{3}=8$, das fünfte $2^{4}=16$ usw.. Es wird also klar, dass die Hochzahl von 2 jedes mal um 1 weniger als die Anzahl des Feldes ist. Das Schachbrett hat 64 Felder, daher werden am letzten Feld $2^{64-1}=2^{63}=9223372036854775808$, also 9 Trillionen Körner sein. Gefragt ist allerdings die Summe. Es gibt einen Weg diese Summe mit einer Formel zu berechnen. Um diese Formel zu finden, benutzen wir den allgemeinen Fall. Wir fangen mit einem Wert w (hier 1) an und jedes mal wird das vorherige Ergebnis mit der gleichen Zahl a multipliziert. Das n-te Glied diese Zahlenfolge wird dann $w\cdot a^{n-1}$. Bei der Summe der Folgeglieder kann w herausgehoben werden: $w\cdot a^{0}+w\cdot a^{1}+w\cdot a^{2}+w\cdot a^{3}+...=w(1+a+a^{2}+a^{3}+...)$. Wir wollen die Summe in Klammer berechnen. Fangen wir mit der einfachen Tatsache an, dass diese Summe gleich sich selbst sein wird: $1+a+a^{2}+a^{3}+...+a^{n-1}=1+a+a^{2}+a^{3}+...+a^{n-1}$ Multiplizieren wir jetzt beide Seiten mit a: $(1+a+a^{2}+a^{3}+...+a^{n-1})\cdot a=(1+a+a^{2}+a^{3}+...+a^{n-1})\cdot a$ Multiplizieren wir jetzt die rechte Seite der Gleichung aus. Dadurch wird die Hochzahl bei jedem Summand um eins mehr: $(1+a+a^{2}+a^{3}+...+a^{n-1})\cdot a=a+a^{2}+a^{3}+...+a^{n}$ Weizen Subtrahieren wir jetzt von beiden Seiten die Zahlenfolge vom Anfang $(1+a+a^{2}+a^{3}+...+a^{n-1})$: $(1+a+a^{2}+a^{3}+...+a^{n-1})\cdot a-(1+a+a^{2}+a^{3}+...+a^{n-1})$$=a+a^{2}+a^{3}+...+a^{n}-(1+a+a^{2}+a^{3}+...+a^{n-1})$ Auf der linke Seite können wir die zweite Klammer mit 1 multiplizieren, auf der rechten die Klammer ausmultiplizieren, dadurch werden alle plus zu minus: $(1+a+a^{2}+a^{3}+...+a^{n-1})\cdot a-(1+a+a^{2}+a^{3}+...+a^{n-1})\cdot 1$$=a+a^{2}+a^{3}+...+a^{n}-1-a-a^{2}-a^{3}-...-a^{n-1}$ Auf der linken Seite können wir jetzt die Klammer herausheben und auf der rechten die Subtraktionen durchführen, wodurch alle Potenzen mit zwei Ausnahmen verschwinden: $(1+a+a^{2}+a^{3}+...+a^{n-1})\cdot (a-1)=a^{n}-1$ Umformen (durch $(n-1)$): $1+a+a^{2}+a^{3}+...+a^{n-1}={\frac {a^{n}-1}{a-1}}$ Letzteres Ergebnis ist die Summenformel einer sogenannten geometrischen Folge (geometrische Summenformel). Etwas abstrakter schreibt man in Mathematik: $\sum \limits _{i=0}^{n-1}a^{i}={\frac {a^{n}-1}{a-1}}$ In der antiken Legende ist a gleich 2, die Summe der ganzen Körner ist daher: ${\frac {2^{64}-1}{2-1}}={\frac {2^{64}-1}{1}}=18446744073709551615\$Körner! Diese Menge entspricht mehr als das 1000-fache der Jahresproduktion heutzutage. Was sollte der König machen? Ein Berater von ihm, hat ihm die Lösung gegeben. Er sollte die Körner eins zu eins zahlen lassen . Folgen Definition Einfache Definition: Eine Folge in der Mathematik ist eine (endliche oder unendliche) Reihenfolge von Objekten, die man aufzählen und möglicherweise auch einordnen kann. Zwei formelle Definitionen von Folgen sind: Als Folge oder Sequenz wird in der Mathematik eine Auflistung von endlich oder unendlich vielen fortlaufend nummerierten Objekten (beispielsweise Zahlen) bezeichnet. Eine Folge ist eine eindeutige Zuordnung zwischen den natürlichen Zahlen $\mathbb {N}$ und den reellen Zahlen $\mathbb {R}$: $n\mapsto a_{n},\ n\in \mathbb {N} ,a_{n}\in \mathbb {R}$ Nehmen wir jetzt als Beispiel eine Anzahl von Farben: {Rot, Blau, Grün, Blau, Schwarz}. Das ist schon eine Folge, in diesem Fall eine endliche. Könnte man eine unendliche Folge mit den Farben machen? Das ist eher eine physikalische als eine mathematische Frage. Da die Wahrnehmungszellen im Auge vermutlich stufenweise funktionieren (was von Quantenphysik bestimmt wird), wird wahrscheinlich die Antwort zu dieser Frage eher so sein: "Man kann wirklich eine riesige Zahl von Farben definieren, sie wird aber nicht unendlich sein". Das ist nicht der Fall mit Zahlen. Da kann man immer eine unendliche Folge aufbauen. Nehmen wir als Beispiel die Brüche von Fünf. Wir können eine endliche Folge definieren: Die erste 8 Brüche von 5 mit einer positive ganze Zahl als Zähler: $\{{\frac {1}{5}},{\frac {2}{5}},{\frac {3}{5}},{\frac {4}{5}},{\frac {5}{5}},{\frac {6}{5}},{\frac {7}{5}},{\frac {8}{5}}\}$. Wir können auch eine unendliche Folge definieren: Alle Brüche von 5 mit einer positive ganze Zahl als Zähler: $\{{\frac {1}{5}},{\frac {2}{5}},{\frac {3}{5}},{\frac {4}{5}},{\frac {5}{5}},{\frac {6}{5}},{\frac {7}{5}},{\frac {8}{5}},\ ...\}$. Wir können allerdings keine Folge definieren, wenn wir in unsere Definition alle Brüche von 5 benutzen. Das würde dann bedeuten, dass wir alle reelle Zahlen als Zähler benutzen sollen. Für die reellen Zahlen gibt es einen Beweis, dass es nicht möglich ist, sie aufzuzählen. Allein sogar die reellen Zahlen zwischen 0 und 1 lassen sich nicht aufzählen! In diesen Beispielen können wir die Glieder der Folge auch einordnen. Das erste Glied der Folge mit den 5 Farben ist Rot, das zweite Blau usw.. Diese Einordnung ist allerdings willkürlich. Bei der Folge mit den Brüchen kann die Einordnung sowohl willkürlich als auch nach einer Regel sein: willkürlich: $\{{\frac {2}{5}},{\frac {8}{5}},{\frac {3}{5}},{\frac {4}{5}},{\frac {7}{5}},{\frac {1}{5}},{\frac {6}{5}},{\frac {5}{5}}\}$. nach einer Regel (vom kleinsten zum größten): $\{{\frac {1}{5}},{\frac {2}{5}},{\frac {3}{5}},{\frac {4}{5}},{\frac {5}{5}},{\frac {6}{5}},{\frac {7}{5}},{\frac {8}{5}},\ ...\}$. Die arithmetische Folge Eine arithmetische Folge ist eine mathematische Folge, die eingeordnet ist und in der zwei nacheinander folgenden Glieder immer die gleiche Differenz aufweisen. Nehmen wir die erste 8 Brüche von 5 mit einer positive ganze Zahl als Zähler: $\left\{{\frac {1}{5}},{\frac {2}{5}},{\frac {3}{5}},{\frac {4}{5}},{\frac {5}{5}},{\frac {6}{5}},{\frac {7}{5}},{\frac {8}{5}}\right\}$ Die Folge ist eingeordnet und die Differenz zwei einander folgenden Glieder ist immer ${\tfrac {1}{5}}$. Die gleiche Folge können wir auch so schreiben: ${0{,}2\,,0{,}4\,,0{,}6\,,0{,}8\,,1,1{,}2\,,1{,}4\,,1{,}6}$ Eine andere arithmetische Folge kann beispielsweise mit 4,1 anfangen, die Differenz 3,3 aufweisen und unendlich sein: $\{4{,}1\,,\ 7{,}4\,,\ 10{,}7\,,\ ...\}$ Die gleiche Folge können wir auch so schreiben: $\{4{,}1+0\cdot 3{,}3\,,\ 4{,}1+1\cdot 3{,}3\,,\ 4{,}1+2\cdot 3{,}3\,,\ 4{,}1+3\cdot 3{,}3\,,\ \ ...\}$ Wie kann man diese Folgen ohne Auflistung ihrer Elemente definieren? Es gibt dafür zumindest zwei Wege: Jedes Glied als Funktion angeben: $a_{n}=a_{1}+(n-1)\cdot d\quad n\in \mathbb {N} _{*}$ wobei d die Differenz ist. Im Fall einer endlichen Folge muss man auch die Anzahl der Glieder angeben: $a_{n}=a_{1}+(n-1)\cdot d\quad n\in \mathbb {N} _{*},n\leq m$ Das erste Glied und jedes folgende Glied mit einer sogenannten rekursiven Formel angeben: $a_{1}=b,a_{n+1}=a_{n}+d\quad b\in \mathbb {R} ,n\in \mathbb {N} _{*}$ wobei d die Differenz ist. Im Fall einer endlichen Folge muss man auch die Anzahl der Glieder angeben: $a_{1},a_{n+1}=a_{n}+d\quad n\in \mathbb {N} _{*},n\leq m$ Für die Folge mit den 8 Brüchen ist in diesem Sinne die Definition mit einer Formel: $a_{n}={\frac {1}{5}}+(n-1)\cdot {\frac {1}{5}}\quad n\in \mathbb {N} _{*},n\leq 8$ Für die Folge mit 3,3 als Anfangsglied ist in diesem Sinne die Definition mit einer rekursiven Formel: $a_{1}=4{,}1,a_{n+1}=a_{n}+3{,}3\quad n\in \mathbb {N} _{*}$ Die geometrische Folge Eine geometrische Folge ist eine mathematische Folge, die eingeordnet ist und in der zwei nacheinander folgenden Glieder immer den gleichen Quotient aufweisen. Nehmen wir die erste 7 Potenzen von 3 mit einer positive ganze Zahl als Hochzahl: $\{3^{1},\ 3^{2},\ 3^{3},\ 3^{4},\ 3^{5},\ 3^{6},\ 3^{7}\}$ Die Folge ist eingeordnet und der Quotient zwei einander folgenden Glieder ist immer 3. Die gleiche Folge können wir auch so schreiben: $\{3,\ 9,\ 27,\ 81,\ 243,\ 729,\ 2187\}$ Eine andere geometrische Folge kann beispielsweise mit 4 anfangen, den Quotient 1,5 aufweisen und unendlich sein: $\{4,\ 6,\ 9,\ 13{,}5\,,\ 20{,}25\,,\ 30{,}375\,,\ ...\}$ Die gleiche Folge können wir auch so schreiben: $\{4\cdot 1{,}5^{0},\ 4\cdot 1{,}5^{1},\ 4\cdot 1{,}5^{2},\ 4\cdot 1{,}5^{3},\ 4\cdot 1{,}5^{4},\ 4\cdot 1{,}5^{5},\ ...\}$ Wie kann man diese Folgen ohne Auflistung ihrer Elemente definieren? Es gibt dafür zumindest zwei Wege: Jedes Glied als Funktion angeben: $a_{n}=a_{0}\cdot q^{n}\quad n\in \mathbb {N}$ wobei d die Differenz ist. Im Fall einer endlichen Folge muss man auch die Anzahl der Glieder angeben: $a_{n}=a_{0}\cdot q^{n}\quad n\in \mathbb {N} ,n\leq m$ Das erste Glied und jedes folgende Glied mit einer sogenannten rekursiven Formel angeben: $a_{0}=b,a_{n+1}=a_{n}\cdot q\quad b\in \mathbb {R} ,n\in \mathbb {N}$ wobei d die Differenz ist. Im Fall einer endlichen Folge muss man auch die Anzahl der Glieder angeben: $a_{0}=b,a_{n+1}=a_{n}\cdot q\quad b\in \mathbb {R} ,n\in \mathbb {N} ,n\leq m$ Für die Folge mit Quotient 3 ist in diesem Sinne die Definition mit einer Formel: $a_{n}=3\cdot 3^{n}\quad n\in \mathbb {N} ,n\leq 6$ Für die Folge mit Quotient 1,5 ist in diesem Sinne die Definition mit einer rekursiven Formel: $a_{0}=4,a_{n+1}=a_{n}\cdot 1{,}5^{n}\quad n\in \mathbb {N}$ Die Fibonacci Folge und der goldene Schnitt Die Fibonacci Folge ist eine berühmte mathematische Zahlenfolge, die sich leicht(er) durch eine rekursive Formel definieren lässt. Das nächste Glied wird als die Summe der zwei vorherigen Glieder definiert. Die zwei ersten Glieder sind entweder 0 und 1 oder 1 und 1: $(0,)\;1,\;1,\;2,\;3,\;5,\;8,\;$$13,\;21,\;34,\;55,\;89,\;144,\;\ldots$ Die Definition durch eine rekursive Formel lautet daher (wenn wir mit 1 und nicht mit 0 anfangen): $F_{0}=1,\;F_{1}=1\;F_{n+2}$$=F_{n}+F_{n+1}\quad n\in \mathbb {N}$ Das dritte Glied ist daher $F_{2}=F_{0}+F_{1}=1+1=2$, das vierte $F_{3}=F_{1}+F_{2}=1+2=2$, das fünfte $F_{4}=F_{2}+F_{3}=2+3=5$ usw.. Die Folge wurde nach einem berühmten Mathematiker des 11.-12. Jahrhunderts genannt, die Folge war allerdings schon seit langem bekannt. Fibonacci hat die Formel benutzt, um Wachstumsprozesse bei Kaninchen zu beschreiben, dass diese Wachstumsprozesse und andere Vorgänge in der Natur diesem Muster folgen war allerdings auch schon bekannt. Eine interessante Eigenschaft der Folge ist, dass der Quotient zwei nacheinander folgenden Glieder der Folge immer näher zum sogenannten goldenen Schnitt sind. Der goldene Schnitt ist eine Zahl. Wenn man eine Strecke in zwei Teilstrecken so teilt, dass der Quotient der Länge der ganzen Strecke zum größten Teil soviel ist, wie der Quotient des größten Teils zum kleinsten, dann ist dieser Quotient der goldene Schnitt. Seine Wert ist: $\phi ={\frac {1+{\sqrt {5}}}{2}}={\frac {2}{{\sqrt {5}}-1}}$ Man kann also beweisen: $\lim _{n\to \infty }{\frac {F_{n+1}}{F_{n}}}=\phi$ Das ist das gleiche, wie der unendliche Kettenbruch: $\phi =1+{\cfrac {1}{1+{\cfrac {1}{1+{\cfrac {1}{1+{\cfrac {1}{\;\,\ddots }}}}}}}}=[1;{\overline {1}}]$ Fibonacci Zahlen werden oft in Kryptographie benutzt. Allerdings kommen in einer großen Anzahl von Phänomenen vor: In der Natur: Die Blätter (Phyllotaxis) oder Fruchtstände vieler Pflanzen sind in Spiralen angeordnet, wobei die Anzahl dieser Spiralen den Fibonacci-Zahlen entsprechen. Die Fibonacci-Folge beschreibt die Ahnenmenge einer männlichen (n = 1) Honigbiene (Apis mellifera) usw.. In Mathematik: Die Summe in bestimmte Diagonalen im Pascalschen Dreieck sind Fibonacci Folgen usw.. Die eulersche und die Kreiszahl als Folgen Die eulersche Zahl ist die Basis der natürlichen Logarithmen: $\log _{e}x=\ln x$ Kehrwertfunktion ${\tfrac {1}{x}}$ Die Logarithmusfunktion ist das Integral der Kehrwertfunktion $f(x)={\tfrac {1}{x}}$: $\int {\frac {1}{x}}\,dx=\ln x+C$ Dadurch können wir die eulersche Zahl definieren: $\int \limits _{1}^{z}{\frac {1}{x}}\,dx=1\Leftrightarrow z=e$ Also die Fläche zwischen der Kurve ${\tfrac {1}{x}}$ und der x-Achse von 1 bis $z$ ist genau dann gleich 1, wenn z gleich $e$ ist. Für die eulersche Zahl gibt es allerdings noch einige andere Definitionen. Hier ist nur eine begrenzte Anzahl davon: Sie ist der Grenzwert der Folge $a_{n}=\left(1+{\tfrac {1}{n}}\right)^{n}$. $e=\lim _{n\to \infty }\left(1+{\frac {1}{n}}\right)^{n}$ Sie ist so viel wie die unendliche Folgesumme (Reihe) $e=\sum _{k=0}^{\infty }{\frac {1}{k!}}$. Sie lässt sich durch folgende unendliche Kettenbruchentwicklung berechnen ${\frac {1}{e-1}}={\cfrac {1}{1+{\cfrac {2}{2+{\cfrac {3}{3+{\cfrac {4}{\;\,\ddots }}}}}}}}$ Die Kreiszahl lässt sich als der Quotient des Umfangs eines Kreises durch seinen Durchmesser definieren. Die Formeln für die Berechnung der Kreiszahl sind i. d. R. kompliziert. Hier ist nur eine begrenzte Anzahl der einfachsten davon: Sie ist der Grenzwert der folgenden Produktfolge: $\pi =2\cdot {\frac {2}{1}}\cdot {\frac {2}{3}}\cdot {\frac {4}{3}}\cdot {\frac {4}{5}}\cdot {\frac {6}{5}}\cdot {\frac {6}{7}}\cdot {\frac {8}{7}}\cdot {\frac {8}{9}}\cdot \dots =\prod \limits _{i=1}^{\infty }{\frac {(2\,i)^{2}}{i^{2}+2\,i}}$ Ein viertel der Kreiszahl ist der Grenzwert der folgenden Folgesumme (Reihe): $\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{2n+1}}={\frac {1}{1}}-{\frac {1}{3}}+{\frac {1}{5}}-{\frac {1}{7}}+{\frac {1}{9}}\mp \cdots ={\frac {\pi }{4}}$ Sie lässt sich durch das folgende unendliche Produkt berechnen: ${\frac {\sqrt {2}}{2}}\cdot {\frac {\sqrt {2+{\sqrt {2}}}}{2}}\cdot {\frac {\sqrt {2+{\sqrt {2+{\sqrt {2}}}}}}{2}}\cdot \dots ={\frac {2}{\pi }}$ Sie lässt sich durch folgende unendliche Kettenbruchentwicklung berechnen: ${\frac {4}{\pi }}=1+{\frac {1^{2}}{2+\textstyle {\frac {3^{2}}{2+\textstyle {\frac {5^{2}}{2+\textstyle {\frac {7^{2}}{2+\textstyle {\frac {9^{2}}{\;\,\ddots }}}}}}}}}}$