MathemaTriX ⋅ Theorie. Reifeniveau 5
| ||||||||||||||||||
|
Inhalt
Ein-Aus- klappen |
| AUFGABEN | ||||||||||||||
|
Grundrechenarten und Bruchrechnungen
[Bearbeiten]Dieses Kapitel fängt im Grundniveau 1 an und wurde im mittleren Niveau 2 vervollständigt.
Schluss und Prozentrechnung
[Bearbeiten]Dieses Kapitel fängt im Grundniveau 1 an und wurde im mittleren Niveau 3 vervollständigt.
Exponential und Logarithmus Funktion
[Bearbeiten]Arbeiten mit Logarithmen
[Bearbeiten]Rechenregeln zwischen Logarithmen
[Bearbeiten]|
|
Hier ein paar Beispiele der Anwendung dieser Regeln:
- Zerlegen Sie folgende Ausdrücke unter Verwendung der Logarithmusregeln in den möglichst einfachsten Logarithmanden.
Da der ganze Numerus mit einer Hochzahl versehen ist, können wir die zweite Regel benutzen:
Für das, was noch in Klammern bleibt, können wir die vierte und die fünfte Regel benutzen:
Im ersten und im dritten Summand haben wir wieder eine Hochzahl, wir können wieder die zweite Regel benutzen:
Wenn der Numerus eine Summe ist , können wir nichts machen, allerdings ist nach der ersten Regel , daher ist das Ergebnis insgesamt:
.
Benutzen wir die vierte und die fünfte Regel um die Produkte bzw. den Bruch zu zerlegen:
Der Numerus des ersten Summanden ist eine Potenz von 5: . Die Wurzel im Numerus des zweiten und des letzten Summanden kann man als Hochzahl schreiben: und . Daher:
Unter Anwendung der zweiten und der ersten Regel bekommen wir dann:
Mit Anwendung der vierten und der zweiten Regel und Zusammenrechnen bekommen wir schließlich:
- Fassen Sie folgenden Ausdruck unter Verwendung der Logarithmusregeln in einen Logarithmanden.
Nach der ersten Regel ist und nach der zweiten , und . Mit Anwendung der vierten und fünften Regel bekommen wir schließlich;
Beweise der Rechenregeln zwischen Logarithmen
[Bearbeiten]Wenn wir bei einem mathematischen Ausdruck eine Rechnung und ihre Gegenrechnung oder eine Funktion und ihre Umkehrfunktion anwenden, bleibt der Ausdruck unverändert. Hier sind ein paar Beispiele[1]:
Der Logarithmus ist die Gegenfunktion der unabhängigen Variable als "Hochzahl", genauer gesagt, der Exponentialfunktion:
(hier für den natürlichen Logarithmus)
Wenn wir also gleichzeitig Funktion und Umkehrfunktion anwenden, dann bleibt der Ausdruck unverändert. Ersetzen wir also in den letzten Ausdrucken durch bzw. durch :
also
Setzten wir in der letzten Gleichung :
also oder
Allgemeiner bedeutet das:
Der Logarithmus seiner Basis ist 1:
Gehen wir zurück zur vorherigen Formel und Benutzen wir letzteres Ergebnis:
Der Logarithmus einer Potenzzahl ist die Hochzahl dieser Potenzzahl mal den Logarithmus ihrer Basis:
Beweis.
Laut Definition des Logarithmus:
(b für Basis, p für Potenzzahl, h für Hochzahl)
Da ist, können wir in der Gleichung dadurch ersetzten:
Mit anderen Symbolen:
Es gilt:
Mit Hilfe der Definition des Logarithmus können wir auch leicht zeigen, dass der Logarithmus von Null gleich 1 ist (für jede Basis):
Der Logarithmus hat irgendwas mit den Hochzahlen zu tun. Wenn wir zwei Potenzzahlen mit der gleichen Basis multiplizieren, dann ist das Ergebnis eine neue Potenzzahl mit der gleichen Basis und Hochzahl die Summer der Hochzahlen: . Mit dieser Tatsache hat die nächste Regel für Logarithmen zu tun:
Der Logarithmus eines Produkts ist die Summe der Logarithmen der Faktoren:
Beweis. Es gilt:
Entsprechend gilt die Regel für die Division:
Der Logarithmus eines Quotients ist die Differenz der Logarithmen des Zählers und des Nenners:
Beweis. Es gilt:
Für eine Basisänderung des Logarithmus gilt:
Beweis: Es gilt:
- ↑ Es gibt immer wieder Voraussetzungen für diese Regeln, die mit den Definitionsmengen zu tun haben, wir werden sie aber hier nicht erwähnen, damit die Sache nicht zu kompliziert wird.
Exponentialfunktion_Diagramm
[Bearbeiten]
Hier werden wir erkunden, wie sich das Diagramm der allgemeinen Exponentialfunktion ändert, wenn wir sogenannten Parameter der Grundfunktion modifizieren:
Die Parameter a und c haben mit dem y-Achsenabschnitt zu tun. Dieser ist der Wert der Funktion an der Stelle Null:
Der y-Achsenabschnitt der allgemeinen Exponentialfunktion ist die Summe der Parameter a und c.
Den Parameter c können wir von zwei Merkmale sofort erkennen:
|
|
Die Funktion wird durch den Parameter c nach oben (c positiv) oder nach unten (c negativ) verschoben. Daher nähert die Funktion nicht die x-Achse selber an, sondern eine Achse die parallel zur x-Achse ist. Im ersten Bild sehen wir die rote Funktion um 1 nach oben verschoben und die blaue um 1 nach unten (also um −1 verschoben). Daher ist c in der roten 1 (Asymptote: y=1) und in der blauen −1 (Asymptote: y=−1). Im zweiten Bild sehen wir genauer die Verschiebung.
Den Parameter a können wir dann erst herausfinden, wenn wir den Parameter c schon kennen. Wir können dann indirekt mit Hilfe des y-Achsenabschnitts den Parameter a berechnen:
|
|
Im ersten Bild sehen wir die Funktionen (rot) und (blau). Hier sind die c Parameter null. Der y-Achsenabschnitt ist in beiden Fällen genau soviel wie der Parameter a, da der Parameter c null ist. Das ist nicht der Fall im zweiten Bild (nur eine rote Funktion). Hier können wir sehen, dass die Asymptote ist. Der y-Achsenabschnitt E(0) ist . Wir können somit a berechnen:
Da hier b eins ist, lautet die Funktion:
Wenn der Parameter a positiv ist, dann liegen alle Werte der Funktion oberhalb der Asymptote . Das macht Sinn, da eine Potenzzahl immer positiv ist, wenn die Basis (hier z) positiv ist, egal was die Hochzahl (hier r) ist. Wenn aber a negativ ist, dann liegen alle Werte unterhalb der Asymptote, wie in den Bildern hier:
|
|
Im ersten Bild sehen wir die Funktionen (rot) und (blau). Hier sind die c Parameter null. Der y-Achsenabschnitt ist in beiden Fällen genau soviel wie der Parameter a, da der Parameter c null ist. Das ist nicht der Fall im zweiten Bild (nur eine rote Funktion). Hier können wir sehen, dass die Asymptote ist. Der y-Achsenabschnitt E(0) ist . Wir können somit a berechnen:
Da hier der Parameter b eins ist, lautet die Funktion:

Der Parameter b zeigt uns quasi wie "breit" die Funktion ist:
|
|
Im ersten Bild sehen wir die Funktionen (rot) und (blau). Hier sind die c Parameter null und a eins. Der y-Achsenabschnitt ist in beiden Fällen eins. Die rote Funktion ist abrupter als die blaue. Wenn der Parameter b negativ ist, werden diese Funktionen auf der y-Achse gespiegelt, wie im zweiten Bild.
|
|
Um den Parameter b zu berechnen, sollen die Parameter a und c schon bekannt sein. Nehmen wir ein Beispiel, wo wir c und a leicht berechnet können: In diesem Bild können wir den Punkt ziemlich genau ablesen. Wenn wir diese Werte in die Funktion einsetzen, können wir auch den Parameter b durch Umformen berechnen:
Punkt also
Arbeiten mit Termen
[Bearbeiten]Dieses Kapitel fängt im im Grundniveau 1 an und wurde im Reifeniveau 3 vervollständigt.
Zahlendarstellungen Mengentheorie und Aussagenlogik
[Bearbeiten]Mengenlehre
[Bearbeiten]Begriffe der Mengenlehre
[Bearbeiten]Eine Menge ist eine Zusammensetzung aus Objekten, die Elemente der Menge genannt werden. Diese "Objekte" können abstrakt ("Ideen") oder konkret ("Gegenstände") sein. Sie dürfen eine Gemeinsamkeit haben, müssen allerdings nicht[1]. Cantor war einer der erster Mathematiker, die sich mit diesem Begriff genauer befasst haben. Er beschrieb eine Menge „naiv“ als eine Zusammenfassung bestimmter, wohlunterschiedener Objekte unserer Anschauung oder unseres Denkens zu einem Ganzen. Wichtig ist also bei einer Menge, dass man seine Elemente unterscheiden und daher auch aufzählen kann. Die Elemente einer Menge werden in Mathematik innerhalb von geschweiften Klammern geschrieben: .
Es gibt eine besondere Menge, die leere Menge. Man kann sie sich vorstellen wie eine leere Schachtel, die hat keinen Inhalt hat. Das Symbol für die leere Menge ist oder . Es muss klar sein: die Menge ist eine Menge, die die leere Menge beinhaltet und daher selber keine leere Menge mehr.
Wichtige Begriffe, die Beziehungen zwischen Mengen beschreiben, sind die Teilmenge, die Schnittmenge, die Vereinigung, die Differenz und das kartesische Produkt.
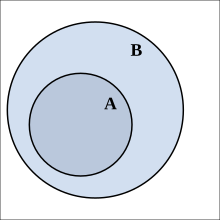
Ein Menge A ist eine Teilmenge einer anderen anderen Menge B, wenn alle Elemente von A auch Elemente von B sind. Das Symbol dafür ist: . Wenn auch gilt, dann sind die Mengen gleich, also jedes Element einer Menge gehört auch der Anderen. In diesem Fall schreibt man: .


Die Schnittmenge von zwei (oder mehrerer) Mengen A und B ist die Menge aller Elemente, die gleichzeitig beiden Mengen gehören. Das Symbol dafür ist: .
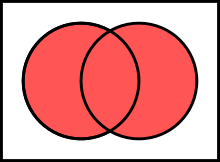

Die Vereinigung von zwei (oder mehrerer) Mengen A und B ist die Menge aller Elemente, die einer der Mengen gehören. Das Symbol dafür ist: .

Die Differenz von zwei Mengen A und B ist die Menge aller Elemente, die zwar zur Menge A gehören aber ohne die Elemente, die doch gleichzeitig zur Menge B gehören. Das Symbol dafür ist: .
Das (kartesische) Produkt zweier Mengen A und B ist die Menge aller Paarelementen, die als erstes Element ein Element von A und als zweites ein Element von B haben. Das Symbol dafür ist: .
- ↑ Man kann trotzdem immer irgendeine Gemeinsamkeit finden: eine Menge von Objekten hat die Gemeinsamkeit, dass sie eben "Objekte" sind.
Mengenlehre Aufgabebeispiel
[Bearbeiten]
Im Diagramm sind mit S1 die Mathematik-StudentInnen gemeint, die Analysis gewählt haben, mit S2 diejenige, die lineare Algebra gewählt haben und mit S3 diejenige, die Zahlentheorie gewählt haben. Die Anzahl der Personen, die durch die weiteren Buchstaben dargestellt werden ist: A=6, B=9, C=13, D=3, E=20, F=33 und G=1.
- Wie viele Personen haben alle drei Fächer gewählt? Beschreiben Sie diese Menge mit Hilfe der Mengen S1, S2 und S3. Beschreiben Sie die gleiche Menge auch mit Hilfe der Mengen A, B, C, D, E, F, G.
- Wie viele Personen haben Analysis oder Zahlentheorie gewählt, ohne lineare Algebra gewählt zu haben? Beschreiben Sie diese Menge mit Hilfe der Mengen S1, S2 und S3. Beschreiben Sie die gleiche Menge auch mit Hilfe der Mengen A, B, C, D, E, F, G.
- Was soll in diesem Zusammenhang bedeuten? Wie viele Personen sind es? Beschreiben Sie die gleiche Menge auch mit Hilfe der Mengen A, B, C, D, E, F, G.
- Was soll in diesem Zusammenhang bedeuten? Wie viele Personen sind es? Beschreiben Sie die gleiche Menge auch mit Hilfe der Mengen A, B, C, D, E, F, G.
- Wie wurden Sie die Menge D mit Hilfe der Mengen S1, S2 und S3 schreiben?
- also 13 Personen.
- also 16 Personen.
- Das sind die Personen, die zumindest eines der beiden Fächer Analysis und lineare Algebra aber doch nicht Zahlentheorie gewählt haben, also . Das sind 56 Personen.
- Das sind die Personen, die gleichzeitig Analysis und Zahlentheorie aber nicht lineare Algebra gewählt haben, also die Menge . Das sind 9 Personen.
Einheiten
[Bearbeiten]Dieses Kapitel fängt im im Grundniveau 2 an und wurde im Reifeniveau 3 vervollständigt.
Statistik und Wahrscheinlichkeitsrechnung
[Bearbeiten]Streumaßen
[Bearbeiten]Streuungsmaßen um den Durchschnitt (um das arithmetische Mittel)
[Bearbeiten]Der Durchschnitt (fachgerecht arithmetisches Mittel genannt) einer Anzahl von Werten ist die Summe dieser Werte durch ihre Anzahl. Nehmen wir zwei einfache Beispiele von Daten und denken wir an einem konkreten Beispiel: Das Gewicht der Personen von zwei Kinder-Teams mit jeweils drei Personen wird gemessen.
Datenreihe 1: 46, 51, 47 (in kg)
Datenreihe 2: 64, 33, 47 (in kg)
Der Durchschnitt (das arithmetische Mittel) in beiden Fällen ist 48 kg. Der Median ist ebenfalls in beiden Fällen gleich (47 kg). Wir merken allerdings, dass zwischen den beiden Verteilungen doch einen Unterschied besteht, der auch durch den Vergleich zwischen Median und Durchschnitt nicht sichtbar wird. In der zweite Verteilung ist der kleinste Wert viel kleiner und der größte viel größer als in der ersten. Für den Vergleich der beiden Verteilungen brauchen wir daher noch etwas, das diesen Unterschied sichtbar macht.
Das einfachste Mittel um diesen Unterschied sichtbar zu machen ist die sogenannte Spannweite. Das ist die Differenz zwischen größten und kleinsten Wert der Verteilung. In der ersten Datenreihe ist die Spannweite 51−46=5 kg, in der zweiten 64−33=31 kg. Der Unterschied zwischen der Spannweiten ist in diesem einfachen Fall groß und aussagekräftig. Es geht aber doch um ein einfaches Beispiel. Für komplexere Beispiele braucht man ein anderes Maß. Dieses ist i. d. R. die sogenannte (empirische) Standardabweichung.

In der ersten Datenreihe ist der Durchschnitt 48. Berechnen wir die Differenz der jeweiligen Werte und des Durchschnitts. Die Differenz des ersten Wertes und des Durchschnitts ist 46−48=−2, die anderen zwei Differenzen sind 51−48=3 und 47−48=−1.
Berechnen wir jetzt die Quadrate dieser Differenzen: (−2)²=4, 3²=9 und (−1)²=1
Somit haben wir die Quadrate der Differenzen der jeweiligen Werte und des Durchschnitts: 4, 4 und 0. Der Durchschnitt ist dann die Summe durch die Anzahl also. Allerdings wird oft aus bestimmten Gründen bei der Berechnung der Varianz besonders bei größeren Datenreihen nicht genau dieser Durchschnitt benutzt, sondern die Summe der Quadrate durch die um eins reduzierte Anzahl n−1 berechnet. Die berechnete Summe der Quadrate wird also nicht durch die Anzahl n dividiert, sondern durch die Anzahl um 1 reduziert (n−1). Als Symbol für die Varianz in diesem Fall wird oft benutzt.
Für die zweite Datenreihe sind die Differenzen: 64−48=16, 33−48=−15 und 47−48=−1. Die Varianz in diesem Fall ist daher:
Für den allgemeinen Fall benutzen wir die Formel:
Erklären wir kurz, was die ganze Symbolik bedeutet: n ist die Anzahl der Werte. Im Nenner steht n−1, es wird also durch die um eins reduzierte Anzahl dividiert. Das Symbol bedeutet Summe. i ist ein Index für den x-Wert, also für einen Wert der Datenreihe. Diese werden von 1 bis n durchnummeriert. Der Strich über das x bedeutet den Durchschnitt der n-Werte, die mit x1, x2, ... , xn dargestellt werden. Der Ausdruck bedeutet daher: Wir berechnen eine Summe, die mit den Werten xi mit i von 1 bis n zu tun hat. Erst durchnummerieren wir diese Werte von 1 bis n (n ist die Anzahl der Werte), also erster Wert , zweiter usw. Für jeden Wert berechnen wir das Quadrat seiner Differenz zum Durchschnitt . Für den ersten Wert ist das , für den zweiten und allgemein . Der Ausdruck kann so abgelesen werden: "Wir berechnen die Differenz jedes Wertes vom Durchschnitt , wir quadrieren die Differenz und am Ende berechnen wir die Summe der Quadrate aller Differenzen, von bis ".
Die (empirische) Standardabweichung lässt sich dann als Wurzel der Formel für die empirischen Varianz berechnen:
In unserem Beispiel sind die Standardabweichungen bzw. . Allein die Tatsache, dass die Standardabweichung die gleichen Einheiten wie die Variable hat (hier kg), im Gegenteil zur Varianz (hier kg²), sollte darauf hinweisen, dass die Standardabweichung ein geeigneteres Instrument als die Varianz für die Beschreibung der Streuung ist.
Wahrscheinlichkeitsverteilungen
[Bearbeiten]Normalverteilung
[Bearbeiten]Definition der Normalverteilung
[Bearbeiten]Wenn wir zufällig irgendeine physikalische Größe in der Natur, beispielsweise die Größe der Personen in einem Ort, messen, werden wir feststellen, dass die Werte etwa "glatt" verlaufen. Damit ist gemeint: es wird mehrere Werte um den Durchschnitt geben und immer weniger, je weiter vom Durchschnitt sich der Wert befindet. Die Verteilung wird etwa viel mehr so: ![]() aussehen und eher nicht so:
aussehen und eher nicht so: ![]() . Das letzte Bild würde im konkreten Beispiel bedeuten, dass es viele kleinen und viele großen Personen gäbe, aber viel weniger die "mittelgroß" wären. So eine Verteilung einer physikalischen Größe wird in der Natur kaum, wenn überhaupt, beobachtet. Je mehrere zufällige Werte vorhanden sind, desto mehr wird die Verteilung zu einer gewisse Kurve neigen, der sogenannten "Normalverteilung":
. Das letzte Bild würde im konkreten Beispiel bedeuten, dass es viele kleinen und viele großen Personen gäbe, aber viel weniger die "mittelgroß" wären. So eine Verteilung einer physikalischen Größe wird in der Natur kaum, wenn überhaupt, beobachtet. Je mehrere zufällige Werte vorhanden sind, desto mehr wird die Verteilung zu einer gewisse Kurve neigen, der sogenannten "Normalverteilung": ![]() . Der erste, der dies beobachtet hat, war Adolph Quetelet im Jahr 1844. Er hat den Brustumfang von mehreren tausend Soldaten gemessen und eine verblüffende Übereinstimmung mit der Normalverteilung festgestellt. Folgendes könnte daher als eine empirische[1] Definition gelten:
. Der erste, der dies beobachtet hat, war Adolph Quetelet im Jahr 1844. Er hat den Brustumfang von mehreren tausend Soldaten gemessen und eine verblüffende Übereinstimmung mit der Normalverteilung festgestellt. Folgendes könnte daher als eine empirische[1] Definition gelten:
Für viele physikalischen Größen gilt, dass ihre Messwerte in der Natur normalverteilt wären, wenn es unendlich viele Werte gäbe.
Die Funktion, die die "Glockenkurve" der Normalverteilung beschreibt, ist selbstverständlich keine lineare und keine Polynomfunktion. Sie ist ziemlich kompliziert und lautet:
ist in dieser Darstellung der Erwartungswert (also der Durchschnitt, der in diesem Fall auch der Median und der Modus ist). ist die Standardabweichung. Der Wert dieser Funktion lässt sich nur annähernd berechnen, daher gibt es für die sogenannte "normierte" Funktion (mit ) entsprechende vorgerechneten Tabellen.
Wie von unserer Beschreibung hier andeuten lässt, war diese Funktion schon lang vor der Entdeckung von Quetelet bekannt. Einige wichtige Wissenschaftler der Mathematik und der Physik haben zu ihrer Entdeckung beigetragen: de Moivre, Poisson, Laplace, Gauß. Die Normalverteilung stellt einen Grenzwert der Binomialverteilung für unendlich viele Proben dar. Als Faustregel für die Anwendung einer Normalverteilung an der Stelle einer Binomialverteilung gilt , wobei n die Anzahl der Versuche und p die entsprechende Wahrscheinlichkeit des entsprechenden Ergebnisses der Binomialverteilung sind. Falls diese Bedingung nicht erfüllt sein sollte, ist die Ungenauigkeit der Näherung immer noch vertretbar, wenn gilt: und zugleich . Eine theoretische Definition der Normalverteilung könnte daher wie im Folgenden lauten:
Die Normalverteilung ist eine Grenzfunktion der Binomialverteilung für unendlich viele Versuche.
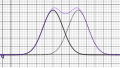
Wenn wir allerdings Messungen eines Merkmals einer Gruppe in der Natur durchführen, müssen wir auf Unterschiede in der Gruppe aufpassen. Es gilt beispielsweise, dass Männer allgemein größer als Frauen sind (durchschnittlich, also nicht alle Männer sind größer als alle Frauen...). Für Männer und für Frauen gibt es dann (zumindest) zwei unterschiedliche Normalverteilungen. Das bedeutet, dass die Verteilung der Größe in der Gesamtbevölkerung doch nicht eine Normalverteilung ist. Die Bilder mit Kombinationen von Normalverteilung hier zeigen das eindeutig.
Die Kombination von Normalverteilungen mit unterschiedlichem Erwartungswert ist keine Normalverteilung mehr.
Um solche Kombinationen zu erkennen gibt es besondere statistische Werkzeuge, die man in einem vertiefenden Studium lernt.
- ↑ empirisch bedeutet "auf die Praxis, die Erfahrung basiert"
Anwendung der Normalverteilung bei gegebenen Erwartungswert und Standardabweichung
[Bearbeiten]Die Normalverteilung ist eine Art Wahrscheinlichkeitsverteilung. Es gibt allerdings einen Grundsätzlichen Unterschied von der Binomialvertielung. Die Binomialverteilung kann durch ein Säulendiagramm dargestellt werden. In diesem Diagramm kann man genau ablesen, wie oft ein gewisser Wert vorkommt. Es gibt in dieser Darstellung sogenannten diskreten Werten. Das bedeutet, dass es beispielsweise die Werte 5 und 6 gibt, ohne dass es einen anderen Werte dazwischen gibt. Die Werte kann man abzählen. Man kann sagen, dass es so und so viele Werte gibt. In der Normalverteilung ist das nicht der Fall. Die Normalverteilung ist eine Grenzfunktion für unendlich viele Werte. Man sagt, dass sie eine "stetige" Funktion ist. Sie ist allerdings ganz symmetrisch, die linke und die rechte Seite sind ein Spiegelbild voneinander. In der Natur sind viele Größen normalverteilt. Wie man die Normalverteilung benutzt, können wir (nur) mit Hilfe eines konkreten Beispiels verstehen.
- Die Größe der männlichen Giraffen ist Normalverteilt mit . Welcher Anteil der Giraffen ist kleiner als 5,62 m?
Um diese Frage zu beantworten, brauchen wir die Standardnormalverteilung. Die Werte einer Normalverteilung können wir nicht genau berechnet. Die Standardnormalverteilung ist die Normalverteilung mit Erwartungswert und Standardabweichung . Für die Standardnormalverteilung wurden die Werte schon gemessen und werden in der folgenden Tabelle[1] angegeben. Mit ihrer Hilfe kann man sagen, welcher Anteil der Werte innerhalb eines gewissen Intervalls liegt.
z \ * 0 1 2 3 4 5 6 7 8 9 0,0* 0,50000 0,50399 0,50798 0,51197 0,51595 0,51994 0,52392 0,52790 0,53188 0,53586 0,1* 0,53983 0,54380 0,54776 0,55172 0,55567 0,55962 0,56356 0,56749 0,57142 0,57535 0,2* 0,57926 0,58317 0,58706 0,59095 0,59483 0,59871 0,60257 0,60642 0,61026 0,61409 0,3* 0,61791 0,62172 0,62552 0,62930 0,63307 0,63683 0,64058 0,64431 0,64803 0,65173 0,4* 0,65542 0,65910 0,66276 0,66640 0,67003 0,67364 0,67724 0,68082 0,68439 0,68793 0,5* 0,69146 0,69497 0,69847 0,70194 0,70540 0,70884 0,71226 0,71566 0,71904 0,72240 0,6* 0,72575 0,72907 0,73237 0,73565 0,73891 0,74215 0,74537 0,74857 0,75175 0,75490 0,7* 0,75804 0,76115 0,76424 0,76730 0,77035 0,77337 0,77637 0,77935 0,78230 0,78524 0,8* 0,78814 0,79103 0,79389 0,79673 0,79955 0,80234 0,80511 0,80785 0,81057 0,81327 0,9* 0,81594 0,81859 0,82121 0,82381 0,82639 0,82894 0,83147 0,83398 0,83646 0,83891 1,0* 0,84134 0,84375 0,84614 0,84849 0,85083 0,85314 0,85543 0,85769 0,85993 0,86214 1,1* 0,86433 0,86650 0,86864 0,87076 0,87286 0,87493 0,87698 0,87900 0,88100 0,88298 1,2* 0,88493 0,88686 0,88877 0,89065 0,89251 0,89435 0,89617 0,89796 0,89973 0,90147 1,3* 0,90320 0,90490 0,90658 0,90824 0,90988 0,91149 0,91309 0,91466 0,91621 0,91774 1,4* 0,91924 0,92073 0,92220 0,92364 0,92507 0,92647 0,92785 0,92922 0,93056 0,93189 1,5* 0,93319 0,93448 0,93574 0,93699 0,93822 0,93943 0,94062 0,94179 0,94295 0,94408 1,6* 0,94520 0,94630 0,94738 0,94845 0,94950 0,95053 0,95154 0,95254 0,95352 0,95449 1,7* 0,95543 0,95637 0,95728 0,95818 0,95907 0,95994 0,96080 0,96164 0,96246 0,96327 1,8* 0,96407 0,96485 0,96562 0,96638 0,96712 0,96784 0,96856 0,96926 0,96995 0,97062 1,9* 0,97128 0,97193 0,97257 0,97320 0,97381 0,97441 0,97500 0,97558 0,97615 0,97670 2,0* 0,97725 0,97778 0,97831 0,97882 0,97932 0,97982 0,98030 0,98077 0,98124 0,98169 2,1* 0,98214 0,98257 0,98300 0,98341 0,98382 0,98422 0,98461 0,98500 0,98537 0,98574 2,2* 0,98610 0,98645 0,98679 0,98713 0,98745 0,98778 0,98809 0,98840 0,98870 0,98899 2,3* 0,98928 0,98956 0,98983 0,99010 0,99036 0,99061 0,99086 0,99111 0,99134 0,99158 2,4* 0,99180 0,99202 0,99224 0,99245 0,99266 0,99286 0,99305 0,99324 0,99343 0,99361 2,5* 0,99379 0,99396 0,99413 0,99430 0,99446 0,99461 0,99477 0,99492 0,99506 0,99520 2,6* 0,99534 0,99547 0,99560 0,99573 0,99585 0,99598 0,99609 0,99621 0,99632 0,99643 2,7* 0,99653 0,99664 0,99674 0,99683 0,99693 0,99702 0,99711 0,99720 0,99728 0,99736 2,8* 0,99744 0,99752 0,99760 0,99767 0,99774 0,99781 0,99788 0,99795 0,99801 0,99807 2,9* 0,99813 0,99819 0,99825 0,99831 0,99836 0,99841 0,99846 0,99851 0,99856 0,99861 3,0* 0,99865 0,99869 0,99874 0,99878 0,99882 0,99886 0,99889 0,99893 0,99896 0,99900 3,1* 0,99903 0,99906 0,99910 0,99913 0,99916 0,99918 0,99921 0,99924 0,99926 0,99929 3,2* 0,99931 0,99934 0,99936 0,99938 0,99940 0,99942 0,99944 0,99946 0,99948 0,99950 3,3* 0,99952 0,99953 0,99955 0,99957 0,99958 0,99960 0,99961 0,99962 0,99964 0,99965 3,4* 0,99966 0,99968 0,99969 0,99970 0,99971 0,99972 0,99973 0,99974 0,99975 0,99976 3,5* 0,99977 0,99978 0,99978 0,99979 0,99980 0,99981 0,99981 0,99982 0,99983 0,99983 3,6* 0,99984 0,99985 0,99985 0,99986 0,99986 0,99987 0,99987 0,99988 0,99988 0,99989 3,7* 0,99989 0,99990 0,99990 0,99990 0,99991 0,99991 0,99992 0,99992 0,99992 0,99992 3,8* 0,99993 0,99993 0,99993 0,99994 0,99994 0,99994 0,99994 0,99995 0,99995 0,99995 3,9* 0,99995 0,99995 0,99996 0,99996 0,99996 0,99996 0,99996 0,99996 0,99997 0,99997 4,0* 0,99997 0,99997 0,99997 0,99997 0,99997 0,99997 0,99998 0,99998 0,99998 0,99998
- Anmerkung: Negative Werte werden aus Gründen der Symmetrie nicht angegeben, weil ist.
Das Symbol "z" zeigt uns hier das Wie-viel-fache der Standardabweichung oberhalb des Erwartungswerts. Die Zeilen zeigen uns das Vielfache bis zur ersten Nachkommastelle, die Spalten geben die zweite Nachkommastelle an. Nehmen wir die vierte Zeile. Hier steht am Anfang links 0,3*. Das Symbol * wird durch die Zahl an der Spalte ersetzt. Nehmen wir die 6-ste Spalte, da oben steht 5. Das Symbol * wird also durch 5 ersetzt. In 0,3* ersetzten wir also * durch 5, dann haben wir 0,35. An dieser Stelle (4-te Zeile, 6-ste Spalte) steht die Zahl 0,63683. Das bedeutet: von Anfang an der Normalverteilung (also von ganz links) bis 0,35 mal die Standardabweichung rechts vom Erwartungswert haben wir 0,63683 aller Fälle (also 63,683%).
Schauen wir jetzt unsere Frage an. Der Erwartungswert ist 5,20 m, die Standardabweichung 0,25 m und es wird der Anteil bis 5,62 m gefragt. 5,62 ist 0,42 (5,62−5,20=0,42) oberhalb des Erwartungswert, also 1,68 mal die Standardabweichung (0,42:0,25=1,68). Die Zweite Nachkommastelle in 1,68 ist 8 und wir werden die entsprechende Spalte in der Tabelle benutzen. In der Tabelle ist 1,6 die 17-te Zeile und 8 die 9-te Spalte. Also das 1,68-fache der Standardabweichung befindet sich an der 17-te Zeile und 9-te Spalte. Da steht die Zahl 0,95352. Das bedeutet: bis 5,62 m Größe haben wir 0,95352 also 95,352 % aller Giraffen. Somit haben wir die Frage beantwortet.
Was ist jetzt, wenn der Grenzwert kleiner als der Erwartungswert ist? In diesem Fall nutzen wir die Symmetrie der Funktion aus, die als Folgerung die Formel, die direkt unterhalb der Tabelle steht, hat:
Wenn in unserem Beispiel der Anteil bis 5,04 m Größe gefragt wird, berechnen wir erst die Differenz vom Erwartungswert, wie vorher: 5,20−5,04=0,16. Das ist das (0,16:0,25=) 0,64-fache der Standardabweichung. 0,6 ist die 7-te Zeile, 4 ist die 5-te Spalte, an dieser Stelle steht 0,73891, also 73,891 %. Das ist allerdings das Ergebnis, wenn wir oberhalb des Erwartungswertes wären. Um den Anteil bis 0,64 mal die Standardabweichung unterhalb des Erwartungswertes müssen wir einfach diese Zahl aus 1 subtrahieren: 1−0,73891=0,26109 also 26,109 % aller Werte befinden sich zur Größe 5,04 m.
Wenn die Frage zwischen zwei Werte ist, dann müssen wir die entsprechenden Anteile einfach subtrahieren. In unserem Beispiel, wenn der Anteil der Giraffen zwischen 5,04 und 5,62 gefragt ist, dann ist es 0,95352−0,26109= 0,69243 also 69,243 %.
- ↑ Tabelle wurde vom Wikibook Statistik übernommen, und das wiederum von Wikipedia
Anwendung der Normalverteilung bei gegebenen Grenzwerten
[Bearbeiten]*Eine Bäckerei produziert Baguettes. Auf der Verpackung steht 450 g. Die Standardabweichung der Masse bei der Produktion ist 12 g. Wie viel muss der Erwartungswert sein, damit weniger als 3,5 % der Produktion unterhalb von 450 g bleibt?
In diesem Fall arbeiten wir erst mit dem Prozentsatz. Da ein Prozentsatz unterhalb des Erwartungswert gegeben ist (3,5%=0,035) und die Tabelle nur Anteile oberhalb dieses Wertes angibt, benutzen wir die Gleichung . Wir suchen daher in der Tabelle 1−0,035=0,965. An der 19. Zeile (1,8*) finden wir an der zweiten und an der dritten Spalte die Werte 0,96485 bzw. 0,96562. Von den beiden Werte ist 0,96485 näher zur 0,965 (0,965−0,96485=0,00015 und 0,96562−0,965=0,00062). Daher nehmen wir mit einer gute Annäherung die zweite Spalte (also die zweite Nachkommastelle wird 1 sein). Der gesuchte Wert wird daher 1,81 mal die Standardabweichung oberhalb des Grenzwertes liegen müssen, damit die Voraussetzung erfüllt werden kann. Das ist dann 1,81·12=21,72≈22 g. Der Erwartungswert muss daher bei ca. 472 g liegen.
- Wie viel muss die Standardabweichung (also die "Genauigkeit" der Produktionsmaschine) sein, damit 94 % aller Baguettes mehr als 452 g sind, wenn der Erwartungswert 483 g ist?
In der Tabelle steht 94 % (also 0,94) an der 16. Zeile zwischen 6. und 7. Spalte. Näher zu 0,94 ist der Wert an der 6. Spalte (0,94−0,93943=0,00057 und 0,94062−0,94=0,00062). Der Abstand zum Erwartungswert muss daher 1,55 mal die Standardabweichung sein. Der tatsächliche Abstand zwischen Grenz- und Erwartungswert ist 483−452=21 g. Das muss ca. das 1,55-fache der Standardabweichung sein, daher soll die Standardabweichung höchstens 13,55 g sein (21:1,55). Vorsichtig sollen wir hier beim Runden sein. 13,55 ist gerundet 14 g, das wäre allerdings oberhalb der Grenze, daher müssen wir doch auf 13 g abrunden.
Geometrische Konstruktionen
[Bearbeiten]Dieses Kapitel fängt im Grundniveau 2 an und wurde im mittleren Niveau 3 vervollständigt.
Geometrie der Ebene
[Bearbeiten]Dieses Kapitel fängt im Grundniveau 2 an und wurde im mittleren Niveau 2 vervollständigt.
Geometrie des Raums
[Bearbeiten]Dieses Kapitel ist nur im mittleren Niveau 3 behandelt.
Diagramme
[Bearbeiten]Boxplot
[Bearbeiten]Streuungsmaßen um den Median (den Zentralwert)
[Bearbeiten]Die Spannweite, also die Differenz zwischen größten und kleinsten Wert ist ein Streuungsmaß auch im Fall des Medians. Ein anderes Maß ist in diesem Fall der Interquartilsabstand (Symbol IQR). Median ist der Wert in der Mitte der geordneten Werte. Wenn wir den ersten viertel der geordneten Werte nehmen, dann ist der Wert am oberen Rand das untere (erste) Quartil. Am oberen Rand der ersten drei Viertel befindet sich das obere (dritte) Quartil[1]. Die Differenz der Werte des oberen und des unteren Quartils ist der Interquartilsabstand.
All diese Sachen können wir in einem sogenannten Boxplot Diagramm darstellen[2]. Das folgende Beispiel beruht auf einer Messreihe mit den folgenden 20 Datenpunkten:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | |
| (unsortiert) | 9 | 6 | 7 | 7 | 3 | 9 | 10 | 1 | 8 | 7 | 9 | 9 | 8 | 10 | 5 | 10 | 10 | 9 | 10 | 8 |
| (sortiert) | 1 | 3 | 5 | 6 | 7 | 7 | 7 | 8 | 8 | 8 | 9 | 9 | 9 | 9 | 9 | 10 | 10 | 10 | 10 | 10 |

Ein Box-Plot hilft dabei sehr schnell einen Überblick über diese Daten zu erhalten. So erkennt man direkt, dass der Median (durchgezogene Linie) genau bei 8,5 liegt und dass je 25 % der Daten unter 7 und über 9,5 liegen, denn dies sind genau die Abmessungen der Box (die "Schachtel" in der Mitte), in der 50 % der Messwerte enthalten sind. Folglich ist auch der Interquartilsabstand, der der Länge der Box entspricht, genau 2,5 (also 9,5−7).
Dieser Box-Plot wurde mit Whiskern [3] bis zu einer Länge des 1,5-fachen Interquartilsabstands erstellt. Diese sind also maximal 3,75 Maßeinheiten lang. Allerdings reichen Whisker stets nur bis zu einem Wert aus den Daten, der sich noch innerhalb dieser 3,75 Einheiten befindet. Der obere Whisker verläuft also nur bis zu 10, da es keinen größeren Wert in den Daten gibt, und der untere Whisker nur bis 5, da der nächstkleinere Wert weiter als 3,75 vom Anfang der Box entfernt ist.
Die Werte von 1 und 3 werden im Box-Plot als Ausreißer markiert, da sie sich nicht innerhalb der Box oder der Whisker befinden. Bei diesen Werten sollte untersucht werden, ob es sich tatsächlich um Ausreißer oder um Tippfehler oder anderweitig auffällige Werte handelt.
- ↑ (als zweite (mittlere) Quartil ist der Median gemeint)
- ↑ Folgender Teil wurde fast ohne Änderungen von wikipedia übernommen.
- ↑ auch "Antennen" genannt, das sind die Strecken bei den Werten 5 und 10 oben und unten vom "Box" im Boxplot
Funktionen
[Bearbeiten]Die quadratische Funktion
[Bearbeiten]Quadratische Funktion Vertiefung
[Bearbeiten]Quadratische Ergänzung
[Bearbeiten]| Eine Funktion der Form wird quadratische Funktion genannt. Ihre Lösungen |
| Der Ausdruck unter der Wurzel wird Diskriminante genannt. |
| Wenn die Diskriminante positiv ist, hat die Funktion zwei Lösungen, wenn null dann eine Lösung und wenn negativ |
Um zu zeigen, warum die Lösungen der quadratischen Funktion durch die angegebene Formel gegeben werden, können wir die sogenannte "quadratische Ergänzung" benutzen.
Um zu verstehen, wie die quadratische Ergänzung funktioniert, nehmen wir ein Beispiel:
Das ist eine quadratische Gleichung aber noch nicht in der allgemeinen Form ax²+bx+c=0. Bringen wir diese Gleichung in diese Form:
Das ist eine quadratische Gleichung mit , und . Obwohl 16 eine Quadratzahl ist, ist ist keine binomische Formel (es sollte sein, also 8 statt 10). Wie kann man jetzt die Lösungen der quadratischen Gleichung finden?
Um das zu finden, machen wir in den vorherigen Rechnungen zwei Schritte zurück.
Letzteres ist doch eine binomische Formel, die plus-minus Formel:
Anstatt haben wir hier , also an der Stelle von ist . Anstatt haben wir 9, also an der Stelle von ist 3 . Es gilt daher:
also oder
Es gibt hier zwei Lösungen, −8 und −2. Es ist leicht festzustellen: Werden die Klammer ausmultipliziert, ergibt sich den quadratischen Term am Anfang:
Um die allgemeine Lösung der abstrakten Gleichung zu finden, werden die hier vorgeführten Schritte durchgeführt, diesmal allerdings mit Symbolen und nicht mit konkreten Zahlen.
Im konkreten Beispiel war der erster Schritt, den Ausdruck zu einer Plus-Minus binomischen Formel umzuwandeln. Wir haben 9 addiert und subtrahiert und dadurch ist eine Differenz von zwei Ausdrucken ( und 9) entstanden: . 5 in ist die Hälfte von 10 in . 10 steht in der allgemeinen Gleichung für b, wir müssen also die Hälfte von b (wie die Hälfte von 10) benutzen:
Wir müssen allerdings die linke Seite der Gleichung mit multiplizieren, damit zumindest die Koeffizient von stimmt. Somit bekommen wir auf der linken Seite folgenden Ausdruck:
, was gleich mit ist.
Jetzt aber stimmt die zweite Koeffizient (von x ohne Quadrat) der allgemeinen Gleichung nicht mehr (sie sollte einfach sein und nicht ). Damit sie auch stimmt, muss im Klammerausdruck an der Stelle von der Ausdruck benutzt werden. Somit haben wir insgesamt:
Bisher haben wir es super geschafft! Wir haben die richtige Koeffizient für und für . Der letzte Schritt ist einfach, da wir "nur" noch am Ende c brauchen:
also ( herausheben)
Wir haben schon die plus-minus binomsiche Formel, was eindeutig wird, wenn wir die zweite Klammer rechts als Quadrat einer Wurzel schreiben:
Der Vorgang, den wir hier vorgeführt haben, wird quadratische Ergänzung genannt.
Lösungsformel der quadratischen Gleichung
[Bearbeiten]Mit Hilfe der quadratischen Ergänzung kann man zeigen, dass:
Die allgemeine quadratische Gleichung kann man daher auch als eine plus-minus binomische Formel schreiben:
Wenn wir die binomische Formel in ihrer Produktform schreiben, bekommen wir:
Ein Produkt ist gleich Null, wenn (zumindest) einer der Faktoren null ist, also hier wenn:
- . Das kann aber nicht gelten, da wir in diesem Fall keine quadratische Funktion haben.
- also
oder wenn:
- also
Die zwei Lösungen können wir mit einem Index versehen und sie zusammengefasst schreiben:
Somit können wir die Formel für die Lösungen einer quadratischen Gleichung (und ihrer entsprechenden quadratischen Funktion) mit Hilfe der quadratischen Ergänzung und der plus-minus binomischen Formel finden.
Scheitelpunkt einer quadratischen Funktion
[Bearbeiten]
Die allgemeine quadratische Funktion kann man daher auch als eine plus-minus binomische Formel schreiben:
Nehmen wir an, dass eine positive Zahl ist. Betrachten wir diese Formel genauer, stellen wir fest, dass sie dann ihren kleinsten Wert annimmt, wenn die erste Klammer null ist. Dass liegt daran, dass die erste Klammer ein Quadrat ist und ihr kleinster Wert nur null sein kann (da das Quadrat einer Zahl nie negativ ist). Die erste Klammer ist auch die einzige, die veränderbar ist, da sie die unabhängige Variable beinhaltet. Wir können dann leicht finden, an welche Stelle das stattfindet und wie viel der Wert der Funktion dann ist:
In diesem Fall ist und daher:
Somit haben wir den Punkt:
So ein Punkt wird Extrempunkt genannt. Wenn positiv ist, ist er ein Minimum, wenn negativ ein Maximum. Die entsprechende Stelle wird Extremstelle genannt.
Die Extremstelle der quadratischen Funktion können wir viel leichter mit Hilfe der ersten Ableitung finden (ohne die quadratische Ergänzung zu benutzen). Da wo die Funktion eine Extremstelle hat, wird sie ihre Richtung im Diagramm ändern. Wäre sie vorher steigend, wird sie dann fallend sein und umgekehrt. Genau am Punkt der Änderung wird sie weder steigend noch fallend sein. Die Steigung also die Ableitung wird null sein, die Tangente der Funktion wird parallel zur x-Achse sein. Um die Stelle zu finden können wir daher die erste Ableitung gleich null setzen. Die erste Ableitung allgemein ist:
Setzen wir diese Ableitung gleich null, ergibt sich:
Wenn wir diesen Wert von in der Funktion einsetzten, bekommen wir nach ein paar Berechnungen den entsprechenden Wert der Funktion:
Der Extrempunkt ist daher (wie es zu erwarten war) wieder:
Quadratische Gleichung Textaufgaben
[Bearbeiten]Lineare Gleichungssysteme
[Bearbeiten]Dieses Kapitel fängt im im Grundniveau 3 an und wurde im Reifeniveau 4 vervollständigt.
Trigonometrische Funktionen
[Bearbeiten]Sinus und Kosinussatz
[Bearbeiten]Beweis des Sinussatzes
[Bearbeiten]Der Sinussatz besagt, dass in jedem Dreieck die Verhältnisse der Sinusse seiner Winkeln zur entsprechenden gegenüberliegenden Seiten gleich zueinander sind:
Selbstverständlich gilt der Satz auch für die Kehrwerte:
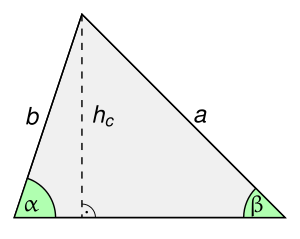
Um den Satz für zwei zufällige Winkel des Dreiecks zu beweisen, reicht es eine Höhe (im Bild die Höhe ) des Dreiecks einzuzeichnen.[1] Diese Höhe zerlegt das Dreieck in zwei rechtwinklige Teildreiecke, in denen man den Sinus von und jeweils als Quotient von Gegenkathete und Hypotenuse ausdrücken kann, nach der Definition von Sinus:
Auflösen nach ergibt:
Durch Gleichsetzen erhält man demnach
Dividiert man nun durch , so erhält man den ersten Teil der Behauptung:
Die Gleichheit mit ergibt sich entsprechend durch Benutzung der Höhe oder .
Beweis des Kosinussatzes
[Bearbeiten]Der Kosinussatz ist eine Verallgemeinerung des Satzes von Pythagoras auf alle Dreiecke. Der besagt, dass das Quadrat von jeder Seite eines zufälligen Dreiecks gleich die Differenz der Summe der Quadrate der anderen zwei Seiten minus das zweifache des Produktes dieser Seiten und des Kosinus der dazwischen liegenden Winkel ist:
Da die Seite c zufällig ausgewählt wird, gilt der Satz auch für die anderen zwei Seiten:
Im folgenden Beweis wird vorausgesetzt.

In den Teildreiecken soll der Satz des Pythagoras angewandt werden, um einen Rechenausdruck für zu finden. Wir zeichnen wieder die Höhe ein. Für das rechte (rechtwinkelige) Dreieck gilt laut Satz von Pythagoras:
Die Seite wird allerdings in der Figur in zwei Teile zerlegt, es gilt daher
Für das linke (auch rechtwinkelige) Dreieck gilt daher:
(nach der binomischen Formel)
Kombinieren wir diese drei Gleichungen, ergibt sich für :
Zusätzlich gilt laut Definition des Kosinus:
Wenn wir dieses Ergebnis in die letzten Gleichung für einsetzten, ergibt sich der Kosinussatz:
Für muss der Beweis geringfügig modifiziert werden. Für ergibt sich der Kosinussatz direkt aus dem Satz des Pythagoras.
Direkte Anwendung des Sinus und des Kosinussatzes
[Bearbeiten]
- Berechnen sie die Diagonalen des abgebildeten Deltoids, wenn die Seite 4,3 cm, die Seite 7,6 cm und der dazwischen liegende Winkel 134° sind.
Mit direkter Anwendung des Kosinussatzes können wir die Diagonale sofort berechnen:
Mit Hilfe des Sinussatzes können wir dann den Winkel berechnen:
Dann können wir auch die andere Diagonale mit Hilfe der Definition von Sinus berechnen:
Trigonometrische Funktionen Diagramm
[Bearbeiten]Parameter im Diagramm der Sinusfunktion
[Bearbeiten]
Hier werden wir erkunden, wie sich das Diagramm der Sinusfunktion ändert, wenn wir sogenannten Parameter der Grundfunktion modifizieren. Allgemein (mit solchen Parametern) ist die Formel für die Sinusfunktion (genauer gesagt: für eine Wellenfunktion in der Mechanik):

ist die sogenannte Amplitude. Sie zeigt uns wie weit nach oben und nach unten der Wert der Funktion schwankt. Sinus (und Kosinus) nehmen Werte zwischen 1 und −1. Das können wir mit Hilfe des Einheitskreises sofort sehen. Wenn wir Sinus mit multiplizieren (und nichts anderes machen) wird die Funktion Werte zwischen und aufnehmen. Im Bild ist (schwarz, Amplitude ), (blau, Amplitude ), (rot, Amplitude ), (grün, Amplitude ).

ist die sogenannte Winkelfrequenz. Sie zeigt uns wie oft innerhalb eines Intervalls des x-Wertes von der y-Wert wieder seinen Anfangswert bekommt. Zwischen Winkelfrequenz und Frequenz gilt: . Der Kehrwert der Frequenz ist die Periode: . Daher gilt auch: . Sinus (und Kosinus) nehmen wiederholt Werte zwischen 1 und −1. Die Periode zeigt uns, nach welcher Änderung des x-Wertes der Wert der Funktion (y-Wert) wieder der gleiche sein wird. Ist (und daher ), dann kommt die Welle im Diagramm öfters vor. Im Bild ist (schwarz, Winkelfrequenz , Periode , Intervall ), (blau, Winkelfrequenz , Periode ), (rot, Winkelfrequenz , Periode .

ist die sogenannte Phase. Sie zeigt uns an welcher Stelle die Funktion "anfängt". Die Sinusfunktion fängt normalerweise mit null und steigend an. Wenn die Phase nicht null ist, dann ist der Wert der Funktion null (und die Funktion steigend) bei . Im Bild ist (schwarz, Phase ), (rot, Phase , der Wert der Funktion ist 0 bei ), (blau, Phase , der Wert der Funktion ist 0 bei .

ist eine Konstante, die das ganze Diagramm nach oben ( positiv) oder nach unten ( negativ) verschiebt. Im Bild ist (schwarz, ), (rot, , Funktion um 0,8 senkrecht nach oben verschoben), (blau, , Funktion um 1,4 senkrecht nach unten verschoben).

Hier sehen wir ein Beispiel, wo alles kombiniert wird. Die Funktion nimmt Werte von −3 bis 1,4. Die gesamte Schwankung (das doppelte der Amplitude) ist daher 4,4 und die Amplitude selber . Die Funktion ist allerdings nach unten verschoben, die Werte schwanken um den Wert −0,8, daher ist die Konstante . Die Phase zu finden ist in diesem Fall ein bisschen komplizierter. Da die Funktion nach unten verschoben ist, müssen wir den Anfang etwas nach unten (bei −0,8) suchen. Dann können wir entdecken, dass der "Anfang" an der Stelle −0,5 ist, daher ist die Phase +0,5. Die rote Funktion lautet daher:
Vektoren
[Bearbeiten]Vektorielle und skalare Größen
[Bearbeiten]Die Größen, die bei ihrer vollständigen Beschreibung auch die Angabe einer Richtung brauchen, nennt man Vektoren. Solche vektrorielle Größen sind die Strecke, die Geschwindigkeit, die Beschleunigung und die Kraft.
Die Größen ohne Richtung im Raum, wie die Zeit, die Masse, die Energie, die Arbeit, die Leistung und den Wirkungsgrad, nennt man Skalare.
Vektor und Punkt
[Bearbeiten]

Ein Punkt ist zwar eine Konstruktion der Phantasie, man kann ihn aber doch in einem Koordinatensystem darstellen. Die Schreibweise eines Punktes mit den Koordinaten und ist oder auch , wobei immer erst die x- und dann die y-Koordinate geschrieben wird. Oft schreibt man auch Strichpunkte (Semikolons) anstelle der Kommata, um Missverständnisse mit Dezimalzahlen zu vermeiden. Um die Position des Punktes im Koordinatensystem zu finden, geht man aus dem Koordinatenursprung rechts so oft wie der x-Wert (links, wenn der x-Wert negativ ist) und nach oben so oft wie der y-Wert (nach unten, wenn der y-Wert negativ ist) angibt. Im Bild 1 z. B. sieht man den Punkt , also 5 Einheiten rechts vom und 3 Einheiten oberhalb des Ursprungs und den Punkt , also 4 Einheiten links (weil der x-Wert negativ ist, also -4) und 2 Einheiten oberhalb. Den idealen dimensionslosen Punkt stellt man im Koordinatensystem eben mit einem Punkt, der doch Dimensionen hat, also mit einem kleinen Kreis oder manchmal auch mit einem kleinen Rhobus usw. dar. Für Punkte im Raum (drei Dimensionen) schreibt man drei Zahlen nebeneinander, die der Reihe nach die x-, y- und z-Koordinate angeben: oder auch .


Ein Vektor ist ein Pfeil im Raum. Einen Vektor schreibt man als Zahlen nebeneinander oder untereinander , wobei wieder erst (links bzw. oben) die x- und dann (rechts bzw. unten) die y-Koordinate geschrieben wird. Der Unterschied in der Schreibweise zum Punkt ist, dass man in der Regel für Punkte einen großen und für Vektoren einen kleinen Buchstabe mit einem Pfeil darüber benutzt, das ist aber nicht immer so.
Im Bild 2 fängt der Vektor am Punkt an. Man geht 3 Einheiten rechts und 4 nach oben (wie bei einem Punkt) und man gelangt an den Punkt . Der Pfeil fängt also am Punkt an und endet am Punkt . Wenn wir vom Punkt P2 den Punkt P1 subtrahieren, wenn wir also die x-Koordinate des Punkts P1 (1) aus der x-Koordinate des Punkts P2 (4) subtrahieren (4-1=3) bekommen wir die x-Koordinate des Vektors zwischen P1 und P2. Wenn wir die y-Koordinate des Punkts P1 (2) aus der y-Koordinate des Punkts P2 (6) subtrahieren (6-2=4) bekommen wir die y-Koordinate des Vektors zwischen P1 und P2 (4). Dieser Vektor ist tatsächlich der Vektor .

Ein Vektor ist aber in der Regel nicht an einem Punkt gebunden. Im Bild 3 wurde der Vektor v verschoben, er fängt am Punkt an und endet am Punkt . Wenn wir hier wieder die entsprechenden Koordinaten der Punkte P4 und P3 subtrahieren, also 2-(-1)=3 für die x-Koordinate und 3-(-1)=4 für die y-Koordinate, bekommen wieder den Vektor .

Im Bild 4 sieht man, dass tatsächlich zwischen den Punkten P1 und P2 einerseits und den Punkten P3 und P4 andererseits der gleiche Vektor v liegt.
Einen Punkt kann man auch mit sogenannten Ortsvektoren darstellen. Diese sind zwar als Vektoren dargestellt sind aber doch an einem Punkt, nämlich den Koordinatenursprung, gebunden, wie im Bild 5.
Der Unterschied also zwischen Punkt und Vektor ist:
Ein Punkt ist an den Koordinatenursprung gebunden, ein Vektor ist nicht unbedingt an einen Punkt gebunden.
Vektoraddition
[Bearbeiten]
Wenn wir zwei Vektoren addieren wollen, addieren wir die x-Koordinate des ersten Vektors zur x-Koordinate des zweiten. So bekommen wir die x-Koordinate der Summe der beiden Vektoren. Dann addieren wir die y-Koordinate des ersten Vektors zur y-Koordinate des zweiten. So bekommen wir die y-Koordinate der Summe der beiden Vektoren.
Im Bild 1 fängt der Vektor u beim Koordinatenursprung und endet 4 Einheiten rechts (x-Koordinate) und 6 nach oben (y-Koordinate) also ist . Der Vektor v fängt am Punkt (4|6) und endet 1 Einheit nach rechts und drei nach unten, am Punkt (5|3), also ist . Wenn wir einerseits die x-Koordinate des Vektors u zur x-Koordinate des Vektors v addieren (4+1=5) und andererseits die y-Koordinate des Vektors u zur y-Koordinate des Vektors v (6-3=3), bekommen wir die entsprechenden Koordinaten der Summe der Vektoren u+v, also ist .


Wenn jemand jetzt aus dem Vektor u den Vektor v subtrahieren will, dann soll man zum Vektor u den Gegenvektor von nämlich den Vektor addieren. Dass der Vektor tatsächlich der Gegenvektor von v ist, kann man im Bild 2 klar sehen (gleicher Vektor in die Gegenrichtung). Das Ergebnis w von u-v sieht man im Bild 3. Tatsächlich ist die x-Koordinate von w die x-Koordinate von u minus die x-Koordinate von v (4-1=3) und die y-Koordinate von w die x-Koordinate von u minus die y-Koordinate von v (6-(-3)=9).


Rein theoretisch könnte man Vektoren ohne Koordinatensystem darstellen und subtrahieren (Bild 4,5: ) oder addieren (Bild 6), in diesem Fall ist es aber nicht klar, welche die x und welche die y Richtung ist und vor allem, welche die Einheit ist! Daher ist es immer notwendig ein Koordinatensystem anzugeben.


Um Vektoren zu addieren, kann man auch ein Parallelogramm benutzen, wie im Bild 7. Dieser Vorgang ist aber aufwendiger, wenn man mehrere Vektoren addieren bzw. subtrahieren will (wie im Bild 6).
Vektor mit Zahl multiplizieren
[Bearbeiten]



Man kann einen Vektor mit einer Zahl multiplizieren. In den Bildern 1 und 2 sieht man das Doppelte bzw. das Dreifache eines Vektors, obwohl hier keine Einheiten oder Achsen gegeben sind. Im Bild 3 sieht man sowohl das Doppelte als auch den Gegenvektor .
Wie multipliziert man eine Zahl mit einem Vektor rechnerisch? Man multipliziert jede Koordinate des Vektors mit der Zahl. Wie man im Bild 4 ablesen kann, ist der Vektor durch die Koordinaten des Vektors je multipliziert mit -1:
Für den Vektor multipliziert man jede Koordinate des Vektors mit 2:
Entsprechend ist es bei den anderen Vektoren:
In der Physik gibt es zwei Arten von Größen: Skalare (z.B. Masse, Zeit, Energie) und Vektoren (z.B. Strecke, Geschwindigkeit, Beschleunigung, Kraft). Wenn man ein Skalar mit einem Vektor multipliziert (z.B. Masse mal Beschleunigung) ist das Ergebnis ein Vektor (in diesem Fall Kraft), dessen Koordinaten wie in diesem Absatz berechnet werden (also Zahl mal jede Koordinate des Vektors).
Betrag eines Vektors
[Bearbeiten]
Der Betrag eines Vektors ist nichts mehr und nichts weniger als seine Länge. Wie man aus dem Bild ablesen kann, kann man die Länge mit Hilfe des Satzes von Pythagoras berechnen. Die Seite a des Rechtwinkeligen Dreiecks ABC ist die y-Koordinate a = uy = 4 des Vektors (die untere Zahl) und die Seite b die x-Koordinate b=ux=3 (die obere Zahl). Daher ist die Länge des Vektors .
Der Gegenvektor hat genau die gleiche Länge, also den gleichen Betrag: .
Richtung eines Vektors und Steigung
[Bearbeiten]

Die Richtung eines zweidimensionalen Vektors hat stark mit der Steigung einer linearen Funktion zu tun. Wenn man von einem Punkt ausgeht und wissen will, in welcher Richtung der Vektor gezeichnet werden muss, kann man einen Schritt nach rechts parallel zur x-Achse machen und dann genau so viel auf der y-Achse, wie die y-Koordinate (untere Zahl) durch die x-Koordinate (obere Zahl).
Eine Darstellung einer Gerade ist auch die „Punkt-Vektor“ Darstellung. In dieser Darstellung der Gerade ist ihre Steigung genau die y-Koordinate (untere Zahl) durch die x-Koordinate (obere Zahl) des Vektors. In so einem Fall wäre die Steigung der entsprechenden Gerade für den Vektor im Bild 1 gleich und im Bild 2 gleich
Orts- und Richtungsvektoren
[Bearbeiten]Wie im Abschnitt über Vektor und Punkt erklärt, kann man einen Punkt auch durch einen vom Koordinatenursprung ausgehenden Vektor darstellen. So einen Vektor nennt man „Ortsvektor“. Um einen Ortsvektor von den anderen Vektoren zu unterscheiden, benutzt man für die anderen, nicht am Koordinatenursprung gebundenen Vektoren den Name „Richtungsvektor“. Wenn man aber das Wort „Vektor“ ohne weitere Bezeichnungen benutzt, ist ein Richtungsvektor gemeint.
Zerlegung eines Vektors zu seinen Komponenten
[Bearbeiten]Einen Vektor kann man zu sogenannten Komponenten zerlegen. Das ist quasi das Gegenteil von Vektoren addieren. Man wählt ein Koordinatensystem (zwei Richtungen auf der Ebene, in der Regel senkrecht zueinander) und findet zwei Vektoren, einen auf jede Achse des Koordinatensystems, dessen Summe der Anfangsvektor ist.



Das Bezugssystem muss aber nicht unbedingt Achsen, die normal aufeinander stehen sein. Das ist der Fall im Bild 3. Hier gelten aber vorherigen Gleichung nicht mehr.
Skalarprodukt von Vektoren
[Bearbeiten]Von den vier Grundrechenarten sind zwischen Vektoren nur drei möglich, die Strichrechnungen (Addition, Subtraktion) und die Multiplikation. Dafür gibt es allerdings zwei Arten von Multiplikation zwischen Vektoren, die sogenannten Skalar- und Kreuzprodukt. Hier werden wir uns mit dem Skalarprodukt beschäftigen, das durch den Punkt der gewöhnlichen Multiplikation dargestellt wird[1]. Es kann zwischen nur zwei Vektoren stattfinden und wird durch die Summe der Produkte der einzelnen Koordinaten der Vektoren berechnet. Das bedeutet: Wenn wir das Skalarprodukt der Vektoren und berechnen wollen, müssen wir die x-Koordinate des Vektors mit der x-Koordinate des Vektors multiplizieren, die y-Koordinate des Vektors mit der y-Koordinate des Vektors auch multiplizieren und die Ergebnisse zusammenrechnen:
Hier ein konkretes Beispiel:
Wir sehen klar: Das Ergebnis eines Skalarproduktes zwischen Vektoren ist kein Vektor mehr, sondern eine Zahl.[2]
- ↑ für das Kreuzprodukt hingegen wird das Symbol benutzt
- ↑ Beim Kreuzprodukt hingegen ist das Ergebnis ein neuer Vektor
Winkelmaß zwischen zwei Vektoren
[Bearbeiten]Der Kosinus des Winkels zwischen zwei Vektoren lässt sich durch folgende Formel berechnen:
Im Zähler steht das Skalarprodukt der beiden Vektoren, im Nenner das Produkt ihrer Beträge. Diese Formel kann man mit Hilfe des Satzes von Pythagoras und der Definition des Kosinus in einem rechtwinkeligen Dreieck zeigen. Der Winkel lässt sich dann leicht mit Hilfe der Umkehrfunktion von Kosinus berechnen:
Hier ein konkretes Beispiel:
Orthogonalitätskriterium zwei Vektoren
[Bearbeiten]Differentialrechnung
[Bearbeiten]Dieses Kapitel fängt im im Reifeniveau 1 an und wird im Reifeniveau 7 weitergeführt.
Integralrechnung
[Bearbeiten]Dieses Kapitel fängt im im Reifeniveau 3 an und wird im Reifeniveau 7 weitergeführt.



















![{\displaystyle \log _{5}\left({\frac {0{,}04}{{\sqrt[{3}]{d^{5}\cdot 5^{d}\cdot 5^{5}}}\ \ }}\cdot 125{\sqrt[{5}]{5}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e02c115ef7d44b4a7e3a5a8ae2c67d80ded2a950)
![{\displaystyle \log _{5}\left({\frac {0{,}04}{{\sqrt[{3}]{d^{5}\cdot 5^{d}\cdot 5^{5}}}\ \ }}\cdot 125{\sqrt[{5}]{5}}\right)=\log _{5}0{,}04-\log _{5}{\sqrt[{3}]{d^{5}\cdot 5^{d}\cdot 5^{5}}}+\log _{5}125+\log _{5}{\sqrt[{5}]{5}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f4a658c60599986f263bf68a86b31a761b01dd7a)

![{\displaystyle {\sqrt[{3}]{d^{5}\cdot 5^{d}\cdot 5^{5}}}=\left(d^{5}\cdot 5^{d}\cdot 5^{5}\right)^{\tfrac {1}{3}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/05bc2f2d8579b6dd40e9c664424f9c2315cd6d72)
![{\displaystyle {\sqrt[{5}]{5}}=5^{\tfrac {1}{5}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/496f39137be415280f48e09c1342a3e6a38decdd)
![{\displaystyle \log _{5}0{,}04-\log _{5}{\sqrt[{3}]{d^{5}\cdot 5^{d}\cdot 5^{5}}}+\log _{5}125+\log _{5}{\sqrt[{5}]{5}}=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0c3e87867e65d7999c4a8fb3d9264c66c694eccc)












![{\displaystyle a+3-3=a\qquad b\cdot t:t=b\qquad ({\sqrt[{n}]{w\ }})^{n}=w\qquad {\sqrt[{n}]{w^{n}\ }}=w}](https://wikimedia.org/api/rest_v1/media/math/render/svg/65ef697e5968913ecf080be618d33517bf5f6a55)

















































































































































































![{\displaystyle a\cdot \left[\left(x+{b \over {2a}}\right)^{2}-\left({{b^{2}-{4ac}} \over {4a^{2}}}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/67fab8b2ea9066c5ad252db3b85cd698adfb28ca)
![{\displaystyle =a\cdot \left[\left(x+{b \over {2a}}\right)^{2}-\left({\sqrt {b^{2}-{4ac} \over {4a^{2}}}}\right)^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d9aa85a3e79b61b330febee0f3c0757df27f7f93)
![{\displaystyle ax^{2}+bx+c=a\cdot \left[\left(x+{b \over {2a}}\right)^{2}-\left({\sqrt {b^{2}-{4ac} \over {4a^{2}}}}\right)^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ea2cbd5d2e60574cc4e4f5dbee20f1c685a0c642)

![{\displaystyle a\cdot \left[\left(x+{b \over {2a}}\right)^{2}-\left({\sqrt {b^{2}-{4ac} \over {4a^{2}}}}\right)^{2}\right]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7e8552a41112983a14c1dccf089fd7b3201d2658)
![{\displaystyle a\cdot \left[\left(x+{b \over {2a}}\right)+\left({\sqrt {b^{2}-{4ac} \over {4a^{2}}}}\right)\right]\cdot }](https://wikimedia.org/api/rest_v1/media/math/render/svg/dc73c9da0f0d9c3d76c6a72523ee3f889d50d3c3)
![{\displaystyle \left[\left(x+{b \over {2a}}\right)-\left({\sqrt {b^{2}-{4ac} \over {4a^{2}}}}\right)\right]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5af93623c8ca04bc407a7bdd8f4660b7f6719865)







![{\displaystyle Q(x)=a\cdot \left[\left(x+{b \over {2a}}\right)^{2}-\left({\sqrt {b^{2}-{4ac} \over {4a^{2}}}}\right)^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/031dd369572f9b7d79e45c8621f2c44d57521db2)


![{\displaystyle Q(x)=a\cdot \left[\left(x+{b \over {2a}}\right)^{2}-\left({\sqrt {b^{2}-{4ac} \over {4a^{2}}}}\right)^{2}\right]=a\cdot \left(0-{b^{2}-{4ac} \over {4a^{2}}}\right)={b^{2} \over {4a}}-c}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2e2a40495eef7fa0ba740ad8485b1a3d9e5c116c)





















































































































































