MathemaTriX ⋅ Theorie. Reifeniveau 7

Hoch

STOPP PUSHBACKS • FREE ASSANGE • FRIEDEN AUF DER WELT ${\color {white}\mathbf {MATHE} \mu \alpha T\mathbb {R} ix}$ DEINE FESTE BEGLEITERIN FÜR DIE SCHULMATHEMATIK EINFACH UND VERSTÄNDLICH GRATIS!* MIT MEHR ALS 200 THEORIE- UND AUFGABEN-ERKLÄRUNGS VIDEOS! Mathe lernen ist wie Fahrradfahren lernen: Du kannst es dir stundenlang erklären lassen, du wirst nie fahren können, wenn du nicht selber zu fahren probierst.

Inhalt Ein-Aus- klappen

AUFGABEN

Niveaus: Grundniveau 1 Grundniveau 2 Grundniveau 3 Mitteniveau 1 Mitteniveau 2 Mitteniveau 3 Reifeniveau 1 Reifeniveau 2 Reifeniveau 3 Reifeniveau 4 Reifeniveau 5 Reifeniveau 6 Reifeniveau 7

Grundrechenarten und Bruchrechnungen

Dieses Kapitel fängt im Grundniveau 1 an und wurde im mittleren Niveau 2 vervollständigt.

Schluss und Prozentrechnung

Dieses Kapitel fängt im Grundniveau 1 an und wurde im mittleren Niveau 3 vervollständigt.

Exponential und Logarithmus Funktion

Dieses Kapitel fängt im Grundniveau 3 an und wurde im Reifeniveau 5 vervollständigt.

Arbeiten mit Termen

Dieses Kapitel fängt im Grundniveau 1 an und wurde im Reifeniveau 3 vervollständigt.

Zahlendarstellungen Mengentheorie und Aussagenlogik

Dieses Kapitel fängt im Grundniveau 2 an und wurde im Reifeniveau 6 vervollständigt.

Einheiten

Dieses Kapitel fängt im Grundniveau 2 an und wurde im Reifeniveau 3 vervollständigt.

Statistik und Wahrscheinlichkeitsrechnung

Dieses Kapitel fängt im Grundniveau 2 an und wurde im Reifeniveau 6 vervollständigt.

Geometrische Konstruktionen

Dieses Kapitel fängt im Grundniveau 2 an und wurde im mittleren Niveau 3 vervollständigt.

Geometrie der Ebene

Dieses Kapitel fängt im Grundniveau 2 an und wurde im mittleren Niveau 2 vervollständigt.

Geometrie des Raums

Dieses Kapitel ist nur im mittleren Niveau 3 behandelt.

Diagramme

Dieses Kapitel fängt im Grundniveau 2 an und wurde im Reifeniveau 5 vervollständigt.

Funktionen

Dieses Kapitel fängt im Grundniveau 3 an und wurde im Reifeniveau 6 vervollständigt.

Lineare Gleichungssysteme

Dieses Kapitel fängt im Grundniveau 3 an und wurde im Reifeniveau 4 vervollständigt.

Trigonometrische Funktionen

Dieses Kapitel fängt im Reifeniveau 1 an und wurde im Reifeniveau 5 vervollständigt.

Vektoren

Dieses Kapitel ist nur im Reifeniveau 5 behandelt.

Differentialrechnung

Kurvendiskussion

Allgemeines zur Kurvendiskussion

Die Ableitung einer Funktion an einem Punkt ist die Steigung der Funktion an diesem Punkt und ist gleich sowohl zur Steigung der Tangente an diesem Punkt als auch zum Tangens des Winkels zwischen dieser Tangente und der x-Achse.

Wenn eine Funktion von links unten nach rechts oben verläuft, ist ihre Steigung (also ihre Ableitung) positiv, im Gegenfall negativ. Der Grenzfall zwischen den beiden Situationen ist, wenn eine Funktion weder nach oben noch nach unten verläuft. Die einzige Möglichkeit in diesem Fall ist, dass sie parallel zur x-Achse verläuft. Logischerweise soll in diesem Fall die Steigung (also die Ableitung) weder positiv noch negativ sein. Die einzige Zahl, die diese Eigenschaft hat, ist Null. Wenn die Steigung (also die Ableitung) einer Funktion an einem Punkt null ist, dann läuft die Tangente der Funktion an dieser Stelle parallel zur x-Achse. In diesem Fall spricht man von einem Extrempunkt oder einem Sattelpunkt.

Extrempunkte sind die Punkte einer Funktion, wo diese ein lokales oder globales Maximum oder Minimum innehat. Die entsprechenden y-Werte sind daher die Extremwerte der Funktion und die x-Werte die Extremstellen. Die Ableitung einer Funktion an solchen Stellen ist Null. Die Tangente an einem solchen Punkt läuft daher parallel zur x-Achse.

Wendepunkte sind Punkte, an denen die Funktion ihre "Biegung" ändert. Wir können uns es so darstellen, dass wir uns von links nach rechts auf der in einem Koordinatensystem dargestellten Kurve der Funktion fahren. Um auf der Kurve zu bleiben, müssen wir mit einem imaginären Lenkrad abbiegen (außer wir befinden uns auf einer Gerade). Müssen wir "nach links abbiegen", dann ist die zweite Ableitung der Funktion positiv, nach rechts ist sie negativ. Der Punkt, wo wir die Richtung von links nach rechts oder umgekehrt ändern müssen, ist ein sogenannter Wendepunkt. An einem Wendepunkt ist die zweite Ableitung der Funktion Null. Wenn an diesem Punkt die Ableitung dazu null ist, dann wird der Punkt dazu Sattelpunkt genannt.

Nehmen wir das konkrete Beispiel des folgenden Bildes:

Kurvendiskussion Erste Ableitung

Ganz links und bis zur Stelle ca. −1,4 (x=−1,4) verläuft die Funktion nach unten, die Steigung (also die Ableitung) ist negativ. Dann läuft sie nach oben bis zur Stelle Null. Die Ableitung (also die Steigung) ist in diesem Intervall positiv. Genau an der Stelle Null wird die Ableitung doch Null, die Tangente der Funktion an dieser Stelle läuft parallel zur x-Achse. Dann allerdings läuft die Funktion weiter nach oben, also die Ableitung ist weiter positiv. Ungefähr an der Stelle 1,4 ändert sich die Richtung wieder nach unten und die Steigung wird negativ bis zur Stelle 2,2 usw.

Kurvendiskussion Zweite Ableitung

Am Anfang muss man "links abbiegen". Die zweite Ableitung ist positiv. Die erste Ableitung wird immer größer. Ungefähr an der Stelle −0,9 fängt man an, "rechts abzubiegen". Die zweite Ableitung ist negativ. Die erste Ableitung wird immer kleiner (egal ob sie positiv oder negativ ist). Das passiert bis an der Stelle 0. Danach muss man wieder "gegensteuern" und "nach links abbiegen". Die zweite Ableitung ist wieder positiv. Das passiert bis ungefähr an der Stelle 0,9. Die zweite Ableitung wird danach negativ erst ca. an der Stelle 1,8 und wieder negativ ca. an der Stelle 2,4.

Kurvendiskussion Extrempunkte

An den Stellen der Änderungen des Vorzeichens der ersten Ableitung wird diese Null sein, also ca. an den Stellen −1,4, 1,4, 2,2 und 2,8. An diesen Stellen wird die erste Ableitung von positiv zu negativ oder umkegehrt. Diese Stellen sind Extrempunkte. An den Stellen −1,4, und 2,2 haben wir jeweils ein lokales Minimum, an den Stellen 1,4 und 2,2 ein lokales Maximum. An diesen Stellen ist also die erste Ableitung null.

Kurvendiskussion Wendepunkte

An den Stellen der Änderungen des Vorzeichens der zweiten Ableitung wird diese Null sein, also ca. an den Stellen −0,9, 0, 0,9, 2,2 und 2,8. An diesen Stellen wird die zweite Ableitung von positiv zu negativ oder umkegehrt. Diese Stellen sind Wendepunkte. An diesen Stellen ist also die zweite Ableitung null.

Kurvendiskussion Sattelpunkte

Wenn sowohl die erste als auch die zweite Ableitung null sind, dann sprechen wir von einem Sattelpunkt. Das passiert in diesem Diagramm an der Stelle 0 (x=0). Allerdings ist der Wert der Funktion an dieser Stelle doch nicht Null (y=f(0)=1).

Kurvendiskussion Nullstellen

Nullstellen sind die Stellen der Funktion, wo die Funktion die x-Achse abschneidet, also wo ihr Wert null ist. Stelle bedeutet x-Wert, Wert der Funktion bedeutet y-Wert. "Der Wert der Funktion ist null" bedeutet, dass wir die Funktion, z.B. f(x) also y, gleich null setzten sollen und dadurch die x-Werte finden, für denen es gilt, dass y gleich null ist. Die Nullstellen im Diagramm ablesen kann man sehr leicht, indem man die Stellen findet, wo die Funktion die x-Achse abschneidet. In unserem Beispiel sind das ungefähr die Stellen (x-Werte auf der x-Achse) −1,6, −1,1, 1,95 und 2,35.

Kurvendiskussion y-Achsenabschnitt

Der y-Achsenabschnitt ist der Wert der Funktion an den Punkt, wo die Funktion die y-Achse abschneidet. Für alle Punkte auf der y-Achse ist der x-Wert null. Um der y-Achsenabschnitt zu finden, reicht daher, den Wert der Funktion (y-Wert) an der Stelle (x-Wert) null zu finden, einfach gesagt, x gleich null in der Funktion setzten. In unserem Beispiel ist der y-Achsenabschnitt gleich 1. Die Funktion schneidet die y-Achse an den Punkt (0|1) ab.

Umkehraufgaben Kurvendiskussion

Theorie zu den Umkehraufgaben der Kurvendiskussion

In den Umkehraufgaben der Kurvendiskussion werden (in der Schulmathematik) die Koeffizienten einer Polynomfunktion gesucht. Das Ziel ist, ein lineares Gleichungssystem zu entwickeln, um diese Koeffizienten zu berechnen. In der (Text-) Aufgabe werden Informationen angegeben, die wir in Gleichungen "übersetzen" müssen. Die Gleichungen müssen um eins mehr als der Grad der Funktion sein, also so viele wie die Koeffizienten. Die Koeffizienten werden dann die gesuchten Variablen des Gleichungssystems darstellen. Zunächst einmal versuchen wir, die Schlüsselwörter zu erörtern, die zur "Übersetzung" der Textaufgabe führen.

Mit den folgenden Ausdrücken ist das gleiche gemeint:

Am Punkt (c|d)$\qquad$Hier ist c der x-Wert der Funktion und d der y-Wert.
Die Funktion hat an der Stelle c den Wert d$\qquad$In diesem Satz ist mit c der x-Wert gemeint und mit d der Wert der Funktion, also der y-Wert.
In beiden Fällen kann der Satz irgendwie indirekter sein, beispielsweise kann "die Funktion die Gerade bla-bla am Punkt bla-bla schneiden". In all diesen Fällen muss die Funktion selber benutzt werden. Wir ersetzten y und x durch ihre Werte und so entsteht eine Gleichung mit den Koeffinzienten als Variablen. Seien a der x-Wert und b der y-Wert, $f(x)=a_{n}\ x^{n}+a_{n-1}\ x^{n-1}+...\ +a_{1}\ x+a_{0}\$ und daher $a_{n},\ a_{n-1},\ ...\ a_{1},\ a_{0}\$die Koeffizienten (wobei n der Grad der Polynomfunktion), dann gilt $f(c)=d\$und daher:

$d=a_{n}\ c^{n}+a_{n-1}\ c^{n-1}+...\ +a_{1}\ c+a_{0}\$

Sonderfälle

x-Achsenabschnitt
Nullstellen
In all diesen Fällen ist gemeint, dass der y-Wert gleich Null ist, also für x=c:

$0=a_{n}\ c^{n}+a_{n-1}\ c^{n-1}+...\ +a_{1}\ c+a_{0}\$
Der einzige Unterschied von der vorherigen Gleichung ist, dass der y-Wert 0 anstatt d ist.

y-Achsenabschnitt
Die Funktion schneidet die y-Achse an ...
(oder Ähnliches)
In all diesen Fällen ist gemeint, dass der x-Wert gleich Null ist. Man kann dann leicht feststellen, dass der y-Wert gleich dem Koeffizienten $a_{0}\$sein wird. f(0)=d und daher:

$d=a_{n}\ 0^{n}+a_{n-1}\ 0^{n-1}+...\ +a_{1}\ 0+a_{0}\ \Rightarrow d=a_{0}$

Mit den folgenden Ausdrücken ist das gleiche gemeint:

(Wert der) Ableitung der Funktion (an einem Punkt oder Stelle)
Steigung der Funktion (an einem Punkt oder Stelle)
Steigung der Tangente der Funktion (an einem Punkt)
Tangens des Winkels zwischen Tangente der Funktion und x-Achse (an einem Punkt oder Stelle).
Wichtiger Hinweis: Wenn die Ableitung an einem Punkt gegeben wird, dann haben wir zwei Informationen gleichzeitig, also eine Gleichung mit Hilfe des Punktes und eine mit Hilfe der Ableitung an dieser Stelle. Das ist allerdings nicht der Fall, wenn nur die Stelle, also der x-Wert, angegeben ist.

In all diesen Fällen muss die Ableitung der Funktion gleich ihren angegebenen Wert und an dieser Stelle gestellt werden. Man muss also erst die allgemeine Ableitung einer Polynomfunktion dieses Grades berechnen:

$f'(x)=a_{n}\ (n)\ x^{n-1}+a_{n-1}\ (n-1)\ x^{n-2}+...\ +a_{2}\cdot 2\ x+a_{1}\$
Die Koeffizient $a_{0}\$kommt nicht mehr vor, da die Ableitung einer Konstante null ist ($a_{0}\$ist eine gesuchte Zahl, also eine Konstante).

Dann setzt man den Wert für die Ableitung und den x-Wert ("Stelle") ein. Seien diese q bzw. p, dann gilt $f'(p)=q\$und daher:

$q=a_{n}\ (n)\ p^{n-1}+a_{n-1}\ (n-1)\ p^{n-2}+...\ +a_{2}\cdot 2\ p+a_{1}$

Sonderfälle

Die Funktion hat einen Extrempunkt (Maximum oder Minimum)
Die Tangente läuft parallel zur x-Achse (oder senkrecht zur y-Achse, oder "steht normal" auf der y-Achse)
Der Tangens ist null
Die Funktion hat einen Sattelpunkt (Sonderfall des Sonderfalls, siehe wieter unten den Text über die zweite Ableitung)

In all diesen Fällen ist gemeint, dass die Ableitung gleich null ist. In der letzten Gleichung schreiben wir daher 0 statt q:

$0=a_{n}\ (n)\ p^{n-1}+a_{n-1}\ (n-1)\ p^{n-2}+...\ +a_{2}\cdot 2\ p+a_{1}$

Weitere Ableitungen

Der Wert der zweiten Ableitung

In diesem Fall müss man die allgemeine Funktion für die erste Ableitung, die wir vorher berechnet haben, noch mal ableiten. Hier ist noch mal die allgemeine erste Ableitung:

$f'(x)=a_{n}\ (n)\ x^{n-1}+a_{n-1}\ (n-1)\ x^{n-2}+...\ +a_{2}\cdot 2\ x+a_{1}\qquad$und hier die Ableitung der Ableitung:

$f''(x)=a_{n}\ (n)\ (n-1)\ x^{n-2}+a_{n-1}\ (n-1)\ (n-2)\ x^{n-3}+...\ +a_{3}\cdot 6\ x+a_{2}\cdot 2\$

Für Ableitungen höheren Grades muss man einfach weiter so die Ableitung der Ableitung berechnen.

Sonderfälle

Die Funktion hat einen Wendepunkt an der Stelle p (an den Punkt (p|r).

Bei einem Wendepunkt ist die zweite Ableitung gleich null:

Zweite Ableitung: $0=a_{n}\ (n)\ (n-1)\ p^{n-2}+a_{n-1}\ (n-1)\ (n-2)\ p^{n-3}+...\ +a_{3}\cdot 6\ p+a_{2}\cdot 2\$

Ist ein Punkt (und nicht einfach eine Stelle) angegeben, dann gibt es auch eine zweite Information und wir können eine zweite Gleichung stellen:

Funktion: $r=a_{n}\ p^{n}+a_{n-1}\ p^{n-1}+...\ +a_{1}\ p+a_{0}\$

Die Funktion hat einen Sattelpunkt an der Stelle p (an den Punkt (p|r).

Bei einem Sattelpunkt ist sowohl die erste als auch die zweite Ableitung gleich null:

Erste Ableitung: $0=a_{n}\ (n)\ p^{n-1}+a_{n-1}\ (n-1)\ p^{n-2}+...\ +a_{2}\cdot 2\ p+a_{1}$

Zweite Ableitung: $0=a_{n}\ (n)\ (n-1)\ p^{n-2}+a_{n-1}\ (n-1)\ (n-2)\ p^{n-3}+...\ +a_{3}\cdot 6\ p+a_{2}\cdot 2\$

Ist ein Punkt (und nicht einfach eine Stelle) angegeben, dann gibt es auch eine dritte Information und wir können eine dritte Gleichung stellen:

Funktion: $r=a_{n}\ p^{n}+a_{n-1}\ p^{n-1}+...\ +a_{1}\ p+a_{0}\$

Umkehraufgaben der Kurvendiskussion Zusammenfassung

Anwendung der Funktion selbst	$f(x)\$allgemein Am Punkt $(x_{wert}|y_{wert})$ Die Funktion hat an der Stelle c ($x_{wert}$) den Wert d ($y_{wert}$) $y_{wert}\$in Abhängigkeit von $x_{wert}$ $y_{wert}\$in Bezug auf $x_{wert}$ je $x_{wert}\$desto $y_{wert}$ $y=a_{n}\ x^{n}+a_{n-1}\ x^{n-1}+...\ +a_{1}\ x+a_{0}\$ $f(x)=0$ x-Achsenabschnitt Nullstellen $0=a_{n}\ x^{n}+a_{n-1}\ x^{n-1}+...\ +a_{1}\ x+a_{0}\$ $f(0)=A_{y}$ y-Achsenabschnitt Die Funktion schneidet die y-Achse an ... (oder Ähnliches) $A_{y}=a_{n}\ 0^{n}+a_{n-1}\ 0^{n-1}+...\ +a_{1}\ 0+a_{0}\ \Rightarrow A_{y}=a_{0}$
Anwendung der ersten Ableitung	$f'(x)\$allgemein (Wert der) Ableitung der Funktion (an einem Punkt oder Stelle) Steigung der Funktion (an einem Punkt oder Stelle) Steigung der Tangente der Funktion (an einem Punkt oder Stelle) knickfrei (gleiche Steigung) Tangens des Winkels zwischen Tangente der Funktion und x-Achse (an einem Punkt oder Stelle) momentane Änderungsrate $f'(x)=a_{n}\ (n)\ x^{n-1}+a_{n-1}\ (n-1)\ x^{n-2}+...\ +a_{2}\cdot 2\ x+a_{1}\$ $f'(x)=0$ Die Funktion hat einen Extrempunkt (Maximum: Hochpunkt oder Minimum: Tiefpunkt) Die Tangente läuft parallel zur x-Achse (oder senkrecht zur y-Achse, oder "steht normal" auf der y-Achse) Der Tangens ist null Die Funktion hat einen Sattelpunkt $0=a_{n}\ (n)\ x^{n-1}+a_{n-1}\ (n-1)\ x^{n-2}+...\ +a_{2}\cdot 2\ x+a_{1}\$
Anwendung der zweiten Ableitung	$f''(x)\$allgemein Der Wert der zweiten Ableitung (an einem Punkt oder Stelle) $f''(x)=a_{n}\ (n)\ (n-1)\ x^{n-2}+a_{n-1}\ (n-1)\ (n-2)\ x^{n-3}+...\ +a_{3}\cdot 6\ x+a_{2}\cdot 2\$ $r=a_{n}\ (n)\ (n-1)\ p^{n-2}+a_{n-1}\ (n-1)\ (n-2)\ p^{n-3}+...\ +a_{3}\cdot 6\ p+a_{2}\cdot 2\$ $f''(x)=0$ Die Funktion hat einen Wendepunkt an der Stelle p (an den Punkt $(p|r)$) Die Funktion hat einen Sattelpunkt an der Stelle p (an den Punkt $(p|r)$) $0=a_{n}\ (n)\ (n-1)\ x^{n-2}+a_{n-1}\ (n-1)\ (n-2)\ x^{n-3}+...\ +a_{3}\cdot 6\ x+a_{2}\cdot 2\$ $0=a_{n}\ (n)\ (n-1)\ p^{n-2}+a_{n-1}\ (n-1)\ (n-2)\ p^{n-3}+...\ +a_{3}\cdot 6\ p+a_{2}\cdot 2\$

Kurvendiskussion Umkehraufgaben

*Eine Funktion vierten Grades hat den Extrempunkt (2|3) und einen Wendepunkt an der Stelle −4. Die Tangente zur Funktion ist parallel zur x-Achse an der Stelle 1. 20 ist eine Nullstelle. Wie lautet die Funktion?

Wir werden die erste (Extrempunkt) und die zweite (Wendepunkt) Ableitung brauchen. Da der Grad der Funktion 4 ist, also da sie 5 Koeffizienten hat, brauchen wir fünf Gleichungen. Die allgemeine Funktion und ihre ersten zwei Ableitungen sind:

$f(x)=a_{4}\ x^{4}+a_{3}\ x^{3}+a_{2}\ x^{2}\ +a_{1}\ x+a_{0}\$

$f'(x)=4\,a_{4}\ x^{3}+3\,a_{3}\ x^{2}+2\,a_{2}\ x\ +a_{1}\$

$f''(x)=12\,a_{4}\ x^{2}+6\,a_{3}\ x+2\,a_{2}$

Mit dem Extrempunkt (2|3) haben wir gleich zwei Informationen, f(2)=3 und f'(2)=0, und daher zwei Gleichungen:

$3=a_{4}\cdot 2^{4}+a_{3}\cdot 2^{3}+a_{2}\cdot 2^{2}\cdot +a_{1}\cdot 2+a_{0}\qquad$und

$0=4\,a_{4}\cdot 2^{3}+3\,a_{3}\cdot 2^{2}+2\,a_{2}\cdot 2\ +a_{1}\$

Mit dem Wendepunkt an der Stelle −4 haben wir noch eine Information, $f''(-4)=0$, und damit die Gleichung:

$0=12\,a_{4}\cdot (-4)^{2}+6\,a_{3}\cdot (-4)+2\,a_{2}$

Die Tangente der Funktion an der Stelle 1 ist parallel zur x-Achse, also ist die erste Ableitung da gleich null:

$0=4\,a_{4}\cdot 1^{3}+3\,a_{3}\cdot 1^{2}+2\,a_{2}\cdot 1\ +a_{1}\$

Letztens ist 20 eine Nullstelle, f(20)=0:

$0=a_{4}\cdot 20^{4}+a_{3}\cdot 20^{3}+a_{2}\cdot 20^{2}\ +a_{1}\cdot 20+a_{0}\$

Damit haben wir folgendes lineares Gleichungssystem, das wir am liebsten mit einem Hilfsmittel lösen:

$3=a_{4}\cdot 2^{4}+a_{3}\cdot 2^{3}+a_{2}\cdot 2^{2}\cdot +a_{1}\cdot 2+a_{0}\qquad$
$0=4\,a_{4}\cdot 2^{3}+3\,a_{3}\cdot 2^{2}+2\,a_{2}\cdot 2\ +a_{1}\$
$0=12\,a_{4}\cdot (-4)^{2}+6\,a_{3}\cdot (-4)+2\,a_{2}$
$0=4\,a_{4}\cdot 1^{3}+3\,a_{3}\cdot 1^{2}+2\,a_{2}\cdot 1\ +a_{1}\$
$0=a_{4}\cdot 20^{4}+a_{3}\cdot 20^{3}+a_{2}\cdot 20^{2}\ +a_{1}\cdot 20+a_{0}\$

Die Lösung des Gleichungssystems ist:

$a_{4}={\frac {157}{2736}},\quad a_{3}=-{\frac {2837}{4788}},\quad a_{2}=-{\frac {265}{21}},\quad a_{1}={\frac {36523}{1197}},\quad a_{0}=-{\frac {4460}{1197}}$

Die Funktion lautet daher:

$f(x)={\frac {157}{2736}}x^{4}-{\frac {2837}{4788}}x^{3}-{\frac {265}{21}}x^{2}+{\frac {36523}{1197}}x-{\frac {4460}{1197}}$

• Eine Funktion dritten Grades hat den Sattelpunkt (−2|4) und den y-Achsenabschnitt −3. Wie lautet die Funktion?

Wir brauchen wieder die allgemeine erste und zweite Ableitung, allerdings brauchen wir hier vier Gleichungen:

Die allgemeine Funktion und ihre ersten zwei Ableitungen sind:

$f(x)=a_{3}\ x^{3}+a_{2}\ x^{2}\ +a_{1}\ x+a_{0}\$

$f'(x)=3\,a_{3}\ x^{2}+2\,a_{2}\ x\ +a_{1}\$

$f''(x)=6\,a_{3}\ x+2\,a_{2}$

Mit dem Sattelpunkt (3|4) haben wir gleich drei Gleichungen, $f(-2)=4$, $f'(-2)=0$ und $f''(-2)=0$, mit dem y-Achsenabschnitt noch eine dazu, $f(0)=-3$:

$4=a_{3}\ (-2)^{3}+a_{2}\ (-2)^{2}\ +a_{1}\ (-2)+a_{0}\$
$0=3\,a_{3}\ (-2)^{2}+2\,a_{2}\ (-2)\ +a_{1}\$
$0=6\,a_{3}\ (-2)+2\,a_{2}$
$-3=a_{0}\$

Die Lösung des Gleichungssystems ist:

$a_{3}=-{\frac {7}{8}},a_{2}=-{\frac {21}{4}},a_{1}=-{\frac {21}{2}},a_{0}=-3$

und die Funktion lautet daher:

$g(x)=-{\frac {7}{8}}x^{3}-{\frac {21}{4}}x^{2}-{\frac {21}{2}}x-3$

Integralrechnung

Rotationskörper

Hier werden wir erkunden, wie das Volumen eines Körpers berechnet werden kann, der durch die Rotation einer Kurve um einer Achse entsteht.

• 
• 
• 

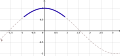
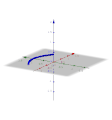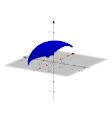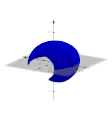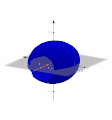
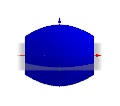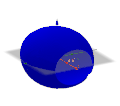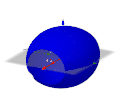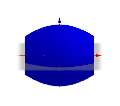
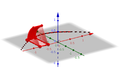
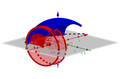
Nehmen wir hier als Beispiel die Kosinusfunktion im ersten Bild, genauer den Teil zwischen −0,9 und 0,9. Im zweiten Bild ist die Ebene des ersten Diagramms der "Boden", die x-Achse ist rot. Um diese Achse lassen wir die Kurve im zweiten Bild drehen. Dadurch entsteht der Körper im dritten Bild (hier allerdings hohl). Wie können wir das Volumen dieses Körpers berechnen? Gehen wir zurück zur Ebene:

• 
• 
• 
• 
• 
• 

Wir nehmen einen Punkt auf der Kurve und formen einen Rechteck. Die Fläche des Rechtecks ist ungefähr so viel wie die Fläche unter der Kurve, es gibt einen kleinen Teil mehr rechts von der Kurve und einen kleinen Teil weniger links (erstes Bild). Im zweiten Bild sehen wir wieder die Ebene als "Boden" und die rote x-Achse. In den restlichen Bildern sehen wir, wie durch die Drehung des Rechtecks ein Zylinder entsteht, der annähernd das gleiche Volumen hat, wie der entsprechenden Teil des blauen Körpers, der durch die Drehung der Kurve entsteht.

Wir können also die Kurve in mehreren kleinen Teilen teilen und dadurch Rechtecke konstruieren, eine Seite deren auf der x-Achse liegt. Wir Teilen die Kurve so, dass diese Seite immer gleich ist: $\Delta x$. In je mehrere Teile wir die x-Achse teilen, desto kleiner wird $\Delta x\$sein und desto genauer wird die Summe der Volumina der dadurch entstehenden Zylinder so viel wie das Volumen der Rotationskörpers sein:

• 
• 
• 

Das Volumen eines Zylinders ist allgemein die Grundfläche (ein Kreis) mal die Höhe. In diesen Zylindern ist die Höhe $\Delta x$, der Radius des Kreises der Grundfläche ist soviel wie $y$, also wie der Wert der Funktion $f(x)$ zwischen den beiden Rändern des Intervalls $\Delta x\$(in diesem Beispiel $\cos x$). Wenn wir das Intervall in n Teilen geteilt haben, ist das Volumen jedes Zylinders:

$V_{n}=\pi \left(f(x_{n})\right)^{2}\cdot \Delta x\quad$(in diesem Beispiel $V_{n}=\pi \cos ^{2}(x_{n})\cdot \Delta x$)

und das ganze Volumen:

$V=\sum _{i=1}^{n}V_{n}=\sum _{i=1}^{n}\pi \left(f(x_{n})\right)^{2}\cdot \Delta x\quad$(in diesem Beispiel $V=\sum _{i=1}^{n}\pi \cos ^{2}(x_{n})\cdot \Delta x$

Für immer größer n wird $\Delta x$ immer kleiner. Ohne hier mathematische Strenge zu verlangen, können wir schreiben:

$\lim _{n\to \infty }\Delta x=dx$

Wir können dann die Summe für verschwindendes $\Delta x$ als Integral "definieren":

$V=\int _{x_{1}}^{x_{2}}\pi \left(f(x)\right)^{2}dx$

In unserem Beispiel ist das:

$V=\int _{-0,9}^{0,9}\pi \cos ^{2}(x)dx\approx 4{,}357\$Einheiten

Rotationsfläche

Folgen

Dieses Kapitel ist nur im Reifeniveau 6 behandelt.