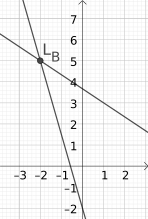MathemaTriX ⋅ Theorie. Mittleres Niveau 3
| ||||||||||||||||||
|
Inhalt
Ein-Aus- klappen |
| AUFGABEN | ||||||||||||||
|
Grundrechenarten und Bruchrechnungen
[Bearbeiten]Dieses Kapitel fängt im Grundniveau 1 an und wurde im mittleren Niveau 2 vervollständigt.
Schluss und Prozentrechnung
[Bearbeiten]Prozentrechnung abstrakt
[Bearbeiten]Prozentrechnung in Geometrie Abstrakt
[Bearbeiten]|
Die Seite einer Figur F ist das 1,5-fache |
A) Er ist 1,5-1=0,5 also 50% mehr.
B) Er ist 0,5 von 1,5 also kleiner.
Der Umfang von G ist daher des Umfangs von F.
C) Die Fläche von F ist das -fache der Fläche von G.
Daher ist sie 2,25-1=1,25=125% größer. Sie ist 225% der Fläche von G.
D) Umgekehrt ist sie 1,25 in 2,25 also kleiner.
Die Fläche von G ist daher der Fläche von F.
E) Der Umfang von F ist 2-1=1=100% und seine Fläche 2²-1=3=300% größer.
Der Umfang von G ist 1 von 2 also
und die Fläche 3 von 4 also kleiner.
Die Fläche von G ist also 25% der Fläche von F.
Prozentrechnung in Statistik Abstrakt
[Bearbeiten]|
In den folgenden Beispielen gehen wir davon aus, dass |
A) Denken wir zunächst einmal mit einer einfachen konkreten Zahl. Sagen wir mal, dass wir 1000 Personen haben. Da Männer und Frauen gleich so viel angenommen sind, wird es dann 500 Männer und 500 Frauen geben. Von den 500 Männern sind 35% Raucher, also 175 Männer. Von der ganzen Bevölkerung rauchen die 27,5% Personen, also im konkreten Beispiel 275 Personen. Da 175 davon Männer sind, werden die restlichen 100 Frauen sein. 100 von 500 Frauen, das sind 20% der Frauen, die rauchen.
Wie können wir das jetzt abstrakt schreiben?
50%(=0,5) sind Männer und 35%(=0,35) davon rauchen. Der Anteil der Raucher in der ganzen Bevölkerung ist daher:
Raucher: 0,5·0,35
Für das Gefragte schreiben wir x, das ist der Anteil der Raucherinnen unter der Frauen, die ebenfalls 50%(=0,5) der Bevölkerung sind. Daher gilt für den Anteil der Raucherinnen in der gesamten Bevölkerung:
Raucherinnen: 0,5·x
Die Summe der beiden Anteile wird der Anteil (27,5%=0,275) der gesamten rauchenden Personen in der gesamten Bevölkerung (100%=1) sein.Wir schreiben also:
B) Man könnte hier sagen, der Unterschied ist 82,4-80=2,4 Jahre. Das stimmt allerdings überhaupt nicht. 80 Jahre ist ein Durchschnitt von rauchenden und nicht rauchenden Personen. Um das Gefragte zu beantworten, brauchen wir keine durchschnittliche Lebenserwartung, sondern die Lebenserwartung der rauchenden Personen. Wir arbeiten in der gleichen Weise, wie in Frage A und bekommen dadurch folgende Gleichung:
Jahre.
Der Lebenserwartungsunterschied ist daher ca. 82,4-73,7=8,7 Jahre.
C) Lebenserwartung Männer: Jahre.
Lebenserwartung Frauen: Jahre.
D) Die RaucherInnenquoten in der höheren Altersstufe sind dafür notwendig.
E) Wir müssen auch wissen, wie andere Krankheiten durchschnittlich für jedes Geschlecht die Lebenserwartung beeinflussen. Dafür können wir den Lebenserwartungsunterschied zwischen Männer und Frauen innerhalb der Gruppe der Nichtraucher und innerhalb der Gruppe der Raucher vergleichen. Sterben alle Raucher am gleichen Alter wie die Raucherinnen? Sterben aller Nichtraucher am gleichen Alter wie die Nichtraucherinnen? Wenn die Antwort zu beiden diesen Fragen ja ist, dann haben wir Gründen zu vermuten, dass das Rauchen der einzige Grund ist, warum Männer früher als Frauen sterben. Da es uns nicht klar ist, ob die offiziellen Daten unter freien Lizenz stehen, machen wir keinen Link dazu, ein Vergleich allerdings mit den tatsächlichen Daten, schließt nicht aus, dass tatsächlich das Rauchen für den Unterschied in der Lebenserwartung zwischen Männer und Frauen verantwortlich ist.
Exponential und Logarithmus Funktion
[Bearbeiten]Dieses Kapitel fängt im im mittleren Niveau 1 an und wird erst im Reifniveau 2 weitergeführt.
Arbeiten mit Termen
[Bearbeiten]Das pascalsche Dreieck Binompotenzen
[Bearbeiten]ist dann kein Binom mehr (drei Summanden). (Hier wird der erweiterte Begriff von Summand benutzt: a+b-c ist die Summe der drei Terme „a“, „b“ und „−c“)
Wir haben bisher nur Binompotenzen mit 2 als Hochzahl gesehen. Es gibt Binompotenzen höheren Grades, also mit einer höheren Hochzahl aus dem Bereich der natürlichen Zahlen:
Bei der Erklärung der binomischer Formeln haben wir das Auflösen von Klammern benutzt. Bei wäre so was schon komplizierter, bei höheren Hochzahl schon ziemlich kompliziert. Um diese Ausdrücke ohne Klammer zu schreiben (Ausmultiplizieren), gibt es einen viel einfacheren Weg, das pascalsche_Dreieck.
Mit Hilfe dieses Dreiecks, kann man die sogenannten Koeffizienten der entstehenden Summanden leicht berechnen.
Das ganze Dreieck ist ein (gleichschenkliches) Zahlendreieck. Die Basis erweitert sich ständig, die Schenkel bestehen aus lauter Einser. Die erste zwei Zeilen sind ein gleichschenkliches Zahlendreieck mit 1 an jedem Eckpunkt.
Für die nächste Zeile schreibt man an den Rändern 1 und für die innere Zahlen addiert man immer jeweils zwei nebenstehenden Zahlen der vorherigen Zeile. Für die dritte Zeile hier schreibt man an den Rändern 1 und in der Mitte addiert man die zwei Einser von oben (Ergebnis 2):

Die vierte und die fünfte Zeile (und alle weitere Zeilen) entstehen in der gleichen Weise:


Wie kann man jetzt ausmultiplizieren?
Man schriebt eine Summe mit 4 Summanden (einen mehr als die Hochzahl des Binoms, hier ein mehr als 3). Jeder Summand besteht aus dem Produkt von a und b mit einer absteigende Hochzahl für a und eine aufsteigende Hochzahl für b. Die erste Hochzahl für a ist die Hochzahl des Binoms (hier 3 absteigend), für b ist sie Null (aufsteigend bis 3):
Wir benutzen dann die vierte Zeile des Dreiecks. Sie hat so viele Zahlen, wie die Anzahl der Summanden (4):
Diese Zahlen werden die Koeffizienten der Summanden sein:
Wenn im Binom Plus steht (a+b), dann steht Plus zwischen allen Summanden. Wenn im Binom Minus steht (a-b), dann alternieren sich plus und minus in der Summe. Berücksichtigen wir auch folgende Tatsachen: und , dann ergibt sich:
und
zusammengefasst:
Für kann man dann genau in der gleichen Weise das Binom leicht ausmultiplizieren. Hier hat man fünf Summanden, also muss die fünfte Zeile des pascalschen Dreiecks benutzt werden (1 4 6 4 1):
Wenn also das Binom (3d−2c)3) ausmultipliziert werden soll, dann wird der Ausdruck für (a−b)3 und an der Stelle von a → 3d benutzt (und an der Stelle von b → 2c).
also
Bruchterme in Brüchen mit gemeinsamen Nenner umwandeln
[Bearbeiten]Im Kapitel über Brüchen haben wir schon gesehen, wie man zwei gleichnamige und zwei ungleichnamige Brüche addiert:
Brüche mit gleichem Nenner:
Brüche mit unterschiedlichen Nennern: Zähler und Nenner des ersten Bruches mit Nenner des zweiten erweitern und entsprechend für den zweiten Bruch!

Dabei ist es nicht wichtig, ob man minus oder plus zwischen den Brüchen hat. Allein der Nenner (ob er der gleiche oder nicht ist) spielt einer Rolle.
Der Vorgang ist genau der gleiche für Bruchterme.
Brüche mit gleichem Nenner:
Brüche mit unterschiedlichen Nennern:
Wenn aber die Sache etwas komplizierter wird, dann benutzt man einen Vorgang, der sehr ähnlich zum Verfahren der Primfaktorzerlegung und ihre Anwendung bei Strichrechnungen zwischen mehreren Brüchen ist.
Für jeden Teilterm, jede Variable, im Nenner, wählt man die höchst Hochzahl die vorkommt. Diese wird dann im gemeinsamen Nenner benutzt. Für a ist sie 3 (a³), für t 7 (t⁷), für x ist die Hochzahl 1(x¹ also x) und für s auch 1 (also s). Der gemeinsame Nenner wird daher a³t⁷xs sein. Den Zähler multipliziert man dann, mit den aus dem Nenner fehlenden Teilen.
Wieso habe wir den Zähler im ersten Bruch (5s) mit ts multipliziert? Wir haben erst den gemeinsamen Nenner (a³t⁷xs) durch den Nenner des Bruches (a³t⁶x) dividiert:
Mit diesem Term (diesem Ergebnis) muss man den Zähler multiplizieren. Den gleichen Prozess haben wir beim zweiten Bruch wiederholt. Dieser Prozess allerdings (gemeinsamen Nenner durch den jeweiligen Nenner dividieren) haben wir auch bei den Strichrechnungen zwischen mehreren Brüchen benutzt, wo wir auch die Primfaktorzerlegung angewandt haben.
Was im Zähler steht, ist nicht so wichtig. Im Nenner allerdings können die Faktoren größere Terme in Klammern sein:
Finden wir erst den gemeinsamen Nenner. Es gibt im Nenner des ersten Bruches die Termen a, w, (t-1), (t+1) und (t-3). Im zweiten Bruch findet man im Nenner noch folgende Terme dazu: p, (q^2+7+r). Wir sollten für den gemeinsamen Nenner die höchste Hochzahl des jeweiligen Terms benutzen. Beispielsweise ist diese für den Term a die Hochzahl 3, für den Term w die Hochzahl 5, für den Term (t+1) die Hochzahl 5 usw. Der gemeinsame Nenner wird dann sein.
Der Zähler des ersten Bruches wird durch den Quotient des gemeinsamen Nenners durch den Nenner des ersten Bruches erweitert:
Entsprechend für den zweiten Bruch:
Nun kann man das Ganze in einem Bruch schreiben:
Bruchtermegleichungen
[Bearbeiten]
Die Schritte, um die Lösung zu finden, sind am Anfang wie die Schritten bei Abschnitt„Bruchterme kürzen“.
- Erster Schritt: Vereinfachen (geht nur im Zähler des ersten Bruches; ist so viel wie ):
- Zweiter Schritt: Herausheben (geht nur im Zähler und im Nenner des ersten Bruches;):
- Dritter Schritt: Nach binomischen Formeln suchen (das geht hier nur im Nenner des Bruches auf der rechten Seite der Gleichung: ):
- Vierter Schritt: Kürzen, was man kürzen kann (das geht in diesem Beispiel beim ersten Bruch: ). Damit ergibt sich:
- Fünfter Schritt: Hat man diese Schritte überprüft, versucht man die Bruchterme auf den gleichen Nenner zu bringen, wie am vorherigen Teilkapitel gezeigt. Hier gibt es im Nenner zwei verschiedenen Terme, und . Der Bruch auf der rechten Seite hat schon beide, man braucht (und darf) ihn NICHT erweitern. Am ersten Bruch fehlt noch der Term und mit diesem muss er erweitert werden. Am zweiten Bruch fehlt der Term und mit diesem muss er erweitert werden.
- Sechster Schritt: Jetzt haben wir überall den gleichen Nenner. Wenn wir beide Seiten der Gleichung (also alle Brüche) mit diesem Nenner multiplizieren, dann wird er überall gekürzt.
- Siebter Schritt: Das vorläufige Ergebnis ist daher die folgende Gleichung, die wir dann mit einfachen Umformungen lösen können:
Die Lösungsmenge, also die Zahlen, die die Bruchtermegleichung am Anfang erfüllen, ist hier nur eine Zahl, die Zahl −2. Man schreibt:
Wie man sieht, ist die Lösung einer Bruchtermegleichung kompliziert. Das Üben und die Erfahrung machen die Sache selbstverständlich einfacher. Es gibt aber doch noch einen Schritt, um so eine Gleichung vollständig zu lösen: Die Definitionsmenge muss vorerst herausgefunden werden. Mit diesem Schritt beschäftigen wir uns im nächsten Teilkapitel.
Polynomdivision
[Bearbeiten]Definitionsmenge
[Bearbeiten]Nehmen wir folgendes Beispiel:
In den Nennern gibt es verschiedene Terme:
Alle diese Terme kann man als Produkte von verschiedenen Faktoren schreiben:
Alle diese Faktoren stehen im Nenner. Es gibt eine Regel in Mathematik, die besagt:
Die Division durch 0 ist nicht definierbar.
Warum das so ist, kann man in der höheren Mathematik zeigen. Der Nenner darf also nicht null sein. In welchen Fällen kann der erste, der zweite oder der dritte Nenner null sein? Dafür setzen wir diese Nenner gleich null!
Wann kann jetzt der erste Ausdruck null sein? Wenn zumindest einer der Faktoren null ist!
In der gleichen Weise für die anderen zwei Nenner:
Der Ausdruck kann nur dann definiert werden, wenn x nicht 0, 1 oder -1 ist. x darf daher alle andere Zahlen sein außer -1, 0 und 1. All die Zahlen, die x sein darf, nennt man Definitionsmenge. Man sagt, dass die Definitionsmenge die Menge der reellen Zahlen außer -1,0 und 1 ist und schreibt:
oder
Die Definitionsmenge anzugeben ist bei jeder Aufgabe sehr wichtig. Nehmen wir das Beispiel am Anfang und setzen wir es gleich null:
Die Lösungsschritte haben wir im vorherigen Absatz gelernt. Die Definitionsmenge ist (wie gerade eben gezeigt) . Wer die Lösungsschritte macht, kommt zum Ergebnis . Dieser Wert gehört aber nicht zur Definitionsmenge. x darf nicht -1 sein, weil in diesem Fall eine Division durch null vorkommt. Man sagt in diesem Fall, dass die Gleichung keine Lösung hat (und sie hat tatsächlich keine Lösung: -1 kann keine Lösung sein!) oder dass die Lösungsmenge die sogenannte leere Menge ist: oder .
Bei manchen Aufgaben kann es sein, dass die allgemeine Definitionsmenge angegeben wird (z.B. die natürliche Zahlen). Wenn man das Beispiel mit den Tischen im Kapitel über lineare Gleichungssysteme betrachtet, kann man feststellen, dass die Antwort nur eine natürliche Zahl sein kann und dass etwas in der Angabe nicht stimmt, wenn das nicht der Fall ist.
Obwohl es nicht Thema diese Buches ist, erwähnen wir hier, dass die Definitionsmenge auch durch Ungleichungen angegeben werden kann. Das ist beispielsweise der Fall, wenn man einen Term in einer quadratischen Wurzel hat. Nehmen wir das folgende Beispiel:
Wir behaupten hier, dass dieser Ausdruck nur dann definiert werden kann[1], wenn der Term unter der Wurzel positiv oder null (anders gesagt: nicht negativ) ist. Das liegt daran, dass die Gegenrechnung der Wurzel das Quadrat ist und das Quadrat von jeder beliebigen Zahl immer positiv ist (oder null, wenn die Zahl null ist). Bei positiven Zahlen ist diese Tatsache klar: + mal + wird + sein. Aber auch bei den negativen Zahlen ist es genauso: − mal − ist auch immer plus! Es gibt also keine Zahl, deren Quadrat negativ ist. In unserem Beispiel muss daher gelten:
Man sagt „x muss größer oder gleich null sein“.
- ↑ genauer gesagt in der Menge der reellen Zahlen. Warum aber das jetzt gesagt werden muss, ist überhaupt nicht Thema dieses Buches
Zahlendarstellungen Mengentheorie und Aussagenlogik
[Bearbeiten]Dieses Kapitel fängt im imGrundniveau 2 an und wird erst im Reifeniveau 5 weitergeführt.
Einheiten
[Bearbeiten]Dieses Kapitel fängt im Grundniveau 2 an und wird erst im Reifeniveau 3 weitergeführt.
Statistik und Wahrscheinlichkeitsrechnung
[Bearbeiten]Dieses Kapitel fängt im Grundniveau 2 an und wird erst im Reifeniveau 1 weitergeführt.
Geometrische Konstruktionen
[Bearbeiten]Dieses Kapitel wird in BRP nicht gefragt. Wenn es dich interessiert hier klicken.
Geometrie der Ebene
[Bearbeiten]Dieses Kapitel fängt im Grundniveau 2 an und wurde im mittleren Niveau 2 vervollständigt.
Geometrie des Raums
[Bearbeiten]Dimension
[Bearbeiten]Wir haben schon in der Geometrie der Ebene den Begriff der Strecke als auch verschiedene Figuren auf einer ebenen Fläche (z.B. Quadrat, Kreis, Dreieck, Rechteck) kennengelernt. Für eine Strecke braucht man nur die Länge angeben (z.B. 2,4dm), dann hat man sie vollständig beschrieben. Alle Strecken mit dieser Länge sind die gleiche Sache (man sagt in Mathematik: Sie sind Kongruent).

mit gleicher Länge
und anderer Breite
Bei einem Rechteck hingegen reicht die Länge nicht aus. Es gibt unendlich viele Rechtecke mit der gleichen Länge und eine andere Breite. Diese Rechtecke sind nicht mehr die gleiche Sache. Sie haben auch einen anderen Flächeninhalt. Sie sind nicht kongruent. Man braucht daher bei Flächen zwei Zahlen, die Abstände beschreiben, beim Rechteck ist das die Länge und die Breite.

Wenn man jetzt eine Figur im Raum betrachtet, z.B. einen Quader, dann reichen die Länge und die Breite wieder nicht aus. Da braucht man noch einen Abstand, die Höhe. Wenn die Höhe anders ist, dann ist auch das Volumen anders.
Die Anzahl der Abstandswerte, die man braucht, um eine Figur vollständig zu beschreiben, nennt man Dimension.[1]
Eine Strecke ist eine eindimensionale Figur: Allein ein Abstand (die Länge), reicht aus, um sie zu beschreiben. Ein Rechteck (und alle ebene Figuren) ist eine zweidimensionale Figur: Man braucht zwei Abstände (Länge und Breite), um sie zu beschreiben. Ein Quader (und alle Figuren, die Raum besetzen) ist eine dreidimensionale Figur: Man braucht drei Abstände (Länge, Breite und Höhe), um sie zu beschreiben. In unserem Bild eines Quaders wird die Länge mit a, die Breite mit b und die Höhe mit c bezeichnet.
Obwohl wir Menschen uns nicht mehrere Dimensionen vorstellen können, gibt es in der Physik theoretische Modelle, die noch mehrere Dimensionen haben. Beispielsweise setzt die allgemeine Relativitätstheorie die Zeit als eine weitere Dimension des sogenannten Zeitraums voraus! Die Stringtheorie kann sogar 11 Dimensionen voraussetzen!
- ↑ Allerdings wird in der Physik nicht nur der Abstand, sondern auch andere Größen als Dimensionsgrundlagen benutzt, z.B. ist in der Relativitätstheorie die Zeit eine vierte Dimension der sogenannten Raumzeit
Körper
[Bearbeiten]Ein Gegenstand in der Geometrie wird Körper genannt, wenn für seine Beschreibung drei Abstände notwendig und hinreichend sind.
Notwendig bedeutet, dass weniger Abstände nicht genügend sind, um den Körper zu beschreiben. Man kann nicht einen Quader nur mit Länge und Breite vollständig beschreiben.
Hinreichend bedeutet, dass man nicht mehrere Abstände oder eine andere Dimension für die Beschreibung braucht. Wenn die Länge, die Breite und die Höhe des Quaders gegeben sind, braucht man nicht auch die Raumdiagonale angeben (sie wird schon von den anderen drei Abständen bestimmt).
Jede dreidimensionale Figur ist ein (geometrischer) Körper. In diesem Text wird auch das Wort „Raumfigur“ dafür benutzt.
Kante
[Bearbeiten]Im Kapitel über die Geometrie der Ebene haben wir den Begriff der Seite einer ebenen Fläche gesehen. Bei einem Quadrat sind alle Seiten gleich, bei einem Rechteck gibt es eine Länge und eine Breite. Die Strecken am Rand einer ebene Figur wurden also Seiten genannt.
Die Strecken am Rand eine Raumfigur werden aber doch Kanten genannt. Das Wort „Seite“ wäre in diesem Fall verwirrend: man wüsste dann nicht, ob mit „Seite“ die Seitenfläche oder die Seitenstrecke gemeint ist. Daher benutzt man das Wort „Kante“ für die Strecken. In unserem Bild eines Quaders wird die Länge mit a, die Breite mit b und die Höhe mit c bezeichnet. a,b und c sind daher Kanten des Quaders. Es gibt in diesem Bild 4 Kanten, die so lang wie a sind, 4 Kanten, die so lang wie b sind, und 4 Kanten, die so lang wie c sind.
Für die ebenen Flächen, die die Figur begrenzen, benutzt man die Worte „Grundfläche“, „Seitenfläche“ und „Deckfläche“. Es gibt selbstverständlich auch Raumfiguren, die von keinen ebenen Flächen begrenzt werden, wie beispielsweise die Kugel.
Ecke und Raumdiagonale
[Bearbeiten]
Oberfläche
[Bearbeiten]Die Grenze einer Raumfigur ist eine Fläche, Oberfläche genannt (in diesem Buch werden wir allerdings das Wort Grenzfläche dafür benutzen). Diese kann aus mehreren ebenen Flächen bestehen, wie bei einem Quader oder einer Pyramide, oder auch eine runde Fläche im Raum sein, wie bei einer Kugel, einem Zylinder oder einem Kegel. Wenn die Grenzfläche der Figur ebene Flächen beinhaltet, dann wird zwischen Grundfläche und Seitenflächen unterschieden.
Grundfläche
[Bearbeiten]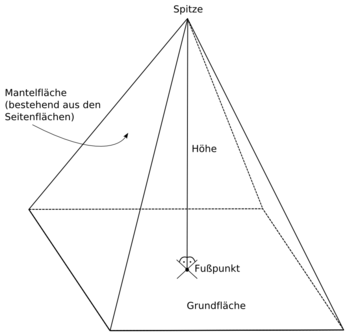
Grundfläche ist die Fläche, die im Bild unten (am Grund) steht. Bei Figuren deren Grenzflächen alle die gleiche Form haben (wie z.B. in einem Quader, wo alle Grenzflächen Rechtecke sind), kann jede beliebige Fläche der Figur als Grundfläche benutzt werden.
Wenn es eine Grenzfläche gibt, die sich von den anderen unterscheidet (wie z.B. bei der Pyramide in unserem Bild: alle Flächen außer einer sind Dreiecke), dann wird i.d.R. diese Fläche als Grundfläche bezeichnet.
Wenn es eine Grundfläche gibt, dann kann ihr gegenüber nur ein Punkt oder eine ganze Fläche stehen. Wenn ihr gegenüber eine ganze Fläche steht, dann nennt man diese Fläche Deckfläche (da sie an der „Decke“ ist). Die Deckfläche kann auch rund sein. Wenn der Grundfläche gegenüber nur ein Punkt liegt (wie in der Pyramide am Bild), dann nennt man diesen Punkt Spitze.
Seitenfläche und Mantel
[Bearbeiten]Wenn es eine Grundfläche gibt, dann nennt man jede der restlichen Flächen Seitenfläche (außer der Deckfläche, wenn es eine gibt). Alle Seitenflächen zusammen nennt man Mantel. Der Mantel kann allerdings auch aus runden und nicht nur ebenen Flächen bestehen, wie z.B. in einem Zylinder (der auch eine Deckfläche hat, die ebenfalls ein Kreis ist) oder einem Kegel (der keine Deckfläche hat, dafür eine Spitze).
Körpernetz
[Bearbeiten]Wenn man die Grenzflächen eines Körpers abwickelt, so dass eine (komplizierte) ebene Figur entsteht, dann nennt man diese ebene Figur Körpernetz (oder einfach Netz). Das ist immer möglich, wenn die Grenzflächen ebene Figuren sind, allerdings nicht immer, wenn die Grenzflächen rund sind. Das ist möglich bei einem Quader, einem Zylinder oder einem Kegel aber nicht möglich bei einer Kugel oder einem Torus.
Gerade und schiefe Körper
[Bearbeiten]-
A: gerades Prisma
B: schiefes Prisma -
Gerade Pyramide
-
Schiefe Pyramide
-
Gerader Kegel
-
Schiefer Kegel
Wenn es bei einem Körper eine Grundfläche gibt, dann gibt es gegenüber entweder eine Fläche oder einen Punkt. Wenn der gegenüberliegende Punkt oder der Mittelpunkt der gegenüberliegenden Fläche direkt oberhalb (also senkrecht nach oben) vom Mittelpunkt der Grundfläche liegen, dann sagt man, dass der Körper gerade ist, sonst dass er schief ist.
Gerade und schiefe Körper
[Bearbeiten]Würfel
[Bearbeiten]-
Würfel
-
Würfelnetz
-
Spielwürfel
Definition
Eine geschlossene Raumfigur, deren Grenzfläche aus 6 kongruente („gleiche“) Quadrate besteht, nennt man Würfel.
Formeln
Mit wird die Länge der Kante bezeichnet.
Volumen:
Oberfläche:
Kantensumme:
Raumdiagonale(rot im Bild):
Flächendiagonale(grün im Bild):
Quader
[Bearbeiten]-
Quader
-
Netz eines Quader
-
Eine quaderförmige
Mauerziegel
Definition
Eine geschlossene Raumfigur, deren Grenzfläche aus 3 Paare paarweise kongruente („gleiche“) gegenüberliegende Rechtecke besteht, nennt man Quader.
Formeln
Mit wird hier die Länge, mit die Breite und mit die Höhe bezeichnet (wie im Bild).
Volumen:
Oberfläche:
Kantensumme:
Raumdiagonale:
Flächendiagonalen: , ,
Prisma
[Bearbeiten]-
Prisma
-
Prismanetz
-
Optisches Prisma
Definition
Eine geschlossene Raumfigur, die durch Parallelverschiebung eines ebenen Vielecks entlang einer nicht in dieser Ebene liegenden Geraden im Raum entsteht, nennt man Prisma. Die Höhe ist der Abstand zwischen Grund- und Deckfläche.
Formeln
Es gibt viele verschiedenen Prismen, daher sollte man dafür die allgemeineren Formeln benutzen, die sich am Ende dieses Teilkapitels befinden.
Pyramide
[Bearbeiten]-
Pyramide
-
Pyramidennetz
-
Einer der ältesten
bekannten Pyramiden -
Maya Pyramide
Definition
Wenn man alle Punkte des Umfangs eines Vieleckes mit einem Punkt (genannt „Spitze“ oder „Scheitel“) außerhalb der Ebene des Vieleckes verbindet, dann entsteht die Grenzfläche einer Pyramide. Das Vieleck bildet dann i.d.R. die Grundfläche, die Dreiecke, die durch die Verbindung des Punktes mit dem Umfang entstehen, sind dann die Seitenflächen. Höhe ist der Abstand zwischen Spitze und Grundfläche.
Formeln
Es gibt viele verschiedenen Pyramiden, daher sollte man dafür die allgemeineren Formeln benutzen, die sich am Ende dieses Teilkapitels befinden.
Zylinder
[Bearbeiten]-
Zylinder
-
Zylindernetz
-
Ein klappbarer (fast) zylinderförmiger Hut
Definition
Eine geschlossene Raumfigur, die durch Parallelverschiebung einer ebenen runden Figur (z.B. eines Kreises oder einer Ellipse) entlang einer nicht in dieser Ebene liegenden Geraden im Raum entsteht, nennt man allgemeinen Zylinder. Das Wort Zylinder allein wird i.d.R. für den Körper benutzt, der durch Parallelverschiebung eines Kreises entsteht. Die Höhe ist der Abstand zwischen Grund- und Deckfläche.
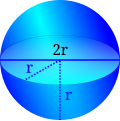
Formeln (für einen geraden Kreiszylinder)
Mit wird hier die Höhe, mit der Radius der Grundfläche bezeichnet (wie im Bild), ist die Mantelfläche:
Volumen:
Oberfläche:
Kegel
[Bearbeiten]-
Gerader Kegel
-
Kegelnetz
-
Spielkegel [1]
- ↑ (die allerdings nicht die Form eines Kegels haben...)
Definition
Wenn man alle Punkte des Umfangs einer runden ebenen Figur mit einem Punkt (genannt „Spitze“ oder „Scheitel“) außerhalb der Figurebene verbindet, entsteht die Grenzfläche eines (allgemeinen) Kegels. Die runde Figur ist dann die Grundfläche und die Fläche, die durch die Verbindung des Punktes mit dem Umfang entsteht, ist der Mantel. Wenn die runde ebene Figur ein Kreis ist, dann spricht man von einem Kreiskegel (in der Schulmathematik oft einfach Kegel genannt). Höhe ist der Abstand zwischen Spitze und Grundfläche. Mit s bezeichnet man die „Mantellinie“ bei einem geraden Kegel.
Formeln (für einen geraden Kegel)
Mit wird hier die Höhe, mit der Radius der Grundfläche bezeichnet (wie im Bild), ist die Mantelfläche:
Volumen:
Oberfläche:
(wobei s die sogenannte „Mantellinie“ ist)
Kugel
[Bearbeiten]-
Kugel
-
Kugel mit Längen- und Breitenkreisen
-
Die Erde mit Längen- und Breitenkreisen
-
Kugelförmige Murmeln
-
Gewehrkugel[1]
-
Ein kugelförmiger Basketball
- ↑ (die allerdings nicht kugelförmig sind)
- ↑ (die allerdings nicht winkeltreu ist)
Für einen Kugel kann man nicht ein Netz auf einer Ebene zeichnen (nur näherungsweise), was der berühmte Mathematiker und Physiker Carl Friedrich Gauß bewiesen hat.
Definition
Eine Raumfigur mit einer Grenzfläche, deren Punkte alle von einem Punkt in der Mitte der Raumfigur (Mittelpunkt genannt) den gleichen Abstand haben (Radius genannt), nennt man Kugel.
Formeln
Mit wird der Radius bezeichnet (wie im Bild).
Volumen:
Oberfläche:
Die platonischen Körper
[Bearbeiten]
|
- ↑ (auch Hexaeder genannt)
Die platonischen Körper sind Raumfiguren, dessen Grenzflächen kongruent („gleich“) zueinander regelmäßige Vielecke sind. Man hat schon in Altertum bewiesen, dass es genau 5 davon gibt: der Würfel, den wir schon gelernt haben (mit 6 Quadrate als Grenzflächen), das Tetraeder (mit vier gleichseitigen Dreiecke als Grenzflächen), das Oktaeder (mit acht gleichseitigen Dreiecke als Grenzflächen), das Dodekaeder (mit zwölf regelmäßigen Fünfecke als Grenzflächen) und das Ikosaeder (mit zwanzig gleichseitigen Dreiecke als Grenzflächen). Da alle Grenzflächen kongruent sind, kann man nicht durch irgendein Merkmal eine Fläche von der anderen oder eine Kante von den andern unterscheiden. Wegen dieser und anderer Eigenschaften haben diese Körper die Philosophen und Wissenschaftler seit der antiken Zeit interessiert.
Eine schöne Animation der Körper und ihrer Körpernetze findet man hier![1]
- ↑ (Vorsicht:dieses Link kann den Browser bei alten Computer verlangsamen)
Andere Figuren
[Bearbeiten]-
Torus
-
Halbkugel
-
Ellipsoid
-
Paraboloid
Selbstverständlich gibt es unendlich viele anderen Raumfiguren, hier erwähnen wir noch den Torus, die Halbkugel, die Ellipsoiden und die Paraboloiden.
Volumen- und Oberflächenregeln
[Bearbeiten]Für alle Körper, die eine Grund- und eine (parellele zur Grundfläche) kongruente („gleiche“) Deckfläche haben, gilt, dass das Volumen die Grundfläche mal die Höhe ist:
Genauer formuliert gilt diese Regel für alle Körper, die durch Parallelverschiebung einer ebenen Fläche entstehen. Für diese Körper gilt dann, dass die Mantelfläche die Summe deren Teilflächen ist und die gesamte Oberfläche . Für die Teilflächen sollte dann man die Formeln aus der Geometrie der Ebene benutzen.
Für alle Körper, die eine Grundfläche und eine gegenüber liegende Spitze haben, gilt, dass das Volumen ein drittel des Produkts der Grundfläche und der Höhe ist:
Genauer gesagt muss dazu gelten, dass die Abstände zwischen Spitze und den Punkten auf dem Umfang der Grundfläche gerade sein sollen. Für diese Körper gilt dann, dass die Mantelfläche die Summe deren Teilflächen ist und die gesamte Oberfläche . Für die Teilflächen sollte dann man die Formeln aus der Geometrie der Ebene benutzen.
Intuitiver Beweis der Formel des Volumens des Quaders
[Bearbeiten]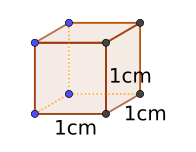
|
|
1 cm³ (auch „Kubikzentimeter“ genannt, Bild links) ist ein Würfel, dessen Kante 1cm ist.
Das Wort „Kubik“ stammt aus dem griechischen Wort für Würfel. Als Hochzahl bedeutet „Kubik“ hoch 3, also Kubikzentimeter (cm³), Kubikmeter (m³) usw.
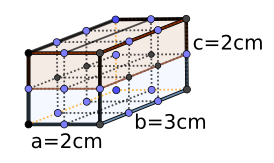
Wie man jetzt im Bild rechts sehen kann, wenn man einen Quader hat, dessen Länge 3cm, dessen Breite 2cm und dessen Höhe 2cm ist, dann beinhaltet dieser Quader 12 Würfel, je 1cm³, also ist das Volumen 12cm³. Man kann daraus folgen, dass das Volumen eines Quaders allgemein die Länge mal die Breite mal die Höhe ist:
Raumgeometrie Anwendung der Formeln
[Bearbeiten]Formel Einsetzen in der Raumgeometrie
[Bearbeiten]

Die Länge eines Lineals ist 3,1 dm, seine Breite 2,5 cm, seine Dicke 2 mm. Berechnen sie die Gesamtlänge seine Kanten, seine Oberfläche und sein Volumen!
Wie wir in der Geometrie der Ebene schon gelernt haben, kann man in solchen Aufgaben das Volumen durch Einsetzen berechnen. Von der Aufgabe kann man schon erschließen, dass das Lineal die Form eines Quaders hat. Hier benutzt man das Wort „Dicke“ anstatt „Höhe“, also wird für diese Dimension ein anderer Name benutzt. Man kann also die Formeln, die in der Formelsammlung für den Quader stehen, benutzen:
Volumen:
Oberfläche:
Kantensumme:
(Mit wird hier die Länge, mit die Breite und mit die Dicke bezeichnet)
Wie aber schon im entsprechenden Kapitel erwähnt, muss man davor warnen, falschen Einheiten anzuwenden! Die Einheiten muss man erst überprüfen und, wenn notwendig, umwandeln. Das ist in dieser Aufgabe schon der Fall:
Wir können alle drei Längenwerte entweder in dm oder in cm oder in mm benutzen. Lass uns hier alle in mm berechnen (wie wir es Kapitel über Einheiten gelernt haben):
Erst jetzt können wir diese Werte in die Formel einsetzen:
Volumen:
Oberfläche:
Kantensumme:
Umformen in der Raumgeometrie konkret
[Bearbeiten]Bei manchen Aufgaben muss man die Formel umformen (wie bei der Geometrie der Ebene), z.B.:

Das Volumen eines (geraden) Zylinders ist 530cm³, seine Höhe 70mm. Wie viel ist seine Fläche?
In der Formelsammlung findet man die Formel für die Fläche:
Oberfläche:
Wenn man die Formel betrachtet, findet man schon das Symbol für die Höhe. Diese aber reicht nicht für die Berechnung des Volumens aus! Man braucht auch den Radius der Grundfläche. Daher wendet man sich an den anderen Vorgaben der Aufgabe. Dort findet man den Wert nicht nur für die Höhe, sondern auch fürs Volumen .
Wir fangen mit der Formel die gegeben ist an.
Hier ist die Formel fürs Volumen gegeben:
Die Werte sowohl fürs Volumen als auch für die Höhe sind zwar gegeben, müssen allerdings übereinstimmen. Wir rechnen erst die 70 mm in cm um (siehe Kapitel „Einheiten umrechnen“):
Jetzt können wir leicht die Oberfläche berechnen, indem wir die entsprechende Formel anwenden:
Umformen in der Raumgeometrie abstrakt
[Bearbeiten]Beim Umformen haben wir am Anfang eine Formel, in der eine bestimmte Variable durch eine Beziehung von anderen Variablen und Zahlen ausgedrückt wird. Diese bestimmte Variable steht allein auf einer Seite (i.d.R. die rechte). Diese Formel wird dann so geändert, dass eine andere Variable der Formel allein auf einer Seite steht. Dafür benutzen wir u.A. die Gegenrechnungen (siehe Kapitel „Umformen“). Z.B. ist plus die Gegenrechnung von minus (und umgekehrt), mal von plus (und umgekehrt), Wurzel von Quadrat (und umgekehrt). „Konkret“ wird in diesem Buch das Umformen dann genannt, wenn die Variablen (außer einer) durch Zahlen ersetzt werden. Wenn dies nicht der Fall ist, wird die Rede von „abstraktem“ Umformen sein. Im letzten Fall bleiben alle Variablen (alle „Buchstaben“) vorhanden. Hier zwei Beispiele aus der Raumgeometrie:
- Radius der Basis eines Zylinders durch das Volumen ausdrücken (und daher auch durch die Höhe).
Hier fangen wir mit der in der [Mathematrix: MA TER/_Formelsammlung_Geometrie|Formelsammlung]] gegebenen Formel fürs Volumen des Zylinders an und formen wir diese um, bis der Radius allein auf einer Seite steht:
- Mantellinie eines Kegels durch seine Oberfläche ausdrücken
(und daher auch durch den Radius der Basis). Hier fangen wir mit der in der [Mathematrix: MA TER/_Formelsammlung_Geometrie|Formelsammlung]] gegebenen Formel für die Oberfläche des Kegels an und formen wir diese um, bis die Mantellinie allein auf einer Seite steht:
Kubikwurzel und weitere Wurzeln
[Bearbeiten]Das Volumen eines Würfels ist 530cm³. Wie viel ist seine Fläche?
Diese Aufgabe ist ähnlich zur Aufgabe im letzten Unterkapitel über Umformen. Die Formeln für den Würfel sind:
.
Man muss erst die Kante des Würfels berechnen, um seine Fläche berechnen zu können. Man kann dafür die Formel fürs Volumen benutzen, , da der Wert des Volumens auch gegeben ist. Welche ist aber die Gegenrechnung von „hoch 3“? Diese Gegenrechnung nennt man Kubikwurzel oder noch besser dritte Wurzel:
Dann kann man leicht die Oberfläche berechnen:
Entsprechend zur Wurzel (die besser Quadratwurzel genannt wird), ist die dritte Wurzel (auch Kubikwurzel genannt) nur dann eine genaue Zahl, wenn die Zahl unter der Wurzel eine sogenannte Kubikzahl ist, wie z.B.:
1(=1³), 8(=2³), 27(=3³), 64(=4³), 125(=5³), 216(=6³), 343(=7³), 512(=8³), 729(=9³), 1000(=10³), 0,008(=0,1³), 9,261(=2,1³)...
Daher gilt:
Die Kubikwurzel von jeder anderen Zahl (die keine Kubikzahl ist) ist eine irrationale Zahl.
Diese Idee der Gegenrechnung kann man auf alle Hochzahlen erweitern:
oder sogar (!):
Zur Vereinfachung der Symbole benutzt man keine Zahl am Anfang des Wurzelzeichens, nur wenn es um die Quadratwurzel geht:
ist gleichbedeutend wie
Herzlichen Dank an alle, deren Bilder ich in diesem Kapitel benutzt habe!
Diagramme
[Bearbeiten]Dieses Kapitel fängt im Grundniveau 2 an und wird im Reifeniveau 3 weitergeführt.
Funktionen
[Bearbeiten]Dieses Kapitel fängt im Grundniveau 3 an und wird im Reifeniveau 1 weitergeführt.
Lineare Gleichungssysteme
[Bearbeiten]Lineare Gleichungssysteme mit 2 Variablen
[Bearbeiten]Additionsverfahren
[Bearbeiten]
Nehmen wir hier die Variable (man kann aber genauso die Variable benutzen). Der y-Koeffizient in der ersten Gleichung ist 3 und in der zweiten 2. Wenn wir den ersten Koeffizient mit 2 multiplizieren und den zweiten mit -3 bekommen wir 6 und ihre Gegenzahl -6. Wenn wir beide Seiten der ersten Gleichung mit 2 multiplizieren, dann haben wir auf beiden Seiten das Gleiche gemacht und beide Seiten werden weiter gleich bleiben (siehe Gegenrechnungen). Ebenfalls wenn wir beide Seiten der zweiten Gleichung mit -3 multiplizieren, bleiben beide Seiten dieser Gleichung gleich:
Wenn wir jetzt die Summe der linken Seiten und die Summe der rechten Seiten beider Gleichungen berechnen, werden die Ergebnisse gleich sein:
Zauberei! Jetzt haben wir nur eine Gleichung mit einem Unbekannten, die wir sofort lösen können!
Wenn wir jetzt eine der beiden Anfangsgleichungen nehmen, können wir auch y berechnen. Nehmen wir die erste:
(x ist -2, wie wir gerade berechnet haben)
|+4
|:3
Die Lösung des Gleichungssystems lautet daher:
und
Tatsächlich kann man diese Werte in beiden Gleichungen einsetzen und feststellen, dass das Ergebnis stimmt. Ersetzen wir in beiden Gleichungen x durch -2 und y durch 5, dann bekommen wir eine wahre Aussage:
Es gibt kein anderes Zahlenpaar, der beide Gleichungen richtig löst, also die Lösung ist eindeutig! Ist es aber immer so? Das ist das Thema des nächsten Unterkapitels.
Lösungsmenge eines linearen Gleichungssystems
[Bearbeiten]| Gleichungssystem A | Gleichungssystem B | |
|---|---|---|
Die Lösung des ersten linearen Gleichungssystems war und , des zweitens und . Geht es aber immer, dass ein Gleichungssystem eine Lösung hat? Die Antwort ist nein. Probieren wir das folgendes Gleichungssystem mit dem Einsetzungsverfahren zu lösen:
| Gleichungssystem C |
|---|
Lösung
→
→ → → !
Man sagt, dass die Aussage am Ende falsch ist. ist doch nicht gleich ! Das bedeutet, dass die beiden Gleichungen, die wir im Gleichungssystem haben ( und ), nicht gleichzeitig erfüllt werden können. Man sagt, dass das Gleichungssystem keine Lösung hat.
Es gibt allerdings noch eine Möglichkeit. Das Gleichungssystem kann unendlich viele Lösungen haben, wie im folgenden Beispiel:
| Gleichungssystem D |
|---|
Lösung
→
→ → →
Man sagt, dass die Aussage am Ende immer wahr ist. Egal wie viel ist, die beiden Gleichungen werden immer gelten. Man soll doch etwas vorsichtig sein. Wenn ist, dann ist (erste Gleichung → → → ). Wenn ist, dann ist (erste Gleichung → → → ). Für jedes gibt es ein bestimmtes und umgekehrt.
Allerdings gilt genau das Gleiche in der zweiten Gleichung: Wenn ist, ist ( → → → ). Wenn ist, dann ist ( → → → ). Egal welchen Wert man für benutzt, wird es für beide Gleichungen der gleiche Wert für als Lösung gelten (und umgekehrt). Es gilt nicht, dass alle Wertepaare (alle Punkte auf der Ebene) Lösungen des Gleichungssystems sind, sondern dass alle Lösungen der einen Gleichung auch Lösungen der anderen Gleichung sind.
Das war allerdings nicht der Fall, als wir eine Lösung des Gleichungssystems hatten (und auf gar keinen Fall, als wir keine Lösung hatten). Nehmen wir beispielsweise das Gleichungssystem A:
6
Da haben wir als Lösung und gefunden. Diese Lösung gilt gleichzeitig für beide Gleichungen. Tatsächlich wenn ist, dann gilt für die erste Gleichung ( → → →) aber auch für die zweite Gleichung ( → → →) . Wenn aber , dann gilt für die erste Gleichung ( → → →) . Für die zweite Gleichung hingegen gilt in diesem Fall: ( → → →) . Die beiden Gleichungen haben den gleichen Wert für y(den Wert 6), nur wenn ist. Man sagt, dass Gleichungssystem A und B eine Lösung haben, Gleichungssystem C keine und Gleichungssystem D unendlich viele Lösungen haben.
Ein lineares Gleichungssystem kann keine, eine oder unendlich viele Lösungen haben.
Viel besser kann man das Ganze verstehen, wenn man die graphischen Lösungen betrachtet.
-
Gleichungssystem A
-
Gleichungssystem B
-
Gleichungssystem C
-
Gleichungssystem D
Im Gleichungssystem A gibt es nur ein Wertepaar, das für beide Funktionen stimmt: . Wenn ist, dann ist für beide Funktionen. Für jeden anderen Wert von x stimmt der Wert von y nicht mehr überein. Beispielsweise für ist für die Funktion und für die Funktion . Es gibt nur ein Wertepaar, das für beide Funktionen eine Lösung ist, und dieses Wertepaar (also der Punkt ) ist die Lösung des Gleichungssystems.
Entsprechend hat auch das Gleichungssystem B nur eine Lösung, den Punkt (Wertepaar) , wie man eindeutig im entsprechenden Bild auch sehen kann. Das ist allerdings nicht der Fall für das Gleichungssystem C. Da laufen die Darstellungen der Funktionen im Koordinatensystem (die Geraden sind) parallel zueinander, sie treffen einander nie. Sie haben daher keinen gemeinsamen Punkt und das Gleichungssystem hat daher keine Lösung (man sagt, dass die Lösung die leere Menge ist). Im Gleichungssystem D hingegen sind alle Punkte der einen Funktion auch Punkte der anderen. Alle Wertepaare, die zu diesen Funktionen gehören, sind daher auch Lösungen des Gleichungssystems D. Das System hat somit unendlich viele Lösungen. Beide Funktionen sind in diesem Fall unterschiedliche Darstellungen der gleichen Funktion. Tatsächlich, wenn man beide Seiten der zweiten Funktion (des Systems D) durch 3 dividiert, bekommt man die erste Funktion:
.
Lösbarkeit eines linearen Gleichungssystems mit 2 Variablen
[Bearbeiten]Man soll zuerst beide Gleichungen in die sogenannte explizite Form umformen, also in der Form, in der y allein auf der linken Seite steht. Nehmen wir die Gleichungssysteme A, C und D des vorherigen Absatzes:
| Gleichungssystem A | Gleichungssystem C | Gleichungssystem D | ||
|---|---|---|---|---|
In der expliziten Form sehen diese Systeme wie im Folgenden aus:
| Gleichungssystem A | Gleichungssystem C | Gleichungssystem D | ||
|---|---|---|---|---|
Bei System A ist die Steigung unterschiedlich (-1 in der ersten Gleichung und -0,6 in der zweiten).
Wenn die Steigung der beiden linearen Funktionen unterschiedlich ist, dann hat das System mit Sicherheit genau eine Lösung.
Bei den Systemen C und D ist die Steigung überall die Gleiche (). Im System C haben die Gleichungen einen anderen y-Achsenabschnitt (+4 und +2). Im System D ist hingegen auch der y-Achsenabschnitt der beiden Gleichungen der gleiche (+4)
Wenn die Steigung der beiden linearen Funktionen die gleiche ist, gibt es zwei Möglichkeiten:
- Ist der y-Achsenabschnitt unterschiedlich, dann gibt es keine Lösung.
- Ist der y-Achsenabschnitt der gleiche, dann gibt es unendlich viele Lösungen.






















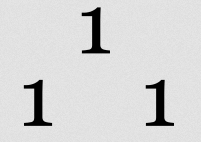












































![{\displaystyle \left[{\frac {2x^{2}-3x+1}{(x+1)\cdot (x-1)}}-{\frac {2x^{2}+2x}{(x-1)\cdot (x+1)}}\right]\cdot (x-1)(x+1)={\frac {2x+15}{(x-1)(x+1)}}\cdot (x-1)(x+1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a8d3bc83087c2d3b64a36e9e800a4f51f1e8b552)






























































![Spielkegel [1]](http://upload.wikimedia.org/wikipedia/commons/thumb/9/92/Bowling-pins.jpg/115px-Bowling-pins.jpg)






![Gewehrkugel[1]](http://upload.wikimedia.org/wikipedia/commons/thumb/7/7e/Projektile_9bzw7%2C62mm.JPG/120px-Projektile_9bzw7%2C62mm.JPG)

![Flächentreue Projektion der Erde[2]](http://upload.wikimedia.org/wikipedia/commons/thumb/f/f2/Goode_homolosine_projection_SW.jpg/120px-Goode_homolosine_projection_SW.jpg)









![Würfel[1]](http://upload.wikimedia.org/wikipedia/commons/thumb/c/cf/Hexahedron_flat_color.svg/91px-Hexahedron_flat_color.svg.png)






























![{\displaystyle a^{3}=V\quad \Leftrightarrow a={\sqrt[{3}]{V}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/13e089531b0b849c30e68a58e08ec463f735480f)
![{\displaystyle a={\sqrt[{3}]{530}}\approx 8,1\ (cm)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/49655481613f3158bf6b0ebfed724cac6bc75745)

![{\displaystyle {\begin{aligned}{\sqrt[{3}]{1}}&=1\\{\sqrt[{3}]{27}}&=3\\{\sqrt[{3}]{343}}&=7\\{\sqrt[{3}]{9{,}261}}&=2{,}1\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ead9293b8d5c52aa98cd099bb701bcace3f323db)
![{\displaystyle {\begin{aligned}{\sqrt[{4}]{a}}&=b&&\rightarrow \quad a=b^{4}\\{\sqrt[{5}]{m}}&=n&&\rightarrow \quad m=n^{5}\\{\sqrt[{-10}]{x}}&=z&&\rightarrow \quad x=z^{-10}\\{\sqrt[{35}]{p}}&=q&&\rightarrow \quad p=q^{35}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f92aae84faa1f8fc8e22c1bff0579f406f9362fd)
![{\displaystyle {\begin{aligned}{\sqrt[{4,3}]{a}}&=b&&\rightarrow \quad a=b^{4,3}\\{\sqrt[{0,3}]{m}}&=n&&\rightarrow \quad m=n^{0,3}\\{\sqrt[{\sqrt {6}}]{x}}&=z&&\rightarrow \quad x=z^{\sqrt {6}}\\{\sqrt[{x}]{p}}&=q&&\rightarrow \quad p=q^{x}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/10a01830f5a736aaff92414b26ff4f0c34067d7b)
![{\displaystyle {\sqrt[{2}]{m}}\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/b4650b423e45e729f221a0e20f736a031e38bfbd)