MathemaTriX ⋅ Theorie nach Thema. Trigonometrische Funktionen

Hoch

STOPP PUSHBACKS • FREE ASSANGE • FRIEDEN AUF DER WELT ${\color {white}\mathbf {MATHE} \mu \alpha T\mathbb {R} ix}$ DEINE FESTE BEGLEITERIN FÜR DIE SCHULMATHEMATIK EINFACH UND VERSTÄNDLICH GRATIS!* MIT MEHR ALS 200 THEORIE- UND AUFGABEN-ERKLÄRUNGS VIDEOS! Mathe lernen ist wie Fahrradfahren lernen: Du kannst es dir stundenlang erklären lassen, du wirst nie fahren können, wenn du nicht selber zu fahren probierst.

Inhalt Ein-Aus- klappen

AUFGABEN

KAPITEL Grundrechenarten Bruchrechnungen $-{\tfrac {\cdot \ +}{\ :\ }}$ Schlussrechnung Prozentrechnung Exponentialfunktion Logarithmus Arbeiten mit Termen $\mathbb {X} ^{2}$ Zahlendarstellungen Mengentheorie Aussagenlogik ${\begin{matrix}\mathbb {R} :=\\\mathbb {Q} \cup \mathbb {I} \end{matrix}}$ Einheiten $cm^{2}$ Statistik und Wahrscheinlichkeit Geometrische Konstruktionen Geometrie der Ebene Geometrie des Raums Diagramme Funktionen $f(x)$ Lineare Gleichungssysteme ${\begin{smallmatrix}{a_{1}\ b_{2}}\\{a_{2}\ b_{2}}\end{smallmatrix}}$ Trigonometrische Funktionen Vektoren Differentialrechnung $^{dy}/_{dx}$ Integralrechnung $\textstyle \int _{a}^{b}dx$ Folgen $a_{n}$ Beweise $a\rightarrow b$

Definition von Sinus Kosinus und Tangens

Definitionen	Trigon. Umkehrf.
Pythagoras abstrakt	Pythagoras konkret

An jedem rechtwinkeligen Dreieck gilt eine gewisse Regel, die schon seit zumindest 4000 Jahren bekannt ist. Diese Regel wurde nach einem griechischen Philosophen genannt: der Pythagoräische Lehrsatz.

In einem rechtwinkeligem Dreieck ist die Summe der Quadrate der Katheten gleich dem Quadrat der Hypotenuse.

Dieser Satz ist verständlicher, wenn wir das erste Dreieck für einen Entwurf des Satzes mit Symbolen benutzen. Wenn a und b die zwei kleineren Seiten des rechtwinkeligen Dreiecks (Katheten genannt) und c die größere (Hypotenuse genannt) sind, ist der entsprechende mathematische Ausdruck:

$a^{2}+b^{2}=c^{2}$

Genauso seit tausenden Jahren bekannt ist eine andere Eigenschaft der geometrischen Figuren und in diesem Fall der rechtwinkeligen Dreiecke. Bei ähnlichen Dreiecken (wenn alle Winkel gleich sind) ist das Verhältnis (der Bruch der Längen) der entsprechenden Seiten konstant. $\textstyle {\frac {b}{c}}\$im ersten Dreieck im Bild ist genauso viel wie $\textstyle {\frac {g}{f}}\$im zweiten. Besonders in rechtwinkeligen Dreiecken bedeutet diese Tatsache, dass:

• Das Verhältnis der dem kleinsten Winkel gegenüberliegenden Seite (hier a) zu Hypotenuse (hier c) eine konstante Zahl für alle ähnlichen rechtwinkeligen Dreiecke ist.
• Das Verhältnis der dem kleinsten Winkel anliegenden Kathete (hier b) zu Hypotenuse eine konstante Zahl für alle ähnlichen rechtwinkeligen Dreiecke ist.

Das entsprechende gilt für den anderen nicht rechten Winkel.

Mit Buchstaben ist dieser Satz viel verständlicher. Im ersten Dreieck gilt: $\ \textstyle {\frac {a}{c}}\$und $\textstyle \ {\frac {b}{c}}\$sind konstant, für alle ähnlichen rechtwinkeligen Dreiecke.

Der erste Bruch wurde Sinus genannt, der zweite Kosinus. Für den kleinsten Winkel (nennen wir ihn $\alpha$) des ersten Bildes gilt also:

$\sin \alpha ={\frac {a}{c}}\$und $\ \cos \alpha ={\frac {b}{c}}\$

Die zwei Dreiecke im Bild sind ähnlich. Die kleinste Kathete a im ersten Dreieck durch seine Hypotenuse, wird so viel sein, wie die kleinste Kathete c im zweiten Dreieck durch seine Hypotenuse:

$\textstyle \sin \alpha ={\frac {a}{c}}={\frac {c}{f}}=\$und $\textstyle \ \cos \alpha ={\frac {b}{c}}={\frac {g}{f}}\$

Somit werden Sinus und Kosinus definiert. Sinus und Kosinus sind die zwei wichtigsten trigonometrischen Funktionen. Formell:

$\sin \theta ={\frac {\text{Gegenkathete}}{\text{Hypotenuse}}}\$und $\ \cos \theta ={\frac {\text{Ankathete}}{\text{Hypotenuse}}}\$

wobei $\theta$ irgendein nicht rechter Winkel in einem Rechtwinkeligen Dreieck.

Für den anderen nicht rechten Winkel des ersten Dreiecks (nennen wir ihn $\beta$) gilt dann:

$\textstyle \sin \beta ={\frac {b}{c}}(=\cos \alpha )\$und $\textstyle \ \cos \beta ={\frac {a}{c}}(=\sin \alpha )$,

da gegenüber von $\beta$ die Seite b ist.

Alle Winkel zusammen in einem Dreieck sind 180°. In einem rechtwinkeligen Dreieck ist einer Winkel 90°, daher sind die anderen zwei zusammen auch 90°. Daher gilt:

$\textstyle \sin \alpha {\frac {b}{c}}=\cos \beta =\cos(90^{\circ }-\alpha )\$und $\textstyle \ \cos \alpha =\sin \beta =\sin(90^{\circ }-\alpha )$.

Mit Hilfe des Pythagoräischen Lehrsatzes ist auch leicht zu zeigen, dass:

$\sin ^{2}x+\cos ^{2}x=1$.

$\sin ^{2}x\$ und $\ \cos ^{2}x\$bedeuten $\ (\sin x)^{2}\$ bzw. $\ (\cos x)^{2}\$.

Beweisen Sie die Gleichung $\sin ^{2}x+\cos ^{2}x=1$ mit Hilfe der entsprechenden Definitionen und des Pythagoras-Satzes! Zeigen Sie dann dazu, dass $\textstyle \ \tan x={\frac {\sin x}{\cos x}}\ \$und $\textstyle \ \tan ^{2}x={\frac {1}{\cos ^{2}x}}-1$ In einem rechtwinkeligen Dreieck mit c als Hypotenuse und a und b als Katheten gilt: $a^{2}+b^{2}=c^{2}$ Für den Winkel α (der Seite a gegenüber) gilt laut Definition: $\sin \alpha ={\frac {a}{c}}\ \rightarrow \ a=c\ \sin \alpha \quad$und $\quad \cos \alpha ={\frac {b}{c}}\ \rightarrow \ b=c\ \cos \alpha$ Daher: $a^{2}+b^{2}=c^{2}\ \rightarrow \ c^{2}\ \sin ^{2}\alpha +c^{2}\cos ^{2}\alpha =c^{2}\ \rightarrow \$ $c^{2}\ (\sin ^{2}\alpha +\cos ^{2}\alpha )=c^{2}\ \rightarrow \ \sin ^{2}\alpha +\cos ^{2}\alpha =1$ c² ist sicherlich nicht null (sonst hätten wir kein Dreieck), daher können wir es wegfallen lassen. Da der Winkel α irgendeine Zahl sein kann, und wir daher ein anders Symbol dafür benutzen dürfen, können wir stattdessen x schreiben: $\sin ^{2}x+\cos ^{2}x=1$ Laut Definition des Tangens ist er so viel wie das Verhältnis der Gegenkathete zur Ankathete. Daher gilt auch: $\tan \alpha ={\frac {a}{b}}={\frac {c\ \sin \alpha }{c\ \cos \alpha }}={\frac {\sin \alpha }{\cos \alpha }}$ Die Kombination der beiden Ergebnissen können wir benutzten, um zu zeigen, dass $\textstyle \ \tan ^{2}x={\frac {1}{\cos ^{2}x}}-1$: $\tan \alpha ={\frac {\sin \alpha }{\cos \alpha }}\Rightarrow \tan ^{2}\alpha ={\frac {\sin ^{2}\alpha }{\cos ^{2}\alpha }}={\frac {1-\cos ^{2}\alpha }{\cos ^{2}\alpha }}={\frac {1}{\cos ^{2}x}}-{\frac {\cos ^{2}\alpha }{\cos ^{2}\alpha }}={\frac {1}{\cos ^{2}x}}-1$

Es gibt allerdings noch eine wichtige Trigonometrische Funktion, der Tangens. Er ist das Verhältnis der Gegen- zu Ankathete:

$\tan \alpha ={\frac {a}{b}}={\frac {c\ \sin \alpha }{c\ \cos \alpha }}={\frac {\sin \alpha }{\cos \alpha }}$

Die Symbole für manche weiteren trigonometrischen Funktionen sind: $\sec ,\ \csc \$ und $\ \cot$. Es gibt allerdings auch die Umkehrfunktionen. Von $\sin ,\ \cos \$und $\ \tan \$ werden sie mit den Symbolen $\arcsin ,\ \arccos \$bzw. $\ \arctan \$ oder $\sin ^{-1},\ \cos ^{-1}\$bzw. $\ \tan ^{-1}\$ (besonders bei Taschenrechnern) dargestellt.

Einheitskreis

Einheitskreis und trigonometrische Funktionen

• 
• 
• 
• 
• 
• 

Der Einheitskreis ist ein in einem Koordinatensystem gezeichneter Kreis. Sein Mittelpunkt ist der Koordinatensystemanfang (also der Punkt (0|0)) und sein Radius ist die Einheit (also 1). Der Radius steht am Anfang auf der x Achse rechts und wird im Gegenuhrzeigesinn gedreht. Dadurch entsteht ein Winkel im Kreis (und ein Punkt P auf dem Kreis), wie im ersten Bild zu sehen ist. Im zweiten Bild sehen wir genauer diese Drehung. Wir sehen auch, dass ein viertel Kreis Drehung einen 90°, ein halber Kreis einen 180°, drei viertel Kreis 270° und ein ganzer Kreis 360° Winkel entsprechen.

Im dritten Bild sehen wir, dass der Sinus gleich der Seite gegenüber dem Winkel ist und der Kosinus gleich der Ankathete. Sinus wird als Gegenkathete durch Hypotenuse definiert: $\textstyle \ \sin \alpha ={\frac {a}{c}}={\frac {a}{1}}=a\$, da die Hypotenuse c in diesem Fall gleich 1 ist. Das Entsprechende gilt für Kosinus: $\textstyle \ \cos \alpha ={\frac {b}{c}}={\frac {b}{1}}=b\$. Die Länge der Seite a ist allerdings auch so viel wie die y-Koordinate des entsprechenden Punktes. Das bedeutet, dass auf der y-Achse der Sinus des Winkels dargestellt wird. Entsprechend wird auf die x-Achse der Kosinus des Winkels dargestellt (die Seite b, also die x-Koordinate des entsprechenden Punktes auf dem Kreis).

Im vierten Bild sehen wir, dass ein Winkel $\theta \$und sein Gegenwinkel $-\theta \$den gleichen Kosinus haben. Da ein ganzer Kreis 360° ist, haben $\theta \$ und $360^{\circ }-\theta \$ den gleichen Kosinus. Im fünften Bild sehen wir, dass ein Winkel $\omega \$und sein Supplementwinkel math>180^\circ -\omega\ </math>den gleichen Sinus haben. Im letzten Bild sehen wir, dass wenn wir eine ganze Drehung (oder mehrere ganzen Drehungen) dazu machen, der neue Winkel sowohl den gleichen Sinus als auch den gleichen Kosinus hat.

Im letzten Bild wird allerdings eine ganze Drehung mit 2π und nicht mit 360° bezeichnet. Das ist eine andere Einheit für die Messung von Winkeln, Radiant genannt. Genauso wie es auf der Welt für die Messung von einer Länge verschiedene Einheiten, wie km oder Meile gibt, gibt es verschiedene Einheiten auch für die Messung einer Drehung (eines Winkels). 2π rads entsprechen einer ganzen Drehung, also 360°.

Radiant

Für jede physikalische Größe gibt es mehrere Einheiten. Für die Länge gibt es beispielsweise die Einheiten Meter, Dezimeter, Zoll, Meile usw.. Die Einheiten gehören zu einem sogenannten Einheitensystem oder metrischen System. Manche Einheiten, wie beispielsweise das Zentimeter oder die Sekunde gehören zu mehreren solchen Systemen.

Für die Messung einer Drehbewegung verwenden wir in der Regel den Winkelgrad. Ein Grad ist $\textstyle {\frac {1}{360}}\$einer ganzen Drehung. Eine ganze Drehung ist damit 360°. Bei Rechnungen in der höheren Mathematik und in der Physik hat sich allerdings gezeigt, dass eine andere Einheit notwendig ist, der Radiant (rad). Eine ganze Drehung ist $2\pi \$rad. Mit Schlussrechnung können wir daher sehr einfach zwischen den beiden Einheiten umrechnen:

${\begin{matrix}2\pi \ {\text{rad}}\\{}\\x\end{matrix}}\quad {\begin{matrix}\cdots \cdots \\\searrow \cdot \\\cdots \cdots \end{matrix}}\quad {\begin{matrix}360^{\circ }\\:\uparrow \\60^{\circ }\end{matrix}}\quad x=\textstyle {\frac {\pi }{3}}\ {\text{rad}}\qquad \qquad \qquad {\begin{matrix}360^{\circ }\\{}\\x\end{matrix}}\quad {\begin{matrix}\cdots \cdots \\\searrow \cdot \\\cdots \cdots \end{matrix}}\quad {\begin{matrix}2\pi \ {\text{rad}}\\:\uparrow \\\pi \ {\text{rad}}\end{matrix}}\quad x=\textstyle 180^{\circ }$

Einheitskreis wichtige Punkte

Der Einheitskreis wird durch die beiden Achsen des Koordinatensystems in vier gleichen Teilen geteilt. Diese Teile werden Quadrante genannt und werden in einer ähnlichen Weise wie der Winkel in diesem Kreis definiert (Gegenuhrzeigersinn, Aufzählungsanfang oben rechts), d.h. der Teil oben rechts (zwischen 0° und 90°) wird erstes, oben links (zwischen 90° und 180°) zweites, unten links (zwischen 180° und 270°) drittes und unten rechts (zwischen 270° und 360° bzw. wieder 0°) viertes Quadrant genannt.

Im Einheitskreis wird der Sinus auf der y-Achse dargestellt. Tatsächlich ist zumindest im ersten Quadrant die Länge der Gegenkathete des Winkels so viel wie die y-Koordinate des entsprechenden Punktes auf dem Einheitskreis. Das gilt für alle Quadrante, allerdings nur für den Betrag der y-Koordinate (die unterhalb der x-Achse doch negativ ist). Das bedeutet:

Der Sinus ist im ersten und zweiten Quadrant positiv, im dritten und vierten negativ.

Entsprechend liegt die Ankathete des Winkels auf der x-Achse, die links von der y-Achse ihre negativen Werte hat. Daher gilt:

Der Kosinus ist im ersten und vierten Quadrant positiv und im zweiten und dritten negativ.

Da der Tangens auch als das Verhältnis von Sinus durch Kosinus definiert kann, ist es leicht auch sein Vorzeichen in den verschiedenen Quadranten zu finden. Im ersten Quadrant sind Sinus und Kosinus positiv, also auch der Tangens, im zweiten ist Sinus positiv und Kosinus negativ, daher ist dort der Tangens negativ ("Plus durch minus ist minus"). Es gilt daher:

Der Tangens ist im ersten und dritten Quadrant positiv und im zweiten und vierten negativ.

Am Einheitskreis gibt es einige besondere Punkte, wie wir im letzten Bild links sehen können. Bei 0 rad (und 0°) ist die y-Koordinate, also Sinus, gleich null und die x-Koordinate, also der Kosinus, so viel wie der Radius, also 1. Bei $\textstyle {\frac {\pi }{2}}\$rad (90°) ist Kosinus null und Sinus 1. Bei $\pi \$rad (180°) ist Kosinus −1 und Sinus wieder null, bei $\textstyle {\frac {3\,\pi }{2}}\$rad (270°) ist wiederum Kosinus null und Sinus −1.

Von der Natur der Definition von Sinus und Kosinus im Einheitskreis wird sichtbar, dass Sinus und Kosinus Werte im Intervall zwischen −1 und 1 annehmen.

Sinus und Kosinus nehmen Werte im Intervall zwischen −1 und 1 an.

Es gibt keinen Winkel (im Bereich der reellen Zahlen) der Sinus oder Kosinus mehr als 1 oder weniger als −1 hat. Das gilt allerdings nicht für den Tangens, der jeden Wert annehmen kann. Beispielsweise, wenn der Winkel nah zu $\textstyle {\frac {\pi }{2}}\$rad (90°) ist, dann nimmt Sinus Werte immer näher zu 1 und Kosinus immer näher zu null an. Daher nimmt Tangens Werte gegen Unendlichkeit an. Bei $\textstyle {\frac {\pi }{2}}\$rad ist allerdings der Tangens nicht mehr definierbar, da Kosinus (der Nenner) null ist.

Ein weiterer interessanter Winkel ist $\textstyle {\frac {\pi }{4}}\$rad (45°). In diesem Fall hat das rechtwinkelige Dreiecke zwei gleichen Winkel, es ist also gleichschenklich. Der Sinus ist in diesem Fall so viel wie der Kosinus $(\textstyle ={\frac {\sqrt {2}}{2}})$ und lässt sich einfach mit Hilfe des Satzes von Pythagoras berechnen. Bei $\textstyle {\frac {\pi }{6}}\$rad (30°) haben wir die Hälfte eines gleichseitigen Dreiecks, die Gegenkathete ist daher die Hälfte der Hypotenuse und der Sinus daher $\textstyle ={\frac {1}{2}}$, so viel wie der Kosinus des Komplementwinkels $\textstyle {\frac {\pi }{3}}\$rad (60°). Der Kosinus von $\textstyle {\frac {\pi }{6}}\$rad (30°) (und der Sinus von $\textstyle {\frac {\pi }{3}}\$rad also von 60°) lässt sich dann leicht mit Hilfe des Pythagorassatzes für Trigonometrie $(\sin ^{2}x+\cos ^{2}x=1)$:
$\textstyle \cos {\frac {\pi }{6}}=\sin {\frac {\pi }{3}}={\frac {\sqrt {3}}{2}}$.
Mit Hilfe des Einheitskreises und Beachtung des Vorzeichens lassen sich dadurch die trigonometrische Zahlen der entsprechenden Winkel in den anderen Quadranten berechnen, also auch die entsprechenden Tangens.

Trigonometrische Funktionen Diagramm

Sinus Diagramm und Einheitskreis

Nehmen wir an, dass ein Punkt P_K sich auf einem Kreis mit konstanter (Winkel- oder Bahn-) Geschwindigkeit bewegt („gleichförmige“ Kreisbewegung) (siehe Animation). P_Y ist die Projektion des Punktes auf der y-Achse. Stellen wir uns vor, dass sich an Punkt P_Y eine Füllfeder befindet und darunter ein bewegendes Papier. Die Füllfeder hinterlässt eine Spur (Punkt P_F) auf dem Papier. Das Ergebnis würde wie auf den folgenden Bildern aussehen.

Die Kurve die entsteht nennt man Kosinusfunktion. Sie (als auch die Sinusfunktion) ist eine sogenannte Winkelfunktion. Winkelfunktionen und Kreisbewegung sind also ganz stark miteinander verbunden. Eigentlich ist die Kreisfunktion eine Kombination von zwei Winkelfunktionen (Sinus und Cosinus) in zwei verschiedenen Richtungen (Senkrecht und Waagerecht). Hier ist noch ein dreidimensionales Bild zur Entstehung der Kosinus Funktion (links) und ein Bild zur Entstehung der Sinus Funktion (rechts).

Winkelfunktionen stellen die Basis für die Beschreibung und das Verständnis der Schwingungen und daher auch der Wellen dar. Eine genauere Beschreibung der Mathematik der Wellen ist aber außerhalb der Ziele dieses Buches. Dafür soll man sich an anderen Quellen wenden, z.B. Wellenfunktion oder Wellengleichung.

Parameter im Diagramm der Sinusfunktion

Das Diagramm der Sinusfunktion $f(x)=\sin x\$sieht wie eine Welle aus:

Hier werden wir erkunden, wie sich das Diagramm der Sinusfunktion ändert, wenn wir sogenannten Parameter der Grundfunktion modifizieren. Allgemein (mit solchen Parametern) ist die Formel für die Sinusfunktion (genauer gesagt: für eine Wellenfunktion in der Mechanik):

$f(x)=A_{0}\sin(\omega x+\phi )+c$

$A_{0}$ ist die sogenannte Amplitude. Sie zeigt uns wie weit nach oben und nach unten der Wert der Funktion schwankt. Sinus (und Kosinus) nehmen Werte zwischen 1 und −1. Das können wir mit Hilfe des Einheitskreises sofort sehen. Wenn wir Sinus mit $A_{0}$ multiplizieren (und nichts anderes machen) wird die Funktion Werte zwischen $-A_{0}$ und $A_{0}$ aufnehmen. Im Bild ist $f_{1}(x)=\sin x$ (schwarz, Amplitude $A_{0}=1$), $f_{2}(x)=2{,}5\sin x$ (blau, Amplitude $A_{0}=2{,}5$), $f_{3}(x)=-0{,}5\sin x$ (rot, Amplitude $A_{0}=-0{,}5$), $f_{4}(x)=-1{,}5\sin x$ (grün, Amplitude $A_{0}=-1{,}5$).

$\omega$ ist die sogenannte Winkelfrequenz. Sie zeigt uns wie oft innerhalb eines Intervalls des x-Wertes von $2\pi$ der y-Wert wieder seinen Anfangswert bekommt. Zwischen Winkelfrequenz und Frequenz $f$ gilt: $\omega =2\pi f$. Der Kehrwert der Frequenz ist die Periode: $T={\tfrac {1}{f}}$. Daher gilt auch: $\omega ={\tfrac {2\pi }{T}}$. Sinus (und Kosinus) nehmen wiederholt Werte zwischen 1 und −1. Die Periode zeigt uns, nach welcher Änderung des x-Wertes der Wert der Funktion (y-Wert) wieder der gleiche sein wird. Ist $f>1$ (und daher $T<1$), dann kommt die Welle im Diagramm öfters vor. Im Bild ist $f_{1}(x)=\sin x$ (schwarz, Winkelfrequenz $\omega =1$, Periode $T=2\pi$, Intervall $=2\pi$), $f2(x)=\sin(2{,}5x)$ (blau, Winkelfrequenz $\omega =2{,}5$, Periode $T=0{,}8\pi$), $f3(x)=\sin {\tfrac {2}{3}}x$ (rot, Winkelfrequenz $\omega ={\tfrac {2}{3}}$, Periode $T=3\pi )$.

$\phi$ ist die sogenannte Phase. Sie zeigt uns an welcher Stelle die Funktion "anfängt". Die Sinusfunktion fängt normalerweise mit null und steigend an. Wenn die Phase nicht null ist, dann ist der Wert der Funktion null (und die Funktion steigend) bei $x=-\phi$. Im Bild ist $f_{1}(x)=\sin x$ (schwarz, Phase $\phi =0$ ), $f2(x)=\sin(x-0{,}5)$ (rot, Phase $\phi =2{,}5$, der Wert der Funktion ist 0 bei $x=0{,}5$ ), $f3(x)=\sin(x+0{,}8)$ (blau, Phase $\phi =0{,}8$, der Wert der Funktion ist 0 bei $x=-0{,}8)$.

$c$ ist eine Konstante, die das ganze Diagramm nach oben ($c$ positiv) oder nach unten ($c$ negativ) verschiebt. Im Bild ist $f_{1}(x)=\sin x$ (schwarz, $c=0$ ), $F2(x)=\sin x+0{,}8)$ (rot, $c=0{,}8$, Funktion um 0,8 senkrecht nach oben verschoben), $F3(x)=\sin x-1{,}4$ (blau, $c=-1{,}4$, Funktion um 1,4 senkrecht nach unten verschoben).

Hier sehen wir ein Beispiel, wo alles kombiniert wird. Die Funktion nimmt Werte von −3 bis 1,4. Die gesamte Schwankung (das doppelte der Amplitude) ist daher 4,4 und die Amplitude selber $A_{0}=2{,}2$. Die Funktion ist allerdings nach unten verschoben, die Werte schwanken um den Wert −0,8, daher ist die Konstante $c=-0{,}8$. Die Phase zu finden ist in diesem Fall ein bisschen komplizierter. Da die Funktion nach unten verschoben ist, müssen wir den Anfang etwas nach unten (bei −0,8) suchen. Dann können wir entdecken, dass der "Anfang" an der Stelle −0,5 ist, daher ist die Phase +0,5. Die rote Funktion lautet daher:

$g(x)=2{,}2\sin(x+0{,}5)-0{,}8$

Beweis des Sinussatzes

Der Sinussatz besagt, dass in jedem Dreieck die Verhältnisse der Sinusse seiner Winkeln zur entsprechenden gegenüberliegenden Seiten gleich zueinander sind:

${\frac {\sin \alpha }{a}}={\frac {\sin \beta }{b}}={\frac {\sin \gamma }{c}}$

Selbstverständlich gilt der Satz auch für die Kehrwerte:

${\frac {a}{\sin \alpha }}={\frac {b}{\sin \beta }}={\frac {c}{\sin \gamma }}$

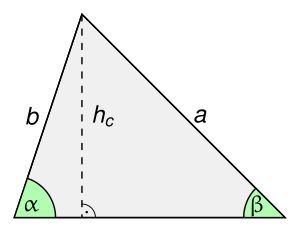
Um den Satz für zwei zufällige Winkel des Dreiecks zu beweisen, reicht es eine Höhe (im Bild die Höhe $h_{c}$) des Dreiecks einzuzeichnen. Diese Höhe zerlegt das Dreieck in zwei rechtwinklige Teildreiecke, in denen man den Sinus von $\alpha$ und $\beta$ jeweils als Quotient von Gegenkathete und Hypotenuse ausdrücken kann, nach der Definition von Sinus:

$\sin \alpha ={\frac {h_{c}}{b}}$

$\sin \beta ={\frac {h_{c}}{a}}$

Auflösen nach $h_{c}$ ergibt:

$h_{c}=b\cdot \sin \alpha$

$h_{c}=a\cdot \sin \beta$

Durch Gleichsetzen erhält man demnach

$a\cdot \sin \beta =b\cdot \sin \alpha$

Dividiert man nun durch $\sin \alpha \cdot \sin \beta$, so erhält man den ersten Teil der Behauptung:

${\frac {a}{\sin \alpha }}={\frac {b}{\sin \beta }}$

Die Gleichheit mit ${\tfrac {c}{\sin \gamma }}$ ergibt sich entsprechend durch Benutzung der Höhe $h_{a}$ oder $h_{b}$.

Beweis des Kosinussatzes

Der Kosinussatz ist eine Verallgemeinerung des Satzes von Pythagoras auf alle Dreiecke. Der besagt, dass das Quadrat von jeder Seite eines zufälligen Dreiecks gleich die Differenz der Summe der Quadrate der anderen zwei Seiten minus das zweifache des Produktes dieser Seiten und des Kosinus der dazwischen liegenden Winkel ist:

$c^{2}=a^{2}+b^{2}-2\,a\,b\,\cos \gamma$

Da die Seite c zufällig ausgewählt wird, gilt der Satz auch für die anderen zwei Seiten:

$b^{2}=a^{2}+c^{2}-2\,a\,c\,\cos \beta$

$a^{2}=b^{2}+c^{2}-2\,b\,c\,\cos \alpha$

Im folgenden Beweis wird $\gamma <90^{\circ }$ vorausgesetzt.

Dreieck

In den Teildreiecken soll der Satz des Pythagoras angewandt werden, um einen Rechenausdruck für $c^{2}$ zu finden. Wir zeichnen wieder die Höhe $h$ ein. Für das rechte (rechtwinkelige) Dreieck gilt laut Satz von Pythagoras:

$h^{2}=b^{2}-e^{2}$

Die Seite $a$ wird allerdings in der Figur in zwei Teile zerlegt, es gilt daher $a=d+e\Rightarrow d=a-e$

Für das linke (auch rechtwinkelige) Dreieck gilt daher:

$c^{2}=h^{2}+d^{2}$

$d^{2}=(a-e)^{2}=a^{2}-2\cdot a\cdot e+e^{2}$ (nach der binomischen Formel)

Kombinieren wir diese drei Gleichungen, ergibt sich für $c^{2}$:

$c^{2}={\overset {b^{2}-e^{2}}{h^{2}}}+{\overset {a^{2}-2\cdot a\cdot e+e^{2}}{d^{2}}}=b^{2}-e^{2}+a^{2}-2\cdot a\cdot e+e^{2}=a^{2}+b^{2}-2\cdot a\cdot e$

Zusätzlich gilt laut Definition des Kosinus:

$\cos \gamma ={\frac {e}{b}}\Rightarrow e=b\cdot \cos \gamma$

Wenn wir dieses Ergebnis in die letzten Gleichung für $c^{2}$ einsetzten, ergibt sich der Kosinussatz:

$c^{2}=a^{2}+b^{2}-2\cdot a\cdot {\overset {b\cdot \cos \gamma }{e}}\Rightarrow c^{2}=a^{2}+b^{2}-2\cdot a\cdot b\cdot \cos \gamma$

Für $\gamma >90^{\circ }$ muss der Beweis geringfügig modifiziert werden. Für $\gamma =90^{\circ }$ ergibt sich der Kosinussatz direkt aus dem Satz des Pythagoras.

Direkte Anwendung des Sinus und des Kosinussatzes

Der Sinus- und der Kosinussatz können bei der Berechnung von verschiedenen Größen in Dreiecken benutzt werden aber auch in Vielecken mit Hilfe von Dreiecken. Wenn in einem Dreieck zwei Seiten und der Winkel dazwischen gegeben sind, dann kann man den Kosinussatz benutzen, in allen anderen Fällen sollte der Sinussatz passend sein.

• Berechnen sie die Diagonalen $d_{1},\ d_{2}$ des abgebildeten Deltoids, wenn die Seite $a$ 4,3 cm, die Seite $b$ 7,6 cm und der dazwischen liegende Winkel $\angle ab$ 134° sind.

Mit direkter Anwendung des Kosinussatzes können wir die Diagonale $d_{1}$ sofort berechnen:

$d_{1}^{2}=a^{2}+b^{2}-2\,a\,b\,\cos(\angle ab)\Rightarrow d_{1}\approx 11{,}0\ {\text{cm}}$

Mit Hilfe des Sinussatzes können wir dann den Winkel $\angle d_{1}b$ berechnen:

${\frac {\sin(\angle d_{1}b)}{a}}={\frac {\sin(\angle ab)}{d_{1}}}\Rightarrow \angle d_{1}b=\arcsin \left({\frac {a\cdot \sin(\angle ab)}{d_{1}}}\right)\Rightarrow \angle d_{1}b\approx 16{,}29^{\circ }$

Dann können wir auch die andere Diagonale mit Hilfe der Definition von Sinus berechnen:

$\sin(\angle d_{1}b)={\frac {\ d_{2}/2\ }{b}}\Rightarrow d_{2}=2\cdot b\cdot \sin(\angle d_{1}b)\Rightarrow d_{2}\approx 4{,}3\ {\text{cm}}$

Vermessungsaufgaben

Trotz GPS werden heutzutage immer noch Abstände mit Hilfe von besonderen Winkelmessgeräten berechnet. Hier sind zwei typische Aufgaben zu diesem Thema. Für ihre Lösung sind der Sinus und/oder der Kosinussatz notwendig.

• Lisa beobachtet die Antenne auf dem Dach eines Gebäudes. Ihre Augen sind 1,73 m hoch, die Antenne selber ist 2,8 m hoch. Den unteren Rand der Antenne sieht Lisa unter einem Höhenwinkel von 67°, den oberen unter 74°. Wie weit vom Gebäude (genauer: vom "Fuß" der Antenne) befindet sich Lisa und wie hoch ist das Gebäude? Machen Sie eine saubere Skizze für die Berechnung!

Der Winkel $\beta \$ist $74^{\circ }-67^{\circ }=7^{\circ }$, der Winkel $\angle ADC=74^{\circ }$. Da $ADC$ ein rechtwinkeliges Dreieck ist, ist der Winkel $\angle ACD=90^{\circ }-74^{\circ }=16^{\circ }$. Mit Hilfe des Sinussatzes können wir dann die Seite $BD$ berechnen:

${\frac {\sin \beta }{\overline {BC}}}={\frac {\sin(\angle ACD)}{\overline {BP}}}\quad \Rightarrow \quad {\overline {BP}}\approx 6{,}33\ m$.

Mit Hilfe der Definition von Sinus und Kosinus können wir dann die Fragen beantworten:

Höhe des Gebäudes:
$\sin \alpha ={\frac {\overline {AB}}{\overline {BP}}}\quad \Rightarrow \quad {\overline {FB}}={\overline {FA}}+{\overline {AB}}\approx 7{,}56\ m$

Abstand:
$\cos \alpha ={\frac {\overline {AD}}{\overline {BP}}}\quad \Rightarrow \quad {\overline {AD}}\approx 2{,}47\ m$

• Vom Gipfel eines 1563 m hohen Berges wird der Abstand zwischen zwei Türmen in einem Tal gemessen, die sich beide auf einer Höhe von 548 m befinden. Zum ersten Turm wird der Tiefenwinkel $\alpha =47^{\circ }$ gemessen und nach Schwenken des Messgerätes um den Horizontalwinkel $\gamma =69^{\circ }$ zum anderen Turm wird dieser unter dem Tiefenwinkel $\beta =49^{\circ }$ gesehen. Wie viel ist der Abstand zwischen den Türmen? Machen Sie eine saubere Skizze für die Berechnung!

Die Strecke ${\overline {BD}}\$ist der Höhenunterschied, also $1563-548=1015\ m$. Mit Hilfe der Definition von Tangens können wir leicht die Strecken ${\overline {BC}},\ {\overline {BF}}\$messen:

$\tan(\angle DCB)={\frac {\overline {DB}}{\overline {BC}}}\quad \Rightarrow \quad {\overline {BC}}\approx 846{,}5\ m$.

$\tan(\angle DFB)={\frac {\overline {DB}}{\overline {BF}}}\quad \Rightarrow \quad {\overline {BF}}\approx 882{,}3\ m$.

Mit Hilfe des Kosinussatzes können wir dann den Abstand zwischen den beiden Türmen berechnen:

${\overline {CF}}^{2}={\overline {BF}}^{2}+{\overline {BC}}^{2}-2\ {\overline {BF}}\ {\overline {BC}}\cos \gamma \approx 1037{,}2\ m$