MathemaTriX ⋅ Theorie nach Thema. Statistik und Wahrscheinlichkeitsrechnung

Hoch

STOPP PUSHBACKS • FREE ASSANGE • FRIEDEN AUF DER WELT ${\color {white}\mathbf {MATHE} \mu \alpha T\mathbb {R} ix}$ DEINE FESTE BEGLEITERIN FÜR DIE SCHULMATHEMATIK EINFACH UND VERSTÄNDLICH GRATIS!* MIT MEHR ALS 200 THEORIE- UND AUFGABEN-ERKLÄRUNGS VIDEOS! Mathe lernen ist wie Fahrradfahren lernen: Du kannst es dir stundenlang erklären lassen, du wirst nie fahren können, wenn du nicht selber zu fahren probierst.

Inhalt Ein-Aus- klappen

AUFGABEN

KAPITEL Grundrechenarten Bruchrechnungen $-{\tfrac {\cdot \ +}{\ :\ }}$ Schlussrechnung Prozentrechnung Exponentialfunktion Logarithmus Arbeiten mit Termen $\mathbb {X} ^{2}$ Zahlendarstellungen Mengentheorie Aussagenlogik ${\begin{matrix}\mathbb {R} :=\\\mathbb {Q} \cup \mathbb {I} \end{matrix}}$ Einheiten $cm^{2}$ Statistik und Wahrscheinlichkeit Geometrische Konstruktionen Geometrie der Ebene Geometrie des Raums Diagramme Funktionen $f(x)$ Lineare Gleichungssysteme ${\begin{smallmatrix}{a_{1}\ b_{2}}\\{a_{2}\ b_{2}}\end{smallmatrix}}$ Trigonometrische Funktionen Vektoren Differentialrechnung $^{dy}/_{dx}$ Integralrechnung $\textstyle \int _{a}^{b}dx$ Folgen $a_{n}$ Beweise $a\rightarrow b$

Lageparameter

Lageparameter Einführung

In der Mathematik, besonders im Bereich der Statistik, gibt es viele sogenannten Mittelwerte. Was ist ein Mittelwert? Wenn man viele Werte (viele Zahlen, die irgendwas messen) hat, dann gibt es eine Zahl, die sich irgendwie in der Mitte dieser Werte befindet. Das ist ein Mittelwert. Es gibt aber verschiedene „Mitten“, also verschiedene Wege um diese Mitte zu berechnen, je nachdem wie das Problem ist. Zwei von diesen Wegen werden wir hier lernen, den Durchschnitt (auch arithmetisches Mittel genannt) und den Median (auch Zentralwert genannt). Wir werden auch den sogenannten Modalwert (Modus) kennenlernen, der zwar kein Mittelwert aber für die Beschreibung von Daten oft hilfreich ist.

Durchschnitt (arithmetisches Mittel)

Fangen wir mit einem Beispiel an:

• Die Familien eines kleinen Dorfes haben Kirschen geerntet. Die Ernte für die verschiedenen Familien war: 54kg, 65kg, 48kg, 76kg, 52kg, 65kg, 45kg. Sie haben allerdings vereinbart, dass jede Familie doch gleich so viele Kirschen bekommt. Wie viel bekommt jede Familie?

Um diese Frage zu beantworten, soll man erst die ganze Ernte berechnen, also die Teilernten addieren. Dann wird die ganze Ernte auf die Anzahl der Familien geteilt. So wird jede Familie gleich so viele Kirschen bekommen. Das Ergebnis nennt man Durchschnitt.

$\mathbf {Durchschnitt} ={\frac {\mathrm {Summe\ der\ Werte} }{\mathrm {Anzahl\ der\ Werte} }}={\frac {54+65+48+76+52+65+45}{7}}\approx 57{,}86$  (das sind kg)

Jede Familie bekommt dann ca. 57,86 kg.

Den Durchschnitt (auch arithmetisches Mittel genannt) mehrerer Werte berechnet man, indem man ihre Summe durch ihre Anzahl (wie viele Werte wir haben) dividiert:

$\mathbf {Durchschnitt} ={\frac {\mathbf {Summe\ der\ Werte} }{\mathbf {Anzahl\ der\ Werte} }}$

Median (Zentralwert)

Den Median (auch Zentralwert genannt) mehrerer Werte findet man, indem man die Werte zuerst der Größe nach ordnet (z.B. vom kleineren zum größeren) und dann den Wert in der Mitte der Reihe wählt.

Ein Beispiel!

• Das Gewicht der Schüler in einer Klasse ist: 54kg, 65kg, 48kg, 76kg, 52kg, 65kg, 45kg. Wie viel ist der Median?

Zuerst der Größe nach ordnen!

45, 48, 52, 54, 65, 65, 76

(ALLE Werte schreiben, also zwei oder mehr mal schreiben, wenn der Wert mehrmals vorkommt; jeden Wert muss man schreiben, so oft wie er vorkommt)

Der Wert in der Mitte ist 54. Es gibt 3 Werte links und 3 Werte rechts. Also 54 ist genau in der Mitte. Daher ist 54kg der Median!

Was ist aber, wenn die Anzahl der Werte eine gerade Zahl ist, wenn wir z.B. 12 Werte haben (12 ist eine gerade Zahl) und nicht 7 wie vorher (7 ist eine ungerade Zahl). Wenn man 7 Werte hat (oder irgendeine andere ungerade Zahl) dann gibt es genau eine Zahl in der Mitte. Bei gerader Anzahl der Werte gibt es doch 2 Zahlen in der Mitte. In diesem Fall wird als Median der Wert definiert, der genau zwischen den beiden Zahlen in der Mitte steht, also der Durchschnitt der beide Zahlen. Schauen wir ein Beispiel an!

• Das Gewicht der Schüler in einer Klasse ist: 52kg, 65kg, 48kg, 76kg, 52kg, 65kg, 45kg, 65kg, 45 kg, 45kg, 78kg, 69kg. Wie viel ist der Median?

Zuerst der Größe nach ordnen!

45, 45, 45, 48, 52, 52, 65, 65, 65, 69, 76, 78

(ALLE Werte schreiben, also jeden Wert schreiben, so oft wie er vorkommt)

Hier gibt es zwei Werte in der Mitte, 52 und 65. Der Median ist genau in der Mitte also die beide Werte addieren und durch 2 dividieren:

$\mathbf {Median} ={\frac {52kg+65kg}{2}}=58{,}5\ kg$

Modus (Modalwert)

Der Modus (auch Modalwert genannt) von mehreren Werten ist der Wert, der am häufigsten vorkommt.

Ein Beispiel!

• Das Gewicht der Schüler in einer Klasse ist: 54kg, 63kg, 48kg, 76kg, 52kg, 63kg, 45kg. Wie viel ist der Modalwert?

Hier kommt 63 zwei mal vor, alle andere Werte kommen nur einmal vor. Daher ist 63kg der Modus.

Was ist aber, wenn mehrere Werte öfters vorkommen? Noch ein Beispiel!

• Das Gewicht der Schüler in einer Klasse ist: 52kg, 65kg, 48kg, 76kg, 52kg, 65kg, 45kg, 65kg, 45 kg, 45kg, 78kg, 69kg.

Hier kommt 45 drei mal vor, 65 drei mal vor, 52 zwei mal vor und die restlichen Werte nur ein mal vor. 45 und 65 kommen am öftesten vor. Daher sind sie beide Modalwerte. 52 hingegen kommt nicht so oft vor wie 45 und 65 (also „nur“ zwei mal), daher ist 52 kein Modalwert. Es gilt also:

Modalwerte (Modi): 45kg und 65kg

Vergleichen von Mittelwerten

 

Weicht der Durchschnitt vom Median stark ab, dann ist die Verteilung ungleichmäßig. Weicht der Durchschnitt vom Median nicht stark ab, dann kann man eine eher gleichmäßiger Verteilung nicht ausschließen. (Vorausgesetzt, dass alle Werte positiv sind)

Um zu verstehen, was das bedeuten soll, schauen wir folgende vier Säulendiagramme an:

• 
  1: Ungleichmäßige Verteilung
• 
  2: relativ gleichmäßige Verteilung
• 
  3: relativ gleichmäßige Verteilung
• 
  4: Ungleichmäßige Verteilung

Nehmen wir an, dass diese vier Bilder die Vermögensverteilung in vier verschiedenen Staaten zeigen. Wenn die verschiedenen Diagramme verglichen werden, wird festgestellt, dass ungleichmäßige Diagramme (wo es weniger großen Werte gibt und viele kleinere) einen größeren Durchschnitt als der Median haben. Je ungleichmäßiger das Diagramm, desto größer der Unterschied zwischen Durchschnitt und Median. Das ist also mit dem ersten Satz dieses Kapitels gemeint: Weicht der Durchschnitt vom Median stark ab, dann ist die Verteilung ungleichmäßig. Weicht der Durchschnitt vom Median nicht stark ab, dann kann man eine eher gleichmäßiger Verteilung nicht ausschließen. Allerdings, wenn es negative Werte gibt, die die größeren Werte ausgleichen, gilt diese Regel nicht mehr.

Im ersten Diagramm kommt der Reihe nach vier mal die eins, vier mal die zwei, vier mal die vier, zwei mal die sechs, ein mal zwanzig und ein mal Hundert. Der Median ist also 3, der Durchschnitt 10. Die Verteilung ist ziemlich ungleichmäßig, Median und Durchschnitt weichen stark ab.

Im zweiten Diagramm kommt der Reihe nach acht mal die sieben, sieben mal die acht und ein mal die achtzehn. Der größte Wert (18) ist ca. 2,5 mal wie der kleinste (7). Der Median ist 7,5 und der Durchschnitt 10. Die Verteilung ist relativ gleichmäßig, der Median und der Durchschnitt sind nah zueinander.

Im dritten Diagramm kommt der Reihe nach acht mal die fünf, zwei mal die zehn, vier mal die fünfzehn und dann ein mal siebzehn und ein mal 23. Der größte Wert (23) ist ca. 4,5 mal wie der kleinste (5). Der Median ist 7,5 und der Durchschnitt 10. Die Verteilung ist relativ ungleichmäßig, der Median und der Durchschnitt sind aber wieder nah zueinander.

Im vierten Diagramm kommt der Reihe nach sechs mal die eins, zwei mal die zwei, sieben mal die zehn und dann ein mal 80. Der größte Wert (80) ist 80 mal wie der kleinste (1). Der Median ist 6 und der Durchschnitt 10. Die Verteilung ist stark ungleichmäßig, der Median und der Durchschnitt sind aber relativ nah zueinander.

Nur im ersten Diagramm weichen Median und Durchschnitt stark voneinander ab, da können wir sicher sein, dass die Verteilung ungleichmäßig ist. In den anderen drei Diagrammen können wir feststellen, dass ein relativ kleiner Unterschied zwischen Median und Durchschnitt nicht aussagekräftig sein kann, da wir sowohl ein relativ gleichmäßige als auch eine relativ ungleichmäßige Verteilung haben können. Aber auch bei großen Unterschieden zwischen Median und Durchschnitt können wir immer noch nicht sagen, ob eine Ungleichmäßigkeit auch innerhalb der obersten Hälfte vorhanden ist oder nicht.Wenn z. B. 50 Werte 1 sind und 49 Werte 1000, dann ist der Durchschnitt (495,45) extrem größer als der Median (1), es sind aber immerhin fast die Hälfte der größeren Werte gleich.

Ein gutes Beispiel solcher Unterschiede ist die Vermögensverteilung in Europa und in der Welt. In Europa ist die Ungleichmäßigkeit in Deutschland und Österreich ziemlich ausgeprägt, wie ein Studium der europäischen Zentralbank gezeigt hat. Das erste Diagramm könnte wohl die Verteilung in diesen zwei Ländern repräsentieren. Was die Welt betrifft, sind nach einigen Studien die Ungleichmäßigkeiten noch (und viel) stärker.

Der Vergleich zwischen Durchschnitt und Median kann seine Aussagekraft über die Ungleichmäßigkeit der Verteilung (sogar völlig) verlieren, wenn manche Werte negativ sind. Das einfachste Beispiel dafür, ist, wenn wir drei Werte haben: −8, 1 und 10. In diesem Fall sind sowohl Durchschnitt als auch Median gleich 1, die Verteilung ist allerdings extrem ungleichmäßig. Beim Vermögen würde diese Verteilung beispielsweise bedeuten, dass eine Person stark verschuldet, eine knapp nicht verschuldet und eine reich ist. Der Vergleich zwischen Median und Durchschnitt ist in diesem Fall nutzlos.

Streumaßen

Streuungsmaßen um den Durchschnitt (um das arithmetische Mittel)

Der Durchschnitt (fachgerecht arithmetisches Mittel genannt) einer Anzahl von Werten ist die Summe dieser Werte durch ihre Anzahl. Nehmen wir zwei einfache Beispiele von Daten und denken wir an einem konkreten Beispiel: Das Gewicht der Personen von zwei Kinder-Teams mit jeweils drei Personen wird gemessen.

Datenreihe 1: 46, 51, 47 (in kg)$\textstyle \qquad \qquad D={\frac {46+51+47}{3}}=48$

Datenreihe 2: 64, 33, 47 (in kg)$\textstyle \qquad \qquad D={\frac {64+33+47}{3}}=48$

Der Durchschnitt (das arithmetische Mittel) in beiden Fällen ist 48 kg. Der Median ist ebenfalls in beiden Fällen gleich (47 kg). Wir merken allerdings, dass zwischen den beiden Verteilungen doch einen Unterschied besteht, der auch durch den Vergleich zwischen Median und Durchschnitt nicht sichtbar wird. In der zweite Verteilung ist der kleinste Wert viel kleiner und der größte viel größer als in der ersten. Für den Vergleich der beiden Verteilungen brauchen wir daher noch etwas, das diesen Unterschied sichtbar macht.

Das einfachste Mittel um diesen Unterschied sichtbar zu machen ist die sogenannte Spannweite. Das ist die Differenz zwischen größten und kleinsten Wert der Verteilung. In der ersten Datenreihe ist die Spannweite 51−46=5 kg, in der zweiten 64−33=31 kg. Der Unterschied zwischen der Spannweiten ist in diesem einfachen Fall groß und aussagekräftig. Es geht aber doch um ein einfaches Beispiel. Für komplexere Beispiele braucht man ein anderes Maß. Dieses ist i. d. R. die sogenannte (empirische) Standardabweichung.

Bei der spitzen Kurve weichen die gemessenen Werte weniger vom Durchschnitt (in der Mitte) ab

Die Standardabweichung ist ein Maß dafür, wie stark die gemessenen Werte vom Durchschnitt (bzw. Erwartungswert) abweichen. Sie ist die Wurzel der sogenannten (empirischen) Varianz. Diese lässt sich ungefähr als arithmetisches Mittel der Quadrate der Differenzen der jeweiligen Werte und des Durchschnitts der Werte. Dieser Satz ist kompliziert, daher erklären wir Schritt zum Schritt, wie die Varianz berechnet wird.

In der ersten Datenreihe ist der Durchschnitt 48. Berechnen wir die Differenz der jeweiligen Werte und des Durchschnitts. Die Differenz des ersten Wertes und des Durchschnitts ist 46−48=−2, die anderen zwei Differenzen sind 51−48=3 und 47−48=−1.

Berechnen wir jetzt die Quadrate dieser Differenzen: (−2)²=4, 3²=9 und (−1)²=1

Somit haben wir die Quadrate der Differenzen der jeweiligen Werte und des Durchschnitts: 4, 4 und 0. Der Durchschnitt ist dann die Summe durch die Anzahl also$\textstyle \ D_{V}={\frac {4+9+1}{3}}=4,{\dot {6}}$. Allerdings wird oft aus bestimmten Gründen bei der Berechnung der Varianz besonders bei größeren Datenreihen nicht genau dieser Durchschnitt benutzt, sondern die Summe der Quadrate durch die um eins reduzierte Anzahl n−1 berechnet. Die berechnete Summe der Quadrate wird also nicht durch die Anzahl n dividiert, sondern durch die Anzahl um 1 reduziert (n−1). Als Symbol für die Varianz in diesem Fall wird oft $s_{x}^{2}\$benutzt.

$s_{x}^{2}={\frac {4+9+1}{3-1}}=7$

Für die zweite Datenreihe sind die Differenzen: 64−48=16, 33−48=−15 und 47−48=−1. Die Varianz in diesem Fall ist daher:

$s_{x}^{2}={\frac {16^{2}+(-15)^{2}+1}{3-1}}=241$

Für den allgemeinen Fall benutzen wir die Formel:

$s_{x}^{2}={\frac {1}{n-1}}\sum \limits _{i=1}^{n}\left(x_{i}-{\overline {x}}\right)^{2}$

Erklären wir kurz, was die ganze Symbolik bedeutet: n ist die Anzahl der Werte. Im Nenner steht n−1, es wird also durch die um eins reduzierte Anzahl dividiert. Das Symbol $\textstyle \ \sum \$bedeutet Summe. i ist ein Index für den x-Wert, also für einen Wert der Datenreihe. Diese werden von 1 bis n durchnummeriert. Der Strich über das x bedeutet den Durchschnitt der n-Werte, die mit x₁, x₂, ... , x_n dargestellt werden. Der Ausdruck $\textstyle \ \sum \limits _{i=1}^{n}\left(x_{i}-{\overline {x}}\right)^{2}\$bedeutet daher: Wir berechnen eine Summe$\textstyle \ \left(\sum \right)\$, die mit den Werten x_i mit i von 1 bis n zu tun hat. Erst durchnummerieren wir diese Werte von 1 bis n (n ist die Anzahl der Werte), also erster Wert $x_{1}$, zweiter $x_{2}\$ usw. Für jeden Wert berechnen wir das Quadrat seiner Differenz zum Durchschnitt ${\overline {x}}$. Für den ersten Wert ist das $\left(x_{1}-{\overline {x}}\right)^{2}$, für den zweiten $\left(x_{2}-{\overline {x}}\right)^{2}\$und allgemein $\left(x_{i}-{\overline {x}}\right)^{2}$. Der Ausdruck $\textstyle \ \sum \limits _{i=1}^{n}\left(x_{i}-{\overline {x}}\right)^{2}\$kann so abgelesen werden: "Wir berechnen die Differenz jedes Wertes $x_{i}$ vom Durchschnitt ${\overline {x}}$, wir quadrieren die Differenz und am Ende berechnen wir die Summe $\textstyle \ \sum \$der Quadrate aller Differenzen, von $\ i=1{\text{:}}\ \left(x_{1}-{\overline {x}}\right)^{2}$ bis $\ i=n{\text{:}}\ \left(x_{n}-{\overline {x}}\right)^{2}$".

Die (empirische) Standardabweichung lässt sich dann als Wurzel der Formel für die empirischen Varianz berechnen:

$s={\sqrt {{\frac {1}{n-1}}\sum \limits _{i=1}^{n}\left(x_{i}-{\overline {x}}\right)^{2}\quad }}$

In unserem Beispiel sind die Standardabweichungen ${\sqrt {7}}\approx 2{,}65\$bzw. ${\sqrt {2}}41\approx 15{,}52$. Allein die Tatsache, dass die Standardabweichung die gleichen Einheiten wie die Variable hat (hier kg), im Gegenteil zur Varianz (hier kg²), sollte darauf hinweisen, dass die Standardabweichung ein geeigneteres Instrument als die Varianz für die Beschreibung der Streuung ist.

Streuungsmaßen um den Median (den Zentralwert)

Den Median (auch Zentralwert genannt) mehrerer Werte findet man, indem man die Werte zuerst der Größe nach ordnet (z.B. vom kleineren zum größeren) und dann den Wert in der Mitte der Reihe wählt.

Die Spannweite, also die Differenz zwischen größten und kleinsten Wert ist ein Streuungsmaß auch im Fall des Medians. Ein anderes Maß ist in diesem Fall der Interquartilsabstand (Symbol IQR). Median ist der Wert in der Mitte der geordneten Werte. Wenn wir den ersten viertel der geordneten Werte nehmen, dann ist der Wert am oberen Rand das untere (erste) Quartil. Am oberen Rand der ersten drei Viertel befindet sich das obere (dritte) Quartil. Die Differenz der Werte des oberen und des unteren Quartils ist der Interquartilsabstand.

All diese Sachen können wir in einem sogenannten Boxplot Diagramm darstellen. Das folgende Beispiel beruht auf einer Messreihe mit den folgenden 20 Datenpunkten:

$i$	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
$x_{i}$ (unsortiert)	9	6	7	7	3	9	10	1	8	7	9	9	8	10	5	10	10	9	10	8
$x_{(i)}$ (sortiert)	1	3	5	6	7	7	7	8	8	8	9	9	9	9	9	10	10	10	10	10

Beispiel für einen Box-Plot

Ein Box-Plot hilft dabei sehr schnell einen Überblick über diese Daten zu erhalten. So erkennt man direkt, dass der Median (durchgezogene Linie) genau bei 8,5 liegt und dass je 25 % der Daten unter 7 und über 9,5 liegen, denn dies sind genau die Abmessungen der Box (die "Schachtel" in der Mitte), in der 50 % der Messwerte enthalten sind. Folglich ist auch der Interquartilsabstand, der der Länge der Box entspricht, genau 2,5 (also 9,5−7).

Dieser Box-Plot wurde mit Whiskern bis zu einer Länge des 1,5-fachen Interquartilsabstands erstellt. Diese sind also maximal 3,75 Maßeinheiten lang. Allerdings reichen Whisker stets nur bis zu einem Wert aus den Daten, der sich noch innerhalb dieser 3,75 Einheiten befindet. Der obere Whisker verläuft also nur bis zu 10, da es keinen größeren Wert in den Daten gibt, und der untere Whisker nur bis 5, da der nächstkleinere Wert weiter als 3,75 vom Anfang der Box entfernt ist.

Die Werte von 1 und 3 werden im Box-Plot als Ausreißer markiert, da sie sich nicht innerhalb der Box oder der Whisker befinden. Bei diesen Werten sollte untersucht werden, ob es sich tatsächlich um Ausreißer oder um Tippfehler oder anderweitig auffällige Werte handelt.

Baumdiagramm

Denken wir an das folgende mathematische Problem:

In einer Urne gibt es 5 schwarze und 4 rote Kugeln. Wir ziehen drei mal zufällig jeweils eine Kugel, ohne sie zurückzulegen. Wie viel ist die Wahrscheinlichkeit, dass: A) alle 3 Kugel rot sind? B) die ersten zwei schwarz und die dritte rot sind? C) wir zwei schwarze und eine rote Kugel ziehen? D) wir zwei rote und eine schwarz Kugel ziehen? E) das Letztere passiert, wenn wir doch zurücklegen?

Am Anfang haben wir 4 roten Kugeln und 9 insgesamt, daher ist die Wahrscheinlichkeit, dass wir eine rote Kugel ziehen $\textstyle {\frac {4}{9}}$. Wenn wir ein rote ziehen, dann gibt es noch 3 roten von insgesamt 8, also sie die Wahrscheinlichkeit $\textstyle {\frac {3}{8}}$. Wir können allerdings alle mögliche Ergebnisse in ein sogenanntes "Baumdiagramm" darstellen, wie im Bild links. Der einzige Pfad, wo drei rote Kugeln gezogen werden, ist der ganz links. Um die Wahrscheinlichkeit, dass drei roten Kugeln gezogen werden, zu berechnen, müssen wir das Produkt der Wahrscheinlichkeiten von jedem Schritt bilden.

Warum multiplizieren wir in diesem Fall? Wir können an ein ganz einfaches Beispiel denken. Denken wir einfach an eine Schokoladentafel. Wenn wir $\textstyle {\frac {2}{5}}\$ davon nehmen, dann haben dieses Bild: . Wenn wir von diesen $\textstyle {\frac {2}{5}}\$ $\ \textstyle {\frac {3}{7}}\$nehmen, dann haben wir ein neues Bild: . Jeder kleiner Teil in diesem neuen Bild ist $\textstyle {\frac {1}{35}}\$ der Schokolade und wir haben 6 solchen Teil. Daher haben wir die beiden Brüchen multipliziert: $\textstyle {\frac {2}{5}}\cdot {\frac {3}{7}}={\frac {6}{35}}$. Genauso ist es mit der Wahrscheinlichkeit. Bei jedem Schritt nehmen wir einen Teil des neuen Teils, wir müssen daher multiplizieren. Somit ist die Antwort zur ersten Frage: $\textstyle {\frac {4}{9}}\cdot {\frac {3}{8}}\cdot {\frac {2}{7}}={\frac {1}{21}}$. Genauso können wir die Antwort zur Frage B finden: $\textstyle {\frac {5}{9}}\cdot {\frac {4}{8}}\cdot {\frac {4}{7}}={\frac {10}{63}}$

Für jeden Pfad müssen wir das Produkt der Wahrscheinlichkeit von jedem Schritt bilden. Wenn aber eine Frage durch verschiedene Pfade erfüllt wird, dann müssen wir die Wahrscheinlichkeiten der unterschiedlichen Pfade addieren. Im Beispiel mit der Schokolade können wir so denken, dass verschiedene Personen die ganze Schokolade (Wahrscheinlichkeit 1) teilen und dass wir dann die Teile von mehrere Personen zusammenrechnen wollen. Das ist der Fall in Fragen C und D. In beiden Fragen gibt es drei Pfade, die das gefragte erfüllen:

• C) ${\frac {5}{9}}\cdot {\frac {1}{2}}\cdot {\frac {4}{7}}+{\frac {5}{9}}\cdot {\frac {1}{2}}\cdot {\frac {4}{7}}+{\frac {4}{9}}\cdot {\frac {5}{8}}\cdot {\frac {4}{7}}$
  $={\frac {10}{63}}+{\frac {10}{63}}+{\frac {10}{63}}={\frac {10}{21}}$
• D) ${\frac {4}{9}}\cdot {\frac {3}{8}}\cdot {\frac {5}{7}}+{\frac {4}{9}}\cdot {\frac {5}{8}}\cdot {\frac {3}{7}}+{\frac {5}{9}}\cdot {\frac {1}{2}}\cdot {\frac {3}{7}}$
  $={\frac {5}{42}}+{\frac {5}{42}}+{\frac {5}{42}}={\frac {5}{21}}$

Für die letzte Fragen müssen wir einfach dazu denken, dass in diesem Fall bei jedem Schritt die Wahrscheinlichkeit gleich bleibt:

• E) ${\frac {4}{9}}\cdot {\frac {4}{9}}\cdot {\frac {5}{9}}+{\frac {4}{9}}\cdot {\frac {5}{9}}\cdot {\frac {4}{9}}+{\frac {5}{9}}\cdot {\frac {4}{9}}\cdot {\frac {4}{9}}$
  $=3\cdot {\frac {80}{729}}={\frac {240}{729}}$

Wahrscheinlichkeitsverteilungen

Binomialverteilung

Die Binomialverteilung ist eine von mehreren sogenannten Wahrscheinlichkeitsverteilungen. Sie dient dazu, die Wahrscheinlichkeit eines gewissen Ereignisses bei bestimmten Zufallsexperimenten zu berechnen. Was das bedeutet, werden wir durch ein einfaches Beispiel erklären.

Wenn wir eine Münze werfen, gibt es zwei mögliche Ereignisse: "Kopf" oder "Zahl". Die Wahrscheinlichkeit des Ereignisses Kopf ist in der Regel 50%, in diesem Fall genau so viel, wie die Wahrscheinlichkeit des Gegenereignisses "nicht Kopf", also des Ereignisses "Zahl". 50% ist 0,5. Beide Ereignisse zusammen, also dass "Kopf" oder "Zahl" herauskommt, haben eine gesamte Wahrscheinlichkeit von 100%, also von 1. In den Wahrscheinlichkeitsverteilungen werden in der Regel reine Zahlen wie 0,5 und 1 statt ihre Prozentdarstellungen (50% bzw. 100%) benutzt.

Der Münzwurf ist ein Zufallsexperiment. Bei einem Wurf wissen wir (normalerweise) nicht, was das Ergebnis sein wird. Wir wissen aber schon, dass die Wahrscheinlichkeit, dass eines der beiden Ergebnissen vorkommt, genau 0,5 ist. Das bedeutet, dass, wenn wir die Münze sehr oft werfen, ungefähr (oder genau) die Hälfte der Ergebnisse wird Kopf sein und die andere Hälfte Zahl. Je öfter wir die Münze werfen, desto näher zu 0,5 wird das Ergebnis Kopf vorkommen.

In diesem Zufallsexperiment gibt es genau zwei mögliche Ergebnisse: Kopf oder Zahl. Wenn ein Würfel geworfen wird, gibt es 6 möglichen Ergebnisse. Die Binomialverteilung beschriebt die Wahrscheinlichkeiten bei Zufallsexperimenten mit genau zwei möglichen Ergebnissen, wie beim Münzwurf. Mit Hilfe der entsprechenden Formel können wir beispielsweise berechnen, wie viel die Wahrscheinlichkeit ist, dass nach 5 Würfen Kopf genau 4 mal vorkommt. Die allgemeine Formel für die Berechnung dieser Wahrscheinlichkeit ist:

$B(k\mid p,n)={\binom {n}{k}}p^{k}(1-p)^{n-k}$

B ist die Wahrscheinlichkeit, die wir berechnen wollen, n ist die Anzahl der Wiederhollungen des Experiments (im Beispiel ist es 5 Würfen), k zeigt uns wie oft das gefragte Ereignis vorkommt (im Beispiel 4 mal Kopf) und p ist die Wahrscheinlichkeit dieses Ereignisses bei einer Wiederholung als reine (und nicht Prozent-) Zahl (in unserem Beispiel die Wahrscheinlichkeit, dass nach einem Wurf Kopf vorkommt, also 0,5). Der Ausdruck $\textstyle \ {\binom {n}{k}}\$ist die sogenannte "Binomialkoeffizient" und lässt sich bei den meisten Taschenrechner mit Hilfe der Taschenrechnerfunktion "nCr" berechnen. Im konkreten Beispiel ist die gefragte Wahrscheinlichkeit:

$B(4\mid 0{,}5,\ 5)={\binom {5}{4}}\cdot 0{,}5^{4}\cdot (1-0{,}5)^{5-4}=5\cdot 0{,}5^{4}\cdot 0{,}5^{1}=0{,}15625$

Welche Möglichkeiten gibt es bei diesem Zufallsexperiment? Dass Kopf genau 0, 1, 2, 3, 4, 5 oder 6 mal vorkommt. Die Summe aller Wahrscheinlichkeiten muss selbstverständlich 1 sein. Probieren wir es aus:

$B(0\mid 0{,}5,\ 5)={\binom {5}{0}}\cdot 0{,}5^{0}\cdot (1-0{,}5)^{5-0}=1\cdot 0{,}5^{0}\cdot 0{,}5^{5}=0{,}03125$

$B(1\mid 0{,}5,\ 5)={\binom {5}{1}}\cdot 0{,}5^{1}\cdot (1-0{,}5)^{5-1}=5\cdot 0{,}5^{1}\cdot 0{,}5^{4}=0{,}15625$

$B(2\mid 0{,}5,\ 5)={\binom {5}{2}}\cdot 0{,}5^{2}\cdot (1-0{,}5)^{5-2}=10\cdot 0{,}5^{2}\cdot 0{,}5^{3}=0{,}3125$

$B(3\mid 0{,}5,\ 5)={\binom {5}{3}}\cdot 0{,}5^{3}\cdot (1-0{,}5)^{5-3}=10\cdot 0{,}5^{3}\cdot 0{,}5^{2}=0{,}3125$

$B(4\mid 0{,}5,\ 5)={\binom {5}{4}}\cdot 0{,}5^{4}\cdot (1-0{,}5)^{5-4}=5\cdot 0{,}5^{4}\cdot 0{,}5^{1}=0{,}15625$

$B(5\mid 0{,}5,\ 5)={\binom {5}{5}}\cdot 0{,}5^{5}\cdot (1-0{,}5)^{5-5}=1\cdot 0{,}5^{5}\cdot 0{,}5^{0}=0{,}03125$

Wenn wir diese Wahrscheinlichkeiten addieren, bekommen wir tatsächlich 1 (was 100% ist, also alle Möglichkeiten):

$0{,}03125+0{,}15625+0{,}3125+0{,}3125+0{,}15625+0{,}03125=1$

Die Wahrscheinlichkeit, dass bei einem Versuch, eines von beiden Ergebnissen vorkommt, ist selbstverständlich nicht immer 0,5 wie beim Münzwurf. Denken wir an eine Urne mit 8 Kugeln, von denen 3 rot und 5 Schwarz sind. Wenn wir zufällig eine Kugel wählen, ist die Wahrscheinlichkeit, dass sie rot ist, nicht mehr 0,5 sondern $\textstyle {\frac {3}{8}}=0{,}375$. Mit Hilfe der Formel können wir dann die Wahrscheinlichkeit berechnen, dass nach 9 mal Ziehen (immer mit Zurücklegen der Kugel) 6 mal rot gezogen wird:

$B(6\mid 0{,}375,\ 9)={\binom {9}{6}}\cdot 0{,}375^{6}\cdot (1-0{,}375)^{9-6}=84\cdot 0{,}375^{6}\cdot 0{,}625^{3}\approx 0{,}057$

Diese Wahrscheinlichkeit ist nicht so groß und das war intuitiv schon zu erwarten, da rot nur 3 in 8 mal vorkommt, also in 9 mal ein bisschen mehr als 3 mal. Wie oft erwarten wir, dass rot nach 9 mal Ziehen vorkommt? Schon ein bisschen mehr als 3 mal aber sicherlich nicht 4 mal. Dieser Wert wird Erwartungswert $\ \mu \$genannt und lässt sich leicht mit der folgenden Formel berechnen:

$\mu =n\cdot p$

In diesem Beispiel ist der Erwartungswert:

$\mu =9\cdot 0{,}375=3{,}375$

Das ist eine Art von Mittelwert. Wenn wir tatsächlich das Experiment durchführen, werden wir allerdings nie diesen Wert bekommen (es ist physikalisch unmöglich, wir können nur ganzen Kugeln ziehen). Die tatsächlichen Ergebnissen werden um diesen Wert sozusagen variieren. Ein Maß für diese Variation ist die sogenannte Standardabweichung:

$\sigma ={\sqrt {n\cdot p\cdot (1-p)\ }}$

Die Standardabweichung ist ein sogenanntes Streuungsmaß. Sie zeigt uns sozusagen, wie viel die tatsächlichen Ergebnissen um den erwarteten "zerstreut" sind.

Wenn wir jetzt die Wahrscheinlichkeit berechnen wollen, dass nach 9 mal Ziehen rot höchsten 7 mal vorkommt, müssen wir alle Wahrscheinlichkeiten bis 7 addieren. In diesem Fall gibt es allerdings einen schnelleren Weg, nämlich mit Hilfe des Gegenereignisses. Wir können die Wahrscheinlichkeit für 8 und für 9 mal berechnen und die Ergebnisse aus 1 subtrahieren:

$P(x\leq 7)=P(x=0)+P(x=1)+P(x=2)+P(x=3)+P(x=4)+P(x=5)+P(x=6)+P(x=7)=\dots$

$\dots =1-P(x\geq 8)=1-P(x=9)-P(x=8)=1-{\binom {9}{9}}\cdot 0{,}375^{9}\cdot (1-0{,}375)^{9-9}-{\binom {9}{8}}\cdot 0{,}375^{8}\cdot (1-0{,}375)^{9-8}\approx 0{,}9977$

also ca. 99,77%!

Normalverteilung

Definition der Normalverteilung

Wenn wir zufällig irgendeine physikalische Größe in der Natur, beispielsweise die Größe der Personen in einem Ort, messen, werden wir feststellen, dass die Werte etwa "glatt" verlaufen. Damit ist gemeint: es wird mehrere Werte um den Durchschnitt geben und immer weniger, je weiter vom Durchschnitt sich der Wert befindet. Die Verteilung wird etwa viel mehr so: aussehen und eher nicht so: . Das letzte Bild würde im konkreten Beispiel bedeuten, dass es viele kleinen und viele großen Personen gäbe, aber viel weniger die "mittelgroß" wären. So eine Verteilung einer physikalischen Größe wird in der Natur kaum, wenn überhaupt, beobachtet. Je mehrere zufällige Werte vorhanden sind, desto mehr wird die Verteilung zu einer gewisse Kurve neigen, der sogenannten "Normalverteilung": . Der erste, der dies beobachtet hat, war Adolph Quetelet im Jahr 1844. Er hat den Brustumfang von mehreren tausend Soldaten gemessen und eine verblüffende Übereinstimmung mit der Normalverteilung festgestellt. Folgendes könnte daher als eine empirische Definition gelten:

Für viele physikalischen Größen gilt, dass ihre Messwerte in der Natur normalverteilt wären, wenn es unendlich viele Werte gäbe.

Die Funktion, die die "Glockenkurve" der Normalverteilung beschreibt, ist selbstverständlich keine lineare und keine Polynomfunktion. Sie ist ziemlich kompliziert und lautet:

$F(x)={\frac {1}{\sqrt {2\pi }}}\int \limits _{-\infty }^{(x-\mu )/\sigma }e^{-{\frac {1}{2}}z^{2}}\mathrm {d} z=\Phi \left({\frac {x-\mu }{\sigma }}\right).$

$\mu \$ist in dieser Darstellung der Erwartungswert (also der Durchschnitt, der in diesem Fall auch der Median und der Modus ist). $\sigma \$ist die Standardabweichung. Der Wert dieser Funktion lässt sich nur annähernd berechnen, daher gibt es für die sogenannte "normierte" Funktion (mit $\mu =0,\ \sigma =1$) entsprechende vorgerechneten Tabellen.

Wie von unserer Beschreibung hier andeuten lässt, war diese Funktion schon lang vor der Entdeckung von Quetelet bekannt. Einige wichtige Wissenschaftler der Mathematik und der Physik haben zu ihrer Entdeckung beigetragen: de Moivre, Poisson, Laplace, Gauß. Die Normalverteilung stellt einen Grenzwert der Binomialverteilung für unendlich viele Proben dar. Als Faustregel für die Anwendung einer Normalverteilung an der Stelle einer Binomialverteilung gilt $np(1-p)\geq 9$, wobei n die Anzahl der Versuche und p die entsprechende Wahrscheinlichkeit des entsprechenden Ergebnisses der Binomialverteilung sind. Falls diese Bedingung nicht erfüllt sein sollte, ist die Ungenauigkeit der Näherung immer noch vertretbar, wenn gilt: $np\geq 4$ und zugleich $n(1-p)\geq 4$. Eine theoretische Definition der Normalverteilung könnte daher wie im Folgenden lauten:

Die Normalverteilung ist eine Grenzfunktion der Binomialverteilung für unendlich viele Versuche.

• 
• 
• 
• 

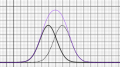
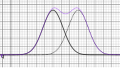
Wenn wir allerdings Messungen eines Merkmals einer Gruppe in der Natur durchführen, müssen wir auf Unterschiede in der Gruppe aufpassen. Es gilt beispielsweise, dass Männer allgemein größer als Frauen sind (durchschnittlich, also nicht alle Männer sind größer als alle Frauen...). Für Männer und für Frauen gibt es dann (zumindest) zwei unterschiedliche Normalverteilungen. Das bedeutet, dass die Verteilung der Größe in der Gesamtbevölkerung doch nicht eine Normalverteilung ist. Die Bilder mit Kombinationen von Normalverteilung hier zeigen das eindeutig.

Die Kombination von Normalverteilungen mit unterschiedlichem Erwartungswert ist keine Normalverteilung mehr.

Um solche Kombinationen zu erkennen gibt es besondere statistische Werkzeuge, die man in einem vertiefenden Studium lernt.

Anwendung der Normalverteilung bei gegebenen Erwartungswert und Standardabweichung

Die Normalverteilung ist eine Art Wahrscheinlichkeitsverteilung. Es gibt allerdings einen Grundsätzlichen Unterschied von der Binomialvertielung. Die Binomialverteilung kann durch ein Säulendiagramm dargestellt werden. In diesem Diagramm kann man genau ablesen, wie oft ein gewisser Wert vorkommt. Es gibt in dieser Darstellung sogenannten diskreten Werten. Das bedeutet, dass es beispielsweise die Werte 5 und 6 gibt, ohne dass es einen anderen Werte dazwischen gibt. Die Werte kann man abzählen. Man kann sagen, dass es so und so viele Werte gibt. In der Normalverteilung ist das nicht der Fall. Die Normalverteilung ist eine Grenzfunktion für unendlich viele Werte. Man sagt, dass sie eine "stetige" Funktion ist. Sie ist allerdings ganz symmetrisch, die linke und die rechte Seite sind ein Spiegelbild voneinander. In der Natur sind viele Größen normalverteilt. Wie man die Normalverteilung benutzt, können wir (nur) mit Hilfe eines konkreten Beispiels verstehen.

• Die Größe der männlichen Giraffen ist Normalverteilt mit $\mu =5{,}20\ m,\ \sigma =0{,}25\ m$. Welcher Anteil der Giraffen ist kleiner als 5,62 m?

Um diese Frage zu beantworten, brauchen wir die Standardnormalverteilung. Die Werte einer Normalverteilung können wir nicht genau berechnet. Die Standardnormalverteilung ist die Normalverteilung mit Erwartungswert $\mu =0\$und Standardabweichung $\sigma =1$. Für die Standardnormalverteilung wurden die Werte schon gemessen und werden in der folgenden Tabelle angegeben. Mit ihrer Hilfe kann man sagen, welcher Anteil der Werte innerhalb eines gewissen Intervalls liegt.

$\Phi _{0;1}(z)\,$

z \ *	0	1	2	3	4	5	6	7	8	9
0,0*	0,50000	0,50399	0,50798	0,51197	0,51595	0,51994	0,52392	0,52790	0,53188	0,53586
0,1*	0,53983	0,54380	0,54776	0,55172	0,55567	0,55962	0,56356	0,56749	0,57142	0,57535
0,2*	0,57926	0,58317	0,58706	0,59095	0,59483	0,59871	0,60257	0,60642	0,61026	0,61409
0,3*	0,61791	0,62172	0,62552	0,62930	0,63307	0,63683	0,64058	0,64431	0,64803	0,65173
0,4*	0,65542	0,65910	0,66276	0,66640	0,67003	0,67364	0,67724	0,68082	0,68439	0,68793
0,5*	0,69146	0,69497	0,69847	0,70194	0,70540	0,70884	0,71226	0,71566	0,71904	0,72240
0,6*	0,72575	0,72907	0,73237	0,73565	0,73891	0,74215	0,74537	0,74857	0,75175	0,75490
0,7*	0,75804	0,76115	0,76424	0,76730	0,77035	0,77337	0,77637	0,77935	0,78230	0,78524
0,8*	0,78814	0,79103	0,79389	0,79673	0,79955	0,80234	0,80511	0,80785	0,81057	0,81327
0,9*	0,81594	0,81859	0,82121	0,82381	0,82639	0,82894	0,83147	0,83398	0,83646	0,83891
1,0*	0,84134	0,84375	0,84614	0,84849	0,85083	0,85314	0,85543	0,85769	0,85993	0,86214
1,1*	0,86433	0,86650	0,86864	0,87076	0,87286	0,87493	0,87698	0,87900	0,88100	0,88298
1,2*	0,88493	0,88686	0,88877	0,89065	0,89251	0,89435	0,89617	0,89796	0,89973	0,90147
1,3*	0,90320	0,90490	0,90658	0,90824	0,90988	0,91149	0,91309	0,91466	0,91621	0,91774
1,4*	0,91924	0,92073	0,92220	0,92364	0,92507	0,92647	0,92785	0,92922	0,93056	0,93189
1,5*	0,93319	0,93448	0,93574	0,93699	0,93822	0,93943	0,94062	0,94179	0,94295	0,94408
1,6*	0,94520	0,94630	0,94738	0,94845	0,94950	0,95053	0,95154	0,95254	0,95352	0,95449
1,7*	0,95543	0,95637	0,95728	0,95818	0,95907	0,95994	0,96080	0,96164	0,96246	0,96327
1,8*	0,96407	0,96485	0,96562	0,96638	0,96712	0,96784	0,96856	0,96926	0,96995	0,97062
1,9*	0,97128	0,97193	0,97257	0,97320	0,97381	0,97441	0,97500	0,97558	0,97615	0,97670
2,0*	0,97725	0,97778	0,97831	0,97882	0,97932	0,97982	0,98030	0,98077	0,98124	0,98169
2,1*	0,98214	0,98257	0,98300	0,98341	0,98382	0,98422	0,98461	0,98500	0,98537	0,98574
2,2*	0,98610	0,98645	0,98679	0,98713	0,98745	0,98778	0,98809	0,98840	0,98870	0,98899
2,3*	0,98928	0,98956	0,98983	0,99010	0,99036	0,99061	0,99086	0,99111	0,99134	0,99158
2,4*	0,99180	0,99202	0,99224	0,99245	0,99266	0,99286	0,99305	0,99324	0,99343	0,99361
2,5*	0,99379	0,99396	0,99413	0,99430	0,99446	0,99461	0,99477	0,99492	0,99506	0,99520
2,6*	0,99534	0,99547	0,99560	0,99573	0,99585	0,99598	0,99609	0,99621	0,99632	0,99643
2,7*	0,99653	0,99664	0,99674	0,99683	0,99693	0,99702	0,99711	0,99720	0,99728	0,99736
2,8*	0,99744	0,99752	0,99760	0,99767	0,99774	0,99781	0,99788	0,99795	0,99801	0,99807
2,9*	0,99813	0,99819	0,99825	0,99831	0,99836	0,99841	0,99846	0,99851	0,99856	0,99861
3,0*	0,99865	0,99869	0,99874	0,99878	0,99882	0,99886	0,99889	0,99893	0,99896	0,99900
3,1*	0,99903	0,99906	0,99910	0,99913	0,99916	0,99918	0,99921	0,99924	0,99926	0,99929
3,2*	0,99931	0,99934	0,99936	0,99938	0,99940	0,99942	0,99944	0,99946	0,99948	0,99950
3,3*	0,99952	0,99953	0,99955	0,99957	0,99958	0,99960	0,99961	0,99962	0,99964	0,99965
3,4*	0,99966	0,99968	0,99969	0,99970	0,99971	0,99972	0,99973	0,99974	0,99975	0,99976
3,5*	0,99977	0,99978	0,99978	0,99979	0,99980	0,99981	0,99981	0,99982	0,99983	0,99983
3,6*	0,99984	0,99985	0,99985	0,99986	0,99986	0,99987	0,99987	0,99988	0,99988	0,99989
3,7*	0,99989	0,99990	0,99990	0,99990	0,99991	0,99991	0,99992	0,99992	0,99992	0,99992
3,8*	0,99993	0,99993	0,99993	0,99994	0,99994	0,99994	0,99994	0,99995	0,99995	0,99995
3,9*	0,99995	0,99995	0,99996	0,99996	0,99996	0,99996	0,99996	0,99996	0,99997	0,99997
4,0*	0,99997	0,99997	0,99997	0,99997	0,99997	0,99997	0,99998	0,99998	0,99998	0,99998

Anmerkung: Negative Werte werden aus Gründen der Symmetrie nicht angegeben, weil $\Phi (-z)=1-\Phi (z)$ ist.

Das Symbol "z" zeigt uns hier das Wie-viel-fache der Standardabweichung oberhalb des Erwartungswerts. Die Zeilen zeigen uns das Vielfache bis zur ersten Nachkommastelle, die Spalten geben die zweite Nachkommastelle an. Nehmen wir die vierte Zeile. Hier steht am Anfang links 0,3*. Das Symbol * wird durch die Zahl an der Spalte ersetzt. Nehmen wir die 6-ste Spalte, da oben steht 5. Das Symbol * wird also durch 5 ersetzt. In 0,3* ersetzten wir also * durch 5, dann haben wir 0,35. An dieser Stelle (4-te Zeile, 6-ste Spalte) steht die Zahl 0,63683. Das bedeutet: von Anfang an der Normalverteilung (also von ganz links) bis 0,35 mal die Standardabweichung rechts vom Erwartungswert haben wir 0,63683 aller Fälle (also 63,683%).

Schauen wir jetzt unsere Frage an. Der Erwartungswert ist 5,20 m, die Standardabweichung 0,25 m und es wird der Anteil bis 5,62 m gefragt. 5,62 ist 0,42 (5,62−5,20=0,42) oberhalb des Erwartungswert, also 1,68 mal die Standardabweichung (0,42:0,25=1,68). Die Zweite Nachkommastelle in 1,68 ist 8 und wir werden die entsprechende Spalte in der Tabelle benutzen. In der Tabelle ist 1,6 die 17-te Zeile und 8 die 9-te Spalte. Also das 1,68-fache der Standardabweichung befindet sich an der 17-te Zeile und 9-te Spalte. Da steht die Zahl 0,95352. Das bedeutet: bis 5,62 m Größe haben wir 0,95352 also 95,352 % aller Giraffen. Somit haben wir die Frage beantwortet.

Was ist jetzt, wenn der Grenzwert kleiner als der Erwartungswert ist? In diesem Fall nutzen wir die Symmetrie der Funktion aus, die als Folgerung die Formel, die direkt unterhalb der Tabelle steht, hat:

$\Phi (-z)=1-\Phi (z)$

Wenn in unserem Beispiel der Anteil bis 5,04 m Größe gefragt wird, berechnen wir erst die Differenz vom Erwartungswert, wie vorher: 5,20−5,04=0,16. Das ist das (0,16:0,25=) 0,64-fache der Standardabweichung. 0,6 ist die 7-te Zeile, 4 ist die 5-te Spalte, an dieser Stelle steht 0,73891, also 73,891 %. Das ist allerdings das Ergebnis, wenn wir oberhalb des Erwartungswertes wären. Um den Anteil bis 0,64 mal die Standardabweichung unterhalb des Erwartungswertes müssen wir einfach diese Zahl aus 1 subtrahieren: 1−0,73891=0,26109 also 26,109 % aller Werte befinden sich zur Größe 5,04 m.

Wenn die Frage zwischen zwei Werte ist, dann müssen wir die entsprechenden Anteile einfach subtrahieren. In unserem Beispiel, wenn der Anteil der Giraffen zwischen 5,04 und 5,62 gefragt ist, dann ist es 0,95352−0,26109= 0,69243 also 69,243 %.

Anwendung der Normalverteilung bei gegebenen Grenzwerten

*Eine Bäckerei produziert Baguettes. Auf der Verpackung steht 450 g. Die Standardabweichung der Masse bei der Produktion ist 12 g. Wie viel muss der Erwartungswert sein, damit weniger als 3,5 % der Produktion unterhalb von 450 g bleibt?

In diesem Fall arbeiten wir erst mit dem Prozentsatz. Da ein Prozentsatz unterhalb des Erwartungswert gegeben ist (3,5%=0,035) und die Tabelle nur Anteile oberhalb dieses Wertes angibt, benutzen wir die Gleichung $\Phi (-z)=1-\Phi (z)$. Wir suchen daher in der Tabelle 1−0,035=0,965. An der 19. Zeile (1,8*) finden wir an der zweiten und an der dritten Spalte die Werte 0,96485 bzw. 0,96562. Von den beiden Werte ist 0,96485 näher zur 0,965 (0,965−0,96485=0,00015 und 0,96562−0,965=0,00062). Daher nehmen wir mit einer gute Annäherung die zweite Spalte (also die zweite Nachkommastelle wird 1 sein). Der gesuchte Wert wird daher 1,81 mal die Standardabweichung oberhalb des Grenzwertes liegen müssen, damit die Voraussetzung erfüllt werden kann. Das ist dann 1,81·12=21,72≈22 g. Der Erwartungswert muss daher bei ca. 472 g liegen.

• Wie viel muss die Standardabweichung (also die "Genauigkeit" der Produktionsmaschine) sein, damit 94 % aller Baguettes mehr als 452 g sind, wenn der Erwartungswert 483 g ist?

In der Tabelle steht 94 % (also 0,94) an der 16. Zeile zwischen 6. und 7. Spalte. Näher zu 0,94 ist der Wert an der 6. Spalte (0,94−0,93943=0,00057 und 0,94062−0,94=0,00062). Der Abstand zum Erwartungswert muss daher 1,55 mal die Standardabweichung sein. Der tatsächliche Abstand zwischen Grenz- und Erwartungswert ist 483−452=21 g. Das muss ca. das 1,55-fache der Standardabweichung sein, daher soll die Standardabweichung höchstens 13,55 g sein (21:1,55). Vorsichtig sollen wir hier beim Runden sein. 13,55 ist gerundet 14 g, das wäre allerdings oberhalb der Grenze, daher müssen wir doch auf 13 g abrunden.

Normalverteilung und Funktionen

*Bei einer Produktionsmaschine hat man festgestellt, dass die Standardabweichung vom Erwartungswert linear abhängig ist: $\textstyle \sigma ={\frac {\mu }{200}}+8$. Wie viel müssen Standardabweichung und Erwartungswert sein, damit 99 % der Produktion oberhalb von 445 g bleibt?

In der Tabelle befindet sich der zu 0,99 näherer Wert an der 24. Zeile und an der 4. Spalte, also 2,33 mal die Standardabweichung. Nach der Angabe müssen daher folgende Bestimmungen gleichzeitig gelten:

$\textstyle \sigma ={\frac {\mu }{200}}+8\quad$und

$\mu -2{,}33\sigma =445$

Die Antwort zu diesem linearen Gleichungssystem ist:

$\mu \approx 469{,}11\qquad \sigma \approx 10{,}35$

Diese Werte können wir auf 469 g und 10 g runden.

Satz von Bayes

Satz von Bayes konkretes Beispiel

Hier werden wir uns mit einem konkreten Beispiel beschäftigen, das mit dem Satz von Bayes nur indirekt zu tun hat. Wir werden also hier diesen Satz nicht benutzen und nicht erklären. Das Beispiel hat ein intuitiv unerwartetes Ergebnis und kann später beim Verständnis des Satzes hilfreich sein.

Die Sensitivität des gewöhnlichen AIDS Tests ist ca. 99,9%, die Spezifität ca. 99,8%. Die Prävalenz im deutschsprachigen Raum ist ca. 0,15%, in Südafrika hingegen ca. 20%. Wie viel ist Wahrscheinlichkeit beim positiven Test, dass die Person tatsächlich krank ist, in diesen Regionen? Bevölkerung DE Raum ca. 100 Mil., Südaf. ca 55 Mil.

Im deutschsprachigen Raum zuerst. Von 100 Millionen Menschen sind
$100000000\cdot 0{,}15\%=100000000\cdot 0{,}0015=150000\$Personen krank.
Von denen werden $150000\cdot 99{,}9\%=150000\cdot 0{,}999=149850\$als positiv
positiv diagnostiziert, die restlichen 150 als negativ.

Gesund sind die restlichen $100000000\cdot 99{,}85\%=100000000\cdot 0{,}9985=99850000\$
Personen. Von denen werden $99850000\cdot 99{,}8\%=99850000\cdot 0{,}998=99650300\$als
negativ diagnostiziert, die restlichen 199700 als positiv.

Die Schritten können wir in der folgenden Abbildung zusammengefasst sehen:

Stellen wir die Ergebnisse in einer Tabelle dar:

$\ _{Krankheit}\diagdown ^{Test}\$	Positiv	Negativ	Teilsummen
Krank	149850	150	150000
Gesund	199700	99650300	99850000
Teilsummen	$\$ 349550 $\$	$\$ 99650450 $\$	$\$ 100000000 $\$

Wenn wir die Spalte mit den positiven Ergebnissen beobachten, stellen
wir fest, dass von den 349550 positiven Tests 149850 tatsächlich krank
sind, also $149850:349550\approx 0{,}4287=42{,}87\%\$

In Südafrika hingegen sieht die Tabelle so aus:

$\ _{Krankheit}\diagdown ^{Test}\$	Positiv	Negativ	Teilsummen
Krank	10989000	11000	11000000
Gesund	88000	43912000	44000000
Teilsummen	$\$ 11077000 $\$	$\$ 43923000 $\$	$\$ 55000000 $\$

Wenn wir die Spalte mit den positiven Ergebnissen beobachten, stellen
wir fest, dass von den 11077000 positiven Tests 10989000 tatsächlich krank
sind, also $10989000:11077000\approx 0{,}9921=99{,}21\%\$

Wir können daher den Schluss ziehen, dass die Aussagekraft eines Krankheitstests
stark von der Häufigkeit der Krankheit in einer Gruppe abhängig sein kann.

Wir sehen daher, dass der Satz von Bayes zu Folgerungen führen kann, die intuitiv nicht so leicht zu verstehen sind.

Satz von Bayes abstraktes Beispiel

Der Satz von Bayes betrifft bedingte Wahrscheinlichkeiten. In (nicht unbedingt verständlichen) Worten besagt der Satz:

Die bedingte Wahrscheinlichkeit eines Ereignisses A unter der Voraussetzung eines Ereignisses B ist so viel wie das Produkt der Wahrscheinlichkeit des Ereignisses B unter der Voraussetzung des Ereignisses A mal die Wahrscheinlichkeit des Ereignisses A durch die Wahrscheinlichkeit des Ereignisses B. Die entsprechende Formel ist:

$P(A\mid B)\;=\;{\frac {P(B\mid A)\cdot P(A)}{P(B)}}$

Nun, um diesen Satz zu verstehen, können wir ein einfaches Beispiel bringen.

In der Klasse W gibt es 15 Mädchen, davon sind 60% Blond, in einer anderen Klasse S gibt es 20 Mädchen, davon sind 35% Blond. Bei einer Party der beiden Klassen (wobei alle Mädchen da sind), spricht jemand mit einer Blondine. Wie viel ist die Wahrscheinlichkeit, dass sie aus der Klasse S kommt?

In der Klasse W sind 60% der 15 Mädchen blond, also 0,6·15=9 Blondinen.
In der Klasse S sind 35% der 20 Mädchen blond, also 0,35·20=7 Blondinen.
Daher sind in der Party insgesamt 9+7=16 Blondinen von insgesamt 15+20=
35 Mädchen. Lass uns die ganzen Zahlen in einer Tabelle schreiben:

$\qquad$ Klasse S Klasse W Teilsummen $\quad$Blond$\quad$ $\qquad 7\qquad$ $\qquad 9\qquad$ $16\$Blondinen insgesamt $\quad$nicht Blond$\quad$ $\qquad 13\qquad$ $\qquad 6\qquad$ $19\$nicht blond insgesamt Teilsummen $20\$Mädchen in Klasse S $15\$Mädchen in Klasse W $35\$Mädchen insgesamt Berechnen wir jetzt die unterschiedlichen Wahrscheinlichkeiten: Mit P(S) wird hier die Wahrscheinlichkeit gezeigt, dass ein Mädchen aus der Klasse S kommt. Insgesamt gibt es 35 Mädchen, davon sind 20 aus der Klasse B, also $\textstyle \ P(S)={\frac {20}{35}}\approx 0{,}5714=57{,}14\%$. Mit P(B) wird hier die Wahrscheinlichkeit gezeigt, dass ein Mädchen blond ist. Insgesamt gibt es 35 Mädchen, davon sind 16 Blondinen, also $\textstyle \ P(B)={\frac {16}{35}}\approx 0{,}4571=45{,}71\%$. Mit P(B|S) wird hier die Wahrscheinlichkeit gezeigt, dass ein Mädchen aus der Klasse S blond ist, formeller ausgedrückt, dass ein Mädchen blond ist unter der Voraussetzung, dass sie aus der Klasse S kommt. Wie wir in der Tabelle sehen können, gibt es in der Klasse S 20 Mädchen, von denen 7 blond sind. Die Wahrscheinlichkeit also, dass unter den Mädchen aus der Klasse S eine Blond ist, ist $\textstyle \ P(B|S)={\frac {7}{20}}=0{,}35=35\%$. Mit P(S|B) wird hier die Wahrscheinlichkeit gezeigt, dass eine Blondine aus der Klasse S kommt, formeller ausgedrückt, dass ein Mädchen aus der Klasse S kommt unter der Voraussetzung, dass sie blond ist. Wie wir in der Tabelle sehen können, gibt es insgesamt 16 Blondinen, von denen 7 aus der Klasse S sind. Die Wahrscheinlichkeit also, dass unter den Blondinen eine aus der Klasse S kommt, ist $\textstyle \ P(S|B)={\frac {7}{16}}=0{,}4375=43{,}75\%$.

P(S|B) ist die gefragte Wahrscheinlichkeit. In der Party gibt es 16 Blondinen, von denen 7 aus der Klasse S kommen. Wenn jemand mit einer Blondine schon spricht, ist die Wahrscheinlichkeit, dass sie aus der Klasse S kommt: $\textstyle \ P(S|B)={\frac {7}{16}}=0{,}4375=43{,}75\%$. Diese Wahrscheinlichkeit ist nicht die gleiche mit der Wahrscheinlichkeit, dass irgendein Mädchen (blond oder nicht) aus der Klasse S kommt. Für diese Wahrscheinlichkeit brauchen wir die ganze Anzahl der Mädchen (35) und die Anzahl der Mädchen in der S Klasse (20): $\textstyle \ P(S)={\frac {20}{35}}\approx 0{,}5714=57{,}14\%$. Wir sehen also: die Wahrscheinlichkeit, dass ein Mädchen aus der Klasse S kommt, unter der Voraussetzung, dass sie Blond ist, hängt von drei Sachen ab: der allgemeine Wahrscheinlichkeit, dass sie Blond ist. der allgemeine Wahrscheinlichkeit, dass sie aus der Klasse S kommt. der Häufigkeit (Wahrscheinlichkeit) der Blondinen in der S Klasse. Schreiben wir den Satz für diesen konkreten Fall: $P(S|B)\;=\;{\frac {P(B|S)\cdot P(S)}{P(B)}}$ Benutzen wir konkrete Zahlen, um diesen Satz zu erklären. Fangen wir mit der gefragten Wahrscheinlichkeit an: $\textstyle \ P(S|B)={\frac {7}{16}}$ Von den 16 Mädchen, die in der Party sind, sind 7 aus der Klasse S. Zähler und Nenner können wir als Bruch (beides durch 1) schreiben und wir können den Zähler mit der Anzahl der Mädchen in der S Klasse (20) erweitern. Daraus entsteht ein Doppelbruch: $\textstyle \ P(S|B)={\frac {7}{16}}={\dfrac {\ \ {\frac {7}{1}}\ \ }{\frac {16}{1}}}={\dfrac {\ \ {\frac {7\cdot 20}{1\cdot 20}}\ \ }{\frac {16}{1}}}={\dfrac {\ \ {\frac {7}{20}}\cdot 20\ \ }{\frac {16}{1}}}$ Der Bruch im Zähler ist die Wahrscheinlichkeit P(B|S), dass ein Mädchen Blond ist, wenn es aus der Klasse S kommt: von den 20 Mädchen in der Klasse S sind 7 Blond. Wir können also diesen Bruch durch P(B|S) ersetzten und den Bruch etwas mehr bearbeiten, indem wir Zähler und Nenner des Doppelbruches mit $\textstyle \ {\frac {1}{35}}\$erweitern: $\textstyle \ P(S|B)={\dfrac {\ \ {\frac {7}{20}}\cdot 20\ \ }{\frac {16}{1}}}={\dfrac {\ \ P(B|S)\cdot {\frac {20}{1}}\ \ }{\frac {16}{1}}}$ $={\dfrac {\ \ P(B|S)\cdot {\frac {20}{1}}\cdot {\frac {1}{35}}\ \ }{{\frac {16}{1}}\cdot {\frac {1}{35}}}}={\dfrac {\ \ P(B|S)\cdot {\frac {20}{35}}\ \ }{\frac {\ \ 16\ \ }{35}}}$ Der Bruch im Zähler $\textstyle \ {\frac {20}{35}}\$ist nichts anders, als die Wahrscheinlichkeit P(S), dass ein Mädchen (blond oder nicht) aus der Klasse S kommt. Es sind ja insgesamt 35 Mädchen, von denen 20 aus der Klasse S sind. Der Bruch im Zähler $\textstyle \ {\frac {16}{35}}\$ist nichts anders, als die Wahrscheinlichkeit P(B), dass ein Mädchen blond ist. Es sind ja insgesamt 35 Mädchen, von denen 16 Blond sind. Wenn wir die Brüche durch die entsprechenden Wahrscheinlichkeiten ersetzten, kommen wir zum Satz von Bayes: $\textstyle \ P(S|B)={\frac {P(B|S)\cdot P(S)}{P(B)}}$

Im allgemeinen Fall wird das Symbol A anstatt B und B anstatt S benutzt:

Satz von Bayes

$P(A\mid B)\;=\;{\frac {P(B\mid A)\cdot P(A)}{P(B)}}$

Die bedingte Wahrscheinlichkeit eines Ereignisses A unter der Voraussetzung eines Ereignisses B ist so viel wie das Produkt der Wahrscheinlichkeit des Ereignisses B unter der Voraussetzung des Ereignisses A mal die Wahrscheinlichkeit des Ereignisses A durch die Wahrscheinlichkeit des Ereignisses B.

Diesen Satz können wir dann direkt in einem abstrakten Beispiel benutzten:

Die Sensitivität des gewöhnlichen AIDS Tests ist ca. 99,9%, die Spezifität ca. 99,8%. Die Prävalenz im deutschsprachigen Raum ist ca. 0,15%, in Südafrika hingegen ca. 20%. Wie viel ist Wahrscheinlichkeit beim positiven Test, dass die Person tatsächlich krank ist, in diesen Regionen? Bevölkerung DE Raum ca. 100 Mil., Südaf. ca 55 Mil.

Wir suchen die Wahrscheinlichkeit P(K|T⁺), dass eine Person Krank (K) ist unter der Voraussetzung, dass der Test Positiv (T⁺) ist. Nach dem Satz von Bayes brauchen wir dafür:

• Die Wahrscheinlichkeit P(T⁺|K) dass ein Test positiv ist, wenn die Person krank ist. Das ist die Sensitivität 99,9%, also 0,999.
• Die Wahrscheinlichkeit P(K) dass eine Person Krank ist. Das ist die Häufigkeit der Krankheit in der Bevölkerung, Prävalenz genannt: 0,15% also 0,0015.
• Die Wahrscheinlichkeit P(T⁺) dass ein Test allgemein in der Bevölkerung positiv ist. Das ist 0,34955 %, also 0,0034955.

$P(K|T^{+})\;=\;{\frac {P(T^{+}|K)\cdot P(K)}{P(T^{+})}}={\frac {0{,}999\cdot 0{,}0015}{0{,}0034955}}\approx 0{,}4287\ {\text{also}}\ 42{,}87\%$

Diese Wahrscheinlichkeit weicht stark von der Sensitivität ab. Intuitiv denken wir, dass wir sicher krank sind, wenn der Test positiv ist, wenn seine Sensitivität so hoch ist (hier 99,9%). Die Sensitivität zeigt allerdings nur wie viel Prozent der Kranken mit dem Test tatsächlich erwischt werden. Das ist aber etwas anderes als der Anteil der Personen mit positivem Test, die tatsächlich krank sind. Nicht nur (fast) alle Kranke werden positiv gezeigt, sondern auch einige Gesunde. Das könnte z.B. daran liegen, dass ein anderer Virus, der keine Krankheit verursacht, Ähnlichkeiten mit dem Krankheitsvirus aufweist. Daher kann der Test manchmal positiv sein, auch wenn die Person nicht krank ist und daher gibt es mehrere Positive als Kranke. Wenn die Krankheit wirklich selten vorkommt, ist die Wahrscheinlichkeit, dass jemand beim positiven Test krank ist, nicht unbedingt so hoch. In unserem (tatsächlichen) Beispiel ist sie weniger als 50%!

Der Satz von Bayes in der Epidemiologie

Regression und Korrelation

Regression

Nehmen wir ein einfaches konkretes Beispiel: die Beziehung zwischen Gewicht und Größe einer Person. Je größer eine Person ist, desto mehr wiegt sie. Man kann sich fragen, ob es möglich ist, diesen Zusammenhang durch eine Funktion zu beschreiben.

cm	kg
173	68
184	103
167	70
172	79
191	100
163	68

• 
• 
• 
• 

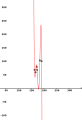
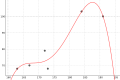
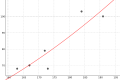
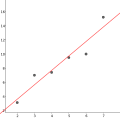
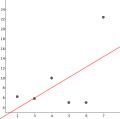
Machen wir das Beispiel noch konkreter: Nehmen wir an, dass wir das Gewicht und die Größe von 6 Personen gemessen und die Ergebnisse in der beiliegenden Tabelle dargestellt haben. Wir können verschiedenen Geraden, die irgendwie zwischen den Daten stehen, benutzten, um einen linearen Zusammenhang darzustellen (erstes Bild). Wie können wir eine Entscheidung über die geeignetste Gerade treffen? Unter anderen der berühmte Mathematiker Carl Friedrich Gauß hat eine Methode entwickelt, um die am besten angepassten Gerade zu finden: die Methode der kleinsten Quadrate. Im zweiten Bild sieht man zwischen jedem Punkt und Gerade eine Strecke, deren Länge die Differenz des y-Wertes des Punktes vom y-Wert der Gerade an dieser Stelle (x-Wert) ist. Nach der Methode der kleinsten Quadrate wird diejenige Gerade gewählt, für die es gilt, dass die Summe der Quadrate dieser Differenzen die kleinste ist. Für unsere Daten ist diese im dritten Bild dargestellt. Man kann allerdings ziemlich leicht feststellen, dass diese Gerade für unseren Zusammenhang nicht gerade die geeignetste ist. Wenn die Gerade verlängert wird (4. Bild), stellt man fest, dass für eine Größe kleiner als ca. 115 cm das Gewicht negativ wird! Das hat selbstverständlich keinen physikalischen Sinn. Ideal wäre die Gerade, wenn sie durch den Punkt (0,0) ginge und für die restlichen Werte die Regel der kleinsten Quadrate erfüllte. So eine Gerade zu finden ist auch möglich, wenn auch ziemlich komplexer und wird hier nicht weiter untersucht.

Für die gegebenen Daten ist also die im dritten Bild dargestellte Gerade die nach dem Kriterium der kleinsten Quadrate die am besten angepasste. Es gibt aber keinen Grund zu denken, dass der Zusammenhang unbedingt linear sein sollte. Sehen noch drei andere Möglichkeiten für unsere Daten:

• 
• 
• 
• 
• 

Um zu entscheiden, ob eine Funktion zu den Daten gut passt, gibt es unterschiedliche Kriterien. Eines davon hat mit der Methode der kleinsten Quadrate zu tun und wird Bestimmtheitsmaß genannt. Das Symbol dafür ist R². Null ist dieses Maß, wenn die Kurve durch alle Datenpunkte geht.

Im 1. Bild sehen wir eine Polynomfunktion, die durch alle Punkte geht. Das ist allerdings keine Überraschung. Für jede Anzahl von Punkte gibt es eine Polynomfunktion, die durch alle Punkte geht, nämlich eine Polynomfunktion, deren Grad um 1 kleiner als die Anzahl der Punkte ist. Wenn wir allerdings diese Funktion außerhalb des Bereichs der gegebenen Punkte betrachten, stellen wir fest, dass sie überhaupt nicht geeignet ist, um unseres Beispiel zu beschreiben, auch wenn das Bestimmtheitsmaß null ist.

Im 2. und 3. Bild sehen wir noch eine Polynomfunktion, diesmal 4. Grades (also um 2 weniger als die Anzahl der Punkte). Wie leicht zu sehen ist, hat sie genau das gleiche Problem wie die Funktion 5. Grades.

Im 4. und 5. Bild sehen wir eine quadratische Funktion, die nach der Methode der kleinsten Quadrate erzeugt wurde. Diese hat immer noch Nachteile, ihre Wert wird beispielsweise ca. unterhalb der Stelle 80 cm größer für fallende Größe, was nicht logisch ist (kleinere Personen und Kinder wiegen ja weniger als größere und nicht mehr). Allerdings ist dieses Modell doch besser als das lineare Modell. Die Werte werden für kleinere Stellen nicht mehr negativ. Es macht auch physikalisch Sinn, wegen der Konstruktion des menschlichen Körpers und die Art in der ein Mensch wächst, dass der Zusammenhang zwischen Gewicht und Größe nicht linear ist. Daher könnte man sich in diesem Fall doch für die quadratische Funktion entscheiden.

Korrelation

Nehmen wir ein einfaches konkretes Beispiel: die Beziehung zwischen Gewicht und Größe einer Person. Je größer eine Person ist, desto mehr wiegt sie. Dieser Zusammenhang lässt sich möglicherweise durch eine lineare Funktion beschreiben. Für die Erzeugung einer solchen linearen Funktion wird i. d. R. die Methode der kleinsten Quadrate angewendet (Regression). Die Frage ist allerdings, wie nah zu einer linearen Funktion die tatsächlichen Daten stehen. Der Korrelationskoeffizient ist ein Maß dieser "Nähe". Schauen wir uns folgende Bilder an:

• 
• 
• 

In allen drei Bildern lautet die lineare Funktion ungefähr $y=2\ x-0{,}4$. Wir können allerdings klar sehen, dass im ersten Bild alle Punkte ziemlich nah zur Gerade sind, im zweiten etwas weiter und im dritten ziemlich weit. Der Korrelationskoeffizient ist im ersten Fall fast 1, im zweiten ca. 0,9 und im dritten weniger als 0,7.

Der Korrelationskoeffizient ist ein Maß der Nähe der Punkte der Datenpaare zur von denen mit Hilfe der Regression erzeugte linearen Funktion.

Der Korrelationskoeffizient hat mit der Steigung der Regressionsgerade das gleiche Vorzeichen, allerdings hat er zur Steigung keinen (anderen) Zusammenhang. Betrachten wir folgende Bilder:

• 
• 
• 

Der Betrag der Korrelationskoeffizient ist in allen Fällen ca. 0,998. Der Koeffizient ist positiv im 1. Bild und negativ in den anderen 2. Die Steigung der Gerade ist im 1. Bild ca. 2, im 2. Bild ca. −0,7 und im 3. Bild ca. −2, obwohl der Korrelationskoeffizient gleich ist.

Der Korrelationskoeffizient hat mit der Steigung der Regressionsgerade außer dem gleichen Vorzeichen gar nichts zu tun.

Man könnte auch denken, dass es keinen Zusammenhang zwischen den dargestellten Größen gibt, wenn der Korrelationskoeffizient null ist. Das ist doch nicht der Fall. Betrachten wir folgende Bilder:

In der dritten Bildreihe sehen wir Punktwolken, die doch einer Funktion entsprechen könnten. Das erste Bild der dritten Bildreihe könnte beispielsweise durch eine Sinusfunktion angenähert werden, das vierte durch eine quadratische, das fünfte durch eine hyperbolische, das sechste durch einen Kreis und das siebte durch vier Kategorien:

Ein Korrelationskoeffizient gleich null schließt einen Zusammenhang der Daten überhaupt nicht aus. Er schließt dann höchstens nur einen linearen Zusammenhang aus.

In der zweiten Bildreihe sehen wir, dass alle Punkte (alle Datenpaare) sich auf einer Gerade befinden. In allen diesen Fällen ist der Korrelationskoeffizient (selbstverständlich) 1 (für positiver Steigung) bzw. −1 (für negative Steigung), auch wenn die Steigung vom Fall zum Fall völlig unterschiedlich ist. In der ersten Bildreihe sehen wir noch eindeutlicher als vorher, dass je mehr die Datenpaaren in einer von einer Gerade entfernte "Punktwolke" dargestellt werden, desto näher zu null der Korrelationskoeffizient ist.

Was könnte der Korrelationskoeffizient für den Zusammenhang zwischen den zwei Größen der Datenpaare bedeuten? Ein Korrelationskoeffizient könnte eine Kausalität bedeuten. Rauchen ist mit einigen Herzerkrankungen stark korreliert und gilt als begründete Ursache (wenn auch eine von mehreren). Rauchen allerdings kann auch zur gelber Färbung der Fingernägel führen. Es gibt daher eine Korrelation zwischen Fingernagelfärbung und Herzerkrankungen. Es gilt aber in diesem Fall eben nicht, dass die Fingernagelfärbung eine Ursache der Herzerkrankungen ist, noch das Gegenteil. In diesem Beispiel wird die Korrelation durch eine gemeinsame Ursache erzeugt. Es kann allerdings auch vorkommen, dass eine Korrelation völlig zufällig ist und dass es keinen Zusammenhang zwischen den korrelierten Größen besteht.