Endomorphismus, Automorphismus – Serlo „Mathe für Nicht-Freaks“
Ein Endomorphismus ist eine lineare Verformung eines Vektorraums . Formal ist ein Endomorphismus eine lineare Abbildung , die auf sich selbst abbildet, d.h. . Ein bijektiver Endomorphismus heißt Automorphismus. Intuitiv ist ein Automorphismus eine lineare Verformung, die man rückgängig machen kann.
Herleitung
[Bearbeiten]Wir kennen schon lineare Abbildungen. Es sind diejenigen Abbildungen zwischen zwei Vektorräumen, welche sich mit der Struktur der Vektorräume vertragen. Wir untersuchen nun ein paar Beispiele von linearen Abbildungen, die wir schon in früheren Artikeln kennengelernt haben.
Beispiele im
[Bearbeiten]Streckung in -Richtung
[Bearbeiten]Zuerst betrachten wir die Streckung eines Vektors in der Ebene um den Faktor in -Richtung. Unsere Abbildung ist damit
Man kann einfach nachprüfen, dass eine lineare Abbildung ist. Wir können wie folgt veranschaulichen: Wir legen ein Schachbrettmuster in die Ebene und wenden auf dieses Schachbrettmuster an.
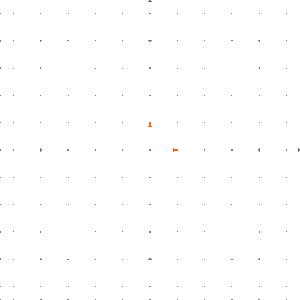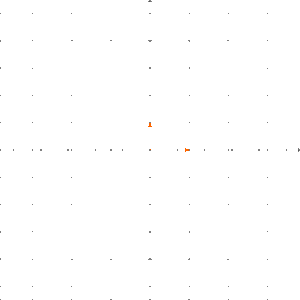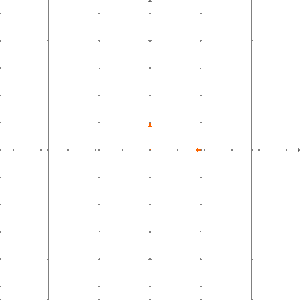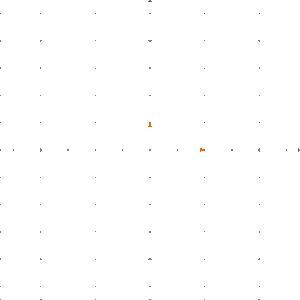
Das Ergebnis ist, dass die Boxen um den Faktor in -Richtung gestreckt werden.
Drehung um den Ursprung
[Bearbeiten]Wir betrachten nun eine Drehung um den Winkel gegen den Uhrzeigersinn mit dem Ursprung als Drehzentrum. Das ist eine Abbildung , die jedem Vektor den um den Winkel gedrehten Vektor zuordnet:
Im Einführungsartikel zu linearen Abbildungen haben wir gesehen, dass Drehungen um den Ursprung linear sind. Wir können uns wie im ersten Beispiel veranschaulichen, indem wir die Abbildung auf das Schachbrettmuster anwenden. Die einzelnen Felder bleiben dann gleich, sie werden nur gedreht.
Projektion auf eine Gerade
[Bearbeiten]
Zuletzt betrachten wir die Abbildung
Die Abbildung „drückt“ Vektoren auf die Gerade . Man kann einfach nachrechnen, dass eine lineare Abbildung ist. Auch diese lineare Abbildung wenden wir auf das Schachbrettmuster an, um sie zu veranschaulichen.

Das gesamte Gitter wird auf die Gerade „plattgedrückt“.
Lineare Verformungen eines beliebigen Vektorraums
[Bearbeiten]In allen obigen Beispielen konnten wir die linearen Abbildungen als Verzerrungen des Schachbrettmusters im visualisieren. Das war möglich, weil alle obigen Funktionen vom wieder in den abbilden. Wir können beliebige lineare Abbildungen als Verformung des Schachbrettmusters veranschaulichen. Die Verformung des Schachbrettmusters zeigt uns, wie die Abbildung auf die Standardbasisvektoren und von und ganzzahlige Vielfache davon wirkt.
Jede lineare Abbildung ist eine lineare Verformung des Raums . Diese Idee wollen wir auf allgemeine Vektorräume verallgemeinern. Wir können uns lineare Abbildungen von nach als lineare Verformungen bzw. Transformationen des Vektorraums vorstellen. Im Gegensatz dazu ist eine lineare Abbildung ein Transport des Vektorraums nach . Wir geben denjenigen linearen Abbildungen, die den Vektorraum verformen, d. h. die von nach abbilden, einen eigenen Namen. Wir nennen eine solche lineare Abbildung Endomorphismus. Also sind Endomorphismen genau die linearen Abbildungen, die den gleichen Definitions- und Zielbereich haben.
Rückgängig machbare Verformungen
[Bearbeiten]In den Beispielen im haben wir gesehen, dass einige Verformungen den Raum erhalten und andere etwas platt drücken. Die Abbildungen, die den Raum erhalten, können wir rückgängig machen. Wenn etwas plattgedrückt wird, ist das nicht möglich, da Information verloren geht. Zum Beispiel geht bei der obigen linearen Abbildung „Projektion auf eine Gerade“ die Information verloren, welche -Komponente der ursprüngliche Vektor hatte. Es ist nicht möglich, den Vektor nach Anwenden der Transformation wieder zurückzugewinnen. Es gibt also Verformungen des Raums, die man rückgängig machen kann, und welche, bei denen das nicht geht. Man kann eine Verformung genau dann rückgängig machen, wenn die dazugehörige Abbildung invertierbar ist. Das gibt uns die Definition einer rückgängig machbaren Verformung des Raums, d. h. ein invertierbarer Endomorphismus. Eine solche Abbildung heißt Automorphismus.
Definition
[Bearbeiten]Definition (Endomorphismus und Automorphismus)
Sei ein -Vektorraum. Eine lineare Abbildung , die auf sich selbst abbildet, heißt Endomorphismus. Die Menge aller Endomorphismen von bezeichnen wir mit .
Einen bijektiven Endomorphismus nennen wir Automorphismus. Die Menge aller Automorphismen von wird mit bezeichnet.
Hinweis
Jeder Automorphismus ist eine bijektive lineare Abbildung und damit auch ein Isomorphismus. Aber nicht jeder Isomorphismus ist ein Automorphismus. Denn Isomorphismen können auch zwei verschiedene Vektorräume aufeinander abbilden.
Beispiele
[Bearbeiten]Beispiele im
[Bearbeiten]Spiegelung
[Bearbeiten]Wir betrachten die lineare Abbildung . Da sie als Definitions- sowie als Bildraum den gleichen Vektorraum hat, ist sie ein Endomorphismus. Die Abbildung hält fest und schickt auf . Damit können wir uns als eine Spiegelung entlang der -Achse vorstellen. Eine Spiegelung können wir rückgängig machen, indem wir ein zweites Mal spiegeln. Das bedeutet, dass selber die zu inverse Abbildung ist. Formal heißt das bzw. . Eine solche Abbildung nennt man auch „selbstinvers.“ Weil ein Inverses besitzt, also invertierbar ist, folgt, dass bijektiv ist. Somit ist auch ein Automorphismus.
Drehung um 90°
[Bearbeiten]Als nächstes betrachten wir den Endomorphismus . Wir wollen zunächst sehen, dass es sich hierbei um eine Drehung um Grad gegen den Uhrzeigersinn handelt. Dazu genügt es zu berechnen, dass auf den Standardbasisvektoren und wie eine solche Drehung wirkt, da wegen der Linearität daraus folgt, dass dann insgesamt eine solche Drehung sein muss. Wir berechnen , sowie , und sehen, dass es sich um die gewünscht Drehung handelt. Auch hier können wir leicht ein Inverses angeben, indem wir „zurückdrehen“ bzw. um Grad im Uhrzeigersinn drehen. Diese Drehung ist durch gegeben. Wir rechnen kurz nach, dass tatsächlich die Inverse von ist: Es gilt
für . Also gilt und ist auch in diesem Beispiel ein Automorphismus.
Scherung
[Bearbeiten]Sei . Wie diese Abbildung den Raum verformt, können wir in der Animation sehen.

Die Transformation sieht umkehrbar aus, d.h. sie sieht aus als wäre sie ein Automorphismus. Das können wir überprüfen, indem wir zeigen, dass injektiv und surjektiv ist.
Um die Injektivität zu zeigen, gucken wir uns den Kern von an, d. h. . Für einen Vektor im Kern, gilt dann . Daraus folgt direkt und damit auch . Somit besteht der Kern nur aus dem Nullvektor und damit ist injektiv.
Um die Surjektivität zu zeigen, nehmen wir uns ein beliebiges und finden ein passendes Urbild unter . Wir suchen also mit . Es ist direkt klar, dass sein muss. Weiterhin muss gelten. Das lässt sich zu umformen. Also ist ein Urbild von . Da beliebig waren, ist surjektiv.
Abbildungen der Form mit heißen Scherungen. Du kannst als Übunsaufgabe zeigen, dass eine Scherung immer ein Automorphismus ist, egal was für eine Zahl ist.
Plattdrücken auf die -Achse
[Bearbeiten]Betrachten wir nun die Abbildung . Diese ist ein Endomorphismus von auf , der jeden Punkt auf der Ebene auf einen Punkt auf der -Achse abbildet. Wir können uns also vorstellen, dass die 2-dimensionale Ebene auf die -Achse „plattgedrückt.“
Da die Punkte in ausschließlich auf die -Achse abbildet, ist keine surjektive Abbildung. Injektiv ist sie auch nicht, denn für jedes können wir unterschiedliche finden, sodass gilt, z.B. und umgekehrt. Also ist kein Automorphismus.

Beispiel im
[Bearbeiten]Betrachten wir nun ein Beispiel im . Wir sehen uns dafür die lineare Abbildung an. Weil den Vektorraum wieder nach abbildet, ist die Abbildung ein Endomorphismus.
Wir wollen nun prüfen, ob auch ein Automorphismus ist. Dafür müssen wir die Surjektivität und Injektivität überprüfen. Für die Injektivität betrachten wir den Kern von , also . Für Vektoren aus dem Kern von gilt also . Daraus können wir direkt schließen, dass und , also , gelten muss. Wir sehen damit, dass der Kern von nicht nur den Nullvektor enthält, sondern auch die Menge aller Vektoren . Somit ist nicht injektiv und kann daher auch nicht bijektiv sein. Insbesondere ist kein Automorphismus.
Anschaulich drückt Vektoren auf die Ebene zusammen. Es gehen somit Informationen verloren. Wenn man einen Vektor hat, kann man nicht mehr auf eindeutige Weise sagen, aus welchem Vektor er unter der Abbildung entstanden ist, da es sehr viele Wege gibt, als Summe zweier Zahlen darzustellen. Beispielsweise gilt .
Beispiel im Folgenraum
[Bearbeiten]Es gibt auch Endomorphismen auf anderen Vektorräumen als und . Für einen beliebigen Körper betrachten wir den Folgenraum
Wir betrachten die Abbildung
wobei
Wenn wir die ersten Folgenglieder ausschreiben, sieht die Abbildung so aus:
Die Abbildung vertauscht also gerade und ungerade Folgenglieder miteinander. Wir begründen kurz, warum linear ist. Die Addition und skalare Multiplikation im Folgenraum ist komponentenweise, d.h. für und und gilt
Da nur die Reihenfolge der Komponenten vertauscht, ist linear. Wir können von auch explizit nachprüfen.
Frage: Wie zeigt man direkt, dass linear ist?
Wir beweisen Additivität und Homogenität von . Seien und und . Dann ist
und
Also ist ein Endomorphismus von . Ist auch ein Automorphismus? Um das zu beantworten, müssen wir überprüfen, ob man rückgängig machen kann. Die Abbildung vertauscht gerade und ungerade Folgenglieder miteinander. Wenn wir die Folgenglieder wieder zurücktauschen, ist wieder rückgängig gemacht. Beim Zurücktauschen werden wieder gerade und ungerade Folgenglieder vertauscht, d.h. das Zurücktauschen ist wieder . Wie beim allerersten Beispiel ist selbstinvers – in Formeln heißt das bzw. . Da invertierbar ist, ist die Abbildung bijektiv. Also ist ein Automorphismus.
Endomorphismen bilden einen Ring mit Eins
[Bearbeiten]Im Artikel Vektorraum linearer Abbildungen haben wir gesehen, dass die Menge der linearen Abbildungen zwischen zwei -Vektorräumen und wieder einen Vektorraum bildet. Da gilt, ist auch die Menge Endomorphismen ein Vektorraum. Das heißt, wir können Endomorphismen eines Vektorraums addieren und mit Skalaren multiplizieren. Insbesondere können wir zwei Endomorphismen und durch Addition verknüpfen und erhalten einen Endomorphismus . Dieser ist durch
definiert, wobei die Addition im Vektorraum bezeichnet.
Lassen sich und auch auf eine andere Art verknüpfen? Intuitiv sind und zwei Verfomungen des Vektorraums . Wir können nun mit den Raum verformen und anschließend das Ergebnis mit verformen. Dabei kommt eine neue Verformung des Vektorraums heraus. Das heißt, wir erhalten wieder einen Endomorphismus von . Diese Abbildung, die aus dem Hintereinanderausführen vom und entsteht, ist die Komposition . Die Komposition von zwei Endomorphismen ist also immer ein Endomorphismus. Zusammengefasst können wir zwei Endomorphismen und verknüpfen, indem wir die Addition oder die Komposition bilden.
Weil wir neben er Addition auch die Komposition als Verknüpfung haben, trägt mehr Struktur als nur die Vektorraumstruktur. Wir werden später beweisen, dass die Menge der Endomorphismen auf mit diesen Verknüpfungen einen Ring bildet. Die Addition im Ring ist dabei die Addition der Abbildungen und die Multiplikation im Ring ist die Komposition der Abbildungen.
Wir überlegen uns nun, ob der Ring eine Eins hat und kommutativ ist. Eine Eins existiert, wenn es ein neutrales Element der Multiplikation gibt. Das heißt, wenn es ein gibt, so dass und für alle gilt. Wir kennen schon eine Abbildung, die diese Eigenschaft erfüllt: die Identität . Das ist eine lineare Abbildung und damit gilt . Also hat der Ring eine Eins.
Ist ein kommutativer Ring? Um das zu beantworten, müssen wir prüfen, ob für alle gilt. Wir überlegen uns das wieder mit Beispielen über . Sei die Projektion auf die -Achse; das heißt, für gilt . Außerdem sei die Drehung um im Urzeigersinn (bzw. um gegen den Uhrzeigersinn) um den Ursprung; das heißt, es gilt . Wir wollen untersuchen, ob gilt. Was machen die Abbildungen und anschaulich? Die Abbildung drückt erst den ganzen Raum auf die -Achse und dreht diese anschließend um im Urzeigersinn. Unser Ergebnis liegt also auf der -Achse.

Die Abbildung dreht zuerst den Raum um im Urzeigersinn und drückt anschließend alles auf die -Achse. Also liegt das Ergebnis der Abbildung auf der -Achse.
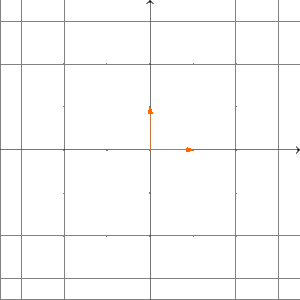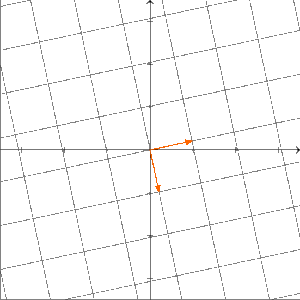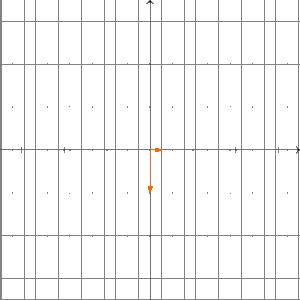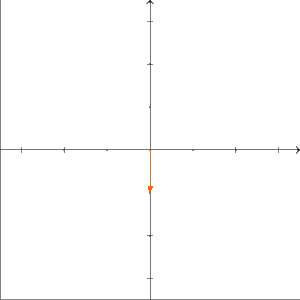
Folglich sind und verschiedene Abbildungen. Deshalb ist kein kommutativer Ring. Allgemeiner gilt: Für jeden Vektorraum mit ist kein kommutativer Ring. Das behandeln wir unten in einer Aufgabe.
Wie oben angekündigt beweisen wir jetzt, dass ein Ring ist:
Satz (Endomorphismenring)
Sei ein Körper und ein -Vektorraum. Dann bildet die Menge der Endomorphismen von zusammen mit Addition und Komposition einen Ring mit Eins.
Für zwei Endomorphismen sind und durch
und für
definiert. Hierbei ist die Addition von .
Beweis (Endomorphismenring)
Damit einen Ring mit Eins bildet, müssen folgende Eigenschaften erfüllt sein:
-
Das Tupel () ist eine abelsche Gruppe.
- Assoziativgesetz der Addition:
- Kommutativgesetz der Addition:
- Existenz eines additiven neutralen Elements:
- Existenz von additiven Inversen:
-
Das Tupel () ist ein Monoid
- Assoziativgesetz der Multiplikation:
- Existenz eines multiplikativen neutralen Elements:
-
Es gelten die Distributivgesetze
- Distributivgesetz I:
- Distributivgesetz II:
Bevor wir mit dem Beweis starten, wollen wir folgende einfache Tatsache im Hinterkopf behalten:
Seien und . Die Abbildungen und bilden Elemente von auf Elemente von ab. Dementsprechend sind Elemente von . Nach Voraussetzung ist ein -Vektorraum. Deshalb können wir die Rechenregeln, die im -Vektorraum gelten, auch auf die Elemente anwenden.
Beweisschritt: () ist eine abelsche Gruppe
Beweisschritt: Assoziativgesetz der Addition
Das Assoziativgesetz der Addition lautet:
Diese Gleichung beweisen wir, indem wir für alle die Gleichung für jeden Vektor beweisen.
Seien daher und . Dann gilt
Damit ist die Assoziativität gezeigt.
Beweisschritt: Kommutativgesetz der Addition
Das Kommutativgesetz der Addition lautet: Diese Gleichung beweisen wir, in dem wir für alle die Gleichung für jedes beweisen.
Seien daher und . Dann gilt
Damit ist die Kommutativität gezeigt.
Beweisschritt: Existenz eines additiven neutralen Elements
Wir müssen folgende Aussage zeigen:
Diese Aussage beweisen wir, in dem wir folgende Aussage zeigen:
Wir wählen , wobei die Nullabbildung von nach ist. Wir zeigen nun, dass das neutrale Element der Addition ist. Seien dafür und . Dann gilt
Das additive neutrale Element ist hier also die Nullabbildung .
Beweisschritt: Existenz von additiven Inversen
Wir müssen folgende Aussage zeigen:
Diese Aussage beweisen wir, in dem wir folgende Aussage zeigen:
Da ein -Vektorraum ist, hat ein beliebiger Vektor ein additive Inverse, nämlich . Es gilt dann . Wir können daher für einen beliebigen Endomorphismus einfach wählen. Das müssen wir nun noch zeigen. Seien dafür und . Dann gilt
Also ist die additive Inverse einer Abbildung die Abbildung .
Wir haben damit bewiesen, dass eine abelsche Gruppe ist.
Diese Aussage hätten wir auch anders zeigen können. Im Artikel Vektorraum linearer Abbildungen haben wir die Menge der linearen Abbildungen zwischen zwei -Vektorräumen und betrachtet. Diese Menge nennen wir . Wir haben gesehen, dass einen -Vektorraum bildet. Es gilt . Also ist auch ein Vektorraum und damit eine abelsche Gruppe.
Beweisschritt: () ist ein Monoid
Beweisschritt: Assoziativgesetz der Multiplikation
Das Assoziativgesetz der Multiplikation in lautet:
Das gilt, da die Komposition von Abbildungen assoziativ ist.
Beweisschritt: Existenz eines multiplikativen neutralen Elements
Wir müssen folgende Aussage zeigen:
Diese Aussage beweisen wir, in dem wir folgende Aussage zeigen:
Wir wählen , wobei die Identität auf ist. Wir wollen noch zeigen, dass das neutrale Element der Multiplikation ist. Seien dafür und . Dann gilt
Also ist das neutrale Element der Multiplikation in gegeben durch die Identität auf , d.h. .
Beweisschritt: Distributivgesetze
Beweisschritt: Distributivgesetz I
Das Distributivgesetz I lautet:
Diese Gleichung beweisen wir, indem wir für alle die Gleichung für jedes zeigen. Seien und . Dann gilt
Damit ist die Distributivität I gezeigt.
Beweisschritt: Distributivgesetz II
Das Distributivgesetz II lautet:
Diese Gleichung beweisen wir, in dem wir die Gleichung für alle und zeigen. Seien dafür und . Dann gilt
Damit ist die Distributivität II gezeigt.
Automorphismen und platt drücken
[Bearbeiten]Der endlichdimensionale Fall
[Bearbeiten]Oben haben wir bereits einige Beispiele von Endo- und Automorphismen untersucht. Dabei haben wir gesehen, dass Endomorphismen, die etwas „plattdrücken“, nicht bijektiv und damit keine Automorphismen sind. Andererseits waren Endomorphismen, die nichts „plattdrücken“, schon Automorphismen.
Frage: Was ist „nichts plattdrücken“ in mathematischer Sprache?
Ein Endomorphismus „drückt nichts platt“, wenn es keinen Vektor gibt, der von auf Null abgebildet wird. Das heißt, für alle Vektoren , gilt . Da eine lineare Abbildung ist, gilt das genau dann, wenn injektiv, also ein Monomorphismus ist.
Bei Endomorphismen von endlich-dimensionalen Vektorräumen ist „nichts plattdrücken“ gleichbedeutend mit „Automorphismus sein“: Sei ein Endomorphismus eines -dimensionalen Vektorraums . Wenn die Abbildung ein Automorphismus ist, ist sie insbesondere injektiv. Also drückt nichts in platt. Wenn wir umgekehrt annehmen, dass nichts plattdrückt, folgt, dass injektiv ist. Damit gehen keine Informationen aus beim Abbilden mit verloren. Daraus können wir schließen, dass das Bild auch -dimensional ist. Also muss gelten. Damit ist auch surjektiv und somit ein Automorphismus.
Wir haben gesehen, dass ein injektiver Endomorphismus über einen endlich-dimensionalen Vektorraum automatisch surjektiv ist. Gilt auch die umgekehrte Aussage? In anderen Worten: Wenn ein surjektiver Endomorphismus eines -dimensionalen Vektorraums ist, folgt dann, dass injektiv ist? Wenn surjektiv ist, gilt und damit . Angenommen ist nicht injektiv. Dann gibt es einen Vektor für den gilt. Dann drückt die Richtung platt, in die zeigt. Das bedeutet, beim Abbilden von durch verlieren wir mindestens eine Dimension von . Folglich wäre dann . Das ist ein Widerspruch zu . Deshalb muss injektiv sein. Also gilt, wenn surjektiv ist, dann ist auch injektiv.
evtl. verweisen auf eine Erklärung im Artikel "Lineare Abbildungen zwischen endlichdimensionalen Vektorräumen", wenn dieser geschrieben ist.
Diese Aussagen zeigen wir in folgendem Satz noch einmal formal.
Satz (Endomorphismen auf endlichdimensionalen Vektorräumen)
Sei ein endlichdimensionaler Vektorraum und ein Endomorphismus. Dann ist äquivalent
- ist ein Isomorphismus
- ist ein Monomorphismus
- ist ein Epimorphismus
Beweis (Endomorphismen auf endlichdimensionalen Vektorräumen)
Wir wissen schon, dass für zwei endlich-dimensionale Vektorräume und mit und eine lineare Abbildung gilt, dass die Aussagen
- ist ein Isomorphismus
- ist ein Monomorphismus
- ist ein Epimorphismus
äquivalent sind. Also folgt für einen Endomorphismus von einem endlich-dimensionalen Vektorraum , dass die drei Aussagen äquivalent sind.
Den Satz für allgemeine lineare Abbildungen verlinken, sobald er geschrieben wurde
Der unendlichdimensionale Fall
[Bearbeiten]Im Unendlichdimensionalen funktioniert das obige Argument nicht mehr. Wir haben im endlichdimensionalen Fall ausgenutzt, dass für einen -dimensionalen Vektorraum und einen Untervektorraum aus schon folgt. Oben haben wir verwendet. In unendlich-dimensionalen Vektorräume gilt das jedoch nicht. Wir können uns das so vorstellen: In einem unendlich-dimensionalen Vektorraum hat ein gleich großer Untervektorraum Platz ohne alles auszufüllen.
Also gilt für Endomorphismen eines unendlichdimensionalen Vektorraums nicht, dass genau dann surjektiv ist, wenn injektiv ist. Um das besser zu verstehen, untersuchen wir nun konkrete Gegenbeispiele.
Beispiel (Ein injektiver Endomorphismus, der nicht surjektiv ist)
Sei der Folgenraum über . Wir definieren den Endomorphismus
Man kann leicht nachprüfen, dass linear ist. Warum ist injektiv? Für mit gilt , also ist . Somit folgt und ist injektiv.
Warum ist nicht surjektiv? Um das zu sehen, müssen wir einen Vektor in finden, den nicht trifft. Sei dafür . Egal welches wir wählen, es gilt für , dass das erste Folgenglied gleich ist. Also wird nie von getroffen. Deshalb ist nicht surjektiv.
Hinweis
Das Vorgehen in diesem Beispiel erinnert an Hilberts Hotel. Dort verschiebt man durch eine Abbildung alle Elemente der Menge um . Die Abbildung ist dabei
Diese Abbildung ist auch injektiv, aber genau wie nicht surjektiv. Der Unterschied ist, dass eine lineare Abbildung zwischen Vektorräumen ist und nur eine Abbildung zwischen Mengen. Wir sehen also hier, dass unendlich-dimensionale Vektorräume ähnlich komische Eigenschaften erfüllen wie unendliche Mengen.
Beispiel (Ein surjektiver Endomorphismus, der nicht injektiv ist)
Wir wählen wieder den Folgenraum über . Wir definieren den Endomorphismus
Also ist für . Wieder kann man leicht nachprüfen, dass linear ist.
Zuerst überprüfen wir, dass surjektiv ist. Sei dafür ein beliebiger Vektor. Wir wollen einen Vektor finden, für den gilt. Dies gilt für und damit ist surjektiv.
Warum ist nicht injektiv? Um das zu sehen, suchen wir ein mit und . Wir wählen dafür . Dann ist , aber . Somit ist nicht injektiv.
Die Automorphismengruppe
[Bearbeiten]Wir wissen, dass die Endomorphismen einen Ring mit Eins bilden. Die Automorphismen sind genau alle invertierbaren Endomorphismen. Deshalb sind die Automorphismen eines Vektorraums genau die Einheiten, d. h. die multiplikativ invertierbaren Elemente, des Endomorphismenrings. Die Multiplikation im Endomorphismenring ist die Komposition von Abbildungen. Im folgenden Satz zeigen wir, dass eine Gruppe bzgl. dieser Multiplikation ist.
Satz (Automorphismengruppe)
Sei ein Körper und ein -Vektorraum. Die Menge bildet eine Gruppe bezüglich der Komposition .
Es gilt zudem .
Beweis (Automorphismengruppe)
Wir müssen folgendes zeigen
- ist abgeschlossen bezüglich
- ist assoziativ
- Es gibt ein neutrales Element bezüglich in
- Jedes Element in hat ein multiplikatives Inverses.
Beweisschritt: Abgeschlossenheit bzgl.
Wir beweisen, dass für alle Automorphismen und auch gilt.
Seien dafür und . Also sind und auch Endomorphismen. Weil ein Ring mit Multiplikation bildet, ist abgeschlossen bezüglich . Also gilt . Wir müssen also nur noch begründen, dass bijektiv ist. Weil und bijektiv sind, gibt es jeweils Inverse und . Wir zeigen nun, dass die Inverse von ist. Es gilt
und
Also hat ein Inverses und ist damit bijektiv. Deshalb ist ein Automorphismus.
Beweisschritt: Assoziativität von
Wir müssen zeigen, dass für alle Automorphismen und folgendes gilt
Die Komposition ist sogar für beliebige Abbildungen assoziativ. Trotzdem begründen wir diese Aussage nochmal. Seien dafür und und ein beliebiger Vektor. Dann gilt
Da die Abbildungen und auf allen Vektoren übereinstimmen, sind sie gleich, d.h. .
Beweisschritt: Existenz eines Neutralen Elements
Wir müssen ein Element finden, so dass für alle gilt .
Wir wählen . Dann gilt und ist linear. Also ist . Außerdem ist bijektiv und deshalb gilt .
Sei . Es gilt
Also ist das neutrale Element in .
Beweisschritt: Existenz Multiplikativer Inverser
Wir beweisen, dass für jedes ein Automorphismus existiert, so dass .
Sei ein Automorphismus. Dann ist bijektiv und somit existiert ein inverse Abbildung , für die gilt . Wir müssen nur noch zeigen, dass . Wir wissen, dass Umkehrabbildungen von linearen Abbildungen linear sind. Folglich ist als Umkehrabbildung der linearen Abbildung auch linear. Außerdem ist auch bijektiv, weil Umkehrabbildung hat. Also gilt und damit ist ein Inverses von in .
Die Automorphismen bilden zwar eine Gruppe, sind aber kein Ring mehr. Das liegt daran, dass keine additive Struktur mehr hat: Wenn wir zwei Automorphismen und von einem Vektorraum haben, muss nicht unbedingt wieder ein Automorphismus sein. Um das konkret zu machen, betrachten wir ein Beispiel:
Beispiel (Summe von Automorphismen, die kein Automorphismus ist)
Wir betrachten den Vektorraum und definieren die Automorphismen
Es ist leicht, zu zeigen, dass und linear und bijektiv sind. Also gilt . Es ist
Da diese Abbildung den Vektor nicht trifft, ist sie nicht surjektiv. Also ist nicht bijektiv und somit kein Automorphismus.
Hinweis
Für keinen Vektorraum gilt, dass abgeschlossen unter Addition ist.
Für Vektorräume mit ist die Automorphismengruppe nicht kommutativ. Wie beim Endomorphismenring ist das Verknüpfen der Abbildungen nicht kommutativ. Das untersuchen wir unten in einer Aufgabe.
Aufgaben
[Bearbeiten]Aufgabe (Automorphismus)
Zeige, dass die Abbildung ein Automorphismus ist.
Lösung (Automorphismus)
Linearität lässt sich leicht nachrechnen. Da Definitions- und Zielbereich gleich sind, ist also ein Endomorphismus.
Wir wollen nun zeigen, dass bijektiv ist. Dazu müssen wir zeigen, dass injektiv und surjektiv ist.
Wir beginnen mit der Injektivität. Seien und mit . Dann gilt für , dass , also und somit . Dies zeigt die Injektivität.
Nun zeigen wir die Surjektivität. Sei dazu . Definiere . Dann gilt . Also ist surjektiv.
Wir haben also gezeigt, dass ein Automorphismus ist.
Aufgabe (Transformation im Raum der Fibonacci-Folgen)
Sei ein Körper und der Vektorraum der Fibonacci-Folgen
wobei der Raum aller Folgen in ist. Zeige:
- ist isomorph zu .
- Es gibt einen Endomorphismus , der die ersten beiden Einträge jeder Folge vertauscht, das heißt, es gilt und für alle .
- ist ein Automorphismus.
Lösung (Transformation im Raum der Fibonacci-Folgen)
Beweisschritt:
Wir zeigen, dass
ein Isomorphismus ist. Die Linearität lässt sich leicht nachrechnen.
Für die Injektivität zeigen wir . Sei also mit , d.h. . Wir zeigen für alle mit vollständiger Induktion. Nach Annahme gilt die Aussage für . Damit ist der Induktionsanfang gezeigt. Sei nun . Für den Beweis des Induktionsschritts müssen wir zeigen und nehmen dafür als Induktionsvoraussetzung an, dass die Aussage für alle gilt. Per Definition der Folge folgt .
Für die Surjektivität benutzen wir, dass jede Folge in durch Angabe der ersten beiden Folgenglieder definiert werden kann: Sei . Wir definieren wie im Beweis der Injektivität induktiv durch , und . Dann gilt und .
Beweisschritt: Es gibt einen Endomorphismus , der die ersten beiden Einträge jeder Folge vertauscht.
Wir benutzen den Isomorphismus aus dem ersten Teil der Aufgabe. Offenbar ist
linear und bildet von nach ab, ist also ein Endomorphismus. Damit ist auch als Verkettung linearer Abbildungen linear. Da von nach abbildet, ist ein Endomorphismus, und per Konstruktion gilt
für alle . Also vertauscht die ersten beiden Einträge jeder Folge.
Beweisschritt: ist ein Automorphismus.
Wir müssen zeigen, dass ein Isomorphismus ist. Da ein Isomorphismus ist, ist ein Isomorphismus genau dann wenn ein Isomorphismus ist. Der Endomorphismus vertauscht einfach nur die beiden Komponenten eines Vektors in , bildet also die (geordnete) Basis von auf die Basis ab. Da eine lineare Abbildung genau dann bijektiv ist, wenn sie Basen auf Basen abbildet, ist ein Isomorphismus.
Aufgabe (Scherungen sind Automorphismen)
Sei ein Skalar. Wir betrachten die Abbildung . Zeige, dass ein Automorphismus ist.
Lösung (Scherungen sind Automorphismen)
Die Linearität von lässt sich leicht nachprüfen. Da den auf sich selbst abbildet, ist ein Endomorphismus und es bleibt lediglich die Bijektivität zu zeigen.
Wir beweisen die Injektivität, indem wir zeigen. Sei , das heißt, es gilt . Wir wollen zeigen. Da gilt, erhalten wir aus der zweiten Vektorkomponente. Daraus folgt nun und es gilt . Damit ist injektiv.
Als zweites müssen wir zeigen, dass surjektiv ist. Sei dafür ; wir müssen zeigen, dass es ein mit gibt. Wenn wir die Definition von einsetzen, muss der gesuchte Vektor damit erfüllen. Das heißt, es muss gelten. Hieraus erhalten wir , also . Setzen wir , so gilt
Also ist surjektiv.
Da bijektiv und ein Endomorphismus ist, ist ein Automorphismus.
Aufgabe (Nicht-Kommutativität im Endomorphismenring)
Sei ein -dimensionaler -Vektorraum mit . Zeige: Der Endomorphismenring ist nicht kommutativ.
Lösung (Nicht-Kommutativität im Endomorphismenring)
Sei eine Basis von , wobei nach Annahme gilt. Wir definieren zwei nichtkommutierende Endomorphismen nach dem Prinzip der linearen Fortsetzung, indem wir die Bilder der Basisvektoren vorgeben: Für setze
und
Die Abbildung vertauscht also die ersten beiden Basisvektoren, während den ersten Basisvektor auf den Nullvektor abbildet. Bei der Definition von und haben wir gebraucht, dass es Basisvektoren gibt. Es gilt für
aber
Da der Basisvektor als Element der Basis von nicht der Nullvektor sein kann, folgt insbesondere
Also gilt . Damit ist der Endomorphismenring nicht kommutativ, falls .
Aufgabe (Kommutativität im Endomorphismenring)
Sei ein eindimensionaler -Vektorraum, d.h. . Zeige: Der Endomorphismenring ist kommutativ.
Lösung (Kommutativität im Endomorphismenring)
Sei eine Basis von und seien beliebig. Endomorphismen sind durch die Bilder der Basisvektoren schon eindeutig bestimmt. Da es wegen nur einen Basisvektor gibt, gilt und damit
für gewisse . Wegen ist jedes von der Form für ein . Mit der Linearität von und der Kommutativität der Multiplikation in folgt
Analog kann man für beliebiges zeigen und es folgt
Somit gilt für alle
wobei wir in die Kommutativität der Multiplikation in ausgenutzt haben.
Hinweis
In den obigen beiden Aufgaben haben wir gesehen, dass kommutativ ist, wenn und nicht kommutativ, wenn . Was gilt für ? Wenn gilt, ist der Nullvektorraum. Es gibt nur einen Endomorphismus über dem Nullraum . Dieser Endomorphismus ist die Nullabbildung . Also gilt . Da der Ring nur aus einem Element besteht, ist kommutativ.
Somit gilt: ist genau dann kommutativ, wenn .






































{\begin{pmatrix}x\\y\end{pmatrix}}&=g{\begin{pmatrix}-y\\x\end{pmatrix}}={\begin{pmatrix}x\\-(-y)\end{pmatrix}}={\begin{pmatrix}x\\y\end{pmatrix}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1825c0a06295d1e4561aac6e6b0a5beb9fdaa2ff)







































_{i}&\mapsto f\left((x_{i})_{i}\right)=(x_{k(i)})_{i},\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4787f55261758fd7de64ad2a8c768550c4686bd5)





![{\displaystyle {\begin{aligned}&f((x_{i})_{i}+(y_{i})_{i})\\[0.3em]&{\color {OliveGreen}\left\downarrow \ {\text{Addition von Folgen}}\right.}\\[0.3em]=&f((x_{i}+y_{i})_{i})\\[0.3em]&{\color {OliveGreen}\left\downarrow \ {\text{Definition von }}f\right.}\\[0.3em]=&(x_{k(i)}+y_{k(i)})_{i}\\[0.3em]&{\color {OliveGreen}\left\downarrow \ {\text{Addition von Folgen}}\right.}\\[0.3em]=&(x_{k(i)})_{i}+(y_{k(i)})_{i}\\[0.3em]&{\color {OliveGreen}\left\downarrow \ {\text{Definition von }}f\right.}\\[0.3em]=&f((x_{i})_{i})+f((y_{i})_{i})\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/67e4fd821c195540f41e768f7939bc6e65252266)
![{\displaystyle {\begin{aligned}&f(\lambda \cdot (x_{i})_{i})\\[0.3em]&{\color {OliveGreen}\left\downarrow \ {\text{Skalare Multiplikation von Folgen}}\right.}\\[0.3em]=&f((\lambda \cdot x_{i})_{i})\\[0.3em]&{\color {OliveGreen}\left\downarrow \ {\text{Definition von }}f\right.}\\[0.3em]=&(\lambda \cdot x_{k(i)})_{i}\\[0.3em]&{\color {OliveGreen}\left\downarrow \ {\text{Skalare Multiplikation von Folgen}}\right.}\\[0.3em]=&\lambda \cdot (x_{k(i)})_{i})_{i}\\[0.3em]&{\color {OliveGreen}\left\downarrow \ {\text{Definition von }}f\right.}\\[0.3em]=&\lambda \cdot f((x_{i})_{i}).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/979d806de1f02dd28926e595763318b965aef0cf)

























































+h)(x)&=(f+g)(x)+_{V}h(x)\\[0.3em]&{\color {OliveGreen}\left\downarrow \ {\text{Definition von }}+\right.}\\[0.3em]&=(f(x)+_{V}g(x))+_{V}h(x)\\[0.3em]&{\color {OliveGreen}\left\downarrow \ {\text{Assoziativität der Addition in }}V\right.}\\[0.3em]&=f(x)+_{V}(g(x)+_{V}h(x))\\[0.3em]&{\color {OliveGreen}\left\downarrow \ {\text{Definition von }}+\right.}\\[0.3em]&=f(x)+_{V}(g+h)(x)\\[0.3em]&{\color {OliveGreen}\left\downarrow \ {\text{Definition von }}+\right.}\\[0.3em]&=(f+(g+h))(x)\\[0.3em]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1993d091e0d08f1e0f0cbe0bbc84ae290a93fee8)



(x)&=f(x)+_{V}g(x)\\[0.3em]&{\color {OliveGreen}\left\downarrow \ {\text{Kommutativität der Addition in }}V\right.}\\[0.3em]&=g(x)+_{V}f(x)\\[0.3em]&{\color {OliveGreen}\left\downarrow \ {\text{Definition von }}+\right.}\\[0.3em]&=(g+f)(x)\\[0.3em]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7455a79ca2a4277888ac58978103139b7e564038)





} }+f)(x)&=0_{\operatorname {Abb(V,V)} }(x)+_{V}f(x)\\[0.3em]&{\color {OliveGreen}\left\downarrow \ {\text{Definition von }}0_{\operatorname {Abb(V,V)} }\right.}\\[0.3em]&=0_{V}+_{V}f(x)\\[0.3em]&{\color {OliveGreen}\left\downarrow \ {\text{Neutrales Element der Addition in }}V\right.}\\[0.3em]&=f(x)\\[0.3em]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0354199aa26d9052d0e245b3f9de01694ebf9b41)





(x)&=f'(x)+_{V}f(x)\\[0.3em]&{\color {OliveGreen}\left\downarrow \ {\text{Definition von }}f'\right.}\\[0.3em]&=-f(x)+_{V}f(x)\\[0.3em]&{\color {OliveGreen}\left\downarrow \ {\text{additive Inverse in }}V\right.}\\[0.3em]&=0_{V}\\[0.3em]&{\color {OliveGreen}\left\downarrow \ {\text{Definition von }}0_{\operatorname {Abb(V,V)} }\right.}\\[0.3em]&=0_{\operatorname {Abb(V,V)} }(x)\\[0.3em]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/65285ff3644b399141a4fb1cc96a54ddab39c33c)









(x)&=(\operatorname {id} _{V}\circ f)(x)\\[0.3em]&{\color {OliveGreen}\left\downarrow \ {\text{Definition von }}\circ \right.}\\[0.3em]&=\operatorname {id} _{V}(f(x))\\[0.3em]&{\color {OliveGreen}\left\downarrow \ {\text{Definition von }}\operatorname {id} _{V}\right.}\\[0.3em]&=f(x)\\[0.3em]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/81b0a75268cc552ceaf8a02c5c9b9f2ef2fa5874)


)(x)&=f((g+h)(x))\\[0.3em]&{\color {OliveGreen}\left\downarrow \ {\text{Definition von }}+\right.}\\[0.3em]&=f(g(x)+_{V}h(x))\\[0.3em]&{\color {OliveGreen}\left\downarrow \ {\text{f ist linear}}\right.}\\[0.3em]&=f(g(x))+_{V}f(h(x))\\[0.3em]&{\color {OliveGreen}\left\downarrow \ {\text{Definition der Komposition}}\right.}\\[0.3em]&=(f\circ g)(x)+_{V}(f\circ h)(x)\\[0.3em]&{\color {OliveGreen}\left\downarrow \ {\text{Definition von }}+\right.}\\[0.3em]&=(f\circ g+f\circ h)(x)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ff4b4bca4d715d1fd15775b93c03fb5a4c84dac8)

\circ h)(x)&=(f+g)(h(x))\\[0.3em]&{\color {OliveGreen}\left\downarrow \ {\text{Definition von }}+\right.}\\[0.3em]&=f(h(x))+_{V}g(h(x))\\[0.3em]&{\color {OliveGreen}\left\downarrow \ {\text{Definition der Komposition }}\right.}\\[0.3em]&=(f\circ h)(x)+_{V}(g\circ h)(x)\\[0.3em]&{\color {OliveGreen}\left\downarrow \ {\text{Definition von }}+\right.}\\[0.3em]&=(f\circ h+g\circ h)(x)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5a1c46d9d034f0133bc59600fccd9ac499c107f8)








































































![{\displaystyle {\begin{aligned}&f\colon \mathbb {R} ^{2}\to \mathbb {R} ^{2},\quad &g\colon \mathbb {R} ^{2}&\to \mathbb {R} ^{2}\\[0.3em]&{\begin{pmatrix}x\\y\end{pmatrix}}\mapsto {\begin{pmatrix}x\\y\end{pmatrix}},&{\begin{pmatrix}x\\y\end{pmatrix}}&\mapsto {\begin{pmatrix}x\\-y\end{pmatrix}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6538b97d067df7a711c22e034505c702782d959a)

![{\displaystyle {\begin{aligned}f+g\colon \mathbb {R} ^{2}&\to \mathbb {R} ^{2}\\[0.3em]{\begin{pmatrix}x\\y\end{pmatrix}}&\mapsto {\begin{pmatrix}2x\\0\end{pmatrix}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a6cd31db458d377a0305d2ef46fa8e829e819d96)





























































































