Konvergenzradius von Potenzreihen – Serlo „Mathe für Nicht-Freaks“

In diesem Kapitel werden wir zeigen, dass jede Potenzreihe $\sum _{k=0}^{\infty }c_{k}x^{k}$ einen Konvergenzradius besitzt. Das ist eine reelle Zahl $R$, so dass die Potenzreihe für alle $x\in \mathbb {R}$ mit $|x|<R$ absolut konvergiert und für alle $x\in \mathbb {R}$ mit $|x|>R$ divergiert. Dabei kann auch $R=0$ und $R=\infty$ gelten. Für den Grenzfall $|x|=R$ kann keine allgemeine Konvergenzaussage getroffen werden. Zur Berechnung des Konvergenzradius werden wir zwei Formeln herleiten. Die Formel von Cauchy-Hadamard $R=1/\limsup _{k\to \infty }{\sqrt[{k}]{|c_{k}|}}$ werden wir aus dem Wurzelkriterium und die Formel von Euler $R=1/\lim _{k\to \infty }\left|{\frac {c_{k+1}}{c_{k}}}\right|$ aus dem Quotientenkriterium herleiten. Außerdem werden wir noch zahlreiche Beispiele zur Berechnung des Konvergenzradius durchdiskutieren.

Definition und Existenz des Konvergenzradius

Wir wissen bereits, dass beispielsweise die geometrische Reihe $\sum _{k=0}^{\infty }x^{k}$ oder die für alle $x\in \mathbb {R}$ mit $|x|<1$ absolut konvergiert und für alle $x\in \mathbb {R}$ mit $|x|>1$ divergiert. Es gilt also $1=\sup \left\{r\in \mathbb {R} \mid \sum _{k=0}^{\infty }r^{k}{\text{ konvergiert absolut}}\right\}$. Die Frage ist nun, ob so eine Grenzzahl, der sogenannte Konvergenzradius, für jede Potenzreihe existiert. Zunächst definieren wir dazu:

Definition (Konvergenzradius)

Sei $(c_{k})_{k\in \mathbb {N} }$ eine Folge und $\sum _{k=0}^{\infty }c_{k}x^{k}$ die zugehörige Potenzreihe. Dann heißt

$R=\sup \left\{r\in \mathbb {R} \mid \sum _{k=0}^{\infty }c_{k}r^{k}{\text{ konvergiert absolut}}\right\}$

der Konvergenzradius der Potenzreihe.

Wir zeigen nun, dass dieser Konvergenzradius tatsächlich für jede Potenzreihe existiert:

Satz (Existenz des Konvergenzradius)

Sei $(c_{k})_{k\in \mathbb {N} }$ eine Folge, $\sum _{k=0}^{\infty }c_{k}x^{k}$ die zugehörige Potenzreihe und $R=\sup\{r\in \mathbb {R} \mid \sum _{k=0}^{\infty }c_{k}r^{k}{\text{ konvergiert absolut}}\}$. Dann gilt:

1. Die Potenzreihe konvergiert für alle $x\in \mathbb {R}$ mit $|x|<R$.
2. Die Potenzreihe divergiert für alle $x\in \mathbb {R}$ mit $|x|>R$.

Beweis (Existenz des Konvergenzradius)

Beweisschritt: Hilfsaussage: Konvergiert die Potenzreihe in $x_{0}\neq 0$ , so konvergiert sie in jedem Punkt $x\in \mathbb {R}$ mit $|x|<|x_{0}|$ absolut.

Da nach Voraussetzung $\sum _{k=0}^{\infty }c_{k}x_{0}^{k}$ konvergiert, ist nach dem Trivialkriterium $(c_{k}x_{0}^{k})_{k\in \mathbb {N} _{0}}$ eine Nullfolge. Da konvergente Folgen beschränkt sind, gibt es eine Schranke $S>0$ mit $|c_{k}x_{0}^{k}|\leq S$. Damit folgt für $x\in \mathbb {R}$ mit $|x|<|x_{0}|$:

$|c_{k}x^{k}|=\left|c_{k}x_{0}^{k}\cdot \left({\frac {x}{x_{0}}}\right)^{k}\right|=|c_{k}x_{0}^{k}|\cdot \underbrace {\left|{\frac {x}{x_{0}}}\right|^{k}} _{=q^{k}}\leq S\cdot q^{k}$

Dabei ist $q=\left|{\frac {x}{x_{0}}}\right|={\frac {|x|}{|x_{0}|}}<1$. Also konvergiert die geometrische Reihe $\sum _{k=0}^{\infty }S\cdot q^{k}=S\cdot \sum _{k=0}^{\infty }q^{k}$ absolut. Mit dem Majorantenkriterium konvergiert die Reihe $\sum _{k=0}^{\infty }c_{k}x_{0}^{k}$ ebenfalls absolut.

Beweisschritt: Ist $x\in \mathbb {R}$ mit $|x|<R$, so konvergiert $\sum _{k=0}^{\infty }c_{k}x^{k}$ absolut.

Sei $x\in \mathbb {R}$ mit $|x|<R=\sup\{r\in \mathbb {R} \mid \sum _{k=0}^{\infty }c_{k}r^{k}{\text{ konvergiert absolut}}\}$. Nach der Definition des Supremums gibt es ein $r\in \mathbb {R}$ mit $|x|<r<R$, für das $\sum _{k=0}^{\infty }c_{k}r^{k}$ konvergiert. Mit der Hilfsaussage aus dem 1. Beweisschritt folgt damit, dass $\sum _{k=0}^{\infty }c_{k}x^{k}$ absolut konvergiert.

Beweisschritt: Ist $x\in \mathbb {R}$ mit $|x|>R$, so divergiert $\sum _{k=0}^{\infty }c_{k}x^{k}$.

Sei $x\in \mathbb {R}$ mit $|x|>R=\sup\{r\in \mathbb {R} \mid \sum _{k=0}^{\infty }c_{k}r^{k}{\text{ konvergiert absolut}}\}$. Wir führen hier einen Widerspruchsbeweis: Wir nehmen an, dass $\sum _{k=0}^{\infty }c_{k}x^{k}$ konvergiert. Nach der Definition des Supremums gibt es erneut ein $r\in \mathbb {R}$ mit $R<r<|x|$. Mit der Hilfsaussage aus dem 1. Beweisschritt konvergiert dann aber $\sum _{k=0}^{\infty }c_{k}r^{k}$. Diese ist aber ein Widerspruch zu $R=\sup\{r\in \mathbb {R} \mid \sum _{k=0}^{\infty }a_{k}r^{k}{\text{ konvergiert absolut}}\}$. Also kann $\sum _{k=0}^{\infty }c_{k}x^{k}$ nicht konvergieren.

Beispiel (Geometrische Reihe und Verwandtes)

• Wir haben oben und im Kapitel zuvor schon gesehen, dass die geometrische Reihe $\sum _{k=0}^{\infty }x^{k}$ den Konvergenzradius $R=1$ hat.
• Ebenso haben die mit der geometrischen Reihe verwandten Reihen $\sum _{k=0}^{\infty }{\frac {x^{k}}{k}}$ und $\sum _{k=0}^{\infty }{\frac {x^{k}}{k^{2}}}$ den Konvergenzradius $R=1$, denn ist $|x|<1$, so gilt $|a_{k}|={\frac {|x|^{k}}{k}}\leq |x|^{k}$ für alle $k\in \mathbb {N}$. Daher konvergiert die Reihe $\sum _{k=0}^{\infty }{\frac {x^{k}}{k}}$ Majorantenkriterium mit der geometrischen Reihe als Majorante. Ist andererseits $|x|>1$, so divergiert $\left({\frac {|x|^{k}}{k}}\right)$ gegen $\infty$, als Quotient der geometrischen Folge $(|x|^{k})$ mit der Potenzfolge $(k^{1})$. Nach dem Trivialkriterium divergiert die Reihe. Bei der Reihe $\sum _{k=1}^{\infty }{\frac {x^{k}}{k^{2}}}$ kann man ganz analog argumentieren.

Hinweis

Im Reelen grenzt der Konvergenzradius anschaulich den Bereich auf der Zahlengerade, in dem die Potenzreihe $\sum \limits _{k=0}^{\infty }c_{k}x^{k}$ absolut konvergiert (das Intervall $]-R;R[$), von den Bereichen ab, in denen die Potenzreihe divergiert (die Intervalle $]-\infty ;-R[$ und $]R;\infty [$).

Veranschaulichung des Konvergenzradius

Hinweis

Analog zum Konvergenradius von Potenzreihen, haben Dirichlet-Reihe, das sind Reihen der Form $\sum \limits _{k=1}^{\infty }{\frac {a_{k}}{k^{s}}}$ mit $s\in \mathbb {Q}$, eine Konvergenzabszisse $\lambda \in \mathbb {R}$, so dass die Reihe für alle $s>\lambda$ konvergiert und für alle $s<\lambda$ divergiert. Wir werden hier Dirichlet-Reihen nicht genauer besprechen, da sie nicht Bestandteil der meisten Analysis-Grundvorlesungen sind. Wer Interesse an Dirichlet-Reihe hat kann sich gerne der entsprechenden Übungsaufgabe widmen.

Veranschaulichung der Konvergenzabszisse

Formeln zur Berechnung des Konvergenzradius

Zur praktischen Anwendung werden wir nun zwei Formeln für den Konvergenzradius herleiten. Dabei werden wir die erste aus dem Wurzelkriterium und die zweite aus dem Quotientenkriterium herleiten.

Einstiegsbeispiel

Dabei schauen wir uns zunächst als konkretes Beispiel die Reihe $\sum _{k=0}^{\infty }a_{k}=\sum _{k=0}^{\infty }\underbrace {\frac {2^{k}}{k}} _{=c_{k}}\cdot x^{k}$ an.

Anwendung des Wurzelkriteriums

Wir erhalten

${\begin{aligned}\limsup _{k\to \infty }{\sqrt[{k}]{|a_{k}|}}&=\limsup _{k\to \infty }{\sqrt[{k}]{\left|{\frac {2^{k}}{k}}\cdot x^{k}\right|}}\\[0.3em]&=\limsup _{k\to \infty }{\sqrt[{k}]{{\frac {2^{k}}{k}}\cdot |x|^{k}}}\\[0.3em]&=\limsup _{k\to \infty }{\frac {\sqrt[{k}]{2^{k}}}{\sqrt[{k}]{k}}}\cdot {\sqrt[{k}]{|x|^{k}}}\\[0.3em]&=\limsup _{k\to \infty }{\frac {2}{\sqrt[{k}]{k}}}\cdot |x|\\[0.3em]&\ {\color {OliveGreen}\left\downarrow \ {\sqrt[{k}]{k}}\to 1{\text{ mit }}k\to \infty \right.}\\[0.3em]&=2\cdot |x|\\[0.3em]&{\begin{cases}<1&{\text{ falls }}|x|<{\frac {1}{2}}\\>1&{\text{ falls }}|x|>{\frac {1}{2}}\end{cases}}\end{aligned}}$

Also konvergiert die Reihe absolut für alle $x\in \mathbb {R}$ mit $|x|<{\frac {1}{2}}$ und divergiert für alle $x\in \mathbb {R}$ mit $|x|>{\frac {1}{2}}$. Sie besitzt damit den Konvergenzradius $R={\frac {1}{2}}$. Da immer ${\sqrt[{k}]{|x|^{k}}}=|x|$ gilt, kann man bei Potenzreihen $\sum _{k=0}^{\infty }c_{k}x^{k}$ auch direkt dem Limes Superior von ${\sqrt[{k}]{|c_{k}|}}$ bilden. Genauer betrachtet gilt

$R={\frac {1}{2}}={\frac {1}{\limsup \limits _{k\to \infty }{\sqrt[{k}]{\frac {2^{k}}{k}}}}}={\frac {1}{\limsup \limits _{k\to \infty }{\sqrt[{k}]{|c_{k}|}}}}$

Diese Formel heißt die Formel von Cauchy-Hadamard. Wir werden sie weiter unten allgemein für jede Potenzreihe beweisen.

Anwendung des Quotientenkriteriums

Hier erhalten wir

${\begin{aligned}\lim _{k\to \infty }\left|{\frac {a_{k+1}}{a_{k}}}\right|&=\lim _{k\to \infty }\left|{\frac {{\frac {2^{k+1}}{k+1}}\cdot x^{k+1}}{{\frac {2^{k}}{k}}\cdot x^{k}}}\right|\\[0.3em]&=\lim _{k\to \infty }{\frac {\frac {2^{k+1}}{k+1}}{\frac {2^{k}}{k}}}\cdot \left|{\frac {x^{k+1}}{x^{k}}}\right|\\[0.3em]&=\lim _{k\to \infty }{\frac {2^{k+1}\cdot k}{2^{k}\cdot k+1}}\cdot {\frac {|x|^{k+1}}{|x|^{k}}}\\[0.3em]&=\lim _{k\to \infty }2\cdot {\frac {k}{k+1}}\cdot |x|\\[0.3em]&\ {\color {OliveGreen}\left\downarrow \ {\frac {k}{k+1}}={\frac {1}{1+{\frac {1}{k}}}}\to {\frac {1}{1+0}}=1{\text{ mit }}k\to \infty \right.}\\[0.3em]&=2\cdot |x|\\[0.3em]&{\begin{cases}<1&{\text{ falls }}|x|<{\frac {1}{2}}\\>1&{\text{ falls }}|x|>{\frac {1}{2}}\end{cases}}\end{aligned}}$

Also folgt ebenso, dass die Reihe für alle $x\in \mathbb {R}$ mit $|x|<{\frac {1}{2}}$ absolut konvergiert und für alle $x\in \mathbb {R}$ mit $|x|>{\frac {1}{2}}$ divergiert. Damit folgt der Konvergenzradius

$R={\frac {1}{2}}={\frac {1}{\lim \limits _{k\to \infty }{\frac {\frac {2^{k+1}}{k+1}}{\frac {2^{k}}{k}}}}}={\frac {1}{\lim \limits _{k\to \infty }\left|{\frac {a_{k+1}}{a_{k}}}\right|}}$

Diese Formel heißt die Formel von Euler. Wir werden diese nun ebenso allgemein beweisen.

Die Formeln von Cauchy-Hadamard und Euler

Nun zeigen wir allgemein

Satz (Die Formeln von Cauchy-Hadamard und Euler)

Sei $\sum _{k=0}^{\infty }c_{k}x^{k}$ eine Potenzreihe und $R=\sup\{r\in \mathbb {R} \mid \sum _{k=0}^{\infty }c_{k}x^{k}{\text{ konvergiert absolut}}\}$ der Konvergenzradius der Potenzreihe. Dann gilt

1. $R={\frac {1}{L}}$ mit $L=\limsup \limits _{k\to \infty }{\sqrt[{k}]{|c_{k}|}}$ (Formel von Cauchy-Hadamard)
2. $R={\frac {1}{q}}$ mit $q=\lim \limits _{k\to \infty }\left|{\frac {c_{k+1}}{c_{k}}}\right|$, falls der Grenzwert existiert (Formel von Euler)

Dabei gilt hier ${\frac {1}{0}}=\infty$ und ${\frac {1}{\infty }}=0$.

Beweis (Die Formeln von Cauchy-Hadamard und Euler)

Beweisschritt: $R={\frac {1}{L}}$ mit $L=\limsup \limits _{k\to \infty }{\sqrt[{k}]{|c_{k}|}}$

Fall 1: $0<L<\infty$

${\begin{aligned}\limsup _{k\to \infty }{\sqrt[{k}]{|c_{k}\cdot x^{k}|}}&=\limsup _{k\to \infty }{\sqrt[{k}]{\left|c_{k}\right|}}\cdot {\sqrt[{k}]{|x|^{k}}}\\[0.3em]&=\underbrace {\limsup _{k\to \infty }{\sqrt[{k}]{\left|c_{k}\right|}}} _{=L}\cdot |x|\\[0.3em]&{\begin{cases}<1&{\text{ falls }}|x|<{\frac {1}{L}}\\>1&{\text{ falls }}|x|>{\frac {1}{L}}\end{cases}}\end{aligned}}$

Mit dem Wurzelkriterium konvergiert die Potenzreihe für alle $x\in \mathbb {R}$ mit $|x|<{\frac {1}{L}}$ und divergiert für alle $x\in \mathbb {R}$ mit $|x|>{\frac {1}{L}}$. Also gilt für den Konvergenzradius $R=\sup\{r\in \mathbb {R} \mid \sum _{k=0}^{\infty }c_{k}x^{k}{\text{ konvergiert absolut}}\}={\frac {1}{L}}$.

Fall 2: $L=\infty$

Für $x\neq 0$ gilt dann

${\begin{aligned}\limsup _{k\to \infty }{\sqrt[{k}]{|c_{k}\cdot x^{k}|}}&=\limsup _{k\to \infty }{\sqrt[{k}]{\left|c_{k}\right|}}\cdot {\sqrt[{k}]{|x|^{k}}}\\[0.3em]&=\underbrace {\limsup _{k\to \infty }{\sqrt[{k}]{\left|c_{k}\right|}}} _{=\infty }\cdot |x|\\[0.3em]&=\infty \end{aligned}}$

Mit dem Wurzelkriterium konvergiert die Potenzreihe für kein $x\in \mathbb {R}$ mit $x\neq 0$. Also gilt für den Konvergenzradius $R=\sup\{r\in \mathbb {R} \mid \sum _{k=0}^{\infty }c_{k}x^{k}{\text{ konvergiert absolut}}\}=0$.

Fall 3: $L=0$

${\begin{aligned}\limsup _{k\to \infty }{\sqrt[{k}]{|c_{k}\cdot x^{k}|}}&=\limsup _{k\to \infty }{\sqrt[{k}]{\left|c_{k}\right|}}\cdot {\sqrt[{k}]{|x|^{k}}}\\[0.3em]&=\underbrace {\limsup _{k\to \infty }{\sqrt[{k}]{\left|c_{k}\right|}}} _{=0}\cdot |x|\\[0.3em]&=0<1\end{aligned}}$

Mit dem Wurzelkriterium konvergiert die Potenzreihe für alle $x\in \mathbb {R}$. Also gilt für den Konvergenzradius $R=\sup\{r\in \mathbb {R} \mid \sum _{k=0}^{\infty }c_{k}x^{k}{\text{ konvergiert absolut}}\}=\infty$.

Beweisschritt: $R={\frac {1}{q}}$ mit $q=\lim \limits _{k\to \infty }\left|{\frac {c_{k+1}}{c_{k}}}\right|$

Fall 1: $0<q<\infty$

${\begin{aligned}\limsup _{k\to \infty }\left|{\frac {c_{k+1}x^{k+1}}{c_{k}x^{k}}}\right|&=\limsup _{k\to \infty }\left|{\frac {c_{k+1}}{c_{k}}}\right|\cdot {\frac {|x|^{k+1}}{|x|^{k}}}\\[0.3em]&=\underbrace {\lim _{k\to \infty }\left|{\frac {c_{k+1}}{c_{k}}}\right|} _{=q}\cdot |x|\\[0.3em]&{\begin{cases}<1&{\text{ falls }}|x|<{\frac {1}{q}}\\>1&{\text{ falls }}|x|>{\frac {1}{q}}\end{cases}}\end{aligned}}$

Mit dem Quotientenkriterium konvergiert die Potenzreihe für alle $x\in \mathbb {R}$ mit $|x|<{\frac {1}{q}}$ und divergiert für alle $x\in \mathbb {R}$ mit $|x|>{\frac {1}{q}}$. Also gilt für den Konvergenzradius $R=\sup\{r\in \mathbb {R} \mid \sum _{k=0}^{\infty }c_{k}x^{k}{\text{ konvergiert absolut}}\}={\frac {1}{q}}$.

Fall 2: $q=\infty$

Für $x\neq 0$ gilt dann

${\begin{aligned}\lim _{k\to \infty }\left|{\frac {c_{k+1}x^{k+1}}{c_{k}x^{k}}}\right|&=\lim _{k\to \infty }\left|{\frac {c_{k+1}}{c_{k}}}\right|\cdot {\frac {|x|^{k+1}}{|x|^{k}}}\\[0.3em]&=\underbrace {\lim _{k\to \infty }\left|{\frac {c_{k+1}}{c_{k}}}\right|} _{=\infty }\cdot |x|\\[0.3em]&=\infty \end{aligned}}$

Mit dem Quotientenkriterium konvergiert die Potenzreihe für kein $x\in \mathbb {R}$ mit $x\neq 0$. Also gilt für den Konvergenzradius $R=\sup\{r\in \mathbb {R} \mid \sum _{k=0}^{\infty }c_{k}x^{k}{\text{ konvergiert absolut}}\}=0$.

Fall 3: $q=0$

${\begin{aligned}\lim _{k\to \infty }\left|{\frac {c_{k+1}x^{k+1}}{c_{k}x^{k}}}\right|&=\lim _{k\to \infty }\left|{\frac {c_{k+1}}{c_{k}}}\right|\cdot {\frac {|x|^{k+1}}{|x|^{k}}}\\[0.3em]&=\underbrace {\lim _{k\to \infty }\left|{\frac {c_{k+1}}{c_{k}}}\right|} _{=0}\cdot |x|\\[0.3em]&=0<1\end{aligned}}$

Mit dem Quotientenkriterium konvergiert die Potenzreihe für alle $x\in \mathbb {R}$. Also gilt für den Konvergenzradius $R=\sup\{r\in \mathbb {R} \mid \sum _{k=0}^{\infty }c_{k}x^{k}{\text{ konvergiert absolut}}\}=\infty$.

Hinweis

Bei den Vor- und Nachteilen der beiden Formeln, verhält es sich genauso als beim Vergleich zwischen Quotienten- und Wurzelkriterium. Mit der Formel von Euler ist der Konvergenzradius im Allgemeinen leichter zu bestimmen, jedoch ist sie nicht immer anwendbar. Und zwar dann, wenn der Grenzwert $\lim \limits _{k\to \infty }\left|{\frac {c_{k+1}}{c_{k}}}\right|$ nicht existiert, oder wenn der Quotient nicht definiert ist. Beispiele dafür sind die Sinus- und Kosinusreihe weiter unten. Ein Beispiel, bei dem die Formel von Euler deutlich einfacher anzuwenden ist, ist die Binomialreihe.

Beispiele

Die geometrische Reihe und Verwandtes

Beispiel (Konvergenzradius der geometrischen Reihe)

Wie wir schon wissen hat die geometrische Reihe $\sum _{k=0}^{\infty }x^{k}=\sum _{k=0}^{\infty }\underbrace {1} _{=c_{k}}\cdot x^{k}$ den Konvergentradius $R=1$. Wir überprüfen dies nochmal mit unseren beiden neuen Formeln:

Die Formel von Cauchy-Hadamard ergibt

$R={\frac {1}{\limsup \limits _{k\to \infty }{\sqrt[{k}]{|c_{k}|}}}}={\frac {1}{\limsup \limits _{k\to \infty }{\sqrt[{k}]{1}}}}={\frac {1}{1}}=1$

Ebenso erhalten wir dies aus der Euler-Formel:

$R={\frac {1}{\lim \limits _{k\to \infty }\left|{\frac {c_{k+1}}{c_{k}}}\right|}}={\frac {1}{\lim \limits _{k\to \infty }{\frac {1}{1}}}}={\frac {1}{1}}=1$

Beispiel (Konvergenzradius von mit der geometrischen Reihe verwandten Reihen)

Ebenso haben die Reihe $\sum _{k=0}^{\infty }{\frac {1}{k}}\cdot x^{k}$ und $\sum _{k=0}^{\infty }{\frac {1}{k^{2}}}\cdot x^{k}$ den Konvergentradius $R=1$.

Die Formel von Cauchy-Hadamard ergibt für die erste Reihe mit $c_{k}={\frac {1}{k}}$:

${\begin{aligned}\limsup _{k\to \infty }{\sqrt[{k}]{|c_{k}|}}&=\limsup _{k\to \infty }{\sqrt[{k}]{\frac {1}{k}}}\\[0.3em]&={\frac {1}{\limsup \limits _{k\to \infty }{\sqrt[{k}]{k}}}}\\[0.3em]&\ {\color {OliveGreen}\left\downarrow \ \lim _{k\to \infty }{\sqrt[{k}]{k}}=1\Longrightarrow \limsup _{k\to \infty }{\sqrt[{k}]{k}}=1\right.}\\[0.3em]&={\frac {1}{1}}\\[0.3em]&=1\end{aligned}}$

Also ist der Konvergenradius gleich $R={\frac {1}{1}}=1$.

Mit der Formel von Euler-Formel ergibt sich ebenso für die zweite Reihe mit $c_{k}={\frac {1}{k^{2}}}$:

${\begin{aligned}\lim _{k\to \infty }\left|{\frac {c_{k+1}}{c_{k}}}\right|&=\lim \limits _{k\to \infty }{\frac {\frac {1}{k+1}}{\frac {1}{k}}}\\[0.3em]&=\lim \limits _{k\to \infty }{\frac {k}{k+1}}\\[0.3em]&=\lim \limits _{k\to \infty }{\frac {1}{1+{\frac {1}{k}}}}\\[0.3em]&\ {\color {OliveGreen}\left\downarrow \ \lim _{k\to \infty }{\frac {1}{k}}=0\right.}\\[0.3em]&={\frac {1}{1+0}}\\[0.3em]&=1\end{aligned}}$

Also ist der Konvergenradius gleich $R={\frac {1}{1}}=1$. Natürlich hätten wir auch den Konvergenzradius der ersten Reihe mit der Formel von Euler und den der zweiten Reihe mit der Formel von Cauchy-Hadamard bestimmen können.

Verständnisfrage: Gib zwei weitere Potenzreihen an, die den Konvergenzradius $R=1$ haben.

Es gibt natürlich unendlich viele Beipiele. Zwei weitere Potenzreihen mit Konvergenzradius $1$ sind beispielsweise $\sum \limits _{k=0}^{\infty }{\frac {1}{k^{3}}}\cdot x^{k}$ und $\sum \limits _{k=0}^{\infty }k\cdot x^{k}$.

Die Binomialreihe

Beispiel (Konvergenzradius der Binomialreihe)

Ein Beispiel einer Potenzreihe, bei dem die Formel von Euler deutlich einfacher anzuwenden ist als die Formel von Cauchy-Hadamrd ist die Binomialreihe $\sum _{k=0}^{\infty }{\binom {s}{k}}\cdot x^{k}$ mit $s\in \mathbb {R}$.

Bei der Formel von Cauchy-Hadamard müssten wir $\limsup \limits _{k\to \infty }{\sqrt[{k}]{|c_{k}|}}=\limsup \limits _{k\to \infty }{\sqrt[{k}]{\left|{\binom {s}{k}}\right|}}$ bestimmen, was nicht so ohne weiteres möglich ist. Die Formel von Euler hingegen ist wesentlich einfacher anzuwenden, denn es ergibt sich

${\begin{aligned}\lim _{k\to \infty }\left|{\frac {c_{k+1}}{c_{k}}}\right|&=\lim \limits _{k\to \infty }{\frac {\left|{\binom {s}{k+1}}\right|}{\left|{\binom {s}{k}}\right|}}\\[0.3em]&\ {\color {OliveGreen}\left\downarrow \ \left|{\binom {s}{k+1}}\right|={\frac {|s\cdot (s-1)\cdot \ldots \cdot (s-k+1)\cdot \overbrace {(s-(k+1)+1)} ^{=(s-k)}|}{1\cdot 2\cdot \ldots \cdot k\cdot (k+1)}}={\frac {|s\cdot (s-1)\cdot \ldots \cdot (s-k+1)|}{1\cdot 2\cdot \ldots \cdot k}}\cdot {\frac {|s-k|}{k+1}}=\left|{\binom {s}{k}}\right|\cdot {\frac {|s-k|}{k+1}}\right.}\\[0.3em]&=\lim \limits _{k\to \infty }{\frac {\left|{\binom {s}{k}}\right|\cdot {\frac {|s-k|}{k+1}}}{\left|{\binom {s}{k}}\right|}}\\[0.3em]&=\lim \limits _{k\to \infty }{\frac {|s-k|}{k+1}}\\[0.3em]&=\lim \limits _{k\to \infty }{\frac {|{\frac {s}{k}}-1|}{1+{\frac {1}{k}}}}\\[0.3em]&\ {\color {OliveGreen}\left\downarrow \ \lim _{k\to \infty }{\frac {1}{k}}=\lim _{k\to \infty }{\frac {s}{k}}=0\right.}\\[0.3em]&={\frac {|0-1|}{1+0}}\\[0.3em]&={\frac {1}{1}}\\[0.3em]&=1\end{aligned}}$

Also hat die Binomialreihe $\sum _{k=0}^{\infty }{\binom {s}{k}}x^{k}$ für alle reellen $s$ ebenfalls den Konvergenzradius $R={\frac {1}{1}}=1$.

Exponential-, Sinus- und Kosinusreihe

Beispiel (Konvergenzradius der Exponentialreihe)

Ein Beispiel einer Potenzreihe, die für alle $x\in \mathbb {R}$ konvergiert ist die Exponentialreihe $\sum _{k=0}^{\infty }{\frac {x^{k}}{k!}}=\sum _{k=0}^{\infty }{\frac {1}{k!}}\cdot x^{k}$.

Bei der Formel von Cauchy-Hadamard müssen wir hier $\limsup \limits _{k\to \infty }{\sqrt[{k}]{|c_{k}|}}=\limsup \limits _{k\to \infty }{\sqrt[{k}]{\frac {1}{k!}}}$ bestimmen, was nicht so einfach ist, außer der Grenzwert $\lim \limits _{k\to \infty }{\sqrt[{k}]{k!}}=\infty$ ist bekannt. Die Formel von Euler hingegen ist erneut ohne weiteres anwendbar und liefert

${\begin{aligned}\lim _{k\to \infty }\left|{\frac {c_{k+1}}{c_{k}}}\right|&=\lim _{k\to \infty }{\frac {\left|{\frac {1}{(k+1)!}}\right|}{\left|{\frac {1}{k!}}\right|}}\\[0.3em]&=\lim _{k\to \infty }{\frac {k!}{(k+1)!}}\\[0.3em]&=\lim _{k\to \infty }{\frac {k!}{k!\cdot (k+1)}}\\[0.3em]&\ {\color {OliveGreen}\left\downarrow \ k!{\text{ kürzen}}\right.}\\[0.3em]&=\lim \limits _{k\to \infty }{\frac {1}{k+1}}\\[0.3em]&=0\end{aligned}}$

Also hat die Exponentialreihe $\sum _{k=0}^{\infty }{\frac {x^{k}}{k!}}$ den Konvergenzradius $R=\infty$.

Beispiel (Konvergenzradius der Sinusreihe)

Ein Beispiel einer Potenzreihe, dbei der die Formel von Euler nicht anwendbar ist, ist die Sinusreihe

$\sum _{k=0}^{\infty }{\frac {(-1)^{k}\cdot x^{2k+1}}{(2k+1)!}}=\sum _{k=0}^{\infty }{\frac {(-1)^{k}}{(2k+1)!}}\cdot x^{2k+1}=x-{\frac {1}{3!}}\cdot x^{3}+{\frac {1}{5!}}\cdot x^{5}-{\frac {1}{7!}}\cdot x^{7}\pm \ldots$

Bei dieser Reihe sind alle geraden Koeffizienten gleich $0$. D.h. es gilt

$\sum _{k=0}^{\infty }{\frac {(-1)^{k}}{(2k+1)!}}x^{2k+1}=\sum _{n=0}^{\infty }c_{n}x^{n}{\text{ mit }}c_{n}={\begin{cases}0&{\text{für}}\ n=2k,\\{\frac {(-1)^{\frac {n-1}{2}}}{n!}}&{\text{für}}\ n=2k+1\end{cases}}$

Die Formel von Euler ist bei dieser Potenzreihe nicht anwendbar, da man im Quotienten $\left|{\frac {c_{n+1}}{c_{n}}}\right|$ durch null teilen würde, falls $n$ gerade ist. Die Formel von Cauchy-Hadamard hingegen ist anwendbar, falls der Grenzwert $\lim \limits _{k\to \infty }{\sqrt[{k}]{k!}}=\infty$ bekannt ist. Denn es gilt

${\begin{aligned}\limsup _{n\to \infty }{\sqrt[{n}]{\left|c_{n}\right|}}&=\limsup _{k\to \infty }{\sqrt[{2k+1}]{\left|c_{2k+1}\right|}}\\[0.3em]&=\limsup _{k\to \infty }{\sqrt[{2k+1}]{\left|{\frac {(-1)^{k}}{(2k+1)!}}\right|}}\\[0.3em]&\ {\color {OliveGreen}\left\downarrow \ |(-1)^{k}|=1\right.}\\[0.3em]&=\limsup _{k\to \infty }{\sqrt[{2k+1}]{\frac {1}{(2k+1)!}}}\\[0.3em]&={\frac {1}{\limsup \limits _{k\to \infty }{\sqrt[{2k+1}]{(2k+1)!}}}}\\[0.3em]&\ {\color {OliveGreen}\left\downarrow \ \lim \limits _{k\to \infty }{\sqrt[{k}]{k!}}=\infty \Longrightarrow \lim \limits _{k\to \infty }{\sqrt[{2k+1}]{(2k+1)!}}=\infty \right.}\\[0.3em]&=0\end{aligned}}$

Also hat die Sinusreihe $\sum _{k=0}^{\infty }{\frac {(-1)^{k}}{(2k+1)!}}x^{2k+1}$ den Konvergenzradius $R=\infty$.

Ein eleganterer und kürzerer Beweis für den Konvergenzradius nutzt das Majorantenkriterium mit der Exponentialreihe als Majorante. Es gilt nämlich mit der Definition der Koeffizienten $c_{n}$ der Sinusreihe von oben:

$|c_{n}x^{n}|=\left\{{\begin{array}{rl}0&{\text{für }}\ n=2k,\\{\frac {1}{n!}}|x|^{n}&{\text{für }}\ n=2k+1\end{array}}\right\}\leq {\frac {1}{n!}}|x|^{n}{\text{ für jedes }}n\in \mathbb {N} _{0}$

Da die Exponentialreihe $\sum _{k=0}^{\infty }{\frac {1}{k!}}x^{k}$ für alle $x\in \mathbb {R}$ absolut konvergiert, konvergiert mit dem Majorantenkriterium die Sinusreihe ebenfalls für jedes $x\in \mathbb {R}$ absolut. Also ist der Konvergenzaradius der Sinusreihe ebenfalls gleich $R=\infty$.

Sehr ähnlich kann man zeigen, dass die Kosinusreihe $\sum _{k=0}^{\infty }{\frac {(-1)^{k}}{(2k)!}}x^{2k}$ ebenfalls den Konvergenzradius $R=\infty$ hat.

Aufgabe (Konvergenzradius der Kosinusreihe)

Bestimme den Konvergenzradius der Kosinusreihe $\sum _{k=0}^{\infty }{\frac {(-1)^{k}}{(2k)!}}x^{2k}$.

Beweis (Konvergenzradius der Kosinusreihe)

Bei der Kosinusreihe

$\sum _{k=0}^{\infty }{\frac {(-1)^{k}}{(2k)!}}\cdot x^{2k}=1-{\frac {1}{2!}}\cdot x^{2}+{\frac {1}{4!}}\cdot x^{4}-{\frac {1}{6!}}\cdot x^{6}\pm \ldots$

Bei dieser Reihe sind alle ungeraden Koeffizienten gleich $0$. D.h. es gilt

$\sum _{k=0}^{\infty }{\frac {(-1)^{k}}{(2k)!}}x^{2k}=\sum _{n=0}^{\infty }c_{n}x^{n}{\text{ mit }}c_{n}={\begin{cases}{\frac {(-1)^{\frac {n}{2}}}{n!}}&{\text{für}}\ n=2k,\\0&{\text{für}}\ n=2k+1\end{cases}}$

Die Formel von Euler ist, wie schon bei der Sinusreihe, auch hier nicht anwendbar, denn im Quotenten $\left|{\frac {c_{n+1}}{c_{n}}}\right|$ ist der Nenner für ungerade $n$ gleich null. Die Formel von Cauchy-Hadamard hingegen ist erneut anwendbar. Es gilt

${\begin{aligned}\limsup _{n\to \infty }{\sqrt[{n}]{\left|c_{n}\right|}}&=\limsup _{k\to \infty }{\sqrt[{2k}]{\left|c_{2k}\right|}}\\[0.3em]&=\limsup _{k\to \infty }{\sqrt[{2k}]{\left|{\frac {(-1)^{k}}{(2k)!}}\right|}}\\[0.3em]&\ {\color {OliveGreen}\left\downarrow \ |(-1)^{k}|=1\right.}\\[0.3em]&=\limsup _{k\to \infty }{\sqrt[{2k}]{\frac {1}{(2k)!}}}\\[0.3em]&={\frac {1}{\limsup \limits _{k\to \infty }{\sqrt[{2k}]{(2k)!}}}}\\[0.3em]&\ {\color {OliveGreen}\left\downarrow \ \lim \limits _{k\to \infty }{\sqrt[{k}]{k!}}=\infty \Longrightarrow \lim \limits _{k\to \infty }{\sqrt[{2k}]{(2k)!}}=\infty \right.}\\[0.3em]&=0\end{aligned}}$

Also hat die Kosinusreihe $\sum _{k=0}^{\infty }{\frac {(-1)^{k}}{(2k)!}}x^{2k}$ ebenfalls den Konvergenzradius $R=\infty$.

Alternativer Beweis (Konvergenzradius der Kosiunsreihe mit Majorantenkriterium)

Erneut können wir alternativ das Majorantenkriterium mit der Exponantialreihe als Majoranten anwenden. Es gilt

$|c_{n}x^{n}|=\left\{{\begin{array}{rl}{\frac {1}{n!}}|x|^{n}&{\text{für }}\ n=2k,\\0&{\text{für }}\ n=2k+1\end{array}}\right\}\leq {\frac {1}{n!}}|x|^{n}{\text{ für jedes }}n\in \mathbb {N} _{0}$

Da die Exponentialreihe $\sum _{k=0}^{\infty }{\frac {1}{k!}}x^{k}$ für alle $x\in \mathbb {R}$ absolut konvergiert, konvergiert mit dem Majorantenkriterium die Kosinusreihe ebenfalls für jedes $x\in \mathbb {R}$ absolut. Der Konvergenzradius ist daher $R=\infty$.

Aufgaben zur Bestimmung des Konvergenzradius

Aufgabe (Konvergenzradius von Potenzreihen)

Bestimme jeweils den Konvergenzradius der folgenden Potenzreihen.

1. $\sum _{k=1}^{\infty }{\frac {x^{k}}{k^{s}}}$ mit $s\in \mathbb {Q}$
2. $\sum _{k=0}^{\infty }k^{k}x^{k}$
3. $\sum _{k=0}^{\infty }{\frac {k!}{k^{k}}}x^{k}$
4. $\sum _{k=0}^{\infty }x^{k!}$
5. $\sum _{k=0}^{\infty }(a^{k}+b^{k})x^{k}$ mit $a>0,\ b>0$

Lösung (Konvergenzradius von Potenzreihen)

• Lösung zu Teilaufgabe 1: Die Formel von Cauchy-Hadamard ergibt mit $c_{k}={\frac {1}{k^{s}}}$:
  ${\begin{aligned}\limsup _{k\to \infty }{\sqrt[{k}]{|c_{k}|}}&=\limsup _{k\to \infty }{\sqrt[{k}]{\frac {1}{k^{s}}}}\\[0.3em]&={\frac {1}{\limsup \limits _{k\to \infty }{\sqrt[{k}]{k^{s}}}}}\\[0.3em]&={\frac {1}{(\limsup \limits _{k\to \infty }{\sqrt[{k}]{k}})^{s}}}\\[0.3em]&\ {\color {OliveGreen}\left\downarrow \ \lim _{k\to \infty }{\sqrt[{k}]{k}}=1\Longrightarrow \limsup _{k\to \infty }{\sqrt[{k}]{k}}=1\right.}\\[0.3em]&={\frac {1}{1^{s}}}\\[0.3em]&=1\end{aligned}}$

  Also ist der Konvergenradius gleich $R={\frac {1}{1}}=1$.

  Alternativ ist die Formel von Euler-Formel anwendbar und ergibt ebenso:

  ${\begin{aligned}\lim _{k\to \infty }\left|{\frac {c_{k+1}}{c_{k}}}\right|&=\lim \limits _{k\to \infty }{\frac {\frac {1}{(k+1)^{s}}}{\frac {1}{k^{s}}}}\\[0.3em]&=\lim \limits _{k\to \infty }{\frac {k^{s}}{(k+1)^{s}}}\\[0.3em]&=\lim \limits _{k\to \infty }{\frac {1}{1+{\frac {1}{k^{s}}}}}\\[0.3em]&\ {\color {OliveGreen}\left\downarrow \ \lim _{k\to \infty }{\frac {1}{k^{s}}}=0\right.}\\[0.3em]&={\frac {1}{1+0}}\\[0.3em]&=1\end{aligned}}$

  Also ist auch hier $R={\frac {1}{1}}=1$.

• Lösung zu Teilaufgabe 2: Hier ist die Formel von Cauchy-Hadamard sogar einfacher. Sie ergibt unmittelbar mit $c_{k}=k^{k}$:
  ${\begin{aligned}\limsup _{k\to \infty }{\sqrt[{k}]{|c_{k}|}}&=\limsup _{k\to \infty }{\sqrt[{k}]{k^{k}}}\\[0.3em]&=\limsup \limits _{k\to \infty }k\\[0.3em]&=\infty \end{aligned}}$

  Also ist der Konvergenradius gleich $R=0$.

  Die Formel von Euler-Formel ist ebenfalls anwendbar, wir benötigen jedoch den Grenzwert $\lim \limits _{k\to \infty }\left(1+{\frac {1}{k}}\right)^{k}=e$. Damit ist

  ${\begin{aligned}\lim _{k\to \infty }\left|{\frac {c_{k+1}}{c_{k}}}\right|&=\lim \limits _{k\to \infty }{\frac {(k+1)^{k+1}}{k^{k}}}\\[0.3em]&=\lim \limits _{k\to \infty }{\frac {(k+1)^{k}\cdot (k+1)}{k^{k}}}\\[0.3em]&=\lim \limits _{k\to \infty }{\frac {(k+1)^{k}}{k^{k}}}\cdot (k+1)\\[0.3em]&=\lim \limits _{k\to \infty }\left({\frac {k+1}{k}}\right)^{k}\cdot (k+1)\\[0.3em]&=\lim \limits _{k\to \infty }\left(1+{\frac {1}{k}}\right)^{k}\cdot (k+1)\\[0.3em]&\ {\color {OliveGreen}\left\downarrow \ \lim \limits _{k\to \infty }\left(1+{\frac {1}{k}}\right)^{k}=e,\ \lim _{k\to \infty }(k+1)=\infty \right.}\\[0.3em]&=\infty \end{aligned}}$

  Also ist auch hier $R=0$.

• Lösung zu Teilaufgabe 3: Die Formel von Cauchy-Hadamard ist hier sehr schwierig anwendbar, denn wir müssten den Grenzwert $\lim \limits _{k\to \infty }{\sqrt[{k}]{\frac {k!}{k^{k}}}}=\lim \limits _{k\to \infty }{\frac {\sqrt[{k}]{k!}}{k}}$ bestimmen, was nicht so ohne Weiteres möglich ist. Die Formel von Euler-Formel ist deutlich einfacher anwendbar. Erneut unter Zuhilfenahme des Grenzwerts $\lim \limits _{k\to \infty }\left(1+{\frac {1}{k}}\right)^{k}=e$ ergibt sich
  ${\begin{aligned}\lim _{k\to \infty }\left|{\frac {c_{k+1}}{c_{k}}}\right|&=\lim \limits _{k\to \infty }{\frac {\frac {(k+1)!}{(k+1)^{k+1}}}{\frac {k!}{k^{k}}}}\\[0.3em]&\ {\color {OliveGreen}\left\downarrow \ {\text{Kehrwert bilden}}\right.}\\[0.3em]&=\lim \limits _{k\to \infty }{\frac {(k+1)!\cdot k^{k}}{(k+1)^{k+1}\cdot k!}}\\[0.3em]&=\lim \limits _{k\to \infty }{\frac {k!\cdot (k+1)\cdot k^{k}}{k!\cdot (k+1)^{k}\cdot (k+1)}}\\[0.3em]&\ {\color {OliveGreen}\left\downarrow \ k!{\text{ und }}(k+1){\text{ kürzen}}\right.}\\[0.3em]&=\lim \limits _{k\to \infty }{\frac {k^{k}}{(k+1)^{k}}}\\[0.3em]&\ {\color {OliveGreen}\left\downarrow \ {\text{erneut Kehrwert bilden}}\right.}\\[0.3em]&=\lim \limits _{k\to \infty }{\frac {1}{\frac {(k+1)^{k}}{k^{k}}}}\\[0.3em]&=\lim \limits _{k\to \infty }{\frac {1}{\left({\frac {k+1}{k}}\right)^{k}}}\\[0.3em]&=\lim \limits _{k\to \infty }{\frac {1}{\left(1+{\frac {1}{k}}\right)^{k}}}\\[0.3em]&\ {\color {OliveGreen}\left\downarrow \ \lim \limits _{k\to \infty }\left(1+{\frac {1}{k}}\right)^{k}=e\right.}\\[0.3em]&={\frac {1}{e}}\end{aligned}}$

  Also ist auch hier $R={\frac {1}{\frac {1}{e}}}=e$.

• Lösung zu Teilaufgabe 4: Bei der Potenzreihe $\sum _{k=0}^{\infty }x^{k!}=\sum _{k=0}^{\infty }1\cdot x^{k!}=\sum _{n=0}^{\infty }c_{n}\cdot x^{n}$ gilt für die Koeffizienten
  $c_{n}={\begin{cases}1&{\text{für}}\ n=k!,\\0&{\text{sonst}}\end{cases}}$

  Die Formel von Euler ist bei dieser Potenzreihe nicht anwendbar, da für alle $n\neq k!$ man im Quotienten $\left|{\frac {c_{n+1}}{c_{n}}}\right|$ durch null teilen würde. Die Formel von Cauchy-Hadamard ist hingegen anwendbar und es gilt

  ${\begin{aligned}\limsup _{n\to \infty }{\sqrt[{n}]{\left|c_{n}\right|}}&=\limsup _{k\to \infty }{\sqrt[{k!}]{\left|c_{k!}\right|}}\\[0.3em]&=\limsup _{k\to \infty }{\sqrt[{k!}]{\left|1\right|}}\\[0.3em]&\ {\color {OliveGreen}\left\downarrow \ {\sqrt[{m}]{1}}=1{\text{ für alle }}m\in \mathbb {N} \right.}\\[0.3em]&=\limsup _{k\to \infty }1\\[0.3em]&=1\end{aligned}}$

  Also hat die Reihe den Konvergenzradius $R={\frac {1}{1}}=1$.

  Alternativ können wir hier auch direkt argumentieren, da die Bauart der Reihe sehr einfach ist:

  1. Ist $|x|<1$, so gilt $|x|^{k!}\leq |x|^{k}$, und da die geometrische Reihe $\sum _{k=0}^{\infty }x^{k}$ für $|x|<1$ absolut konvergiert, konvergiert die Reihe $\sum _{k=0}^{\infty }x^{k!}$ mit dem Majorantenkriterium ebenfalls absolut.
  2. Ist $|x|>1$, so gilt $|x|^{k!}>1$, also kann $(x^{k!})$ keine Nullfolge sein. Mit dem Trivialkriterium divergiert die Reihe daher in diesem Fall.

  Also folgt so ebenfalls $R=1$.

• Lösung zu Teilaufgabe 5: Bei dieser Potenzreihe ist die Formel von Euler nicht geeignt, da mit $c_{k}=a^{k}+b^{k}$ der Quotient $\left|{\frac {c_{k+1}}{c_{k}}}\right|$ schwer zu untersuchen ist. Bei der Formel von Cauchy-Hadamard erhalten wir die Folge ${\sqrt[{k}]{c_{k}}}={\sqrt[{k}]{a^{k}+b^{k}}}$. Diese lässt sich mit Hilfe einer Fallunterscheidung untersuchen:
  1. Ist $a<b$, so gilt: $b={\sqrt[{k}]{b^{k}}}\leq {\sqrt[{k}]{a^{k}+b^{k}}}\leq {\sqrt[{k}]{b^{k}+b^{k}}}={\sqrt[{k}]{2b^{k}}}={\sqrt[{k}]{2}}\cdot {\sqrt[{k}]{b^{k}}}={\sqrt[{k}]{k}}\cdot b$. Wegen $\lim \limits _{k\to \infty }{\sqrt[{k}]{k}}=1$ folgt nun mit dem Der Sandwichsatz $\lim \limits _{k\to \infty }{\sqrt[{k}]{a^{k}+b^{k}}}=b$.
  2. Ist $b<a$, so gilt analog: $a={\sqrt[{k}]{a^{k}}}\leq {\sqrt[{k}]{a^{k}+b^{k}}}\leq {\sqrt[{k}]{a^{k}+a^{k}}}={\sqrt[{k}]{2a^{k}}}={\sqrt[{k}]{2}}\cdot {\sqrt[{k}]{a^{k}}}={\sqrt[{k}]{k}}\cdot b$. Wegen $\lim \limits _{k\to \infty }{\sqrt[{k}]{k}}=1$ folgt nun mit dem Der Sandwichsatz $\lim \limits _{k\to \infty }{\sqrt[{k}]{a^{k}+b^{k}}}=a$.
  Insgesamt ergibt sich $\limsup \limits _{k\to \infty }{\sqrt[{k}]{|c_{k}|}}=\lim \limits _{k\to \infty }{\sqrt[{k}]{|c_{k}|}}=\max\{a;b\}$. Für den Konvergenzradius der Potenzreihe folgt damit
  $R={\frac {1}{\max\{a;b\}}}=\min \left\{{\frac {1}{a}};{\frac {1}{b}}\right\}$

Ähnliche, ganz hervoragende, Aufgaben zum Potenzradius finden sich am Ende des Kapitels im Aufgabenteil.

Verhalten auf dem Rand des Konvergenzradius

Am Beipiel der drei Potenzreihen $\sum \limits _{k=0}^{\infty }x^{k}$, $\sum \limits _{k=0}^{\infty }{\frac {1}{k}}x^{k}$ und $\sum \limits _{k=0}^{\infty }{\frac {1}{k^{2}}}x^{k}$ kann man erkennen, dass das Verhalten auf dem Rand der Konvergenzradius (hier $|x|=1$) sehr unterschiedlich sein kann:

• Für die geometrische Reihe $\sum \limits _{k=0}^{\infty }x^{k}$ gilt: Sowohl für $x=-1$ also auch für $x=1$ divergieren die Reihen $\sum \limits _{k=0}^{\infty }(-1)^{k}$ und $\sum \limits _{k=0}^{\infty }1^{k}=\sum \limits _{k=0}^{\infty }1$ jeweils mit dem Trivialkriterium, da die Folgen $((-1)^{k})$ und $(1)$ keine Nullfolgen sind.
• Für die Reihe $\sum \limits _{k=1}^{\infty }{\frac {1}{k}}x^{k}$ gilt: Für $x=-1$ konvergiert die Reihe $\sum \limits _{k=0}^{\infty }(-1)^{k}{\frac {1}{k}}$ mit dem Leibniz-Kriterium, da die Folge $\left({\frac {1}{k}}\right)$ eine monoton fallende Nullfolgen ist. Für $x=1$ hingegen ergibt sich die harmonische Reihe $\sum \limits _{k=1}^{\infty }{\frac {1}{k}}$, welche bekanntlich divergiert.
• Für die Reihe $\sum \limits _{k=1}^{\infty }{\frac {1}{k^{2}}}x^{k}$ gilt: Sowohl für $x=-1$ als auch für $x=1$ konvergiert die Reihe. Für $x=1$ ergibt sich die Reihe der reziproken Quadratzahlen $\sum \limits _{k=0}^{\infty }{\frac {1}{k^{2}}}$, welche bekanntlich (absolut) konvergiert. Ebenso konvergiert für $x=-1$ die Reihe $\sum \limits _{k=1}^{\infty }(-1)^{k}{\frac {1}{k^{2}}}$, wegen $\left|(-1)^{k}{\frac {1}{k^{2}}}\right|={\frac {1}{k^{2}}}$ und da jede absolut konvergente Reihe konvergiert.

Eine Reihe , die ebenfalls den Konvergenzradius $R=1$ hat, deren Konvergenzverhalten auf dem Rand des Konvergenzradius jedoch schwieriger zu bestimmen ist, ist die Binomialreihe $\sum \limits _{k=0}^{\infty }{\binom {s}{k}}x^{k}$. Für den Fall $s>0$ kann man dazu das Konvergenzkriterium von Raabe verwenden. Ebenso kann man für verschiedene Werte von $s\in \mathbb {R}$ die Konvergenz auch mit dem Majoranten- bzw. Leibniz-Kriterium bestimmen. Siehe hierzu die entsprechende Übungsaufgabe im Aufgabenteil.

Hinweis

Hat eine Potenzreihe $\sum \limits _{k=0}^{\infty }c_{k}x^{k}$ den Konvergenzradius $R$, so kann keine allgemeine Aussage über das Konvergenzverhalten der Potenzreihe für $|x|=R$ gemacht werden.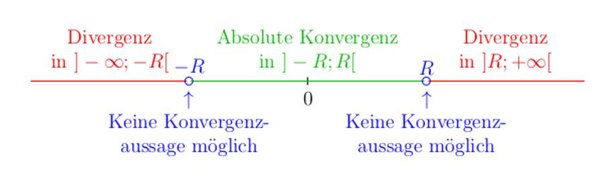

Veranschaulichung des Konvergenzradius mit Randwerten

Für Potenzreihen mit Konvergenzradius $R=1$ wollen wir noch festhalten:

1. Ist $x=1$, so ergibt sich die Reihe $\sum \limits _{k=0}^{\infty }c_{k}\cdot 1^{k}=\sum \limits _{k=0}^{\infty }c_{k}$. Diese Reihe kann dann mit den bekannten Konvergenzkriterien untersucht werden.
2. Ist $x=-1$, so ergibt sich die Reihe $\sum \limits _{k=0}^{\infty }(-1)^{k}c_{k}$. Nach dem Leibniz-Kriterium konvergiert die Reihe, falls $(c_{k})$ eine monoton fallende Nullfolge ist.