Geometrische Reihe – „Mathe für Nicht-Freaks“

Die geometrische Reihe hat die Form $\sum _{k=0}^{\mathrm{\infty }}{q}^k$. Sie ist eine wichtige Reihe, die dir häufig in Beweisen und Herleitungen begegnen wird. Außerdem kann man mit der geometrischen Reihe Konvergenzkriterien wie das Quotienten- oder das Wurzelkriterium beweisen.

Geometrische Summenformel

Ein Video zur Erklärung der Geometrischen Reihe.(YouTube-Video vom Kanal Quatematik)

Wir wiederholen die geometrische Summenformel. Mit dieser Formel können wir die Partialsummen der geometrischen Reihe explizit ausrechnen. Beweisen wir nun die geometrische Summenformel:

Satz (Geometrische Summenformel)

Für alle reellen $q\ne 1$ und für alle $n\in {\mathbb{N}}_0$ ist:

$\sum _{k=0}^n{q}^k=\frac{1-q^{n+1}}{1-q}$

Beweis (Geometrische Summenformel)

Es ist

$\begin{array}{cc}\sum _{k=0}^n{q}^k& =1+q+q^2+\cdots +q^n\\ & \downarrow \text{beide Seiten mit }q\text{ multiplizieren}\\ ⟹q\cdot \sum _{k=0}^n{q}^k& =q+q^2+q^3+\cdots +q^{n+1}\\ & \downarrow \text{zweite von erster Gleichung subtrahieren}\\ ⟹\sum _{k=0}^n{q}^k-q\cdot \sum _{k=0}^n{q}^k& =(1+q+\cdots +q^n)-(q+q^2+\cdots +q^{n+1})\\ & =1-q^{n+1}\\ & \downarrow \text{links }\sum _{k=0}^n{q}^k\text{ ausklammern}\\ ⟹(1-q)\cdot \sum _{k=0}^n{q}^k& =1-q^{n+1}\\ & \downarrow \cdot \frac{1}{1-q}\text{, da }q\ne 1\\ ⟹\sum _{k=0}^n{q}^k& =\frac{1-q^{n+1}}{1-q}\\ \end{array}$

Geometrische Reihe

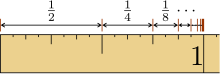
Song über die geometrische Reihe (Youtube-Video von DorFuchs)

Die geometrische Reihe $\sum _{k=0}^{\mathrm{\infty }}{r}^k$ für $r=\frac{1}{2}$, $r=\frac{1}{3}$ oder $r=\frac{1}{4}$ konvergiert.

Wir betrachten zwei Fälle: $|q|<1\text{ und }|q|\ge 1$.

Fall $|q|<1$

Kommen wir zur geometrischen Reihe $\sum _{k=0}^{\mathrm{\infty }}{q}^k$. Wir betrachten zunächst den Fall $|q|<1$ und damit $q\ne 1$, da wir nur in diesem Fall die geometrische Summenformel anwenden können. Mit dieser Formel können wir die Partialsumme explizit berechnen. Wir erhalten:

$\begin{array}{cc}\sum _{k=0}^{\mathrm{\infty }}{q}^k& ={\left(\sum _{k=0}^n{q}^k\right)}_{n\in \mathbb{N}}\\ & \downarrow \text{Geometrische Summenformel }(q\ne 1)\\ & ={\left(\frac{1-q^{n+1}}{1-q}\right)}_{n\in \mathbb{N}}\end{array}$

Die geometrische Reihe konvergiert also genau dann, wenn die Folge ${\left(\frac{1-q^{n+1}}{1-q}\right)}_{n\in \mathbb{N}}$ konvergiert. Dies ist genau dann der Fall, wenn ${\left(q^n\right)}_{n\in \mathbb{N}}$ eine konvergente Folge ist. Nun wissen wir, dass ${\left(q^n\right)}_{n\in \mathbb{N}}$ gegen $0$ konvergiert, wenn $|q|<1$ ist, und gegen $1$ konvergiert, wenn $q=1$ ist. Den Fall $q=1$ haben wir in diesem Abschnitt aber ausgeschlossen. Damit erhalten wir zunächst:

Wenn $|q|<1$ ist, dann konvergiert die geometrische Reihe $\sum _{k=0}^{\mathrm{\infty }}{q}^k$.

Berechnen wir nun den Grenzwert der geometrischen Reihe für $|q|<1$:

$\begin{array}{cc}\sum _{k=0}^{\mathrm{\infty }}{q}^k& =\underset{n\to \mathrm{\infty }}{lim}\sum _{k=0}^n{q}^k\\ & =\underset{n\to \mathrm{\infty }}{lim}\frac{1-q^{n+1}}{1-q}\\ & \downarrow \text{Grenzwertsätze}\\ & =\frac{1-\underset{n\to \mathrm{\infty }}{lim}{q}^{n+1}}{1-q}\\ & \downarrow |q|<1\\ & =\frac{1-0}{1-q}\\ & =\frac{1}{1-q}\end{array}$

Aufgabe (Alternativer Beweis für die Konvergenz der geometrischen Reihe)

Zeige, dass die geometrische Reihe $\sum _{k=0}^{\mathrm{\infty }}{q}^k$ für $|q|<1$ gegen $\frac{1}{1-q}$ konvergiert.

Wie kommt man auf den Beweis? (Alternativer Beweis für die Konvergenz der geometrischen Reihe)

Wir müssen zeigen, dass es zu jedem $ϵ>0$ ein $N\in \mathbb{N}$ gibt, so dass

$|\sum _{k=0}^n{q}^k-\frac{1}{1-q}|<ϵ$ für alle $n\ge N$

Mit der geometrischen Summenformel gilt nun

$|\sum _{k=0}^n{q}^k-\frac{1}{1-q}|=|\frac{1-q^{n+1}}{1-q}-\frac{1}{1-q}|=\left|\frac{1-q^{n+1}-1}{1-q}\right|=\left|\frac{q^{n+1}}{1-q}\right|=\frac{1}{1-q}\cdot |q^{n+1}|$

Da die geometrische Folge $(q^n{)}_{n\in \mathbb{N}}$ für $|q|<1$ gegen Null konvergiert, gilt dies auch für $(q^{n+1}{)}_{n\in \mathbb{N}}$. Also gibt es zu jedem $\widetilde{ϵ}>0$ ein $\tilde{N}\in \mathbb{N}$ mit

$|q^{n+1}-0|<\widetilde{ϵ}$ für alle $n\ge \tilde{N}$

Weil $\frac{1}{1-q}$ konstant ist, gibt es auch ein $N\in \mathbb{N}$ mit

$\frac{1}{1-q}\cdot |q^{n+1}|<ϵ$ für alle $n\ge N$

Damit folgt die Behauptung.

Beweis (Alternativer Beweis für die Konvergenz der geometrischen Reihe)

Sei $ϵ>0$ gegeben. Die geometrische Folge $(q^n{)}_{n\in \mathbb{N}}$ konvergiert für $|q|<1$ gegen null. Wegen $|q|<1$ gibt es für $\widetilde{ϵ}:=(1-q)\cdot ϵ>0$ ein $N\in \mathbb{N}$ mit

$|q^n|<\widetilde{ϵ}$ für alle $n\ge N$

Mit der geometrischen Summenformel folgt dann für alle $n\ge N$

$\begin{array}{cc}& |\sum _{k=0}^n{q}^k-\frac{1}{1-q}|=|\frac{1-q^{n+1}}{1-q}-\frac{1}{1-q}|\\ =& \frac{1}{1-q}\cdot |q^{n+1}|\\ & \downarrow n+1\ge N\\ <& \frac{1}{1-q}\cdot \widetilde{ϵ}\\ & \downarrow \widetilde{ϵ}=(1-q)\cdot ϵ\\ =& \frac{1}{1-q}\cdot (1-q)\cdot ϵ=ϵ\end{array}$

Somit folgt für den Grenzwert der Reihe: $\sum _{k=0}^{\mathrm{\infty }}{q}^k=\frac{1}{1-q}$.

Fall $|q|\ge 1$

Bei $|q|\ge 1$ gilt für alle $k\in {\mathbb{N}}_0$, dass $\left|q^k\right|\ge 1$. Also ist die Folge ${\left(q^k\right)}_{k\in {\mathbb{N}}_0}$ keine Nullfolge. Damit divergiert die Reihe $\sum _{k=0}^{\mathrm{\infty }}{q}^k$ nach dem sogenannten Trivialkriterium, das wir später noch genauer betrachten.

Um die Divergenz zu veranschaulichen, betrachten wir den Fall für ein positives $q$, also $q\ge 1$. So folgt für alle $k\in \mathbb{N}\text{, dass }{q}^k\ge 1$. Damit können wir die Partialsummen abschätzen: $\sum _{k=1}^n{q}^k\ge \sum _{k=1}^{n}1=n$ Also ist die Folge der Partialsummen durch die Folge $(n{)}_{n\in \mathbb{N}}$ nach unten beschränkt. Da $(n{)}_{n\in \mathbb{N}}$ divergiert, divergiert auch die Reihe $\sum _{k=0}^{\mathrm{\infty }}{q}^k$ als Folge der Partialsummen.

Zusammenfassung

Fassen wir das bereits Bewiesene zusammen: Für $|q|>1$, $q=-1$ und $q=1$ divergiert die geometrische Reihe. Diese drei Fälle können wir in der Bedingung $|q|\ge 1$ zusammenfassen. Für den Fall $|q|<1$ konvergiert die geometrische Reihe und hat als Grenzwert $\frac{1}{1-q}$:

Satz (Geometrische Reihe)

Die geometrische Reihe $\sum _{k=0}^{\mathrm{\infty }}{q}^k$ konvergiert genau dann, wenn $|q|<1$ ist. Sie hat dann den Wert $\frac{1}{1-q}$:

$\sum _{k=0}^{\mathrm{\infty }}{q}^k=\{\begin{array}{cc}\frac{1}{1-q}& ;|q|<1\\ \text{divergent}& ;|q|\ge 1\end{array}$

Beispiel (Geometrische Reihe)

Für $q=\frac{1}{2}$, $q=-\frac{1}{2}$ und $q=2$ gilt

$\begin{array}{cc}\sum _{k=0}^{\mathrm{\infty }}{\left(\frac{1}{2}\right)}^k& =1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\dots =\frac{1}{1-\frac{1}{2}}=\frac{1}{\frac{1}{2}}=2\\ \sum _{k=0}^{\mathrm{\infty }}{(-\frac{1}{2})}^k& =1-\frac{1}{2}+\frac{1}{4}-\frac{1}{8}+\frac{1}{16}-\dots =\frac{1}{1+\frac{1}{2}}=\frac{1}{\frac{3}{2}}=\frac{2}{3}\\ \sum _{k=0}^{\mathrm{\infty }}{2}^k& =1+2+4+8+16+\dots \text{ divergiert}\end{array}$

Beispielaufgaben

Beispielaufgabe 1

Aufgabe (Beispiele geometrischer Reihen)

Berechne die Grenzwerte folgender Reihen:

1. $\sum _{k=0}^{\mathrm{\infty }}\frac{1}{3^k}$
2. $\sum _{k=0}^{\mathrm{\infty }}\frac{2^k}{3^k}$
3. $\sum _{k=0}^{\mathrm{\infty }}\frac{(-2{)}^k}{3^k}$
4. $\sum _{k=1}^{\mathrm{\infty }}\frac{1}{2^k}$
5. $\sum _{k=4}^{\mathrm{\infty }}\frac{1}{3^{k-2}}$

Lösung (Beispiele geometrischer Reihen)

Lösung Teilaufgabe 1:

$\begin{array}{cc}\sum _{k=0}^{\mathrm{\infty }}\frac{1}{3^k}& =\sum _{k=0}^{\mathrm{\infty }}\frac{1^k}{3^k}\\ & =\sum _{k=0}^{\mathrm{\infty }}{\left(\frac{1}{3}\right)}^k\\ & \downarrow \sum _{k=0}^{\mathrm{\infty }}{\left(\frac{1}{3}\right)}^k=\frac{1}{1-\frac{1}{3}}=\frac{1}{\frac{2}{3}}=\frac{3}{2}\\ & =\frac{3}{2}\end{array}$

Lösung Teilaufgabe 2:

$\begin{array}{cc}\sum _{k=0}^{\mathrm{\infty }}\frac{2^k}{3^k}& =\sum _{k=0}^{\mathrm{\infty }}{\left(\frac{2}{3}\right)}^k\\ & \downarrow \sum _{k=0}^{\mathrm{\infty }}{\left(\frac{2}{3}\right)}^k=\frac{1}{1-\frac{2}{3}}=\frac{1}{\frac{1}{3}}=3\\ & =3\end{array}$

Lösung Teilaufgabe 3:

$\begin{array}{cc}\sum _{k=0}^{\mathrm{\infty }}\frac{(-2{)}^k}{3^k}& =\sum _{k=0}^{\mathrm{\infty }}{(-\frac{2}{3})}^k\\ & \downarrow \sum _{k=0}^{\mathrm{\infty }}{(-\frac{2}{3})}^k=\frac{1}{1-(-\frac{2}{3})}=\frac{1}{1+\frac{2}{3}}=\frac{1}{\frac{5}{3}}=\frac{3}{5}\\ & =\frac{3}{5}\end{array}$

Lösung Teilaufgabe 4:

Illustration für $\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\dots =1$

Man beachte, dass diese Reihe bei 1 und nicht bei 0 beginnt! Dementsprechend müssen wir die Reihe zuerst umformen, bevor wir die obige Formel anwenden können:

$\begin{array}{cc}\sum _{k=1}^{\mathrm{\infty }}\frac{1}{2^k}& =\left(\sum _{k=0}^{\mathrm{\infty }}\frac{1}{2^k}\right)-\frac{1}{2^0}\\ & =\left(\sum _{k=0}^{\mathrm{\infty }}{\left(\frac{1}{2}\right)}^k\right)-1\\ & \downarrow \sum _{k=0}^{\mathrm{\infty }}{\left(\frac{1}{2}\right)}^k=\frac{1}{1-\frac{1}{2}}=2\\ & =2-1=1\end{array}$

Lösung Teilaufgabe 5:

Bei dieser Reihe führen wir zunächst eine Indexverschiebung durch und formen anschließend um:

$\begin{array}{cc}\sum _{k=4}^{\mathrm{\infty }}\frac{1}{3^{k-2}}& \underset{\text{schiebung}}{\stackrel{\text{Indexver-}}{=}}\left(\sum _{k=2}^{\mathrm{\infty }}\frac{1}{3^k}\right)\\ & =\left(\sum _{k=0}^{\mathrm{\infty }}\frac{1}{3^k}\right)-\frac{1}{3^0}-\frac{1}{3^1}\\ & =\left(\sum _{k=0}^{\mathrm{\infty }}{\left(\frac{1}{3}\right)}^k\right)-1-\frac{1}{3}\\ & \downarrow \sum _{k=0}^{\mathrm{\infty }}{\left(\frac{1}{3}\right)}^k=\frac{1}{1-\frac{1}{3}}=\frac{3}{2}\\ & =\frac{3}{2}-1-\frac{1}{3}\\ & =\frac{1}{2}-\frac{1}{3}\\ & =\frac{3}{6}-\frac{2}{6}=\frac{1}{6}\end{array}$

Hinweis

Eine ähnliche Aufgabe befindet sich im Aufgabenteil am Ende des Kapitels.

Beispielaufgabe 2

Aufgabe (Sonderfälle geometrischer Reihen)

Seien $M,N\in \mathbb{N}$ mit $N\ge 2$ und $M<N$. Finde Formeln für die geometrischen Reihen

1. $\sum _{k=0}^{\mathrm{\infty }}\frac{1}{N^k}$ und $\sum _{k=0}^{\mathrm{\infty }}\frac{(-1{)}^k}{N^k}$
2. $\sum _{k=0}^{\mathrm{\infty }}\frac{M^k}{(M+1{)}^k}$ und $\sum _{k=0}^{\mathrm{\infty }}(-1{)}^k\frac{M^k}{(M+1{)}^k}$
3. $\sum _{k=0}^{\mathrm{\infty }}\frac{M^k}{N^k}$ und $\sum _{k=0}^{\mathrm{\infty }}(-1{)}^k\frac{M^k}{N^k}$

Lösung (Sonderfälle geometrischer Reihen)

Lösung Teilaufgabe 1:

$\begin{array}{cc}\sum _{k=0}^{\mathrm{\infty }}\frac{1}{N^k}& =\sum _{k=0}^{\mathrm{\infty }}{\left(\frac{1}{N}\right)}^k\\ & \downarrow \text{geometrische Reihe mit }q=\frac{1}{N}\\ & =\frac{1}{1-\frac{1}{N}}=\frac{1}{\frac{N-1}{N}}=\frac{N}{N-1}\end{array}$

und

$\begin{array}{cc}\sum _{k=0}^{\mathrm{\infty }}\frac{(-1{)}^k}{N^k}& =\sum _{k=0}^{\mathrm{\infty }}{(-\frac{1}{N})}^k\\ & \downarrow \text{geometrische Reihe mit }q=-\frac{1}{N}\\ & =\frac{1}{1+\frac{1}{N}}=\frac{1}{\frac{N+1}{N}}=\frac{N}{N+1}\end{array}$

Lösung Teilaufgabe 2:

$\begin{array}{cc}\sum _{k=0}^{\mathrm{\infty }}\frac{M^k}{(M+1{)}^k}& =\sum _{k=0}^{\mathrm{\infty }}{\left(\frac{M}{M+1}\right)}^k\\ & \downarrow \text{geometrische Reihe mit }q=\frac{M}{M+1}\\ & =\frac{1}{1-\frac{M}{M+1}}=\frac{1}{\frac{1}{M+1}}=M+1\end{array}$

und

$\begin{array}{cc}\sum _{k=0}^{\mathrm{\infty }}(-1{)}^k\frac{M^k}{(M+1{)}^k}& =\sum _{k=0}^{\mathrm{\infty }}{(-\frac{M}{M+1})}^k\\ & \downarrow \text{geometrische Reihe mit }q=-\frac{M}{M+1}\\ & =\frac{1}{1+\frac{M}{M+1}}=\frac{1}{\frac{2M+1}{M+1}}=\frac{M+1}{2M+1}\end{array}$

Lösung Teilaufgabe 3:

$\begin{array}{cc}\sum _{k=0}^{\mathrm{\infty }}\frac{M^k}{N^k}& =\sum _{k=0}^{\mathrm{\infty }}{\left(\frac{M}{N}\right)}^k\\ & \downarrow \text{geometrische Reihe mit }q=\frac{M}{N}\\ & =\frac{1}{1-\frac{M}{N}}=\frac{1}{\frac{N-M}{N}}=\frac{N}{N-M}\end{array}$

und

$\begin{array}{cc}\sum _{k=0}^{\mathrm{\infty }}(-1{)}^k\frac{M^k}{N^k}& =\sum _{k=0}^{\mathrm{\infty }}{(-\frac{M}{N})}^k\\ & \downarrow \text{geometrische Reihe mit }q=-\frac{M}{N}\\ & =\frac{1}{1+\frac{M}{N}}=\frac{1}{\frac{N+M}{N}}=\frac{N}{N+M}\end{array}$

Beispielaufgabe 3

Aufgabe (Verschiebung des Startindex in geometrischer Reihe)

Sei $q\in ℝ$ mit $|q|<1$. Bestimme eine Formel für jede der folgenden drei Reihen

1. $\sum _{k=1}^{\mathrm{\infty }}{q}^k$
2. $\sum _{k=2}^{\mathrm{\infty }}{q}^k$
3. $\sum _{k=m}^{\mathrm{\infty }}{q}^k$ für $m\in \mathbb{N}$

Lösung (Verschiebung des Startindex in geometrischer Reihe)

Lösung Teilaufgabe 1:

$\begin{array}{cc}\sum _{k=1}^{\mathrm{\infty }}{q}^k& =\left(\sum _{k=0}^{\mathrm{\infty }}{q}^k\right)-q^0\\ & =\left(\sum _{k=0}^{\mathrm{\infty }}{q}^k\right)-1\\ & \downarrow \sum _{k=0}^{\mathrm{\infty }}{q}^k=\frac{1}{1-q}\\ & =\frac{1}{1-q}-1\\ & =\frac{1}{1-q}-\frac{1-q}{1-q}\\ & =\frac{1-(1-q)}{1-q}\\ & =\frac{q}{1-q}\end{array}$

Lösung Teilaufgabe 2:

$\begin{array}{cc}\sum _{k=2}^{\mathrm{\infty }}{q}^k& =\left(\sum _{k=0}^{\mathrm{\infty }}{q}^k\right)-q^0-q^1\\ & =\left(\sum _{k=0}^{\mathrm{\infty }}{q}^k\right)-1-q\\ & \downarrow \sum _{k=0}^{\mathrm{\infty }}{q}^k=\frac{1}{1-q}\\ & =\frac{1}{1-q}-1-q\\ & =\frac{1}{1-q}-\frac{1-q}{1-q}-\frac{q(1-q)}{1-q}\\ & =\frac{1-(1-q)-q(1-q)}{1-q}\\ & =\frac{1-1+q-q+q^2}{1-q}\\ & =\frac{q^2}{1-q}\end{array}$

Lösung Teilaufgabe 3:

Für $|q|<1$ und $m\in \mathbb{N}$ gilt

$\begin{array}{cc}\sum _{k=m}^{\mathrm{\infty }}{q}^k& =\left(\sum _{k=0}^{\mathrm{\infty }}{q}^k\right)-\sum _{k=0}^{m-1}{q}^k\\ & \downarrow \sum _{k=0}^{\mathrm{\infty }}{q}^k=\frac{1}{1-q}\text{ und }\sum _{k=0}^{m-1}{q}^k=\frac{1-q^m}{1-q}\\ & =\frac{1}{1-q}-\frac{1-q^m}{1-q}\\ & =\frac{1-(1-q^m)}{1-q}\\ & =\frac{1-1+q^m}{1-q}\\ & =\frac{q^m}{1-q}\end{array}$

Beispielaufgabe 4

Aufgabe (Reihen, die mit der geometrischen Reihe verwandt sind)

Löse folgende drei Aufgaben:

1. Zeige für alle reellen $q\ne 1$ und $n\in \mathbb{N}$ die Gleichung $\sum _{k=0}^n(k+1)q^k=\frac{1-(n+2)q^{n+1}+(n+1)q^{n+2}}{(1-q{)}^2}$.
2. Zeige für alle $q\in ℝ$ mit $|q|<1$ die Gleichung $\sum _{k=0}^{\mathrm{\infty }}(k+1)q^k=\frac{1}{(1-q{)}^2}$.
3. Berechne die Reihen $\sum _{k=0}^{\mathrm{\infty }}\frac{k+1}{2^k}$ und $\sum _{k=1}^{\mathrm{\infty }}\frac{k}{2^k}$.

Lösung (Reihen, die mit der geometrischen Reihe verwandt sind)

Lösung Teilaufgabe 1:

Die Aussage ist für alle $q\in ℝ$ und $n\in \mathbb{N}$ äquivalent zu

$(1-q{)}^2\cdot \sum _{k=0}^n(k+1)q^k=1-(n+2)q^{n+1}+(n+1)q^{n+2}$

Die linke Seite lässt sich nun wie folgt in die rechte umrechnen:

$\begin{array}{cc}(1-q{)}^2\cdot \sum _{k=0}^n(k+1)q^k& =(1-2q+q^2)\cdot \sum _{k=0}^n(k+1)q^k\\ & =(1-q-(q-q^2))\cdot \sum _{k=0}^n(k+1)q^k\\ & =(1-q)\cdot \sum _{k=0}^n(k+1)q^k-(q-q^2)\cdot \sum _{k=0}^n(k+1)q^k\\ & =\sum _{k=0}^n(k+1)q^k-\sum _{k=0}^n(k+1)q^{k+1}-[\sum _{k=0}^n(k+1)q^{k+1}-\sum _{k=0}^n(k+1)q^{k+2}]\\ & =1+2q+3q^2+4q^3+\dots +n{q}^{n-1}+(n+1)q^n\\ & -q-2q^2-3q^3-\dots -(n-1)q^{n-1}-n{q}^n-(n+1)q^{n+1}\\ & -[q+2q^2+3q^3+\dots +(n-1)q^{n-1}+n{q}^n+(n+1)q^{n+1}\\ & -q^2-2q^3-\dots -(n-2)q^{n-1}-(n-1)q^n-n{q}^{n+1}-(n+1)q^{n+2}]\\ & =1+q+q^2+q^3+\dots +q^{n-1}+q^n-(n+1)q^{n+1}\\ & -[q+q^2+q^3+\dots +q^{n-1}+q^n+q^{n+1}-(n+1)q^{n+2}]\\ & \downarrow \text{Teleskopsumme}\\ & =1-(n+2)q^{n+1}+(n+1)q^{n+2}\end{array}$

Lösung Teilaufgabe 2:

Im Kapitel Beispiele von Grenzwerten hatten wir $\underset{n\to \mathrm{\infty }}{lim}n{q}^n=0$ für $|q|<1$ gezeigt. Aus den Grenzwertregeln folgt damit $\underset{n\to \mathrm{\infty }}{lim}n{q}^{n+1}=q\cdot \underset{n\to \mathrm{\infty }}{lim}n{q}^n=0$ und $\underset{n\to \mathrm{\infty }}{lim}(n+1)q^{n+2}=0$. Daher ist

$\begin{array}{cc}\sum _{k=0}^{\mathrm{\infty }}(k+1)q^k& =\underset{n\to \mathrm{\infty }}{lim}\sum _{k=0}^n(k+1)q^k\\ & =\underset{n\to \mathrm{\infty }}{lim}\frac{1-(n+2)q^{n+1}+(n+1)q^{n+2}}{(1-q{)}^2}\\ & \downarrow \text{Grenzwertsätze}\\ & =\frac{1-\underset{n\to \mathrm{\infty }}{lim}(n+2)q^{n+1}+\underset{n\to \mathrm{\infty }}{lim}(n+1)q^{n+2}}{(1-q{)}^2}\\ & =\frac{1-0+0}{(1-q{)}^2}\\ & =\frac{1}{(1-q{)}^2}\end{array}$

Lösung Teilaufgabe 3:

Mit der Formel aus Teilaufgabe 2 ergibt sich mit $q=\frac{1}{2}$:

$\begin{array}{cc}\sum _{k=0}^{\mathrm{\infty }}\frac{k+1}{2^k}& =\sum _{k=0}^{\mathrm{\infty }}(k+1){\left(\frac{1}{2}\right)}^k\\ & \downarrow \text{Teilaufgabe 2}\\ & =\frac{1}{(1-\frac{1}{2}{)}^2}\\ & =\frac{1}{(\frac{1}{2}{)}^2}=\frac{1}{\frac{1}{4}}=4\end{array}$

Weiter gilt mit $q=\frac{1}{2}$:

$\begin{array}{cc}\sum _{k=1}^{\mathrm{\infty }}\frac{k}{2^k}& \underset{\text{schiebung}}{\stackrel{\text{Indexver-}}{=}}\sum _{k=0}^{\mathrm{\infty }}(k+1){\left(\frac{1}{2}\right)}^{k+1}\\ & =\sum _{k=0}^{\mathrm{\infty }}(k+1){\left(\frac{1}{2}\right)}^k\frac{1}{2}\\ & =\frac{1}{2}\sum _{k=0}^{\mathrm{\infty }}(k+1){\left(\frac{1}{2}\right)}^k\\ & \downarrow \text{Teilaufgabe 2}\\ & =\frac{1}{2}\frac{1}{(1-\frac{1}{2}{)}^2}\\ & =\frac{1}{2}\frac{1}{\frac{1}{4}}=\frac{4}{2}=2\end{array}$

Lösung (Reihen, die mit der geometrischen Reihe verwandt sind, Alternative für Teilaufgabe 1)

Die zu zeigende Gleichung können wir direkt rekonstruieren, indem wir wie beim Beweis der geometrischen Summelformel vorgehen: Es gilt

$\sum _{k=0}^n(k+1)q^k=1+2q+3q^2+4q^3+5q^4+\dots +n{q}^{n-1}+(n+1)q^n$

Indem wir beide Seiten mit $q$ multiplizieren, erhalten wir

$q\cdot \sum _{k=0}^n(k+1)q^k=q+2q^2+3q^3+4q^4+5q^5+\dots +n{q}^n+(n+1)q^{n+1}$

Nun können wir die beiden Gleichungen voneinander subtrahieren

$\begin{array}{cc}\sum _{k=0}^n(k+1)q^k-q\cdot \sum _{k=0}^n(k+1)q^k& =(1+2q+3q^2+4q^3+\dots +n{q}^{n-1}+(n+1)q^n)\\ & -(q+2q^2+3q^3+4q^4+\dots +n{q}^n+(n+1)q^{n+1})\\ & =1+q+q^2+q^3+\dots +q^{n-1}+q^n-(n+1)q^{n+1}\\ \end{array}$

Jetzt klammern wir auf der linken Seite $\sum _{k=0}^n(k+1)q^k$ aus.

$\begin{array}{cc}(1-q)\cdot \sum _{k=0}^n(k+1)q^k& =1+q+q^2+q^3+\dots +q^{n-1}+q^n-(n+1)q^{n+1}\\ & \downarrow \cdot \frac{1}{1-q}\\ ⟹\sum _{k=0}^n(k+1)q^k& =\frac{1+q+q^2+q^3+\dots +q^{n-1}+q^n-(n+1)q^{n+1}}{1-q}\\ & \downarrow \text{mit }1-q\text{ erweitern und ausmultiplizieren}\\ & =\frac{1-(n+2)q^{n+1}+(n+1)q^{n+2}}{(1-q{)}^2}\\ \end{array}$

Lösung (Reihen, die mit der geometrischen Reihe verwandt sind, Alternative für Teilaufgabe 3)

Wir rechnen:

$\begin{array}{cc}\sum _{k=1}^{\mathrm{\infty }}\frac{k}{2^k}& =\sum _{k=0}^{\mathrm{\infty }}k{\left(\frac{1}{2}\right)}^k\\ & =\sum _{k=0}^{\mathrm{\infty }}(k+1-1){\left(\frac{1}{2}\right)}^k\\ & \downarrow \text{Reihen }\sum _{k=0}^{\mathrm{\infty }}(k+1){\left(\frac{1}{2}\right)}^k\text{ und }\sum _{k=0}^{\mathrm{\infty }}{\left(\frac{1}{2}\right)}^k\text{ konvergieren}\\ & =\sum _{k=0}^{\mathrm{\infty }}(k+1){\left(\frac{1}{2}\right)}^k-\sum _{k=0}^{\mathrm{\infty }}{\left(\frac{1}{2}\right)}^k\\ & \downarrow \text{Teilaufgabe 2 mit }q=\frac{1}{2}\\ & =\frac{1}{(1-\frac{1}{2}{)}^2}-\sum _{k=0}^{\mathrm{\infty }}{\left(\frac{1}{2}\right)}^k\\ & \downarrow \text{geometrische Reihe}\\ & =\frac{1}{(1-\frac{1}{2}{)}^2}-\frac{1}{1-\frac{1}{2}}\\ & =\frac{1}{\frac{1}{4}}-\frac{1}{\frac{1}{2}}=4-2=2\end{array}$

Hinweis

Genau wie in Teilaufgabe 3 lässt sich allgemein für $|q|<1$ zeigen:

$\sum _{k=1}^{\mathrm{\infty }}k{q}^k=\frac{q}{(1-q{)}^2}$