MathemaTriX ⋅ Diagramme
Erscheinungsbild
| ||||||||||||||||||
|
|
| AUFGABEN |
Säulendiagramm
[Bearbeiten]Säulendiagramm
[Bearbeiten]Mittelwerte bei einem Säulendiagramm
[Bearbeiten]Ablesen
Erstellen
D Ö R F E R 3 1 5 5 4 3 4 6 7 8 Toten pro Dorf
R Ä Ü M E 1 2 5 5 3 0 1 2 4 8 Betten pro Raum
T I S C H E 4 5 1 4 1 0 1 2 3 9 Personen/Tisch
P E R S O N 3 5 1 5 1 0 1 2 3 14 Part./Person
K I N D E R 5 2 3 5 2 4 5 6 7 8 Tonnen/Kind
T Ö P F E 3 2 2 5 4 0 3 5 7 8 Blumen pro Topf
M Ü T T E R 6 6 5 1 1 1 2 3 6 7 Kinder/Mutter
K I N D E R 3 5 1 5 1 0 1 2 3 14 Bücher pro Kind
Liniendiagramm
[Bearbeiten]- Tausende Jahre her.
- Tausende Jahre her.
- War nicht
Lineare Funktion Diagramm
[Bearbeiten]- ca. 2500 €, 3700 €, −600 € bzw. −1200 €
- ca. 1 t, 1200 €
- ca. 2,6, 3,8 bzw. 5,8 t
- ca.60, 50, 35 bzw. 10 Hz
- ca. 70 Hz, 140 cm
- ca. 100, 60, 40 bzw. 120 cm
- ca. 85, 70, bzw. 52 g/L
- ca. 100 g/L, 250 °C
- ca. 0, 75, 100 bzw. 150 °C
- ca. 71 Jahre
- ca. 77 Jahre
- ca. 30 Zig./Tag
- ca. 34 Zig./Tag
- ca. 85 Jahre
- ca. 71 Jahre
- ca. 77 Jahre
- ca. 30 Zig./Tag
- ca. 34 Zig./Tag
- ca. 85 Jahre
Kreisdiagramm
[Bearbeiten]Boxplot
[Bearbeiten]Einführung
[Bearbeiten]Matura
[Bearbeiten]- j n j n j n n j n
- Es ist nicht sicher, ob die gleiche Person in beiden Fällen die entsprechenden Punkte hatte
- ja, über 19
- ja, unter 5,5
- Nein, wir wissen nicht, wo 20% der Personen liegen
- Falsch, es gibt zumindest 1 Person von 50%, die weniger als 12 Punkte hat
- zweite
- nein
- [47;50][45;47]
- 42
- ja
- nein
- nein, liegt innerhalb des gleichen Quartils
- n n j n j j n j n(82)
- Falsch, auch bei einem Diagramm ist die niedrigste Punkteanzahl zumindest 42
- ja, die Grenze wird nicht erreicht, etwa über 104
- ja, die Grenze wird nicht erreicht, unter 41
- ja, sogar zumindest 75%
- ja, egal ob der Median zwischen zwei Werten oder nicht liegt haben wir 50% oder mehr Personen mit 56 oder mehr Punkten
- zweite
- nein
- [37;39][32;37]
- 47
- ja
- ja
- möglich, wenn 42 genau der Median ist und nicht oberhalb des Medians als Wert wiederholt wird
Diagramme
[Bearbeiten]Diagramme 1
[Bearbeiten]- 9 m
- senkrecht: an der gleichen Höhe bleiben
der Rest hinunter klettern - Auf der x-Achse ein Teil zwischen 0 und 3
- Auf der x-Achse genau zwischen 0 und 3
- 0,06 m/s
- ja, z.B. Keller
- D
- H
- S
- C: Wendepunkt, Stelle ein weniger als
E: Hochpunkt, an der Stelle , Stelle auch Median und Modus - Keine
- kg (oder g)
- von links: 2,4-3-3,6 kg
- flacher
- rechts verschoben
- 2,5
- Auf der x-Achse, 8 kleine Einheiten links und rechts von
- C: Wendepunkt, Stelle ein weniger als
Diagramme 2
[Bearbeiten]- 1957
- nein, wir müssen die y-Werte vergleichen
- ca. 90 Millionen Feinunzen
- Absolute Änderung der Goldreserven zwischen 1976 und 1999
- ca. 0.0828
- ca. 8,28% weniger
- Momentane Änderung der Goldreserven in Millionen Feinunzen pro Jahr im Jahr 1994
- ca. 14 Millionen Feinunzen pro Jahr
- nach ca. 10 Jahren
- fast konstant bei 950 Millionen Feinunzen
- ca. 350 Millionen Feinunzen pro Jahr
- Die Goldförderung in Tonnen pro Jahr in Abhängigkeit vom Jahr
- Die Masse des gefördeten Goldes in Tonnen, mit Integral
- Wie schnell sich die Geschwindigkeit, mit der Gold gefördert wird (Goldförderung), ändert, Ableitung der Kurve
- Wie schnell sich die Geschwindigkeit, mit der Gold gefördert wird (Goldförderung), zwischen zwei Daten durchschnittlich ändert. Z.B. hat sich die Goldförderung (Geschwindigkeit, mit der Gold gefördert wird) zwischen 1910 und 1940 ca. verdopplelt
- Die größte absolute Änderung findet zwischen 1980 und 1990 statt, die größte relative anscheinend doch zwischen 1930 und 1940
- Wie schnell sich die Geschwindigkeit, mit der Gold gefördert wird (Goldförderung), zwischen 1900 und 2000 durchschnittlich ändert
- relative Änderung des verbliebenen Sauerstoffs zwischen ca. 1,5-te und 7-te Stunde
- ca. nach 11,5 Stunden
- Mittlere Abnahme der Sauerstoffsmenge in g pro Stunde zwischen 2. und 13. Stunde.
- in etwa:

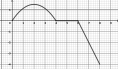
- ca. 5,3
- Punkte (4|4) und (0|8) mit einer Gerade verbinden
- Gerade verschieben, bis sie die Kurve s nur berührt und nicht mehr schneidet oder rechnerisch:
- Steigung k zwischen (4|4) und (0|8) berechnen
- Funktion s finden
- s ableiten
- löse von s'=k

- 1250 €
- 1 t
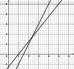
- ca. 2,3 t
- Löse Geogebra:
- x ja (Kosten), y eher nicht
- 1,8 die erste, 4 die zweite
Diagramme 3
[Bearbeiten]- Die Steigung der Gerade ist 0,5, also 50%
- Z

- also alle Katzen die (ggf. auch) rot sind und dazu auch alle, die gleichzeitig weiß und schwarz sind.
- bzw.
- ab den 2,65-ten bis zum 80,6-ten Tag
- Sie wachsen unendlich, das ist einfach unmöglich. Auch für kurze Zeit nicht geeignet, genau wegen falscher Konnotationen[1]
- Geogebra, Tabelle, exp(Höhe→x)→nein
- für 2 Punktpaare→Nein
- 30,31%(109,11°), 19,42%(69,91°), 31,58%(113,68°), 18,69%(67,30°)
- D=nicht ablesbar , Med=45 , Q1=42 , Q3=47 , IQR=5, Span=14 , Max=50 , Min=36; 1. Quartil liegt zwischen zwei Werten!
- ii, iii, vii, ix
- A=B=F=G, C=E
- 8,5⋅10⁸, das 3.
L ist Luftdruck in Atm
h ist die Höhe, eine Einheit ist 50 km- der y-AA zeigt uns den Luftdruck, wenn die Höhe null ist (also auf der Oberfläche)
die Steigung zeigt uns, wie viel der Luftdruck (in atm) pro 50 km fällt
- Naki

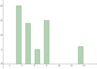
- alle Werte in cm
Schwarz:
, , Med=8 , Max=14 , Min=5,5;
rot:
D=6,5 , Med=6,5 , Span=0 , Max=6,5 , Min=6,5; - die 4.
- Standardabweichung bzw. Wahrscheinlichkeit, dass nach 12 Mal Wählen, zumindest 6 (also mehr als 5) Teile grün sind
- y-Achsenabschnitt : Todesalter der nicht-Raucher, Steigung : wie viele Jahre früher pro Zigarette man stirbt

- Null und 3,2
- ca. 5,63 km
(im Diagramm ablesbar)- 5 mit 4 B., 7 mit 8 B.
- →nicht arithm. →geom.
→arithm. →nicht geom. - 22,5 bzw 2,8
- 11 m=1100 cm, Radius daher 550 cm, also das 110-fache; Oberfläche: also das 12100-fache
B Blutdruck in mmHg
v Volumen in ml- Nullstelle: Volumen des verlorenen Blutes, wenn der Blutdruck Null ist
Steigung: wie viel der Blutdruck in mmHg pro ml verlorenen Blutes fällt
- ↑ viel geeigneter ist eine sogenannte S-Funktion, deren erste Hälfte allerdgins doch von eine exponentielle gut angenähert werden kann
























































































































































