MathemaTriX ⋅ Zahlendarstellungen Mengentheorie und Aussagenlogik

STOPP PUSHBACKS • FREE ASSANGE • FRIEDEN AUF DER WELT

${\color {white}\mathbf {MATHE} \mu \alpha T\mathbb {R} ix}$	DEINE FESTE BEGLEITERIN
	FÜR DIE SCHULMATHEMATIK

EINFACH UND
VERSTÄNDLICH

GRATIS!^*

STARTEN!

MIT MEHR ALS 200 THEORIE- UND AUFGABEN-ERKLÄRUNGS VIDEOS!

Mathe lernen ist wie Fahrradfahren lernen: Du kannst es dir stundenlang erklären lassen, du wirst nie fahren können, wenn du nicht selber zu fahren probierst.

AUFGABEN

KAPITEL

Grundrechenarten Bruchrechnungen	$-{\tfrac {\cdot \ +}{\ :\ }}$
Schlussrechnung Prozentrechnung
Exponentialfunktion Logarithmus
Arbeiten mit Termen	$\mathbb {X} ^{2}$
Zahlendarstellungen Mengentheorie Aussagenlogik	${\begin{matrix}\mathbb {R} :=\\\mathbb {Q} \cup \mathbb {I} \end{matrix}}$
Einheiten	$cm^{2}$
Statistik und Wahrscheinlichkeit
Geometrische Konstruktionen
Geometrie der Ebene
Geometrie des Raums
Diagramme
Funktionen	$f(x)$
Lineare Gleichungssysteme	${\begin{smallmatrix}{a_{1}\ b_{2}}\\{a_{2}\ b_{2}}\end{smallmatrix}}$
Trigonometrische Funktionen
Vektoren
Differentialrechnung	$^{dy}/_{dx}$
Integralrechnung	$\textstyle \int _{a}^{b}dx$
Folgen	$a_{n}$
Beweise	$a\rightarrow b$

Zahlendarstellungen[Bearbeiten]

(Dekadisches oder) Dezimalsystem[Bearbeiten]

Darstellungen einer Zahl im Dezimalssystem[Bearbeiten]

Die römische Zahlendarstellung[Bearbeiten]

Die griechische Zahlendarstellung[Bearbeiten]

Die Geschichte von Null[Bearbeiten]

Binäre Zahlen[Bearbeiten]

Weitere Zahlensysteme[Bearbeiten]

Zahlenmengen[Bearbeiten]

Zur welchen Zahlenmengen gehören folgende Zahlen?
$\quad$	$\ \ \ \mathbb {N} \ \ \$	$\ \ \ \mathbb {Z} \ \ \$	$\ \ \ \mathbb {Q} \ \ \$	$\ \ \ \mathbb {I} \ \ \$	$\ \ \ \mathbb {R} \ \ \$
$\textstyle {\frac {5}{13}}$	✘	✘	✔	✘	✔
$\textstyle {\frac {26}{13}}$	✔	✔	✔	✘	✔
$\textstyle -{\frac {\sqrt {5}}{13}}$	✘	✘	✘	✔	✔
${\sqrt {7}}$	✘	✘	✘	✔	✔
$-{\sqrt {196}}$	✘	✔	✔	✘	✔
${\sqrt {-4}}$	✘	✘	✘	✘	✘
${\sqrt {169}}$	✔	✔	✔	✘	✔
$\textstyle -{\frac {26}{13}}$	✘	✔	✔	✘	✔

Zur welchen Zahlenmengen gehören folgende Zahlen?
$\quad$	$\ \ \ \mathbb {N} \ \ \$	$\ \ \ \mathbb {Z} \ \ \$	$\ \ \ \mathbb {Q} \ \ \$	$\ \ \ \mathbb {I} \ \ \$	$\ \ \ \mathbb {R} \ \ \$
$\textstyle {\frac {\sqrt {0{,}25}}{13}}$	✘	✘	✔	✘	✔
$\textstyle {\sqrt {33}}$	✘	✘	✘	✔	✔
$\textstyle -{\sqrt {441}}$	✘	✔	✔	✘	✔
${\sqrt {-9}}$	✘	✘	✘	✘	✘
$6$	✔	✔	✔	✘	✔
$\textstyle {\frac {\sqrt {11}}{13}}$	✘	✘	✘	✔	✔
$\textstyle {\frac {65}{13}}$	✔	✔	✔	✘	✔
$\textstyle -{\frac {8}{4}}$	✘	✔	✔	✘	✔

Zur welchen Zahlenmengen gehören folgende Zahlen?
$\quad$	$\ \ \ \mathbb {N} \ \ \$	$\ \ \ \mathbb {Z} \ \ \$	$\ \ \ \mathbb {Q} \ \ \$	$\ \ \ \mathbb {I} \ \ \$	$\ \ \ \mathbb {R} \ \ \$
${\sqrt {144}}$	✔	✔	✔	✘	✔
$\textstyle +{\frac {39}{3}}$	✔	✔	✔	✘	✔
$\textstyle {\frac {13}{6{,}5}}$	✔	✔	✔	✘	✔
$\textstyle -{\frac {\sqrt {81}}{13}}$	✘	✘	✔	✘	✔
$\textstyle {\frac {\sqrt {8}}{13}}$	✘	✘	✘	✔	✔
${\sqrt {289}}$	✔	✔	✔	✘	✔
$-{\sqrt {-6}}$	✘	✘	✘	✘	✘
${\sqrt {4}}$	✔	✔	✔	✘	✔

Zur welchen Zahlenmengen gehören folgende Zahlen?
$\quad$	$\ \ \ \mathbb {N} \ \ \$	$\ \ \ \mathbb {Z} \ \ \$	$\ \ \ \mathbb {Q} \ \ \$	$\ \ \ \mathbb {I} \ \ \$	$\ \ \ \mathbb {R} \ \ \$
$\textstyle {\frac {0{,}5}{\sqrt {0{,}0625}}}$	✔	✔	✔	✘	✔
$\textstyle -{\frac {38}{3}}$	✘	✘	✔	✘	✔
$\textstyle -{\frac {52}{1{,}3}}$	✘	✔	✔	✘	✔
$\textstyle {\frac {\sqrt {169}}{13}}$	✔	✔	✔	✘	✔
$\textstyle {\frac {\sqrt {-9}}{13}}$	✘	✘	✘	✘	✘
$28$	✔	✔	✔	✘	✔
$-{\sqrt {(-25)(-4)}}$	✘	✔	✔	✘	✔
${\sqrt {18}}$	✘	✘	✘	✔	✔

Zur welchen Zahlenmengen gehören folgende Zahlen?
$\quad$	$\ \ \ \mathbb {N} \ \ \$	$\ \ \ \mathbb {Z} \ \ \$	$\ \ \ \mathbb {Q} \ \ \$	$\ \ \ \mathbb {I} \ \ \$	$\ \ \ \mathbb {R} \ \ \$
$\textstyle {\frac {11}{7}}$	✘	✘	✔	✘	✔
$\textstyle {\frac {28}{7}}$	✔	✔	✔	✘	✔
$\textstyle -{\frac {\sqrt {7}}{15}}$	✘	✘	✘	✔	✔
${\sqrt {15}}$	✘	✘	✘	✔	✔
$-{\sqrt {625}}$	✘	✔	✔	✘	✔
${\sqrt {-121}}$	✘	✘	✘	✘	✘
${\sqrt {256}}$	✔	✔	✔	✘	✔
$\textstyle -{\frac {45}{15}}$	✘	✔	✔	✘	✔

Zur welchen Zahlenmengen gehören folgende Zahlen?
$\quad$	$\ \ \ \mathbb {N} \ \ \$	$\ \ \ \mathbb {Z} \ \ \$	$\ \ \ \mathbb {Q} \ \ \$	$\ \ \ \mathbb {I} \ \ \$	$\ \ \ \mathbb {R} \ \ \$
$\textstyle {\frac {\sqrt {0{,}09}}{11}}$	✘	✘	✔	✘	✔
$\textstyle {\sqrt {70}}$	✘	✘	✘	✔	✔
$\textstyle -{\sqrt {1600}}$	✘	✔	✔	✘	✔
${\sqrt {-25}}$	✘	✘	✘	✘	✘
$6$	✔	✔	✔	✘	✔
$\textstyle {\frac {\sqrt {33}}{33}}$	✘	✘	✘	✔	✔
$\textstyle {\frac {60}{12}}$	✔	✔	✔	✘	✔
$\textstyle -{\frac {33}{11}}$	✘	✔	✔	✘	✔

Zur welchen Zahlenmengen gehören folgende Zahlen?
$\quad$	$\ \ \ \mathbb {N} \ \ \$	$\ \ \ \mathbb {Z} \ \ \$	$\ \ \ \mathbb {Q} \ \ \$	$\ \ \ \mathbb {I} \ \ \$	$\ \ \ \mathbb {R} \ \ \$
${\sqrt {81}}$	✔	✔	✔	✘	✔
$\textstyle +{\frac {70}{5}}$	✔	✔	✔	✘	✔
$\textstyle {\frac {23}{11{,}5}}$	✔	✔	✔	✘	✔
$\textstyle -{\frac {\sqrt {144}}{12}}$	✘	✘	✔	✘	✔
$\textstyle {\frac {\sqrt {27}}{9}}$	✘	✘	✘	✔	✔
${\sqrt {324}}$	✔	✔	✔	✘	✔
$-{\sqrt {-35}}$	✘	✘	✘	✘	✘
${\sqrt {49}}$	✔	✔	✔	✘	✔

Zur welchen Zahlenmengen gehören folgende Zahlen?
$\quad$	$\ \ \ \mathbb {N} \ \ \$	$\ \ \ \mathbb {Z} \ \ \$	$\ \ \ \mathbb {Q} \ \ \$	$\ \ \ \mathbb {I} \ \ \$	$\ \ \ \mathbb {R} \ \ \$
$\textstyle {\frac {0{,}2}{\sqrt {0{,}01}}}$	✔	✔	✔	✘	✔
$\textstyle -{\frac {45}{6}}$	✘	✘	✔	✘	✔
$\textstyle -{\frac {42}{1{,}4}}$	✘	✔	✔	✘	✔
$\textstyle {\frac {\sqrt {289}}{17}}$	✔	✔	✔	✘	✔
$\textstyle {\frac {\sqrt {-16}}{4}}$	✘	✘	✘	✘	✘
$41$	✔	✔	✔	✘	✔
$-{\sqrt {(-16)(-9)}}$	✘	✔	✔	✘	✔
${\sqrt {12}}$	✘	✘	✘	✔	✔

Mengenlehre[Bearbeiten]

Begriffe der Mengenlehre[Bearbeiten]

Mengenlehre Aufgabebeispiel[Bearbeiten]

1. $C=S1\bigcap S2\bigcap S3\$ also 13 Personen.
2. $G\bigcup B\bigcup A=\left(S1\bigcup S3\right)\setminus S2\$ also 16 Personen.
3. Das sind die Personen, die zumindest eines der beiden Fächer Analysis und lineare Algebra aber doch nicht Zahlentheorie gewählt haben, also $G\bigcup F\bigcup E$ . Das sind 54 Personen.
4. Das sind die Personen, die gleichzeitig Analysis und Zahlentheorie aber nicht lineare Algebra gewählt haben, also die Menge $B$ . Das sind 9 Personen.
5. $\left(S3\bigcap S2\right)\setminus S1\$
6. a=8, b=3
  c=4, d=4
7. ca. 15,79%
1. A=8, B=43
  C=37, D=27
  E=35, F=0
  U=S1, V=S2, W=S3
2. keine:177, eine:80
3. $\left(S\bigcup P\right)\setminus M\$
4. Personen die kaum trainieren und viel rauchen aber nicht so viel Fett oder Fleisch essen
5. Die Grüne Fläche
6. Die gelbe Fläche
7. Die Personen die viel Fett oder Fleisch essen ohne die Personen, die viel rauchen oder kaum trainieren
1. $S1\bigcap S2\bigcap S3\ =\emptyset \ =A\bigcap B\$ oder jede zufällige Schnittmenge der Mengen A bis F, also keine Person.
2. $A\bigcup D=S1\setminus S2\$ also 27 Personen.
3. Das sind die Personen, die zumindest eines der beiden Parteien Lila oder Blau mögen aber die Grüne Partei doch nicht, also $A\bigcup B\bigcup C$ . Das sind 67 Personen.
4. Das sind die Personen, die sowohl die grüne und als auch die lila Partei mögen, allerdings ohne die blaue Partei zu mögen, also die Menge $D$ . Das sind 7 Personen.
5. $\left(S3\bigcap S2\right)\setminus S1\$
6. a=2, b=3
  c=4, d=8
7. ca. 23,53%
1. A=14, B=1
  C=24, D=3
  E=36, F=19, G=22
  U=S1, V=S2, W=S3
2. 72
3. $\left(M\bigcup P\right)\setminus \left(S\bigcap M\right)\$
4. Personen die kaum trainieren und viel rauchen ohne die Personen die sowohl kaum trainieren als auch so viel Fett oder Fleisch essen
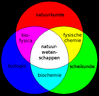5. Entsprechend rot, gelb und grün
6. Die Grüne Fläche
7. Die Personen die viel Fett oder Fleisch essen und viel rauchen aber doch trainieren
1. $B=S1\bigcap S2\bigcap S3\ =S3$ also 29 Personen.
2. $C\bigcup A=\left(S1\bigcup S3\right)\setminus S2\$ also 72 Personen.
3. Das sind die Personen, die zumindest eines der beiden Fächer Analysis und lineare Algebra gewählt haben allerdings ohne Zahlentheorie gewählt zu haben, also $A\bigcup C\bigcup D$ ( $C$ ist im Bild ohne $B$ gemeint). Das sind 125 Personen.
4. Das sind die Personen, die gleichzeitig Analysis und Zahlentheorie aber nicht lineare Algebra gewählt haben. Das ist die leere Menge: $\left(S3\bigcap S1\right)\setminus S2=\emptyset$ , also keine Person.
5. $S2\setminus S1\$
6. ja, z.B. : $\Omega _{2}=S1,\ \Omega =S2,\ \Omega _{1}=S3$
1. $C=S1\bigcap S2\bigcap S3\$ also 21 Personen.
2. $G\bigcup B\bigcup A=\left(S1\bigcup S3\right)\setminus S2\$ also 17 Personen.
3. Das sind die Personen, die zumindest eine der beiden Eigenschaften "Fleischesser" oder "oft fliegen" aufweisen aber doch nicht mit dem Auto zur Arbeit fahren, also $G\bigcup F\bigcup E$ . Das sind 55 Personen.
4. Das sind die Personen, die gleichzeitig die Eigenschaften "Fleischesser" und "zur Arbeit mit dem Auto" aufweisen aber nicht so oft fliegen, also die Menge $B$ . Das sind 9 Personen.
5. $\left(S3\bigcap S2\right)\setminus S1\$
6. 12 Personen

Aussagenlogik[Bearbeiten]

Mengenlehre und Aussagenlogik[Bearbeiten]

1. $(A\cup B)\setminus C=(x|(x\in A\lor x\in B)\land x\notin C$
1. $(A\cap B)\cup C=(x|(x\in A\land x\in B)\lor x\notin C$
1. $(C\cup B)\setminus A=(x|(x\in C\lor x\in B)\land x\notin A$
1. $(A\cup B)\cap C=(x|(x\in A\lor x\in B)\land x\in C$
1. $(A\setminus B)\cap C=(x|(x\in A\land x\notin B)\land x\in C$
1. $A\cup (B\setminus C)=(x|x\in A\lor (x\in B\land x\notin C)$

Wahrheitstabellen[Bearbeiten]

$a$	$b$	$c$	$\ a\Rightarrow c\$	$\ b\land c\$	$\ (a\Rightarrow c){\dot {\lor }}(b\land c)\$
Belegung			Untersuchung
w	w	w	w	w	f
w	w	f	f	f	f
w	f	w	w	f	w
w	f	f	f	f	f
f	w	w	w	w	f
f	w	f	w	f	w
f	f	w	w	f	w
f	f	f	w	f	w

$a$	$b$	$c$	$\ a\Leftrightarrow c\$	$\ b\land \neg c\$	$(a\Leftrightarrow c)\lor \neg (b\land \neg c)$
Belegung			Untersuchung
w	w	w	w	f	w
w	w	f	f	w	f
w	f	w	w	f	w
w	f	f	f	w	f
f	w	w	f	f	w
f	w	f	w	f	w
f	f	w	w	f	w
f	f	f	w	f	w

$a$	$b$	$c$	$\ a\lor c\$	$\ \neg b\land c\$	$(a\lor c){\dot {\lor }}(\neg b\land c)$
Belegung			Untersuchung
w	w	w	w	f	w
w	w	f	w	f	w
w	f	w	w	w	f
w	f	f	w	f	w
f	w	w	w	f	w
f	w	f	f	f	f
f	f	w	w	w	f
f	f	f	f	f	f

$a$	$b$	$c$	$\ a\Leftarrow c\$	$\ b\land c\$	$(a\Leftarrow c)\lor \neg (b\land c)$
Belegung			Untersuchung
w	w	w	w	w	w
w	w	f	w	f	w
w	f	w	w	f	w
w	f	f	w	f	w
f	w	w	f	w	f
f	w	f	w	f	w
f	f	w	f	f	w
f	f	f	w	f	w

$a$	$b$	$c$	$\ a{\dot {\lor }}c\$	$\ b\Leftrightarrow c\$	$(a{\dot {\lor }}c)\land (b\Leftrightarrow c)$
Belegung			Untersuchung
w	w	w	f	w	f
w	w	f	w	f	f
w	f	w	f	f	f
w	f	f	w	w	w
f	w	w	w	w	w
f	w	f	f	f	f
f	f	w	w	f	f
f	f	f	f	w	f

$a$	$b$	$c$	$\ \neg a{\dot {\lor }}\neg c$	$\ b\land c\$	$(\neg a{\dot {\lor }}\neg c)\Leftrightarrow (b\land c)$
Belegung			Untersuchung
w	w	w	f	w	f
w	w	f	w	f	f
w	f	w	f	f	w
w	f	f	w	f	f
f	w	w	w	w	w
f	w	f	f	f	w
f	f	w	w	f	f
f	f	f	f	f	w

BILDERVERZEICHNIS

ÖFFNE DEIN HORIZONT!
LERNE MIT MATHEMATRIX!

\quad

\quad

\quad

$\mathbf {MATHE} \mu \alpha T\mathbb {R} ix$
LOGO	CH DE AT

SPENDEN
Der Hauptautor ggf. das Team verdient zwar nicht viel, braucht allerdings dein Geld eigentlich nicht. Wenn du aber doch meinst, dass gute Arbeit belohnt werden soll und dieses Projekt gut findest, kannst du immer in diesem Link spenden. Das ist allerdings vielleicht die einzige Einrichtung mit völliger Transparenz, wo du genau weißt, was mit deinem Geld passiert.