Benutzer:Dirk Hünniger/mnf
Über das Projekt
[Bearbeiten]
Was ist Mathematik?
[Bearbeiten]Was ist Mathematik?
[Bearbeiten]Die Mathematik ist eine für unser Leben unentbehrliche Wissenschaft. Sie hilft uns, zu vielen Fragen und Problemen Lösungen zu finden und ist für zahlreiche weitere Wissenschaften unersetzlich. Für einige Menschen besitzt sie sogar einen Wert an sich. Dabei ist die Frage, was Mathematik ist, gar nicht leicht zu beantworten. Was macht also die Mathematik aus und womit beschäftigt sie sich?
Historisch ist die Mathematik aus der Untersuchung von geometrischen Figuren und dem Rechnen mit Zahlen entstanden. Heute beschäftigt sie sich in unterschiedlichen Teilgebieten mit abstrakten Strukturen, die in der Regel durch einige wenige Grundaussagen beschrieben werden. Diese Grundaussagen heißen Axiome und alle weiteren Eigenschaften und Gesetzmäßigkeiten der Struktur werden aus den Axiomen mit Hilfe der Logik hergeleitet. Ein Beispiel für eine solche Struktur sind die natürlichen Zahlen, die durch die Peano-Axiome beschrieben werden. Ein anderes Beispiel ist die euklidische Geometrie, die durch Hilberts Axiomensystem charakterisiert wird.
Wie funktioniert Mathematik?
[Bearbeiten]
Jede mathematische Theorie besitzt dabei ihre eigenen Axiome. Theorien bauen auch oftmals aufeinander auf, indem sie die Axiome einer Theorie um neue erweitern. Ob die Theorie dabei in sich stimmig ist, also keine Widersprüche erzeugt, zeigt sich erst im Laufe ihrer Entwicklung. Innerhalb einer Theorie werden aus den Axiomen weitere Aussagen hergeleitet, die man Theoreme oder Sätze nennt. Aus den neu gewonnenen Theoremen und den ursprünglichen Axiomen werden weitere Theoreme bewiesen, über die weitere Theoreme bewiesen werden und so fort. Am Ende hat man so eine Vielzahl von Sätzen hergeleitet, die eine mathematische Theorie ausmachen.
Oft wird der Aufbau einer mathematischen Theorie mit dem eines Gebäudes verglichen. Das Fundament bilden die Axiome. Darauf setzen die Theoreme auf und die Beweise sind der Mörtel, welcher alles zusammenhält. Am Ende entsteht so ein komplettes mathematisches Gebäude, die mathematische Theorie. Die Aufgabe des Mathematikers ist hier ähnlich der eines Maurers. Er findet und setzt Axiome für neue Theorien (Fundament legen) und beweist neue Theoreme (neue Steine mit Mörtel auf die Wand mauern).
Ziel einer mathematischen Theorie ist es, gewisse abstrakte Strukturen zu beschreiben und Vorhersagen über diese Strukturen zu machen. Die natürlichen Zahlen mit ihren Rechengesetzen oder Wahrscheinlichkeitsbetrachtungen sind Beispiele für solche Strukturen. Die Axiome einer Theorie legen die betrachtete Struktur fest und die Theoreme sind zusätzliche Eigenschaften der Struktur. Indem Theoreme aus den Axiomen logisch hergeleitet sind, ist garantiert, dass die Struktur die Eigenschaften besitzt, welche durch die Theoreme beschrieben werden. Dies begründet auch das Vorgehen des Beweisens. Immer, wenn man etwas findet, das alle Axiome einer Theorie erfüllt, sind dafür alle Theoreme der Theorie anwendbar, ohne dass man dies extra nachprüfen muss.
Bei der Erforschung einer mathematischen Theorie sieht man oft Muster, die häufig oder in „natürlicher Weise“ auftreten. Man gibt ihnen dann Namen, um sie einfach und kurz bezeichnen zu können. So werden neue Objekte definiert. Diese Definitionen sind entscheidend dafür, dass man kurz und trotzdem exakt über mathematische Theorien sprechen kann. Wenn wir zum Beispiel wissen, was die natürlichen Zahlen sind und wie man sie in Faktoren zerlegen kann, so stoßen wir auf die Struktur der Primzahlen (Zahlen, die sich nur durch eins und sich selbst teilen lassen). Ob und wann eine bestimmte Definition sinnvoll ist, ist durchaus nicht immer leicht zu beantworten. In Bezug auf die Primzahlen erwies es sich später als vorteilhaft, sie wie folgt zu definieren: „Eine Primzahl ist eine natürliche Zahl, die genau 2 Teiler hat.“ Weil die Eins jetzt keine Primzahl mehr ist, kann z. B. eindeutig (bis auf die Reihenfolge) durch das Produkt von vier Primzahlen () dargestellt werden. Bei der Beschäftigung mit mathematischen Objekten erkennt man oft weitere Muster. Beispielsweise sieht man bei Primzahlen, dass es sehr viele von ihnen gibt. Man gelangt so zur Vermutung: Möglicherweise gibt es unendlich viele Primzahlen. Ganz gleich, wie offensichtlich eine Vermutung sein kann: Man muss sie nach den strengen Prinzipien der Logik beweisen.
Oft sind mathematische Theorien durch Naturbeobachtungen oder „die Welt um uns herum“ motiviert. So erhält man intuitive Ideen von Strukturen, die man mathematisch beschreiben will. Welche Axiome man als Grundlage einer Theorie wählen sollte, ist keine einfache Frage. Ein Beispiel sind die natürlichen Zahlen: Früh begegnet uns die Idee des Zählens und wir vergleichen Mengen, indem wir die Anzahl ihrer Elemente bestimmen. Ebenso ist uns klar, wie man Zahlen addieren kann. Die Aufgabe eines Mathematikers besteht nun darin, die Struktur der natürlichen Zahlen durch Axiome zu beschreiben. Dazu werden einige einleuchtende Eigenschaften der natürlichen Zahlen festgehalten. Als Mathematiker muss man nun die „richtigen“ Axiome finden, um die Struktur vollständig zu beschreiben. Sie müssen unabhängig voneinander sein und es sollten möglichst wenige davon gesetzt werden.
Sind die Axiome aber erst einmal gesetzt, so existieren sie unabhängig von der „Welt um uns herum“ – und alle daraus logisch ableitbaren Schlussfolgerungen ebenso. Anders als formulierte Naturgesetze der Physik oder Chemie können sie nicht durch spätere Experimente widerlegt werden, sondern gelten als „unbedingt wahr“. In diesem Moment löst sich die Mathematik von den Naturbeobachtungen und ist deshalb streng genommen auch keine Naturwissenschaft mehr. Von einigen wird die Mathematik deshalb den Geisteswissenschaften zugeordnet. Heutzutage wird sie oftmals als Strukturwissenschaft bezeichnet. Wenn die Gesetze der Logik universelle Gültigkeit haben (also zu jeder Zeit und an jedem Ort stimmen), so müsste jede andere Gesellschaft, wenn sie von denselben Axiomen ausgeht, dieselbe Mathematik entwickeln wie wir – ganz egal, ob es sich dabei um Menschen oder eine außerirdische Intelligenz handeln würde. Einmal bewiesene Aussagen haben innerhalb einer mathematischen Theorie eine ewige Gültigkeit und sind nicht mehr widerlegbar.
Die Frage, ob die Logik wirklich so universell ist und welche Axiome zu wählen sind, ist jedoch eine heikle und durchaus philosophische Frage. Als Grundlage des mathematischen Schlussfolgerns wird heutzutage die formale Logik verwendet. Die Logik – traditionell ein Teil der Philosophie – ist heute ein fester Bestandteil der Mathematik. Als axiomatische Grundlage verwendet man in der modernen Mathematik die Axiome der Mengenlehre nach Ernst Zermelo und Abraham Adolf Fraenkel (kurz: ZF) und zumeist das Auswahlaxiom (ZFC, vom englischen choice). Letzteres Axiom ist nicht völlig unumstritten, da sich damit teilweise kontraintuitive Ergebnisse beweisen lassen. Andererseits ist das Auswahlaxiom jedoch für viele Bereiche der Mathematik unerlässlich.
Wird Mathematik entdeckt oder erschaffen?
[Bearbeiten]Diese Frage ist eher philosophischer Natur. Es gibt hierzu zwei unterschiedliche Positionen. In der ersten, der so genannten platonischen Sichtweise sind mathematische Objekte universell vorhanden und werden vom Mathematiker entdeckt. Der Konstruktivismus demgegenüber nimmt die Position ein, dass Mathematik von Menschen erschaffen wird: Ein mathematisches Objekt kann nur dann existieren, wenn man weiß, wie es konstruiert wird. Der Mathematiker Leopold Kronecker tätigte hierzu auch den Ausspruch: „Die ganzen Zahlen hat der liebe Gott gemacht, alles andere ist Menschenwerk.“ Hier betont Kronecker den konstruktiven Charakter der Mathematik, nennt aber mit den ganzen Zahlen auch ein für ihn platonisches Element.
Welche Sichtweise du der Mathematik gegenüber einnimmst, ist dir frei überlassen.[1]
Mathematik und die Natur
[Bearbeiten]Es ist tatsächlich bemerkenswert, dass sich die Natur durch unsere Mathematik sehr gut beschreiben lässt. Galileo Galilei schrieb dazu: „Das Buch der Natur ist mit mathematischen Symbolen geschrieben.“ Fast alle Wissenschaften nutzen die Mathematik, um mit ihr Modelle über ihr jeweiliges Forschungsfeld zu erstellen: Die Physik, die Chemie, die Biologie, die Wirtschaftswissenschaften und die Geographie zählen dabei noch zu den „direktesten Anwendern“. Jedoch praktisch alle empirischen Wissenschaften führen Beobachtungen durch und brauchen die Hilfsmittel der Statistik, um ihre Aussagen überprüfen zu können.
Dass sich die mehr oder weniger alltäglichen Phänomene mit Hilfe von Mathematik gut erklären lassen, mag vielleicht nicht verwundern: Schließlich wurde die Mathematik entwickelt, um solche Phänomene zu beschreiben. Es ist jedoch erstaunlich, wie universell die Methoden der Mathematik sind. Sie sind auch auf neuere Beobachtungen anwendbar und auf Phänomene, die nichts mit unserem Alltag zu tun haben: die Berechnungen von Planetenbahnen etwa oder elektromagnetische Felder und Ströme. Diese Dinge wurden entdeckt, als die Mathematik schon entwickelt war und nicht „mal eben angepasst“ werden konnte. Noch viel verblüffender ist die Tatsache, dass Mathematiker manchmal völlig abstrakte Konzepte entwickeln, ohne über eine mögliche Anwendung nachzudenken und diese Strukturen sich erst lange Zeit später in Naturbeobachtung wiederfinden, sozusagen „in der Natur realisiert“ sind. Hierfür gibt es streng genommen keinerlei logischen Grund. Schon Albert Einstein stellte sich die Frage, wie es kommt, dass die Mathematik „auf die Gegenstände der Wirklichkeit so vortrefflich passt.“
Viele mathematische Bereiche hängen auch sehr eng mit Naturbeobachtungen zusammen. Deswegen unterscheidet man häufig die reine von der angewandten Mathematik. Die Abgrenzung ist dabei oftmals unscharf, doch gibt es einige Forschungszweige, die man klar der einen oder der anderen Richtung zuweisen kann. „Algebra“ und „Zahlentheorie” zählen beispielsweise zur reinen Mathematik. Die Frage, wie man mit Hilfe von Computern am effizientesten Klimasimulationen durchführen kann, ist jedoch sicherlich angewandt und fällt in den Bereich der „Numerik“.
Teilgebiete der Mathematik
[Bearbeiten]Die ältesten Teilgebiete der Mathematik sind die Geometrie und die Zahlentheorie. Die Geometrie beschäftigt sich mit Figuren in der Ebene wie Dreiecken oder Kreisen und mit Körpern im Raum wie Pyramiden, Quadern oder Kugeln. Die Zahlentheorie, auch Arithmetik genannt, untersucht die Eigenschaften der Zahlen, vor allem der natürlichen Zahlen , und die damit verbundenen Rechengesetze. Diese beiden Teilgebiete werden schon seit tausenden von Jahren betrieben. Sie waren nicht nur den Babyloniern, den Ägyptern und den Griechen bekannt, sondern auch den Chinesen, Indern und den Mayas.
Die grundlegenden Gebiete der modernen Mathematik sind Analysis und Lineare Algebra. Sie werden an den Hochschulen in der Regel als mehrsemestrige Kurse angeboten. Schwerpunkt in der Analysis sind Grenzwertprozesse wie Ableitungen oder Integrale. Die Lineare Algebra behandelt demgegenüber Vektorräume und lineare Abbildungen zwischen diesen Vektorräumen.
Eine Sonderrolle als Teilgebiete der Mathematik spielen seit dem 20. Jahrhundert die Logik und die Mengenlehre. Sie haben eine Doppelrolle: sie sind einerseits Teilgebiete der Mathematik und nutzen mathematische Methoden, stellen aber andererseits die Grundlagen für die gesamte Mathematik zur Verfügung. Die rasante Entwicklung der Naturwissenschaften, der Technik und der Informatik machte ein Nachdenken über die Grundlagen der Mathematik, und damit eine Beschäftigung mit Logik und Mengenlehre, notwendig.
Aus den Anfängen der Mathematik hat sich eine Vielzahl von weiteren Teilgebieten entwickelt. Der Brockhaus[2] nennt 11 Teilgebiete:
- Geometrie
- Zahlentheorie
- Algebra
- Mengenlehre
- Logik
- Analysis
- Funktionentheorie, -analysis
- Topologie, Graphentheorie
- Wahrscheinlichkeitstheorie und Statistik
- Komplexitätstheorie
- Numerische Mathematik
Im Wikipedia-Artikel „Teilgebiete der Mathematik“ werden 21 Teilgebiete genannt.
In der Funktionentheorie werden komplexe Funktionen analysiert. Die Topologie beschäftigt sich mit der Verformung von Körpern, die Graphentheorie mit Knoten und Kanten. Die Wahrscheinlichkeitstheorie untersucht zufällige Ereignisse, die Statistik entwickelt Methoden zur Auswertung von Messdaten. In der Numerischen Mathematik werden Berechnungsverfahren ermittelt und die Komplexitätstheorie untersucht den Aufwand von Rechenverfahren.
Charakteristisch für die Mathematik sind fließende Übergänge von einem Teilgebiet zum anderen. Immer wieder werden die in einem Teilgebiet entwickelten Methoden auch in anderen Teilgebieten verwendet. Daher ist es kaum möglich, die Teilgebiete exakt voneinander abzugrenzen.
Aussagenlogik
[Bearbeiten]
In den beiden vorangegangenen Kapiteln hast du Aussagen und Junktoren kennengelernt. Mit Hilfe der Junktoren kann man aus Aussagen weitere Aussagen erzeugen. Wir hatten auch gesehen, dass in der Mathematik eine formalisierte Sprache benutzt wird. Das hat mehrere Gründe:
- Zum einen ist unsere natürliche Sprache nicht eindeutig. Die Eindeutigkeit der Begriffe und Zusammenhänge ist aber für die Mathematik ganz wesentlich.
- Zum anderen werden in der Mathematik viele abstrakte Sachverhalte beschrieben und analysiert, für die neue Begriffe mit einer genau festgelegten Bedeutung benötigt werden.
Deshalb benutzt die Mathematik eine künstliche Sprache, die als formale Sprache bezeichnet wird. Wir werden diese Sprache schrittweise vorstellen und beginnen damit in diesem Kapitel. Die weiteren Schritte folgen in der Prädikatenlogik und in der Klassenlogik.
Die folgenden Definitionen erscheinen sehr formal, insbesondere dann, wenn ihr zum ersten Mal damit konfrontiert werdet. Diese formale Strenge hilft jedoch dabei, Fehlschlüsse zu vermeiden und die Mathematik auf eine sichere Grundlage zu stellen.
Die Sprache der Aussagenlogik
[Bearbeiten]Für die Logik ist die formale Sprache besonders wichtig, denn mit Hilfe der Logik werden ja die mathematischen Beweise geführt. Beweise verlaufen nach ganz bestimmten Regeln. Das Einhalten dieser Regeln muss automatisiert nachprüfbar sein! Und das geht in einer formalisierten Sprache am besten. Die Sprache, in der Aussagen mit Junktoren verknüpft werden, ist die Sprache der Aussagenlogik. Wie unsere natürliche Sprache hat sie ein Alphabet:
Definition (Alphabet der Aussagenlogik)
Die Sprache der Aussagenlogik hat drei Arten von Zeichen:
- die Aussagenkonstanten , und ,
- die Junktoren , , , , und ,
- die Klammern und .
Die Zeichen heißen (Wahr) und (Falsch), die Junktoren (Negation), (Konjunktion), (Disjunktion), (Kontravalenz), (Implikation) und (Äquivalenz).
Anmerkung: Genau genommen bestehen die Konstanten selbst aus mehreren Zeichen, dem Buchstaben und einer Zahl. Wir wollen die Konstanten hier aber als eine Einheit betrachten. Es ist nicht weiter wichtig, wie sie genau realisiert werden. Wichtig ist nur, dass wir ausreichend viele Konstanten haben und bei Bedarf immer noch ein paar neue hinzunehmen können.
Aus diesen Zeichen können nach bestimmten Regeln Wörter gebildet werden, die in diesem Zusammenhang Formeln oder wohlgeformte Zeichenreihen genannt werden. Zeichenreihen entstehen einfach dadurch, dass Zeichen aus dem Alphabet hintereinander geschrieben werden, zum Beispiel so: . Aber das ist keine Formel!
Definition (Formeln der Aussagenlogik)
Die Formeln der Aussagenlogik werden nach folgenden Regeln gebildet:
- Jede Aussagenkonstante ist eine Formel, und sind Formeln.
- Ist eine Formel, so ist auch eine Formel.
- Sind und Formeln, so sind auch , , , und Formeln.
Es gibt keine weiteren Formeln.
Eine solche Definition wird rekursiv (lat. zurückgehend) genannt, weil bei der Erzeugung weiterer Formeln auf bereits erzeugte Formeln zurückgegriffen wird.
Beispiel für eine Formel
[Bearbeiten]Um zu zeigen, wie diese Regeln angewendet werden, zeigen wir, dass eine Formel der Aussagenlogik ist:
| Zeile | Formel | Begründung |
|---|---|---|
| 1 | nach Regel 1, ist eine Aussagenkonstante | |
| 2 | nach Regel 1, ist eine Aussagenkonstante | |
| 3 | nach Regel 3 angewendet auf Zeile 1 und 2 | |
| 4 | nach Regel 2 angewendet auf Zeile 3 | |
| 5 | nach Regel 3 angewendet auf Zeile 1 und 2 | |
| 6 | nach Regel 3 angewendet auf Zeile 4 und 5 |
Beweis über den Aufbau der Formeln
[Bearbeiten]Die rekursive Definition der Formeln erlaubt ein besonderes Beweisverfahren. Um eine Behauptung für alle Formeln zu beweisen, genügen zwei Schritte:
- Im ersten Schritt wird die Behauptung für die Aussagenkonstanten und für und gezeigt.
- Im zweiten Schritt wird gezeigt, dass sich die Behauptung unter den Regeln vererbt. Das heißt Folgendes:
- Wenn die Behauptung für eine Formel gilt, dann gilt sie auch für die Formel .
- Wenn die Behauptung für die Formeln und gilt, dann gilt sie auch für die Formel , , , und .
Es ist klar, dass die Behauptung dann für alle Formeln gelten muss, denn Formeln können ja nur aufgrund dieser Regeln entstehen! Wir zeigen als Beispiel den folgenden einfachen Satz:
Satz
Jede Formel enthält genauso viele linke wie rechte Klammern.
Beweis
- Für beliebige Aussagenkonstanten und für und ist das richtig, denn sie enthalten gar keine Klammern.
- Wenn genauso viele linke wie rechte Klammern enthält, dann gilt das auch für , denn bei der Bildung der Negation kommen keine Klammern dazu. Haben schließlich und jeweils gleich viele linke wie rechte Klammern, so kommen bei genau eine linke und eine rechte Klammer dazu. Also bleiben es gleich viele. So ist es auch bei den weiteren Regeln für , , und . ✔
Klammerersparnis, Schreibweisen
[Bearbeiten]Bei der Schreibweise von Formeln lassen wir die Außenklammern in der Regel weg und erlauben uns auch andere Freiheiten. Es muss nur immer klar sein, welche Formel im Sinne der obigen Definition gemeint ist. Natürlich übernehmen wir auch die Bindungsregeln aus dem Kapitel über Junktoren, um Klammern wegzulassen:
- Negation
- Konjunktion
- Disjunktion
- Implikation
- Äquivalenz
Falls es dem Verständnis dient, setzen wir auch zusätzliche Klammern.
Aussagen formalisieren
[Bearbeiten]Wir greifen nun einige Aussagen auf, die wir schon im Kapitel Junktoren angesprochen haben. Wenn wir Aussagen formalisieren, dann heißt das nichts anderes, als sie in eine Formel zu übersetzen, die der Aussage möglichst gut entspricht.
Beispiel 1: Zwei Aussagen werden mit dem Junktor und verbunden.
„ ist kleiner als und ist gerade.“
Zurzeit haben wir nur die Möglichkeit, die beiden Aussagen durch eine Konstante wiederzugeben, sagen wir durch („ ist kleiner als “) und („ ist gerade“). Dann lautet die formalisierte Aussage einfach:
Da es hierbei auf die Konstanten und gar nicht ankommt, verwendet man einfach auch die Variablen und und schreibt für die formalisierte Aussage. Wir wissen aber aus dem Zusammenhang, dass damit eine exakte Formel der Aussagenlogik gemeint ist.
Anmerkung: Wir werden in den Kapiteln Prädikatenlogik und Klassenlogik weitere Möglichkeiten kennenlernen, Aussagen besser zu formalisieren.
Verständnisfrage: Formalisiere die folgenden Aussagen:
- Wenn Berlin in Deutschland liegt und der Rhein durch Deutschland fließt, dann liegt Berlin am Rhein.
- Teilt eine natürliche Zahl , dann wird entweder von oder von geteilt.
- Es gibt unendlich viele Primzahlen.
Antwort:
- Sei Berlin liegt in Deutschland, Der Rhein fließt durch Deutschland, Berlin liegt am Rhein. Dann lautet die Formalisierung . Die Außenklammern haben wir nach der Klammerersparnisregel weggelassen.
- , wobei , und bedeuten. Hier haben wir für die Konstanten einfach anstelle von verwendet, weil ja klar ist, dass damit in diesem Zusammenhang Aussagenkonstanten gemeint sind.
- Diese Aussage enthält keine Junktoren. In der Aussagenlogik kann man sie nur durch eine Konstante formalisieren.
Teilformeln
[Bearbeiten]Beim rekursiven Aufbau einer Formel erhält man zwischendurch weitere Formeln. Diese Formeln werden Teilformeln genannt. Die genaue Definition ist natürlich ebenfalls rekursiv. Teilformeln, die keine echten Teilformeln haben, heißen atomare Formeln.
Definition (Teilformeln, atomare Formeln)
- Die Aussagenkonstanten und die Formeln und sind atomare Formeln und Teilformeln von sich selbst.
- Die Teilformeln von sind die Teilformeln von und selbst. Die Teilformeln von , , , und sind die Teilformeln von und , sowie und selbst.
Verständnisfrage: Welche Teilformeln hat die im Beispiel oben erstellte Formel ?
Antwort:
Atomere Formeln: und . Weitere Teilformeln: , , und die Formel selbst.
Junktor
[Bearbeiten]Junktoren sind bestimmte Symbole in der Aussagenlogik, die Aussagen miteinander verbinden oder in eine Beziehung stellen. Das Wort Junktor stammt vom lateinischen Wort „iungere“ ab, was so viel wie „verknüpfen, verbinden“ bedeutet. Junktoren kann man deshalb gut mit Bindewörtern vergleichen, wie sie in natürlichen Sprachen vorkommen (Beispiele für Bindewörter sind „und“, „oder“, „aber“). Während Junktoren in der Logik Aussagen miteinander verknüpfen, verbinden Bindewörter einzelne Satzteile in einer natürlichen Sprache. Dementsprechend gibt es (wie du noch sehen wirst) in der deutschen Sprache für Junktoren ein äquivalentes oder ähnliches Bindewort.
Es gibt aber einen entscheidenden Unterschied: Die Bedeutung eines Junktors ist eindeutig definiert, wohingegen Bindewörter oftmals eine unterschiedliche Bedeutung (je nach Kontext, in dem sie verwendet werden) besitzen. So bedeutet „oder“ im Satz „Gehst du nun ins Kino oder bleibst du zu Hause?“, dass die angesprochene Person die Entscheidung hat, entweder ins Kino zu gehen oder zu Hause zu bleiben (es geht nur eines von beiden). Im Satz „Er freut sich über seinen Lottogewinn oder seine neue Freundin“ besitzt „oder“ eher die Bedeutung eines „und/oder“ (die Person kann sich sowohl über den Lottogewinn als auch über die neue Freundin freuen). Im Satz „Gehst du nun ins Kino oder ins Restaurant?“ kann „oder“ sowohl ausschließend als auch einschließend gemeint sein.
Es ist wichtig, dass du die Definitionen und Eigenschaften der einzelnen Junktoren genau kennst (insbesondere diejenigen Eigenschaften, die scheinbar der Intuition widersprechen), da dir sonst leicht Fehler in der Anwendung passieren. Es ist auch wichtig, dass du klar zwischen Bindewörtern der natürlichen Sprache und aussagelogischen Junktoren unterscheidest.
Einführende Beispiele
[Bearbeiten]Nimm als Beispiel die folgenden zwei Aussagen:
Aussage : „ ist durch 2 teilbar.“
Aussage : „ ist gerade.“
Diese beiden Aussagen kannst du miteinander verknüpfen, indem du den Junktor „und“ verwendest. Du erhältst dadurch die Aussage: „ ist durch 2 teilbar und ist gerade.“ Beachte dabei, dass hier „und“ als Junktor verwendet wird. Du kannst aber auch die beiden Aussagen auf eine ganz andere Art und Weise miteinander verknüpfen, nämlich: „Wenn durch 2 teilbar ist, dann ist gerade.“ Hier ist der Junktor der „Wenn-dann“-Junktor, der beide Aussagen miteinander verknüpft. Beide Beispiele zur Übersicht:
Aussage „ und “:
Aussage „Wenn , dann “:
Für Junktoren werden Symbole verwendet. So ist für den Junktor „und“ das Symbol und für den „Wenn-dann“-Junktor das Symbol gebräuchlich. Damit können obige beide Aussagen folgendermaßen dargestellt werden:
Aussage „ und “:
Aussage „Wenn , dann “:
Offene Frage: Überlege dir einige mathematische Aussagen. Welche Verknüpfungen sind in diesen Aussagen enthalten? Welche verknüpften Teilaussagen kannst du ausmachen?
Verständnisfrage: Nimm den Satz: „Wenn eine natürliche Zahl ist und gerade ist, dann ist durch 2 teilbar.“ Wie kannst du diesen Satz in Teilaussagen und Junktoren zerlegen?
Und mit Symbolen:
Junktoren verbinden nur Aussagen
[Bearbeiten]Du solltest dir auch merken, dass Junktoren nur Aussagen miteinander verbinden. Die durch den Junktor verbundenen Teile müssen also selbst wieder Aussagen und keine Satzfragmente oder Ähnliches sein. Nimm hierzu den Beispielsatz:
„7 und 42 sind natürliche Zahlen.“
Hier ist „und“ kein Junktor! Wenn dem so wäre, dann müssten die Satzteile „7“ sowie „42 sind natürliche Zahlen“ Aussagen sein, was sie aber nicht sind:
Anders sieht die Sache aus, wenn man obigen Satz leicht umformuliert:
„7 ist eine natürliche Zahl und 42 ist eine natürliche Zahl.“
Hier ist „und“ ein Junktor, weil die einzelnen Teile wiederum Aussagen sind:
Du siehst an obigem Beispiel gut, dass nicht jedes Bindewort der natürlichen Sprache automatisch ein Junktor ist und dass sauber zwischen Junktoren und deren zugeordneter Übersetzung unterschieden werden muss.
Die Junktoren
[Bearbeiten]Im Folgenden stellen wir die für die Mathematik wichtigsten Junktoren vor. Um eine übersichtliche Notation zu erreichen, werden wir, wie es in der Mathematik üblich ist, als Platzhalter für Aussagen Großbuchstaben wie , und verwenden. Beachte, dass diese Platzhalter auch für Aussagen stehen können, die selbst wieder eine Verknüpfung von mehreren Aussagen sind. Neben jedem Junktor findest du eine sogenannte Wahrheitstabelle des jeweiligen Junktors. Sie gibt den Wahrheitswert der zusammengesetzten Aussage in Abhängigkeit der Wahrheitswerte der einzelnen Teilaussagen wieder. steht dabei für „wahr“ und steht für „falsch“.
Negation – die Verneinung einer Aussage
[Bearbeiten]Der erste Junktor, den wir vorstellen, ist die Verneinung einer Aussage, welche Negation genannt wird. Die Negation kehrt den Wahrheitswert einer Aussage um: Aus „wahr“ wird durch Negation „falsch“ und analog aus „falsch“ wird „wahr“. Mit anderen Worten: Eine negierte Aussage ist genau dann wahr, wenn die Aussage falsch ist. Dies kannst du auch rechts der Wahrheitstabelle zur Negation entnehmen. Das Symbol der Negation ist . Wenn du also die Verneinung einer Aussage ausdrücken möchtest, so schreibst du auf (gesprochen „nicht A“). Es gibt aber auch die Notation (gesprochen „A quer“) beziehungsweise , um die Negation von aufzuschreiben.

Es ist wichtig, dass du lernst, wie man eine Aussage richtig negiert. So ist zum Beispiel die Negation der Aussage „Es regnet“ nicht die Aussage „Es scheint die Sonne“, sondern die Aussage „Es regnet nicht“. Es könnte ja zum Beispiel sein, dass es bewölkt ist, es aber nicht regnet. Um eine logische Aussage zu negieren, gibt es einfache Umformungsregeln, die du beachten musst. Diese werden wir später im Kapitel „Aussagen negieren“ erklären.
Konjunktion – die Und-Verknüpfung
[Bearbeiten]Eine wichtige Verknüpfung zwischen zwei Aussagen und ist die Konjunktion, die Und-Verknüpfung „ und “. Das Symbol für „und“ ist (als Merkhilfe kannst du an ein großes A vom Englischen „and“ für „und“ denken). Wenn du also notieren möchtest, dass sowohl die Aussage als auch die Aussage wahr ist, schreibst du . Wie du aus der Wahrheitstabelle entnehmen kannst, ist eine Aussage dann und nur dann wahr, wenn sowohl als auch wahr sind. Wenn bereits eine der beiden Teilaussagen falsch ist, ist die gesamte Aussage falsch. Dies deckt sich mit dem alltäglichen Gebrauch des Bindewortes „und“.
Disjunktion – die Oder-Verknüpfung
[Bearbeiten]Außerdem kann man Aussagen noch über eine Oder-Verknüpfung miteinander verbinden. Dazu gibt es in der Logik die Disjunktion mit dem Symbol . Wenn du sagen möchtest, dass mindestens eine der beiden Aussagen , wahr ist, schreibst du („ oder “ ausgesprochen).
Beachte: In der Umgangssprache besitzt „oder“ zwei verschiedene Lesarten: So benutzen wir „oder“ im Sinne von „und/oder“ („Dieses Angebot richtet sich an junge Leute oder Kunstinteressierte.“) und in der Bedeutung als „entweder oder“ („Kommst du mit? Ja oder nein?“). Die Disjunktion ist das nicht-ausschließende Oder im Sinne von „mindestens“ („Der Bus hält, wenn jemand einsteigen oder jemand aussteigen will“).
Kontravalenz – die Entweder-oder-Verknüpfung
[Bearbeiten]Die Kontravalenz ist ein Junktor im Sinne einer Entweder-oder-Verknüpfung. Man benutzt für sie das Symbol („exklusiv oder“). Eine Aussage ist genau dann wahr, wenn entweder oder , aber nicht beide Aussagen gleichzeitig wahr sind. Die Kontravalenz entspricht damit dem ausschließenden Oder im Sinne von „Dieses Jahr gewinnt (entweder) Bayern oder Dortmund die deutsche Fußballmeisterschaft“. Die Kontravalenz wird in der Mathematik seltener verwendet als die Disjunktion.
Implikation – die Wenn-dann-Verknüpfung
[Bearbeiten]Eine wichtige Verknüpfung in der Aussagenlogik ist die Implikation, welche als Wenn-dann-Verknüpfung aufgefasst werden kann. Ihr Symbol ist ; weitere weniger gebräuchliche Schreibweisen sind und . So bezeichnet die Aussage „Wenn , dann “. Weitere Sprechweisen für sind „Aus folgt “, „ impliziert “, „ ist eine hinreichende Bedingung für “ und „ ist eine notwendige Bedingung für “. Dabei wird Prämisse und Konklusion genannt:

Die Bedeutung von ist demnach, dass wenn bereits die Aussage gilt, auch die Aussage gelten muss. Dabei muss aber kein kausaler Zusammenhang zwischen und vorliegen (was du vielleicht durch die Formulierung „Wenn , dann “ vermuten könntest). So ist die Aussage („Aus folgt “) eine wahre Aussage, auch wenn aus der Tatsache, dass ist, nicht kausal die Tatsache folgt, dass ist.
Leicht begeht man bei der Implikation den Fehler zu glauben, dass dann auch gelten müsse. So gehen einige davon aus, dass aus dem Satz „Wenn es regnet, ist die Straße nass“ folgen müsse, dass, wenn die Straße nass ist, es auch regne. Dies ist aber nicht der Fall! So kann die Straße aufgrund einer Straßenreinigung nass sein oder es kann vor kurzem geregnet haben, ohne dass es momentan regnet.
Warnung
Viele mathematische Sätze sind als Implikationen definiert (aus gewissen Bedingungen folgt eine Tatsache ). Deshalb ist es wichtig, dass du dir merkst, dass eine Implikation nicht umkehrbar ist (der Pfeil geht schließlich nur von nach und nicht umgekehrt). Sonst passiert es dir schnell, dass du Fehler in deinen Beweisen machst.
Frage: Überlege dir selbst mathematische Beispiele, mit denen du andere Leute überzeugen kannst, dass Implikationen im Allgemeinen nicht umkehrbar sind.
Ein Beispiel ist die Implikation „Wenn viel Schnee draußen liegt, ist es kalt“. Die Umkehrung wäre „Wenn es kalt ist, dann liegt Schnee draußen”. Nun hat jeder von uns schon kalte Tage ohne Schnee erlebt, womit die umgekehrte Implikation nicht wahr sein kann.
Ein weiteres Beispiel ist:
Die Umkehrung wäre die Aussage:
Wenn die Ableitung einer Funktion an der Stelle gleich null ist, dann ist in differenzierbar und besitzt in ein lokales Extremum.
Ein Gegenbeispiel ist die Funktion . Bei dieser Funktion ist die erste Ableitung bei null, da und ist, aber diese Funktion besitzt keine lokale Extremstelle bei .
Beachte auch, dass nach der Wahrheitstabelle die Implikation bereits dann wahr ist, wenn die Prämisse falsch ist. So ist die Aussage („Wenn ist, dann ist “) eine wahre Aussage, auch wenn ist. Dieses Prinzip der Implikation wird ex falso quodlibet genannt oder zu Deutsch: „Aus Falschem folgt Beliebiges.“ Demnach ist eine Implikation nur dann und genau dann falsch, wenn die Prämisse wahr ist und die Konklusion falsch ist. Diese Tatsache kann zu recht kontraintuitiven Aussagen führen, die aber dennoch wahr sind. Betrachte dazu folgende Verständnisfrage:
Verständnisfrage: Welche der folgenden Aussagen sind wahr und welche sind falsch?
- Wenn Berlin in England liegt, ist Schnee schwarz.
- Wenn Berlin in England liegt, ist Schnee weiß.
- Wenn Berlin in Deutschland liegt, ist Schnee schwarz.
- Wenn Berlin in Deutschland liegt, ist Schnee weiß.
- Wenn der Mond aus grünem Käse besteht, ist heute Sonntag.
Antwort: Die Aussagen (1) und (2) sind wahr, weil bereits die Prämisse „Berlin liegt in England“ falsch ist. Auch Aussage (4) ist wahr, weil sowohl die Prämisse als auch die Konklusion wahr ist. Nur Aussage (3) ist falsch (Prämisse ist wahr und Konklusion falsch). Aussage (5) ist an jedem Tag wahr.
Äquivalenz – die Genau-dann-wenn-Verknüpfung
[Bearbeiten]Der letzte Junktor, den wir vorstellen möchten, ist die Äquivalenz. Die Äquivalenz wird mit dem Doppelpfeil dargestellt. Die Sprechweise von ist dabei „Genau dann , wenn “, „ ist gleichwertig mit “ oder „ ist äquivalent zu “. Eine Aussage ist genau dann und nur dann wahr, wenn die beiden Aussagen und denselben Wahrheitswert besitzen. Ist eine der beiden Aussagen wahr und die andere falsch, ist falsch. Die Äquivalenz wird auch Bijunktion genannt.
Die Bedeutung der Aussage ist dabei, dass aus der Aussage die Aussage folgt und dass aus der Aussage die Aussage folgt. Dies erkennst du auch am Doppelpfeil – während bei der Äquivalenz der Pfeil von nach und umgekehrt geht, geht der Pfeil in der Implikation nur in eine Richtung (und zwar von der Prämisse zur Konklusion). Die Äquivalenz drückt damit eine Gleichwertigkeit zwischen zwei Aussagen aus, da zwei in Äquivalenz stehende Aussagen immer denselben Wahrheitswert besitzen (genau so ist die Äquivalenz definiert).
Verständnisfrage: Überlege dir Beispiele für eine Äquivalenzbeziehung.
Ein einfaches Beispiel aus der Mathematik ist
„Genau dann wenn durch 2 teilbar ist, ist gerade.“
Ein weiteres Beispiel aus dem Alltag ist
„Genau dann wenn Schaltjahr ist, hat der Februar 29 Tage.“
Ein Schaltjahr ist nämlich als ein solches Jahr definiert, wo der Februar 29 Tage hat[3].
Verständnisfrage: Sei . Ist dann notwendige oder hinreichende Bedingung von und wie sieht es umgekehrt aus?
Weil bei aus die Aussage folgt und umgekehrt, ist sowohl notwendige als auch hinreichende Bedingung für und umgekehrt.
Bindungsreihenfolge der Junktoren (Präzedenzregeln)
[Bearbeiten]Aus der Arithmetik kennst du bereits das Phänomen, dass bestimmte Operatoren stärker binden als andere. So bindet die Multiplikation stärker als die Addition („Punktrechnung geht vor Strichrechnung“). Beispielsweise muss man als lesen. Jedoch ist diese Bindungsreihenfolge in der Logik nicht immer komplett und du musst Klammern einsetzen, um dem Leser die richtige Bindungsreihenfolge zu zeigen. Folgende Bindungsreihenfolge ist aber allgemein akzeptiert:
Negation bindet stärker als Konjunktion und Disjunktion bindet stärker als Implikation und Äquivalenz
Manchmal wird auch eine vollständige Bindungsreihenfolge definiert. Diese lautet dann meistens (der am stärksten bindende Junktor steht am Anfang):
- Negation
- Konjunktion
- Disjunktion
- Implikation
- Äquivalenz
Die Kontravalenz hat keinen festen Platz in der obigen Liste. Sie bindet stärker als die Implikation und schwächer als die Negation. Wenn aber die Kontravalenz zusammen mit der Disjunktion oder der Konjunktion auftritt, solltest du deinen Ausdruck entsprechend Klammern[4].
Nach obiger Bindungsreihenfolge muss also die Aussage als gelesen werden. Ich empfehle dir aber (und werde dies auch im Buch umsetzen), bei der Unterscheidung der Bindung zwischen Konjunktion und Disjunktion sowie zwischen Implikation und Äquivalenz Klammern einzusetzen.
Wenn mehrere Implikationen nacheinander ohne Klammerung verwendet werden, gilt in der Literatur meistens folgende Definition:
Verständnisfrage: Wie musst du die Klammern in folgenden Ausdrücken richtig setzen (nach der vollständigen Liste zur Bindungsreihenfolge)?
Antwort:
Quantor
[Bearbeiten]Was sind Quantoren?
[Bearbeiten]Neben den Junktoren gibt es noch eine zweite wichtige Gruppe von logischen Symbolen, die Quantoren. Während Junktoren Aussagen miteinander verknüpfen, legen Quantoren fest, für welche Objekte einer Grundmenge eine Aussageform gilt. Eine Aussageform ist dabei ein sprachlich sinnvoller Ausdruck, in dem die Variable vorkommt und der durch Belegung dieser Variablen mit einem konkreten Wert in eine Aussage übergeht. So sind die Ausdrücke
ist eine gerade Zahl
und
ist ein Mensch
Beispiele für solche Aussageformen , die von der Variablen abhängen.
Wir möchten den Begriff „Quantor“ an einem Beispiel erklären. Stelle dir dazu vor, wir verwenden gerade die Menge der reellen Zahlen. Dies bedeutet, dass alle Variablen, die wir benutzen, nur mit reellen Zahlen belegt werden sollen. Betrachte nun folgende Aussage:
Für alle gilt, dass ist.
In diesem Beispiel ist „für alle“ ein Quantor, der Allquantor. Er behauptet, dass die Aussageform für alle Belegungen der Variablen wie zum Beispiel , oder gültig sein soll. Wir können also folgende Struktur der obigen Aussage erkennen:
Wie auch bei Junktoren werden für Quantoren bestimmte Symbole verwendet. Für den Allquantor ist das Symbol am geläufigsten. So kann die obige Aussage „Für alle gilt, dass ist“ auch so geschrieben werden:
Wir können aber auch andere Quantoren zur Bindung der Variablen in der Aussageform verwenden. Anstatt auszudrücken, dass die Aussageform für alle Belegungen von gültig ist, können wir auch sagen, dass diese Aussageform für mindestens eine reelle Zahl wahr ist. Dieser Quantor „es gibt mindestens ein“ wird Existenzquantor genannt und hat das Symbol . So besitzt die Aussage „Es gibt mindestens ein mit “ folgende Struktur:
Formal aufgeschrieben wird daraus:
Verständnisfrage: Sind obige Aussagen und für reelle Zahlen wahr oder falsch?
- Die Aussage ist falsch, da sie für die erlaubte Belegung nicht stimmt. Es ist nämlich .
- Die Aussage ist wahr. Die Zahl ist nämlich eine reelle Zahl mit . Damit existiert (mindestens) eine reelle Zahl, welche die Aussageform erfüllt.
Arten von Quantoren
[Bearbeiten]Allquantor
[Bearbeiten]| Symbol: | |
| Bedeutung: | „für alle“ oder „für jede(s)“ |
| Schreibweise: |
Im vorherigen Abschnitt hast du den Allquantor bereits kennen gelernt. Sein Symbol ist (ein umgedrehtes A – „für Alle“). Die Schreibweise des Allquantors ist . Dies bedeutet „Für alle gilt “ oder „Für jedes gilt “. Dabei ist eine beliebige Aussageform, in der die Variable vorkommt. In der Literatur ist auch die Schreibweise zu finden, die wir aber in diesem Projekt nicht verwenden werden.
Die Menge der Objekte, auf die sich der Quantor bezieht, muss eindeutig bestimmt sein (und kann sich zum Beispiel aus dem Kontext ergeben). Wenn du eben natürliche Zahlen behandelst, so behauptet eine Aussage , dass die Aussageform für alle Belegungen von aus den natürlichen Zahlen zu einer wahren Aussage wird. Untersuchst du reelle Zahlen, so behauptet , dass die Aussageform für alle reellen Zahlen zu einer wahren Aussage wird.
Wenn du die Bezugsmenge des Allquantors explizit angeben möchtest oder musst, kannst du die deutlichere Schreibweise verwenden. Sie ist eine Kurzschreibweise für und bedeutet: „Für alle aus der Menge gilt die Aussage .“
Aufgabe: Überlege dir einige (mathematische) Aussagen, in denen du den Allquantor verwenden kannst und schreib diese auf.
Folgende Beispiele können mit dem Allquantor aufgeschrieben werden:
- Für jedes Auto gilt: Es fährt oder es steht.
- Für alle reellen Zahlen und alle natürlichen Zahlen ist .
- Alle Schwäne sind weiß.
Aufgabe: Wie lauten die obigen Aussagen in Quantorenschreibweise?
Existenzquantor
[Bearbeiten]| Symbol: | |
| Bedeutung: | es existiert mindestens ein |
| Schreibweise: |
Dieser Quantor wird für Aussagen folgender Form verwendet: „Es gibt mindestens ein , so dass gilt“. Dieser Quantor heißt Existenzquantor. Sein Symbol ist ein horizontal gespiegeltes E, welches für „es Existiert mindestens ein“ steht. Analog zum Allquantor haben Existenzaussagen die Form . Diese Schreibweise steht für „Es gibt mindestens ein , so dass gilt“ oder „Es existiert mindestens ein , für welches gilt“. Auch hier ist eine Variable und eine Aussageform, die von abhängt. In der Literatur kannst du auch die Schreibweise finden.
Wie auch beim Allquantor muss die Bezugsmenge des Quantors klar sein (z. B. aus dem Kontext). Muss die Bezugsmenge explizit angegeben werden, so kannst du die Schreibweise verwenden. Sie ist eine Kurzschreibweise für und bedeutet: „Es gibt mindestens ein aus der Menge , für welches die Aussage wahr ist“.
Hinweis
In der Mathematik gibt es folgende Konvention: Eine Aussage der Form „Es gibt ein …“ ist immer als Aussage der Form „Es gibt mindestens ein …“ zu verstehen.
Verständnisfrage: Übersetze folgende Aussagen in die formelle Schreibweise mit dem Existenzquantor:
- Es gibt eine Zahl , so dass ist.
- Es gibt schöne Männer.
- Jeder Mensch besitzt einen Seelenverwandten.
Antwort:
Eindeutiger Existenzquantor
[Bearbeiten]| Symbol: | |
| Bedeutung: | es existiert genau ein |
| Schreibweise: |
Der letzte Quantor, den wir dir vorstellen möchten, ist der eindeutige Existenzquantor . Die Schreibweise zu diesem Quantor (der auch Eindeutigkeitsquantor genannt wird) ist . Dies bedeutet so viel wie
(*) Es gibt genau ein , so dass die Aussageform für dieses eine wahre Aussage ist.
Beachte den Unterschied zwischen dem Existenzquantor und dem eindeutigen Existenzquantor: Während beim Existenzquantor die Aussageform für mindestens eine Belegung von gilt, gilt beim eindeutigen Existenzquantor die Aussageform für genau eine Belegung von aus der Grundmenge.
Auch bei diesem Quantor muss sich die Bezugsmenge durch den Kontext ergeben. Wenn du sie explizit angeben möchtest, kannst du die Schreibweise verwenden. Sie ist eine Kurzschreibweise für und bedeutet: „Es gibt genau ein aus der Menge , für welches die Aussage wahr ist.“ Alternative und in der Literatur auch verbreitete Schreibweisen für den eindeutigen Existenzquantor sind und .
Verständnisfrage: Überlege dir, ob folgende Aussagen wahr sind:
Antwort:
- Wahr. Da und ist, gibt es mit mindestens eine reelle Zahl, deren Quadrat gleich 4 ist.
- Falsch. Es ist und . Somit gibt es kein eindeutiges Element mit .
- Wahr. ist nämlich die einzige natürliche Zahl, deren Quadrat gleich ist. Beachte hier, dass keine natürliche Zahl ist.
Der eindeutige Existenzquantor lässt sich mit Hilfe des Existenzquantors und des Allquantors beschreiben, nämlich so:
(**) Es gibt mindestens ein mit und wenn zwei Objekte und die Aussageformen und erfüllen, so sind sie gleich.
Die Formulierungen (*) und (**) beschreiben genau denselben Sachverhalt! Das ist der Grund dafür, dass der Quantor üblicherweise wie folgt definiert wird:
Definition (Eindeutiger Existenzquantor)
Damit ist auch klar, wie Aussagen mit zu beweisen sind:
- Zunächst wird bewiesen,
- anschließend wird gezeigt, dass aus und für beliebige und die Gleichheit folgt.
Notation
[Bearbeiten]Für Ausdrücke mit Quantoren werden in der Literatur verschiedene Schreibweisen verwendet[5]. So findet man anstelle vom Ausdruck auch die Notationen:
Gleiches gilt für den Existenzquantor :
Manchmal werden in der Literatur auch Existenzquantoren der Art bzw. verwendet. Ihre Bedeutung ist:
- bedeutet, es gibt genau Objekte mit der Eigenschaft
- bedeutet, es gibt höchstens Objekte mit der Eigenschaft
- bedeutet, es gibt mindestens Objekte mit der Eigenschaft
Wir werden in diesem Projekt aber die Schreibweise und verwenden. Auch kann man aufeinanderfolgende Quantoren vom selben Typ zusammenfassen, indem man die verschiedenen eingeführten Variablen durch Kommata trennt. So kannst du anstelle von auch folgende Schreibweise benutzen: . Analog kann man anstelle von auch kürzer schreiben.
Aussageform und Substitution
[Bearbeiten]Du hast dich vielleicht schon darüber gewundert, dass wir manchmal den Begriff „Aussage“ und manchmal den Begriff „Aussageform“ benutzen. Der Unterschied liegt darin, dass Aussageformen freie Variablen besitzen, während in Aussagen keine freien Variablen vorkommen. Doch was sind freie Variablen?
Freie und gebundene Variablen
[Bearbeiten]Variablen sind Platzhalter (Leerstellen) in einem sprachlichen Ausdruck, die für Elemente der Grundmenge stehen. Sie können durch Quantoren oder andere Operatoren gebunden werden. Die Bedeutung der gebundenen Variablen ist an den Operator gekoppelt, in dessen Wirkungsbereich sie liegen. So besagt , dass die Aussage zutrifft, egal welches Element aus dem Grundbereich für genommen wird. dagegen heißt nur, dass es wenigstens ein Element aus dem Grundbereich gibt, für das zutrifft. Eine Variable, die nicht gebunden ist, heißt frei.
So ist die Variable im Ausdruck frei und im Ausdruck durch den Allquantor gebunden. Aber nicht nur Quantoren können Variablen binden. Auch durch Mengenausdrücke der Form oder durch Summen können Variablen gebunden werden. Solltest du Summen oder Mengen noch nicht kennen: Kein Problem. Diese werden wir später behandeln. Generell gilt:
Definition (Freie und gebundene Variablen)
Eine Variable ist gebunden, wenn sie durch einen mathematischen Operator (z. B. einen Quantor) eingeführt wurde und im Wirkungsbereich dieses Operators liegt. Ansonsten ist eine Variable eine freie Variable.
Hier noch einige Beispiele:
Beispiel (freie und gebundene Variablen)
Verständnisfrage: Welche der Variablen in den folgenden Ausdrücken sind frei und welche sind gebunden?
Antwort:
Terme
[Bearbeiten]Variablen sind Platzhalter für Elemente aus einem Grundbereich. Grundbereiche in der Mathematik sind häufig die Zahlbereiche , , , oder . Es kann aber auch eine ganz andere Menge der Grundbereich sein, beispielsweise die Menge aller Menschen, Autos oder Musikinstrumente. Ausdrücke, die Elemente aus dem Grundbereich bezeichnen, werden Terme genannt. Mit Hilfe von Operationssymbolen (auch Verknüpfungen genannt) wie , und werden aus Termen weitere Terme gebildet. Zu einem Operationssymbol gehört eine natürliche Zahl als Stellenzahl, die angibt, wie viele Terme zu einem neuen Term verknüpft werden. Die Terme, die verknüpft werden, heißen Argumente, das Ergebnis der Verknüpfung Resultat.
Beispiel (Operationssymbole)
- Das Pluszeichen „“ ist 2-stellig und macht aus zwei Zahlen eine dritte, die Summe: .
- Das Vorzeichen „“ ist 1-stellig: . Das Subtraktionszeichen „“ dagegen ist 2-stellig: .
- Beim größten gemeinsamen Teiler „“ und beim kleinsten gemeinsamen Vielfachen „“ werden die Argumente in der Regel dahinter notiert: und .
- Die Potenz ist 2-stellig, aber das Operationssymbol wird gar nicht notiert. Stattdessen wird die Verknüpfung durch das Hochstellen widergegeben: .
- Der Durchschnitt „“ und die Vereinigung „“ von Mengen sind 2-stellige Verknüpfungen: und .
- Das Komplement einer Menge „“ ist 1-stellig und wird häufig hochgestellt hinter dem Argument notiert: .
- Bei mehrstelligen Verknüpfungen stehen die Argumente in Klammern hinter dem Symbol:
Bei 2-stelligen Operationssymbolen werden die Klammern weggelassen, wenn sie nicht erforderlich sind.
Definition (Term)
Terme sind sprachliche Ausdrücke, die eine Zahl oder ein anderes Objekt bezeichnen. Insbesondere sind Variable Terme. Mit Hilfe von Verknüpfungen können aus Termen weitere Terme gebildet werden.
Terme treten oftmals als Teile von Aussagen auf.
Beispiel (Terme)
Einige Terme aus diesen Beispielen enthalten weitere Terme: So enthält der Term „“ die Terme „“ und „“ und der Term „“ enthält die Terme „“ und „“.
Prädikate
[Bearbeiten]Von Verknüpfungen sind Prädikate (auch Relationssymbole genannt) zu unterscheiden. Prädikate haben wie Verknüpfungen eine Stellenzahl. Die Argumente von Prädikaten sind ebenfalls Terme, aber das Resultat ist eine Aussage oder eine Aussageform. Beispiele für Prädikate sind größer-gleich () und die Teilmengenbeziehung ().
Definition (Prädikat)
Prädikate verbinden Terme zu Aussagen bzw. Aussageformen. Sie haben eine Stellenzahl. Ist ein -stelliges Prädikat, so heißt , dass auf zutrifft. 2-stellige Prädikate werden meist zwischen die Argumente geschrieben.
Hinweis
Die Schreibweise von Prädikaten ist genau dieselbe wie bei Verknüpfungen! Es muss also aus dem Zusammenhang erschlossen werden, was von beiden gemeint ist.
Beispiel (Prädikat)
Aussageformen, Formeln
[Bearbeiten]Mit Hilfe der Begriffe freie und gebundene Variable können wir definieren, was Aussageformen sind:
Definition (Aussageform, Formeln)
Aussageformen sind sprachliche Ausdrücke mit freien Variablen, die durch Belegung dieser Variablen mit konkreten Werten in eine Aussage übergehen.
Als Oberbegriff von Aussagen und Aussageformen ist die Bezeichnung Formel üblich:
Definition (Formel)
Eine Formel ist eine Aussage oder eine Aussageform und damit ein Oberbegriff für beide Konzepte. Jede Formel ist damit entweder eine Aussage oder eine Aussageform.
Verständnisfrage: Welche der folgenden formalen Ausdrücke sind Aussagen und welche sind Aussageformen?
Antwort:
- Aussageform ( und kommen frei im Ausdruck vor)
- Aussageform ( kommt frei im Ausdruck vor)
- Aussage (keine freien Variablen)
- Aussageform ( kommt frei im Ausdruck vor)
- Aussage (keine freien Variablen)
Der Wahrheitsgehalt der obigen Aussagen und Aussageformen hängt jeweils von der gewählten oder vorgegebenen Grundmenge ab.
Substitution von Termen für Variablen
[Bearbeiten]Ersetzt man in einem Ausdruck eine freie Variable durch einen Term, so nennt man diesen Vorgang Substitution. Das kommt beispielsweise beim Lösen von Gleichungssystemen vor. Beispiel:
Aus der 2. Gleichung erhalten wir , was wir als Substitution nutzen können. Daher ersetzen wir in Gleichung 1. die Variable durch den Term und erhalten so: , woraus sich schließlich ergibt.
Beim Substituieren musst du darauf achten, dass du nur und wirklich nur freie Variablen durch den entsprechenden Term ersetzt. Gebundene und quantifizierte Variablen müssen unangetastet bleiben. Beispiel:
Beachte, dass die gebundene Variable nicht verändert wurde. Wenn im Substitutionsterm freie Variablen vorkommen, die in der Aussageform bereits gebunden sind, dann müssen diese gebundenen Variablen umbenannt werden. Es dürfen nämlich durch die Substitution keine Variablen gebunden werden, die vorher frei waren:
Im obigen Beispiel wird durch die Substitution die freie Variable neu eingeführt. Jedoch ist in der ursprünglichen Aussageform bereits durch den Existenzquantor gebunden. Deswegen muss die gebundene Variable umbenannt werden (hier in die Variable ). Würde man dies nicht tun, dann würde die freie Variable ebenfalls gebunden werden, was bei einer Substitution nicht erlaubt ist.
Definition (Substitution)
Gegeben sei ein Ausdruck mit der freien Variablen und ein beliebiger Term . Dann entsteht der Ausdruck durch die Substitution dadurch, dass alle Vorkommen von durch ersetzt werden. Sollten durch die Substitution freie Variable gebunden werden, so sind die gebundenen Variablen vorher umzubenennen.
Eine andere Schreibweise für diese Substitution ist , für den substituierten Term .
Verständnisfrage: Wie lauten folgende Aussageformen beziehungsweise Aussagen nach der Substitution?
- für die Substitution
- für die Substitution
- für die Substitution
- für die Substitution
Antwort:
- . In der Aussage ist keine freie Variable und kann daher nicht ersetzt werden.
Verständnisfrage: Wieso können sich Aussagen durch eine Substitution nicht ändern?
Weil Aussagen per Definition keine freien Variablen besitzen und nur freie Variable substituiert werden, bleiben Aussagen bei einer Substitution unverändert.
Tautologie
[Bearbeiten]Tautologie
[Bearbeiten]
Es gibt Aussagen, die sind immer wahr. Das klassische Beispiel hierfür ist die Bauernregel: „Wenn der Hahn kräht auf dem Mist, dann ändert sich das Wetter oder es bleibt wie es ist.“ stehe für die Aussage „Der Hahn kräht auf dem Mist“ und für „Das Wetter ändert sich“, dann können wir diese Bauernregel folgendermaßen formalisieren:
Da Aussagen entweder „wahr“ oder „falsch“ sind, ist leicht zu sehen, dass die Bauernregel immer wahr ist. Dabei kommt es überhaupt nicht darauf an, ob der Hahn kräht oder nicht. Denn oder – eine dieser beiden Aussagen ist wahr. Es spielt auch keine Rolle, was genau mit gemeint ist: es muss nur eine Aussage sein! könnte auch für die Behauptung stehen: „Es gibt kleine, grüne Männchen auf dem Mars.“
Woran liegt es, dass diese Aussage immer wahr ist? Es liegt daran, wie die Aussage mit Junktoren aus Teilaussagen zusammengebaut ist. Wir wissen, dass die Negation den Wahrheitswert umdreht: aus wird und umgekehrt aus wird . Die Oder-Verbindung wird wahr, wenn eine der beiden Teilaussagen wahr ist. Also ist immer wahr. Die Implikation ist nur dann falsch, wenn die Prämisse wahr ist und die Konklusion falsch ist. In unserem Beispiel aber ist die Konklusion immer wahr. Daher ist auch immer wahr. Mit Junktoren zusammengesetzte Aussagen, die immer wahr sind, werden Tautologien oder auch allgemeingültige Aussagen genannt:
Definition (Tautologie)
Eine mit Junktoren zusammengesetzte Aussage heißt tautologisch oder allgemeingültig, wenn sie bei jeder möglichen Interpretation seiner Teilaussagen mit Wahrheitswerten wahr ist.
Besonders wichtige Tautologien sind Äquivalenzen. Zwei Aussagen und sind nämlich genau dann äquivalent, wenn die zusammengesetzte Aussage eine Tautologie ist. Das wird oft bei Beweisen genutzt. Statt direkt die Aussage zu beweisen, wird eine dazu äquivalente Aussage gezeigt.
Beispiel (Äquivalente Aussagen)
Die folgenden drei Aussagen sind äquivalent:
- (Kontraposition)
- (Widerspruchsbeweis)
Es sind also tautologisch:
Eine alternative Formulierung des Widerspruchbeweises ist im Übrigen .
Überprüfung einer Tautologie
[Bearbeiten]Wir werden jetzt drei Möglichkeiten vorstellen, wie du überprüfen kannst, ob eine Aussage eine Tautologie ist oder nicht. Alle diese Möglichkeiten sollen am Beispiel der Kontraposition demonstriert werden.
Wahrheitstabelle erstellen
[Bearbeiten]Eine Methode ist es, eine Wahrheitstabelle für die zu untersuchende Aussage aufzustellen, vgl. Kapitel „Wahrheitstabelle“. Wenn in der letzten Spalte der Wahrheitstabelle nur „wahr“ als resultierender Wahrheitswert auftritt, ist die untersuchte Aussage eine Tautologie. Sobald ein resultierender Wahrheitswert „falsch“ ist, ist die Aussage keine Tautologie.
Aufgabe: Stelle die Wahrheitstabelle für auf.
Ergebnis: Die Aussage ist eine Tautologie.
Aufgabe: Stelle die Wahrheitstabelle für auf.
Ergebnis: Die Aussage ist keine Tautologie.
Aufgabe: Stelle die Wahrheitstabelle für auf.
Ergebnis: Die Aussage ist eine Tautologie.
Aufgabe: Stelle die Wahrheitstabelle für auf.
Ergebnis: Die Aussage ist eine Tautologie.
Äquivalenzumformungen verwenden
[Bearbeiten]Wenn du die Tautologie einer Äquivalenz beweisen musst, kannst du versuchen, die Aussage durch bereits bekannte Äquivalenzbeziehungen in die Aussage umzuformen. Für unser Beispiel nehmen wir an, dass wir die folgenden Äquivalenzen bereits kennen:
- (Umformung der Implikation)
- (Kommutativität von )
Mit diesen beiden Äquivalenzen können wir die Kontraposition beweisen:
Baummethode
[Bearbeiten]Diese Methode ist eine Art des Widerspruchsbeweises. Du beweist hier, dass eine Aussage eine Tautologie ist, indem du zeigst, dass diese Aussage nie falsch sein kann, weil sich sonst ein Widerspruch ergibt. Dabei zerlegst du die zu untersuchende Aussage schrittweise in ihre Teilaussagen und schaust dir nur diejenigen Fälle an, die zu einer falschen Aussage führen würden.
Nehmen wir an, dass falsch ist. Dann muss entweder falsch sein und wahr sein oder umgekehrt. Im ersten Fall muss und sein. Dies ist aber ein Widerspruch dazu, dass wahr ist (weil für und die Aussage falsch ist).
Im zweiten Fall muss und sein. Dies bedeutet und . Aber auch das führt zu einem Widerspruch, weil ist (für und ist die Aussage falsch). Schematisch könnte man dies in einem Baum darstellen (deswegen auch der Name). Dabei stellt jeder Ast einen zu betrachtenden Fall dar:
Liste von Tautologien
[Bearbeiten]Assoziativgesetze
[Bearbeiten]Bei der Disjunktion und bei der Konjunktion ist es egal, in welcher Reihenfolge du die Aussagen auswertest:
Kommutativgesetze
[Bearbeiten]Bei der Disjunktion und bei der Konjunktion ist es egal, in welcher Reihenfolge die einzelnen Teilaussagen verknüpft werden. Dies ist in der deutschen Sprache nicht unbedingt der Fall. Betrachte dazu folgende zwei Aussagen, welche in der Bedeutung einen leichten Unterschied aufweisen: „Ralf aß Haferbrei und er bekam Bauchschmerzen“ und „Er bekam Bauchschmerzen und Ralf aß Haferbrei“.
Distributivgesetze
[Bearbeiten]Eine Disjunktion kann in eine Konjunktion hineingezogen werden und umgekehrt.
Absorptionsgesetze
[Bearbeiten]Idempotenzgesetze
[Bearbeiten]Doppelte Verneinung
[Bearbeiten]Satz vom ausgeschlossenen Dritten
[Bearbeiten]- (lateinisch: tertium non datur, übersetzt: ein Drittes gibt es nicht.)
Satz vom Widerspruch
[Bearbeiten]Durch Anwendung der de Morganschen Regel, der doppelten Verneinung und der Kommutativität lässt sich der Satz vom Widerspruch in den Satz vom ausgeschlossenen Dritten umformen:
Die de-Morgansche Regel
[Bearbeiten]Bei der Negation einer Und- beziehungsweise einer Oder-Verknüpfung wird die Negation reingezogen und die Klammer aufgelöst. Aus einem wird dabei ein und umgekehrt.
Negation von Implikation und Äquivalenz
[Bearbeiten]Prinzip der Kontraposition
[Bearbeiten]Diese Äquivalenz wird oft genutzt, um eine Implikation zu beweisen, Redewendung: Beweis der Kontraposition.
Beweis durch Widerspruch
[Bearbeiten]Auch mit Hilfe der folgenden Äquivalenz kann eine Implikation bewiesen werden, Redewendung: Beweis durch Widerspruch.
Darstellung von Implikation und Äquivalenz
[Bearbeiten]Mit Hilfe dieser Gesetze kann die Implikation und die Äquivalenz auf Aussagen mit anderen Junktoren zurückgeführt werden.
Gesetze mit Wahr und Falsch
[Bearbeiten]Im Folgenden steht für „wahr“ und für „falsch“. und können als 0-stellige Junktoren angesehen werden.
- (Aus Falschem folgt Beliebiges.)
- (Wird gelegentlich als Definition für verwendet.)
Aussagen formalisieren
[Bearbeiten]Wir möchten nun zeigen, wie Aussagen in natürlicher Sprache in die formale Schreibweise der Logik übersetzt und wie umgekehrt formale Ausdrücke in die natürliche Sprache umformuliert werden können. Hier kann wie beim Lernen einer Fremdsprache vorgegangen werden: Die einzelnen Wörter und Satzfragmente in natürlicher Sprache übersetzt man in die dazu äquivalente Form der Logik und umgekehrt. Dabei werden zur Übung auch Ausdrücke betrachtet, wie sie in der Analysis 1 betrachtet werden.
Vokabelliste
[Bearbeiten]Die folgende Vokabelliste listet Satzfragmente in natürlicher Sprache mit ihren Übersetzungen in der formalen Ausdrucksweise der Logik gleich:
| natürliche Sprache | formale Schreibweise |
|---|---|
| nicht | |
| und | |
| oder („oder“ im Sinne von „und/oder“) | |
| Wenn , dann | |
| dann, wenn | |
| Aus folgt | |
| impliziert | |
| ist hinreichend für | |
| ist notwendig für | |
| Genau dann , wenn | |
| Dann und nur dann , wenn | |
| ist gleichwertig mit | |
| ist äquivalent zu | |
| ist notwendig und hinreichend für | |
| Für alle ist | |
| Jedes erfüllt | |
| Es ist für alle | |
| Für alle aus ist | |
| Jedes der Menge erfüllt | |
| Es ist für alle | |
| Für alle ab ist | |
| Jedes größer oder gleich erfüllt | |
| Es gibt ein mit | |
| Es existiert ein , so dass gilt | |
| Für mindestens ein gilt | |
| Es gibt ein aus mit | |
| Für mindestens ein gilt | |
| Es gibt ein ab mit | |
| Für wenigstens ein ab gilt | |
| Es gibt genau ein mit | |
| Es existiert genau ein , so dass gilt | |
| Für genau ein gilt | |
| Es gibt genau ein aus mit | |
| Für genau ein gilt |
Beispiele
[Bearbeiten]Übersetzung von formaler in natürliche Sprache
[Bearbeiten]Wir möchten dir an Beispielen zeigen, wie du die obige Vokabelliste anwenden kannst, um Aussagen aus der formalen in die natürliche Sprache zu übersetzen.
Beispiel (Beispiel 1: Übersetzung von formaler in natürliche Sprache)
Wir übersetzen nun die Aussage schrittweise in natürliche Sprache:
Beispiel (Beispiel 2: Übersetzung von formaler in natürliche Sprache)
Das folgende Beispiel zeigt die schrittweise Übersetzung der Aussage
in die Aussage „Für jede reelle Zahl gibt es eine reelle Zahl mit “:
Übersetzung von natürlicher in formale Sprache
[Bearbeiten]Bei der Übersetzung einer Aussage aus natürlicher Sprache in die formale Schreibweise gehen wir die umgekehrte Richtung der obigen beiden Beispiele. Auch hier kann mit Hilfe der Vokabelliste schrittweise die Aussage übersetzt werden. Gegebenenfalls müssen wir die Aussage zunächst umformulieren, damit die Regeln aus der Vokabelliste anwendbar sind. Das folgende Beispiel demonstriert eine solche Übersetzung:
Beispiel (Übersetzung von natürlicher in formale Sprache)
Das folgende Beispiel demonstriert die Formalisierung der Aussage „Alle ungeraden Zahlen ab 3 sind Primzahlen“. Dabei nutzen wir das Prädikat , welches für „ ist eine Primzahl“ steht:
Übungsaufgaben
[Bearbeiten]Verständnisfrage: Übersetze folgende Aussagen der formalen Logik in die natürliche Sprache
1. Aussage:
2. Aussage:
3. Aussage:
Verständnisfrage: Übersetze folgende Aussagen der natürlichen Sprache in die formale Schreibweise der Logik
- Zu jedem gibt es ein , so dass für alle die Ungleichung erfüllt ist.
- Zu jedem und gibt es ein , so dass für alle mit .
- Für jeden Menschen gibt es einen anderen, der ihn liebt.
Antwort:
Häufige Fehler beim Übersetzen
[Bearbeiten]| Aussage in natürlicher Sprache | Erklärung | ||
|---|---|---|---|
| und sind reelle Zahlen. | Der Junktor kann nur Aussagen miteinander verbinden. | ||
| Für alle natürlichen Zahlen und ganzen Zahlen gilt … | Wird „und“ für eine Aufzählung benutzt, dann darf es nicht mit übersetzt werden. | ||
| Für alle mit gilt … | oder auch |
Das Symbol aus der Mengenschreibweise kann nicht für Aussagen eingesetzt werden. Hier ist eine Implikation notwendig. | |
| Es ist für alle . | . | . | Die Quantoren müssen immer vor dem Ausdruck stehen, den sie quantifizieren. |
Aussagen negieren
[Bearbeiten]In diesem Kapitel werden wir dir erklären, wie du mathematische Aussagen und Aussageformen negieren kannst. Hierzu werden wir den Weg über die formale Schreibweise gehen, weil Ausdrücke dieser Schreibweise leichter zu negieren sind. Das liegt daran, dass Aussagen in der formalen Schreibweise durch einfache Umformungsregeln negiert werden können. Dies ist deutlich einfacher als Ausdrücke intuitiv zu negieren.
Du kannst ja einmal versuchen, folgende Beispiele zu negieren. Du wirst sehen, dass die intuitive Negation nicht einfach ist (an dieser Stelle wird nicht erwartet, dass du bereits die folgenden Ausdrücke negieren kannst). Die ersten beiden Aussageformen stammen im Übrigen aus der Analysis 1 und werden dir damit im weiteren Studium durchaus begegnen. Versuche also mal folgende Ausdrücke zu negieren:
- Zu jedem gibt es ein , sodass für alle die Ungleichung erfüllt ist.
- Zu jedem und gibt es ein , sodass für alle mit .
- Für jeden Menschen gibt es einen anderen, der ihn liebt.
Die Negation dieser Ausdrücke findest du später im Abschnitt „Beispiele“.
Allgemeine Vorgehensweise
[Bearbeiten]Um nun eine in natürlicher Sprache gegebene Aussage zu negieren, kannst du folgendermaßen vorgehen:
Sollte die Aussage in formaler Schreibweise vorliegen, dann entfallen der erste und der letzte Schritt. Diese beiden Schritte, also die Übersetzung von natürlicher in formale Schreibweise und umgekehrt, erklären wir dir im Kapitel „Aussagen formalisieren“.
Umformungsregeln zum Negieren
[Bearbeiten]Wie wir bereits gesagt haben, gelten Regeln zur Negation von Aussagen in formaler Schreibweise. Diese sind:
| Form der Negation | umgeformte Aussage | Bedeutung |
|---|---|---|
| Nicht oder nicht . | ||
| Nicht und nicht . | ||
| Obwohl , gilt nicht . | ||
| Entweder oder (aber nicht beides gleichzeitig). | ||
| Genau dann , wenn nicht . | ||
| Genau dann nicht , wenn . | ||
| Es gibt ein mit nicht . | ||
| Es gibt ein mit nicht . | ||
| Für alle ist nicht . | ||
| Für alle ist nicht . | ||
| Für jedes gilt: hat nicht die Eigenschaft oder es gibt ein von verschiedenes mit der Eigenschaft . | ||
| Es gibt kein oder mindestens zwei mit . |
Wieso sind die Umformungsregeln so? Das liegt daran, dass die Aussagen der ersten Spalte äquivalent zu den Aussagen der zweiten Spalte sind. Dies bedeutet, dass die Aussagen der ersten Spalte genau dann wahr sind, wenn die entsprechenden Aussagen der zweiten Spalte wahr sind. Wenn du dir die umgeformten Aussagen anschaust, dann siehst du, dass die Negation in den Teilaussagen weitergereicht wird. So können die Ausdrücke schrittweise durch die Umformungsregeln negiert werden, bis am Ende die Negationszeichen ganz innen stehen.
Bei der Negation der Äquivalenz kannst du dir im Übrigen aussuchen, ob du diese Aussage zu oder zu oder zu umformst. Die erste Umformung ist einfacher, verwendet aber die Kontravalenz . Diese wird in der Mathematik nicht häufig verwendet und möglicherweise wurde sie nicht in deiner Vorlesung besprochen.
Zur Regel mit dem eindeutigen Existenzquantor
[Bearbeiten]Bei der Regel mit dem eindeutigen Existenzquantor haben wir ausgenutzt, dass wir auch folgendermaßen schreiben können:
Diese Aussage kann nun mit den anderen Umformungsregeln negiert werden, sodass man dann am Ende erhält:
Man kann auch einen anderen Weg gehen: Man fängt mit der Aussage
„Es gibt genau ein mit .“
an und negiert diese intuitiv zu
„Es gibt kein oder mindestens zwei mit .“
Diese Aussage in der Prädikatenlogik formalisiert lautet
Dies ist dann die zweite Möglichkeit, um einen Ausdruck mit einem eindeutigen Existenzquantor zu negieren.
Beispiele
[Bearbeiten]Ausführliches Beispiel
[Bearbeiten]Betrachten wir zunächst folgende Aussage
„Zu jedem gibt es ein , das kleiner als ist.“
Diese lässt sich mit den Methoden aus dem Kapitel „Aussagen formalisieren“ umschreiben. Die formalisierte Aussage lautet
Diese lässt sich nun schrittweise negieren, indem die obigen Umformungsregeln verwendet werden:
Das Ergebnis ist damit die Aussage . Die Negation der obigen wahren Aussage führt damit zu der falschen Aussage:
„Es gibt ein , so dass alle größer oder gleich sind.“
Beispiele aus der Einleitung
[Bearbeiten]Betrachten wir nun das erste Beispiel aus der Einleitung:
Zu jedem gibt es ein , sodass für alle die Ungleichung erfüllt ist.
Zum Negieren der Aussage gehen wir schrittweise wie im ersten Beispiel vor:
Übungsaufgabe
[Bearbeiten]Aufgabe
Negiere folgende Aussagen:
- Für alle gibt es ein , sodass .
- Für alle und gibt es ein , sodass für alle mit .
- Für jeden Menschen gibt es einen anderen, der ihn liebt.
Lösung
Erste Aussage:
Zweite Aussage:
Dritte Aussage:
Vierte Aussage:
Beweis
[Bearbeiten]Was sind Beweise?
[Bearbeiten]
Ein Beweis ist eine fehlerfreie Herleitung eines mathematischen Satzes aus Axiomen und bereits bewiesenen Aussagen. Er besteht aus endlich vielen Teilschritten, wobei bei jedem Teilschritt streng logisch eine neue Aussage aus den vorhergehenden Aussagen geschlossen wird. Beweise spielen damit eine wichtige Rolle in der Mathematik, denn jeder neue Satz einer Theorie muss durch einen Beweis begründet werden. Um Sätze beweisen zu können oder auch Beweise nachvollziehen zu können, ist es notwendig, die Beweistechniken zu kennen.
Wie ist ein Beweis aufgebaut? Die Voraussetzungen, von denen wir beim Beweis eines Satzes ausgehen, nennt man Prämissen. Dies sind Aussagen, die entweder Axiome der Theorie oder bereits bewiesene Sätze sind. Aus diesen Prämissen werden nun durch logische Schlussfolgerungen weitere Aussagen hergeleitet, aus denen wiederum durch logische Schlussfolgerungen neue Aussagen hergeleitet werden usw. Am Ende dieser Herleitungen steht die zu beweisende Aussage. Durch einen solchen Beweis (der in der rechten Abbildung skizziert ist) hat man nun folgende Aussage bewiesen:
Wie können logische Schlussfolgerungen aussehen? Stelle dir vor, du hast bereits die Implikation „Wenn , dann “ als Satz in deiner Theorie bewiesen oder es ist ein Axiom deiner Theorie oder eine Tautologie. Nimm außerdem an, du hast die Aussage bereits hergeleitet oder sie ist eine Prämisse deines Beweises. Da nun sowohl die Aussage als auch die Aussage „Wenn , dann “ gilt, kannst du dir aus beiden Aussagen die Aussage logisch erschließen und deinem Beweis hinzufügen.
Neben Implikationen können auch Äquivalenzen zur logischen Schlussfolgerung herangezogen werden. Denn wenn eine Äquivalenz gilt, so gilt sowohl die Implikation als auch die Implikation , die für logische Schlussfolgerungen nach dem obigen Prinzip verwendet werden können.
Das Ende eines Beweises wird oft durch „qed“ gekrönt. Dies steht für quod erat demonstrandum und bedeutet so viel wie „was zu beweisen war“. Auch die Symbole □ bzw. ■ sind als Markierungen für ein Beweisende verbreitet.
Beispiel
[Bearbeiten]Stelle dir vor, du möchtest folgenden Satz beweisen:
Dabei sind , und reelle Zahlen. Bei diesem Satz ist Prämisse und die zu beweisende Aussage. Wenn der Satz direkt bewiesen wird, so sieht der Beweis folgendermaßen aus (im nächsten Kapitel wird beschrieben, was ein „direkter Beweis“ ist):
Wir stellen dir nun einen möglichen Beweis für obigen Satz vor. Wundere dich nicht, wenn der Beweis „vom Himmel zu fallen“ scheint. Im nächsten Abschnitt werden wir erklären, warum der Beweis so aufgebaut werden musste. Dort erklären wir auch, wie man den Beweis selbst finden kann. Lies dir also erst einmal nur den Beweis durch und versuche, dessen Schlussfolgerungen nachzuvollziehen.
Beweis
Es ist (Quadratzahlen sind stets nichtnegativ). Diese Ungleichung lässt sich umformen:
Nun ist nach Voraussetzung , also . Wenn wir nun für die Variable einsetzen, erhalten wir die Ungleichung:
Dieser Beweis lässt sich folgendermaßen in einem Diagramm skizzieren:

Wenn Beweise vom Himmel fallen
[Bearbeiten]Vielleicht kennst du dieses Gefühl: Du lernst gerade einen neuen Beweis kennen und fragst dich, wie der Autor sich den Beweis „ausgedacht“ hat. Der Beweis scheint vom Himmel gefallen zu sein oder einem göttlichen Einfall entsprungen.
Bevor du dir das nächste Mal diese Frage stellst, solltest du dir Folgendes vor Augen halten: Der Beweis ist eine fehlerfreie Herleitung der Richtigkeit einer Aussage. Es ist kein Lösungsweg, sondern nur das Endergebnis eines Lösungsweges. Beweise erklären in der Regel nicht, wie man diese gefunden hat oder finden kann. Durch Beweise können zwar mathematische Konzepte und Zusammenhänge erklärt werden, dies ist aber kein wesentliches Ziel eines Beweises.
In den seltensten Fällen kann ein Mathematiker einen Beweis sofort führen (sofern er den Beweis des Satzes nicht bereits kennt). In der Regel muss er sich erst einmal auf einem Schmierblatt Gedanken über den Satz machen. Wenn er irgendwann, irgendwie (und dies kann durchaus sehr, sehr lange dauern) einen Beweis gefunden hat, schreibt er diesen als Endergebnis auf. Auch ist oft der Weg, wie der Beweis geführt wird, ein ganz anderer, als der, auf dem ein Mathematiker im Lösungsweg auf den Beweis gekommen ist. Einem Außenstehenden, der nur den Beweis, aber nie den eigentlichen Lösungsweg zu Gesicht bekommen hat, stellt sich da natürlich die Frage, wie „man auf den Beweis kommt“.
Betrachten wir das obige Beispiel: den Beweis des Satzes . Wir haben den Beweis mit der wahren Aussage begonnen. Ein Leser kann sich hier durchaus fragen, wie wir auf diese Ungleichung gekommen sind. Diese Frage löst sich auf, wenn wir zeigen, was auf dem Schmierblatt stand (wie unser Lösungsweg aussah):
Schmierblatt (ordentlich aufgeschrieben):
Es fällt einiges auf: Zum einen siehst du, dass der Lösungsweg auf dem Schmierblatt nicht perfekt ist. So mussten wir erst quadratisch ergänzen, bevor wir erkannt haben, dass ist. Einem findigen Mathematiker würde dies sofort auffallen. Zum anderen ist dieser Lösungsweg nicht für einen Beweis geeignet: Er beginnt nicht mit der Prämisse des Satzes, sondern mit dem, was wir beweisen möchten. Dies ist problematisch, denn man kann einen Beweis schlecht mit dem beginnen, was man eigentlich zeigen möchte. Am Ende erhalten wir zwar eine wahre Aussage, aber sie ist nicht die Aussage, die wir beweisen möchten. Da wir nicht deutlich gemacht haben bzw. überlegt haben, dass die Termumformungen umkehrbar sind (die Pfeile zeigen nur „nach unten“), können wir mit Hilfe des Schmierblattes nicht begründen, dass man von der unteren wahren Aussage die zu beweisende Aussage herleiten kann.
Du siehst: Das, was wir auf dem Schmierblatt geschrieben haben, ist für einen Beweis ungeeignet. Deswegen mussten wir den Beweis (mit Hilfe dessen, was auf dem Schmierblatt stand) anders formulieren. Wir haben mit der wahren Aussage begonnen und aus dieser schrittweise die Zielaussage hergeleitet.
Das Schmierblatt erklärt nun, wieso wir mit angefangen haben und wie wir auf diese Ungleichung gekommen sind. Leider wird in den seltensten Fällen neben dem Beweis eines Satzes auch der Lösungsweg dargestellt oder die Idee dahinter genannt. Oftmals muss der Leser selbst herausfinden, wie man auf einen bestimmten Beweis selbst kommen kann, was sehr schwer sein kann. Wir werden uns in diesem Buch darum bemühen, Beweise so zu formulieren, dass aus ihnen auch die Idee dahinter leicht herausgelesen werden kann.
Direkter und indirekter Beweis
[Bearbeiten]Es gibt zwei wichtige Arten von Beweisen: direkte Beweise und indirekte Beweise (auch Widerspruchsbeweise genannt).
Direkter Beweis
[Bearbeiten]Beim direkten Beweis wird der zu beweisende Satz direkt bewiesen. Dies bedeutet, dass man mit den Voraussetzungen von beginnt und aus diesen die zu beweisende Aussage direkt durch logische Schlussfolgerungen herleitet. Ein direkter Beweis nimmt also folgende Form an:
Beispiel
[Bearbeiten]Betrachten wir ein Beispiel. Stelle dir vor, wir müssen den Satz
„Die Summe von drei aufeinanderfolgenden natürlichen Zahlen ist durch 3 teilbar.“
beweisen. Dieser Satz lässt sich folgendermaßen als Implikation formulieren:
„Wenn eine natürliche Zahl ist, dann ist durch 3 teilbar.“
In dieser Implikation ist „ ist eine natürliche Zahl“ die Prämisse und „ ist durch 3 teilbar“ die Konklusion. Ein direkter Beweis hätte also folgende Form:
Ein solcher Beweis könnte so aussehen (Implikationen der logischen Schlussfolgerungen sind orange):
Anstatt deinen Beweis so wie obigen zu strukturieren, kannst du ihn auch als Fließtext schreiben (dies ist meistens kompakter):
„Sei eine natürliche Zahl. Damit ist auch eine natürliche Zahl und somit durch 3 teilbar. Da ist, ist durch 3 teilbar.“
Widerspruchsbeweis
[Bearbeiten]Neben dem direkten Beweis gibt es eine zweite Art des Beweises, den Widerspruchsbeweis oder indirekten Beweis. Wenn du einen mathematischen Satz indirekt beweisen möchtest, so führst du seine Negation durch logische Schlussfolgerungen zu einem Widerspruch. Dabei nenne ich im Folgendem Widerspruchsannahme. Ein Widerspruchsbeweis hat also folgende Form:
Um einen Widerspruchsbeweis erfolgreich durchzuführen, musst du zunächst den zu beweisenden Satz richtig negieren. Wie du dies machen kannst, kannst du im Abschnitt „Aussagen negieren“ nachlesen.
Doch wie haben wir den Satz bewiesen, wenn wir die Widerspruchsannahme zu einem Widerspruch geführt haben? Wenn du die Widerspruchsannahme zu einem Widerspruch geführt hast, so weißt du, dass falsch sein muss, also ist. Damit ist die doppelte Verneinung von wahr (). Nun ist eine Tautologie, was du an folgender Wahrheitstabelle erkennst:
Da eine Tautologie ist, ist dann und nur dann wahr, wenn wahr ist (siehe Definition der Äquivalenz). Wir haben durch den Widerspruchsbeweis bewiesen, dass wahr ist (da falsch ist). Damit muss aber wegen obiger Tautologie wahr sein. Genau dies ist zu zeigen, wenn wir den Satz beweisen wollen.
Beispiel
[Bearbeiten]Stelle dir vor, wir wollen den Satz
„Die Summe von drei aufeinanderfolgenden natürlichen Zahlen ist durch 3 teilbar.“
durch einen Widerspruchsbeweis beweisen (diesen Satz haben wir bereits oben direkt bewiesen). Diesen Satz können wir als Implikation definieren:
„Wenn eine natürliche Zahl ist, dann ist durch 3 teilbar.“
Um diese Implikation indirekt zu beweisen, müssen wir zunächst die Widerspruchsannahme formulieren, also die obige Implikation negieren. Wir erhalten:
Widerspruchsannahme: „ ist eine natürliche Zahl und ist nicht durch 3 teilbar.“
Diese Annahme müssen wir nun durch logische Schlussfolgerungen zu einem Widerspruch führen. Eine solche Herleitung könnte so aussehen:
Auch diesen Beweis kannst du in einem Fließtext schreiben:
Widerspruchsannahme: Sei eine natürliche Zahl und nicht durch 3 teilbar. Wegen ist nicht durch 3 teilbar. Damit ist keine natürliche Zahl, da, wenn eine natürliche Zahl wäre, so wäre durch 3 teilbar. Wenn keine natürliche Zahl ist, ist auch keine natürliche Zahl. Dies ist aber ein Widerspruch dazu, dass nach Widerspruchsannahme eine natürliche Zahl ist ↯.
Fallunterscheidung und Kontraposition
[Bearbeiten]Neben den verschiedenen Arten mathematischer Beweise gibt es einige Methoden, die du in Beweisen verwenden kannst: die vollständige Fallunterscheidung, der Beweis durch Kontraposition und die vollständige Induktion. Diese Liste ist nicht vollständig und es gibt gewiss vielfältige Wege einen Beweis zu führen. Dennoch kann dir der nachfolgende Abschnitt als Inspirationsquelle für eigene Beweise dienen.
Vollständige Fallunterscheidung
[Bearbeiten]Bei vollständiger Fallunterscheidung wird der Beweis in eine endliche Anzahl von Fällen aufgeteilt. Für jeden der Fälle muss der zu beweisende Satz unter zusätzlicher Annahme der Fallbedingung bewiesen werden. Ein Beweis durch vollständige Fallunterscheidung hat damit folgende Form:
Mit dem einfachsten Fall kann man beginnen; manchmal fließen die hierbei gewonnenen Erkenntnisse bei der Bearbeitung anderer Fälle ein. Insofern kann eine relativ schwierige Gesamtaufgabe in mehrere leichter zu lösende Teilaufgaben reduziert werden gemäß dem Motto: teile und herrsche!
Zu achten ist darauf, dass bei der Aufteilung des Beweises in unterschiedliche Fälle der zu beweisende Satz vollständig abgedeckt wird. So kann z. B. beim Beweis eines Satzes, der für alle ganzen Zahlen gelten soll, eine Aufteilung in positive und negative Zahlen sinnvoll sein. Dann muss aber auch das Auftreten der Zahl Null als dritter Fall bewiesen werden.
Beispiel
[Bearbeiten]Als Beispiel beweisen wir folgenden Satz mit Hilfe vollständiger Fallunterscheidung (Quelle: Wikipedia-Artikel „Beweis (Mathematik)“):
„Ist eine Primzahl ungleich zwei, dann gibt es eine natürliche Zahl mit oder .“
Wir werden folgende vier Fälle unterscheiden:
Da eine natürliche Zahl ist (nur natürliche Zahlen können per Definition Primzahlen sein), muss einer der obigen vier Fälle auftreten. Unsere Fallunterscheidung ist damit vollständig. Betrachten wir nun die vier Fälle:
Fall 1:
ist durch 4 teilbar und damit keine Primzahl. Somit ist die Prämisse der zu beweisenden Implikation falsch und damit die gesamte Implikation wahr.
Fall 2:
Die Konklusion der zu beweisenden Implikation und damit die gesamte Implikation ist wahr.
Fall 3:
Es ist . Damit ist durch 2 teilbar. Da nach Voraussetzung der zu beweisenden Implikation ist, kann keine Primzahl sein. Somit ist die Prämisse der zu beweisenden Implikation falsch und damit die gesamte Implikation wahr.
Fall 4:
Die Konklusion der zu beweisenden Implikation und damit die gesamte Implikation ist wahr.
In jedem der Fälle konnten wir beweisen, dass unter der Bedingung der jeweiligen Fallunterscheidung die zu beweisende Implikation wahr ist. Da unsere Fallunterscheidung vollständig ist, ist die zu beweisende Implikation unabhängig vom jeweiligen Fall wahr.
Beweis durch Kontraposition
[Bearbeiten]Der Beweis durch Kontraposition ist eine Beweismethode, die für Beweise von Implikationen der Form verwendet werden können. Diese Beweismethode basiert auf der Tautologie .
Verständnisfrage: Zeige, dass die Aussage eine Tautologie ist.
Um zu zeigen, dass eine Tautologie ist, können wir die Wahrheitstabelle dieser Aussage aufstellen und uns überzeugen, dass der resultierende Wahrheitswert immer wahr ist:
Die Aussage ist also eine Tautologie und damit immer wahr. Dies bedeutet, dass dann und nur dann wahr ist, wenn wahr ist. Wenn wir also einen Satz der Form beweisen wollen, können wir alternativ auch die Aussage beweisen. Beim Beweis durch Kontraposition macht man genau dies: Anstatt einen Satz der Form direkt zu beweisen, wird die Aussage bewiesen.
Um also Kontraposition erfolgreich anwenden zu können, musst du wissen, wie man Aussagen richtig negiert. Dies kannst du im Abschnitt „Aussagen negieren“ nachlesen.
Beispiel
[Bearbeiten]Als Beispiel wollen wir folgenden Satz mit Hilfe der Kontraposition beweisen (im Folgenden gehe ich davon aus, dass eine Quadratzahl, also ein Element der Menge ist):
„Ist gerade, dann ist gerade.“
Dieser Satz hat die Form einer Implikation mit:
Um diesen Satz durch Kontraposition beweisen zu können, müssen wir erst einmal die Aussage , also die Negation der Aussagen und bestimmen:
Damit erhalten wir für :
Diesen Satz werden wir direkt beweisen. Wir suchen also einen Beweis der Form
Beweis: Sei eine natürliche Zahl und ungerade. Wir müssen nun zeigen, dass ungerade ist. Da ungerade ist, gibt es eine natürliche Zahl mit . Damit ist
Also ist eine ungerade Zahl. q. e. d.
Vollständige Induktion
[Bearbeiten]Die Vollständige Induktion wird im nächsten Abschnitt dieses Buches ausführlich vorgestellt. Zur Vollständigkeit nenne ich hier nur das Prinzip dieser Beweismethode:
Definition (Vollständige Induktion)
Sei eine Aussageform in der freien Variablen . Sei (oder ) eine wahre Aussage (Induktionsanfang) und die Implikation für alle erfüllt (Induktionsschritt), dann ist die Aussageform allgemeingültig in .
Vollständige Induktion
[Bearbeiten]Die vollständige Induktion ist eine wichtige Beweismethode, die dir in deinem Studium noch häufig begegnen wird. Dabei kann man ihre Wirkungsweise gut mit dem Dominoeffekt vergleichen. Doch wie sieht ein „Beweis mit dem Dominoeffekt“ konkret aus? Betrachten wir zunächst eine Beispielaufgabe, die mit Hilfe der vollständigen Induktion gelöst werden kann.
Eine Beispielaufgabe
[Bearbeiten]
Unsere Beispielaufgabe ist die „Gauß'sche Summenformel“, auch „kleiner Gauß“ genannt. Sie heißt so, weil der neunjährige Carl Friedrich Gauß diese Summenformel in einer Mathestunde entdeckt hat (Gauß ist der geniale Mathematiker, dessen Gesicht später den Zehn-Mark-Schein in Deutschland zieren sollte). Laut Anekdote[6] konnte der kleine Gauß die Summe der ersten natürlichen Zahlen sofort und ohne längeres Rechnen angeben.
Seine Idee war dabei, dass es zwischen genau Paare von Zahlen gibt, deren Summe ist: , , und so weiter bis . Wenn man seinen „Trick“ verallgemeinert, kommt man auf folgende Formel:
Für jede natürliche Zahl ist die Summe gleich .
Gut. Wir könnten nun anfangen, diese Behauptung für einzelne natürliche Zahlen zu beweisen:
Für :
, stimmt ✔
Für :
, stimmt auch ✔
und so weiter und so fort…
Doch dies ist keine Möglichkeit, einen Beweis zu führen, da es unendlich viele natürliche Zahlen gibt und es daher grundsätzlich unmöglich ist, alle Summen auszurechnen (denk an die armen Mitschüler von Gauß, wie sie versucht haben, die einzelnen Zahlen nacheinander aufzusummieren). Wir brauchen also eine andere Lösungsmethode. Wir haben dir in der Einleitung dieses Kapitels gesagt, dass diese Aufgabe durch vollständige Induktion gelöst werden kann und dass diese Beweismethode einem Dominoeffekt ähnelt. Doch wie lässt sich ein Dominoeffekt in dieser Aufgabe ausnutzen? Analysieren wir dazu die Aufgabe:
Wenn du dir die Aufgabe durchliest, wirst du erkennen, dass es in der Aufgabenstellung eine freie Variable gibt (die natürliche Zahl ). Wenn du für diese freie Variable einen bestimmten Wert einsetzt, entsteht eine konkrete Aussage. Durch Nachrechnen kannst du feststellen, ob diese Aussage wahr oder falsch ist. Wenn du z. B. für die Zahl einsetzt, entsteht die (wahre) Aussage:
Die Summe ist gleich .
Ein solcher Ausdruck, der eine (oder auch mehrere) freie Variable enthält und der durch Belegung dieser Variablen mit Werten in eine Aussage übergeht, wird Aussageform genannt und mit bezeichnet. heißt so viel wie: Eine Aussageform mit dem Namen und der freien Variablen , also in Abhängigkeit von . Die obige Aussage wäre demnach . Hier einige weitere Beispiele:
lautet: Die Summe ist gleich .
lautet: Die Summe ist gleich .
Unsere Aufgabe ist es, zu beweisen, dass die Aussageform bei Einsetzung aller natürlichen Zahlen immer eine wahre Aussage ergibt. Eine solche Aussageform, die für alle natürlichen Zahlen stets eine wahre Aussage liefert, nennt man „allgemeingültig in “.

Doch wie kann man jetzt den Dominoeffekt ins Spiel bringen? Dazu werden wir eine Analogie zwischen der Aussageform und einer Dominoreihe finden: Stelle dir dazu eine unendlich lange Dominoreihe vor, die irgendwo im Raum anfängt. Diese Dominoreihe ist durchnummeriert (der erste Dominostein ist die Eins, der zweite die Zwei und so weiter). Nun führen wir eine Beziehung zwischen der Dominoreihe und der zu beweisenden Aussageform ein. Wir sagen, dass der erste Dominostein für die Aussage steht, der zweite Dominostein für die Aussage und so weiter. Gehen wir nun davon aus, dass beim Fallen eines Dominosteins die Wahrheit der ihm zugewiesenen Aussage bewiesen ist. Wenn also Dominostein Nummer umfällt, ist die Aussage wahr und beim Fall von Dominostein Nummer ist die Aussage wahr.

Wir haben nun das Problem der Aufgabe auf das von uns aus der Kindheit bekannte Problem zurückgeführt, eine Dominoreihe zum Umfallen bringen zu wollen.
Frage: Was musst du tun, damit alle Dominosteine umfallen? Wie muss dazu die Dominoreihe aufgebaut sein?
Wenn du darüber nachdenkst, kommst du auf zwei Bedingungen, die du erfüllen musst, damit alle Dominosteine umfallen.
- Du musst den ersten Dominostein umstoßen.
- Die Dominoreihe muss so aufgebaut sein, dass beim Fall eines Dominosteins auch sein Nachfolger umfällt.
Wenn beide Bedingungen eingehalten werden, fallen alle Steine in der Dominoreihe nacheinander um („Dominoeffekt“). Du musst also dafür Sorge tragen, dass beides erfüllt ist.
Frage: Wie lauten die beiden Lösungsschritte aus der Antwort der eben gestellten Frage, wenn wir diese in das Ausgangsproblem zurückübersetzen, die Allgemeingültigkeit einer Aussageform zu beweisen?
- Erster Lösungsschritt: Zeige, dass die Aussageform für erfüllt ist.
- Zweiter Lösungsschritt: Zeige, dass unter der Annahme, dass die Aussageform für ein beliebiges erfüllt ist, die Aussageform auch für den Nachfolger erfüllt sein muss.

Dass durch den Beweis dieser beiden Lösungsschritte die Aufgabe gelöst ist, kannst du folgendermaßen erkennen: Zunächst wird im ersten Lösungsschritt gezeigt, dass die Behauptung für wahr ist. Wenn wir nun dieses Wissen auf den zweiten Lösungsschritt anwenden (wenn also ist), folgt, dass die Behauptung auch für wahr sein muss. Wenn wir nochmal den zweiten Lösungsschritt anwenden, folgt die Wahrheit für und bei nochmaliger Anwendung für und so weiter…
Wir müssen also die obigen beiden Lösungsschritte beweisen, um die Aufgabe zu lösen. Hier ist der Beweis mit den beiden notwendigen Lösungsschritten:
1. Lösungsschritt: Für lautet die zu beweisende Aussage . Durch Nachrechnen der rechten Seite, zeigt man, dass diese Aussage wahr ist.
2. Lösungsschritt: Gehen wir davon aus, dass die Aussage für bereits bewiesen ist. Gehen wir also davon aus, dass gilt:
Wir müssen nun die Summenformel für beweisen. Wir müssen also beweisen, dass gilt:
Durch Termumformungen zeigen wir nun, dass die linke Seite der Gleichung gleich der rechten Seite der Gleichung ist. Wir müssen also Termumforungen der folgenden Form finden:
Die notwendigen Termumformungen sind:
Unter Annahme der gegebenen Gleichung können wir also die linke Seite der Zielgleichung in die rechte Seite der Zielgleichung umformen. Damit haben wir die Zielgleichung bewiesen.
Wir haben so eine kurze und elegante Lösung der Aufgabe gefunden (Gauß' Lehrer wäre sicherlich stolz auf uns ![]() ).
).
Das Prinzip der vollständigen Induktion
[Bearbeiten]
Doch was ist nun das Prinzip der vollständigen Induktion? Dazu schauen wir uns die obige Beispielaufgabe an und versuchen, das dabei verwendete Beweisprinzip zu verallgemeinern.
Zunächst stellen wir fest, dass es sich um eine Aussageform handelt, deren einzige freie Variable eine natürliche Zahl ist. Die Aufgabe besteht nun darin, zu beweisen, dass die Aussageform für alle natürlichen Zahlen erfüllt ist, also allgemeingültig in ist.
Nun haben wir im ersten Schritt bewiesen, dass die Aussageform für die kleinste natürliche Zahl erfüllt ist (in unserem obigen Beispiel war diese kleinste natürliche Zahl die Eins; in bestimmten Fällen kann es aber auch eine andere natürliche Zahl sein, je nachdem, wie die zu beweisende Aufgabe lautet). Dieser Schritt wird Induktionsanfang genannt und entspricht in unserer obigen Analogie dem Umstoßen des ersten Dominosteins.
Im zweiten Schritt haben wir bewiesen, dass, wenn die Aussageform für eine beliebige natürliche Zahl erfüllt ist, sie auch für erfüllt sein muss. Dieser Schritt wird Induktionsschritt genannt und entspricht in unserer obigen Analogie der Tatsache, dass die Dominoreihe so aufgebaut sein muss, dass beim Fall eines Dominosteins auch der nächste Dominostein umfallen muss. Die dabei getroffene Annahme, dass die Aussageform für ein beliebiges erfüllt ist, nennt man Induktionsvoraussetzung oder auch Induktionsannahme (das war die gegebene Gleichung im zweiten Lösungsschritt). Die unter Annahme der Induktionsvoraussetzung zu beweisende Aussage wird Induktionsbehauptung genannt (das war unsere obige Zielgleichung). Der Induktionsschritt hat also die Form:
Im Folgenden werden wir nur noch den Begriff „Induktionsvoraussetzung“ verwenden. Fassen wir zusammen: Die vollständige Induktion lässt sich beim Beweis der Allgemeingültigkeit von Aussageformen anwenden, deren eine freie Variable eine natürliche Zahl ist. Zum Beweis durch vollständige Induktion musst du folgendes leisten:
- Induktionsanfang: Beweise, dass eine wahre Aussage ist.
- Induktionsschritt: Beweise, dass wenn wahr ist, auch wahr sein muss. Dabei können folgende Teilschritte identifiziert werden:
- Induktionsvoraussetzung: Die Aussage ist wahr für ein beliebiges .
- Induktionsbehauptung: Die Aussage ist wahr.
- Beweis des Induktionsschritts: Beweise, dass unter Annahme der Induktionsvoraussetzung die Induktionsbehauptung wahr ist.
Der Induktionsschritt hat dementsprechend folgende Form:
Oftmals (insbesondere bei einfacheren Aufgaben) werden Induktionsvoraussetzung und Induktionsbehauptung weggelassen, wenn sie dem Autor zu trivial erscheinen, als dass sie ausführlich erwähnt werden müssten. Auch der Induktionsanfang bzw. der Induktionsschritt werden manchmal nicht ausgeführt. Oft geben Lehrbuchautoren nur den Hinweis, dass eine bestimmte Aufgabe durch vollständige Induktion bewiesen werden kann und überlassen dem Leser die Auseinandersetzung mit dem jeweiligen Beweis. In diesem Kapitel werden aber alle Teilschritte der vollständigen Induktion ausgeführt.
Wenn wir nun die obige Beweismethode in mathematischer Sprache formulieren, erhalten wir die Definition der vollständigen Induktion.
Definition (Vollständige Induktion)
Sei eine Aussageform mit der freien Variable . Sei eine wahre Aussage (Induktionsanfang) und die Implikation für alle erfüllt (Induktionsschritt), dann ist die Aussageform allgemeingültig in .
Einige Fragen zur vollständigen Induktion
[Bearbeiten]Frage: Muss man zum Beweis mit vollständiger Induktion immer den Induktionsanfang und den Induktionsschritt durchführen oder kann man sich auch unter Umständen einen der beiden Schritte sparen?
Zur vollständigen Induktion gehören immer Induktionsanfang und Induktionsschritt. Wenn du einen der beiden Schritte weglassen würdest, wäre deine Lösung unvollständig und besäße damit keine Beweiskraft.
Die Antwort auf diese Frage kannst du dir auch über die Analogie zur Dominoreihe überlegen: Wenn du den Induktionsanfang weglässt, entspricht dies der Tatsache, dass du den ersten Dominostein nicht umstößt, was zur Folge hat, dass kein Dominostein umfällt.
Wenn du den Induktionsschritt weglässt, könntest du nach der Analogie nicht gewährleisten, dass ein Dominostein beim Umfallen auch seinen Nachfolger mitreißt. Damit könntest du nicht garantieren, dass alle Dominosteine umfallen (zwei Dominosteine könnten zum Beispiel zu weit voneinander entfernt stehen). Deine Lösung hätte dann keine Beweiskraft.
Frage: Da die Dominoreihe unendlich ist, benötigt sie auch unendlich lange zum Umfallen. Dies würde bedeuten, dass ein Beweis mit vollständiger Induktion nie vollständig wäre (da zu keiner Zeit alle Steine umgefallen sind). Heißt das nicht, dass man die vollständige Induktion nie zu Ende führen kann?
Diese Frage zeigt eine der Grenzen der Dominoanalogie. Die Zeit, die ein Dominostein benötigt, um umzufallen und dabei den nächsten Stein anzustoßen, ist für die Mathematik nicht relevant. Es ist nur wichtig, dass jeder Stein in endlich vielen Schritten fällt.
Beispiele vollständiger Induktion
[Bearbeiten]Schema zum Beweis mit vollständiger Induktion
[Bearbeiten]Die folgende Übersicht hilft dir, einen Beweis mit Hilfe vollständiger Induktion zu führen, wie sie im Abschnitt „Prinzip der vollständigen Induktion“ definiert wurde. Zwar kannst du viele Induktionsbeweise nach diesem Schema lösen, aber es gibt auch Ausnahmen!
Lösungsweg: Beweis auf Schmierblatt finden
[Bearbeiten]Kein Beweis fällt vom Himmel – so auch kein Induktionsbeweis. Bevor du den gesuchten Beweis aufschreiben kannst, musst du ihn erst einmal finden (klingt logisch, oder? ![]() ). Das folgende Schema soll dir dabei helfen. Die einzelnen Fragen beziehungsweise Schritte kannst du auf Schmierpapier oder im Kopf durchführen. In den nächsten Abschnitten wird dieses Schema an typischen Induktionsaufgaben erklärt und exemplarisch angewandt.
). Das folgende Schema soll dir dabei helfen. Die einzelnen Fragen beziehungsweise Schritte kannst du auf Schmierpapier oder im Kopf durchführen. In den nächsten Abschnitten wird dieses Schema an typischen Induktionsaufgaben erklärt und exemplarisch angewandt.
| Fragen/Schritt | Anmerkungen |
|---|---|
| Über welche Variable wird die Induktion geführt? | Oftmals ist diese Variable (hat sich so etabliert). Dies muss aber nicht sein und ist aufgabenabhängig. |
| Wie lautet die Aussageform, deren Allgemeingültigkeit zu beweisen ist? | Mach dir klar, wie die Aussageform aussieht, deren Allgemeingültigkeit du beweisen möchtest/musst. |
| Fragen/Schritt | Anmerkungen |
|---|---|
| Welchen Wert hast du für die Induktionsvariable im Induktionsanfang? Welches ist die kleinste natürliche Zahl für den Induktionsanfang? | Meistens geht aus der Aufgabenstellung hervor, wie der Induktionsanfang lautet. Manchmal ist dies aber nicht der Fall und du musst den Induktionsanfang selbst herausfinden, etwa durch Probieren. |
| Wie lautet die zu beweisende Aussage für den Induktionsanfang | Setze in die Aussageform die oben gefundene Zahl für den Induktionsanfang ein. |
| Finde einen Beweis für den Induktionsanfang | Hier musst du den Beweis für die oben gefundene Aussage finden. Bei Gleichungen bzw. Ungleichungen gelingt dir dies zum Beispiel dadurch, dass du beide Seiten dieser Gleichung oder Ungleichung ausrechnest und die dadurch entstanden Werte vergleichst. |
| Fragen/Schritt | Anmerkungen |
|---|---|
| Wie lautet die Induktionsvoraussetzung? | — |
| Wie lautet die Induktionsbehauptung? | Achte darauf, dass du die Induktionsbehauptung richtig formulierst, dass du also Klammern um setzt. Wenn du zum Beispiel die zu bearbeitende Aussageform lautet „ ist ungerade“ lautet die Induktionsbehauptung nicht „ ist ungerade“, sondern „ ist ungerade“. |
| Finde den Beweis für den Induktionsschritt | Finde den Beweis dafür, dass unter Annahme der Induktionsvoraussetzung die Induktionsbehauptung gilt. Hier ist Kreativität gefragt, denn es gibt kein Beweisschema F. Aber meistens kannst du Aufgaben des gleichen oder ähnlichen Typs auf ähnliche Weise lösen (natürlich nicht immer). Das heißt, wenn du schon einige Induktionsbeweise gesehen oder durchgeführt hast, wird es dir leichter fallen, ähnliche Aufgaben zur vollständigen Induktion zu lösen. Es heißt mal wieder: Übung macht den Meister! |
Beweis aufschreiben
[Bearbeiten]Nachdem du dir den Beweis im Kopf oder auf Schmierpapier überlegt hast, geht es nun darum, einen sauberen und formal richtigen Beweis aufzuschreiben. Das folgende Schema gibt dir eine mögliche Struktur vor, wie du dies machen kannst:
Aussageform, deren Allgemeingültigkeit für bewiesen werden soll:
<Aussageform aufschreiben, welche bewiesen werden soll>
1. Induktionsanfang:
<gefundenen Beweis für den Induktionsanfang aufschreiben>
2. Induktionsschritt:
2a. Induktionsvoraussetzung:
<Induktionsvoraussetzung formulieren>
2b. Induktionsbehauptung:
<Induktionsbehauptung formulieren>
2c. Beweis des Induktionsschritts:
<gefundenen Beweis für den Induktionsschritt aufschreiben>
Bedenke, dass das obige Beweisschema nur eine Möglichkeit ist, einen Beweis für vollständige Induktion aufzuschreiben, an dem du dich aber gut orientieren kannst. Sollten dir mal in einer Klausur, Test oder ähnlichem ein paar Punkte der vollständigen Induktion fehlen, schreibe die restlichen trotzdem auf. Oft werden sie auch schon bewertet.
Beweis einer Summenformel
[Bearbeiten]Als erste Beispielaufgabe wähle ich den Beweis einer Summenformel, da dies ein typisches Anwendungsgebiet der vollständigen Induktion ist. Aber auch Produktgleichungen kannst du auf eine ähnliche Art lösen. Unsere Beispielaufgabe lautet:
„Beweise durch vollständige Induktion, dass für alle natürlichen Zahlen ist.“
Beweisfindung auf dem Schmierblatt
[Bearbeiten]Notwendige Vorüberlegungen
[Bearbeiten]Frage: Über welche Variable wird die Induktion geführt?
Frage: Wie lautet die zu beweisende Aussageform?
Der Doppelpunkt steht dabei für „ist definiert durch“.
Induktionsanfang
[Bearbeiten]Frage: Was ist die kleinste sinnvoll einsetzbare natürliche Zahl für ?
Nach der Aufgabenstellung ist , also . Die kleinste, sinnvoll einsetzbare natürliche Zahl ist damit die , womit die Induktion startet.
Frage: Wie lautet die zu beweisende Aussage für den Induktionsanfang?
Nach dem Einsetzen der für in der Aussageform erhalten wir die Aussage:
Aufgabe: Finde einen Beweis für den Induktionsanfang.
Bei Summenformeln musst du die im Induktionsanfang entstandene Gleichung verifizieren. Dies erreichst du durch Nachrechnen der beiden Seiten der Gleichung, welche identisch sein müssen. Bei unserer Aufgabe erhalten wir für den linken Term der Gleichung:
Für den rechten Term der Gleichung erhalten wir:
Damit stimmen beide Seiten der obigen Gleichung überein, so dass wahr ist.
Induktionsschritt
[Bearbeiten]Frage: Wie lautet die Induktionsvoraussetzung?
Die Induktionsvoraussetzung lautet . Wir benutzen hier den Variablennamen , weil der Name bereits als Laufindex in der Summe vorkommt.
Frage: Wie lautet die Induktionsbehauptung?
Die Induktionsbehauptung lautet .
Aufgabe: Finde den Beweis für den Induktionsschritt.
Wir müssen nun beweisen, dass unter Annahme der Induktionsvoraussetzung die Induktionsbehauptung gilt. Bei Summenformeln können meistens folgende Schritte identifiziert werden:
1. Zerlege die Summe der Induktionsbehauptung so, dass du die Induktionsvoraussetzung anwenden kannst.
Dazu musst du von der Summe so viele Summanden extra schreiben (oder in einer eigenen Summe zusammenfassen), dass die restliche Summe der Summe in der Induktionsvoraussetzung entspricht:
2. Induktionsvoraussetzung anwenden.
Nun kann die Induktionsvoraussetzung verwendet werden:
Somit müssen wir jetzt folgende Gleichheit beweisen:
3. Termumformungen finden, um eine Seite der Gleichung in die andere zu überführen.
Wie du auf die notwendigen Termumformungen kommst wird im Abschnitt „Terme – Notwendige Termumformungen finden“ beschrieben. Du kannst die obige Gleichung durch Termumformumgen zum Beispiel so beweisen:
Beweis aufschreiben
[Bearbeiten]Nun kann der Beweis nach dem obigen Schema aufgeschrieben werden.
Aussageform, deren Allgemeingültigkeit für bewiesen werden soll:
1. Induktionsanfang:
Für gilt:
Damit ist wahr.
2. Induktionsschritt:
2a. Induktionsvoraussetzung:
2b. Induktionsbehauptung:
2c. Beweis des Induktionsschritts:
Es gilt:
Damit ist die Induktionsbehauptung bewiesen.
Beweise von Ungleichungen
[Bearbeiten]Ungleichung mit Summenformel
[Bearbeiten]Aufgabe
[Bearbeiten]Beweise, dass für alle die Ungleichung gilt.
Lösungsweg
[Bearbeiten]Ungleichungen zu beweisen, ist ein weiteres Problem, bei der die vollständige Induktion oftmals eingesetzt wird. Hier sind die notwendigen Termumformungen meist raffinierter als beim Beweis von Summenformeln und man muss geschickte Abschätzungen für Terme finden.
Diese Beispielaufgabe beschreibt eine wichtige Abschätzung der harmonischen Reihe, die noch später im Buch relevant wird (die Folge nennt man harmonische Folge, die Summe über diese Folge wird dementsprechend harmonische Reihe genannt). Die Aussageform, deren Allgemeingültigkeit zu beweisen ist, lautet:
Frage: Wie lautet der Induktionsanfang?
Fangen wir wie immer mit dem Induktionsanfang an. Wie oben ist die kleinste sinnvoll einsetzbare Zahl für die . Die Aussage für , die wir beweisen müssen, lautet:
Nun Rechnen wir die linke Seite der Ungleichung aus und erhalten:
Da ist, ist damit die Ungleichung für und somit der Induktionsanfang bewiesen.
Nun geht es mit dem Induktionsschritt weiter. Nach Induktionsvoraussetzung nehmen wir an, dass für ein bestimmtes gültig ist. Unsere Aufgabe ist es, zu beweisen, dass unter dieser Annahme auch gültig sein muss (beachte, dass wir für die Induktionsbehauptung überall durch ersetzt haben). Da wir in der vollständigen Induktion irgendwie die Induktionsvoraussetzung verwenden müssen, sollten wir die Summe so zerlegen, dass die Summe der Induktionsvoraussetzung auftritt (mal schauen, ob uns das gelingt und weiterhilft). Es ist .
Die rechte Seite der Ungleichung lässt sich auch als Summe schreiben (dadurch können wir beide Seiten besser miteinander vergleichen). Es ist und somit lautet unsere zu beweisende Ungleichung:
Wir wissen nach der Induktionsvoraussetzung bereits, dass ist. Wenn wir nun beweisen könnten, dass wäre, wäre unsere Induktionsbehauptung bewiesen. Hier brauchen wir eine geschickte Abschätzung der Summe. Wir wissen, dass die Summanden mit wachsendem immer kleiner werden. Da wir die Summe nach unten abschätzen müssen, könnten wir alle Summanden mit dem kleinsten in der Summe vorkommenden Summanden abschätzen. Dies gibt uns die Möglichkeit, die Summe zu vereinfachen und daraus vielleicht eine Abschätzung zu bekommen. Der kleinste Summand wäre . Da sich mit die Summe wahrscheinlich besser zusammenfassen lässt und ist, versuchen wir mal die Abschätzung mit . Wir erhalten:
Frage: Wie viele Summanden hat nun die Summe ?
Die Summe hat Summanden.
Damit ergibt sich die Ungleichung:
Somit haben wir den Beweis für die Induktionsbehauptung gefunden.
Beweis
[Bearbeiten]Die Aussageform, deren Allgemeingültigkeit zu beweisen ist, lautet:
1. Induktionsanfang:
Für ist
2a. Induktionsvoraussetzung:
Sei .
2b. Induktionsbehauptung:
Wenn ist, dann ist .
2c. Beweis der Induktionsbehauptung:
Zunächst gilt für alle :
Damit ist wegen der Induktionsvoraussetzung:
Ungleichung ohne Summenformel
[Bearbeiten]Aufgabe
[Bearbeiten]Bestimmen Sie alle für die gilt:
Lösungsweg
[Bearbeiten]Vorüberlegung: Wie kommen wir an unsere , welche die Ungleichung erfüllen?
Zunächst können wir für die ersten natürlichen Zahlen überprüfen, ob sie die Bedingung erfüllen:
Die Aussage ist für und wahr. Wir vermuten deswegen, dass die Ungleichung für alle erfüllt ist.
Beweis
[Bearbeiten]Die Ungleichung ist für alle erfüllt.
Aussageform, deren Allgemeingültigkeit für mit bewiesen werden soll:
1. Induktionsanfang:
2. Induktionsschritt:
2a. Induktionsvoraussetzung:
2b. Induktionsbehauptung:
2c. Beweis des Induktionsschritts:
Aus der Induktionsvoraussetzung wissen wir bereits, dass gilt. Beweisen wir nun deswegen die fehlende Ungleichung:
Die untere Ungleichung kann direkt miteinander verglichen werden und ist insbesondere für alle wahr.
Beweis von Teilbarkeit
[Bearbeiten]Aufgabe
[Bearbeiten]Beweise, dass alle Zahlen der Form mit durch 6 teilbar sind.
Lösungsweg
[Bearbeiten]Als letztes Beispiel betrachten wir eine Aufgabe zur Teilbarkeit.
Frage: Über welche Variable ist die Induktion zu führen?
Die Induktionsvariable ist .
Frage: Wie lautet die Aussageform, deren Allgemeingültigkeit zu beweisen ist?
Im Induktionsanfang musst du wie bei den obigen Beispielen die kleinste sinnvoll einsetzbare Zahl einsetzen und die so ausgerechnete Zahl auf die gewünschte Teilbarkeit überprüfen (beachte dabei, dass jede ganze Zahl ein Teiler von ist).
Frage: Wie lautet der Induktionsanfang?
Der Induktionsanfang ist laut Aufgabenstellung für zu führen. Wir erhalten , was durch sechs teilbar ist.
Frage: Wie lautet die Induktionsvoraussetzung?
Die Zahl ist durch 6 teilbar.
Frage: Wie lautet die Induktionsbehauptung?
Die Zahl ist durch 6 teilbar.
Im Beweis des Induktionsschritts hilft es meist, den erhaltenen Term, den du auf Teilbarkeit überprüfen sollst, durch Termumformungen auf eine Summe zu bringen, bei der du weißt, dass jeder seiner Summanden durch die gewünschte Zahl teilbar ist. Versuche dabei die Summe in so eine Struktur zu bringen, dass du die Induktionsvoraussetzung verwenden kannst.
Frage: Wie lautet der Beweis für den Induktionsschritt?
Wir erhalten nach obiger Vorgehensweise:
Nach Induktionsvoraussetzung wissen wir, dass durch 6 teilbar ist. Der Summand ist auch durch sechs teilbar. Und wie sieht es mit aus? Da entweder oder gerade ist, ist entweder oder durch zwei teilbar. Damit muss auch durch 6 teilbar sein.
Beweis
[Bearbeiten]Aufgabe: Schreibe den Beweis auf.
Die Aussageform, deren Allgemeingültigkeit zu beweisen ist, lautet:
1. Induktionsanfang:
Für ist durch 6 teilbar.
2a. Induktionsvoraussetzung:
Es ist durch 6 teilbar.
2b. Induktionsbehauptung:
ist durch 6 teilbar.
2c. Beweis der Induktionsbehauptung:
Es ist . Normalerweise würdest du jetzt Potenzen von m zusammenfassen zu . Das ist zwar richtig, aber nicht zielführend. Vielmehr musst du den Term der Induktionsvoraussetzung ins Spiel bringen, hier durch Umordnen, so dass sich ergibt. Am Term kannst du nicht sofort ablesen, dass er für alle durch 6 teilbar ist. Ein weiterer Induktionsbeweis lässt sich jedoch vermeiden, denn wenn du ausklammerst , ist die Teilbarkeit sofort zu erkennen, weil m oder m+1 durch 2 teilbar ist. Damit sind alle 3 Summanden von durch 6 teilbar und der Induktionsbeweis in allen Einzelheiten nachvollziehbar geführt.
Mengenlehre
[Bearbeiten]Erklärung und Definition
[Bearbeiten]
Der Begriff der Menge ist eines der wichtigsten und grundlegendsten Konzepte der Mathematik. Das ist auch der Grund, warum er dir schon so früh im Studium begegnet. Doch was ist eine Menge?
Hierzu möchten wir die originale Definition von Georg Cantor, dem Begründer der Mengenlehre, aus dem Jahr 1895 verwenden:

Definition (Naive Definition einer Menge von Cantor)
„Unter einer ‚Menge‘ verstehen wir jede Zusammenfassung von bestimmten wohlunterschiedenen Obje[k]ten uns[e]rer Anschauung oder unseres Denkens (welche die ‚Elemente‘ von genannt werden) zu einem Ganzen.“[7]
Eine Menge ist also der Zusammenschluss von verschiedenen Objekten zu einem neuen Objekt, welches all die zusammengeschlossenen Objekte umfasst. Betrachte hierzu folgende Polygone:

Diese Polygone wurden zu einer Menge zusammengeschlossen, was durch die Ellipse angedeutet wird. Hier könnte man sich die Menge als eine Art „Behältnis“ vorstellen, welche alle Polygone als Inhalt enthält. Dieses Bild ist jedoch nicht ganz korrekt. Ein Behältnis bleibt nämlich dasselbe, auch wenn man seinen Inhalt ändert. Dies ist bei Mengen anders: Diese ändern ihre Identität, wenn man neue Elemente hinzufügt oder bestehende entfernt.
Die Vorstellung einer Menge als „Inhalt eines Behältnisses“ ist hier besser. Wenn du also eine Menge von verschiedenen Objekten hast, so kannst du dir diese Menge als Inhalt eines Behältnisses vorstellen. Dabei ist die Menge ein Objekt, welches den Inhalt des Behältnisses darstellt und nicht das Behältnis selbst:
-
Eine Beispielmenge
-
Dieselbe Menge als imaginäre Box
-
Bessere Vorstellung: Menge als Inhalt einer imaginären Box
Diese Vorstellung entspricht in etwa dem alltäglichen Gebrauch des Begriffs „Menge“. Nimm den alltäglichen Begriff einer „Menschenmenge in einem Stadion“ als anschauliches Beispiel:
-
Eine Menschenmenge in einem Stadion
Niemand würde diese Menge mit dem Stadion, was in unserem Beispiel quasi das Behältnis ist, gleichsetzen. Vielmehr entspricht die (Menschen-)Menge im Stadion der Zusammenfassung von allen Personen innerhalb des Stadions zu einem Ganzen. Diese Menge kann man dabei als „Inhalt des Stadions“ auffassen, wobei wir für dieses Beispiel alle anderen Gegenstände innerhalb des Stadions nicht beachten. Wenn neue Personen das Stadion betreten oder verlassen, dann ändert sich auch die Menge der Leute im Stadion. Genauso verändern Mengen in der Mathematik ihre Identität, wenn Elemente entfernt oder hinzugefügt werden.
Beachte, dass wir in diesem Beispiel mit der Menschenmenge im Stadion was anderes als die Anzahl der Leute im Stadion meinen. Unsere Menge ändert sich, wenn beispielsweise eine Person das Stadion verlässt und danach eine andere Person das Stadion betritt. Genauso ist es auch in der Mathematik: Wenn du innerhalb einer Menge ein Objekt mit einem anderen austauscht, dann veränderst du die Identität dieser Menge. Ignoriere bitte auch Unzulänglichkeiten, die in diesem anschaulichen Beispiel aus mathematischer Sicht stecken. Beispielsweise haben wir nicht geklärt, was ein Mensch ist und was seine Identität ausmacht.
Anders als in der realen Welt, wo Behältnisse und damit ihre Inhalte räumlich begrenzt sind, können Mengen beliebig groß sein und unendlich viele Elemente umfassen. Auch müssen ihre Elemente keine gemeinsamen Eigenschaften besitzen. Sie können sehr unterschiedlich sein.
Grundlegende Notationen für Mengen
[Bearbeiten]
Zur Bezeichnung von Mengen werden in der Regel Großbuchstaben verwendet. Wenn die Elemente einer Menge selbst keine Mengen sind, nutzt man für sie oft Kleinbuchstaben. Man schreibt – „ ist ein Element von “, wenn eines der Objekte bezeichnet, das in der Menge enthalten ist. Ist dies nicht der Fall, schreibt man – „ ist kein Element von “.
Das Element-Symbol wurde im Übrigen 1889 von Giuseppe Peano in seiner Arbeit Arithmetices principia nova methodo exposita eingeführt. Es ist eine veränderte Darstellung des Anfangsbuchstaben ε (Epsilon) vom griechischen Wort εστί („estí“, was „ist“ bedeutet)[8].
Beispiele für Mengen
[Bearbeiten]Stelle dir folgende Ansammlung von Objekten vor:

Aus dieser Ansammlung können wir die vier Objekte Trommel, Spielkarte, Digitalkamera und Gitarre zu einer Menge zusammenfassen:
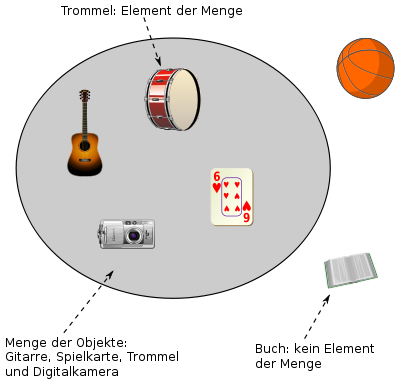
Wenn wir die gerade von uns gebildete Menge mit bezeichnen, so können wir aufschreiben:
– „Die Trommel ist ein Element der Menge .“
– „Das Buch ist kein Element der Menge .“
Verständnisfrage: Sei die im obigen Beispiel gebildete Menge. Welche der folgenden Aussagen sind wahr?
Antwort:
- wahr
- falsch
- falsch
- falsch
Zahlenbereiche als Mengen
[Bearbeiten]Auch Zahlenbereiche werden in der Mathematik als Mengen aufgefasst. So ist die Menge der natürlichen Zahlen die Zusammenfassung aller Zahlen zu einer Menge. Diese Menge wird mit dem Buchstaben mit (meistens links) doppelter Vertikalen notiert. Auch andere Zahlenbereiche werden als Mengen aufgefasst:
| Zahlenbereich | Symbol |
|---|---|
| Natürliche Zahlen | |
| Ganze Zahlen | |
| Rationale Zahlen | |
| Reelle Zahlen | |
| Komplexe Zahlen |
Verständnisfrage: Welche der folgenden Aussagen sind wahr?
Antwort:
- wahr: ist eine natürliche Zahl.
- falsch: ist keine natürliche Zahl.
- falsch: ist eine natürliche Zahl. Also ist die Aussage, dass diese nicht in sei, falsch.
- wahr: ist keine natürliche Zahl.
Die Extensionalität von Mengen
[Bearbeiten]Die Identität einer Menge manifestiert sich allein dadurch, welche Objekte sie enthält. Zwei Mengen sind nämlich genau dann gleich, wenn sie dieselben Elemente besitzen. Diese beiden Mengen sind dann ein- und dasselbe Objekt. So gibt es beispielsweise nur eine Menge, welche genau die Zahlen und enthält. Mehrere Mengen mit denselben Elementen kann es nicht geben.
Wenn es auch nur ein Objekt gibt, welches Element der einen Menge, aber nicht der anderen ist, dann sind beide Mengen verschieden. Diese Eigenschaft von Mengen wird Extensionalitätsprinzip oder auch Extensionalitätsaxiom genannt. Sie lässt sich wie folgt formalisieren:
Definition (Extensionalitätsprinzip)
Für zwei beliebige Mengen und gilt:
Übersetzt bedeutet obige Formel:
Würden wir Mengen, die über unterschiedliche Eigenschaften definiert sind, als unterschiedlich betrachten (eine solche Mengenlehre wäre intensional), wäre sie für die Mathematik nicht brauchbar. Wie aber aus dem obigen Extensionalitätsprinzip hervorgeht, ist es für die Identität einer Menge egal, wie sie gebildet wurde. Es ist nur wichtig zu wissen, welche Elemente sie umfasst.
Beispiel
In unserer Mengenlehre ist die Menge aller Lösungen der Gleichung identisch mit der Menge aller Lösungen der Gleichung . Dies ist die Menge bestehend aus den Zahlen und . In einer intensionalen Mengenlehre wäre dies nicht zwangsläufig der Fall, da beide Mengen durch unterschiedliche Eigenschaften definiert sind.
Wozu braucht man Mengen in der Mathematik?
[Bearbeiten]Mengen werden dir in allen Teilgebieten der Mathematik begegnen. Sie sind ein praktisches Hilfsmittel und mit ihnen können komplexe Sachverhalte kurz und prägnant ausgedrückt werden. Auch können mit Mengen neue Objekte konstruiert oder Konzepte modelliert werden. Beispielsweise nutzt die Topologie Mengen, um Nachbarschaftsbeziehungen auszudrücken und auch die in der Algebra studierten Strukturen wie Gruppen oder Körper werden als Mengen definiert.
Daneben ist die Mengenlehre selbst ein etabliertes Teilgebiet der Mathematik. Hier haben Mathematiker gezeigt, dass alle wesentlichen Konzepte der Mathematik allein mit Mengen modelliert werden können. Trotz des simplen Charakters ist der Mengenbegriff also sehr mächtig. So kann beispielsweise jede Zahl als ein komplexes Mengengebilde dargestellt werden[9]. Über die Mengenlehre können so Grundfragen der Mathematik beantwortet werden (eben weil man sich auf den Standpunkt stellen kann, alles in der Mathematik sei Menge)[10]. Beispielsweise besitzt die Mengenlehre Mittel, um für eine Aussage zu beweisen, dass sie innerhalb eines gegebenen Axiomensystems weder beweisbar noch widerlegbar ist[11].
Wenn man sich die Einfachheit und die Bedeutung der Mengenlehre vor Augen hält, dann wundert es schon ein wenig, dass die Mengenlehre eine für die Mathematik recht junge Theorie ist.
Teilmenge und echte Teilmenge
[Bearbeiten]Beziehungen zwischen Mengen
[Bearbeiten]Stelle dir zwei Mengen und in einem Mengendiagramm vor. Es gibt mehrere Möglichkeiten, wie diese beiden Mengen zueinander liegen können. und könnten sich überlappen, könnte komplett in liegen oder es gibt eine andere Lage zueinander. Einige dieser Zusammenhänge treten so häufig in der Mathematik auf, dass sie eigene Bezeichnungen bekommen haben. Diese sind:
| Mengendiagramm | Bezeichnung |
|---|---|
 |
ist eine Teilmenge von |
 |
und sind disjunkte Mengen. |
Teilmenge
[Bearbeiten]Definition und Beispiele
[Bearbeiten]

Wenn alle Elemente einer Menge auch Elemente einer Menge sind, so wird eine Teilmenge der Menge genannt. Hierfür schreibt man . Es ist also genau dann eine Teilmenge von , wenn sie einen Teil der Menge von umfasst. Betrachte hierzu die folgenden zwei Mengen:
Da alle Streichinstrumente auch Instrumente sind, sind alle Elemente von auch Elemente von . Damit ist eine Teilmenge von . Weitere Sprechweisen für sind:
ist eine Untermenge von
und
ist eine Obermenge von
Erläutern wir diese Sprechweise noch einmal an dem Beispiel von gerade eben. Zweifellos wird man erkennen, dass die Menge der Instrumente alle Streichinstrumente aus umfasst und darüber hinaus noch weitere Elemente enthält. Ordnen wir die Mengen und nun nach der Allgemeinheit ihrer Bezeichnung an (absteigend von allgemein nach spezifisch):
- Menge : Instrumente
- Menge : Streichinstrumente
„Instrument“ ist ein Oberbegriff für „Streichinstrumente“. Dementsprechend muss eine Obermenge von sein. Analog ist „Streichinstrumente“ ein Unterbegriff von „Instrumente“, weswegen auch eine Untermenge von ist. Du kannst es dir auch räumlich vorstellen: die Menge steht über und ist daher eine Obermenge von , während als Untermenge unter steht. Bei unterschiedlichen Mengen umfasst also die größere Obermenge die kleinere Untermenge.
Auch die gegenteilige Beziehung von zwei Mengen ist mathematisch darstellbar. Möchtest du etwa betonen, dass keine Teilmenge der Menge ist, so kannst du schreiben. Beispiel:
Fassen wir das bereits Gesagte in einer Definition zusammen:
Definition (Teilmenge)
Die Menge ist eine Teilmenge der Menge genau dann, wenn alle Elemente der Menge auch Elemente der Menge sind. Man schreibt , wenn eine Teilmenge von ist.
Es ist also:
Mit Erklärung:
Einige Beispiele:
Beispiel (Teilmenge)
Anmerkungen zu den Beispielen:
Beispiel 3: ist die Menge der natürlichen Zahlen und die Menge der ganzen Zahlen. Da jede natürliche Zahl auch eine ganze Zahl ist, ist eine Teilmenge von .
Beispiel 4: ist die Menge aller negativen, ganzen Zahlen. Da nicht negativ ist, ist und damit keine Teilmenge von .
Beispiel 5: Jede Menge ist Teilmenge von sich selbst (siehe spätere Verständnisfrage).
Das fünfte Beispiel zeigt exemplarisch, dass jede Menge Teilmenge von sich selbst ist. Es ist also für alle Mengen . Folglich:
Instrumente sind somit eine Teilmenge von Instrumente. Im ersten Moment mag dies ungewohnt klingen. Für die Mathematik hat sich diese Konvention aber als sinnvoll erwiesen, weil so unnötige Fallunterscheidungen, ob zwei Mengen gleich sind oder nicht, vermieden werden. Mit dem Begriff der echten Teilmenge (siehe unten) gibt es einen Begriff, der die Gleichheit der beiden Mengen ausschließt.
Verständnisfrage: Warum ist jede Menge Teilmenge von sich selbst?
Damit ist, muss nach Definition gelten:
Jedes Element aus ist auch Element aus
Dies ist aber für alle Mengen erfüllt.
Identität von Mengen zeigen
[Bearbeiten]Um die Identität zweier Mengen und zu zeigen, geht man häufig in zwei Schritten vor. Man zeigt zunächst, dass eine Teilmenge von ist, und später im zweiten Schritt, dass eine Teilmenge von ist. Für zwei Mengen und gilt nämlich folgende Äquivalenz:
Satz (Identität von Mengen)
Zwei Mengen und sind genau dann identisch, wenn eine Teilmenge von und eine Teilmenge von ist.
Verdeutlichen wir uns diese Tatsache erneut an einem Beispiel. Nehme hierzu die beiden Mengen:
Damit eine Teilmenge von ist, müssen alle Instrumente aus der ersten Menge auch in der zweiten enthalten sein. Analog müssen alle Instrumente der zweiten Menge auch in der ersten Menge enthalten sein, damit die zweite Menge eine Teilmenge der ersten Menge ist. Dies ist genau dann und nur dann möglich, wenn beide Mengen identisch sind.
Beweis (Identität von Mengen)
Nach dem Extensionalitätsprinzip für Mengen gilt:
Transitivität der Teilmengenbeziehung
[Bearbeiten]
Es ist auch möglich, mehrere Teilmengenbeziehungen hintereinander aufzuführen:
Diese Schreibweise ergibt Sinn, weil aus und folgt, dass ist. Obige Teilmengenkette impliziert also:
Dieser Zusammenhang ist in allgemeiner Form auch im Bild rechts dargestellt. Die beschriebene Eigenschaft nennt man „Transitivität der Teilmengenbeziehung“:
Satz (Transitivität der Teilmengenbeziehung)
Die Teilmengenbeziehung ist transitiv. Das bedeutet, dass wenn und ist, auch ist.
Beweis (Transitivität der Teilmengenbeziehung)
Sei beliebig. Wegen ist . Wegen ist . Damit ist jedes Element aus auch Element aus , was zu beweisen war.
Echte Teilmenge
[Bearbeiten]Definition und Erklärung
[Bearbeiten]
Ist eine Menge eine Teilmenge der Menge und , so nennt man eine echte Teilmenge der Menge . Um deutlich zu machen, dass eine echte Teilmenge von ist, schreibt man .
Definition (Echte Teilmenge)
Die Menge ist eine echte Teilmenge der Menge genau dann, wenn eine Teilmenge der Menge und nicht identisch mit ist. Die Schreibweise ist hierfür .
Oben haben wir bereits gesehen, dass jede Menge Teilmenge von sich selbst ist. Beispielsweise ist:
Beide Mengen sind identisch, da die darin enthaltenen Elemente exakt übereinstimmen. Umgangssprachlich sollte aber ein „Teil“ nicht identisch mit dem Ganzen sein. Um bei Teilmengen die Gleichheit beider Mengen auszuschließen, gibt es den Begriff der echten Teilmenge. Im obigen Beispiel liegt demnach keine echte Teilmenge vor. Anders ist es dagegen im folgenden Beispiel:
Der Unterschied wird anhand der Schreibweise deutlich:
| Schreibweise | Bedeutung | Bemerkung |
|---|---|---|
| ist eine Teilmenge von | der Fall ist hier möglich | |
| ist eine echte Teilmenge von | hier ist garantiert , es gibt also ein Element mit |
Hinweis
In mathematischer Literatur findet man auch die Schreibweise . Jedoch wird diese Schreibweise nicht in einer einheitlichen Definition gebraucht. So verwenden einige Autoren diese Schreibweise in der Bedeutung „ ist eine Teilmenge von “ und andere in der Bedeutung „ ist eine echte Teilmenge von “. Wegen dieser Uneindeutigkeit werden wir in diesem Buch auf diese Schreibweise verzichten.
Satz (echte Teilmengenbeziehung)
Ist eine echte Teilmenge von , so hat wenigstens ein zusätzliches Element, formalisiert:
Beweis (echte Teilmengenbeziehung)
Sei eine echte Teilmenge von . Dann ist insbesondere . Wäre , gälte und somit , da bereits ist. Also gilt , und nach den Umformungsregeln zum Negieren folgt daraus: .
Beispiele
[Bearbeiten]Betrachte zunächst folgende Beispiele:
Beispiel (echte Teilmenge)
- ist keine echte Teilmenge der Menge
- ist keine echte Teilmenge der Menge
Anmerkungen zu den Beispielen:
Beispiel 3: Der hier dargestellte Zusammenhang wird auch oben bei dem Abschnitt zu Venn-Diagrammen schön illustriert.
Beispiel 4: Entspricht dem eingangs erwähnten Instrumentenbeispiel, lediglich werden hier Zahlen statt Instrumente gebraucht.
Um den Unterschied der Begriffe „Teilmenge“ und „echte Teilmenge“ deutlich zu machen, kannst du folgende Mengen betrachten:
ist eine Teilmenge von und weil zusätzliche Elemente besitzt, ist auch eine echte Teilmenge von . Außerdem ist auch eine Teilmenge von . Weil aber und identisch sind, ist keine echte Teilmenge von :
-
A ist eine echte Teilmenge von B
-
C ist keine echte Teilmenge von B
Verständnisfragen zur Teilmenge
[Bearbeiten]Verständnisfrage: Welche der folgenden Aussagen sind wahr?
Antwort:
- wahr
- falsch
- falsch
- falsch
Verständnisfrage: Es ist . Ist dann oder ?
Aus folgt, dass jedes Objekt , welches die Eigenschaft erfüllt, auch die Eigenschaft erfüllt. Damit ist die richtige Antwort.
Wenn du also mal zeigen möchtest, dass für zwei Mengen und die Beziehung erfüllt ist, so kannst du zeigen.
Verständnisfrage: Es seien und verschiedene Objekte. Welche der folgenden Aussagen ist wahr?
Zunächst sollte man sich vergegenwärtigen, was die einzelnen Mengen bedeuten:
- – die Menge, die die Objekte und als Elemente besitzt.
- – die Menge, die die Objekte und sowie die Menge als Elemente besitzt.
Nun kann der Wahrheitswert der einzelnen Aussagen bestimmt werden:
- – falsch, da die Menge kein Element von ist.
- – wahr, weil alle Elemente von auch Elemente von sind.
- – falsch, weil gleich ist und damit ist keine echte Teilmenge von .
- – wahr, weil ein Element von ist.
- – wahr, weil alle Elemente von , nämlich die Objekte und , auch Elemente von sind.
- – wahr, weil alle Elemente von , nämlich die Objekte und , auch Elemente von sind und weil ungleich ist.
Verständnisfrage: Lässt sich ein Beispiel für zwei Mengen und finden, für welche und gilt?
Ja. Es ist und für und .
Verständnisfrage: Gegeben sei die Menge . Welche der folgenden Aussagen ist wahr?
Antworten:
- wahre Aussage: ist in enthalten und damit ist eine Teilmenge von . Alternativ kann man auch argumentieren, dass jede Menge eine Teilmenge von sich selbst ist.
- falsche Aussage: Die Menge ist identisch zu und damit keine echte Teilmenge von .
- wahre Aussage: Die leere Menge ist Teilmenge jeder Menge.
- wahre Aussage: Die leere Menge ist Teilmenge von , aber nicht identisch mit . Damit ist die leere Menge eine echte Teilmenge von .
Verständnisfrage: Welche der folgenden Aussagen ist wahr?
Antworten:
- wahre Aussage: Die leere Menge ist Teilmenge jeder Menge und damit auch eine Teilmenge der leeren Menge.
- falsche Aussage: Keine Menge ist eine echte Teilmenge von sich selbst. Dies gilt auch für die leere Menge.
Verständnisfrage: Ist die echte Teilmengenbeziehung transitiv?
Ja, wenn und gilt, dann auch . Beweis: aus folgt und aus folgt . Mit der Transitivität von ergibt sich . Wegen gibt es ein mit . Da aber alle Elemente von in liegen, liegt . Also gilt: .
Disjunkte Mengen und paarweise disjunkte Mengensysteme
[Bearbeiten]Disjunkte Mengen
[Bearbeiten]Erklärung und Beispiele
[Bearbeiten]Zwei Mengen und , die keine gemeinsamen Elemente besitzen, nennt man disjunkt. Für disjunkte Mengen gibt es auch die Bezeichnungen elementfremd oder durchschnittsfremd. Das Wort „disjunkt“ leitet sich dabei vom lateinischen Wort „disiunctum“ ab, was soviel wie „getrennt“ bedeutet. Nehme als Beispiel die folgenden zwei Mengen
Diese beiden Mengen sind nicht disjunkt, weil sie das „Klavier“ als gemeinsames Objekt besitzen. Demgegenüber sind aber die folgenden beiden Mengen disjunkt, weil sie keine gemeinsamen Elemente besitzen:
Weitere Beispiele:
-
Die Menge mit der Spielkarte und dem Buch ist disjunkt zur Menge mit der Gitarre und der Trommel.
-
Ein weiteres Beispiel für zwei disjunkte Mengen
-
Disjunkte Mengen im Mengendiagramm
Definition
[Bearbeiten]Der Schnitt ist die Menge aller gemeinsamen Elemente von und . Zwei Mengen sind also genau dann disjunkt, wenn die Menge kein Element besitzt. Eine solche Menge ohne Elemente nennt man „leere Menge“, welche als notiert wird. Es ist also:
Definition (disjunkte Menge)
Zwei Mengen nennt man disjunkt, wenn sie keine gemeinsamen Elemente besitzen:
Verständnisfragen
[Bearbeiten]Verständnisfrage: Welche der folgenden Paare von Mengen sind disjunkt?
- und
- und
- und
- und
- und
Antwort:
- und sind nicht disjunkt, weil sie beide als Element besitzen.
- und sind disjunkt, weil sie keine gemeinsamen Elemente besitzen.
- und sind nicht disjunkt, weil sie zum Beispiel die Zahl als gemeinsames Element besitzen.
- und sind disjunkt, weil ist.
- und sind nicht disjunkt, weil sie als gemeinsames Element besitzen.
Folgende Fragen setzen voraus, dass du den Begriff der Schnittmenge und der leeren Menge schon kennst (siehe die nächsten Kapitel). Du kannst diese Fragen also gerne überspringen, wenn du diese Begriffe noch nicht kennen solltest.
Verständnisfrage: Mit welchen Mengen ist disjunkt?
ist mit jeder Menge disjunkt, weil ist.
Verständnisfrage: Wann ist eine Menge zu sich selbst disjunkt?
Eine Menge ist genau dann zu sich selbst disjunkt, wenn ist. Wegen ist dies genau dann der Fall, wenn ist:
Verständnisfrage: Nehme die zwei Mengen und . Unter welchen Umständen sind diese beiden Mengen disjunkt?
Diese beiden Mengen sind genau dann disjunkt, wenn ist.
Paarweise disjunkte Mengensysteme
[Bearbeiten]
Ein Mengensystem , also eine Menge von Mengen, nennt man paarweise disjunkt, wenn jeweils zwei verschiedene Mengen disjunkt sind. Egal welche zwei unterschiedlichen Mengen und aus ausgewählt werden, diese beiden Mengen besitzen keine gemeinsamen Elemente. Zum Beispiel ist folgendes Mengensystem paarweise disjunkt:

Demgegenüber ist das folgende Mengensystem nicht paarweise disjunkt, weil sich die Mengen und überschneiden:

Wir fassen zusammen:
Definition (paarweise disjunktes Mengensystem)
Ein Mengensystem ist paarweise disjunkt, wenn alle verschiedenen Mengen disjunkt sind. Es gilt also:
Verständnisfrage: Sei ein Mengensystem besteht aus nur einer Menge . Ist paarweise disjunkt?
Ja, jedes Mengensystem bestehend aus nur einem Element ist paarweise disjunkt. Es gibt keine zwei verschiedenen Mengen und damit muss für keine Mengenpaare geprüft werden, ob sie disjunkt sind, oder nicht.
Verständnisfrage: Sei das leere Mengensystem. Ist paarweise disjunkt?
Ja, auch das leere Mengensystem ist paarweise disjunkt. Die zu prüfende Aussage ist eine All-Aussage über die leere Menge und damit wahr.
Verständnisfrage: Sei ein paarweise disjunktes Mengensystem. Ist dann immer ?
Nein. Wir haben eben erfahren, dass jedes einelementige Mengensystem paarweise disjunkt ist. Es ist also für jede Menge paarweise disjunkt. Sei nun eine nicht leere Menge und . Es ist
Es gibt also paarweise disjunkte Mengensysteme, deren Schnitt nicht leer ist.
Potenzmenge
[Bearbeiten]Definition
[Bearbeiten]
Die Potenzmenge einer Menge ist die Menge aller Teilmengen der Menge . Es ist also . Neben sind noch die Schreibweisen und gebräuchlich.
Einfach ausgedrückt: Die Potenzmenge ist die Menge aller möglichen Kombinationen der einzelnen Elemente einer Menge. Im vorherigen Kapitel wurde bereits die Teilmenge erläutert. Die Potenzmenge umfasst alle möglichen Teilmengen, die sich aus den Elementen von bilden lassen. Dazu zählt auch die leere Menge .
Definition (Potenzmenge)
Die Potenzmenge einer Menge ist die Menge aller Teilmengen dieser Menge:
Hinweis
Es ist , was man nicht mit der leeren Menge verwechseln darf. ist die einelementige Menge, die die leere Menge als einziges Element enthält.
Beispiele
[Bearbeiten]Wenden wir die Definition nun in einem Beispiel an. Gegeben sei die Menge folgender Instrumente:
besitzt zwei Elemente. Damit kommen als Teilmengen von nur solche Mengen infrage, die entweder null, eins oder zwei Elemente enthalten. Insgesamt wirst du für folgende vier Teilmengen finden:
- Die leere Menge ist die einzige Teilmenge von ohne Elemente: .
- Die zwei einelementigen Teilmengen von sind und :
- Als einzige zweielementige Teilmenge von kommt die Menge selbst infrage:
Alle vier Teilmengen können wir nun in die Potenzmenge zusammenfassen:
Weitere Beispiele sind:
Beispiel (Potenzmenge)
In der folgenden Animation ist die Erstellung der Potenzmenge dargestellt:
Eigenschaften und Verständnisfragen
[Bearbeiten]Wenn du dir die obigen Beispiele anschaust, dann ist die Anzahl der Elemente der bisherigen Potenzmengen stets eine Potenz von . Dies ist nicht verwunderlich, denn es gilt allgemein:
Satz (Größe der Potenzmenge einer endlichen Menge)
Sei eine beliebige endliche Menge mit Elementen. Dann hat die Potenzmenge genau Elemente.
Beweis (Größe der Potenzmenge einer endlichen Menge)
Um eine Teilmenge zu bilden, ist für jedes der Elemente von zu entscheiden, ob es zur Teilmenge gehört oder nicht. Daher gibt es dafür genau Möglichkeiten.
Bei dem obigen Instrumentenbeispiel ist beispielsweise . Damit muss die Potenzmenge Elemente besitzen. Die Beispielmenge hat drei Elemente und acht Teilmengen (x, y und z seien alle verschieden).
Verständnisfrage: Wie sehen folgende Potenzmengen aus? Wie viele Elemente besitzen die Potenzmengen?
Antwort:
- , die Potenzmenge besitzt zwei Elemente.
- , die Potenzmenge besitzt vier Elemente.
- , die Potenzmenge besitzt ein Element.
Verständnisfrage: Welche der folgenden Aussageformen sind für alle Mengen erfüllt?
Antworten:
- Allgemeingültige Aussageform
- Nicht allgemeingültige Aussageform
- Nicht allgemeingültige Aussageform
- Allgemeingültige Aussageform
- Allgemeingültige Aussageform
- Allgemeingültige Aussageform
Begründungen für die Antworten:
- Für jede Menge ist . Jede Menge ist also eine Teilmenge von sich selbst. Damit ist nach Definition auch stets .
- Nimm als Gegenbeispiel . Es ist die zweielementige Menge . Nun ist genau dann , wenn ein Element von ist. Es ist zwar aber . Die Potenzmenge besteht nämlich nur aus den beiden Mengen und , die beide ungleich sind (beachte . Also kann keine Teilmenge von sein. Zwar ist jede Menge Teilmenge von sich selbst, aber nicht jede Menge ist Teilmenge seiner Potenzmenge.
- Nimm als Gegenbeispiel . Es ist . Die leere Menge ist also das einzige Element von . Damit ist aber (die Menge der leeren Menge) kein Element von .
- Es ist genau dann , wenn ist. Wir haben bereits gesehen, dass stets Element von seiner Potenzmenge ist. Damit ist die Aussageform allgemeingültig.
- Es ist für jede Menge . Demnach ist auch für alle Mengen .
- Die leere Menge ist Teilmenge von jeder Menge. Da auch eine Menge ist, ist auch .
Verständnisfrage: Wie sieht die Menge aus?
Die leere Menge ist die einzige Teilmenge der leeren Menge und deswegen ist . Die einelementige Menge hat die zwei Teilmengen und . Also ist .
Verständnisfrage: Wie viele Elemente besitzt die Menge ?
Um die Anzahl der Elemente zu bestehen, können wir schrittweise vorgehen:
- besitzt null Elemente. Damit besitzt Element.
- besitzt dann Elemente.
- besitzt dann Elemente.
Die Menge besitzt also vier Elemente.
Leere Menge
[Bearbeiten]Mathe für Nicht-Freaks: Leere Menge
Verknüpfungen zwischen Mengen
[Bearbeiten]Einleitendes Beispiel
[Bearbeiten]Symmetrische Differenz
[Bearbeiten]Stelle dir vor, du hast eine Grundmenge gegeben:
In dieser Grundmenge gibt es eine Menge :
Und eine Menge :
Beide Mengen haben teilweise gemeinsame Elemente, es gibt aber auch Objekte, die nur in einer der beiden Mengen enthalten sind. Insgesamt ergibt sich also folgendes Bild:
Stelle dir nun vor, wir möchten die Menge aller Objekte beschreiben, die Elemente genau einer der Mengen und sind:
Diese Menge wird symmetrische Differenz der Mengen und genannt. Man schreibt für diese symmetrische Differenz . Hier ist eine Verknüpfung zwischen zwei Mengen. Der Operator verknüpft nämlich zwei Mengen und zu der neuen Menge . Die neue Menge enthält dabei alle Objekte, die Elemente genau einer der Mengen und sind. Dass eine Verknüpfung ist, ist analog dazu, dass die Addition + eine Verknüpfung ist. So wie die Addition + zwei Zahlen und zu einer neuen Zahl verknüpft, genauso verknüpft auch die symmetrische Differenz zwei Mengen und zu einer neuen Menge . Beispiel:
Genauso wie die Addition aus den beiden Zahlen und die Summe macht, verknüpft die symmetrische Differenz die beiden Mengen und zur neuen Menge .
Komplement
[Bearbeiten]Schauen wir uns noch ein weiteres Beispiel an: Stelle dir vor, wir wollen alle Objekte der Grundmenge beschreiben, die nicht in enthalten sind:
Diese Menge aller Objekte der Grundmenge, die nicht in enthalten sind, wird Komplement von genannt. Für diese Menge schreibt man . Während im obigen Beispiel der Operator war, ist hier der Operator. Im Unterschied zu wirkt auf nur einer Menge. Während nämlich zwei Mengen und zu einer neuen Menge verknüpft, nimmt nur eine Menge und macht daraus die neue Menge .
Überblick zu allen Mengenverknüpfungen
[Bearbeiten]So wie die symmetrische Differenz und das Komplement gibt es mehrere auf Mengen definierten Verknüpfungen. In der nachfolgenden Übersicht geben wir zunächst eine Übersicht über die wichtigsten Mengenverknüpfungen. In den nächsten Kapiteln werden wir diese dann einzeln vorstellen.
| Name der Verknüpfung | Schreibweise | Aussprache | Mengendiagramm | Definition | Erklärung |
|---|---|---|---|---|---|
| Durchschnitt | „ geschnitten “ | 
|
Die Menge aller Objekte, die sowohl in der Menge als auch in der Menge enthalten sind | ||
| Vereinigung | „ vereinigt “ | 
|
Die Menge aller Objekte, die in der Menge oder in der Menge enthalten sind (hier ist „oder“ als „und/oder“, also als einschließendes Oder, zu lesen) | ||
| Differenz | „ ohne “ | 
|
Die Menge aller Objekte, die in der Menge enthalten sind und keine Elemente der Menge sind | ||
| Symmetrische Differenz | „symmetrische Differenz von und “ | 
|
Die Menge aller Objekte, die in genau einer der Mengen und enthalten sind, also entweder in A oder in B, aber nicht in beiden | ||
| Komplement | „Komplement von “ | 
|
Die Menge aller Objekte (der Grundmenge), die keine Elemente von sind |
Tupel und geordnetes Paar
[Bearbeiten]Geordnetes Paar
[Bearbeiten]
Geordnete Paare begegnen uns bereits in der Schule: sie werden benötigt, um Koordinaten anzugeben, zum Beispiel beim "Schiffe versenken". Um ein Feld auf dem 10 mal 10 großen Spielfeld zu bestimmen, werden zwei Angaben benötigt: die Zeile und die Spalte. Zeilen sind hier mit einem großen Buchstaben benannt, Spalten haben Nummern . Wird vom Gegner das Feld aufgerufen, ist das Dreier-Schiff versenkt:

Ein anderes Beispiel ist das zweidimensionale Koordinatensystem für die reellen Zahlen, in dem die Punkte durch ein Paar reeller Zahlen angegeben werden. Dabei ist die Reihenfolge der Koordinaten wichtig! Der Punkt ist ein anderer als der Punkt . Es dürfen auch beide Koordinaten gleich sein, das ist beispielsweise beim Ursprung des Koordinatensystems der Fall.
Definition (Geordnetes Paar)
bezeichnet das geordnete Paar aus den Objekten und . Dabei ist die erste oder linke Komponente, die zweite oder rechte Komponente. Zwei geordnete Paare sind sind nur dann gleich, wenn beide Komponenten gleich sind:
Für geordnete Paare werden oft auch spitze Klammern oder andere besondere Klammern verwendet.
Warnung
Das geordnete Paar darf nicht mit der Zweiermenge verwechselt werden! Während bei geordneten Paaren die Reihenfolge relevant ist und beispielsweise , spielt die Reihenfolge in der Menge keine Rolle. Hier ist .
Verständnisfrage: Welche Bedingungen müssen für und gelten, damit folgende Paare gleich sind?
- und
- und
- und
Antwort:
- Es ist genau dann, wenn und .
- Es ist genau dann, wenn .
- Es ist, da anderenfalls und gelten müsste.
n-Tupel
[Bearbeiten]
Der Begriff des geordneten Paares lässt sich verallgemeinern. Werden drei Komponenten betrachtet, erhält man Tripel, mit vier Komponenten Quadrupel, usw. Allgemein kann man zu jeder natürlichen Zahl sogenannte -Tupel betrachten. Sie sollen die folgende Bedingung erfüllen:
Zwei -Tupel sind nur dann gleich, wenn sie komponentenweise gleich sind, formalisiert:
n-Tupel lassen sich mit Hilfe von geordneten Paaren darstellen. Für 3-Tupel setzt man , für 4-Tupel , usw. So kann man schrittweise für alle natürlichen Zahlen n-Tupel erklären. Sind n-Tupel definiert, erzeugt man (n+1)-Tupel durch: . Diese Art der Definition wird rekursiv genannt:
Definition (Rekursive Definition der -Tupel ())
Rekursionsanfang: Für sei das 2-Tupel das geordnete Paar.
Rekursionsschritt: Seien -Tupel bereits definiert. Dann definieren wir -Tupel durch:
Wir müssen nun nachweisen, dass diese Definition tatsächlich das leistet, was wir von -Tupeln erwarten. Nämlich das zwei -Tupel nur dann gleich sind, wenn alle Komponenten des Tupels gleich sind.
Satz
Für zwei -Tupel gilt:
Beweis
Induktion über :
Induktionsanfang: Für folgt die Behauptung aus der Definition des geordneten Paares.
Induktionsschritt: Die Behauptung gelte für . Dann folgt für :
Beweisende ✔
Alternative Definition der Tupel
[Bearbeiten]Die Definition der -Tupels mit Hilfe des geordneten Paares hat zur Folge, dass jedes -Tupel ein geordnetes Paar ist. Für die meisten Zwecke ist das nicht störend und die gesamte elementare Theorie der Relationen und Funktionen kann darauf aufgebaut werden. Es gibt aber auch eine schärfere Tupel-Definition, die eine zusätzliche Forderung an die Gleichheit von Tupeln stellt:
Definition (Alternative Definition der Gleichheit von Tupeln)
Zwei Tupel beliebiger Stellenzahl sind dann und nur dann gleich, wenn sie
- dieselbe Stellenzahl haben und
- komponentenweise gleich sind.
Formalisiert:
Kartesisches Produkt
[Bearbeiten]Kartesisches Produkt
[Bearbeiten]Das kartesische Produkt ist eine besondere Verknüpfung zwischen zwei Mengen. Die Schreibweise für das kartesische Produkt zwischen den Mengen und ist (ausgesprochen: „ kreuz “). Das kartesische Produkt ist die Menge aller geordneten Paare mit und . So ist beispielsweise:
Beispiele/Übungsaufgabe: Schreibe folgende kartesische Produkte aus.
Antwort:
Definition (kartesisches Produkt)
Das kartesische Produkt zweier Mengen und ist die Menge aller geordneten Paare wobei ein Element der Menge und ein Element der Menge ist:
Verständnisfrage: Sei eine endliche Menge mit Elementen und eine endliche Menge mit Elementen. Wie viele Elemente enthält die Menge ?
Seien bis die Elemente der Menge und bis die Elemente der Menge . Dann sieht so aus:
Man sieht, dass es für jedes genau verschiedene mit gibt. Damit enthält genau verschiedene geordnete Paare als Elemente.
Man kann auch das kartesische Produkt von mehr als zwei Mengen bilden. Analog zum Fall von zwei Mengen ist das kartesische Produkt der drei Mengen , und gleich der Menge aller 3-Tupel mit , und :
Verständnisfrage: Was ist ?
Allgemein ist das kartesische Produkt der Mengen bis die Menge aller n-Tupel mit , und so weiter bis :
Für kartesische Produkte von Mengen mit sich selber gibt es eine abkürzende Schreibweise: Es ist , und so weiter. Allgemein ist
Verständnisfrage: Was ist ?
Produktschreibweise
[Bearbeiten]Für das kartesische Produkt von mehreren Mengen, gibt es auch die kompaktere Schreibweise . Diese ist definiert durch
Du siehst, dass die obige Schreibweise ähnlich dem Produkt reeller Zahlen ist, welches du vielleicht schon aus der Schule kennst. Der Unterschied ist der, dass hier anstatt Zahlen Mengen verknüpft werden und die Verknüpfung nicht die Multiplikation sondern das kartesische Produkt ist.
Relation
[Bearbeiten]Wie können Eigenschaften und Beziehungen modelliert werden?
[Bearbeiten]Im vorherigem Kapitel haben wir das Konzept der Menge kennengelernt, mit der Objekte zu einem Ganzen zusammengefasst werden können. In diesem Kapitel werden wir uns damit beschäftigen, wie Eigenschaften von und Beziehungen zwischen Objekten modelliert werden können. Diese Eigenschaften von bzw. Beziehungen zwischen Objekten werden Relationen genannt. Hierzu werden wir uns zunächst einige Beispiele anschauen, um dann das Konzept der Relationen einzuführen.
Modellierung von Eigenschaften
[Bearbeiten]
Sei die Menge aller zur Zeit lebenden Menschen. Wir wollen nun das (biologische) Geschlecht der Menschen beschreiben. Dabei soll angenommen werden, dass jeder Mensch entweder männlich oder weiblich aber nicht beides gleichzeitig ist. Wie können wir das Geschlecht eines Menschen mit Hilfe von Mengen beschreiben?
Eine in der Mathematik häufig benutzte Möglichkeit ist folgende: Wir definieren eine neue Menge , die genau all diejenigen Menschen enthält, die wir als weiblich bezeichnen wollen. Die Menge ist also definiert durch . Damit können wir schreiben, um auszudrücken, dass weiblich ist.
Ein Vorteil dieser Modellierung ist der, dass wir Mengenverknüpfungen verwenden können, um neue Eigenschaften zu beschreiben. So ist die Menge aller männlichen Menschen, da wir davon ausgehen, dass jeder nicht weibliche Mensch männlich ist. Damit können wir für „ ist männlich“ schreiben.
Wir fassen zusammen: Wenn wir eine Grundmenge haben und in ihr eine Eigenschaft beschreiben wollen, so können wir eine neue Menge definieren, die genau all diejenigen Objekte aus enthält, die diese Eigenschaft besitzen.
Modellierung von zweistelligen Beziehungen
[Bearbeiten]
Sei wieder die Menge aller Menschen, die zur Zeit leben. Wie kann nun die Liebesbeziehung zwischen zwei Menschen beschrieben werden? Wie können wir also modellieren, dass ein Mensch einen anderen Menschen liebt?
Auch hierfür führen wir eine neue Menge ein: Die Menge soll genau all diejenigen Paare von Menschen enthalten, für die gilt, dass die Person liebt. Wir definieren damit . So können wir schreiben, um auszudrücken, dass den Menschen liebt. Damit haben wir eine Modellierung für die Liebesbeziehung gefunden.
Rechts siehst du ein Beispiel für eine solche Modellierung. Du siehst, dass Kristina und Max sowie Julia und Anna ein Liebespärchen sind. Hannes ist zwar in Max verliebt, jedoch wird seine Liebe nicht erwidert. Stefan liebt keine Person der Grundmenge und wird auch von keiner anderen Person geliebt.
Verständnisfrage: Wieso werden für die Beziehung „ liebt “ Paare und nicht Mengen verwendet?
Bekanntermaßen ist bei der aufzählenden Mengenschreibweise die Reihenfolge der Objekte irrelevant. So ist . Jedoch ist die Beziehung „ liebt “ zwischen den Personen und eine andere Beziehung als „ liebt “. Dementsprechend können Mengen der Form nicht zur Beschreibung der Liebesbeziehung herangezogen werden.
Im Gegensatz zu Mengen besitzen Paare die notwendige Eigenschaft, dass die Reihenfolge ihrer Komponenten für die Identitätsbeziehung relevant ist. So ist dann und nur dann, wenn und ist.
Zusammenfassung: Um eine zweistellige Beziehung in einer Grundmenge zu modellieren, können wir eine neue Menge definieren, die all diejenigen Paare der Objekte und aus enthält, die in Beziehung zueinander stehen. Damit ist .

Mit der Liebesbeziehung haben wir ein Beispiel für eine Beziehung von Objekten innerhalb einer Menge kennen gelernt. Wie können wir Beziehungen von Objekten unterschiedlicher Mengen modellieren?
Nehmen wir hierzu die Beziehung „ studiert “. Dabei sei die Menge der Menschen und die Menge der Studienfächer. Um nun die Beziehung „ studiert “ zu beschreiben, definieren wir eine neue Menge derjenigen Paare mit und , so dass der Mensch das Fach studiert. So wird die Beziehung „ studiert “ modelliert durch die Menge . Es ist damit .
Auf der linken Seite siehst du ein konkretes Beispiel für diese Art der Modellierung. Hier sind Hannes, Anna und Julia Studenten, während Max nicht studiert. Hannes studiert Geografie und Anna und Julia studieren Mathematik. Das Studienfach Kommunikationswissenschaften wird in unserem Beispiel von niemandem studiert.
Hinweis
In unseren Beispielen gehen wir davon aus, dass immer eindeutig festgestellt werden kann, ob eine Person eine andere Person liebt beziehungsweise ob eine Person ein konkretes Fach studiert. In der Realität sind diese Fragen aber selten eindeutig beantwortbar. Auch haben wir nicht spezifiziert, welche Art von Liebe wir meinen. Zählt beispielsweise die Liebe von Eltern zu ihren Kindern auch dazu?
Obige Relationen stellen nur einführende Beispiele dar. Übersehe bitte die Unzulänglichkeiten, die diese Relationen haben.
Modellierung von dreistelligen Beziehungen
[Bearbeiten]
Zum Schluss schauen wir uns ein Beispiel für eine Beziehung an, in der drei Objekte involviert sind. Ein Beispiel für eine solche Beziehung ist die Relation „ lernt beim Lehrer “. Dabei sind und Menschen der Menge und ein Schulfach der Menge .
Diese Beziehung beschreiben wir über ein 3-Tupel. Wir definieren eine neue Menge von 3er-Tupeln mit und für die gilt, dass der Mensch beim Lehrer das Schulfach lernt. Es ist also .
Auf der rechten Seite siehst du eine Abbildung, die diese Modellierung veranschaulicht. Hier ist Anna Lehrerin der Fächer Mathematik und Geografie. Julia ist Schülerin im Mathematikunterricht und Hannes Schüler im Geografieunterricht bei Anna. Max ist weder Schüler noch Lehrer. Außerdem gibt es in unserem Beispiel weder Schüler noch Lehrer für das Fach Kunst.
Definitionen
[Bearbeiten]Aus den obigen Beispielen lässt sich ein Prinzip ablesen, wie Relationen in der Mathematik modelliert werden. Sei dazu eine -stellige Relation zwischen den Mengen bis . Dies bedeutet, dass eine Relation ist, die zwischen Objekten bis besteht und dass , , …, ist. Wie wird in der Mathematik modelliert?
wird modelliert als Menge von -Tupeln der Objekte bis mit , , …, . Dabei enthält genau diejenigen -Tupel von Objekten, die in Relation zueinander stehen. Somit ist eine Teilmenge des kartesischen Produkts . Zur Erinnerung: ist die Menge aller -Tupel mit , , …, . Die Relation ist daher eine Teilmenge von .
Definition (Relation)
Eine -stellige Relation zwischen Objekten der Mengen bis ist eine Teilmenge des kartesischen Produkts .
Diese Art der Relation kann nicht die Qualität einer Relation beschreiben. Entweder stehen bestimmte Objekte in Relation zueinander oder nicht, aber sie können nicht mehr oder weniger in Relation zueinander stehen. Im Beispiel der Liebesbeziehung bedeutet dies, dass entweder die Person liebt oder nicht. Jedoch können wir mit Hilfe der obigen Definition nicht beschreiben, dass die Person mehr liebt als die Person oder dass die Person mag, aber nicht liebt.
Die häufigste Art der Relation ist die binäre Relation:
Definition (binäre Relation)
Eine binäre Relation ist eine zweistellige Relation. Eine binäre Relation ist damit eine Beziehung, die zwischen Objekten zweier Mengen und existiert und damit eine Teilmenge des kartesischen Produkts .
Für eine binäre Relation gibt es eine eigene Schreibweise für die Relation zwischen zwei Objekten und . Um auszudrücken, dass mit in Relation steht, kann man neben auch schreiben. Ein Beispiel hierfür ist die Relation , die „ ist kleiner als “-Relation auf den reellen Zahlen (hier ist „“ das Zeichen für die Relation). Anstatt nun zu schreiben (was bedeutet, dass 2 kleiner als 3 ist), kann man auch schreiben, wie du es bereits aus der Schule kennst.
Frage: Sei . Wie sehen folgende Relationen als Mengen von Tupeln aus?
- : „ ist eine gerade Zahl.“
- : „ ist eine Quadratzahl.“
- : „ ist kleiner als “
- : „ ist ein Teiler von “ oder gleichwertig „die Division durch hinterlässt keinen Rest“
- : „“
Antwort:
Binäre Relation
[Bearbeiten]Binäre Relationen sind zweistellige Relationen, also Teilmengen des kartesischen Produkts der Mengen und .
Homogene und heterogene Relationen
[Bearbeiten]Eine binäre Relation heißt homogen, wenn die Mengen und identisch sind. Im Fall nennt man die Relation heterogen.
Homogene Relationen beschreiben damit Beziehungen innerhalb einer Menge und heterogene Relationen beschreiben Beziehungen von Objekten aus unterschiedlichen Mengen.
Verständnisfrage: Welche der folgenden Relationen ist homogen und welche sind heterogen?
- „Die Person liebt die Person “
- „Die natürliche Zahl ist kleiner als die rationale Zahl “
- „Die natürliche Zahl teilt die natürliche Zahl “
- „Die Personen und sind in derselben Klasse“
- „Die Person studiert das Fach “
Antwort:
- homogen
- heterogen
- homogen
- homogen
- heterogen
Darstellung endlicher binärer Relationen
[Bearbeiten]Es gibt zwei wesentliche Möglichkeiten, binäre Relationen zwischen endlichen Mengen darzustellen: Pfeildiagramme und Relationsmatrizen. Diese möchten wir dir anhand der folgenden Relationen vorstellen:
- heterogene Relation : „Der Fluss fließt im Land “, wobei ein Fluss der Menge und ein Land der Menge ist.
- homogene Relation : „ ist ein Nachfolger von “ auf der Grundmenge .
Pfeildiagramm
[Bearbeiten]Die erste Möglichkeit der Darstellung sind Pfeildiagramme. Hier werden alle Objekte, die in Relation zueinander stehen, durch Pfeile miteinander verbunden. So sieht die heterogene Relation „Der Fluss fließt im Land “ im Pfeildiagramm so aus:

Da die zweite Relation „ ist ein Nachfolger von “ homogen ist, kann hier auf die Darstellung zweier Mengen verzichtet werden:
Verständnisfrage: Erstelle die Pfeildiagramme für folgende binäre Relationen auf der Grundmenge
- ist größer als
- ist ein Teiler von
- ergibt bei Division mit 2 denselben Rest wie
Relationsmatrix
[Bearbeiten]Bei der Relationsmatrix wird eine Tabelle für die Relation aufgestellt. Hier wird in jeder Zelle eingetragen, ob das Objekt der aktuellen Spalte mit dem Objekt der aktuellen Zeile in Relation steht. Die Relation „Der Fluss fließt im Land “ sieht als Relationsmatrix so aus:
| Irland | Deutschland | Niederlande | Ukraine | |
| Donau | X | X | ||
| Elbe | X | |||
| Nil | ||||
| Rhein | X | X |
Die Relationsmatrix der Relation „ ist ein Nachfolger von “ auf der Menge ist folgende:
| 1 | 2 | 3 | 4 | |
| 1 | ||||
| 2 | X | |||
| 3 | X | |||
| 4 | X |
Die Hauptdiagonale in der Relationsmatrix zu einer homogenen Relation ist die Menge der Zellen, bei denen die Objekte der Spalte dieselben sind wie die Objekte der Zeile:
| 1 | 2 | 3 | n | ||
| 1 | Haupt- | ||||
| 2 | dia- | ||||
| 3 | gona- | ||||
| n | le |
Verständnisfrage: Erstelle die Relationsmatrizen für folgende binäre Relationen auf der Grundmenge
- ist größer als
- ist ein Teiler von
- ergibt bei Division mit 2 denselben Rest wie
Relationsmatrix für die Relation „ ist größer als “ auf der Grundmenge :
| 1 | 2 | 3 | 4 | |
| 1 | ||||
| 2 | X | |||
| 3 | X | X | ||
| 4 | X | X | X |
Relationsmatrix für die Relation „ ist ein Teiler von “ auf der Grundmenge :
| 1 | 2 | 3 | 4 | |
| 1 | X | X | X | X |
| 2 | X | X | ||
| 3 | X | |||
| 4 | X |
Relationsmatrix für die Relation „ ergibt bei Division mit 2 denselben Rest wie “ auf der Grundmenge :
| 1 | 2 | 3 | 4 | |
| 1 | X | X | ||
| 2 | X | X | ||
| 3 | X | X | ||
| 4 | X | X |
Wichtige Begriffe
[Bearbeiten]Bildmenge
[Bearbeiten]
Wir betrachten nochmals die Relation „Der Fluss fließt im Land “. Wir möchten jetzt zu einem bestimmten Fluss alle Länder wissen, durch die er fließt. Für die Donau stellen wir beispielsweise fest, dass sie durch Deutschland und die Ukraine fließt. Anders ausgedrückt: Die Donau steht mit Deutschland und der Ukraine in Relation.
Wir können zu einem beliebigen Element aus der Grundmenge alle Elemente heraussuchen, die mit in Relation stehen. Diese Menge wird als Bildmenge oder als das Bild von bezeichnet. Für das Bild von unter der Relation schreibt man . Der Ausdruck bezeichnet also die Menge aller Elemente, die mit in Relation stehen. Er ist eigentlich recht intuitiv, denn ist die Menge aller , die nach dem stehen können, wo also eine wahre Aussage ist.
Du wirst vielleicht schon den Bildbegriff für Funktionen kennen, welcher die Menge aller Funktionswerte für eine gegebene Menge von Argumenten ist. Dies ist kein Zufall, denn Funktionen können als spezielle binäre Relationen aufgefasst werden (solche, bei dem es für jedes genau ein mit gibt). Der Begriff der Bildmenge für Relationen ist in diesem Fall mit der Bildmenge der Funktion identisch. Der Begriff des Bildes einer Relation ist damit eine Verallgemeinerung des Bildes von Funktionen.
Im Folgenden bezeichnet eine binäre Relation zwischen den Mengen und .
Definition (Bildmenge eines Elements)
Zu einem bezeichnet das Bild von unter die Menge aller , die mit in Relation stehen:
Verständnisfrage: Was ist , also das Bild vom Rhein unter
Es ist .
Verständnisfrage: Sei . Was ist ?
Weil und ist, ist .
Die obige Definition von Bild beschränkt sich auf einen einzigen Eingabewert. Es sollte auch möglich sein ein Bild für beliebig viele Elemente zu erhalten, also für eine Menge von Eingabewerten. Dazu suchen wir uns einfach alle Elemente heraus, die mindestens mit einem dieser Eingabewerten in Relation stehen. Wenn wir beispielsweise das Bild der Donau und des Rheins wissen wollen, dann ist dies die Menge . Deutschland steht sowohl mit der Donau und dem Rhein in Relation und gehört somit zur gesuchten Bildmenge. Die Ukraine steht mit der Donau in Relation, womit es auch Element der Bildmenge ist (es steht mit mindestens einem Eingabewert in Relation). Gleiches gilt für Niederlande, die mit dem Rhein in Relation steht.
Definition (Bildmenge einer Menge)
Zu bezeichnet das Bild von unter die Menge aller , die mit mindestens einem Element aus in Relation stehen:
Urbild
[Bearbeiten]Wenn wir für ein beliebiges Objekt die Objekte heraussuchen können, die mit diesem in Relation stehen, können wir das natürlich in „beide Richtungen“ tun. Stelle dir vor, wir suchen jetzt nicht mehr zu einem Fluss die dazugehörigen Länder, sondern wir haben ein Land und wollen die Flüsse wissen, die in diesem Land fließen. Dies entspricht der Suche nach dem Urbild. Beispielsweise ist das Urbild der Ukraine die Donau. Für das Urbild von schreibt man . Dabei ist die Menge aller Objekte die vor stehen können, also die Menge aller mit .
Definition (Urbildmenge)
Zu einem bezeichnet das Urbild von unter die Menge aller , die mit in umgekehrter Relation stehen:
Verständnisfrage: Was ist ?
.
Einschränkung einer Relation
[Bearbeiten]Ist eine Relation auf , so lässt sich diese auf eine Teilmenge reduzieren. Die so entstehende Relation enthält nur die Paare von , deren Elemente in liegen. Die reduzierte Relation heißt Einschränkung:
Definition (Einschränkung einer Relation)
Ist und so heißt die Einschränkung von auf . Häufig wird die Einschränkung einer Relation ebenfalls mit bezeichnet.
Offensichtlich gilt .
Beispiel (Einschränkung einer Relation)
sei die Kleiner-Gleich-Relation auf den reellen Zahlen , also .
Dann ist die Kleiner-Gleich-Relation auf den natürlichen Zahlen und die Kleiner-Gleich-Relation auf den ganzen Zahlen .
Konverse Relation
[Bearbeiten]Es ist auch möglich, eine Relation umzukehren. Eine solche umgekehrte Relation wird konverse oder auch inverse Relation genannt. Sie entsteht anschaulich dadurch, dass man alle Pfeile im Pfeildiagramm umdreht. Bezüglich der konversen Relation steht genau dann in Relation zu , wenn bezüglich der ursprünglichen Relation mit in Beziehung steht.
Definition (Konverse Relation)
Sei eine Relation. Die konverse Relation kehrt alle Tupel aus um. Es ist genau dann , wenn ist.
Beispiel (Konverse Relationen)
Die Relation „ ist ein Nachfolger von “ hat die konverse Relation „ ist ein Vorgänger von “. Es ist beispielsweise (3 ist Nachfolger von 2). Damit ist (2 ist Vorgänger von 3).
Ein weiteres Beispiel: Es gilt (2 teilt 8), also gilt für die Konverse . Konkret heißt das: ist ein Vielfaches von .
Bei der Definition des Urbildes haben wir gesagt, dass wir alle Elemente suchen, die in umgekehrter Richtung in Relation stehen. Dies war wenig intuitiv. Allerdings kann man sich das jetzt mithilfe der konversen Relation klar machen. Denn das Urbild einer Relation ist einfach das Bild der konversen Relation. Beschrieben ist es aber schon fast schwerer zu sehen als wenn man einfach die Definitionen hinschreibt und umformt:
Das Bild der konversen Relation ist . Das ist aber gemäß unserer bisherigen Definitionen die selbe Menge wie (hier haben wir die Definition der konversen Relation eingesetzt). Der letzte Ausdruck entspricht der Definition des Urbilds für .
Äquivalenzrelation
[Bearbeiten]Einführendes Beispiel
[Bearbeiten]
Oftmals verhalten sich verschiedene Objekte in bestimmten Aspekten gleich oder besitzen gleiche, beziehungsweise sehr ähnliche Eigenschaften. So ist das Ergebnis einer Drehung von dasselbe wie bei einer Drehung von . Exemplare von Büchern derselben ISB-Nummer besitzen denselben Inhalt und Autor. In diesem Kapitel wirst du die mathematischen Werkzeuge kennen lernen, mit denen du solche Äquivalenzen zwischen Objekten einer Grundmenge sauber beschreiben kannst.

Eine Beziehung, die die Gleichwertigkeit zwischen Objekten unter bestimmten Aspekten ausdrückt, wird Äquivalenzrelation genannt. Wir werden sehen, dass folgende Relation auf der Grundmenge aller bisher gedruckter Buchexemplare eine Äquivalenzrelation ist:
und besitzen dieselbe ISB-Nummer.
Frage: Welche Eigenschaften besitzt diese Relation?
Die Relation ist
- reflexiv: Für jedes Buchexemplar gilt: und besitzen dieselbe ISB-Nummer. Sprich: ein Buchexemplar hat immer dieselbe ISB-Nummer wie es selbst.
- nicht irreflexiv: Weil die Grundmenge nicht leer ist, gibt es mindestens ein Buchexemplar . Dieses steht mit sich selbst in Relation, weil die Relation reflexiv ist, und damit ist die Relation nicht irreflexiv.
- symmetrisch: Wenn und dieselbe ISB-Nummer besitzen, dann besitzen auch und dieselbe ISB-Nummer.
- nicht antisymmetrisch: Es gibt mindestens zwei verschiedene Buchexemplare und , die dieselbe ISB-Nummer besitzen. Für diese beiden Exemplare steht zwar in Relation zu und in Relation zu , aber es ist .
- transitiv: Wenn die Buchexemplare und dieselbe ISB-Nummer besitzen und die Buchexemplare und dieselbe ISB-Nummer besitzen, dann besitzen auch und dieselbe ISB-Nummer.
- nicht linear: Nehme zwei verschiedene Buchexemplare und , so dass beide eine verschiedene ISB-Nummer haben. Dann steht weder mit noch mit in Relation. Damit ist die Relation nicht linear.
Wir werden sehen, dass die Eigenschaften der Reflexivität, Symmetrie und Transitivität der obigen Relation, genau diejenigen sind, die hinreichend und notwendig für eine Äquivalenzrelation sind.

Es gibt eine weitere Möglichkeit, Äquivalenzrelationen zu beschreiben: Die Möglichkeit, die Grundmenge in verschiedene disjunkte Teilmengen zu zerlegen. Nehmen wir wieder das obige Beispiel mit den Büchern. Stell dir vor, wir fassen alle Exemplare in eine Menge zusammen, die dieselbe ISB-Nummer besitzen. Es kommen also genau dann zwei Bücher und in dieselbe Menge, wenn sie dieselbe ISB-Nummer besitzen, wenn also in Relation zu steht. Eine so entstandene Teilmenge werden wir später Äquivalenzklasse nennen.
Das Ergebnis ist eine Zerlegung der Grundmenge aller gedruckter Buchexemplare in disjunkte Teilmengen. Jede dieser Teilmengen steht für ein konkretes Schriftwerk eines Autors. Denn jede ISB-Nummer bezeichnet eindeutig ein solches Schriftwerk und jede Teilmenge enthält genau diejenigen Exemplare, die dieselbe ISB-Nummer besitzen. Man kann diese Teilmengen nun als neue Objekte betrachten. Dadurch erhältst du die Menge aller Schriftwerke. Jedes Schriftwerk ist dabei als Menge, nämlich der Menge aller Exemplare dieses Schriftwerks, modelliert. Durch eine Zerlegung einer Menge mit Hilfe einer Äquivalenzrelation können also neue Objekte modelliert werden (dies ist eine gängige Vorgehensweise in der Mathematik).
Definitionen
[Bearbeiten]Äquivalenzrelation
[Bearbeiten]Eine Äquivalenzrelation ist folgendermaßen definiert:
Definition (Äquivalenzrelation)
Eine Äquivalenzrelation ist eine homogene, binäre Relation auf einer Grundmenge, die folgende Eigenschaften besitzt:
- reflexiv: "Für jedes Element aus der Grundmenge gilt: "
- symmetrisch: "Für je zwei Elemente aus der Grundmenge gilt: "
- transitiv: "Für je drei Elemente aus der Grundmenge gilt: und "
Zwei Elemente, die bezüglich einer Äquivalenzrelation in Relation stehen, heißen äquivalent. Wenn zwei Elemente und äquivalent zueinander bezüglich einer Äquivalenzrelation sind, schreibt man oft oder einfach anstatt der sonst üblichen Schreibweise beziehungsweise .
Verständnisfrage: Was musst du tun, wenn du entscheiden sollst, ob eine Relation eine Äquivalenzrelation ist oder nicht?
Verständnisfrage: Welche der folgenden Relationen ist eine Äquivalenzrelation?
- „ und gehen in dieselbe Klasse“ auf der Menge aller Schüler einer Schule
- „“ auf der Menge der ganzen Zahlen
- „ und sind ungerade“ auf der Menge
- „ und besitzen denselben Rest bei der Division durch zwei“ auf der Menge
- „“ auf einer beliebigen, nicht leeren Grundmenge
Antwort:
- Äquivalenzrelation
- keine Äquivalenzrelation (die Relation ist nicht symmetrisch – so ist zwar , aber nicht auch )
- keine Äquivalenzrelation (die Relation ist nicht reflexiv – beispielsweise steht 2 nicht mit sich selbst in Relation)
- Äquivalenzrelation
- Äquivalenzrelation
Verständnisfrage: Wie viele totale Äquivalenzrelationen auf einer Grundmenge gibt es? (Eine Relation ist total, wenn für jeweils zwei Elemente und mindestens ein Element mit einem anderen in Relation steht. Sprich es gilt oder .)
Sei eine Äquivalenzrelation auf der Grundmenge . Seien beliebig. Da total ist, steht in Relation zu oder in Relation zu . Sei oBdA . Auf Grund der Symmetrie ist dann aber auch . Damit steht jedes Element mit jedem anderen Element in Relation.
Es gibt also genau eine totale Äquivalenzrelation auf einer Grundmenge , nämlich , bei der jedes Element mit jedem anderen in Relation steht.
Äquivalenzklasse
[Bearbeiten]Im obigen Beispiel haben wir durch die Äquivalenzrelation die Grundmenge in disjunkte Teilmengen zerlegt, indem wir alle Buchexemplare in einer Teilmenge zusammengefasst haben, die in Relation steht. Eine solche Teilmenge wird Äquivalenzklasse genannt und mit bezeichnet:
Definition (Äquivalenzklasse)
Eine Äquivalenzklasse ist die Menge aller Elemente der Grundmenge , die zum Element äquivalent sind:
Wenn du die Relation explizit angeben musst, kannst du auch schreiben. Es ist dann
Das Element in der Schreibweise nennt man Repräsentant oder Vertreter. Ist unsere obige Definition für Äquivalenzklassen korrekt im Sinne, dass wenn und äquivalent zueinander sind? Dies beantwortet der folgende Satz:
Satz
Ist , dann ist .
Beweis
Sei . Zu zeigen ist, dass und ist. Sei also beliebig. Es gilt damit . Da außerdem ist, folgt aus der Transitivität der Äquivalenzrelation, dass auch ist. Dies bedeutet aber . Da beliebig war, ist .
Dass auch ist, kannst du analog beweisen.
Es gilt auch die Umkehrung des obigen Satzes:
Satz
Aus folgt .
Beweis
Sei . Damit ist , also für alle . Nun ist , da aufgrund der Reflexivität der Äquivalenzrelation. Daraus folgt, dass und somit nach Definition ist.
Zusammen ergeben die vorherigen beiden Sätze folgenden wichtigen Satz:
Satz (Zusammenhang zwischen Äquivalenz der Repräsentanten und der Äquivalenzklassen)
Für Äquivalenzklassen und deren Vertreter gilt folgender Zusammenhang:
Greift man aus jeder Äquivalenzklasse ein Element heraus, so erhält man ein Vertretersystem:
Definition (Vertretersystem, Repräsentantensystem)
Ist eine Äquivalenzrelation auf , so ist ein Vertretersystem (oder Repräsentantensystem) eine Teilmenge von , die aus jeder Äquivalenzklasse von genau ein Element enthält.
Verständnisfrage: Wie sehen die Äquivalenzklassen der folgenden Äquivalenzrelationen aus? Gib ein mögliches Vertretersystem an.
- „ und gehen in dieselbe Klasse“ auf der Menge aller Schüler einer Schule
- „ und besitzen denselben Rest bei der Division durch zwei“ auf der Menge
- „“ auf einer beliebigen, nicht leeren Grundmenge
Antwort:
- Die Menge der Äquivalenzklassen ist die Menge aller Klassen der Schule. Dabei ist jede Klasse als Menge aller Schüler modelliert, die diese Klasse besuchen. Ein mögliches Vertretersystem ist die Menge aller Klassensprecher.
- Es gibt zwei Äquivalenzklassen: Die Menge aller Zahlen, die restlos durch 2 geteilt werden können, und die Menge aller Zahlen, die bei Division durch 2 den Rest 1 lassen. Damit zerfällt die Grundmenge in die Menge der geraden und in die Menge der ungeraden Zahlen. Ein Vertretersystem ist z.B.
- Jede Äquivalenzklasse ist einelementig. Die Grundmenge zerfällt also in die Menge (Beachte, dass dies eine Menge von einelementigen Mengen ist. Die Zerlegungsmenge ist ungleich der Grundmenge). Das einzige Vertretersystem ist selbst.
Zerlegung einer Menge
[Bearbeiten]Oft haben wir bereits von der Zerlegung einer Menge gesprochen (welche in der Mengenlehre auch Partition genannt wird). Eine Zerlegung ist eine Aufteilung einer Grundmenge in verschiedene Teilmengen, so dass jedes Element aus der Grundmenge in genau einer Teilmenge enthalten ist. Eine Zerlegung kann man also als eine Menge von Teilmengen der Grundmenge auffassen. Damit garantiert ist, dass jedes Element der Grundmenge in genau einer Teilmenge enthalten ist, müssen zusätzliche Bedingungen erfüllt sein, die in der folgenden Definition zusammengefasst sind:
Definition (Zerlegung einer Menge)
Eine Zerlegung einer Menge ist eine Menge von Teilmengen von (also ), welche folgende Bedingungen erfüllt:
-
Die Vereinigung aller Mengen von ergibt die Menge :
-
Alle Mengen von sind paarweise disjunkt:
-
Alle Mengen von sind nicht leer:
Im nächsten Abschnitt werden wir den Zusammenhang zwischen Äquivalenzrelation und der durch ihr definierten Zerlegung genauer untersuchen. Alternativ kann die Zerlegung durch folgende Aussagen charakterisiert werden:
- ,
- ,
- .
Zusammenhang zwischen Äquivalenzrelationen und der Zerlegung einer Menge
[Bearbeiten]Wollen wir nun den Zusammenhang zwischen Äquivalenzrelationen und der Zerlegung einer Menge untersuchen. Im einführenden Beispiel haben wir gesehen, dass eine Äquivalenzrelation eine Zerlegung der Grundmenge definiert, indem man alle äquivalenten Elemente in einer Teilmenge, der Äquivalenzklasse, zusammenfasst. Eine solche Zerlegung einer Menge durch eine Äquivalenzrelation wird mit bezeichnet und in bestimmten Kontexten der Mathematik Quotientenraum oder Faktorraum genannt. Die Zerlegung der Grundmenge ist also:
Doch ist dies wirklich eine Zerlegung im Sinne der obigen Definition? Beweisen wir es:
Satz (Äquivalenzrelationen induzieren eine Zerlegung)
Sei eine Äquivalenzrelation auf der Grundmenge . Dann ist die Menge aller Äquivalenzklassen eine Zerlegung der Grundmenge.
Beweis (Äquivalenzrelationen induzieren eine Zerlegung)
Um zu zeigen, dass eine Zerlegung von ist, müssen wir folgende Behauptungen beweisen:
Beweisschritt:
Es ist genau dann , wenn und wenn ist.
Beweisschritt:
Jede Äquivalenzklasse ist nach Definition eine Teilmenge von . Damit ist auch die Vereinigung aller Äquivalenzklassen eine Teilmenge von .
Beweisschritt:
Sei beliebig. Da auf Grund der Reflexivität von das Element in Relation zu sich selbst steht, ist . Nun ist und damit
Da beliebig war, ist .
Beweisschritt:
Seien mit . Dann ist und für ein .
Widerspruchsbeweis: Sei . Dann gibt es ein mit und . Damit ist und . Aus der Transitivität folgt und damit aus dem Satz über den Zusammenhang zwischen Äquivalenzklassen und der Äquivalenz der Repräsentanten des vorherigem Abschnitts. Jedoch ist ein Widerspruch zu Annahme , so dass sein muss.
Beweisschritt:
Sei beliebig. Dann ist für ein . Wegen der Reflexivität von der Äquivalenzrelation ist und damit . Daraus folgt, dass insbesondere ist.
Doch wie sieht es umgekehrt aus? Kannst du aus einer vorgegebenen Partition einer Menge so eine Äquivalenzrelation definieren, dass ist?
Frage: Wie kann eine solche Äquivalenzrelation aussehen?
Damit die induzierte Menge der Äquivalenzrelation gleich der Partitionsmenge sein kann, muss für alle gelten:
Damit gibt es nur einen möglichen Kandidaten einer Äquivalenzrelation:
Satz (Jede Zerlegung induziert eine Äquivalenzrelation)
Sei eine Menge und eine Zerlegung dieser Menge. Dann gibt es genau eine Äquivalenzrelation , die diese Zerlegung induziert, für die also ist. Diese Äquivalenzrelation ist definiert durch:
Beweis (Jede Zerlegung induziert eine Äquivalenzrelation)
Sei eine Menge und eine Zerlegung dieser Menge.
Beweisschritt: Existenz einer Äquivalenzrelation, die diese Zerlegung induziert
Wir definieren die Relation über folgende Definition:
Beweisschritt: ist eine Äquivalenzrelation
Beweisschritt: ist reflexiv
Sei beliebig. Da die Vereinigung aller Mengen von die Grundmenge ergibt, gibt es eine Menge mit . Damit ist
Beweisschritt: ist symmetrisch
Sei beliebig. Es ist
Beweisschritt: ist transitiv
Sei mit und . Dann gibt es ein und ein mit und . Damit ist , da sowohl ein Element von als auch ein Element von ist. Da eine Partition ist, muss sein. Daraus folgt und damit .
Beweisschritt:
Sei und beliebig.
Beweisschritt:
Sei beliebig, also . Dann gibt es ein mit . Da und ist, ist . Daraus folgt , weil verschiedene Mengen von disjunkt sind. Damit ist , was zu beweisen war.
Beweisschritt:
Sei beliebig. Damit ist sowohl als auch ein Element von und damit . Daraus folgt . Da beliebig war, ist .
Aus den Behauptungen (2.1) und (2.2) folgt, dass ist.
Beweisschritt:
Beweisschritt:
Sei beliebig. Da ist, gibt es ein mit . Aus der Behauptung (2) folgt, dass und damit ist.
Beweisschritt:
Sei beliebig. Da alle Mengen aus nach Definition nicht leer sind, gibt es ein mit . Aus Behauptung (2) folgt, dass und damit ist.
Die Behauptung (3) folgt direkt aus Behauptung (3.1) und (3.2).
Beweisschritt: Eindeutigkeit dieser Äquivalenzrelation
Sei eine weitere Äquivalenzrelation mit . Sei beliebig. Es gilt dann
Induzierte Äquivalenzrelation
[Bearbeiten]Hinweis
Wir benutzen hier den Begriff der Funktion, der erst später definiert wird.
Das Nachrechnen, dass eine gegebene Relation wirklich eine Äquivalenzrelation ist, benutzt oft ein Standardschema, was wir in diesem Satz zusammenfassen:
Satz
Seien nichtleere Mengen und eine Abbildung.
Auf sei eine Äquivalenzrelation gegeben. Wir definieren für die Relation .
Dann ist eine Äquivalenzrelation. Diese nennen wir "die durch induzierte Äquivalenzrelation".
Beweis
Wir müssen die drei Eigenschaften einer Äquivalenzrelation nachprüfen. Seien also
Beweisschritt: Reflexivität
, da reflexiv ist. Das ist nach Definition von äquivalent zu , also ist reflexiv.
Beweisschritt: Symmetrie
Gelte für und . Wir zeigen .
Also ist symmetrisch.
Beweisschritt: Transitivität
Sei und . Wir zeigen, dass .
Also ist transitiv.
Damit ist eine Äquivalenzrelation auf .
Hinweis
Die häufigste Anwendung ist die, wo auf der Menge die Relation die Gleichheit "" ist. Ist dann noch surjektiv, so ist keine Urbildmenge für leer und die Äquivalenzklassen in sind gerade die Urbilder der Elemente von . In diesem Fall kann man den Beweis schneller führen, wenn man nachrechnet, dass die Urbilder der Elemente von eine Zerlegung der Menge erzeugen.
Beispiel (Induzierte Äquivalenzrelation in )
Wähle , und die Funktion, die jeder natürlichen Zahl den Rest bei der Division durch 3 zuordnet. Dann besteht aus den Äquivalenzklassen
(Rest 0)
(Rest 1)
(Rest 2)

Beispiel (Induzierte Äquivalenzrelation im )
Seien und . Außerdem definiere mit . Die Funktion ist wegen sicher surjektiv. Die Äquivalenzklassen sind Geraden parallel zu der Urspungsgeraden , auf denen den konstanten Wert hat.
Warum sind Äquivalenzklassen interessant?
[Bearbeiten]In vielen Fällen betrachtet man Äquivalenzklassen auf einer Menge mit einer durch einer oder mehrere Verknüpfungen definierten Struktur, wie Gruppe oder Vektorraum.
Dort betrachtet man Äquivalenzrelationen, wo man die Verknüpfungen der Grundmenge auf die Äquivalenzklassen "transportieren" kann. Als Teaser: wenn man in dem letzten Beispiel irgendeinen Vektor des mit zu einen beliebigen anderen Vektor mit addiert, erhält man immer einen Vektor der Klasse mit , egal, welche Vektoren man nimmt.
Genauso landet man immer in der Klasse mit , wenn man einen beliebigen Vektor der Klasse mit mit multipliziert.
Das wird später im Kapitel Faktorraum genauer untersucht.
Ordnungsrelation
[Bearbeiten]Ordnungen sind eine besondere Klasse binärer, homogener Relationen. Sie sind eine Verallgemeinerung der Ordnungsrelationen wie oder , die du bereits für die Zahlbereiche , und kennst. Mit Hilfe von Ordnungsrelationen können Elemente einer Grundmenge ihrer Größe nach geordnet und miteinander verglichen werden.
Um eine Ordnung auf einer Menge zu definieren, reicht es, eine der beiden Relationen oder zu definieren. Die jeweils andere Relation lässt sich dann mit den folgenden Beziehungen darauf zurückführen:
- genau dann, wenn und ,
- genau dann, wenn oder .
Ordnungsrelationen lassen sich umdrehen: so wird aus der Kleiner-Gleich-Relation die Grösser-Gleich-Relation und aus der Echt-Kleiner-Relation wird die Echt-Größer-Relation . In Listen im Internet kann in der Regel gewählt werden, ob die Ergebnisse aufsteigend oder absteigend sortiert werden sollten.
Ordnungsrelationen gibt es auch außerhalb der Zahlen. So sind beispielsweise die Wörter im Lexikon alphabetisch geordnet.
Totalordnung
[Bearbeiten]
Totalordnungen sind direkte Verallgemeinerungen der Kleiner-Gleich-Relation auf den Zahlen. Genau wie andere binäre homogene Relationen wird die Totalordnung über ihre Eigenschaften bestimmt.
Frage: Welche Eigenschaft besitzt die Relation auf den Zahlbereichen , und ?
| Eigenschaft der Relation | Begründung |
|---|---|
| reflexiv | Für alle ist . |
| antisymmetrisch | Aus und folgt |
| transitiv | Aus und folgt |
| linear | Für alle reellen Zahlen und ist oder |
| nicht irreflexiv | Diese Relation ist reflexiv und die Grundmenge ist nicht leer |
| nicht symmetrisch | Gegenbeispiel: Es ist aber und damit kann die Relation nicht symmetrisch sein |
Eine Relation ist dann eine Totalordnung, wenn sie diejenigen vier Eigenschaften hat, die auch die Kleiner-Gleich-Relation für die Zahlen besitzt:
Definition (Totalordnung)
Eine Totalordnung auf ist eine binäre und homogene Relation auf der Grundmenge , die folgende Eigenschaften besitzt:
- (Reflexivität)
- (Antisymmetrie)
- (Transitivität)
- (Linearität)
Da eine Totalordnung die direkte Verallgemeinerung der Ordnung auf der Zahlengeraden ist, welche eine „Linie“ ist, wird eine Totalordnung auch lineare Ordnung genannt.
Hinweis
In der Mathematik wird das Adjektiv „linear“ mehrfach verwendet. So kennst du „lineare Funktionen“ aus der Schule und in der linearen Algebra gibt es den Begriff der „linearen Abbildung”. Diese Begriffe haben aber nichts mit dem Begriff der „linearen Ordnung“ zu tun!
Beispiel (Totalordnung)
- Die Relation auf der Grundmenge ist eine Totalordnung.
- Die Relation auf der Grundmenge ist eine Totalordnung.
- Die Relation auf der Grundmenge ist eine Totalordnung.
- Die alphabetische Ordnung der Wörter in einem Lexikon ist eine Totalordnung
Die Ordnungen auf den Zahlbereichen , und sind zwar alle Totalordnungen, aber sie unterscheiden sich auch! So hat ein kleinstes Element, nämlich die , aber weder noch haben ein kleinstes Element. In gibt es zwischen zwei verschiedenen Elementen mit immer ein weiteres Element mit , und . Das gilt für und nicht.
Satz
Sei eine Totalordnung auf der Menge und eine Teilmenge von . Dann ist die Einschränkung von auf eine Totalordnung auf .
Beweis
Die Einschränkung von auf ist . Die vier Eigenschaften der Totalordnung auf gelten natürlich auch für die Teilmenge . Also ist eine Totalordnung auf .
Wie bereits gesagt, ist auch die Umkehrung einer Totalordnung wieder eine Totalordnung:
Aufgabe: Sei eine Totalordnung. Beweise, dass dann auch die konverse Relation definiert durch eine Totalordnung ist.
Beweisschritt: ist reflexiv
Wir müssen beweisen, dass für alle aus der Grundmenge gilt. Nun gilt nach Definition genau dann, wenn ist. Wir wissen aber bereits, dass reflexiv ist, und damit auch, dass für alle gilt. Es folgt die Reflexivität von .
Beweisschritt: ist antisymmetrisch
Auch dies folgt aus der Antisymmetrie von . Für gilt nämlich . Setzen wir ein, folgt für alle und der Grundmenge. Dies ist die Antisymmetrieeigenschaft von .
Beweisschritt: ist transitiv
Sei und . Nach Definition ist dann und . Es folgt aus der Transitivität von . Damit gilt aber auch nach der Definition von . Ingesamt haben wir so gezeigt und damit die Transitivität von .
Beweisschritt: ist linear
Von wissen wir bereits, dass es linear ist. Also gilt für zwei und : oder . Nach Definition von gilt dann auch für alle und : oder . Dies ist die Linearitätseigenschaft von .
Definition (Weitere Ordnungsrelationen auf Grundlage der Totalordnung)
Sei eine Totalordnung auf der Grundmenge . Dann sind die weiteren Ordnungsrelationen und auf folgendermaßen definiert:
Während ebenfalls eine Totalordnung ist, ist das bei und nicht der Fall. Diese beiden Relationen sind strikte Totalordnungen:
Strikte Totalordnung
[Bearbeiten]Analog zur Totalordnung, soll auch die Relation die Kleiner-Relation der reellen Zahlen verallgemeinern. Wenn eine Relation das tut, nennt man sie strikte Totalordnung. Welche Eigenschaften muss nun aber besitzen, um als strikte Totalordnung zu gelten?
Frage: Welche Eigenschaften besitzt die Relation auf den Zahlbereichen , und ?
| Eigenschaft der Relation | Begründung |
|---|---|
| irreflexiv | Für alle ist . |
| antisymmetrisch | Ist , so folgt automatisch . Damit kann und nie gleichzeitig auftreten. Somit ist die Implikation stets wahr, weil die Prämisse stets falsch ist (siehe Abschnitt zur Implikation). |
| asymmetrisch | Die Kleiner-Relation ist antisymmetrisch und irreflexiv. |
| transitiv | Aus und folgt . |
| konnex | Für zwei verschiedene Zahlen und gilt entweder oder . |
| trichotom | Die Kleiner-Relation ist asymmetrisch und konnex. |
| nicht linear | Für die Zahlen und gilt weder noch . |
| nicht reflexiv | Es ist beispielsweise . |
| nicht symmetrisch | Es ist beispielsweise , aber nicht auch . |
Aus dem Abschnitt zu den Eigenschaften binärer Relationen wissen wir, dass eine binäre Relation genau dann trichotom ist, wenn sie gleichzeitig irreflexiv, asymmetrisch, konnex und antisymmetrisch ist. Dementsprechend müssen wir von einer binären Relation nur die Trichotomie und die Transitivität fordern und es folgt dann bereits, dass diese Relation genau dieselben Eigenschaften wie die Echt-Kleiner-Relation besitzt. Deswegen wählen wir die Trichotomie und die Transitivität als die charakteristischen Eigenschaften einer strikten Totalordnung:
Definition (strikte Totalordnung)
Eine binäre und homogene Relation auf der Grundmenge heißt strikte Totalordnung, wenn folgende Eigenschaften besitzt:
- (Transitivität)
- (Trichotomie)
Das Symbol ist dabei die Kontravalenz, also die Entweder-Oder-Verknüpfung zwischen Aussagen. Wir zeigen nun, dass die mit Hilfe einer Totalordnung definierte Relation eine strikte Totalordnung ist.
Satz
Sei eine Totalordnung auf und die Relation wie folgt definiert: . Dann ist eine strikte Totalordnung auf .
Beweis
Zu zeigen ist, dass transitiv und trichotom ist.
Beweisschritt: ist transitiv
Gelte . Nach Definition von gilt dann: . Mit der Transitivität von folgt . Weiterhin folgt aus mit der Antisymmetrie von . Da gilt, muss gelten. Wäre nun , würde daraus folgen - Widerspruch! Also gilt . Insgesamt haben wir gezeigt, was nach Definition von gerade ist.
Beweisschritt: ist trichotom
Gelte , dann gilt nach Definition von weder noch . Gelte nun . Mit der Linearität von gilt . Wegen der Antisymmetrie von kann aber wegen nicht beides gelten, also: . Daraus folgt . In beiden Fällen gilt also .
Aufgabe: Sei eine Totalordnung. Beweise, dass dann auch die Relation definiert durch eine strikte Totalordnung ist.
Sei eine Totalordnung auf . Wie im vorigen Abschitt gezeigt ist dann auch mit eine Totalordnung auf . Die Definition von lässt sich wie folgt umschreiben: , also gilt . Nunmehr folgt der Beweis genauso wie eben für gezeigt.
Sobald eine strikte Totalordnung definiert wurde, können ähnlich wie bei der Totalordnung weitere Ordnungsrelationen auf zurückgeführt werden:
Definition (Weitere Ordnungsrelationen auf Grundlage der strikten Totalordnung)
Sei eine strikte Totalordnung auf der Grundmenge . Dann sind die weiteren Ordnungsrelationen , und auf folgendermaßen definiert:
Aufgabe: Sei eine strikte Totalordnung. Beweise, dass dann auch die Relation definiert durch eine Totalordnung ist.
Zu zeigen ist, dass reflexiv, antisymmetrisch, transitiv und linear ist.
Beweisschritt: ist reflexiv
Es gilt , also auch .
Beweisschritt: ist antisymmetrisch
Gelte . Nach Definition von gilt dann: . Wegen der Trichotomie von können aber nicht und gemeinsam gelten oder eine der beiden Ungleichungen zusammen mit der Gleichung, also folgt .
Beweisschritt: ist transitiv
Gelte . Dann gilt nach Definition von . Ist folgt , also gilt . Ist , folgt ebenfalls und damit . Gelte also und . Dann gelten und und mit der Transitivität von folgt und somit auch .
Beweisschritt: ist linear
Mit der Trichotomie von gilt entweder oder oder . Im ersten Fall gilt , ebenso im zweiten Fall. Im zweiten Fall gilt zusätzlich . Im dritten Fall gilt . Insgesamt gilt .
Die Beweis, dass eine Totalordnung ist verläuft analog.
Aufgabe: Sei eine strikte Totalordnung. Beweise, dass dann auch die Relation definiert durch eine strikte Totalordnung ist.
Zu zeigen ist, dass transitiv und trichotom ist.
Beweisschritt: ist transitiv
Sei . Nach Definition von gilt dann auch: . Mit der Transitivität von folgt daraus , also gilt .
Beweisschritt: ist trichotom
Es gilt . Nach Definition von folgt daraus: , das ist die Trichotomie von .
Aufgabe: Sei eine Totalordnung auf der Menge und wie üblich definiert. Zeige:
Beweis:
Gilt , so gilt nach Definition und . Aus folgt wegen der Antisymmetrie . Da nicht gilt, muss gelten. Gelte nun . Dann folgt mit der Linearität . Gälte , dann folgte mit der Reflexivität ↯. Also gilt und insgesamt folgt .
Aufgabe: Sei eine transitive binäre Relation auf der Menge und wie üblich definiert. Zeige: Gilt , so ist eine Totalordnung auf .
Beweis:
Mit der Definition von lautet die Voraussetzung:
Da transitiv ist, sind nur noch die drei anderen Eigenschaften zu zeigen.
Beweisschritt: Reflexivität
Für den Spezialfall ist die linke Seite von (*) immer falsch. Also ist auch die rechte Seite falsch und es gilt die Reflexivität: .
Beweisschritt: Antisymmetrie
Gelte . Dann ist (*) nur wahr, wenn gilt. Das zeigt die Antisymmetrie.
Beweisschritt: Linearität
Gilt , dann gilt auch , also die Linearität. Gelte nun . Dann liefert (*) , also ebenfalls die Linearität.
Also ist eine Totalordnung. ✔
Zusammenhang von strikter Totalordnung zur Totalordnung
[Bearbeiten]In den vorherigen beiden Abschnitten haben wir dargelegt, wie man aus einer Totalordnung und einer strikten Totalordnung einer Menge die jeweils andere Ordnung definieren kann. Es fehlt aber noch der Beweis, dass beide Wege gleichwertig sind, dass es also egal ist, welchen Weg man geht. Um dies zu zeigen, muss Zweierlei gezeigt werden:
- Sei eine Totalordnung, von der man die strikte Totalordnung über bildet. Wenn man nun wieder die von induzierte Totalordnung über bildet, dann müssen die beiden Relationen und identisch sein. Es muss also gelten .
- Analoges muss gelten, wenn man bei einer strikten Totalordnung beginnt und über den Zwischenschritt der von induzierten Totalordnung die von induzierte strikte Totalordnung bildet: .
Beweis
Sei eine Totalordnung und definiert über , wobei definiert ist über .
Beweisschritt:
Es gilt:
Den letzten Beweisschritt wollen wir näher ausführen: Um die Äquivalenz zu zeigen, müssen wir die beiden Implikationen und beweisen. Die erste Implikation ist klar, weil unabhängig von der Aussage stets wahr ist. Wenn wir in der zweiten Implikation mit der Prämisse starten, dann ist einer der beiden Fälle und wahr. In beiden Fällen gilt , denn im ersten Fall gilt es sowieso und im zweiten Fall folgt es aus der Reflexivität von .
Sei nun eine strikte Totalordnung. Sei die von induzierte Totalordnung mit . Sei wiederum definiert über .
Beweisschritt:
Es gilt:
Halbordnung
[Bearbeiten]Es gibt Relationen, die bis auf die Linearität alle Eigenschaften der Totalordnung erfüllen. Damit verhalten sie sich fast wie Totalordnungen. Jedoch können bei diesen Relationen nicht alle Paare von Elemente der Grundmenge miteinander verglichen werden. Diese Relationen werden Halbordnungen oder partielle Ordnungen genannt (eben weil diese Ordnungen nur „zur Hälfte“ Totalordnungen sind):
Definition (Halbordnung)
Eine Halbordnung ist eine binäre und homogene Relation auf der Grundmenge , die folgende Eigenschaften besitzt:
- reflexiv
- antisymmetrisch
- transitiv
Beispiel (Halbordnung)
- Die Ist-Teiler-von-Beziehung auf ist eine Halbordnung.
- Die Teilmengenbeziehung auf jeder Menge von Mengen ist eine Halbordnung.
Aus der Definition folgt, dass jede Totalordnung eine Halbordnung ist. Aber nicht jede Halbordnung ist eine Totalordnung.
Aufgabe: Gib ein Beispiel für eine Halbordnung an, die keine Totalordnung ist.
Die Teilmengenbeziehung auf der Potenzmenge ist eine Halbordnung, aber keine Totalordnung. So gilt für die Mengen und weder noch und damit ist keine totale Relation.
Quasiordnung
[Bearbeiten]
Noch allgemeiner sind Quasiordnungen, auch Präordnungen genannt. Bei ihnen wird die Antisymmetrie nicht mehr verlangt.
Definition (Quasiordnung)
Eine Quasiordnung ist eine binäre und homogene Relation auf der Grundmenge , die folgende Eigenschaften besitzt:
- reflexiv
- transitiv
Beispiel (Quasiordnung)
- Die Ist-Teiler-von-Beziehung auf ist eine Quasiordnung.
Diese Relation ist nicht antisymmetrisch, denn es gilt beispielsweise und aber nicht . Auf dagegen ist die Relation eine Halbordnung.
Der Begriff der Quasiordnung verallgemeinert nicht nur den der Halbordnung, sondern zugleich auch den der Äquivalenzrelation.
Nachweis von Ordnungsrelationen
[Bearbeiten]Wenn du die Aufgabe hast zu entscheiden, ob eine gegebene Relation eine Totalordnung bzw. eine Halbordnung ist, so musst du schauen, ob diese Relation alle notwendigen Eigenschaften für diese Art von Relation erfüllt. Der folgende Entscheidungsbaum demonstriert dir die Vorgehensweise:
Beispielaufgabe
[Bearbeiten]Aufgabe
Ist die Relation „ ist eine Teilmenge von “ auf der Grundmenge , der Menge aller Teilmengen von , eine Halbordnung bzw. eine Totalordnung?
Lösung
Hier kannst du schrittweise vorgehen:
Beweisschritt: Ist die Relation reflexiv?
Ja, die Relation ist reflexiv, denn jede Menge ist nach Definition eine Teilmenge von sich selbst (Für alle Mengen gilt ).
Beweisschritt: Ist die Relation antisymmterisch?
Ja, die Relation ist antisymmetrisch, weil aus und die Gleichheit folgt.
Beweisschritt: Ist die Relation transitiv?
Ja, die Relation ist transitiv, weil aus und die Beziehung folgt.
Beweisschritt: Ist die Relation linear?
Nein, die Relation ist nicht linear. So ist weder noch ist .
Beweisschritt: Ist die Relation eine Halbordnung bzw. eine Totalordnung?
Da die Relation reflexiv, antisymmetrisch und transitiv ist, ist sie eine Halbordnung. Da die Relation aber nicht linear ist, ist sie keine Totalordnung.
Abbildung
[Bearbeiten]Abbildung, Funktion
[Bearbeiten]Ein zentrales Konzept der Mathematik ist die Abbildung, die auch Funktion genannt wird. Abbildungen sind eindeutige Zuordnungen zwischen zwei Mengen und . Dies bedeutet, dass jedem Element durch die Abbildung genau ein Element zugeordnet wird. Ein Beispiel hierfür ist die Quadratfunktion von der Menge in die Menge , die jeder reellen Zahl ihre Quadratzahl zuordnet. Die Schreibweise für Abbildungen von nach ist:
Ausgesprochen wird dieser Ausdruck so:
Die Menge heißt Definitionsbereich von und ist die Zielmenge der Abbildung. Die Elemente aus dem Definitionsbereich von werden Argument genannt und jedes durch die Abbildung getroffene Element heißt Funktionswert zum Argument .
Hinweis
Die Begriffe „Abbildung“ und „Funktion“ sind beide in der Mathematik üblich und bedeuten genau dasselbe.
In der Zielmenge müssen nicht alle Elemente Funktionswerte sein.
Hier besteht der Definitionsbereich aus vier Elementen. Die Zielmenge ist . und sind Funktionswerte. Die Zahl dagegen nicht, denn keine Zahl ergibt bei Division durch den Rest . Also sind nicht alle Elemente in Funktionswerte.
Die Pfeile geben die Zuordnung wider: sie gehen vom Argument zum Funktionswert und verbinden so ein Paar. Wir können daher die Zuordnung als eine Menge von Paaren aus Argument und Funktionswert beschreiben: . Mengen von Paaren haben wir bereits im Kapitel Relation kennengelernt. Abbildungen sind also Relationen! Aber nicht jede Relation ist eine Abbildung. Damit eine Relation eine Abbildung ist, muss jedes Element in in Relation mit genau einem Element in sein
Fassen wir noch einmal zusammen, was eine Funktion ausmacht: Die Paare bilden eine Relation . Diese Relation hat eine spezielle Eigenschaft: zu jedem Element gibt es genau ein Element mit . Im Pfeildiagramm erkennst du dies daran, dass von jedem Element des Definitionsbereichs genau ein Pfeil ausgeht. Im Koordinatensystem muss es zu jedem -Wert genau einen -Wert geben.

Wir definieren daher Abbildungen als eine Relationen mit der oben genannten Eigenschaft:
Definition (Abbildung, Funktion)
Eine Abbildung oder Funktion aus der Menge in die Menge ist eine Relation mit folgender Eigenschaft:
- zu jedem Element gibt es genau ein Element mit .
Dieses eindeutige Element wird mit bezeichnet und Funktionswert von genannt. ist der Definitionsbereich, ist die Zielmenge der Funktion. Die Zuordnung kann zusätzlich angegeben werden: oder auch so .
Beispiel (Quadratfunktion)
Jeder reellen Zahl wird ihr Quadrat zugeordnet:
Funktionen werden häufig im Koordinatensystem veranschaulicht, wie in der Darstellung der Funktion rechts. Dabei werden die Paare als Koordinaten aufgefasst. Diese Punktemenge wird dann als Graph der Funktion bezeichnet.
Verständnisfrage: Welche der folgenden Pfeildiagramme stellen Abbildungen aus der Menge in die Menge dar?
-
Pfeildiagramm 1
-
Pfeildiagramm 2
-
Pfeildiagramm 3
-
Pfeildiagramm 4
Antwort:
- Pfeildiagramm 1: Abbildung
- Pfeildiagramm 2: partielle Abbildung (dem Objekt wird kein Element aus zugeordnet)
- Pfeildiagramm 3: keine Abbildung (dem Element werden mehrere Elemente aus zugeordnet und dem Objekt wird kein Element aus zugeordnet)
- Pfeildiagramm 4: Abbildung
Definitions- und Wertebereich
[Bearbeiten]Ist eine Funktion von nach , so ist der Definitionsbereich von
Der Wertebereich einer Funktion ist als die Menge der Funktionswerte definiert:
Definition (Wertebereich einer Funktion)
sei eine Funktion. Dann ist der Wertebereich von die Menge aller Elemente für die es ein Argument gibt, formalisiert:
Es gilt .
Einschränkung einer Funktion
[Bearbeiten]Definition (Einschränkung einer Funktion)
Sei eine Funktion und eine Teilmenge von . Dann ist die Einschränkung von auf die Funktion, die auf mit übereinstimmt:
Für die eingeschränkte Funktion gilt: .
ist tatsächlich eine Funktion.
Gleichheit von Abbildungen
[Bearbeiten]Es ist nicht sofort klar, wann zwei Abbildungen gleich sind. Ähnlich wie bei Mengen müssen wir definieren, wann zwei Abbildungen gleich sind.
Definition (Gleichheit von Abbildungen)
Zwei Abbildungen und sind gleich, wenn , und für alle gilt .
Sind zwei Funktionen gleich, so sind auch die Definitionsbereiche und die Wertebereiche gleich. Bei der Gleichheit kommt es nicht darauf an, ob die Zuordnungsvorschriften und gleich formuliert sind!
Beispiel
Die folgenden Funktionen sind gleich:
Bild und Urbild
[Bearbeiten]Zwei wesentliche Begriffe im Zusammenhang mit Abbildungen ist der Begriff des Bildes und der Begriff des Urbilds:
Definition (Bild)
Sei eine Funktion und eine Teilmenge. Das Bild ist die Menge aller Funktionswerte mit :
Notation: Es ist üblich, sowohl für den Funktionswert eines Elementes , als auch für das Bild einer Teilmenge die gleiche Schreibweise zu verwenden, nämlich mit runden Klammern. Aus dem Zusammenhang muss dann klar werden, was jeweils gemeint ist. Einige Autor*innen verwenden daher für das Bild einer Teilmenge eckige Klammern: .

Beispiel (Bild)
Sei . Es ist
Definition (Urbild)
Das Urbild einer Abbildung und einer Menge ist die Menge aller Argumente , die durch in die Menge abgebildet werden:
Beachte, dass auch Elemente enthalten kann, die durch nicht getroffen werden. Betrachte dazu die Abbildung auf der rechten Skizze. Die Zahl wird nicht getroffen und die Zahl besitzt als Funktionswert nur das Argument . Dementsprechend gilt für das Urbild .
Beispiel (Urbild)
Sei . Es ist
Warnung
Es besteht Verwechslungsgefahr zwischen dem Urbild , der Umkehrfunktion und dem multiplikativen Inversen .
Aufgabe
Sei
Bestimme folgende Bilder und Urbilder (beachte die unterschiedlichen Definitions- und Zielmengen der Abbildungen!):
Lösung
-
Da der gesamte Definitionsbereich von ist, müssen hier alle Funktionswerte bestimmt werden, die durch getroffen werden. Generell ist das Ergebnis der (reellwertigen) Quadratfunktion stets nicht negativ. Also ist das Bild eine Teilmenge von .
Nun kann man auch zeigen, dass alle nicht-negativen Zahlen durch getroffen werden.
Sei hierfür eine nicht negative Zahl. Es ist dann stets im Definitionsbereich von enthalten. Da ist, gibt es ein Argument, welches von auf abgebildet wird. Also gilt .
-
Wir müssen nur die Funktionswerte von und überprüfen. Es ist und .
Damit wird nur getroffen und es gilt .
-
Wenn wir alle Beträge der ganzen Zahlen bilden, erhalten wir die Menge der natürlichen Zahlen zusammen mit der Null, deshalb gilt:
-
Wir nutzen die Definition des Bildes . Da die Aussage immer falsch ist, folgt .
-
Bei der Quadratfunktion wird sowohl als auch auf abgebildet. Es ist nämlich sowohl sowie . Da beide Zahlen und im Defintionsbereich von sind, sind beide Zahlen im Urbild enthalten.
Nun suchen wir alle mit , also . Da nicht sein darf, bleibt nur die Möglichkeit übrig.
Damit ist das gesuchte Urbild.
-
Der Definitionsbereich von besteht nur aus der Menge . Diese Zahlen werden durch den Betrag auf die Menge abgebildet. Da die Menge in enthalten, ist der komplette Definitionsbereich das gesuchte Urbild, also
-
Bei der Betragsfunktion wird für ein beliebiges nicht-negatives sowohl als auch auf abgebildet. Damit ist das Urbild von .
-
Wir benutzen die Definition des Urbilds: . Die Aussage ist für alle falsch. Somit folgt .
Eigenschaften von Abbildungen
[Bearbeiten]sei eine Funktion von der Menge in die Menge . Es gelte also: .
Injektiv
[Bearbeiten]

Wenn eine Funktion verschiedene Argumente stets auf verschiedene Funktionswerte abbildet, wird sie injektiv genannt. Im Pfeildiagramm injektiver Funktionen treffen niemals zwei Pfeilspitzen auf denselben Funktionswert.
Definition (Injektiv)
Eine Funktion ist injektiv, wenn sie verschiedene Argumente auf verschiedene Werte abbildet:
Zum Nachweis der Injektivität wird häufig die Kontraposition verwendet: .
Beispiel (Injektiv)
- ist nicht injektiv, denn alle Werte bis auf werden zweimal getroffen. Es gilt ja beispielsweise .
- ist injektiv, denn aus folgt .
Surjektiv
[Bearbeiten]
Eine Funktion ist surjektiv, wenn alle Elemente von von der Funktion getroffen werden. Anders ausgedrückt: zu jedem Element gibt es ein Argument , mit .
Definition (Surjektiv)
Eine Funktion ist surjektiv, wenn alle Elemente von getroffen werden:
Beispiel (Surjektiv)
- ist surjektiv, denn für ein beliebiges ist .
- ist nicht surjektiv, denn die Quadratfunktion auf wird niemals negativ.
Verständnisaufgabe: Ist surjektiv?
Nein, da weder noch in liegen. Das heißt liegt nicht im Bild von .
Satz (Surjektivität)
.
Beweis (Surjektivität)
Die Behauptung folgt mit der Definition des Wertebereichs: der umfasst alle Werte, die getroffen werden.
Bijektiv
[Bearbeiten]
Eine Funktion kann sowohl injektiv als auch surjektiv sein. Man nennt diese Eigenschaft bijektiv. Im Pfeildiagramm ist dann jedes Element von mit genau einem Element von verbunden. Mit Hilfe von bijektiven Funktionen können Mengen hinsichtlich ihre Größe verglichen werden: gibt es eine Bijektion von auf , so haben die beiden Mengen und gleichviele Elemente. Wir werden den Größenvergleich zwischen Mengen im Kapitel Mächtigkeit von Mengen ausführlich behandeln.
Definition (Bijektiv)
Eine Funktion ist bijektiv von auf , wenn sie injektiv und surjektiv ist. Das heißt, jedem Element von wird genau ein Element von zugeordnet:
Beispiel (Bijektiv)
- ist bijektiv.
- ist bijektiv.
- ist nicht bijektiv.
-
f : Gerade
-
g : Parabel 3. Grades
-
h : Sinuskurve
Beweis
- Im Koordinatenkreuz ist diese Funktion eine Gerade mit Steigung und um eine Einheit nach oben verschoben. Wir zeigen die Injektivität: aus folgt und daraus . Für die Surjektivität sei eine beliebige reelle Zahl gegeben. Dann definieren wir das Argument und rechnen nach: . Also werden alle reellen Zahlen getroffen.
- In gleicher Weise zeigt man die Bijektivität von , das ist eine Parabel 3. Grades.
- Der Graph von ist die Sinuskurve. Die nimmt bekanntlich alle Werte zwischen und an. Also ist surjektiv auf dem Intervall . ist aber nicht injektiv, denn ist periodisch, das heißt, diese Werte werden immer wieder angenommen.
Funktionskomposition
[Bearbeiten]
Seien zwei Abbildungen und gegeben. Dann können wir die beiden Funktionen nacheinander ausführen. Wir bilden zunächst ein mit ab und erhalten . Dann können wir darauf anwenden und erhalten . Insgesamt ergibt sich . Das führt zum Begriff der Komposition von Funktionen
Definition (Komposition von Abbildungen)
Die Komposition zweier Abbildungen und ist die Abbildung .
Gelesen wird so: erst , dann oder auch: nach .
Hinweis
Beachte, dass in der Schreibweise für die Funktionskomposition diejenige Funktion, die zuerst angewandt wird, rechts steht (Hier musst du also „von rechts nach links“ lesen). Die Schreibweise meint also, dass auf erst und danach angewandt wird. Es ist also .
Verständnisfrage: Sei und . Berechne
Antwort:
Verständnisfrage: Seien und zwei Abbildungen von nach . Gilt dann ? Wieso?
Nein, dies ist nicht der Fall. Sei zum Beispiel und . Dann ist nämlich
und
Hier sieht man, dass ist. Beispielsweise ist .
Satz (Existenz der Umkehrfunktion)
Ist bijektiv, so gibt es eine eindeutige Funktion mit für alle und für alle .
Beweis (Existenz der Umkehrfunktion)
Beweisschritt: Existenz
Wir definieren für das eindeutige mit . Die gewünschten Identitäten folgen unmittelbar.
Beweisschritt: Eindeutigkeit
Sind zwei solche Funktionen, so .
Definition (Umkehrfunktion)
Für eine bijektive Funktion bezeichnen wir mit die eindeutige Funktion aus obigem Satz. Diese Funktion nennen wir die Umkehrfunktion von .
Aufgaben
[Bearbeiten]Aufgabe (Komposition surjektiver Abbildungen)
Seien und zwei Abbildungen. Seien und surjektiv. Zeige, dass surjektiv ist.
Wie kommt man auf den Beweis? (Komposition surjektiver Abbildungen)
Da und sind, dann ist mit für alle (Nach Definition von Funktionskomposition).
Wir müssen überprüfen, dass alle Elemente durch getroffen werden:
Wir suchen für alle ein Element mit .
Da surjektiv ist, gibt es für alle ein Element mit .
Da surjektiv ist, gibt es für alle ein Element mit .
Nun kann man zeigen, dass für alle gilt:
Also ist die Funktion surjektiv.
Lösung (Komposition surjektiver Abbildungen)
ist surjektiv
ist surjektiv
Aus(*) und (**) gilt:
Dann für alle gibt es mit .Also ist surjektiv.
Aufgabe (Komposition injektiver Abbildungen)
Seien und zwei Abbildungen. Seien und injektiv. Zeige, dass injektiv ist.
Wie kommt man auf den Beweis? (Komposition injektiver Abbildungen)
Da und sind, dann ist mit für alle (Nach Definition von Funktionskomposition).
Wir müssen überprüfen, dass für alle zwei Elemente mit gilt :
ist injektiv, dann für alle zwei Elemente mit gilt .
ist injektiv, dann für alle zwei Elemente mit gilt .
Nun kann man zeigen, dass für alle zwei Elemente gilt:
Also ist die Funktion injektiv.
Lösung (Komposition injektiver Abbildungen)
ist injektiv ) ...(*)
ist injektiv ) ...(**)
Aus(*) und (**) gilt: .
Dann für alle gilt: .
Also ist die Funktion injektiv.
Aufgabe
Seien und zwei Abbildungen. Wenn und surjektiv sind, folgt daraus, dass surjektiv ist? Begründe deine Antwort.
Lösung
Wenn wir zeigen wollen, dass eine Funktion nicht surjektiv ist, reicht es ein einziges Gegenbeispiel zu finden. Seien die drei Mengen mit . Die formale Definition für Funktionskomposition lautet mit für alle . dann in unserem Gegenbeispiel haben wir . Beachte, dass die Funktionen und surjektiv sind, weil alle Elemente von durch und getroffen werden. Aber die Funktion ist nicht surjektiv, denn es gibt eine Element , die nicht Funktionswert durch ist. Es gilt, dass nicht unbedingt surjektiv ist.
Aufgabe
Seien und zwei Abbildungen. Wenn injektiv ist, folgt daraus, dass injektiv ist? Begründe deine Antwort.
Lösung
Die Antwort ist ja, was wir im Folgenden beweisen werden. Seien , wobei . Wir zeigen, dass . Weil , gilt
Da injektiv ist, folgt aus der Definition, dass . Somit ist injektiv.
Verknüpfung
[Bearbeiten]Definition der Verknüpfung
[Bearbeiten]Verknüpfungen sind dir bereits aus der Schule bekannt. Beispiele hierfür sind Addition und Multiplikation. Diese Verknüpfungen können wir als spezielle Abbildungen betrachten. Schauen wir uns dazu als Beispiel die Verknüpfung der Addition auf den reellen Zahlen genauer an:
Die Addition verknüpft zwei Zahlen und zu einer neuen Zahl . Wir können somit die Addition als Abbildung vom nach auffassen. (Wiederholung: ist die Menge aller geordneter Paare mit und ). Der Definitionsbereich ist , weil bei der Addition zwei reelle Zahlen miteinander verknüpft werden. Die Zielmenge ist , da das Ergebnis der Addition zweier reeller Zahlen wieder eine reelle Zahl ist. Damit ist die Addition eine Abbildung . Analog lässt sich auch die Multiplikation als Abbildung von nach mit der Zuordnungsvorschrift auffassen.
Das obige Beispiel können wir nun verallgemeinern. Statt betrachten wir jetzt irgendeine Grundmenge . Die Addition ist eine Verknüpfung, die zwei Objekte zu einem neuen Objekt der Grundmenge verknüpft - wir wollen jetzt aber den allgemeineren Fall betrachten, dass eine Verknüpfung Objekte zu einem neuen Objekt verknüpft. Analog zu unserem Beispiel ist dann eine solche Verknüpfung eine Abbildung , welche auch -stellige Verknüpfung genannt wird. Ein Synonym für das Wort „Verknüpfung“ ist der Begriff „Operation“
Definition (Verknüpfung)
Eine -stellige Verknüpfung auf einer Grundmenge ist eine Abbildung .
Verständnisfrage: Zähle Beispiele für Verknüpfungen auf.
- Addition , Multiplikation und Potenzbildung sind zweistellige Verknüpfungen auf .
- Quadratfunktion , Betragsfunktion und Sinusfunktion sind einstellige Verknüpfungen auf .
- Funktionskomposition von reellwertigen Funktionen ist eine binäre Verknüpfung auf der Menge aller Funktionen .
- Vereinigung, Differenz, Durchschnitt sind binäre Verknüpfungen auf der Potenzmenge einer gegebenen Grundmenge.
- Komplementbildung ist eine einstellige Verknüpfungen auf der Potenzmenge einer gegebenen Grundmenge.
Binäre Verknüpfungen
[Bearbeiten]Für zweistellige Verknüpfungen wird auch der Begriff binäre Verknüpfung gebraucht:
Definition (binäre Verknüpfung)
Eine binäre Verknüpfung ist eine zweistellige Verknüpfung. Eine binäre Verknüpfung auf einer Grundmenge ist damit eine Abbildung .
Betrachten wir eine binäre Verknüpfung auf einer Grundmenge . Damit lässt sich als eine Abbildung auffassen. Du kannst dir als eine Maschine vorstellen, die zwei Elemente und aus der Menge nimmt und daraus ein Element aus erzeugt:

Für binäre Verknüpfungen wird oft die Schreibweise verwendet. Hier steht stellvertretend für eine beliebige Verknüpfung wie die Addition oder die Multiplikation . Diese Schreibweise sollte nicht mit der Funktionskomposition verwechselt werden, die auch das Symbol verwendet (Zwar ist die Funktionskomposition eine binäre Verknüpfung, aber nicht jede binäre Verknüpfung ist eine Funktionskomposition).
Eigenschaften binärer Verknüpfungen
[Bearbeiten]Sei im Folgenden eine beliebige Verknüpfung auf einer Grundmenge . Wir betrachten nun die sogenannte Kommutativität beziehungsweise Assoziativität der binären Verknüpfung.
Kommutativität
[Bearbeiten]Betrachten wir die Maschinenvorstellung einer binären Verknüpfung. Bei einer binären Verknüpfung besitzt die Maschine zwei Eingänge. In diese können wir zwei Objekte und aus der Grundmenge stecken. Ein Element stecken wir links in unsere Maschine und das andere rechts:

Ist die Reihenfolge, in der wir die Argumente in die Maschine stecken, egal? Kommt immer dasselbe raus, wenn wir und vertauschen?

Es gibt solche Verknüpfungen, bei dem die Reihenfolge der Argumente egal ist. Bei solchen Verknüpfungen ist stets unabhängig davon, welche Argumente und gewählt wurden. Ein Beispiel hierfür ist die Addition auf den reellen Zahlen. Für die Addition gilt nämlich stets .
Weil diese Eigenschaft praktisch ist, bekommt sie einen eigenen Namen. Wir sprechen hier von Kommutativität beziehungsweise nennen solche Verknüpfungen kommutative Verknüpfungen. Der Begriff kommt vom lateinischen Wort commutare, was „vertauschen“ bedeutet. Es ist also:
Definition (Kommutativität)
Eine binäre Verknüpfung heißt kommutativ, wenn für alle gilt: .
Beispiel (Beispiel und Nichtbeispiel für Kommutativität)
- Die Addition auf den reellen Zahlen ist kommutativ. Für alle reellen Zahlen und ist nämlich .
- Die Subtraktion auf den reellen Zahlen ist nicht kommutativ. So ist , aber , also .
Assoziativität
[Bearbeiten]Was passiert, wenn wir mehr als zwei Objekte miteinander verknüpfen wollen? Nehmen wir die Addition als Verknüpfung und betrachten wir die Summe . Wie können wir diese Operation ausführen, wenn die Addition als zweistellige Verknüpfung definiert ist, also genau zwei Argumente zu einem Ergebnis zusammenfasst?
Hier haben wir zwei Möglichkeiten: Zum einen können wir zunächst die Summe von und bilden und dann hinzuaddieren. So berechnen wir . Zum anderen kann zunächst und miteinander addiert werden, um danach die Summe aus und dem Ergebnis der ersten Summe zu bilden. Hier wird gerechnet.
So haben wir bei jeder Verknüpfung zwei Möglichkeiten, um zu berechnen. Zum einen kann dieser Ausdruck als und zum anderen als berechnet werden. Im folgenden Diagramm sind beide Möglichkeiten mit dem Maschinenmodell dargestellt. Dabei stellt sich die Frage: Ist es egal, welche der beiden Methoden wir verwenden? Ist das Endergebnis gleich, egal in welcher Reihenfolge die einzelnen Verknüpfungen ausgerechnet werden?

Bei der Addition ist es egal, in welcher Reihenfolge die Verknüpfungen ausgerechnet werden. So ist für alle reellen Zahlen , und . Verknüpfungen wie die Addition, bei der die Reihenfolge der Verknüpfungsausrechnung egal ist, nennt man assoziativ. Das Wort kommt vom lateinischen associare und bedeutet „vereinigen“ beziehungsweise „verbinden“.
Definition (Assoziativität)
Eine binäre Verknüpfung heißt assoziativ, wenn für alle gilt: .
Beispiel (Beispiel und Gegenbeispiel für Assoziativität)
- Die Addition auf den reellen Zahlen ist assoziativ. Die Aussage, dass für alle reellen Zahlen , und ist, nennt man auch Assoziativgesetz.
- Die Subtraktion auf den reellen Zahlen ist nicht assoziativ. So ist , aber . Es ist also .
Weil bei einer assoziativen Verknüpfung die Reihenfolge egal ist, in der die einzelnen Verknüpfungen ausgewertet werden, können wir Klammern weglassen. Dies gilt für drei und auch für mehr Operanden. Du kannst dann also statt oder auch einfach schreiben. Beachte, dass eine Schreibweise wie ohne Klammern nur dann sinnvoll ist, wenn die Verknüpfung assoziativ ist. Bei nicht assoziativen Verknüpfungen musst du immer die Klammern setzen.
Übungsaufgaben
[Bearbeiten]Kommutativität und Assoziativität
[Bearbeiten]Aufgabe
Welche der folgenden Verknüpfungen sind kommutativ und welche sind assoziativ?
- Addition auf
- Subtraktion auf
- Multiplikation auf
- Potenzbildung auf (x positiv, da sonst keine Verknüpfung)
- Funktionskomposition
- Durchschnitt auf der Potenzmenge einer Menge
Lösung
| binäre Verknüpfung | assoziativ | kommutativ |
|---|---|---|
| Addition auf | X | X |
| Subtraktion auf | ||
| Multiplikation auf | X | X |
| Potenzbildung auf | ||
| Funktionskomposition | X | |
| Durchschnitt auf der Potenzmenge einer Menge | X | X |
Eigenschaften von Verknüpfungen
[Bearbeiten]Aufgabe (Einige Beispiele für Verknüpfungen)
Wir betrachten die folgenden drei Verknüpfungen:
- auf
- auf
- auf
Entscheide, ob die folgenden Aussagen wahr oder falsch sind:
- Die Verknüpfung ist auf kommutativ.
- Die Verknüpfung ist auf assoziativ.
- Es gibt eine ganze Zahl , sodass für alle gilt: und .
- Zu jedem gibt es ein , sodass gilt: .
- Die Verknüpfung ist auf kommutativ.
- Die Verknüpfung ist auf assoziativ.
- Es gibt eine reelle Zahl , sodass für alle gilt: und .
- Es gibt , , und , sodass gilt:
- Die Verknüpfung ist auf kommutativ.
- Die Verknüpfung ist auf assoziativ.
- Es gibt eine natürliche Zahl , sodass für alle gilt: und .
Lösung (Einige Beispiele für Verknüpfungen)
-
Wahr: Wir überprüfen, ob für alle gilt:
- Linke Seite:
- Rechte Seite:
-
Wahr: Wir überprüfen, ob für alle gilt: . Die linke Seite ist:
Und auf der rechten Seite erhalten wir:
Da Addition und Multiplikation in kommutativ sind, können wir die Reihenfolge der Terme vertauschen. Wir sehen dann schnell, dass linke und rechte Seite übereinstimmen. Daher ist die Verknüpfung auf kommutativ.
-
Wahr: Wir überprüfen, ob es eine ganze Zahl gibt, sodass für jede ganze Zahl gilt: und .
Erste Gleichung:
Dies muss nun für alle gelten. Also setzen wir 1 als Wert für ein, denn die Gleichung muss insbesondere auch dann gelten. Damit erhält man die Gleichung: . Also ist . Bisher haben wir nur ein Element gefunden, das die Gleichung für erfüllt. Deswegen prüfen wir jetzt, ob die Gleichung mit für alle ganzen Zahlen gilt. Wir setzen in die Verknüpfung ein und erhalten die allgemeingültige Aussageform . Damit haben wir gezeigt, dass die erste Gleichung für alle ganzen Zahlen gilt.
Zweite Gleichung:
Wir gehen vor wie bei der ersten Gleichung: Da auch die zweite Gleichung für alle gelten muss, muss insbesondere auch für die folgende Gleichung richtig sein: . Daraus folgt unmittelbar . Umgekehrt erfüllt auch die Gleichung für beliebige Werte .
-
Falsch: Wir wollen herausfinden, ob es für jede ganze Zahl eine ganze Zahl gibt, sodass und ist. Betrachten wir zuerst die erste Gleichung:
Achtung: Auf den ersten Blick sieht die letzte Zeile dieser Gleichungsumformung so aus, als ob wir für jede Zahl auch eine Zahl berechnen könnten, die erfüllt. Aber die Zahl muss auch eine ganze Zahl sein. Das ist zum Beispiel für nicht der Fall, wie wir durch Einsetzen in sehen: Hier ist . Also haben wir ein Gegenbeispiel zu unserer Aussage gefunden, weil es zu kein ganzzahliges gibt, sodass gilt.
-
Wahr: Wir müssen überprüfen, ob für alle gilt:
- Linke Seite:
- Rechte Seite:
-
Falsch: Wir wollen überprüfen, ob die Verknüpfung assoziativ ist, also ob für alle gilt:
- Linke Seite:
- Rechte Seite:
Vergleichen wir diese Seiten, dann vermuten wir schnell, dass diese nicht übereinstimmen. Wir können konkrete Werte für einsetzen und sehen
Also ist die Verknüpfung nicht assoziativ.
-
Falsch: Wir müssen untersuchen, ob es eine reelle Zahl gibt, sodass für alle gilt: und . Die beiden Gleichungen sind äquivalent, da wir ja schon gesehen haben, dass die Verknüpfung kommutativ ist. Wir kümmern uns also nur um die Gleichung . Willst du ein solches finden oder seine Existenz widerlegen, gehst du immer gleich vor: Du nimmst die Gleichung und stellst sie um, damit du Dinge über erfahren kannst. Da die Gleichung für alle gelten muss, kannst du auch konkrete Werte für einsetzen und so etwas über erfahren.
Probieren wir das einfach mal aus. Wir betrachten die Gleichung und stellen sie um:
Diese Gleichung soll also für alle gelten. Du musst nur zwei verschiedene Werte von einsetzen und schon siehst du, dass das unmöglich ist. Wie sollte denn gleichzeitig (für ) und (für ) gelten? Also existiert kein mit der geforderten Eigenschaft.
-
Wahr: Zunächst solltest du erkennen, dass diese Aussage zwar sehr ähnlich zur Assoziativität aussieht, aber der Allquantor durch einen Existenzquantor ersetzt wurde. Wir müssen also nur ein Beispiel von Zahlen finden, das die altbekannte Eigenschaft erfüllt.
Als wir gezeigt haben, dass nicht assoziativ ist, haben wir die die beiden obigen Terme ausgerechnet:
Wie kannst du jetzt und wählen, damit die beiden rechten Seiten gleich sind? Du könntest zum Beispiel wählen. Und schon hast du die Existenz der Zahlen bewiesen und bist fertig.
-
Falsch: Wir wollen untersuchen, ob die Gleichung für alle natürlichen Zahlen und erfüllt ist. Wie üblich setzen wir zunächst die Verknüpfungsvorschrift ein und erhalten:
- Linke Seite:
- Rechte Seite
Also ist die Verknüofung nicht kommutativ.
-
Falsch: Wir müssen wieder das Assoziativgesetz für beliebige nachrechnen.
- Linke Seite:
- Rechte Seite:
- Linke Seite:
- Rechte Seite:
-
Falsch: Wir müssen wieder prüfen, ob eine natürliche Zahl existiert, sodass für alle gilt. Wir betrachten zunächst nur die linke Gleichung und wollen einsehen, dass es kein gibt, das diese Gleichung im Allgemeinen erfüllt. Wie immer stellen wir die Gleichung dafür um:
Nun sollen wir also einen festen Wert finden, der gleich ist – und zwar für alle natürlichen Zahlen . Wir müssen nur zwei verschiedene Werte einsetzen und sehen schon, dass das nicht funktionieren kann. Du solltest dir auch bewusst sein, dass die Zahl in jedem Fall eine natürliche Zahl sein müsste.
Hinweis
Das Element in 3. nennen wir neutrales Element bezüglich in . Neutrale Elemente spielen eine wichtige Rolle in der Algebra. Genauso ist in 7. das neutrale Element bezüglich in , in 11. bezüglich in .
Mächtigkeit von Mengen
[Bearbeiten]Warnung
Das folgende Kapitel enthält stark kontraintuitive Aussagen. Beim Lesen kann es zu Erstaunen und Verblüffung kommen. Ihr Geist wird sich mit der Zeit an diese Aussagen gewöhnen.
In diesem Kapitel werden wir uns mit der Frage beschäftigen, wann zwei Mengen gleich groß sind. Hier werden wir insbesondere „unendliche“ Mengen auf ihre Größe untersuchen. Dabei werden wir auf Ergebnisse stoßen, die scheinbar paradox sind und unserer Erwartung widersprechen. Dies ist auch der Grund, warum viele Mathematiker die Frage nach der Größe unendlicher Mengen vermieden haben oder ihre erste Beantwortung durch Georg Cantor (1845-1918) abgelehnt haben. So schrieb Carl Friedrich Gauß (1777-1855):
„Ich verabscheue es, wenn ein unendliches Objekt wie ein vollständig gegebenes Objekt verwendet wird. In der Mathematik ist diese Operation verboten; das Unendliche ist eine Redensart.“[12]
Wir werden in diesem Kapitel sehr ausführlich das Unendliche untersuchen.
Bevor wir aber der Frage nach der Größe unendlicher Mengen nachgehen, beantworte bitte für dich folgende Fragen (du kannst auch „aus dem Bauch heraus“ antworten):
Beantworte intuitiv: Welche der folgenden Mengen ist größer? Welche der folgenden Mengen besitzt mehr Elemente?
- Menge der natürlichen Zahlen oder die Menge der Quadratzahlen
- Menge der natürlichen Zahlen oder die Menge der ganzen Zahlen
- Menge der natürlichen Zahlen oder die Menge der rationalen Zahlen
- Menge der natürlichen Zahlen oder die Menge der reellen Zahlen
Diese Fragen werden wir in diesem Kapitel beantworten.
Wann sind zwei Mengen gleich groß?
[Bearbeiten]
Wann besitzen zwei Mengen und gleich viele Elemente? Im Fall, dass und endliche Mengen sind, ist diese Frage einfach zu beantworten: Man zählt die Elemente beider Mengen und vergleicht diese Anzahl miteinander. Doch diese Methode kann nicht auf den Fall übertragen werden, dass eine der beiden Mengen unendlich ist.
Nun könnte man annehmen, dass alle unendlichen Mengen gleich groß sind. Schließlich bezeichnen wir die Größe dieser Menge in unserer Alltagssprache mit demselben Wort: „Unendlich“. Wir werden aber sehen, dass diese Annahme zu nicht sinnvollen Ergebnissen führen würde und dass es unterschiedliche Arten der Unendlichkeit gibt.
Da das Zählen der Elemente bei unendlichen Mengen fehlschlägt, müssen wir eine andere Methode finden, Mengen miteinander zu vergleichen. Schauen wir uns ein Beispiel aus der endlichen Welt an: Stell dir vor, dass du zwei Kisten mit unterschiedlich großen Steinen hast und wissen willst, in welcher Kiste mehr Steine sind. Leider hast du keinerlei Messgeräte und zählen kannst du auch nicht. Wie kannst du vorgehen?
Frage: Wie kannst du feststellen, in welcher Kiste mit unterschiedlich großen Steinen mehr Steine sind, ohne dass du zählst oder irgendwelche Hilfsmittel benutzt?

Eine Möglichkeit ist folgende: Du kannst die Steine beider Kisten so nebeneinander packen, dass jeweils ein Stein der einen Kiste neben einem Stein der anderen Kiste liegt. Ist eine Kiste leer und bleiben in der anderen Kiste Steine übrig, so besitzt die zweite Kiste mehr Steine als die erste. Werden beide Kisten gleichzeitig leer, so waren in den beiden Kisten dieselbe Anzahl von Steinen.
Was haben wir hier gemacht? Wir haben zwei endliche Mengen und , die wir vergleichen wollen. Nun haben wir nacheinander jeweils ein Element und ein Element einander zugeordnet. Dabei war diese Zuordnung eineindeutig. „Eineindeutig“ bedeutet, dass dem Element ein eindeutiges und dem Element ein eindeutiges Element zugeordnet wird. Waren wir damit in dem Sinn erfolgreich, dass wir jedem ein eindeutiges und jedem ein eindeutiges zuordnen konnten, dann sind beide Mengen gleich groß. Ist eine solche eineindeutige Zuordnung zwischen den Mengen und unmöglich, sind beide Mengen unterschiedlich groß.
Eine solche eineindeutige Zuordnung zwischen zwei Mengen ist aber nichts anderes als eine bijektive Abbildung zwischen diesen beiden Mengen. Dementsprechend sind zwei endliche Mengen genau dann gleich groß, wenn es zwischen ihnen eine bijektive Abbildung gibt. Dieses Merkmal gleich großer endlicher Mengen kann auch auf unendliche Mengen übertragen werden.
Bei der Übertragung auf unendliche Mengen müssen wir aber vorsichtig sein. Es tritt nämlich etwas auf, was bei endlichen Mengen nicht auftritt. Bei endlichen Mengen ist es egal, wie wir die Elemente der Mengen paarweise zuordnen. Bei unendlichen Mengen ist es nicht egal, wie die folgenden Beispiele zeigen:
Beispiel
Wir betrachten die Menge der natürlichen Zahlen mit Null und ohne Null.
- Die Funktion ist injektiv, aber nicht surjektiv.
- Die Funktion ist bijektiv.
Im Beispiel 1 ist die Zahl kein Bild der Funktion . Bei dieser Zuordnung bleibt die Zahl übrig. Im Beispiel 2 gilt , aber ist bijektiv und bei dieser Zuordnung bleiben keine Elemente übrig. Also ist eine echte Teilmenge zur gesamten Menge "gleich groß". Wir können daher nicht verlangen, dass alle injektiven Funktionen zwei gleichgroße unendliche Mengen bijektiv aufeinander abbilden. Es muss genügen, wenn wir eine bijektive Abbildung finden, damit zwei unendliche Mengen gleich groß sind.
Hinweis
Unendliche Mengen können injektiv in eine echte Teilmenge abgebildet werden.
Wir haben also eine Methode gefunden, zwei Mengen miteinander zu vergleichen: Zwei Mengen sind genau dann gleich groß, wenn eine bijektive Abbildung zwischen ihnen möglich ist. An dieser Stelle möchten wir noch darauf hinweisen, dass in der Mathematik eher von der Mächtigkeit als von der Größe von Mengen die Rede ist. So würde ein Mathematiker anstatt „zwei Mengen sind gleich groß“ eher „zwei Mengen sind gleichmächtig“ sagen.
Definition (Gleichmächtigkeit von Mengen)
Zwei Mengen und sind dann und nur dann gleichmächtig, wenn es zwischen ihnen eine bijektive Abbildung gibt:
Sind zwei Mengen nicht gleichmächtig, dann bleiben beim Vergleich bei einer der beiden Mengen Elemente übrig. Wir erhalten dann keine bijektive Abbildung, sondern nur eine injektive. Ist Injektiv, haben wir aber allen Elementen aus ein Element aus zugeordnet, so ist auf jeden Fall nicht mächtiger als . Wir definieren daher:
Definition (Mächtigkeit von Mengen)
Eine Mengen ist mächtiger als eine Menge , wenn es eine injektive Abbildung gibt. wird dann schmächtiger als genannt:
Beachte, dass diese Definition den Fall der Gleichmächtigkeit einschließt! Den Zusammenhang zwischen den beiden Definitionen liefert der Äquivalenzsatz von Cantor-Bernstein-Schröder:
Satz (Äquivalenzsatz von Cantor-Bernstein-Schröder)
Ist schmächtiger als und schmächtiger als , dann sind und gleichmächtig:
Dieser Satz liefert ein weiteres Kriterium dafür, wie die Gleichmächtigkeit zweier Mengen bewiesen werden kann. Indem nämlich zwei Funktionen angegeben werden: und . Den Beweis des Äquivalenzsatzes führen wir hier.
Beispiele
[Bearbeiten]Schauen wir uns nun die obigen Beispiele an, bei denen du dich intuitiv entscheiden solltest, welche Menge mehr Elemente enthält.
Menge der natürlichen Zahlen und Menge der Quadratzahlen
[Bearbeiten]Welche Menge ist nun größer: Die Menge der natürlichen Zahlen oder die Menge der Quadratzahlen ? Ist es möglich, eine Bijektion zwischen und zu finden?
Ja, es gibt eine bijektive Abbildung zwischen und , nämlich die Abbildung . Also die Abbildung
Es gibt also eine Abbildung, die jeder natürlichen Zahl eine eineindeutige Quadratzahl zuordnet. So sieht man, dass es genauso viele natürliche Zahlen gibt, wie es Quadratzahlen gibt. Dies ist ein erstes überraschendes Ergebnis: Denn aus der Tatsache, dass die Menge der Quadratzahlen eine echte Teilmenge der natürlichen Zahlen ist und dass es in den meisten endlichen Teilmengen der natürlichen Zahlen mehr natürliche Zahlen als Quadratzahlen gibt, könnte man vermuten, dass die Menge der natürlichen Zahlen mehr Elemente enthält als die Menge der Quadratzahlen. Dies ist aber, wie wir gerade gesehen haben, nicht der Fall.
Du siehst: Für unendliche Mengen ist der in der endlichen Welt gültige Satz „Ist eine echte Teilmenge der Menge , dann besitzt mehr Elemente als “ nicht mehr anwendbar.
Menge der natürlichen Zahlen und Menge der ganzen Zahlen
[Bearbeiten]Kommen wir zum nächsten Beispiel:
Frage: Sind die Menge der natürlichen Zahlen und die Menge der ganzen Zahlen gleich groß?
Auch diese beiden Mengen sind gleich groß. Eine bijektive Abbildung zwischen der Menge der natürlichen Zahlen und der Menge der ganzen Zahlen ist die Abbildung
oder in einer Formel
Menge der natürlichen Zahlen und Menge der rationalen Zahlen
[Bearbeiten]Auch die Menge der rationalen Zahlen ist gleich mächtig mit der Menge der natürlichen Zahlen. Hier ist es jedoch nicht so einfach, selbst auf den Beweis zu kommen. Zunächst musst du die rationalen Zahlen in eine geschickte zweidimensionale Anordnung bringen:
Nun kannst du bei 0 beginnend die obige Anordnung der rationalen Zahlen so abzählen, dass jeder rationalen Zahl im Schema genau eine eindeutige natürliche Zahl zugeordnet wird:
So erhältst du folgende Abbildung der natürlichen Zahlen in die Menge der rationalen Zahlen:
Durch diese Abbildung werden zwar alle rationalen Zahlen mindestens einmal getroffen (die Abbildung ist surjektiv), aber es gibt verschiedene natürliche Zahlen, die auf dieselbe rationale Zahl abgebildet werden (die Abbildung ist nicht injektiv). So wird der 5 und der 7 dieselbe rationale Zahl -1 zugeordnet. Um nun auch die Abbildung injektiv (und damit insgesamt bijektiv) zu machen, überspringen wir beim Abzählen diejenigen rationalen Zahlen, die nicht vollständig gekürzt sind:
So erhalten wir folgende bijektive Abbildung zwischen und :
Es ist also möglich, bijektiv auf abzubilden. Dies beweist, dass und gleich mächtig sind, also dieselbe Anzahl an Elementen besitzen. Auch dies ist eine stark kontraintuitive Feststellung, denn allein im Intervall gibt es unendlich viele rationale, aber nur zwei natürliche Zahlen.
Zur Übung kannst du nun folgende Aufgabe lösen:
Frage: Welche Menge ist größer: oder , die Menge der positiven rationalen Zahlen?
Auch die beiden Mengen und sind gleich mächtig. Um dies zu zeigen, wählen wir folgendes Schema zur Anordnung der positiven rationalen Zahlen:
Um eine bijektive Abbildung von nach zu erhalten, zählen wir die rationalen Zahlen im Schema diagonal beginnend bei ab, wobei wir nicht vollständig gekürzte Brüche überspringen:
So haben wir folgende bijektive Abbildung zwischen und gefunden, die beweist, dass beide Mengen gleich mächtig sind:
Das hier vorgestellte Vefahren wird auch Cantors erstes Diagonalargument genannt.
Menge der natürlichen Zahlen und Menge der reellen Zahlen
[Bearbeiten]Als letztes Beispiel vergleichen wir die Menge der natürlichen Zahlen mit der Menge der reellen Zahlen. Hier werden wir sehen, dass es mehr reelle als natürliche Zahlen gibt. Doch wie kann man beweisen, dass und nicht gleich mächtig sind?
Wir werden diesen Beweis in zwei Schritten führen: Zunächst zeigen wir, dass die Menge der reellen Zahlen und das offene Intervall gleich mächtig sind. Danach zeigen wir, dass und nicht gleich mächtig sind. So haben wir gezeigt, dass auch und nicht gleich mächtig sind (wären und gleich mächtig, so wären auch und gleich mächtig, was wir aber widerlegt haben).
Frage: Wieso sind und gleich mächtig? Wie sieht eine bijektive Abbildung zwischen und aus?
Wir wissen, dass der Tangens eine bijektive Abbildung von nach ist. Diese Funktion können wir nutzen, um eine bijektive Abbildung zu basteln. Durch die Zuordnung wird das Intervall bijektiv auf verschoben. Wenn man nun noch den Tangens anwendet, entsteht eine bijektive Abbildung :
Alternativ können wir mit dem Arkustangens eine bijektive Abbildung konstruieren:
Nun müssen wir beweisen, dass und nicht gleich mächtig sein können, dass es also keine bijektive Abbildung gibt.
Sei dazu eine beliebige Abbildung. Wir können nun die einzelnen Funktionswerte dieser Funktion in ihrer Dezimalentwicklung in einer unendlich langen Liste untereinander schreiben:
Dabei steht die Variable für die Ziffer aus der Menge , die bei der Dezimalentwicklung der Zahl an der -ten Nachkommastelle auftritt. Sollte eine Dezimalentwicklung einer reellen Zahl abbrechen, so füllen wir diese mit Nullen auf. So wird aus der Dezimalentwicklung 0,25 der Zahl die Dezimalentwicklung
Wäre beispielsweise , , und , so würden die ersten vier Zeilen unserer Liste so aussehen:
Nun konstruieren wir mit Hilfe der Liste eine neue Zahl , welche im offenen Intervall liegt und nicht in der Liste enthalten ist. Dabei gehen wir nach folgendem Algorithmus vor:
- Wir setzen , wenn und , wenn ist. Damit ist .
- Wir setzen , wenn und , wenn ist. Damit ist .
- Wir setzen , wenn und , wenn ist. Damit ist .
Die allgemeine Regel zur Konstruktion von lautet dabei:
- Setze , wenn ist und setze ansonsten .
Diese Regel garantiert, dass sich von jedem für unterscheidet, da sich in seiner Dezimalbruchentwicklung an der -ten Nachkommastelle von unterscheidet.
Hinweis
Es gibt eine Möglichkeit, bei der zwei unterschiedliche Dezimalbruchentwicklungen dieselbe Zahl bezeichnen. Dies kann nämlich dann und nur dann auftreten, wenn eine der beiden Dezimalbruchentwicklungen mit lauter 9ern endet. So ist beispielsweise:
Da wir aber die Unterscheidung in und machen und in der Dezimalbruchentwicklung von nur 5er und 4er nach dem Komma auftreten, kann dieser Fall in unserem Beweis nicht auftreten.
In unserem obigen Beispiel würden die ersten 4 Nachkommastellen von lauten:
Außerdem ist eine reelle Zahl im Intervall , da als Nachkommastellen nur 4er und 5er auftreten und da keine Vorkommastellen ungleich Null besitzt. ist auch nicht in unserer Liste enthalten, was bedeutet, dass es nicht durch die Funktion getroffen wird. Dies bedeutet aber, dass nicht surjektiv ist. Also ist sicher nicht bijektiv.
Da dieser Beweis für jede Abbildung funktioniert, gibt es keine bijektive Abbildung zwischen der Menge der natürlichen Zahlen und der Menge der reellen Zahlen. Dies beweist, dass beide Mengen nicht gleich mächtig sind, dass es also unterschiedliche Arten der Unendlichkeit gibt. Es gibt natürlich eine injektive Abbildung von in , nämlich die Identität: . Also ist echt mächtiger als .
Der obige Beweis wurde von Georg Cantor 1877 entdeckt und wird Cantors zweites Diagonalargument genannt.
Abzählbarkeit und Überabzählbarkeit
[Bearbeiten]Wir haben in den Beispielen zwei verschiedene Größen von unendlichen Mengen kennengelernt: die Abzählbarkeit und die Überabzählbarkeit. Eine Menge ist abzählbar unendlich, wenn sie gleichmächtig mit der Menge ist. Dies bedeutet, dass alle Elemente dieser Menge in einer unendlichen Liste aufgeschrieben werden können. Dies ist gleichwertig damit, dass man alle Elemente dieser Menge abzählen kann (ihr also eine eineindeutige Indexnummer zuordnen kann).
Eine höchstens abzählbare Menge ist entweder endlich oder abzählbar unendlich. Eine überabzählbare Menge ist eine Menge, die nicht höchstens abzählbar, also mächtiger als die Menge der natürlichen Zahlen ist. Eine solche Menge kann nicht in einer unendlichen Liste aufgeschrieben werden. Dafür ist sie einfach zu groß.
Hinweis
In der Literatur wird der Begriff „abzählbar“ nicht eindeutig verwendet. Manchmal bedeutet dieser Begriff „abzählbar unendlich“ und manchmal „höchstens abzählbar“.
Die Begriffe dieses Abschnitts treten in der Mathematik oft und an verschiedenen Stellen auf. Deshalb ist es wichtig, dass du lernst, mit diesen Begriffen umzugehen.
Beispiel (abzählbar unendliche und überabzählbar unendliche Mengen)
- Die Mengen , und sind abzählbar unendlich.
- Die Mengen und sind überabzählbar unendlich.
Äquivalenzsatz von Cantor-Bernstein-Schröder
[Bearbeiten]Satz (Äquivalenzsatz von Cantor-Bernstein-Schröder)
Ist schmächtiger als und schmächtiger als , dann sind und gleichmächtig:
Wir beweisen den Satz in mehreren Schritten und zeigen zunächst die Äquivalenz mit dem Zwischenmengensatz.[13]
Satz (Zwischenmengensatz)
Liegt eine Menge zwischen einer Menge und einem injektiven Bild von , so sind und gleichmächtig.
Wir zeigen zunächst, dass der Äquivalenzsatz und der Zwischenmengensatz äquivalent sind:
Satz
Beweis
"": Es gelte der Äquivalenzsatz von Cantor-Bernstein-Schröder. Weiterhin sei und es gelte . Setze , dann bildet injektiv in ab. Mit bildet auch injektiv in ab. Mit dem Satz von Cantor-Bernstein-Schröder folgt .
"": Gelte nun der Zwischenmengensatz, sowie injektiv und Injektiv. Dann ist auch die Verkettung injektiv und es gilt: . Mit dem Zwischenmengensatz folgt . ✔
Für den Beweis des Zwischenmengensatzes definieren wir noch eine spezielle Halbordnung:
Definition (Spezielle Halbordnung)
Es sei eine Funktion von in . Dann ist die Menge der Fixpunkte von . Für zwei beliebige Funktionen und ist die Relation wie folgt definiert:
besagt, dass mehr Fixpunkte als hat, aber ansonsten mit übereinstimmt.
Aufgabe: Zeige, dass eine Halbordnung ist.
Zu zeigen ist, ist reflexiv, transitiv und antisymmetrisch.
reflexiv: Es gilt und , also auch .
transitiv: Gelte und . Dann folgt und . Daraus ergibt sich . Für ist kein Fixpunkt von und auch kein Fixpunkt von . Also folgt und somit .
antisymmetrisch: Gelte und . Dann gilt und also . Daher stimmen beide Funktionen überein und es gilt: .
Die Beweisidee ist folgende: wir betrachten alle injektiven Funktionen , die zwar mehr Fixpunkte haben als die gegebene Funktion , aber ausserhalb dieser Fixpunkte mit übereinstimmen. Je mehr Fixpunkte diese Funktionen haben, desto weniger Funktionswerte stimmen mit überein. Unter diesen Funktionen gibt es (hoffentlich) welche, deren Bildbereich weitere Elemente von umfasst. Diese müssen Fixpunkte sein, denn ansonsten sind keine Abweichungen von erlaubt. Wenn es unter den betrachteten Funktionen eine gibt, in deren Bildbereich alle Elemente von liegen, haben wir eine Bijektion gefunden.
Beweis (Zwischenmengensatz, Äquivalenzsatz)
Sei nun und gelte . Sei weiterhin:
ist die Menge aller injektiven Funktionen , die mehr Fixpunkte als haben. Es gilt , denn ist nach Voraussetzung Injektiv, und es gilt . Wir definieren:
ist die Fixpunktmenge aller Funktionen aus . Es gilt , denn wenn gibt es ein dessen Fixpunkt ist und da gilt . Wir definieren schliesslich die gesuchte Bijektion:
, da injektiv ist, und es gilt nach Definition von :
Da ja , wie oben gezeigt, gilt . Wir zeigen nun: . Seien und gelte . Sind , dann folgt . Sind folgt aus der Injektivität von . Bleibt als letzter Fall und . Dann gibt es mit und es folgt: mit der Injektivität von . Insgesamt haben wir gezeigt:
Als letzten Schritt beweisen wir, dass surjektiv auf ist und zeigen dazu . Wir definieren die Funktion wie folgt:
ist injektiv wegen der Injektivität von . Weiterhin gilt , denn hat allenfalls mehr Fixpunkte als und für gilt . Mit folgt daraus wegen wegen der Transitivität von . Insgesamt haben wir gezeigt: . Daraus folgt mit () und mit der Antisymmetrie von ergibt sich . Nach Definition von gilt und mit der Gleichheit folgt . Das ist aber nur möglich, wenn gilt, also: . Also:
Damit ist der Beweis des Zwischenmengensatzes und des Äquivalenzsatzes von Cantor-Bernstein-Schröder beendet. ✔
Beispiel
[Bearbeiten]Wir verwenden die Bezeichnungen wie im Beweis des Zwischenmengensatzes.
Beispiel (Zwischenmengensatz)
Es sei die Menge der natürlichen Zahlen, die Menge der natürlichen Zahlen größer oder gleich und die Funktion, die jede Zahl um 2 erhöht. ist injektiv und es gilt:
ist eine echte Obermenge von , denn die ist kein Bild unter . Wir definieren folgendermassen:
ist injektiv und alle ungeraden Zahlen sind Fixpunkte. Auf den geraden Zahlen stimmt mit überein. Da keine Fixpunkte hat, gilt also . somit gilt . Da ist, ist eine Bijektion auf .
Mehr Fixpunkte als kann aber keine Funktion aus haben, denn die geraden Zahlen können keine Fixpunkte sein. Das folgt durch Induktion: ist kein Fixpunkt, denn , tritt also nicht als Bild auf. Sei nun gerade und nach Induktionsvoraussetzung kein Fixpunkt. Dann ist das Bild von aber . Also kann auch kein Fixpunkt sein. Daher ist in diesem Beispiel tatsächlich die Funktion, deren Existenz im Beweis gezeigt wird.

Vertiefung zum Thema Mächtigkeit
[Bearbeiten]Wir haben definiert, dass zwei Mengen und genau dann gleichmächtig sind, wenn es zwischen ihnen eine bijektive Abbildung gibt: . Die Relation ist eine Äquivalenzrelation auf der Klasse aller Mengen.
Hinweis
Die Klasse aller Mengen ist zu groß für eine Menge, sie ist eine echte Klasse, vgl. "Axiomatische Mengenlehre".
Aufgabe: Zeige dass eine Äquivalenzrelation ist.
Um zu zeigen, dass eine Relation eine Äquivalenzrelation ist, müssen wir zeigen, dass sie reflexiv, symmetrisch und transitiv ist. Im folgenden seien beliebige Mengen.
Reflexiv: Die Identitätsabbildung ist eine Bijektion der Menge auf sich. Also gilt .
Symmetrisch: Gelte . Dann gibt es eine bijektive Abbildung . Daher ist die Umkehrfunktion ebenfalls bijektiv und bildet die Menge auf die Menge ab: . Also gilt .
Transitiv: Gelte und . Dann gibt es bijektive Abbildungen und . Die Komposition dieser beiden Abbildungen ist als Komposition zweier bijektiven Abbildungen ebenfalls bijektiv und bildet auf ab: . Also gilt . ✔
Da die Relation eine Äquivalenzrelation ist, zerfällt die Klasse aller Mengen unter dieser Relation in Äquivalenzklassen gleichmächtiger Mengen. Da diese Äquivalenzklassen ebenfalls echte Klassen sind, geht man zu einem Repräsentantensystem über, den sogenannten Kardinalzahlen:
Definition (Kardinalzahlen)
Die Kardinalzahlen sind Mengen und bilden ein Repräsentantensystem für die Äquivalenzklassen gleichmächtiger Mengen.[14]
Anmerkung: Die Schreibweise sollte nicht mit den mit den Betragsstrichen oder der Determinantenfunktion aus der Linearen Algebra verwechselt werden.
Definition (Ordnung der Kardinalzahlen)
Die folgende Definition ist repräsentantenunabhängig:
Es ist leicht zu zeigen, dass die Relation reflexiv und transitiv ist. Die Antisymmetrie folgt mit dem Äquivalenzsatz von Cantor-Bernstein-Schröder. ist also eine Halbordnung. Mit dem Auswahlaxiom kann man zeigen, dass eine Totalordnung ist:
Satz
ist eine Totalordnung auf den Kardinalzahlen.
Kardinalzahlen lassen sich also der Größe nach vergleichen. Sie sind verallgemeinerte natürliche Zahlen, die die Mächtigkeit einer Menge beschreiben. Im Fall einer endlichen Menge ist ihre Kardinalzahl nichts anderes als die Anzahl ihrer Elemente. Die endlichen Kardinalzahlen sind also die natürlichen Zahlen . Beispielsweise ist und .
ist die kleinste Mächtigkeit, die eine unendliche Menge haben kann: man kann zeigen, dass jede unendliche Menge eine Mächtigkeit größer oder gleich besitzt. Außerdem hat Cantor im Satz von Cantor gezeigt, dass jede Potenzmenge mächtiger als ihre zugrunde liegende Menge ist. Man kann zeigen, dass ist. Es gibt also unendlich viele unendliche Kardinalzahlen!
Die unendlichen Kardinalzahlen werden mit bezeichnet (der Buchstabe Aleph ist der erste Buchstabe des hebräischen Alphabets). Es ist . Es stellt sich nun die Frage, ob ist. Oder – anders formuliert – ob es eine Menge gibt, die mächtiger als , aber weniger mächtig als ist. Cantor vermutete, dass dies nicht der Fall ist, konnte seine Vermutung aber nicht beweisen. Diese Vermutung wird Kontinuumshypothese genannt. Es stellte sich jedoch heraus, dass diese Hypothese in der Mengenlehre mit den Axiomen von Zermelo-Fraenkel einschliesslich Auswahlaxiom weder beweisbar noch widerlegbar ist.
Generell kann man sich fragen, ob zwischen der Kardinalzahl einer unendlichen Menge und der ihrer Potenzmenge noch weitere Kardinlzahlen liegen. Falls nicht, wäre gerade usw. Das ist die allgemeine Kontinuumshypothese (GCH, General Continuum Hypothesis). Aber da schon die einfache Kontinuumshypothese in ZFC nicht beweisbar ist, ist es die allgemeine auch nicht. Sie kann aber widerspruchsfrei zu den ZFC-Axiomen zugefügt werden, d. h. wenn ZFC widerspruchsfrei ist, dann ist es auch ZFC + GCH.
Terme
[Bearbeiten]Terme sind mathematische Ausdrücke, die aus Zahlen, Funktionszeichen (wie , usw.), Variablen und Klammern gebildet werden können. Terme können durch Termumformungen verändert werden.
Notwendige Termumformungen finden
[Bearbeiten]Aufgabe
[Bearbeiten]Finde die notwendigen Termumformungen, um den Term in den Term umzuwandeln.
Herangehensweise
[Bearbeiten]Eine solche Problemstellung wird dir sicherlich häufig im Studium begegnen. Oftmals bekommst du, während du den Beweis für einen Satz suchst, einen Term α heraus und stehst vor dem Problem, zu beweisen, dass dieser gleich einem gewissen Term β ist (so wie ihn zum Beispiel die Aufgabe fordert). Du musst also eine Kette von Termumformungen finden, so dass
Um dieses Problem zu lösen, kannst du folgendermaßen vorgehen: Du schreibst beide Terme nebeneinander und versuchst beide durch Termumformungen auf die gleiche Gestalt zu bringen. Also in etwa so:
Die Lösung ergibt sich dann, indem du aufschreibst
Aufgabe: Finde die notwendigen Termumformungen für die obige Aufgabe heraus.
Mit der obigen Methode erhältst du folgende Lösung:
Damit ergibt sich folgende Lösung:
Gleichungen
[Bearbeiten]Gleichungen sind Aussagen oder Aussageformen, die die Gleichheit zwischen zwei Termen ausdrücken. Die allgemeine Form von Gleichungen ist
wobei und Terme sind.
Ungleichungen machen vergleichende Aussagen über zwei Terme. Hier steht an der Stelle des Gleichheitszeichens eines der Ordnungsrelationen , , oder .
Umformungen
[Bearbeiten]Durch Umformungen kann eine Gleichung in eine neue Gleichung umgeformt werden. Dabei muss gelten, dass immer dann, wenn erfüllt ist, zwangsläufig auch die Gleichung erfüllt sein muss. Man schließt also aus der Annahme der Gleichung auf die neue Gleichung .
Eine Gleichungsumformung von nach ist also nichts anderes als die Implikation , welche wahr sein muss (also eine Tautologie sein muss).
Ein Beispiel: Immer dann, wenn ist, ist (es ist ). Damit kann die Gleichung aus der Gleichung geschlossen werden beziehungsweise in umgeformt werden.
Ein häufiges Problem ist das Separieren/Isolieren („auf eine Seite bringen“) einer Variablen aus einer Ausgangsgleichung. Hier hat man eine Ausgangsgleichung mit mindestens einer Variablen gegeben, von der man weiß, dass sie erfüllt sein muss (Beispiel: ). Nun möchte man wissen, welche Werte eine bestimmte Variable (in Abhängigkeit der anderen Variablen) annehmen kann, sodass die Ausgangsgleichung mit diesen Werten erfüllt ist (Welche Werte für erfüllen die Ausgangsgleichung ?). Hier kann man schrittweise die Ausgangsgleichung in andere Gleichungen umformen, bis man eine Gleichung erhält, in der die gewünschte Variable auf einer Seite separiert ist. So können wir folgendermaßen nach umformen:
Insgesamt haben wir so die Implikation bewiesen. Wir wissen damit, dass immer dann, wenn ist, auch die Gleichung erfüllt sein muss. Doch haben wir damit auch bewiesen, dass unter der Annahme von die ursprüngliche Ausgangsgleichung erfüllt ist?
Nein, dies haben wir nicht. Genauso, wie Implikationen im Allgemeinen nicht umkehrbar sind, sind auch Gleichungsumformungen im Allgemeinen nicht umkehrbar. So ist eine nicht umkehrbare Gleichung. Es ist also .
Frage: Wieso ist die Umformung nicht umkehrbar?
Nicht immer dann, wenn gilt, gilt auch die Gleichung . So ist für zwar , aber . Damit ist die Implikation falsch, also nicht in umformbar.
Oben haben wir gezeigt, dass in umformbar ist, aber noch nicht, dass aus auch immer die Gleichung folgt. Dies müssen wir nachholen (obige Umformung in umgekehrter Reihenfolge, da jeder Einzelschritt umkehrbar ist):
Als Quintessenz dieses Abschnitts solltest du dir merken:
Hinweis
Gleichungsumformungen sind im Allgemeinen nicht umkehrbar.
Frage: Du hast die Ausgangsgleichung ( und sind Terme, bei denen in mindestens einem Term die Variable vorkommt). Aus ihr hast du die Lösungen , bis durch einfache Gleichungsumformungen gewonnen ( sind Terme ohne Variable ). Du hast also gezeigt . Sind dann bis alle Lösungen der Ausgangsgleichung für die Variable ? Wieso?
Nein, dies ist nicht der Fall. Zwar folgt aus die Aussage , und damit sind bis mögliche Kandidaten für Lösungen. Jedoch müssen sie die Ausgangsgleichung nicht lösen.
Ein Beispiel: Du weißt, dass es keine reelle Zahl gibt, die die Gleichung löst. Jedoch kannst aus der Ausgangsgleichung Gleichungsumformungen durchführen, die dich auf die Pseudolösungen und führen:
Wenn du nur einfache Gleichungsumformungen verwendest, musst du also immer überprüfen, ob deine gefunden Lösungen auch wirklich die Ausgangsgleichung lösen.
Äquivalenzumformungen
[Bearbeiten]Oben hast du gesehen, dass nicht alle Gleichungsumformungen umkehrbar sind. Deswegen werden all diejenigen Umformungen, die umkehrbar sind, unter dem Begriff Äquivalenzumformung zusammengefasst. Äquivalenzumformungen sind also diejenigen Umformungen , bei denen auch die Umkehrung erfüllt ist. Es gilt so insgesamt die Äquivalenz (daher der Name „Äquivalenzumformung“).
Wir können die Lösungen für aus der Gleichung direkt durch Äquivalenzumformung gewinnen (und sparen uns so den sonst notwendigen Rückweg):
Frage: Welche der folgenden Gleichungsumformungen sind Äquivalenzumformungen?
- Addition mit einem beliebigen Term auf beiden Seiten
- Subtraktion mit einem beliebigen Term auf beiden Seiten
- Multiplikation mit einem beliebigen Term auf beiden Seiten
- Division mit einem beliebigen Term ungleich Null auf beiden Seiten
- beide Seiten quadrieren
- beide Seiten hoch drei nehmen
- auf beiden Seiten den Betrag nehmen
| Umformung | Äquivalenzumformung | keine Äquivalenzumformung |
|---|---|---|
| Addition mit einem beliebigen Term auf beiden Seiten | ✔ | |
| Subtraktion mit einem beliebigen Term auf beiden Seiten | ✔ | |
| Multiplikation mit einem beliebigen Term auf beiden Seiten | ✘ | |
| Division mit einem beliebigen Term ungleich Null auf beiden Seiten | ✔ | |
| beide Seiten quadrieren | ✘ | |
| beide Seiten hoch drei nehmen | ✔ | |
| auf beiden Seiten den Betrag nehmen | ✘ |
Frage: Wieso ist die Multiplikation mit einem Term keine Äquivalenzumformung?
Wenn man beide Seiten einer Gleichung mit Null multipliziert, so ist die resultierende Gleichung stets , also immer wahr. Dies ist auch dann der Fall, wenn die ursprüngliche Gleichung falsch ist bzw. nicht erfüllbar ist.
Beispiel: Es gibt keine reelle Zahl mit . So ist nicht aus herleitbar (aus einer wahren Aussage können keine falschen Aussagen hergeleitet werden). Jedoch ist eine gültige Gleichungsumformung. Diese ist aber nicht umkehrbar, da ihre Umkehrung lauten würde, was aber für alle eine falsche Aussage ist.
Frage: Welche Eigenschaften muss eine Funktion erfüllen, damit
- eine gültige Gleichungsumformung ist?
- eine Äquivalenzumformung ist?
Für jede Funktion ist eine gültige Gleichungsumformung. Denn eine Funktion ordnet jedem Argument einen eindeutigen Funktionswert zu. Dies bedeutet insbesondere, dass, wenn ist, auch sein muss, also erfüllt ist.
Für eine Funktion ist genau dann eine Äquivalenzumformung, wenn injektiv ist. Gerade haben wir gesehen, dass eine gültige Gleichungsumformung ist. Sie ist eine Äquivalenzumformung, wenn auch eine gültige Gleichungsumformung ist. Diese Forderung ist aber nichts anderes als die Definition der Injektivität für die Funktion .
Summe und Produkt
[Bearbeiten]Motivation
[Bearbeiten]Wenn eine Summe viele Summanden hat, ist es unpraktisch, alle Summanden aufzuschreiben. Hier brauchst du eine abkürzende Schreibweise. Analoges gilt auch für Produkte, die viele Faktoren besitzen. Möglichkeiten solcher verkürzenden Summen- und Produktschreibweisen werden dir in diesem Kapitel vorgestellt.
Um lange Summen und Produkte abzukürzen, kannst du einzelne Summanden bzw. Faktoren auslassen. Beispielsweise kannst du die Summe der Zahlen eins bis hundert so aufschreiben:
Diese Schreibweise hat den Vorteil, dass sie intuitiv ist. Du kannst sie verwenden, ohne sie dem Leser extra erklären zu müssen. Auch der Umgang mit ihr ist im Regelfall nicht schwer. Das sind die Gründe, weshalb wir im Folgenden des Öfteren auf diese Schreibweise zurückgreifen werden. Jedoch hat sie einen entscheidenen Nachteil: Sie ist nicht eindeutig. Betrachte dazu folgendes Beispiel:
Beispiel: Wie lautet die Summe ausgeschrieben?
Ein mögliches Ergebnis ist (Summe der ersten acht natürlichen Zahlen). Ein weiteres mögliches Ergebnis ist (Summe der ersten vier Potenzen von zwei).
Wie das obige Beispiel zeigt, ist die Schreibweise mit Auslassungen ungenau: Es ist nicht eindeutig definiert, welche Summanden oder Faktoren zu ergänzen sind. Deswegen ist sie in den Augen der Mathematik kein guter Kandidat, um sie als abkürzende Schreibweise für lange Summen und Produkte einzusetzen. Es gibt jedoch eine andere Schreibweise, die dieses Problem der Ungenauigkeit nicht hat. Diese werden wir dir in den nächsten Abschnitten vorstellen.
Die Summenschreibweise
[Bearbeiten]Hier ein Beispiel einer Summenschreibweise mit Hilfe des Summenzeichens:

Diese Schreibweise besteht aus dem großen griechischen Buchstaben Σ (Sigma). Dem Summenzeichen Σ folgt ein Funktionsterm (hier ist es ). Unter dem Summenzeichen steht eine neue, zuvor noch nicht benutzte Variable, die als Laufindex, Laufvariable oder Summationsvariable bezeichnet wird. Unter dem Summenzeichen steht außerdem der Startwert der Laufvariablen. Das ist der kleinste ganzzahlige Wert, den die Laufvariable annehmen kann. Über dem Summenzeichen steht der Endwert der Laufvariablen. Auch dieser ist eine ganze Zahl und steht für den größten Wert, den die Laufvariable annehmen kann. Der Laufindex läuft nun vom Start- zum Endwert und nimmt nacheinander jede ganze Zahl zwischen diesen beiden Werten an (daher der Name „Laufindex“ bzw. „Laufvariable“). Für jeden der Werte, den die Laufvariable annimmt, wird ein Summand geschrieben. Der Funktionsterm nach dem Summenzeichen gibt dabei an, welcher Wert für diesen Summanden aufgeschrieben werden soll. Dazu wird der aktuelle Wert der Laufvariablen in den Funktionsterm eingesetzt und das Ergebnis als Summand notiert.
In unserem Beispiel ist die Laufvariable . Diese läuft vom Startwert bis zum Endwert und nimmt dabei nacheinander die Werte , , , und an. Der Funktionsterm, der angibt, welcher Summand aufgeschrieben werden soll, ist . Wir erhalten für den Summanden , für den Summanden , für den Summanden und so weiter… Insgesamt erhalten wir so die Summe:
In der folgenden Animation siehst du nochmals die Funktionsweise der Summenschreibweise :
Damit ergibt sich folgende Definition der Summe:
Definition (Summenschreibweise)
ist eine Kurzschreibweise für die Summe
Hinweis
In der Literatur findest du häufig die Schreibweise anstelle von . Hier ist eine Kurzschreibweise für . Die Schreibweise meint wie eine Zuordnungsvorschrift, die der Laufvariablen den Wert für den aktuellen Summanden zuordnet.
Verständnisaufgabe: Schreibe folgende Summen in der Summenschreibweise
Antwort:
- oder auch
Verständnisaufgabe: Wie lauten folgende Summen ausgeschrieben?
Wir erhalten folgende Summen:
Die Produktschreibweise
[Bearbeiten]
Die Produktschreibweise funktioniert analog zur Summenschreibweise. Der Unterschied ist, dass anstatt summiert, multipliziert wird – insgesamt also anstatt einer Summe ein Produkt beschrieben wird. Anstelle des Sigmazeichens Σ wird ein großes Pi Π verwendet. In der Produktschreibweise ist zum Beispiel:
In der folgenden Animation ist die Wirkungsweise der Produktschreibweise dargestellt, welche analog zur Summenschreibweise funktioniert:
Definition (Produktschreibweise)
ist eine Kurzschreibweise für das Produkt
Auch hier findest du in der Literatur häufig die Schreibweise an Stelle von .
Verständnisaufgabe: Schreibe folgende Produkt in der Produktschreibweise:
Antwort:
Verständnisaufgabe: Wie lauten folgende Produkte ausgeschrieben?
Wir erhalten folgende Produkte:
Leere Summe/Leeres Produkt
[Bearbeiten]Doch was passiert, wenn man die Summe bzw. das Produkt nicht auschreiben kann, weil der Startwert für die Laufvariable größer als der Endwert ist? Summen, die einen größeren Startwert als Endwert haben, nennt man leere Summe und Produkte mit einem größeren Start- als Endwert nennt man leeres Produkt, weil die Indexmenge, also die Menge der Werte, welche die Laufvariable durchläuft, „leer“ ist. Im Fall leerer Produkte und Summen gibt es in der Mathematik eine Konvention, die sich als sinnvoll erwiesen hat. Man ordnet einer Summe, bei der der Startwert größer dem Endwert ist, den Wert zu. Einem Produkt mit größerem Start- als Endwert wird der Wert zugeordnet. Du kannst dir hier als Eselsbrücke merken: Leeren Produkten/Summen wird eine solche Zahl zugeordnet, die das Ergebnis bei der entsprechenden Verknüpfung nicht verändert (wenn man zu einer Zahl addiert, ändert sich diese Zahl nicht und auch die Multiplikation mit verändert eine Zahl nicht).
Definition (Leere Summe)
Eine Summe, deren Startwert für die Laufvariable größer dem Endwert ist, nennt man leere Summe. Ihr wird der Wert Null zugeordnet.
Definition (Leeres Produkt)
Ein Produkt, dessen Startwert für die Laufvariable größer dem Endwert ist, nennt man leeres Produkt. Ihm wird der Wert Eins zugeordnet.
Beispiel
- und
- und
Doppelsumme und Doppelprodukt
[Bearbeiten]Doppelsummen und -produkte entstehen, wenn in der Summe oder dem Produkt wieder eine Summe oder ein Produkt definiert ist. Diese kannst du ausrechnen, indem du von außen nach innen die einzelnen Summen und Produkte auflöst:
Verständnisfrage: Schreibe folgende Doppelsummen und -produkte aus.
Antwort:
Beachte, dass – wie in der zweiten Teilaufgabe – die in einem Produkt geschachtelte Summe Vorrang hat, und deswegen ausgeschrieben geklammert werden muss.
Rekursive Definition der Summe und des Produkts
[Bearbeiten]Es gibt ein Problem mit den obigen Definitionen für Summen und Produkte, das wir dir nicht verschweigen möchten. Wie dir vielleicht bereits aufgefallen ist, haben wir zur Definition der Summen- und Produktschreibweise selbst Summanden und Faktoren ausgelassen, obwohl wir bereits festgestellt haben, dass das ungenau ist. Um uns nun von dieser Ungenauigkeit zu befreien, müssen wir eine Definition der Summen- und Produktschreibweise finden, die ohne Auslassungen auskommt.
Hier bietet sich eine rekursive Definition an. Solch eine Definition vollzieht sich in zwei Schritten: Dem Rekursionsschritt und dem Rekursionsanfang. Im Fall der Summe bzw. des Produkts lautet die rekursive Definition:
Definition (Rekursive Definition der Summe)
Die Summe ist definiert durch:
- Rekursionsschritt: Für ist
- Rekursionsanfang: Für ist
Definition (Rekursive Definition des Produkts)
Das Produkt ist definiert durch:
- Rekursionsschritt: Für ist
- Rekursionsanfang: Für ist
Zunächst fällt auf, dass die Definition des Rekursionsanfangs bei Summe und Produkt der obigen Definition der leeren Summe bzw. des leeren Produkts entspricht. Du siehst hier also eine erste Anwendung dieser Definition.
Um die rekursive Definition einer Summe (und eines Produkts) zu verstehen, kann man sich anschauen, wie mit Hilfe dieser Definition eine konkrete Summe ausgerechnet wird. Betrachten wir hierzu die Summe . Nach dem, was wir im Abschnitt zur Summenschreibweise gelernt haben, erwarten wir für diese Summe das Ergebnis
Wie lässt sich diese Summe aus der rekursiven Definition der Summe gewinnen? Hierzu muss solange der Rekurionsschritt auf die Summe angewandt werden, bis der Rekursionsanfang verwendet werden kann. Dieses Vorgehen ist im Einzelnen in der folgenden Animation dargestellt:
Du siehst: Zunächst wird die Summe mit dem Endwert auf eine Summe mit dem Endwert zurückgeführt, indem die Definition des Rekursionsschrittes angewandt wird (setze und ). Auf die verbleibende Summe mit Endwert wird nochmals der Rekursionsschritt angewandt und es entsteht eine Summe mit Endwert . Auf diese Summe wird nochmals der Rekursionsschritt angewandt. Die so entstandene Summe hat den Endwert , also einen kleineren Endwert als der Startwert . So ist die Bedingung für den Rekursionsanfang erfüllt und wir können die restliche Summe durch ersetzen. Die Rekursion bricht ab.
Analog funktioniert die rekursive Definition des Produkts: Wenn wir ein Produkt gegeben haben, so wird mit Hilfe des Rekursionschritts das Produkt schrittweise auf ein Produkt mit immer kleinerem Endwert zurückgeführt. Irgendwann ist der Endwert des verbleibenden Produkts kleiner als der Startwert. Es wird der Rekursionsanfang angewendet, womit die Rekursion abbricht.
Verständnisaufgabe: Wende die rekursive Definition auf folgende Summen/Produkte an:
Beim ersten Produkt erhält man:
Die zweite Summe ist bereits leer. Damit beginnt (und endet direkt) die Rekursion mit dem Rekursionsanfang:
Und beim letzten Produkt ist das Ergebnis:
Alternative Summen-/Produktschreibweise
[Bearbeiten]
Es gibt auch eine alternative Schreibweise für Summen und Produkte, die mächtiger ist als die oben vorgestellte Schreibweise. Auf die Nennung des Start- und Endwertes wird bei dieser Schreibweise verzichtet. Stattdessen definiert man unter der Summe eine Bedingung, die als (mathematische) Aussage formuliert wird. Als Laufvariable dient in dieser Schreibweise diejenige Variable, die in der Bedingung neu eingeführt wird (demzufolge muss in der Bedingungsaussage genau eine Variable neu eingeführt werden). Die Laufvariable nimmt nun in einer beliebigen Reihenfolge alle ganzzahligen Werte an, die die gestellte Bedingung erfüllen. Wegen der Kommutativität der Addition und der Multiplikation ist es auch kein Problem, dass die Reihenfolge der Summanden bzw. der Faktoren nicht spezifiziert ist. Nun wird wie in der oben definierten Summen-/Produktschreibweise für jeden Wert der Laufvariablen ein Summand aufgeschrieben. Auch hier gibt der Funktionsterm bzw. die Zuordnungsvorschrift nach der Summe an, welcher Wert als Summand für welchen Wert der Laufvariable aufgeschrieben wird.
Es ist auch möglich, dass in der alternativen Summen-/Produktschreibweise über mehrere Variablen summiert wird. Betrachte hierzu das Beispiel
In dieser Summe wird über alle Paare natürlicher Zahlen summiert, für die die Aussage erfüllt ist. Das trifft genau auf die Paare und , und , und sowie und zu. Damit ergibt sich obige Summe zu
Verständnisfrage: Was ist ?
Die Variablen können bei der Bedingung folgende Werte annehmen:
Damit erhält man für die Summe
Verständnisfrage: Was ist ?
Für die Bedingung müssen gleichzeitig folgende Ungleichungen erfüllt sein:
Damit sind folgende Paare für möglich:
Das Ergebnis lautet damit:
Fakultät
[Bearbeiten]Die Fakultät ist nichts anderes als eine Kurzschreibweise für das Produkt . Die Fakultät ist insbesondere für die Kombinatorik wichtig, da sie die Anzahl der verschiedenen Anordnungen einer -elementigen Menge wiedergibt. So stößt man in der Wahrscheinlichkeitsrechnung, der Statistik und auch in anderen Bereichen der Mathematik immer wieder auf die Fakultät. Schauen wir uns aber zunächst ihre Definition an, bevor wir uns ihrer Anwendung zuwenden.
Herleitung
[Bearbeiten]
Nehmen wir eine beliebige Menge. Wie viele Möglichkeiten gibt es, diese anzuordnen? Eine solche Fragestellung ergibt sich, wenn uns zum Beispiel bei einer Menge von Läufern die Anzahl der möglichen Startverteilungen oder bei einem Gruppenfoto die Anzahl der Aufstellungen der Personen interessiert. Welche Objekte wir betrachten, hat keinen Einfluss auf ihre Anordnungsmöglichkeiten. Ausschlaggebend ist nur ihre Anzahl. Wir suchen also eine Funktion , so dass die Anzahl der unterschiedlichen Möglichkeiten ist, die Elemente einer -elementigen Menge anzuordnen.
Um diese Funktion zu finden, gehen wir induktiv vor. Zunächst beginnen wir bei der kleinsten Menge mit nur einem Element () und versuchen durch sukzessives Einfügen neuer Elemente auf den Ergebnissen der vorherigen Schritte aufzubauen. Der Einfachheit halber betrachten wir nur Mengen der Form , da nur die Anzahl an Elementen relevant ist.
Beginnen wir mit der einelementigen Menge . Diese kann man nur auf eine Art anordnen, da sie nur ein Element besitzt:
Fügen wir der Menge ein Element hinzu und betrachten nun die Menge . Die neue Zahl kann ich an zwei Orten platzieren – vor und nach der :
Beim Hinzufügen des dritten Elements gehen wir auf dieselbe Weise vor: Die neuen Anordnungsmöglichkeiten erzeugen wir durch Einfügen des neu hinzukommenden Elements (der ) an allen möglichen Stellen in den bereits bestehenden Anordnungen von zwei Elementen. Zunächst sieht man, dass man die Zahl an drei Stellen einfügen kann: links, mittig, rechts. Außerdem gibt es bereits zwei mögliche Anordnungen der Zahlen . Damit erhalten wir ingesamt neue Anordnungsmöglichkeiten:
Für eine -elementige Menge lautet das Verfahren also: „Erzeuge alle Anordnungen der Menge, indem du das neue Element, , an allen möglichen Stellen in alle möglichen Permutationen der Menge ohne einfügst.“ Wir haben so induktiv alle Permutationen einer -elementigen Menge erzeugt. Wir wollen unserer Funktion nun einen Namen geben: Die von uns gesuchte Funktion wird Fakultät genannt und wird üblicherweise in der Postfix-Notation geschrieben.
Kehren wir zurück zur Erzeugungsvorschrift: Es gibt Möglichkeiten die neue Zahl zu platzieren, wobei es bereits Anordnungsmöglichkeiten der restlichen Zahlen gibt. So ergibt sich die Rekursionsformel:
Mit haben wir den Rekursionsanfang gefunden (es gibt eine Anordnungsmöglichkeit für eine einelementige Menge). Diese rekursive Berechnungsvorschrift können wir als Produkt auch explizit aufschreiben:
Unsere Baumdarstellung zeigt, dass die Fakultät schneller als jede Potenz wächst. Exponentieller Wachstum der Form entspricht der Anzahl der Blätter auf der -ten Ebene eines Baumes mit konstantem Verzweigungsgrad . Der Fakultätsbaum jedoch hat einen Verzweigungsgrad, der mit jeder neuen Ebene um zunimmt. Die Fakultät wächst also in der Großenordnung wie die Funktion .
Definition
[Bearbeiten]
Die Fakultät ist definiert als
Das auftretende Produkt mit der Pünktchen-Schreibweise können wir exakter als endliches Produkt notieren:
Es fehlt noch der Ausdruck . Was soll hier das Ergebnis sein? In der Schreibweise mit dem endlichen Produkt ergibt sich ein leeres Produkt:
Dieses Produkt ist leer, weil der Startwert des Laufindex größer als dessen Endwert ist. Wir hatten bereits festgelegt, dass das leere Produkt immer ist. Wir können also definieren:
Die letzte Gleichung können wir auch so interpretieren: Es gibt genau eine Möglichkeit eine leere Menge anzuordnen, nämlich mit der leeren Anordnung. Fassen wir das Gesagte zusammen:
Definition (Fakultät)
Für eine natürliche Zahl ist ihre Fakultät definiert durch:
Es ist .

Schauen wir uns einige Beispiele an:
Beispiel (Beispiele zur Fakultät)
Es ist
Die Fakultät wächst dabei sehr schnell. So ist und , also eine Zahl mit 157 Ziffern im Dezimalsystem. Die Stirlingformel ist eine Möglichkeit, die Fakultät zu approximieren. Diese Approximation zeigt, dass die Fakultät schneller als exponentielle Funktionen wächst.
Rekursive Definition der Fakultät
[Bearbeiten]Die Fakultät kann auch rekursiv definiert werden. Hierfür benötigen wir einen Rekursionsschritt und -anfang. Beim Rekursionsschritt wird angegeben, wie mit Hilfe von berechnet werden kann:
Frage: Wie kann mit Hilfe von berechnet werden?
Es ist
Der Rekursionsschritt lautet also
Mit Hilfe des obigen Rekursionsschritts kann auf zurückgeführt werden. Dieses wiederum kann durch berechnet werden, weil ist und so weiter. Es entsteht so eine Kette von Berechnungen, wobei in jedem Schritt die Fakultät einer Zahl mit Hilfe der Fakultät des Vorgängers berechnet wird.
Diese Berechnungskette muss aber irgendwann einmal abbrechen. Hierfür benötigen wir den Rekursionsanfang. Dabei müssen wir für die kleinste Zahl , für die die Fakultät sinnvoll definiert werden kann, den Ausdruck angeben. Diese kleinste Zahl ist . Nun wissen wir aber bereits aus dem obigen Abschnitt, dass ist. Damit ergibt sich folgende rekursive Definition der Fakultät:
Definition (Rekursive Definition der Fakultät)
Die Fakultät ist rekursiv definiert durch:
Die Wirkungsweise der rekursiven Definition lässt sich gut an einem Beispiel nachvollziehen. Hier wird solange der Rekursionsschritt angewendet, bis der Rekursionsanfang benutzt werden kann:
Verständnisfrage: Warum ist ?
Dies ergibt sich direkt aus dem Rekursionsschritt . In dieser Gleichung setzt man anstelle von einfach ein. Dies ergibt
Verständnisfrage: Vereinfache folgende Ausdrücke:
Es ist
Verständnisaufgabe: Beweise .
Aus der dritten binomischen Formel wissen wir . Damit ist
Dabei haben wir ausgenutzt, dass nach der Definition der Fakultät ist.
Anwendungen der Fakultät
[Bearbeiten]Wie bereits erwähnt, tritt die Fakultät häufig bei Wahrscheinlichkeitsrechnungen und in der Statistik auf. Die Ursache dafür liegt an folgendem Satz aus der Kombinatorik (die Kombinatorik beschäftigt sich mit der Frage nach der Anzahl möglicher Anordnungen und bildet damit die Grundlage der Wahrscheinlichkeitsrechnung).
Satz (Anordnungen einer endlichen Menge)
Die Anzahl aller Anordnungen einer endlichen Menge mit Elementen ist .
Dies bedeutet, dass die Anzahl der Permutationen einer Menge mit Elementen gleich ist. Mit Hilfe dieses Satzes können nun folgende Fragen beantwortet werden: Wie viele mögliche Anordnungen von Spielkarten gibt es? Wenn ich Bierflaschen habe, wie viele Reihenfolgen gibt es, diese Bierflaschen zu trinken? Auf wie viele unterschiedliche Routen kann man elf Sehenswürdigkeiten besichtigen?
Wie kommt man auf den Beweis? (Anordnungen einer endlichen Menge)
Schauen wir uns zunächst einige Beispiele an. Betrachte dazu die Menge und .
Frage: Wie viele Anordnungen dieser beiden Mengen gibt es und welche sind das?
Die Anzahl der verschiedenen Anordnungen dieser beiden Mengen lässt sich am besten dadurch bestimmen, indem wir alle möglichen Anordnungen systematisch aufschreiben. Fangen wir mit der Menge an. Die Menge besitzt folgende mögliche Anordnungen:
Wir haben sechs mögliche Anordnungen gefunden (was entspricht). Analog können wir alle möglichen Anordnungen der 4-elementigen Menge finden:
Wir haben verschiedene Möglichkeiten der Anordnung gefunden (was entspricht). Wenn man sich nun die gefundene Systematik zum Notieren aller Anordnungen anschaut, kann man ein induktives Prinzip erkennen.
Schauen wir uns die Anordnungen der zweiten Menge an. Zunächst haben wir vier Möglichkeiten die erste Zahl zu bestimmen (jede Spalte). Danach haben wir in den Zeilen jeder Spalte alle Kombinationsmöglichkeiten der restlichen drei Zahlen systematisch aufgeschrieben. Da es für drei Zahlen genau sechs Möglichkeiten gibt (wie bei Menge bestimmt), kommen wir auf insgesamt Möglichkeiten. Diese Argumentation entspricht einem Beweis mit vollständiger Induktion.
Beweis (Anordnungen einer endlichen Menge)
Aussageform, deren Allgemeingültigkeit für bewiesen werden soll:
Es gibt Möglichkeiten eine -elementige Menge anzuordnen.
1. Induktionsanfang:
Für eine einelementige Menge gibt es nur eine Anordnungsmöglichkeit. Da außerdem ist, ist die Aussageform für wahr.
2. Induktionsschritt:
2a. Induktionsvoraussetzung:
Es gibt Möglichkeiten eine -elementige Menge anzuordnen.
2b. Induktionsbehauptung:
Es gibt Möglichkeiten eine -elementige Menge anzuordnen.
2c. Beweis des Induktionsschritts:
Für eine -elementige Menge gibt es Möglichkeiten die erste Position zu besetzen. Für jede dieser Möglichkeiten müssen die restlichen Positionen besetzt werden, wobei es nach Induktionsvoraussetzung dafür genau Möglichkeiten gibt. Damit ist die Gesamtzahl aller möglichen Anordnungen einer -elementigen Menge genau .
Jetzt können wir auch unsere obigen Fragen beantworten: Es gibt verschiedene Anordnungen von Spielkarten, verschiedene Reihenfolgen, Bierflaschen zu trinken und verschiedene Routen, um Sehenswürdigkeiten zu besuchen.
Binomialkoeffizient
[Bearbeiten]Herleitung und Definition
[Bearbeiten]Frage: Was ist wahrscheinlicher: Beim Lotto zu gewinnen oder vom Blitz getroffen zu werden?
Das wirst du nach Lektüre dieses Kapitels beantworten können.
Damit du diese Frage beantworten kannst, musst du erst einmal die Wahrscheinlichkeit eines Lottogewinns wissen. Wie groß ist also die Wahrscheinlichkeit, 6 Richtige aus 49 Möglichkeiten zu raten? Zur Antwort dieser Frage benötigen wir die Anzahl der verschiedenen Möglichkeiten, 6 Zahlen aus 49 möglichen zu wählen. Hier kommt der Binomialkoeffizient ins Spiel. Er ist nämlich definiert als:
Definition (Binomialkoeffizient)
Der Binomialkoeffizient gibt für natürliche Zahlen und an, wie viele Möglichkeiten es gibt, Objekte aus Objekten auszuwählen. Damit gibt der Binomialkoeffizient an, wie viele -elementige Teilmengen aus einer -elementigen Menge gebildet werden können.
Man schreibt für den Binomialkoeffizienten . Dieser wird „n über k“ oder „k aus n“ ausgesprochen (Die deutsche Lotterie wird auch 6 aus 49 genannt). Der Binomialkoeffizient verdankt seinen Namen der Tatsache, dass er als Koeffizient im binomischen Lehrsatz auftritt. Aber dazu im nächsten Kapitel mehr.
Unsere Aufgabe ist es, den Binomialkoeffizienten zu bestimmen. Gehen wir dazu schrittweise vor: Zunächst ist es wichtig, dass du streng zwischen den Begriffen Anordnung und Kombination unterscheidest. Der Unterschied zwischen diesen zwei Begriffen ist der, dass bei einer Anordnung auf die Reihenfolge der Objekte geachtet wird, bei einer Kombination nicht. So sind zwar die Anordnungen und verschieden, die Kombinationen und aber gleich.
Frage: Wie viele Anordnungen von 6 Zahlen aus 49 Möglichkeiten gibt es?
An der ersten Stelle können 49 verschiedene Zahlen stehen. Wenn die erste Stelle besetzt ist, gibt es für jede dieser Besetzung 48 verschiedene Möglichkeiten, die zweite Stelle zu besetzen. Dementsprechend gibt es verschiedene Möglichkeiten die ersten zwei Stellen zu belegen. Analog gibt es für die ersten drei Stellen verschiedene Möglichkeiten der Belegung und so weiter. Damit gibt es für sechs Stellen verschiedene Belegungen, also verschiedene Anordnungen.
Jedoch ist beim Lotto die Reihenfolge der gezogenen Zahlen irrelevant. In den oben gefundenen Anordnungen gibt es viele, die zur gleichen Kombination gehören. Dementsprechend die Frage:
Frage: Wie viele Kombinationen von 6 Zahlen aus 49 Möglichkeiten gibt es?
Nimm eine beliebige Kombination von 6 Zahlen aus 49 Möglichkeiten. Wir haben bereits gesehen, dass in der bereits beschriebenen Menge aller Anordnungen diese Kombination öfter vorkommt. Wie oft ist dies? Nehmen wir eine konkrete Kombination der 6 Zahlen. Jede Anordnung dieser 6 Zahlen kommt in der obigen Menge aller Zahlen genau einmal vor. Nun gibt es nach dem Satz über die Anzahl der Anordnungen einer endlichen Menge für eine Kombination mit 6 Elementen genau verschiedene Anordnungen. Man muss also die obige Gesamtzahl aller Anordnungen durch 720 teilen und erhält das gewünschte Ergebnis. Es gibt damit verschiedene Kombinationen von 6 Zahlen aus 49.
Mit Hilfe des obigen Lösungswegs können wir auch eine allgemeine Formel für die Berechnung des Binomialkoeffizienten finden. Hierzu benötigen wir eine Fallunterscheidung in und . Betrachten wir zunächst den Fall, dass größer als ist:
Frage: Was ist der Binomialkoeffizient , wenn ist?
Nach obiger Definition entspricht der Binomialkoeffizient der Anzahl der verschiedenen Kombinationen von Objekten aus verschiedenen Objekten. Da größer als ist, gibt es keine Kombination von Objekten aus möglichen (So kannst du keine Kombination von 11 Elementen aus 4 dir zur Verfügung stehenden bilden). Damit ist für der Binomialkoeffizient .
Und nun zum Fall, dass und ist:
Aufgabe: Berechne allgemein für und , indem du analog zur obigen Herleitung für vorgehst.
Die Anzahl der verschiedenen Anordnungen von Elementen aus einer -elementigen Menge entspricht nach obiger Herleitung dem Produkt . Dieses Produkt kann auch in der Produktschreibweise als geschrieben werden. Dieses Produkt muss noch durch die Anzahl der verschiedenen Anordnungen einer Kombination geteilt werden, die ist (siehe Anordnungssatz aus dem Kapitel „Fakultät“). Damit erhalten wir:
Wenn wir dieses Ergebnis mit erweitern, erhalten wir die in Lehrbüchern übliche Definition des Binomialkoeffizienten:
Frage: Der letzte Fall: Wie sieht es im Fall aus?
Es gibt nur eine 0-elementige Menge, die leere Menge . Per Definition ist die leere Menge Teilmenge jeder Menge, insbesondere jeder -elementigen Menge. Damit ist Anzahl der 0-elementigen Kombinationen einer -elementigen Menge gleich 1 (es gibt nur die leere Kombination ). Es ist also für alle . Dies erhält man auch, wenn man mit der obigen Definition ausrechnet (siehe Binomialkoeffizient - Rechenregeln).
Zusammengefasst erhalten wir folgende alternative Definition des Binomialkoeffizienten:
Definition (Lehrbuchdefinition des Binomialkoeffizienten)
Für zwei natürliche Zahlen mit ist der Binomialkoeffizient definiert durch:
Für ist
Hier einige Beispiele:
Beispiel (Beispiele zum Binomialkoeffizienten)
Hinweis
Es gibt auch eine verallgemeinerte Definition des Binomialkoeffizienten. Mit diesem wirst du aber am Anfang des Studiums kaum in Berührung kommen, weswegen ich ihn weglasse.
Und was ist nun wahrscheinlicher: Blitzschlag oder Lottogewinn?
[Bearbeiten]Wie oben berechnet, gibt es verschiedene Kombinationen von 6 Zahlen beim Lottospiel.
Frage: Wie hoch ist die Wahrscheinlichkeit beim Lottospielen 6 Richtige zu bekommen?
Die Wahrscheinlichkeit, beim Lotto zu gewinnen, ist
Und wie hoch ist nun die Wahrscheinlichkeit vom Blitz getroffen zu werden? Um diese Frage zu beantworten, müssen wir sie konkretisieren: Wie hoch ist die Wahrscheinlichkeit in Deutschland innerhalb eines Jahres vom Blitz getroffen zu werden?. Nach dem Wikipedia-Artikel gibt es durchschnittlich 3 bis 7 Todesfälle durch Blitzschlag in Deutschland pro Jahr. In diesem Artikel ist die Rede von 4 bis 5 Todesfällen und Herr Krämer nennt so um die 10 Todesfälle jährlich (Leider konnte ich nur Angaben zu den jährlichen Todesfällen finden. Es wird sicherlich mehrere Menschen geben, die vom Blitz getroffen, aber nicht gestorben sind). Bei gut 82 Millionen Einwohner in Deutschland ergibt dies mit durchschnittlich 5 Todesfällen im Jahr eine Wahrscheinlichkeit von , in Deutschland innerhalb eines Jahres vom Blitz tödlich getroffen zu werden, also ungefähr die Wahrscheinlichkeit im Lotto zu gewinnen. Wenn man noch annimmt, dass die Anzahl der nicht-tödlichen Blitzschläge auf Menschen mindestens genauso hoch ist wie die Anzahl der jährlichen Todesfälle, ergibt dies eine Wahrscheinlichkeit von mindestens , im Jahr vom Blitz getroffen zu werden. Dementsprechend ist es wahrscheinlicher, in Deutschland innerhalb eines Jahres vom Blitz getroffen zu werden, als bei einem einzigen Tipp 6 Richtige im Lotto zu haben. Beachte, dass wir in der obigen Rechnung nur die Wahrscheinlichkeit eines einzigen Lottotipps berechnet haben. Wenn jemand im Jahr öfter Lotto spielt oder mehr Lottotipps bei einer Ziehung einreicht, dann ist seine Gesamtgewinnwahrscheinlichkeit, mit mindestens einem Tipp zu gewinnen, größer als .
Binomischer Lehrsatz
[Bearbeiten]Der binomische Lehrsatz
[Bearbeiten]Sicherlich sind dir die binomischen Formeln noch aus der Schule bekannt. Ich kann mir gut vorstellen, dass dein Mathe-Lehrer sie in seinen Unterrichtsstunden hoch und runter gebetet hat. Nicht ohne Grund! Denn immer wieder helfen sie dir die binomischen Formeln geschickt umzuformen und Beweise einfach zu führen. Hier zur Wiederholung die drei binomischen Formeln, welche für alle gelten:
Denk immer an diese Formeln. Wenn du zum Beispiel auf Terme wie triffst, kannst du sie auch als schreiben. Manchmal kannst du so schwierige Terme vereinfachen oder zusammenfassen. Doch nun zum Thema dieses Kapitels: Wie lauten die binomischen Formeln für größere Potenzen als der 2?. Wir wollen also eine allgemeine Lösungsformel für den Term für finden.
Hinweis
Denk daran, wenn wir wissen, was ist, wissen wir auch, was ist. Denn wir können als schreiben und für können wir die gefundene Formel anwenden. Dies gilt insbesondere auch für die obigen binomischen Formeln. So folgt wegen die zweite binomische Formel direkt aus der ersten.
Schauen wir uns ein Beispiel an: Wir wollen wissen, was ist. Hierzu müssen wir den Term ausmultiplizieren, wie es in der folgenden Animation gezeigt wird:
Wir erhalten so den Term . Es fällt auf, dass für jeden Summanden der Gesamtsumme die Summe der Exponenten von und gleich 3 ist. Dies leuchtet ein. Wir nehmen nämlich, wenn wir das Produkt ausmultiplizieren, aus jedem der Terme entweder ein oder ein (in jeden Summanden kommen insgesamt 3 Faktoren oder vor). Die Summe der Exponenten beider Variablen muss also gleich 3 sein. Es müssen so nur noch die Koeffizienten der einzelnen Summanden bestimmt werden.
Wir sind nun bereit für den allgemeinen Fall. Wir wollen wissen:
Wir wissen, dass das Ergebnis eine Summe von Potenzen in und ist. Die Summe der Exponenten in jedem Summanden ist gleich . Alle Potenzen besitzen also die Form , wobei eine natürliche Zahl ist (die 0 ist mit eingeschlossen). Wir müssen noch die Koeffizienten dieser Potenzen bestimmen. Betrachten wir einige Beispiele. Der Koeffizient von muss 1 sein. Denn wenn wir diese Potenz erhalten wollen, müssen wir aus allen Termen die Variable wählen:
Analog ist auch der Koeffizient für 1. Doch wie lautet allgemein der Koeffizient für den Term ? Dazu müssen wir aus den Termen -mal die Variable und -mal die Variable wählen. Doch wie viele Möglichkeiten gibt es aus Termen -mal eine Variable auszuwählen? Fällt dir etwas auf? Genau, dies ist der im vorherigen Abschnitt diskutierte Binomialkoeffizient ! Dementsprechend ist der Koeffizient von gleich (Deshalb auch der Name: Binomialkoeffizient!). Wir erhalten:
Satz (Der binomische Lehrsatz)
Für alle reellen Zahlen und und für alle natürlichen Zahlen gilt:
Folgerungen aus dem binomischen Lehrsatz
[Bearbeiten]Mit Hilfe des binomischen Lehrsatzes kannst du nun weitere Antworten auf Fragen der Kombinatorik finden. Stell dir vor, du hast eine beliebige, endliche Menge gegeben. Wie viele Teilmengen kannst du aus dieser Menge bilden? Wir wissen bereits, dass die Anzahl der -elementigen Teilmengen von dem Binomialkoeffizienten entspricht ( ist die Anzahl der Elemente der Menge ). Um die Gesamtzahl aller Teilmengen der Menge zu finden, müssen wir die Summe über die Anzahl aller -elementigen Teilmengen von mit bilden. Wir erhalten (Anmerkung: ist Potenzmenge von , also die Menge aller Teilmengen von . Dementsprechend ist die Anzahl aller Teilmengen von .):
Frage: Was ist das Ergebnis der obigen Summe? Vergleiche dazu die obige Summe mit dem binomischen Lehrsatz!
Die obige Summe entsteht aus dem binomischen Lehrsatz für und . Dementsprechend ist .
Satz (Größe der Potenzmenge einer endlichen Menge)
Sei eine beliebige endliche Menge. Dann ist .
Und wie sieht es mit der folgenden Summe aus?
Frage: Wie lautet das Ergebnis der obigen Summe?
Die obige Summe entsteht aus dem binomischen Lehrsatz für und . Das Ergebnis der Summe lautet dementsprechend:
Rechenregeln für den Binomialkoeffizienten
[Bearbeiten]In diesem Kapitel stelle ich dir die wichtigsten Eigenschaften des Binomialkoeffizienten vor.
Rechenregeln in der Übersicht
[Bearbeiten]Es sei im Folgendem und eine natürliche Zahl, wobei und hier auch Null sein dürfen. Außerdem sei . Es gelten nun folgende Regeln:
- für
Einige der obigen Gleichungen können gut aus der Anschauung des Binomialkoeffizienten erklärt werden, dass der Anzahl der -elementigen Teilmengen einer -elementigen Menge entspricht:
- weil eine -elementige Menge nur eine -elementige Teilmenge enthält (nämlich die Menge ).
- . Zu jeder Teilmenge von mit Elementen existiert deren Komplement, welches Elemente enthält. Somit ist die Anzahl der unterschiedlichen Teilmengen gleich.
- . Stellen wir uns Mengen vor, wobei und ein zuvor nicht in enthaltenes Element ist. Dann ist der erste Summand die Anzahl der -elementigen Teilmengen von - fügt man aber jeder dieser Mengen das neue Element hinzu, sind diese nun -elementige Teilmengen von . Zusammen mit den -elementigen Teilmengen ohne (der zweite Summand), erhalten wir das Ergebnis.
Andere Rechenregeln sind aber nicht so offensichtlich. Hier kann im Beweis auf die Fakultätsdefinition des Binomialkoeffizienten zurückgegriffen werden.
Pascalsches Dreieck
[Bearbeiten]

Das pascalsche Dreieck ist eine grafische Anordnung der Binomialkoeffizienten in einem Dreieck:
Wenn man die Binomialkoeffizienten ausrechnet, dann ergibt sich folgendes Dreieck:
Die Regel ermöglicht es, den Binomialkoeffizienten als Summe der beiden direkt oberhalb liegenden Binomialkoeffizienten zu berechnen:

Das Besondere am pascalschen Dreieck ist, dass man an ihm direkt die Binomalkoeffizienten und damit die Vorfaktoren beim Ausklammern von Potenzen der Form ablesen kann. Beispielsweise lautet die Zeile für :
Dies ist die vierte Zeile, weil die erste Zeile im Dreieck zu gehört. Damit wissen wir ohne Nachrechnen:
Der Sinn des pascalschen Dreiecks ist es also, die Vorfaktoren beim Ausklammern von Potenzen der Form einfach ablesen zu können. Das Dreieck wurde im Übrigen nach Blaise Pascal benannt, der es 1655 in einem seiner Bücher veröffentlichte. Es wurde aber bereits früher von anderen Mathematikern eingesetzt[15].
Beweise zu den Rechenregeln
[Bearbeiten]Regel 1 und 2
[Bearbeiten]Satz
Es gelten die beiden Formeln und .
Beweis
Die obigen Gleichungen ergeben sich durch Ausnutzung der Fakultätsdefinition des Binomialkoeffizienten:
und
Regel 3
[Bearbeiten]Satz
Es ist .
Wie kommt man auf den Beweis?
Um die notwendigen Termumformungen zu finden, beginnen wir am besten mit dem Term (weil dieser komplizierter ist als und deswegen die Umformung von zu wahrscheinlich einfacher ist als umgekehrt):
Der Term kann nun vereinfacht werden:
Der Term unterscheidet sich kaum von . Im Nenner müssen nur noch die beiden Faktoren vertauscht werden:
Damit haben wir alle notwendigen Termumformungen für den Beweis gefunden ![]() .
.
Beweis
Die Formel kann folgendermaßen bewiesen werden:
Regel 4
[Bearbeiten]Satz
Es ist .
Wie kommt man auf den Beweis?
Zunächst können wir beide Binomialkoeffizienten ausschreiben:
Beide erhaltene Terme können soweit wie möglich vereinfacht werden:
Die vereinfachten Terme stimmen überein, also müssen auch und identisch sein. Im Beweis müssen wir nun die verwendeten Termumformungen aufschreiben, mit denen in umgeformt werden kann.
Beweis
Es ist
Regel 5
[Bearbeiten]Satz
Sei mit . Es ist dann .
Wie kommt man auf den Beweis?
Zum Beweis der Gleichung gehen wir schrittweise vor:
Frage: Wie lautet die zu beweisende Gleichung, nachdem man auf beiden Seiten die Definition eingesetzt hat?
Aufgabe: Versuche durch Termumformungen die gerade gefundene Gleichung zu beweisen.
Beweis
Es ist
- ↑ Mit der Frage "Sind die mathematischen Erkenntnisse erfunden oder werden sie gefunden?" beschäftigt sich auch der italienische Autor Mario Livio in seinem Buch "Ist Gott ein Mathematiker?" (ISBN: 9783423348003). Auch der erstaunliche Zusammenhang zwischen Natur und Mathematik wird von Livio ausführlich diskutiert und mit den Lebensgeschichten großer Denker wie Pythagoras, Platon, Newton und Einstein bereichert.
- ↑ Brockhaus.de, Teilgebiete der Mathematik im Überblick
- ↑ Siehe Wikipedia-Artikel „Schaltjahr“
- ↑ Siehe hierzu die Diskussion https://de.wikibooks.org/w/index.php?title=Benutzer_Diskussion:Stephan_Kulla&oldid=712748#Kontravalenz_Bindungsstaerke
- ↑ Siehe Abschnitt „Notation“ des englischsprachigen Wikipedia-Artikels „Quantifier (logic)“
- ↑ Siehe Abschnitt „Herkunft der Bezeichnung“ des Wikipedia-Artikels „Gaußsche Summenformel“.
- ↑ Georg Cantor: Beiträge zur Begründung der transfiniten Mengenlehre. In: Mathematische Annalen 46 (1895), S. 31.
- ↑ Siehe auch Wikipedia-Artikel zum „Elementzeichen“
- ↑ Siehe Von Neumanns Modell der natürlichen Zahlen und Dedekindsche Schnitte
- ↑ Siehe Abschnitt „Bedeutung“ im Wikipedia-Artikel zur Zermelo-Fraenkel-Mengenlehre
- ↑ So konnte gezeigt werden, dass die Kontinuumshypothese in ZFC weder beweis- noch widerlegbar ist.
- ↑ Spektrum der Wissenschaft Spezial: Das Unendliche (Mai 2001). Seite 14. ISSN 0943-7096
- ↑ Wolfgang Rautenberg, Uber den Cantor-Bernsteinschen Aquivalenzsatz, Berlin 2007,[PDF]
- ↑ Auf eine genaue Definition der Kardinalzahlen verzichten wir hier. Üblicherweise werden Kardinalzahlen als spezielle Ordinalzahlen definiert.
- ↑ Siehe hierzu den Wikipedia-Artikel „Pascalsches Dreieck“.























































![{\displaystyle {\begin{aligned}\overbrace {\left(\underbrace {x{\text{ ist eine natürliche Zahl}}} _{\mathrm {Teilaussage} }\ \underbrace {\mathrm {und} } _{\mathrm {Junktor} }\ \underbrace {x\mathrm {\ ist\ gerade} } _{\mathrm {Teilaussage} }\right)} ^{\mathrm {Teilaussage} }\\[0.5em]\qquad \overbrace {\mathrm {Wenn\ } \ldots \mathrm {,\ dann\ } \ldots } ^{\mathrm {Junktor} }\qquad \overbrace {x\mathrm {\ ist\ durch\ } 2\mathrm {\ teilbar} } ^{\mathrm {Teilaussage} }\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/93b0537a34d8f0235e09c34dd512d1699de6613f)



































































































































































































































![{\displaystyle {\begin{aligned}&A\Rightarrow B\\&{\color {RedOrange}\updownarrow {\text{ Umformung nach 1.}}}\\[0.3em]\Leftrightarrow \quad &\neg A\lor B\\&{\color {RedOrange}\updownarrow {\text{ Kommutativität nach 2.}}}\\[0.3em]\Leftrightarrow \quad &B\lor \neg A\\&{\color {RedOrange}\updownarrow {\text{ Umformung nach 1.}}}\\[0.3em]\Leftrightarrow \quad &\neg B\Rightarrow \neg A\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7fe101798c8407b1c7f3b4821a0efb6296a58f6d)









































![{\displaystyle {\begin{aligned}&a<b\land b<c\Rightarrow a<c\\[0.5em]&\quad {\color {Purple}\downarrow \,{\mathsf {Bindungsreihenfolge\,beachten}}}\\[0.5em]&(a<b\land b<c)\Rightarrow a<c\\[0.5em]&\quad {\color {Purple}\downarrow \,A\Rightarrow B\longleftrightarrow {\text{Wenn }}A{\text{, dann }}B}\\[0.5em]&{\text{Wenn }}a<b\land b<c{\text{, dann }}a<c\\[0.5em]&\quad {\color {Purple}\downarrow \,A\land B\longleftrightarrow A{\text{ und }}B}\\[0.5em]&{\text{Wenn }}a<b{\text{ und }}b<c{\text{, dann }}a<c\\[0.5em]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4a3b2ba6b30b303a023ca77a9a7b51e654e2b89a)


![{\displaystyle {\begin{aligned}&\forall x\in \mathbb {R} \,\exists y\in \mathbb {R} :\,x+y=0\\[0.5em]&\quad {\color {Purple}\downarrow \,\forall x\in \mathbb {R} :A(x)\longleftrightarrow {\text{Für alle }}x{\text{ aus }}\mathbb {R} {\text{ gilt }}A(x)}\\[0.5em]&{\text{Für alle }}x{\text{ aus }}\mathbb {R} {\text{ gilt }}\exists y\in \mathbb {R} :\,x+y=0\\[0.5em]&\quad {\color {Purple}\downarrow \,\exists y\in \mathbb {R} :A(y)\longleftrightarrow {\text{Es gibt mindestens ein }}y{\text{ aus }}\mathbb {R} {\text{ mit }}A(y)}\\[0.5em]&{\text{Für alle }}x{\text{ aus }}\mathbb {R} {\text{ gilt }}({\text{Es gibt mindestens ein }}y{\text{ aus }}\mathbb {R} {\text{ mit }}x+y=0)\\[0.5em]&\quad {\color {Purple}\downarrow \,{\mathsf {Aussage\ sch{\ddot {o}}ner\ formulieren}}}\\[0.5em]&{\text{Für jede reelle Zahl }}x{\text{ gibt es eine reelle Zahl }}y{\text{ mit }}x+y=0\\[0.5em]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/691b5ffa62abd3d2dce53e1a535d2867b07612f1)

![{\displaystyle {\begin{aligned}&{\text{Alle ungeraden Zahlen ab 3 sind Primzahlen}}\\[0.3em]&\quad {\color {Purple}\left\downarrow \,{\mathsf {Allquantor}}\,\forall \;{\mathsf {eingef{\ddot {u}}hrt\,und\,Text\,umformuliert}}\right.}\\[0.3em]&\forall x:({\text{ist}}\,x\,{\text{ungerade und ist}}\,x\,{\text{größer als oder gleich}}\,3,\,{\text{dann ist}}\,x\,{\text{Primzahl}})\\[0.3em]&\quad {\color {Purple}\left\downarrow \,{\mathsf {Junktoren}}\,\land \;{\mathsf {und}}\,\Rightarrow \,{\mathsf {eingesetzt}}\right.}\\[0.3em]&\forall x:(x\,{\text{ist ungerade}}\land \,x\,{\text{ist größer als oder gleich}}\,3\Rightarrow x\,{\text{ist Primzahl}})\\[0.3em]&\quad {\color {Purple}\left\downarrow \,{\mathsf {Pr{\ddot {a}}dikate}}\,\geq \;{\mathsf {und}}\,P\,{\mathsf {eingesetzt,mit}}\,P:={\text{ist Primzahl}}\right.}\\[0.3em]&\forall x:(x\,{\text{ist ungerade}}\land \,x\geq 3\Rightarrow P(x))\\&\quad {\color {Purple}\left\downarrow \,(x\,{\text{ist ungerade}})\,{\mathsf {umgeschrieben}}\right.}\\[0.3em]&\forall x:(({\text{es gibt keine Zahl, die mit 2 multipliziert x ergibt)}}\land \,x\geq 3\Rightarrow P(x))\\&\quad {\color {Purple}\left\downarrow \,{\mathsf {Negation}}\,\neg \,{\mathsf {eingesetzt}}\right.}\\[0.3em]&\forall x:(\neg ({\text{es gibt eine Zahl die mit 2 multipliziert x ergibt}})\land \,x\geq 3\Rightarrow P(x))\\&\quad {\color {Purple}\left\downarrow \,{\mathsf {Existenzquantor}}\,\exists \,{\mathsf {eingesetzt}}\right.}\\[0.3em]&\forall x:(\neg \exists y:{\text{2 mal y ist x}}\land \,x\geq 3\Rightarrow P(x))\\&\quad {\color {Purple}\left\downarrow \,{\mathsf {Multiplikation}}\,\cdot \,{\mathsf {und}}\,={\mathsf {eingesetzt}}\right.}\\[0.3em]&\forall x:(\neg \exists y:2\cdot y=x\land \,x\geq 3\Rightarrow P(x))\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e476762bd2eac7850d1c6a7a004668f564b00bd)



![{\displaystyle {\begin{array}{l}\exists y\in \mathbb {R} \,\forall x\in \mathbb {R} :\,x+y=x\\[0.5em]\quad \downarrow \\[0.5em]{\text{Es gibt ein }}y\in \mathbb {R} {\text{, so dass }}\forall x\in \mathbb {R} :\,x+y=x.\\[0.5em]\quad \downarrow \\[0.5em]{\text{Es gibt ein }}y\in \mathbb {R} {\text{, so dass für alle }}x\in \mathbb {R} {\text{ gilt, dass }}x+y=x.\\[0.5em]\quad \downarrow \\[0.5em]{\text{Es gibt eine reelle Zahl }}y{\text{,}}\\[0.5em]{\text{so dass für alle reellen Zahlen }}x{\text{ die Gleichung }}x+y=x{\text{ erfüllt ist.}}\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0d64cb5303660c93d7a13b3c4cf64b025f4dedd6)
![{\displaystyle {\begin{array}{l}a>0\land b>0\Rightarrow a+b>0\\[0.5em]\quad \downarrow \\[0.5em]{\text{Wenn }}a>0\land b>0{\text{ ist, dann ist }}a+b>0.\\[0.5em]\quad \downarrow \\[0.5em]{\text{Wenn }}a>0{\text{ und }}b>0{\text{ ist, dann ist }}a+b>0.\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4d388db9872fdeef2ff29943516dc82459968938)
![{\displaystyle {\begin{array}{l}\forall \epsilon >0\,\exists \delta >0\,\forall x,y\in D:\,|x-y|<\delta \Rightarrow |f(x)-f(y)|<\epsilon \mathrm {.} \\[0.5em]\quad \downarrow \\[0.5em]{\text{Zu jedem }}\epsilon >0\,\exists \delta >0:\,\forall x,y\in D:\,|x-y|<\delta \Rightarrow |f(x)-f(y)|<\epsilon \mathrm {.} \\[0.5em]\quad \downarrow \\[0.5em]{\text{Zu jedem }}\epsilon >0{\text{ gibt es ein }}\delta >0{\text{,}}\\[0.5em]{\text{so dass }}\forall x,y\in D:\,|x-y|<\delta \Rightarrow |f(x)-f(y)|<\epsilon \mathrm {.} \\[0.5em]\quad \downarrow \\[0.5em]{\text{Zu jedem }}\epsilon >0{\text{ gibt es ein }}\delta >0{\text{,}}\\[0.5em]{\text{so dass für alle }}x,y\in D{\text{ gilt: }}|x-y|<\delta \Rightarrow |f(x)-f(y)|<\epsilon \mathrm {.} \\[0.5em]\quad \downarrow \\[0.5em]{\text{Zu jedem }}\epsilon >0{\text{ gibt es ein }}\delta >0{\text{,}}\\[0.5em]{\text{so dass für alle }}x,y\in D{\text{ gilt: Wenn }}|x-y|<\delta {\text{ ist, dann ist }}|f(x)-f(y)|<\epsilon \mathrm {.} \\[0.5em]\quad \downarrow \\[0.5em]{\text{Zu jedem }}\epsilon >0{\text{ gibt es ein }}\delta >0{\text{,}}\\[0.5em]{\text{so dass für alle }}x,y\in D{\text{ mit }}|x-y|<\delta {\text{ gilt }}|f(x)-f(y)|<\epsilon \mathrm {.} \end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8c90e19d5e18012ec2715afdff522a0ed33477db)


























![{\displaystyle {\begin{aligned}{\begin{array}{l}{\text{Negation einer Aussage in natürlicher Sprache.}}\\[0.5em]\qquad {\color {Orange}\left\downarrow {\text{Übersetzung}}\right.}\\[0.5em]{\text{Negation einer Aussage in formaler Sprache.}}\\[0.5em]\qquad {\color {Orange}\left\downarrow {\text{schrittweise Anwendung von Umformungsregeln}}{\color {White}{\text{Ü}}}\right.}\\[0.5em]{\text{negierte Aussage in formaler Sprache.}}\\[0.5em]\qquad {\color {Orange}\left\downarrow {\text{Übersetzung}}\right.}\\[0.5em]{\text{negierte Aussage in natürlicher Sprache.}}\\[0.5em]\end{array}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7b1c27d1db54580ad847f36b439e42e8e040aec5)



























![{\displaystyle {\begin{array}{l}\neg (\forall x\,\exists y:y<x)\\[0.5em]\qquad {\color {Gray}\left\downarrow \ {\text{Umformungsregel: }}\neg (\forall x:A(x))\iff \exists x:\neg A(x)\right.}\\[0.5em]\exists x:\neg (\exists y:y<x)\\[0.5em]\qquad {\color {Gray}\left\downarrow \ {\text{Umformungsregel: }}\neg (\exists x:A(x))\iff \forall x:\neg A(x)\right.}\\[0.5em]\exists x\,\forall y:\neg (y<x)\\[0.5em]\qquad {\color {Gray}\left\downarrow \ \neg (y<x)\iff y\geq x\right.}\\[0.5em]\exists x\,\forall y:y\geq x\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/88acf55e3fe8ec228cf414b58e900721fc3edb1e)

![{\displaystyle {\begin{array}{l}{\text{Negation der Aussage: Zu jedem }}\epsilon >0{\text{ gibt es ein }}N\in \mathbb {N} {\text{,}}\\[0.3em]{\text{sodass für alle }}n\geq N{\text{ die Ungleichung }}|a-a(n)|<\epsilon {\text{ erfüllt ist.}}\\[1em]\qquad {\color {Gray}\left\downarrow \ {\text{Übersetzung in formale Schreibweise}}\right.}\\[1em]\neg \left(\forall \epsilon >0\,\exists N\in \mathbb {N} \,\forall n\in \mathbb {N} :\,n\geq N\implies |a-a(n)|<\epsilon \right)\\[1em]\qquad {\color {Gray}\left\downarrow \ {\text{Umformungsregel: }}\neg (\forall x:A(x))\iff \exists x:\neg A(x)\right.}\\[1em]\exists \epsilon >0:\neg \left(\exists N\in \mathbb {N} \,\forall n\in \mathbb {N} :\,n\geq N\implies |a-a(n)|<\epsilon \right)\\[1em]\qquad {\color {Gray}\left\downarrow \ {\text{Umformungsregel: }}\neg (\exists x:A(x))\iff \forall x:\neg A(x)\right.}\\[1em]\exists \epsilon >0\,\forall N\in \mathbb {N} :\neg \left(\forall n\in \mathbb {N} :\,n\geq N\implies |a-a(n)|<\epsilon \right)\\[1em]\qquad {\color {Gray}\left\downarrow \ {\text{Umformungsregel: }}\neg (\forall x:A(x))\iff \exists x:\neg A(x)\right.}\\[1em]\exists \epsilon >0\,\forall N\in \mathbb {N} \,\exists n\in \mathbb {N} :\,\neg \left(n\geq N\implies |a-a(n)|<\epsilon \right)\\[1em]\qquad {\color {Gray}\left\downarrow \ {\text{Umformungsregel: }}\neg (A\implies B)\iff A\land \neg B\right.}\\[1em]\exists \epsilon >0\,\forall N\in \mathbb {N} \,\exists n\in \mathbb {N} :\,n\geq N\land \neg \left(|a-a(n)|<\epsilon \right)\\[1em]\qquad {\color {Gray}\left\downarrow \ \neg \left(|a-a(n)|<\epsilon \right)\iff |a-a(n)|\geq \epsilon \right.}\\[1em]\exists \epsilon >0\,\forall N\in \mathbb {N} \,\exists n\in \mathbb {N} :\,n\geq N\land |a-a(n)|\geq \epsilon \\[1em]\qquad {\color {Gray}\left\downarrow \ {\text{Übersetzung in natürliche Sprache}}\right.}\\[1em]{\text{Es gibt ein }}\epsilon >0{\text{, sodass es für alle }}N\in \mathbb {N} {\text{ ein }}n\in \mathbb {N} {\text{ mit }}n\geq N{\text{ und }}|a-a(n)|\geq \epsilon {\text{ gibt.}}\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c63c686ce2724c0517791d37661f9045fd4dac28)




![{\displaystyle {\begin{array}{l}{\text{Negation der Aussage: Für alle }}R>0{\text{ gibt es ein }}n\in \mathbb {N} {\text{, sodass }}|x_{n}|\geq R\mathrm {.} \\[1em]\qquad {\color {Gray}\left\downarrow \ {\text{Übersetzung in formale Schreibweise}}\right.}\\[1em]\neg \left(\forall R>0\,\exists n\in \mathbb {N} :|x_{n}|\geq R\right)\\[1em]\qquad {\color {Gray}\left\downarrow \ {\text{Umformungsregel: }}\neg (\forall x:A(x))\iff \exists x:\neg A(x)\right.}\\[1em]\exists R>0:\neg \left(\exists n\in \mathbb {N} :|x_{n}|\geq R\right)\\[1em]\qquad {\color {Gray}\left\downarrow \ {\text{Umformungsregel: }}\neg (\exists x:A(x))\iff \forall x:\neg A(x)\right.}\\[1em]\exists R>0\,\forall n\in \mathbb {N} :\neg \left(|x_{n}|\geq R\right)\\[1em]\qquad {\color {Gray}\left\downarrow \ {\text{Umformungsregel: }}\neg (|x_{n}|\geq R)\iff |x_{n}|<R\right.}\\[1em]\exists R>0\,\forall n\in \mathbb {N} \,:|x_{n}|<R\\[1em]\qquad {\color {Gray}\left\downarrow \ {\text{Übersetzung in natürliche Sprache}}\right.}\\[1em]{\text{Es gibt ein }}R>0{\text{, so dass für alle }}n\in \mathbb {N} {\text{, }}|x_{n}|<R{\text{ gilt.}}\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/df33d63fb9fb268096a5423310e4c7ad839e3ffa)
![{\displaystyle {\begin{array}{l}{\text{Negation der Aussage: Für alle }}\epsilon >0{\text{ und }}x\in D{\text{ gibt es ein }}\delta >0{\text{,}}\\[1em]{\text{sodass }}|f(x)-f(y)|<\epsilon \ {\text{für alle }}y\in D{\text{ mit }}|x-y|<\delta \mathrm {.} \\[1em]\qquad {\color {Gray}\left\downarrow \ {\text{Übersetzung in formale Schreibweise}}\right.}\\[1em]\neg \left(\forall \epsilon >0\,\forall x\in D\,\exists \delta >0\,\forall y\in D:|x-y|<\delta \implies |f(x)-f(y)|<\epsilon \right)\\[1em]\qquad {\color {Gray}\left\downarrow \ {\text{Umformungsregel: }}\neg (\forall x:A(x))\iff \exists x:\neg A(x)\right.}\\[1em]\exists \epsilon >0:\neg \left(\forall x\in D\,\exists \delta >0\,\forall y\in D:|x-y|<\delta \implies |f(x)-f(y)|<\epsilon \right)\\[1em]\qquad {\color {Gray}\left\downarrow \ {\text{Umformungsregel: }}\neg (\forall x:A(x))\iff \exists x:\neg A(x)\right.}\\[1em]\exists \epsilon >0\,\exists x\in D:\neg \left(\exists \delta >0\,\forall y\in D:|x-y|<\delta \implies |f(x)-f(y)|<\epsilon \right)\\[1em]\qquad {\color {Gray}\left\downarrow \ {\text{Umformungsregel: }}\neg (\exists x:A(x))\iff \forall x:\neg A(x)\right.}\\[1em]\exists \epsilon >0\,\exists x\in D\,\forall \delta >0:\neg \left(\forall y\in D:|x-y|<\delta \implies |f(x)-f(y)|<\epsilon \right)\\[1em]\qquad {\color {Gray}\left\downarrow \ {\text{Umformungsregel: }}\neg (\forall x:A(x))\iff \exists x:\neg A(x)\right.}\\[1em]\exists \epsilon >0\,\exists x\in D\,\forall \delta >0\,\exists y\in D:\neg \left(|x-y|<\delta \implies |f(x)-f(y)|<\epsilon \right)\\[1em]\qquad {\color {Gray}\left\downarrow \ {\text{Umformungsregel: }}\neg (A\implies B)\iff A\land \neg B\right.}\\[1em]\exists \epsilon >0\,\exists x\in D\,\forall \delta >0\,\exists y\in D:|x-y|<\delta \land \neg \left(|f(x)-f(y)|<\epsilon \right)\\[1em]\qquad {\color {Gray}\left\downarrow \ {\text{Umformungsregel: }}\neg (|f(x)-f(y)|<\epsilon )\iff |f(x)-f(y)|\geq \epsilon \right.}\\[1em]\exists \epsilon >0\,\exists x\in D\,\forall \delta >0\,\exists y\in D:|x-y|<\delta \land |f(x)-f(y)|\geq \epsilon \\[1em]\qquad {\color {Gray}\left\downarrow \ {\text{Übersetzung in natürliche Sprache}}\right.}\\[1em]{\text{Es gibt ein }}\epsilon >0{\text{ und ein }}x\in D{\text{,}}\\[1em]{\text{so dass für alle }}\delta >0{\text{ es ein }}y\in D{\text{ mit }}|x-y|<\delta {\text{ und }}|f(x)-f(y)|\geq \epsilon {\text{ gibt.}}\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1cb53d37d08cbe665c631cb475b653af6bf8a6e4)
![{\displaystyle {\begin{array}{l}{\text{Negation der Aussage: Für jeden Menschen gibt es einen anderen, der ihn liebt.}}\\[1em]\qquad {\color {Gray}\left\downarrow \ {\text{Übersetzung in formale Schreibweise. Sei }}M{\text{ die Menge aller Menschen.}}\right.}\\[1em]\neg \left(\forall x\in M\,\exists y\in M:y{\text{ liebt }}x\right)\\[1em]\qquad {\color {Gray}\left\downarrow \ {\text{Umformungsregel: }}\neg (\forall x:A(x))\iff \exists x:\neg A(x)\right.}\\[1em]\exists x\in M:\neg \left(\exists y\in M:y{\text{ liebt }}x\right)\\[1em]\qquad {\color {Gray}\left\downarrow \ {\text{Umformungsregel: }}\neg (\exists x:A(x))\iff \forall x:\neg A(x)\right.}\\[1em]\exists x\in M\,\forall y\in M:\neg \left(y{\text{ liebt }}x\right)\\[1em]\qquad {\color {Gray}\left\downarrow \ {\text{Übersetzung in natürliche Sprache}}\right.}\\[1em]{\text{Es gibt einen Menschen, so dass alle Menschen ihn nicht lieben.}}\\[1em]\qquad {\color {Gray}\left\downarrow \ {\text{Umformulierung}}\right.}\\[1em]{\text{Es gibt einen Menschen, den }}{\mathit {kein\ Mensch}}{\text{ liebt.}}\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c900f2297c7ffef625a3d57802ab3e55aa7e68cc)
![{\displaystyle {\begin{array}{l}\neg (\forall x\exists y:A(x)\implies B(y))\\[1em]\qquad {\color {Gray}\left\downarrow \ {\text{Umformungsregel: }}\neg (\forall x:A(x))\iff \exists x:\neg A(x)\right.}\\[1em]\exists x\,\neg (\exists y:A(x)\implies B(y))\\[1em]\qquad {\color {Gray}\left\downarrow \ {\text{Umformungsregel: }}\neg (\exists x:A(x))\iff \forall x:\neg A(x)\right.}\\[1em]\exists x\forall y:\neg (A(x)\implies B(y))\\[1em]\qquad {\color {Gray}\left\downarrow \ {\text{Umformungsregel: }}\neg (A\implies B)\iff (A\land \neg B)\right.}\\[1em]\exists x\forall y:\left(A(x)\land \neg B(y)\right)\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1cd0b4630b29112790e6c4b9bc4bc161aa2d0cb2)






![{\displaystyle {\begin{array}{ll}&\left(x-{\tfrac {k}{2}}\right)^{2}\geq 0\\[0.4em]\Rightarrow \ &x^{2}-kx+\left({\tfrac {k}{2}}\right)^{2}\geq 0\\[0.4em]\Rightarrow \ &\left({\tfrac {k}{2}}\right)^{2}\geq kx-x^{2}\\[0.4em]\Rightarrow \ &\left({\tfrac {k}{2}}\right)^{2}\geq x\cdot (k-x)\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a54f77163386c41cabb69035e458b9e62369bc63)



![{\displaystyle {\begin{array}{l}\left({\tfrac {k}{2}}\right)^{2}\geq xy\\[0.5em]\qquad \left\downarrow \ k=x+y\Rightarrow y=k-x\right.\\[0.5em]\left({\tfrac {k}{2}}\right)^{2}\geq x\cdot (k-x)\\[0.5em]\qquad \downarrow \\[0.5em]\left({\tfrac {k}{2}}\right)^{2}\geq xk-x^{2}\\[0.5em]\qquad \downarrow \\[0.5em]x^{2}-kx+\left({\tfrac {k}{2}}\right)^{2}\geq 0\\[0.5em]\qquad \left\downarrow {\text{ quadratische Ergänzung}}\right.\\[0.5em]\left(x-{\tfrac {k}{2}}\right)^{2}-\left({\tfrac {k}{2}}\right)^{2}+\left({\tfrac {k}{2}}\right)^{2}\geq 0\\[0.5em]\qquad \downarrow \\[0.5em]\left(x-{\tfrac {k}{2}}\right)^{2}\geq 0\qquad {\text{(wahre Aussage)}}\\[0.5em]\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/582482c5dec37e044f87ae6c5e2fb1e02ba51988)



















![{\displaystyle {\begin{array}{c}{\text{Prämissen}}\\[2ex]{\begin{array}{c}{\text{Fall }}F_{1}:\\{\color {Orange}|}\\{\color {Orange}{\text{logische}}}\\{\color {Orange}{\text{Schlussfolgerungen}}}\\{\color {Orange}\downarrow }\\{\text{zu beweisende Aussage}}\end{array}}{\begin{array}{c}{\text{Fall }}F_{2}:\\{\color {Orange}|}\\{\color {Orange}{\text{logische}}}\\{\color {Orange}{\text{Schlussfolgerungen}}}\\{\color {Orange}\downarrow }\\{\text{zu beweisende Aussage}}\end{array}}\ldots {\begin{array}{c}{\text{Fall }}F_{n}:\\{\color {Orange}|}\\{\color {Orange}{\text{logische}}}\\{\color {Orange}{\text{Schlussfolgerungen}}}\\{\color {Orange}\downarrow }\\{\text{zu beweisende Aussage}}\end{array}}\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bf02969cd919a5581f3c35f1b4bceb808db49ea7)












![{\displaystyle {\sqrt[{2}]{n}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/982b437319c71ee5c834f6b28e818772a2a05240)
![{\displaystyle \underbrace {n{\text{ ist gerade}}} _{=\ A}\Rightarrow \ \underbrace {{\sqrt[{2}]{n}}{\text{ ist gerade}}} _{=\ B}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ea9bab96851d63ec01f0f4ad20fd183eab122353)

![{\displaystyle {\begin{aligned}\neg B&=\neg \left({\sqrt[{2}]{n}}{\text{ ist gerade}}\right)\\&={\sqrt[{2}]{n}}{\text{ ist ungerade}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/12dd28dc26c38e771d84bb5de62720ad32903045)
![{\displaystyle \left({\sqrt[{2}]{n}}{\text{ ist ungerade}}\right)\Rightarrow \left(n{\text{ ist ungerade}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e6a6f9295ffece067e1640f3d93855d49d0faff1)
![{\displaystyle {\begin{array}{c}{\sqrt[{2}]{n}}{\text{ ist ungerade}}\\{\color {Orange}|}\\{\color {Orange}{\text{logische Schlussfolgerungen}}}\\{\color {Orange}\downarrow }\\n{\text{ ist ungerade}}\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/49cbbfb2aeeb711315db6718ce73517634c7f06b)

![{\displaystyle {\sqrt[{2}]{n}}=2\cdot k+1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fe7fe60f2c7c5efbd0330ee8a9d0693199b3a6a4)
![{\displaystyle {\begin{aligned}n&=\left({\sqrt[{2}]{n}}\right)^{2}\\&=\left(2\cdot k+1\right)^{2}\\&=4k^{2}+4k+1\\&=2\cdot \underbrace {\left(2k^{2}+2k\right)} _{=:\ m}+1\\&=2\cdot m+1\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9126b6161fd5cf22034bd01e192237bb2a7ef1ae)












































![{\displaystyle {\begin{aligned}\overbrace {1+2+3+\dots +k+(k+1)} ^{\text{linke Seite der Zielgleichung}}&={\color {OliveGreen}(1+2+3+\dots +k)}+(k+1)\\[0.5em]&\qquad {\color {OliveGreen}\downarrow \ {\text{Gegebene Gleichung einsetzen}}}\\[0.5em]&={\color {OliveGreen}{\frac {k\cdot (k+1)}{2}}}+(k+1)\\[0.5em]&={\frac {k\cdot (k+1)}{2}}+{\frac {2\cdot (k+1)}{2}}\\[0.5em]&={\frac {k\cdot (k+1)+2\cdot (k+1)}{2}}\\[0.5em]&\qquad {\color {Gray}\left\downarrow \ a\cdot b=b\cdot a\right.}\\[0.5em]&={\frac {(k+1)\cdot k+(k+1)\cdot 2}{2}}\\[0.5em]&\qquad {\color {Gray}\left\downarrow \ (k+1){\text{ ausklammern}}\right.}\\[0.5em]&={\frac {(k+1)\cdot (k+2)}{2}}\\[0.5em]&\qquad {\color {Gray}\left\downarrow \ k+2=(k+1)+1\right.}\\[0.5em]&=\underbrace {\frac {(k+1)\cdot ((k+1)+1)}{2}} _{\text{rechte Seite der Zielgleichung}}\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d46e653cfc718faf1a64ecdcc5e4ed067234b567)


























![{\displaystyle {\begin{aligned}\sum _{k=1}^{l+1}(2k-1)^{2}&=\left(\sum _{k=1}^{l}(2k-1)^{2}\right)+(2\cdot (l+1)-1)^{2}\\[0.3em]&{\color {OliveGreen}\left\downarrow \ {\text{Induktionsvoraussetzung verwenden}}\right.}\\[0.3em]&={\frac {l\cdot (2l-1)\cdot (2l+1)}{3}}+(2\cdot (l+1)-1)^{2}\\&={\frac {l\cdot (2l-1)\cdot (2l+1)+3\cdot (2l+1)^{2}}{3}}\\[0.3em]&{\color {OliveGreen}\left\downarrow \ (2l+1){\text{ ausklammern}}\right.}\\[0.3em]&={\frac {(2l+1)\cdot {\Big (}l\cdot (2l-1)+3\cdot (2l+1){\Big )}}{3}}\\&={\frac {(2l+1)\cdot (2l^{2}-l+6l+3)}{3}}\\&={\frac {(2l+1)\cdot (2l^{2}+2l+3l+3)}{3}}\\&={\frac {(2l+1)\cdot (2l\cdot (l+1)+3\cdot (l+1))}{3}}\\&={\frac {(l+1)\cdot (2l+1)\cdot (2l+3)}{3}}\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5ebe36ef0e60799ef45792427eddbc181082be45)




























![{\displaystyle {\begin{array}{lrcl}&{\dfrac {4^{2}}{2+1}}&<&{\dfrac {(2\cdot 2)!}{(2!)^{2}}}\\[5pt]\iff &{\dfrac {16}{3}}&<&{\dfrac {4!}{4}}\\[5pt]\iff &{\dfrac {64}{12}}&<&{\dfrac {72}{12}}\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cf93750de009b958848589ec7da438c706ae2136)

![{\displaystyle {\begin{array}{lrcl}&{\dfrac {4^{n+1}}{n+2}}&<&{\dfrac {\left(2(n+1)\right)!}{\left((n+1)!\right)^{2}}}\\[5px]\iff &{\dfrac {4^{n}\cdot 4}{n+2}}&<&{\dfrac {(2n+2)!}{((n+1)!)^{2}}}\\[5px]\iff &{\dfrac {4(n+1)}{n+2}}\cdot {\dfrac {4^{n}}{n+1}}&<&{\dfrac {(2n+2)(2n+1)(2n)!}{((n+1)\cdot n!)^{2}}}\\[5px]\iff &{\dfrac {4(n+1)}{n+2}}\cdot {\dfrac {4^{n}}{n+1}}&<&{\dfrac {(2n+2)(2n+1)(2n)!}{(n+1)^{2}\cdot (n!)^{2}}}\\[5px]\iff &\color {OliveGreen}{\dfrac {4(n+1)}{n+2}}\cdot \color {Orange}{\dfrac {4^{n}}{n+1}}&<&\color {OliveGreen}{\dfrac {(2n+2)(2n+1)}{(n+1)^{2}}}\cdot \color {orange}{\dfrac {(2n)!}{(n!)^{2}}}\\[5px]\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/956dfef985f9fd86aceaa217e1488465d8668e70)

![{\displaystyle {\begin{array}{lrcl}&{\dfrac {4(n+1)}{n+2}}&<&{\dfrac {(2n+2)(2n+1)}{(n+1)^{2}}}\\[5pt]\iff &4(n+1)^{3}&<&(2n+2)(2n+1)(n+2)\\[5pt]\iff &4(n+1)^{3}&<&2(n+1)\cdot 2\left(n+{\dfrac {1}{2}}\right)\cdot (n+2)\\[5pt]\iff &(n+1)^{3}&<&(n+1)\left(n+{\dfrac {1}{2}}\right)(n+2)\\[5pt]\iff &(n+1)^{2}&<&\left(n+{\dfrac {1}{2}}\right)(n+2)\\[5pt]\iff &n^{2}+2n+1&<&n^{2}+{\dfrac {5}{2}}n+1\\[5pt]\iff &2n&<&{\dfrac {5}{2}}n\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/722b0f0bc0f5edd5dbe892f0bc95033efb6d4051)








































![{\displaystyle {\begin{array}{c}\underbrace {A=B} _{A{\text{ ist identisch zu }}B}\\[2em]\underbrace {:\iff } _{\text{ nach Definition genau dann, wenn }}\\[2em]\underbrace {\forall x:(x\in A\iff x\in B)} _{{\text{für alle }}x{\text{ gilt: }}x{\text{ ist genau dann Element von }}A{\text{, wenn es Element von }}B{\text{ ist und umgekehrt.}}}\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd1cb6e2d1607e72887d90a1d4010a76e6515877)




![{\displaystyle {\begin{aligned}A&=\{x\,|\,x{\text{ ist ein Streichinstrument}}\}\\&=\{{\text{Geige, Viola, Cello}},\ldots \}\\[0.2em]B&=\{x\,|\,x{\text{ ist ein Instrument}}\}\\&=\{{\text{Trommel, Geige, Viola, Gitarre, Cello, Klavier}},\ldots \}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d044f799c792ca44d8129e0d4f2fef325629bb44)



![{\displaystyle {\begin{array}{c}\underbrace {A\subseteq B} _{A{\text{ ist Teilmenge von }}B}\\[2em]\underbrace {\iff } _{\text{ genau dann, wenn }}\\[2em]\underbrace {\forall x:(x\in A\Rightarrow x\in B)} _{{\text{Für alle }}x{\text{ gilt: Wenn }}x{\text{ ein Element von }}A{\text{ ist, dann ist es auch ein Element von }}B}\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2e48d8ad6b2adb91d0a08b01ef76c8ae509e3a66)



























































































































































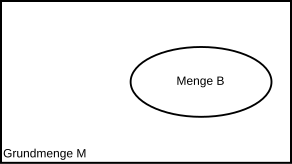












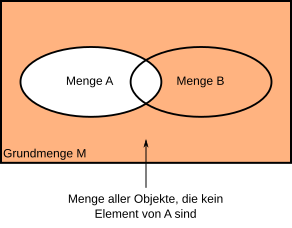






































![{\displaystyle {\begin{aligned}&(x_{1},x_{2},\dots ,x_{n},x_{n+1})=(y_{1},y_{2},\dots ,y_{n},y_{n+1})\\[0.3em]&{\color {BurntOrange}\left\updownarrow \ {\mathsf {Definition\;des\;Tupels}}\right.}\\[0.3em]\Leftrightarrow \;&((x_{1},x_{2},\dots ,x_{n}),x_{n+1})=((y_{1},y_{2},\dots ,y_{n}),y_{n+1})\\[0.3em]&{\color {BurntOrange}\left\updownarrow \ {\mathsf {Gleichheit\;des\;geordneten\;Paares}}\right.}\\[0.3em]\Leftrightarrow \;&(x_{1},x_{2},\dots ,x_{n})=(y_{1},y_{2},\dots ,y_{n}){\mathsf {\;und\;}}x_{n+1}=y_{n+1}\\[0.3em]&{\color {BurntOrange}\left\updownarrow \ {\mathsf {Induktionsvoraussetzung}}\right.}\\[0.3em]\Leftrightarrow \;&\forall k\leq n:x_{k}=y_{k}{\mathsf {\;und\;}}x_{n+1}=y_{n+1}\\[0.3em]&{\color {BurntOrange}\left\updownarrow \ {\mathsf {logische\;Umformung}}\right.}\\[0.3em]\Leftrightarrow \;&\forall k\leq n+1:x_{k}=y_{k}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c9d85fabfa38e40d2f5eeef0bbda5d6fce78e7cc)























![{\displaystyle {\begin{aligned}\{1,\,2\}\times \{3,\,4\}\times \{5,\,6\}=\{&(1,\,3,\,5);\,(1,\,3,\,6);\\[0.3em]&(1,\,4,\,5),\,(1,\,4,\,6),\\[0.3em]&(2,\,3,\,5),\,(2,\,3,\,6),\\[0.3em]&(2,\,4,\,5),\,(2,\,4,\,6)\}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/98631c7ffa59e769c92f8b5be10adf4e564e8c0d)












![{\displaystyle {\begin{aligned}\{1,\,2\}^{3}=\{1,\,2\}\times \{1,\,2\}\times \{1,\,2\}=\{&(1,\,1,\,1),\,(1,\,1,\,2),\\[0.3em]&(1,\,2,\,1),\,(1,\,2,\,2),\\[0.3em]&(2,\,1,\,1),\,(2,\,1,\,2),\\[0.3em]&(2,\,2,\,1),\,(2,\,2,\,2)\}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f88abd4ff7afdbfd2a704acdb83ebb2989afbf7f)






















































































































![{\displaystyle [x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/07548563c21e128890501e14eb7c80ee2d6fda4d)
![{\displaystyle [x]:=\{y\in M\,|\,y\sim x\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e665ff6d7154b198135b70c30c329952ee70220d)
![{\displaystyle [x]_{R}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d056fbad1d0b1c96edffb0fd0a1de8c2c00ec283)
![{\displaystyle [x]_{R}:=\{y\in M\,|\,y\sim _{R}x\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a6a16b1c37765e5090d56f2bffceb8a9dfc18ead)
![{\displaystyle [x]=[y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c34866e2a1216182b168dc1e272b0b02f1aab3a)
![{\displaystyle [x]\subseteq [y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4044b09c892280324baed37803bc2090935cedf8)
![{\displaystyle [y]\subseteq [x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ac2e8afc1de2256507f713d34dc61c6cc7c3b7a5)
![{\displaystyle a\in [x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/05b02437c238452a7cd8dbb82cd1cd934c8e380b)


![{\displaystyle a\in [y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6620c98bbacf4088ff62169b2ca876bcf5cce5fa)
![{\displaystyle x\in [x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/171880f55704b7119665c4bf008a08c02f00e9da)
![{\displaystyle x\in [y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8c97e1e00ad3bbee9f19110b07b1d5919ff41159)
![{\displaystyle [x]=[y]\iff x\sim y}](https://wikimedia.org/api/rest_v1/media/math/render/svg/01400b3e054161d1cc2ed3b4fb6358535335ed09)












![{\displaystyle {M/{\sim }}:=\{[x]\,|\,x\in M\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/04208fed7323862596e7462126eebb4f5ed61c27)
![{\displaystyle {M/{\sim _{R}}}:=\{[x]_{R}\,|\,x\in M\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7e9eb1dadd24dcae85e77b2e7c85d7099a11d6f9)




![{\displaystyle [x]\in P}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a879f0507d97feab501ded9760a8676e2f5b445b)
![{\displaystyle x\in [x]\subseteq \bigcup _{A\in P}A\implies x\in \bigcup _{A\in P}A}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f986e59a66668889d93b646a1ae474215b61fe6b)

![{\displaystyle A=[x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2cc2360da551f120152ad04072d8da887b136e1b)
![{\displaystyle B=[y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6d23de58718d213078a2482d6476309b00de627f)
![{\displaystyle A\cap B=[x]\cap [y]\neq \emptyset }](https://wikimedia.org/api/rest_v1/media/math/render/svg/70cf8087e730778b290f84e7e7c942751c0fcf60)

![{\displaystyle A=[x]=[y]=B}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4c009e4190a987dc70ba3e96983d838e73265b4a)

![{\displaystyle A=[x]\neq \emptyset }](https://wikimedia.org/api/rest_v1/media/math/render/svg/9f7cba1c0f36d7fb019b01ad8fe0fd5032c61a32)





![{\displaystyle {\begin{aligned}x\sim y&\iff \exists A\in P:x,y\in A\\[0.3em]&\iff \exists A\in P:y,x\in A\\[0.3em]&\iff y\sim x\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9590540976e33189910fd672193873aa3d5f286c)








![{\displaystyle \forall A\in P:\forall x\in A:[x]=A}](https://wikimedia.org/api/rest_v1/media/math/render/svg/89f12906e0bb84d3da3ec2ad8fee56768419d39f)
![{\displaystyle [x]\subseteq A}](https://wikimedia.org/api/rest_v1/media/math/render/svg/87662bb481ccffceb5b3ddcba6044d129ddf241e)
![{\displaystyle y\in [x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5c147835b2190d9bdd96df91bb70b34e3f655302)


![{\displaystyle A\subseteq [x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f76cdb2e0efea4ff4b7e79febad65356382d0852)


![{\displaystyle [x]=A}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c67ce5908dc00ce5c74736cff858abbb1e2dd377)

![{\displaystyle [x]\in M/{\sim }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9f83381ad95113cb29dc477ed998f08b78f1b627)
![{\displaystyle [x]=A\in P}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1a3babc9ce147cd9ef3539ba17b08c9e33734194)

![{\displaystyle A=[x]\in M/{\sim }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/62e4214881a93eec1ac7abbbb738b294d4684045)


![{\displaystyle {\begin{aligned}x\sim _{2}y&\iff \exists [a]\in M/{\sim _{2}}:x,y\in [a]\\[0.3em]&\ \left\downarrow \ P=M/{\sim _{2}}\right.\\[0.3em]&\iff \exists A\in P:x,y\in A\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/586e6cac5f307b10503f40e7773061400af3816e)










![{\displaystyle {\begin{aligned}&\ x\sim _{M}y\\[0.3em]&\ {\color {OliveGreen}\downarrow {\text{Definition von }}{\sim _{M}}}\\[0.3em]\implies &\ f(x)\sim _{N}f(y)\\[0.3em]&\ {\color {OliveGreen}\downarrow {\sim _{N}}{\text{ ist symmetrisch}}}\\[0.3em]\implies &\ f(y)\sim _{N}f(x)\\[0.3em]&\ {\color {OliveGreen}\downarrow {\text{Definition von }}{\sim _{M}}}\\[0.3em]\implies &\ y\sim _{M}x\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/580bd47877ad97e28401fd9d7d94ac0949bb285b)


![{\displaystyle {\begin{aligned}&\ x\sim _{M}y{\text{ und }}y\sim _{M}z\\[0.3em]&\ {\color {OliveGreen}\downarrow {\text{nach Definition von }}{\sim _{M}}}\\[0.3em]\implies &\ f(x)\sim _{N}f(y){\text{ und }}f(y)\sim _{N}f(z)\\[0.3em]&\ {\color {OliveGreen}\downarrow {\sim _{N}}{\text{ ist transitiv}}}\\[0.3em]\implies &\ f(x)\sim _{N}f(z)\\[0.3em]&\ {\color {OliveGreen}\downarrow {\text{nach Definition von }}{\sim _{M}}}\\[0.3em]\implies &\ x\sim _{M}z\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7db00bcacd925016114f51113c1f04e982fc2225)



















































































































![{\displaystyle {\begin{aligned}&\;x\leq _{2}y\\[0.3em]&\;{\color {Orange}\left\updownarrow \ {\mathsf {Definition\;von\;\leq _{2}}}\right.}\\[0.3em]\Leftrightarrow &\;x<y\lor x=y\\[0.3em]&\;{\color {Orange}\left\updownarrow \ x<y\Leftrightarrow x\leq _{1}y\land x\neq y\right.}\\[0.3em]\Leftrightarrow &\;(x\leq _{1}y\land x\neq y)\lor x=y\\[0.3em]&\;{\color {Orange}\left\updownarrow \ {\mathsf {Distributivgesetz:\;}}(A\land B)\lor C\Leftrightarrow (A\lor C)\land (B\lor C)\right.}\\[0.3em]\Leftrightarrow &\;(x\leq _{1}y\lor x=y)\land (x\neq y\lor x=y)\\[0.3em]&\;{\color {Orange}\left\updownarrow \ A\lor \neg A{\mathsf {\;ist\;eine\;Tautologie\;(immer\;wahr)}}\right.}\\[0.3em]\Leftrightarrow &\;(x\leq _{1}y\lor x=y)\land {\mathsf {W}}\\[0.3em]&\;{\color {Orange}\left\updownarrow \ A\land {\mathsf {W}}\Leftrightarrow A\right.}\\[0.3em]\Leftrightarrow &\;x\leq _{1}y\lor x=y\\[0.3em]&\;{\color {Orange}\left\updownarrow \ \leq _{1}{\mathsf {\;ist\;reflexiv}}\right.}\\[0.3em]\Leftrightarrow &\;x\leq _{1}y\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/45e9cc0201b4b604bf2b2741eb9167f9a1cb2f93)








![{\displaystyle {\begin{aligned}&\;x<_{2}y\\[0.3em]&\;{\color {Orange}\left\updownarrow \ {\mathsf {Definition\;von\;<_{2}}}\right.}\\[0.3em]\Leftrightarrow &\;x\leq y\land x\neq y\\[0.3em]&\;{\color {Orange}\left\updownarrow \ x\leq y\Leftrightarrow x<_{1}y\lor x=y\right.}\\[0.3em]\Leftrightarrow &\;(x<_{1}y\lor x=y)\land x\neq y\\[0.3em]&\;{\color {Orange}\left\updownarrow \ {\mathsf {Distributivgesetz:\;}}(A\lor B)\land C\Leftrightarrow (A\land C)\lor (B\land C)\right.}\\[0.3em]\Leftrightarrow &\;(x<_{1}y\land x\neq y)\lor (x=y\land x\neq y)\\[0.3em]&\;{\color {Orange}\left\updownarrow \ A\land \neg A{\mathsf {\;ist\;immer\;falsch\;}}({\mathsf {F}})\right.}\\[0.3em]\Leftrightarrow &\;(x<_{1}y\land x\neq y)\lor {\mathsf {F}}\\[0.3em]&\;{\color {Orange}\left\updownarrow \ A\lor F\Leftrightarrow A{\mathsf {\;ist\;eine\;Tautologie}}\right.}\\[0.3em]\Leftrightarrow &\;(x<_{1}y\land x\neq y)\\[0.3em]&\;{\color {Orange}\left\updownarrow \ <_{1}{\mathsf {\;ist\;irreflexiv}}\right.}\\[0.3em]\Leftrightarrow &\;x<_{1}y\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/47500c73bfaeef65821770a62839cbf7a55d3220)



























































![{\displaystyle f[A]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/35ed71bdb47bfe4c79812b2740415da6f8914c21)





















![{\displaystyle g^{-1}\left([0,5]\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b944e43938aeca9b94cfd1a2397dd986ec82fdb5)
![{\displaystyle h^{-1}\left([0,5]\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1f09688ac278fa4775bea40b8ac54ad0c8045fd1)

























![{\displaystyle [0,5]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/466c74a63ec8b8422ccb96c6bc5140dca45b5593)
![{\displaystyle g^{-1}\left([0,5]\right)=\{-1,\,0,\,1\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9123bdd537a3aee9121c9bd7a29285fcc3de8967)


![{\displaystyle h^{-1}\left([0,5]\right)=[-5,5]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ab05a5782fb7e4998d2d49b4fb464e6a30c198d2)
























![{\displaystyle h:\mathbb {R} \to [-1,1];x\mapsto \sin(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b3ae4fb74e1253aac9059a8615f8b956964d73fb)







![{\displaystyle [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01)












































































































































































![{\displaystyle {\begin{array}{ccccccccc}1&2&3&4&5&6&7&8&\cdots \\[0.3em]\updownarrow &\updownarrow &\updownarrow &\updownarrow &\updownarrow &\updownarrow &\updownarrow &\updownarrow &\cdots \\[0.3em]1&4&9&16&25&36&49&64&\cdots \end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ec62aac93c8e4ab359a3a2b29d0b89078e6c4c83)
![{\displaystyle {\begin{array}{ccccccccc}1&2&3&4&5&6&7&8&\cdots \\[0.3em]\updownarrow &\updownarrow &\updownarrow &\updownarrow &\updownarrow &\updownarrow &\updownarrow &\updownarrow &\cdots \\[0.3em]0&-1&1&-2&2&-3&3&-4&\cdots \\\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3c36be9385aa9afd457aa197f7d30aba092c572e)


![{\displaystyle {\begin{array}{clclclccclclclc}\cdots &-{\tfrac {1}{3}}&&-{\tfrac {1}{2}}\ _{\color {Blue}(6)}&{\color {MidnightBlue}\leftarrow }&-{\tfrac {1}{1}}\ _{\color {Blue}(5)}&&0\ _{\color {Blue}(1)}&{\color {MidnightBlue}\rightarrow }&{\tfrac {1}{1}}\ _{\color {Blue}(2)}&&{\tfrac {1}{2}}\ _{\color {Blue}(13)}&{\color {MidnightBlue}\rightarrow }&{\tfrac {1}{3}}\ _{\color {Blue}(14)}&\cdots \\[0.3em]&&&{\color {MidnightBlue}\downarrow }&&{\color {MidnightBlue}\uparrow }&&&&{\color {MidnightBlue}\downarrow }&&{\color {MidnightBlue}\uparrow }&&{\color {MidnightBlue}\downarrow }&\\[0.3em]\cdots &-{\tfrac {2}{3}}&&-{\tfrac {2}{2}}\ _{\color {Blue}(7)}&&-{\tfrac {2}{1}}\ _{\color {Blue}(4)}&{\color {MidnightBlue}\leftarrow }&{\color {MidnightBlue}-}&{\color {MidnightBlue}-}&{\tfrac {2}{1}}\ _{\color {Blue}(3)}&&{\tfrac {2}{2}}\ _{\color {Blue}(12)}&&{\tfrac {2}{3}}\ _{\color {Blue}(15)}&\cdots \\[0.3em]&&&{\color {MidnightBlue}\downarrow }&&&&&&&&{\color {MidnightBlue}\uparrow }&&{\color {MidnightBlue}\downarrow }&\\[0.3em]\cdots &-{\tfrac {3}{3}}&&-{\tfrac {3}{2}}\ _{\color {Blue}(8)}&{\color {MidnightBlue}\rightarrow }&-{\tfrac {3}{1}}\ _{\color {Blue}(9)}&{\color {MidnightBlue}-}&{\color {MidnightBlue}-}&{\color {MidnightBlue}\rightarrow }&{\tfrac {3}{1}}\ _{\color {Blue}(10)}&{\color {MidnightBlue}\rightarrow }&{\tfrac {3}{2}}\ _{\color {Blue}(11)}&&{\tfrac {3}{3}}\ _{\color {Blue}\cdots }&\cdots \\[0.3em]&\vdots &&\vdots &&\vdots &&&&\vdots &&\vdots &&{\color {MidnightBlue}\downarrow }&\\\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e1f49961729b204c7246fcf0c9e8658cb5cbe372)
![{\displaystyle {\begin{array}{ccccccccccc}{\color {Blue}1}&{\color {Blue}2}&{\color {Blue}3}&{\color {Blue}4}&{\color {Blue}5}&{\color {Blue}6}&{\color {Blue}7}&{\color {Blue}8}&{\color {Blue}9}&{\color {Blue}10}&{\color {Blue}\dotsb }\\[0.3em]{\color {MidnightBlue}\downarrow }&{\color {MidnightBlue}\downarrow }&{\color {MidnightBlue}\downarrow }&{\color {MidnightBlue}\downarrow }&{\color {MidnightBlue}\downarrow }&{\color {MidnightBlue}\downarrow }&{\color {MidnightBlue}\downarrow }&{\color {MidnightBlue}\downarrow }&{\color {MidnightBlue}\downarrow }&{\color {MidnightBlue}\downarrow }&{\color {MidnightBlue}\downarrow }\\[0.3em]0&{\tfrac {1}{1}}&{\tfrac {2}{1}}&-{\tfrac {2}{1}}&-{\tfrac {1}{1}}&-{\tfrac {1}{2}}&-{\tfrac {2}{2}}&-{\tfrac {3}{2}}&-{\tfrac {3}{1}}&{\tfrac {3}{1}}&\dotsb \\\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b647ffd578f9b89a4c3f4d5a4e0147271155ca63)
![{\displaystyle {\begin{array}{clclclccclclclc}\cdots &-{\tfrac {1}{3}}&&-{\tfrac {1}{2}}\ _{\color {Blue}(6)}&{\color {MidnightBlue}\leftarrow }&-{\tfrac {1}{1}}\ _{\color {Blue}(5)}&&0\ _{\color {Blue}(1)}&{\color {MidnightBlue}\rightarrow }&{\tfrac {1}{1}}\ _{\color {Blue}(2)}&&{\tfrac {1}{2}}\ _{\color {Blue}(11)}&{\color {MidnightBlue}\rightarrow }&{\tfrac {1}{3}}\ _{\color {Blue}(12)}&\cdots \\[0.3em]&&&{\color {MidnightBlue}\downarrow }&&{\color {MidnightBlue}\uparrow }&&&&{\color {MidnightBlue}\downarrow }&&{\color {MidnightBlue}\uparrow }&&{\color {MidnightBlue}\downarrow }&\\[0.3em]\cdots &-{\tfrac {2}{3}}&&-{\tfrac {2}{2}}\ _{\color {Blue}(\cdot )}&&-{\tfrac {2}{1}}\ _{\color {Blue}(4)}&{\color {MidnightBlue}\leftarrow }&{\color {MidnightBlue}-}&{\color {MidnightBlue}-}&{\tfrac {2}{1}}\ _{\color {Blue}(3)}&&{\tfrac {2}{2}}\ _{\color {Blue}(\cdot )}&&{\tfrac {2}{3}}\ _{\color {Blue}(13)}&\cdots \\[0.3em]&&&{\color {MidnightBlue}\downarrow }&&&&&&&&{\color {MidnightBlue}\uparrow }&&{\color {MidnightBlue}\downarrow }&\\[0.3em]\cdots &-{\tfrac {3}{3}}&&-{\tfrac {3}{2}}\ _{\color {Blue}(7)}&{\color {MidnightBlue}\rightarrow }&-{\tfrac {3}{1}}\ _{\color {Blue}(8)}&{\color {MidnightBlue}-}&{\color {MidnightBlue}-}&{\color {MidnightBlue}\rightarrow }&{\tfrac {3}{1}}\ _{\color {Blue}(9)}&{\color {MidnightBlue}\rightarrow }&{\tfrac {3}{2}}\ _{\color {Blue}(10)}&&{\tfrac {3}{3}}\ _{\color {Blue}\cdots }&\cdots \\[0.3em]&\vdots &&\vdots &&\vdots &&&&\vdots &&\vdots &&{\color {MidnightBlue}\downarrow }&\\\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/995e7c8e8dce67e67f033689feca805f5ca7d453)
![{\displaystyle {\begin{array}{cccccccccccc}{\color {Blue}1}&{\color {Blue}2}&{\color {Blue}3}&{\color {Blue}4}&{\color {Blue}5}&{\color {Blue}6}&{\color {Blue}7}&{\color {Blue}8}&{\color {Blue}9}&{\color {Blue}10}&{\color {Blue}11}&{\color {Blue}\cdots }\\[0.3em]{\color {MidnightBlue}\downarrow }&{\color {MidnightBlue}\downarrow }&{\color {MidnightBlue}\downarrow }&{\color {MidnightBlue}\downarrow }&{\color {MidnightBlue}\downarrow }&{\color {MidnightBlue}\downarrow }&{\color {MidnightBlue}\downarrow }&{\color {MidnightBlue}\downarrow }&{\color {MidnightBlue}\downarrow }&{\color {MidnightBlue}\downarrow }&{\color {MidnightBlue}\downarrow }&{\color {MidnightBlue}\downarrow }\\[0.3em]0&{\tfrac {1}{1}}&{\tfrac {2}{1}}&-{\tfrac {2}{1}}&-{\tfrac {1}{1}}&-{\tfrac {1}{2}}&-{\tfrac {3}{2}}&-{\tfrac {3}{1}}&{\tfrac {3}{1}}&{\tfrac {3}{2}}&{\tfrac {1}{2}}&\cdots \\\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/90e91a9f1f991aa52082c3622fb82e2c224c9231)
![{\displaystyle [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)




![{\displaystyle {\begin{array}{cccccccccccccccc}{\color {Blue}1}&{\color {Blue}2}&{\color {Blue}3}&{\color {Blue}4}&{\color {Blue}5}&{\color {Blue}6}&{\color {Blue}7}&{\color {Blue}8}&{\color {Blue}9}&{\color {Blue}10}&{\color {Blue}11}&{\color {Blue}\cdots }\\[0.3em]{\color {MidnightBlue}\downarrow }&{\color {MidnightBlue}\downarrow }&{\color {MidnightBlue}\downarrow }&{\color {MidnightBlue}\downarrow }&{\color {MidnightBlue}\downarrow }&{\color {MidnightBlue}\downarrow }&{\color {MidnightBlue}\downarrow }&{\color {MidnightBlue}\downarrow }&{\color {MidnightBlue}\downarrow }&{\color {MidnightBlue}\downarrow }&{\color {MidnightBlue}\downarrow }&{\color {MidnightBlue}\downarrow }\\[0.3em]1&{\tfrac {1}{2}}&2&3&{\tfrac {1}{3}}&{\tfrac {1}{4}}&{\tfrac {2}{3}}&{\tfrac {3}{2}}&4&5&{\tfrac {1}{5}}&\cdots \\\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ff76ab879ca9fb460b3c88fcbe34a26e2a80d300)








![{\displaystyle {\begin{aligned}f(1)&=0,\ a_{11}\ a_{12}\ a_{13}\ a_{14}\dots \\[0.3em]f(2)&=0,\ a_{21}\ a_{22}\ a_{23}\ a_{24}\dots \\[0.3em]f(3)&=0,\ a_{31}\ a_{32}\ a_{33}\ a_{34}\dots \\[0.3em]f(4)&=0,\ a_{41}\ a_{42}\ a_{43}\ a_{44}\dots \\[0.3em]&\ \,\vdots \end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f1cbc3c432b586c97047b75a4a950d9baa92d662)










![{\displaystyle {\begin{aligned}f(1)&=0,\ 5\ 0\ 0\ 0\dots \\[0.3em]f(2)&=0,\ 7\ 5\ 0\ 0\dots \\[0.3em]f(3)&=0,\ 3\ 3\ 3\ 3\dots \\[0.3em]f(4)&=0,\ 1\ 4\ 1\ 5\dots \\[0.3em]&\ \,\vdots \end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a9cba41a70bfbb08e00674d5f71f5be9db56eda1)























![{\displaystyle {\begin{aligned}f(1)&=0,\ {\color {Red}5}\ 0\ 0\ 0\dots \\[0.3em]f(2)&=0,\ 7\ {\color {Blue}5}\ 0\ 0\dots \\[0.3em]f(3)&=0,\ 3\ 3\ {\color {OliveGreen}3}\ 3\dots \\[0.3em]f(4)&=0,\ 1\ 4\ 1\ {\color {RedOrange}5}\dots \\[0.3em]&\ \,\vdots \\\\x&=0,\ {\color {Red}4}\ {\color {Blue}4}\ {\color {OliveGreen}5}\ {\color {RedOrange}4}\dots \\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4ab36be0c09cfa6046084f6e98d063ca688929e7)




![{\displaystyle A\supseteq B\supseteq f[A]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/09ad29794c4b6fc4161db980dd9bb5d86d11ef55)

![{\displaystyle B\supseteq f[A]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d1631daf51d33ecaaeecdbec7598967a98997cee)










































































































![{\displaystyle {\begin{array}{rcl}{\frac {n\cdot (n+1)\cdot (4n-1)}{6}}+2n\cdot (n+1)+(n+1)&&{\frac {(n+1)\cdot (n+2)\cdot (4n+3)}{6}}\\[0.5em]{\frac {n\cdot (n+1)\cdot (4n-1)}{6}}+(n+1)\cdot (2n+1)&&{\frac {(n+1)\cdot (n+2)\cdot (4n+3)}{6}}\\[0.5em]{\frac {n\cdot (n+1)\cdot (4n-1)+6\cdot (n+1)\cdot (2n+1)}{6}}&&{\frac {(n+1)\cdot (n+2)\cdot (4n+3)}{6}}\\[0.5em]{\frac {(n+1)\cdot (n\cdot (4n-1)+6\cdot (2n+1))}{6}}&&{\frac {(n+1)\cdot (n+2)\cdot (4n+3)}{6}}\\[0.5em]{\frac {(n+1)\cdot (4n^{2}-n+12n+6)}{6}}&&{\frac {(n+1)\cdot (4n^{2}+3n+8n+6)}{6}}\\[0.5em]{\frac {(n+1)\cdot (4n^{2}+11n+6)}{6}}&=&{\frac {(n+1)\cdot (4n^{2}+11n+6)}{6}}\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a914783fb4332f07bc713aa2e5ae141cbb5a8411)
![{\displaystyle {\begin{aligned}{\frac {n\cdot (n+1)\cdot (4n-1)}{6}}+2n\cdot (n+1)+(n+1)&={\frac {n\cdot (n+1)\cdot (4n-1)}{6}}+(n+1)\cdot (2n+1)\\[0.5em]&={\frac {n\cdot (n+1)\cdot (4n-1)+6\cdot (n+1)\cdot (2n+1)}{6}}\\[0.5em]&={\frac {(n+1)\cdot (n\cdot (4n-1)+6\cdot (2n+1))}{6}}\\[0.5em]&={\frac {(n+1)\cdot (4n^{2}-n+12n+6)}{6}}\\[0.5em]&={\frac {(n+1)\cdot (4n^{2}+3n+8n+6)}{6}}\\[0.5em]&={\frac {(n+1)\cdot (n+2)\cdot (4n+3)}{6}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/af68cdb07ce498fdeb4742afd8951cd4008862a7)










![{\displaystyle {\begin{array}{lrll}&3s+t&=s-t&{\color {Gray}\left|\ -t{\text{ auf beiden Seiten}}\right.}\\[0.3em]\Rightarrow \ &3s&=s-2t&{\color {Gray}\left|\ -s{\text{ auf beiden Seiten}}\right.}\\[0.3em]\Rightarrow \ &2s&=-2t&{\color {Gray}\left|\ {}\cdot {\tfrac {1}{2}}{\text{ auf beiden Seiten}}\right.}\\[0.3em]\Rightarrow \ &s&=-t\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8f638d043ebaa554e1fc767c202448df4b8b00aa)







![{\displaystyle {\begin{array}{lrll}&s&=-t&{\color {Gray}\left|\ {}\cdot 2{\text{ auf beiden Seiten}}\right.}\\[0.3em]\Rightarrow \ &2s&=-2t&{\color {Gray}\left|\ +s{\text{ auf beiden Seiten}}\right.}\\[0.3em]\Rightarrow \ &3s&=s-2t&{\color {Gray}\left|\ +t{\text{ auf beiden Seiten}}\right.}\\[0.3em]\Rightarrow \ &3s+t&=s-t\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/697c8bc0785a1e28396e9b41307822679ca721fb)













![{\displaystyle {\begin{array}{lrlcll}&x^{2}&=-1&&&{\color {Gray}\left|\ {\text{Quadrieren}}\right.}\\[0.3em]\Rightarrow \ &x^{4}&=1&&&{\color {Gray}\left|\ {\text{vierte Wurzel ziehen}}\right.}\\[0.3em]\Rightarrow \ &x&={\sqrt[{4}]{1}}&\lor &x=-{\sqrt[{4}]{1}}\\[0.3em]\Rightarrow \ &x&=1&\lor &x=-1\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fd25fc88cadbc62dba7781ace6c486e176af1894)


![{\displaystyle {\begin{array}{lrll}&3s+t&=s-t&{\color {Gray}\left|\ -t{\text{ auf beiden Seiten}}\right.}\\[0.3em]\Leftrightarrow \ &3s&=s-2t&{\color {Gray}\left|\ -s{\text{ auf beiden Seiten}}\right.}\\[0.3em]\Leftrightarrow \ &2s&=-2t&{\color {Gray}\left|\ {}\cdot {\tfrac {1}{2}}{\text{ auf beiden Seiten}}\right.}\\[0.3em]\Leftrightarrow \ &s&=-t\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dd2d244e233b5b48d5bb06baf131d47410cd53cf)





















































































![{\displaystyle {\begin{aligned}&\prod _{l=-1}^{0}(l-1)\\[0.5em]&{\color {Gray}\left\downarrow \ {\text{Rekursionsschritt: }}\prod _{l=-1}^{0}(l-1)=\left(\prod _{l=-1}^{-1}(l-1)\right)\cdot (0-1)\right.}\\[0.5em]=\ &\left(\prod _{l=-1}^{-1}(l-1)\right)\cdot (0-1)\\[0.5em]&{\color {Gray}\left\downarrow \ {\text{Rekursionsschritt: }}\prod _{l=-1}^{-1}(l-1)=\left(\prod _{l=-1}^{-2}(l-1)\right)\cdot (-1-1)\right.}\\[0.5em]=\ &\left(\prod _{l=-1}^{-2}(l-1)\right)\cdot (-1-1)\cdot (0-1)\\[0.5em]&{\color {Gray}\left\downarrow \ {\text{Rekursionsanfang: }}\prod _{l=-1}^{-2}(l-1)=1\right.}\\[0.5em]=\ &1\cdot (-1-1)\cdot (0-1)\\=\ &1\cdot (-2)\cdot (-1)=2\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c53c492bf6b8b8beb95ff60d8acdf894367b68e7)

![{\displaystyle {\begin{aligned}&\prod _{m=5}^{5}(m-n)^{k}\\[0.5em]&{\color {Gray}\left\downarrow \ {\text{Rekursionsschritt: }}\prod _{m=5}^{5}(m-n)^{k}=\left(\prod _{m=5}^{4}(m-n)^{k}\right)\cdot (5-n)^{k}\right.}\\[0.5em]=\ &\left(\prod _{m=5}^{4}(m-n)^{k}\right)\cdot (5-n)^{k}\\[0.5em]&{\color {Gray}\left\downarrow \ {\text{Rekursionsanfang: }}\prod _{m=5}^{4}(m-n)^{k}=1\right.}\\[0.5em]=\ &1\cdot (5-n)^{k}\\=\ &(5-n)^{k}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/274590a9762abd0e9d3fd8822137fba078aa3124)




































![{\displaystyle {\begin{aligned}n!&=n\cdot (n-1)!=n\cdot (n-1)\cdot (n-2)!=\ldots \\[0.5em]&=n\cdot (n-1)\cdot (n-2)\cdot \ldots \cdot 1\\[0.5em]&=\prod _{i=1}^{n}i\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a9779d9226bfc35f059499c71e9c4ad979505eee)



































































































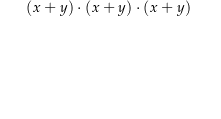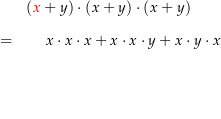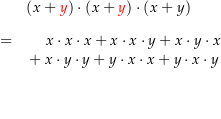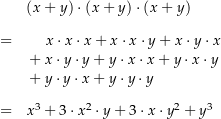


















































![{\displaystyle {\begin{aligned}&{\frac {n!}{k!\cdot (n-k)!}}+{\frac {n!}{(k+1)!\cdot (n-k-1)!}}\\[0.5em]&\qquad {\color {Gray}\left\downarrow \ {\text{Brüche gleichnamig machen}}\right.}\\[0.5em]=\ &{\frac {n!\cdot (k+1)}{(k+1)!\cdot (n-k)!}}+{\frac {n!\cdot (n-k)}{(k+1)!\cdot (n-k)!}}\\[0.5em]=\ &{\frac {n!\cdot (k+1)+n!\cdot (n-k)}{(k+1)!\cdot (n-k)!}}\\[0.5em]&\qquad {\color {Gray}\left\downarrow \ {\text{Zähler zusammenfassen}}\right.}\\[0.5em]=\ &{\frac {n!\cdot (k+1+n-k)}{(k+1)!\cdot (n-k)!}}\\[0.5em]=\ &{\frac {n!\cdot (n+1)}{(k+1)!\cdot (n-k)!}}\\[0.5em]=\ &{\frac {(n+1)!}{(k+1)!\cdot (n-k)!}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/40513076754f3d592d3a03bfb3649a5717744d8d)
![{\displaystyle {\begin{aligned}&{\binom {n}{k}}+{\binom {n}{k+1}}\\[0.5em]=\ &{\frac {n!}{k!\cdot (n-k)!}}+{\frac {n!}{(k+1)!\cdot (n-k-1)!}}\\[0.5em]&\qquad {\color {Gray}\left\downarrow \ {\text{Brüche gleichnamig machen}}\right.}\\[0.5em]=\ &{\frac {n!\cdot (k+1)}{(k+1)!\cdot (n-k)!}}+{\frac {n!\cdot (n-k)}{(k+1)!\cdot (n-k)!}}\\[0.5em]=\ &{\frac {n!\cdot (k+1)+n!\cdot (n-k)}{(k+1)!\cdot (n-k)!}}\\[0.5em]&\qquad {\color {Gray}\left\downarrow \ {\text{Zähler zusammenfassen}}\right.}\\[0.5em]=\ &{\frac {n!\cdot (k+1+n-k)}{(k+1)!\cdot (n-k)!}}\\[0.5em]=\ &{\frac {n!\cdot (n+1)}{(k+1)!\cdot (n-k)!}}\\[0.5em]=\ &{\frac {(n+1)!}{(k+1)!\cdot (n-k)!}}\\[0.5em]&\qquad {\color {Gray}\left\downarrow \ {\text{Im Nenner}}+1-1{\text{ einfügen}}\right.}\\[0.5em]=\ &{\frac {(n+1)!}{(k+1)!\cdot ((n+1)-(k+1))!}}\\[0.5em]=\ &{\binom {n+1}{k+1}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ded4a6437d3187e3c4dc33cdcf4365178f43dbdf)