MathemaTriX ⋅ Theorie nach Thema. Funktionen

Hoch

STOPP PUSHBACKS • FREE ASSANGE • FRIEDEN AUF DER WELT ${\color {white}\mathbf {MATHE} \mu \alpha T\mathbb {R} ix}$ DEINE FESTE BEGLEITERIN FÜR DIE SCHULMATHEMATIK EINFACH UND VERSTÄNDLICH GRATIS!* MIT MEHR ALS 200 THEORIE- UND AUFGABEN-ERKLÄRUNGS VIDEOS! Mathe lernen ist wie Fahrradfahren lernen: Du kannst es dir stundenlang erklären lassen, du wirst nie fahren können, wenn du nicht selber zu fahren probierst.

Inhalt Ein-Aus- klappen

AUFGABEN

KAPITEL Grundrechenarten Bruchrechnungen $-{\tfrac {\cdot \ +}{\ :\ }}$ Schlussrechnung Prozentrechnung Exponentialfunktion Logarithmus Arbeiten mit Termen $\mathbb {X} ^{2}$ Zahlendarstellungen Mengentheorie Aussagenlogik ${\begin{matrix}\mathbb {R} :=\\\mathbb {Q} \cup \mathbb {I} \end{matrix}}$ Einheiten $cm^{2}$ Statistik und Wahrscheinlichkeit Geometrische Konstruktionen Geometrie der Ebene Geometrie des Raums Diagramme Funktionen $f(x)$ Lineare Gleichungssysteme ${\begin{smallmatrix}{a_{1}\ b_{2}}\\{a_{2}\ b_{2}}\end{smallmatrix}}$ Trigonometrische Funktionen Vektoren Differentialrechnung $^{dy}/_{dx}$ Integralrechnung $\textstyle \int _{a}^{b}dx$ Folgen $a_{n}$ Beweise $a\rightarrow b$

Funktion allgemein

Wenn man z.B. die Temperaturen um gewissen Uhrzeiten an einem Tag misst, dann hat man schon eine Art von Funktion. Man sagt, dass die Temperatur die abhängige Variable ist und die Uhrzeit die unabhängige. Für jeden Wert der unabhängigen Variable gibt es einen Wert der abhängigen Variable aber für jeden Wert der abhängigen Variable kann es keine, eine oder mehrere Werte der unabhängigen Variable geben.

In unserem Beispiel: für jede Uhrzeit gibt es genau eine Temperatur (es kann nicht mehrere geben), eine Temperatur aber kann nie, einmal oder mehrmals vorkommen. Man kann die ganze Information in einer Tabelle schreiben und mit Hilfe der Tabelle, kann man auch ein Diagramm erstellen:

Wie man im Diagramm ablesen kann, es gibt nur eine Temperatur für jede Uhrzeit (z.B. um 10 Uhr ist die Temperatur 14°C und nicht gleichzeitig 18°C) aber für jede Temperatur kann es keine (z.B. 5°C gibt es nicht), eine (z.B. 10° C gibt es nur um 6 Uhr) oder mehrere Zeiten (z.B. 15°C kommt 2 mal vor, man kann sogar raten, dass es die gleiche Temperatur irgendwann zwischen 10 Uhr und 12 Uhr gab!).

Lineare Funktion

Was ist eine lineare Funktion

Wenn das Diagramm einer Funktion eine Gerade ist, dann geht es um eine sogenannte lineare Funktion. Ein lineare Funktion hat die allgemeine Form:

y=s x +A

wo y die abhängige Variable ist, x die unabhängige Variable und s und A irgendwelche Konstanten (Zahlen, die sich nicht ändern, wie die Variablen). So sind die folgende Funktionen linear:

y=3x – 2$\qquad$ y=-0,5x+130 $\qquad$y= ¾ x – 2,3$\qquad$ y=-√3 x -5

In der ersten Funktion y=3x – 2 ist s=3 und A=-2.

In der zweiten Funktion y=-0,5x+130 ist s=-0,5 und A=130.

In der dritten Funktion y= ¾ x – 2,3 ist s= ¾ und A=-2,3.

In der vierten Funktion y=-√3 x -5 ist s=-√3 und A=-5.

Selbstverständlich kann man statt x und y andere Symbole benutzen:

y=3x – 2, a=3b – 2 und V=3h – 2 sind Darstellungen der gleichen Funktion, es werden nur andere Symbole für x und y benutzt. y= ¾ x – 2,3 ist doch eine andere Funktion, weil s und A (die Konstanten) anders sind. Wenn allein s oder allein A oder beide s und A in zwei Funktionen anders sind, dann haben wir zwei unterschiedlichen linearen Funktion. Wenn s und A in zwei Funktionen gleich sind, dann haben wir die gleiche Funktion, egal welche Symbole wir für x und y benutzen.

In einer linearen Funktion  $\textstyle y=s\cdot x+A$  wird die Konstante, mit der x multipliziert wird (hier mit s bezeichnet), Steigung der Funktion genannt. Die Steigung ist ein sehr wichtiger Begriff in der höheren Mathematik. Die Konstante, die dann addiert wird (hier mit A bezeichnet) nennt man y-Achsenabschnitt. Man muss auch sagen: in verschiedenen Staaten benutzt man unterschiedliche Symbole für s und A, z.B.

$y=mx+n$

Hier ist dann m die Steigung und n der y-Achsenabschnitt (Gebrauch in Deutschland) .

$y=kx+d$

Hier ist dann k die Steigung und d der y-Achsenabschnitt (Gebrauch in Österreich) .

$y=mx+q$

Hier ist dann m die Steigung und q der y-Achsenabschnitt (Gebrauch in der Schweiz) .

$y=mx+b$

Hier ist dann m die Steigung und b der y-Achsenabschnitt (Gebrauch in Spanien) .

$y=ax+b$

Hier ist dann a die Steigung und b der y-Achsenabschnitt (Gebrauch in Frankreich und auf Englisch) .

Tabelle für eine lineare Funktion erstellen

Für jede Funktion kann man eine Tabelle machen. Diese Tabelle kann man dann als Punkte in einem Diagramm darstellen. Als Beispiel benutzen wir die Funktion y=3x – 2:

Diagramm einer linearen Funktion mit Hilfe von zwei Punkten erstellen

Um diese Funktion in einem Diagramm darzustellen braucht man nur zwei Punkte. Einen Punkt schreibt man mit einem Wertepaar P:(x|y), wobei erst immer der x-Wert geschrieben wird und dann der y-Wert (innerhalb von Klammern). Benutzen wird beispielsweise P_A:(-1|-5) und P_B:(2|4) (erstes Bild). Mit Hilfe dieser Punkte kann man eine Gerade ziehen (zweites Bild). Wie man dann feststellen kann, liegen alle Wertepaare der Tabelle auf dieser Gerade! (Drittes Bild)

• 
• 
• 

Das ist genau die Sache. Alle Wertepaare einer linearen Funktion liegen auf der gleichen Gerade! Die Darstellung einer linearen Funktion auf einem Koordinatensystem ist eine Gerade!

Eine lineare Funktion mit Hilfe von zwei Punkten ermitteln

Lineare Funktion

Wenn man zwei Punkte einer linearen Funktion hat, kann man nicht nur die entsprechende Gerade im Diagramm zeichnen, sondern auch die Funktion selber finden, wenn man sie nicht kennt. Nehmen wir die folgenden zwei Punkte P und Q, die man auch vom Diagramm ablesen kann:

$P:(2|4),\ Q:(5|-2)$

Mit Hilfe der beide Punkten kann man die Funktion in einem Koordinatensystem darstellen, wie im Bild. Wie viel ist die Steigung dieser Funktion und wie viel der y-Achsenabschnitt?

Die allgemeine Gleichung einer linearen Funktion ist:

$\ y=s\ x+A$

wobei hier mit s die Steigung gemeint ist und mit A der y-Achsenabschnitt.

Um die Steigung und den y-Achsenabschnitt der im Diagramm dargestellten Funktion zu berechnen, werden wir hier das sogenannte Gleichsetzungsverfahren benutzen. Setzen wir die Wertepaare für die zwei gegebenen Punkten in der allgemeinen Gleichung der linearen Funktion ein:

$\left|{\begin{array}{lrl}P(x|y)&y&=s\ x+A\\P(2|4)&4&=s\ 2+A&\\P(5|-2)&-2&=s\ 5+A\\\end{array}}\right|\quad {\begin{array}{l}\\\mathbf {I} \\\mathbf {II} \end{array}}$
Formen wir beide Gleichungen auf A um:
$\left({\begin{array}{rl}4&=s\cdot 2+A\\-2&=s\cdot 5+A\\\end{array}}\right)\ {\begin{array}{l}|-s\cdot 2\ {\text{also}}\ -2\ s\\|-s\cdot 5\ {\text{also}}\ -5\,s\\\end{array}}$
$\Leftrightarrow \left({\begin{array}{rl}4-2\,s&=\mathbf {A} \\-2-5\,s&=\mathbf {A} \\\end{array}}\right)$
Da die rechten Seiten der Gleichungen gleich sind (beide A), sollen auch die linken gleich sein.
${\begin{array}{rll}4-2\,s&=-2-5\,s\quad &|-4+5s\\3\,s&=-6\quad &|:3\\s&=-2&\end{array}}$
und daher
$\quad A=4-2\,s=4-2\cdot (-2)=8$
Die Funktion lautet daher:

$y=-2\ x+8\qquad$

Für die direkte Berechnung der Steigung s gibt es allerdings eine Formel. Es gilt:

$s={\frac {\Delta y}{\Delta x}}$

wobei Δy die Differenz der y-Werte der zwei Punkte und Δx die Differenz der x-Werte ist.

In unserem Beispiel sind die Punkte $P:(2|4)$ und $Q:(5|-2)$, also die y-Werte 4 und -2 und die x-Werte 2 und 5. Die entsprechenden Differenzen sind: Δy=4 − ( − 2)=6 und Δx=2-5=-3. Daher ist die Steigung der abgebildeten linearen Funktion, die durch die Punkte P und Q geht:

$\textstyle s={\frac {\Delta y}{\Delta x}}={\frac {6}{-3}}=-2$

Die Steigung und ihre Zusammenhänge ==== ===== Beweis der Formel der Steigung einer linearen Funktion =

Zeigen Sie, dass die Steigung s einer linearen Funktion $\textstyle s={\frac {\Delta y}{\Delta x}}\ \$ist.

Wir benutzen hier 2 Punkte, wie in der entsprechenden Aufgabe mit konkreten Zahlen. Diesmal benutzen wir Symbole statt konkreten Zahlen.

$\quad$ $\left|{\begin{array}{lrl}P(x|y)&y&=s\ x+A\\P(x_{1}|y_{1})&y_{1}&=s\ x_{1}+A&\\P(x_{2}|y_{2})&y_{2}&=s\ x_{2}+A\\\end{array}}\right|\quad {\begin{array}{l}\\\mathbf {I} \\\mathbf {II} \end{array}}$

Wir formen beide Gleichungen auf A um:
$\left({\begin{array}{rl}y_{1}&=s\cdot x_{1}+A\\y_{2}&=s\cdot x_{2}+A\\\end{array}}\right)\ {\begin{array}{l}|-s\cdot x_{1}\ \\|-s\cdot x_{2}\ \\\end{array}}$
$\Leftrightarrow \left({\begin{array}{rl}y_{1}-s\ x_{1}&=\mathbf {A} \\y_{2}-s\ x_{2}&=\mathbf {A} \\\end{array}}\right)$
Da die rechten Seiten der Gleichungen gleich sind (beide A),
sollen auch die linken gleich sein.
${\begin{array}{rll}y_{1}-s\ x_{1}&=y_{2}-s\ x_{2}\quad &|-y_{1}+s\ x_{2}\\s\ x_{2}-s\ x_{1}&=y_{2}-y_{1}&|{\text{s herausheben}}\\s\ (x_{2}-x_{1})&=y_{2}-y_{1}\quad &|:(x_{2}-x_{1})\\s&={\frac {y_{2}-y_{1}}{x_{2}-x_{1}}}&\end{array}}$
Das Symbol $\ \Delta \$bedeutet Differenz. $\Delta y=y_{2}-y_{1}\$und $\Delta x=x_{2}-x_{1}$, daher:
$\quad$Steigung$\ s={\frac {\Delta y}{\Delta x}}$

Zusammenhang linearer Funktion und direkter Proportionalität

Die direkte Proportionalität ist eine lineare Funktion, deren y-Achsenabschnitt A null ist. Wenn wir für die Steigung der linearen Funktion das Symbol s und für den y-Achsenabschnitt das Symbol A, dann lautet die allgemeine Darstellung:

y= s·x + A

Wenn der y-Achsenabschnitt null ist, dann haben wir eine direkte Proportionalität:

y= s·x

Die Steigung ist in diesem Fall das Verhältnis (Quotient) zwischen abhängiger und unabhängiger Variable:

${\text{s}}={\frac {\text{y}}{\text{x}}}$

Es gibt allerdings noch einen Zusammenhang zwischen direkter Proportionalität und linearer Gleichung. Die Steigung ist das Verhältnis zwischen Änderung der unabhängigen und Änderung der abhängigen Variable:

${\text{s}}={\frac {\Delta {\text{y}}}{\Delta {\text{x}}}}$

Das bedeutet, dass eine direkte Proportionalität zwischen den beiden Änderungen besteht:

${\Delta {\text{y}}}={\text{s}}\cdot {\Delta {\text{x}}}$

Zusammenhang linearer Funktion und Ähnlichkeit ebener Figuren

Alle hier gleichfarbigen Figuren sind zueinander ähnlich.

Zwei Figuren sind ähnlich, wenn die eine eine Vergrößerung der andere ist. Bei Figuren mit Winkeln bedeutet das, dass entsprechende Winkel gleich bleiben, die Verhältnisse (Quotienten) der entsprechenden Seiten zu einander ebenfalls.

Wenn man das große und das kleine Dreieck im Bild hier links vergleicht, dann stellt man fest, dass alle entsprechenden Winkel gleich sind (A mit D, B mit E und C mit F). Dreieck DEF ist eine Vergrößerung des Dreiecks ABC. Nehmen wir an, dass Seite DE 1,5 mal so groß wie Seite AB ist, also DE=1,5·AB. Dann muss das gleiche ebenfalls zwischen BC und EF gelten, also EF=1,5·BC. Für die Verhältnisse (Quotienten) gilt dann:

${\frac {DE}{AB}}=1,5$ und ${\frac {EF}{BC}}=1,5$

also, die Quotienten der entsprechenden Seiten sind gleich!

Seite DE ist allerdings 1,5 mal die Seite AB, also um 50% größer als AB. Das gilt allerdings genauso für Seiten EF und BC, also EF ist 50% größer als BC. Man stellt daher fest, dass bei der Ähnlichkeit von Figuren eine direkte Proportionalität (eine lineare Funktion mit y-Achsenabschnitt gleich null) für die Längen der Seiten vorliegt: wird eine Seite größer, dann wird die andere auch und zwar um den gleichen Prozentsatz!

Einheiten der Steigung

Steigung einer Gerade: $a={\frac {\Delta y}{\Delta x}}$

Steigung in einem s-t Diagramm

Die Steigung einer Gerade ist allgemein die Differenz zwei y-Werte durch die Differenz der entsprechenden x-Werte, also ein Differenzenquotient (Bild links). Da bei einem s-t Diagramm auf der y-Achse die Strecke dargestellt wird und bei der x die Zeit (Bild rechts), ergibt sich der Quotient:

Steigung: $\qquad {\frac {\Delta y}{\Delta x}}={\frac {\Delta s}{\Delta t}}$

Der letzte Quotient ist nichts anders als die mittlere Geschwindigkeit:

${\bar {v}}={\frac {\Delta s}{\Delta t}}$

Daher:

Die Steigung in einem s-t Diagramm zeigt uns die Geschwindigkeit

Im konkreten Beispiel rechts: s₁ ist zwei Einheiten, s₂ 5 Einheiten. Wenn die Einheiten der y-Achse Meter (m) sind, ist Δs=3 m. Entsprechend, wenn die Einheit auf der x-Achse Sekunde (s) ist, dann ist Δt=6 s. Die Steigung und daher auch die Geschwindigkeit ist in diesem Fall

${v}={\frac {\Delta s}{\Delta t}}={\frac {3m}{6s}}=0,5{\frac {m}{s}}$

Steigung einer Gerade: $s={\frac {\Delta y}{\Delta x}}$

Steigung in einem v-t Diagramm

Entsprechend können wir die physikalische Größe und die Einheiten der Steigung in einem v-t Diagramm finden. Da bei einem v-t Diagramm auf der y-Achse die Geschwindigkeit dargestellt wird und bei der x die Zeit (Bild rechts), ergibt sich der Quotient:

Steigung $\ s={\frac {\Delta y}{\Delta x}}={\frac {\Delta v}{\Delta t}}$</math>

Die Steigung zeigt uns in diesem Fall eine Änderung der Geschwindigkeit, also eine Beschleunigung:

$\alpha ={\frac {\Delta v}{\Delta t}}$

Daher:

Die Steigung in einem v-t Diagramm zeigt uns die Beschleunigung

Im konkreten Beispiel rechts: $v_{1}$ ist 2 Einheiten, $v_{2}$ 5 Einheiten, daher, wenn die Einheiten m/s (Meter pro Sekunde) sind, ist $\Delta s=3\ m/s$, und für Sekunde als Einheit auf der x-Achse ist $\Delta t=6\ s$. Die Steigung und daher auch die Beschleunigung ist in diesem Fall:

$\alpha ={\frac {\Delta v}{\Delta t}}={\frac {3\ m/s}{6\ s}}=0{,}5{\frac {\ m/s}{6\ s}}=0{,}5\ m/s^{2}$

Von diesen Beispielen wird daher klar:

Die Steigung ist eine Änderungsrate, sie zeigt wie schnell sich die Größe der y-Achse in Bezug auf die Größer der x-Achse ändert. Die Einheiten der Steigung sind daher die Einheiten der y-Achse durch die Einheiten der x-Achse.

Noch zwei Beispiele: Wenn auf der y-Achse Kraft (in Newton) dargestellt wird und auf der x Fläche (in m²), dann ist die physikalische Größe der Steigung Druck (also Kraft durch Fläche) und die Einheit Pa (Pascal, also Newton durch m²). Wenn auf der y-Achse Masse (in kg) steht und auf der x Volumen (in $\ell$), dann ist die physikalische Größe der Steigung Dichte (also Masse durch Volumen) und ihre Einheiten kg/$\ell$.

Textaufgaben zu den linearen Funktionen

Bei den Textaufgaben über lineare Funktionen wird es normalerweise zwei Konstanten geben (also zwei Zahlen). Die Einheit einer der Zahlen wird normalerweise durch eine Änderungsrate (ein Verhältnis, einen Quotient von zwei anderen Einheiten) ausgedrückt. Diese Konstante (diese Zahl mit der Einheit "etwas" pro "etwas anderes") wird die Steigung sein, also der Koeffizient der unabhängigen Variable (i.d.R $x$). Die Einheit der Steigung wird die Form Einheit A durch Einheit B haben. Die Einheit B (z.B. Sekunde oder Meter) ist die Einheit der unabhängigen Variablen (i.d.R. $x$).

Die andere Konstante wird dann der y-Achsenabschnitt sein. Die Einheit des y-Achsenabschnitts ist auch die Einheit der abhängigen Variable und auch die erwähnte Einheit A bei der Steigung. Damit haben wir alle Elemente in einem mathematischen Zusammenhang „übersetzt“.

• Beim Taxifahren ist die Grundgebühr 4€ und jede Minute kostet dann 0,5€. Stelle diesen Zusammenhang als lineare Funktion dar.

Lösung:

Hier sind zwei Zahlen angegeben: 4€ und 0,5€. Über 0,5€ ist aber auch gesagt, dass man "jede Minute" 0,5€ zahlt. Anders ausgedrückt sind es 0,5€ pro Minute. Einheit A (€) durch Einheit B (min). Das heißt, es geht um eine Änderungsrate. 0,5 soll also unsere Steigung sein. Dann ist die Grundgebühr der y-Achsenabschnitt. Die abhängige Variable wird also in € ausgedrückt (wie die Grundgebühr und die Einheit A oben in der Steigung), die unabhängige in Minuten (wie die Einheit B, die Einheit, die in der Steigung unten steht). Für beide Variablen kann man frei irgendwelche Symbole auswählen, gewöhnlich sollen sie auch sinnvoll sein, z.B. hier K für die Kosten und t für die Zeit (Englisch: time):

K(t)= 0,5 t + 4 (t in Minuten, K in €)

Man soll auch eine Entscheidung über das Vorzeichen der Steigung treffen. Das ist eher einfach. Wenn es klar ist, dass die abhängige Variable (z.B. y, hier die Kosten K) auch größer wird, wenn die unabhängige (z.B. x, hier die Zeit t) größer wird, dann ist die Steigung positiv. Bei den Kosten ist es klar, dass sie immer mehr werden, wenn die Fahrt länger dauert. Also ist die Steigung positiv.

Wenn aber es klar ist, dass die unabhängige Variable kleiner wird, wenn die unabhängige größer wird, dann ist die Steigung negativ. Schauen wir ein entsprechendes Beispiel.

• Eine Kerze mit einer Länge von 1,8 dm wird angezündet. Dabei brennt sie stündlich um ca. 0,9 cm ab. Stelle diesen Zusammenhang als lineare Funktion dar.

Hier ist 0,9 cm eine Änderungsrate, also 0,9 cm pro Stunde. 0,9 ist also die Steigung. Die Kerze wird aber immer kürzer, also wird die Steigung negativ sein. 1,8 dm wird unserer y-Achsenabschnitt sein. Wir wählen L für die Länge und t für die Zeit aus:

L(t)= - 0,9 t + 18 (t in Stunden, L in cm)

Vorsicht!

Man soll immer die Einheiten schreiben und die richtigen Einheiten benutzen.

Wenn man beispielsweise für den Abstand die Einheit Meter benutzt, muss man alle angegebene Abstände in Meter umwandeln, wenn sie nicht schon in Meter angegeben sind. Der vorsichtige Leser hat vielleicht gemerkt, dass der y-Achsenabschnitt in der Funktion 18 und nicht 1,8 ist. Wir haben erst die 1,8dm in 18cm umgewandelt! Das ist notwendig, weil die Steigung in cm (und nicht dm) pro Stunde gegeben ist. Ähnlich, wenn der Wert für die Zeit in Minuten gegeben ist, muss man sie erst in Stunden umwandeln (die Steigung ist ja pro Stunden). Darauf muss man also immer aufpassen!

Schauen wir ein etwas komplexeres Beispiel.

• Der Druck in der Atmosphäre eines Planeten ist durch eine lineare Funktion angegeben. Auf 50km Höhe ist er 3 Atm, auf 200 km 1,8 Atm. Wie viel ist der Druck

1. auf der Oberfläche des Planeten?
2. auf 300 km Höhe?
3. 50 km unterhalb der Oberfläche?

In diesem Fall muss man erst die lineare Funktion mit Hilfe der beiden Punkte finden. Der aufmerksame Leser hat vielleicht schon gesehen, dass die gegebenen Punkte hier $P_{1}\ (50|3),\ \ P_{2}\ (200|1{,}8)$ sind. Wie im vorherigen Teil gezeigt, man kann die Funktion in zwei verschiedenen Weisen finden:

Man kann das lineare Gleichungssystem lösen:

P(x|y)	x	y	y=mx+n
P(50|3)	50	3	3=m·50+n
Q(200|1,8)	200	1,8	−1,8=m·200+n

oder man kann direkt die Formel für die Steigung benutzen:

$m={\frac {\Delta y}{\Delta x}}$

und dann den y-Achsenabschnitt finden.

Selbstverständlich bekommt man in beiden Fällen die gleiche Antwort:

m=-0,008 und n=3,4 also

$y=-0{,}008x+3,4$

Mit Hilfe der Funktion kann man jetzt die Fragen beantworten.

• Auf der Oberfläche ist die Höhe (also der x-Wert) Null. Das ist der y-Achsenabschnitt, also 3,4 Atm
• In der zweiten Frage setzt man die 300 km für den x-Wert ein: $y=-0{,}008\cdot 300+3,4=1$, also 1 Atm.
• In der dritten Frage muss man denken, dass unterhalb der Oberfläche die Höhe negativ sein wird: $y=-0{,}008\cdot (-50)+3,4=3,8$ also 3,8 Atm.

Darstellungen der linearen Funktion

Es gibt verschiedene Weisen eine lineare Funktion anzugeben. Hier werden nur manche davon angegeben.

Die explizite Form

Die Darstellung y=a⋅x+b der linearen Funktion nennt man explizite Form.

In dieser Form steht die abhängige Variable y auf der rechten Seite und auf der linken die unabhängige Variable x - mit einer Konstante a (bzw. d, m usw.) vor ihr - plus eine zweite Konstante b (bzw. d, n usw.). Es gibt aber auch andere Darstellungen der linearen Funktion.

Die implizite Form

Die implizite Form ist:

a⋅x+b⋅y+c=0   (oder   a⋅x+b⋅y=c)

Die Parameterform (Vektorform)

Die Parameterform wird durch zwei Gleichungen angegeben:

$x=a_{1}\cdot t+b_{1}$

$y=a_{2}\cdot t+b_{2}$

Die Variable t nennt man Parameter

Das gleich kann man in der sogenannten Vektorform darstellen:

$\textstyle \mathbf {X} =\mathbf {A} \ \cdot t+\mathbf {B} \$

$\textstyle \mathbf {X} ,\ \mathbf {A} ,\$und $\ \mathbf {B} \$sind Vektoren, nämlich $\textstyle {\binom {x_{1}}{x_{2}}},\ {\binom {a_{1}}{a_{2}}},\ {\binom {b_{1}}{b_{2}}}$:

$\textstyle {\binom {x_{1}}{x_{2}}}={\binom {a_{1}}{a_{2}}}\ \cdot t+{\binom {b_{1}}{b_{2}}}\$

Diese Darstellung ist gleichbedeutend mit den folgenden zwei Gleichungen:

$x_{1}=a_{1}\cdot t+b_{1}$

$x_{2}=a_{2}\cdot t+b_{2}$

Es ist oft so in der Vektorrechnung, dass die Achsen des Koordinatensystems durchnummeriert werden. Hier steht $x_{1}\$an der Stelle von $x\$und $x_{2}\$an der Stelle von $y$.

Graphische Darstellung

Drei verschieden lineare Funktionen

Wie schon beschrieben kann man Geometrie und Algebra kombinieren. Wir haben dort gesehen, dass die algebraische Form eines Kreises x²+y²=r² ist.

Die geometrische Form einer linearen Gleichung in einem kartesischen Koordinatensystem ist eine Gerade:

In diesem Bild haben die rote und die grüne Gerade den gleichen y-Achsenabschnitt, die rote und die blaue die gleiche Steigung (sie sind parallel). Die blaue und die grüne haben einen gemeinsamen Punkt bei (-4/3|-5/3)

Umwandeln von einer Form zu einer anderen

Im folgenden werden die unterschiedlichen Symbole für die explizite Form benutzt, die in den verschiedenen deutschsprachigen Staaten benutzt werden. Nochmal:

y=k⋅x+d     ist gleich wie     y=m⋅x+n     ist gleich wie     y=m⋅x+q

Wichtig ist nur zu wissen:

Die Konstante, die in der explizite Form mit x multipliziert wird, ist die Steigung. (in der Schweiz und in Deutschland m, in Österreich k - in der Regel!)

Die Konstante, die zu diesem Produkt addiert wird, ist der y-Achsenabschnitt. (in der Schweiz q, in Deutschland n, in Österreich d - in der Regel!)

Explizite zur impliziten Form

y=k⋅x+d ⇔ -k⋅x+y-d=0

Das ist schon die implizite Form   a⋅x+b⋅y+c=0   mit

-k statt a (Konstante vor x in der impliziten Form),

1 statt b (Konstante vor y in der impliziten Form) und

-d statt c (Konstante ohne Variable in der impliziten Form).

Explizite zur Parameterform

y=m⋅x+n

Wenn wir x=t stellen, dann haben wir schon die Parameterform:

x=t y=m⋅t+n

Vektorform:$\quad {\binom {x}{y}}={\binom {1}{m}}\cdot t+{\binom {0}{n}}$

Vergleichen wir das mit dem allgemeineren Parameterform (x=a₁⋅t+b₁  und  y=a₂⋅t+b₂), dann stellen wir fest, dass hier a₁=1, b₁=0, a₂=m und b₂=n ist.

Implizite zur expliziten Form

a⋅x+b⋅y+c=0

Mit unseren Kenntnissen können wir diese Gleichung auf y umformen:

a⋅x+b⋅y+c=0   ⇔   b⋅y=-c-a⋅x und daher:

$\mathbf {y={\frac {-a}{b}}\cdot x+{\frac {-c}{b}}}$

Das ist die explizite Form mit -a/b als Steigung (m, k usw.) und -c/b als y-Achsenabschnitt (n,p,d usw.).

Implizite zur Parameterform

Man nimmt das Ergebnis aus dem letzten Abschnitt und wandelt diese explizite in die Parameterform:

$\mathbf {x=t}$ $\mathbf {y={\frac {-a}{b}}\cdot t+{\frac {-c}{b}}}$

Vektorform:$\quad {\binom {x}{y}}={\binom {1}{-{\frac {a}{b}}}}\cdot t+{\binom {0}{-{\frac {c}{b}}}}$

Parameter- zur expliziten Form

x=a1⋅t+b1 y=a2⋅t+b2

Vektorform:$\quad {\binom {x}{y}}={\binom {a_{1}}{a_{2}}}\cdot t+{\binom {b_{1}}{b_{2}}}$

Man formt die erste Gleichung auf t um und setzt dieses t in die zweite Gleichung ein:

$t={\frac {1}{a_{1}}}\cdot x-{\frac {b_{1}}{a_{1}}}\quad \Rightarrow \quad y=a_{2}\cdot \left({\frac {1}{a_{1}}}\cdot x-{\frac {b_{1}}{a_{1}}}\right)+b_{2}\quad \Rightarrow$

$\mathbf {y={\frac {a_{2}}{a_{1}}}\cdot x+{\frac {a_{1}\cdot b_{2}-a_{2}\cdot b_{1}}{a_{1}}}}$

Die Steigung in der Parameterform ist daher $\mathbf {\frac {a_{2}}{a_{1}}}$ und

der y-Achsenabschnitt ist $\mathbf {\frac {a_{1}\cdot b_{2}-a_{2}\cdot b_{1}}{a_{1}}}$

Parameter- zur impliziten Form

Man benutzt die Gleichung    $y=a_{2}\cdot \left({\frac {1}{a_{1}}}\cdot x-{\frac {b_{1}}{a_{1}}}\right)+b_{2}$    aus dem letzten Abschnitt und formt sie um:

$\mathbf {a_{2}\cdot x-a_{1}\cdot y+(a_{1}\cdot b_{2}-a_{2}\cdot b_{1})=0}$

Das ist schon die implizite Form   a⋅x+b⋅y+c=0   mit

$a_{2}$ statt a (Konstante vor x in der impliziten Form),

$-a_{1}$ statt b (Konstante vor y in der impliziten Form) und

$(a_{1}\cdot b_{2}-a_{2}\cdot b_{1})$ statt c (Konstante ohne Variable in der impliziten Form).

Die lineare Funktion graphisch darstellen

Durch die Definition der Gerade versteht man, dass zwei Punkte ausreichen, um eine Gerade eindeutig zu definieren. Ein Punkt ist durch zwei Werte bestimmt, die x-Koordinate und die entsprechende y-Koordinate. Um zwei Punkte einer linearen Funktion zu finden, reicht es daher aus, willkürlich zwei Werte für x in der Funktion einzugeben und die entsprechende Werte für y finden. Diese zwei Punkte zeichnet man dann im Koordinaten System. Die Gerade, die durch diese zwei Punkte läuft, entspricht der gegebenen linearen Funktion.

Lösung(en) einer Funktion

Schnittpunkte von Funktionen

Diagramm

Text

Hier sind ein paar Beispiele von Funktionen:

f(x)=3x−5 $\qquad$ K(s)=3s+1,5 $\qquad$ V(r,h)=πr²(r+h)

h(t)=14− 3t $\qquad$ ρ(m,V)=${\frac {m}{V}}$

Oft haben wir erwähnt, dass wenn nichts zwischen zwei mathematischen Ausdrücken steht, eine Multiplikation gemeint ist. In diesen Fällen ist allerdings nicht so. Mit dem Symbol f(x) ist eine Funktion f gemeint, wo die abhängige Variable durch f (in diesem Fall auch y) und die unabhängige durch x symbolisiert wird. f(x) bedeutet so viel wie „f in Abhängigkeit von x“. Entsprechend könnte K(s) die Kosten einer Taxifahrt in Abhängigkeit vom Abstand s bedeuten, V(r,h) das Volumen V eines zusammengesetzten geometrischen Körpers in Abhängigkeit von dem Radius r und der Höhe h, h(t) die Höhe einer Kerze in Abhängigkeit von der Zeit oder ρ(m,V) die Dichte in Abhängigkeit von der Masse und das Volumen. Selbstverständlich können alle diese Symbole auch etwas anderes als Kosten, Volumen, Radius, Zeit usw. bedeuten und jedes Symbol kann mal die unabhängige und mal die abhängige Variable sein (wie hier mit dem Volumen). In der Symbolik a(u) ist das (oder die) Symbol im Klammer (hier u) die unabhängige Variable, die auf der x-Achse dargestellt wird und das Symbol außerhalb (vor) der Klammer (hier a) die abhängige.

In einer Funktion kann es für jeden Wert der unabhängigen Variable genau einen Wert der abhängigen geben, für jeden Wert der abhängigen allerdings keine, eine oder mehrere Werte der unabhängigen. Die Menge der Werte der unabhängigen Variable wird Definitionsmenge genannt, die Menge der Werte der abhängigen Zielmenge. Obwohl für die Zielmenge oft das Wort Wertemenge benutzt wird, sind in der Schulmathematik i.d.R. nur die Werte der Zielmenge, die tatsächlich einem Wert der Definitionsmenge entsprechen, mit Wertemenge gemeint. Im Bild ist A die Definitionsmenge, B die Zielmenge und {b,c,d} die Wertemenge. B kann in diesem Fall nicht die Definitionsmenge sein, da {b} zwei Werten von A entspricht. Mit dem Wort „Stelle“ ist ein Wert aus der Definitionsmenge gemeint („x-Wert“), mit dem Ausdruck „Wert der Funktion“ ein Wert aus der Zielmenge („y-Wert“). Wenn der Wert einer Funktion (y-Wert) an einer gewissen Stelle gefragt wird, dann muss man die unabhängige Variable in der Funktion durch ihren angegebenen Wert („Stelle“, x-Wert) ersetzen. Wenn z.B. die Funktion g(a)=a²+4a−11 ist, dann ist der Wert der Funktion an der Stelle 2 gleich g(2)=2²+4·2−11 also 1. Wie zu sehen ist, haben wir bei g(2) überall, wo in der Funktion g(a)=a²+4a−11 das a steht, dieses durch 2 ersetzt und damit den Wert der Funktion an dieser Stelle berechnet. Es gilt daher in dieser Funktion: g(2)=1.

Mit dem Begriff „Lösungen“ einer Funktion sind die Stellen (x-Werte) der Funktion gemeint, wo die Funktion gleich Null ist, also wo die x-Achse von der Funktion geschnitten oder berührt wird und wo der y-Wert Null ist. Im Diagramm sind die Punkte B, C, D und E Lösungen der Funktion, die durch die Kurve dargestellt wird. Der Punkt F ist die Lösung der Funktion, die mit einer Gerade dargestellt wird. Wenn nicht ein Diagramm sondern der "algebraische" Ausdruck der Funktion gegeben ist, dann sollen wir die Funktion gleich Null setzen, um die Lösungen zu finden. Beispielsweise müssen wir die Funktion k(x)=x⁴−5x³+4x gleich Null setzen, u ihre Lösungen (Nullstellen) zu finden:

0=x⁴−5x³+4x

Diese Gleichung stimmt für x gleich ca. −0,83, 0, 1 und ca. 4,83. Diese Stellen (: Werte von x) sind die Lösungen der Funktion (Nullstellen: Stellen, also Werten von x, wo die Funktion, also die Werte von y, Null ist).

Der y-Achsenabschnitt für eine Gerade haben wir schon gelernt, für die Kurve im Diagramm ist er der Punkt A. An diesem Punkt ist der x-Wert Null (wie allerdings auf der ganzen y-Achse). Wenn wir den Wert der Funktion g(a)=a²+4a−11 a an der Stelle 0 (x-Wert, also die unabhängige Variable ist Null, also hier a=0), dann bekommen wir den Wert g(0)=0²+4∙0−11=−11. Alle Teilterme, die x haben, werden bei der Berechnung des y-Achsenabschnitts einfach ausgelassen (da sie mit Null multipliziert werden). Der y-Achsenabschnitt der Kurve im Diagramm ist 1 (Punkt A), der Gerade 13 (nicht sichtbar).

Lösung eines Gleichungssystems sind die Punkte, wo die Funktionen einander schneiden. Im Bild sind es die Punkte G, H, I. Da schneiden die Kurve und die gerade einander. Um diese Punkte zu finden, werden die beide Funktionen gleich zueinander gestellt. Wenn z.B. die Kurve k(x)=x⁵+4x³-3x²+1 wäre und die Gerade f(x)=−2x+13, dann schreibt man: k(x)=f(x) also x⁵+4x³-3x²+1=−2x+13 und löst diese Gleichung. Das funktioniert, weil die beiden Funktionen an den Schnittpunkten die gleichen y-Werte haben (also ist an diesen Punkten tatsächlich k(x)=f(x)) und auch die gleichen x-Werte.

Der Punkt K gehört zur Kurve aber nicht zur Gerade, Punkt J gehört zu keiner der beiden Funktionen. Um herauszufinden, ob ein Punkt zu einer Funktion gehört, setzen wir in der Funktion den Wert von x ein und vergleichen wir das Ergebnis (y-Wert) mit dem y-Wert des Punktes. Wenn diese dann übereinstimmen, dann gehört der Punkt zur Funktion, sonst nicht.

Die quadratische Funktion

Die quadratische Gleichung

Eine Funktion der Form $\ Q(x)=ax^{2}+bx+c\$ wird quadratische Funktion genannt. Ihre Lösungen (Nullstellen) werden durch die folgende Formel angegeben:

$x_{1,2}={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}$

Der Ausdruck unter der Wurzel wird Diskriminante $D\$ genannt.

$D={b^{2}-4ac}$

Wenn die Diskriminante positiv ist, hat die Gleichung zwei Lösungen, wenn null dann eine Lösung und wenn negativ keine (da es keine Wurzel von negativen Zahlen gibt).

Eine Polynomfunktion ist eine Funktion von einer Summe von Potenzfunktionen, deren Hochzahlen natürliche Zahlen sind:

$P(x)=a_{n}x^{n}+a_{n-1}x^{n-1}+...+a_{2}x^{2}+a_{1}x+a_{0}$

n ist die größte Hochzahl und bestimmt den sogenannten Grad der Funktion (für a_n≠0), a_n, a_n-1, … , a₀ sind die sogenannten Koeffizienten. Wenn n=2 ist, dann ist von einer quadratische Funktion die Rede:Q(x)= ax²+bx+c

Wir beschäftigen uns in diesem Kapitel mit den Lösungen einer quadratischen Funktion, also mit den Stellen der Funktion, wo ihre Wert Null ist. Wir setzen daher die Funktion gleich Null. Die entsprechende Gleichung wird quadratische Gleichung genannt:

ax²+bx+c=0

Fangen wir mit einem einfachen Beispiel an:

x²=9

Die Gegenrechnung von Quadrat ist die Wurzel:

$x={\sqrt {9}}\$ also x=3

Ist das jetzt die einzige Lösung dieser Gleichung? Nein. Auch der Wert −3 ist eine Lösung der Gleichung:

(−3)²=9

Daher ist es notwendig, bei solchen Fällen beide Lösungen zu schreiben:

$x=\pm {\sqrt {9}}$ also sowohl +3 als auch −3

Allerdings haben wir die quadratische Gleichung in der folgenden Form geschrieben:

ax²+bx+c=0

In der Gleichung x²=9 haben wir rechts doch nicht null sondern 9. Wie so haben wir behauptet, dass es um eine quadratische Gleichung geht? Das wird klar, wenn 9 auf die andere Seite gebracht wird:

x²−9=0

Das ist eine quadratische Gleichung mit a=1, b=0 und c=−9. Das ist allerdings auch die plus-minus binomische Formel, die als Produkt geschrieben werden kann:

x²−9=0 → (x+3)(x−3)=0 also x=−3 oder x=3

Wir haben also gesehen, dass die quadratische Funktion f(x)=x²−9, also die entsprechende Gleichung x²−9=0, zwei Lösungen hat. Ist das immer der Fall, dass eine quadratische Funktion und die entsprechende Gleichung zwei Lösungen hat? Nehmen wir folgendes Beispiel:

x²+10x+25=0

Das ist eine quadratische Gleichung mit a=1, b=10 und c=25. Der Term links ist wieder eine binomische Formel, die plus Formel:

x²+10x+25=0 → (x+5)²=0 → (x+5)(x+5)=0 also x=−5

Wie zu sehen ist, gibt es hier nur eine (sozusagen doppelte) Lösung, nämlich x=−5. Nehmen wir noch ein Beispiel:

x²=−3

Die Gegenrechnung ist die Wurzel:

$x={\sqrt {-9}}\$

Die Wurzel von negativen Zahlen ist (in der Menge der reellen Zahlen) nicht definierbar. Eine Erklärung ist, dass das Quadrat von allen Zahlen (positiven und negativen) nie negativ sein kann. Beispielsweise ist 3²=9 positiv aber (−3)²=9 auch. Daher hat die Gleichung x²=−3 keine Lösung. Bringen wir in der Gleichung die 3 auf die andere Seite:

x²+3=0

Vergleichen wir das mit der allgemeinen quadratischen Gleichung:

ax²+bx+c=0

sehen wir, dass in x²+3=0 das a gleich 1, das b gleich 0 und das c gleich 3 sein soll. So haben wir eine quadratische Gleichung mit a=1, b=0 und c=3. Diese Gleichung hat allerdings keine Lösung (in der Menge der reellen Zahlen). Wir haben also in den vorherigen Beispielen gesehen:

Eine quadratische Gleichung (und die entsprechende Funktion) kann keine, eine oder zwei Lösungen haben.

Es gibt eine Formel für die Lösungen der allgemeiner quadratische Funktion ax²+bx+c=0:

$x_{1,2}={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}$

Der Ausdruck unter der Wurzel wird Diskriminante D genannt.

$D={b^{2}-4ac}$

Wenn die Diskriminante positiv ist, hat die Gleichung zwei Lösungen $\textstyle \left(x_{1,2}={\frac {-b\pm {\sqrt {D}}}{2a}}\right)$, wenn null dann eine Lösung $\textstyle \left(x_{1,2}=-{\frac {b}{2a}}\right)$und wenn negativ keine (da es keine Wurzel von negativen Zahlen gibt). In unseren Beispielen:

• x²=9 also x²−9=0 Hier ist a=1, b=0 und c=−9.
  Diskriminante: D=b²−4ac=0²−4·1·(−9)=36>0 (positiv). Es gibt daher 2 Lösungen.

• (x+5)²=0 also x²+10x+25=0 Hier ist a=1, b=10 und c=25.
  Diskriminante: D=b²−4ac=10²−4·1·25=100−100=0 (null). Es gibt daher 1 Lösung.

• x²=−3 also x²+3=0 Hier ist a=1, b=0 und c=3.
  Diskriminante: D=b²−4ac=0²−4·1·3=−12<0 (negativ). Es gibt daher keine Lösung.

• (x+5)²=9 also x²+10x+16=0 Hier ist a=1, b=10 und c=16.
  Diskriminante: D=b²−4ac=10²−4·1·16=100−64=36>0 (positiv). Es gibt daher 2 Lösungen.

Quadratische Gleichung Textaufgaben

Hier entsteht ein Musterbeispiel (Ausnahmsweise mit Erklärung)

Quadratische Funktion Vertiefung

Quadratische Ergänzung

Eine Funktion der Form $\ Q(x)=ax^{2}+bx+c\$ wird quadratische Funktion genannt. Ihre Lösungen (Nullstellen) werden durch die folgende Formel angegeben:

$x_{1,2}={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}$

Der Ausdruck unter der Wurzel wird Diskriminante $D\$ genannt.

$D={b^{2}-4ac}$

Wenn die Diskriminante positiv ist, hat die Funktion zwei Lösungen, wenn null dann eine Lösung und wenn negativ keine (da es keine Wurzel von negativen Zahlen gibt).

Um zu zeigen, warum die Lösungen der quadratischen Funktion durch die angegebene Formel gegeben werden, können wir die sogenannte "quadratische Ergänzung" benutzen.

Um zu verstehen, wie die quadratische Ergänzung funktioniert, nehmen wir ein Beispiel:

$(x+5)^{2}=9$

Das ist eine quadratische Gleichung aber noch nicht in der allgemeinen Form ax²+bx+c=0. Bringen wir diese Gleichung in diese Form:

$(x+5)^{2}=9\rightarrow (x+5)^{2}-9=0\rightarrow x^{2}+10x+25-9=0\rightarrow x^{2}+10x+16=0$

Das ist eine quadratische Gleichung mit $a=1$, $b=10$ und $c=16$. Obwohl 16 eine Quadratzahl ist, ist $x^{2}+10x+16$ ist keine binomische Formel (es sollte $x^{2}+8x+16$ sein, also 8 statt 10). Wie kann man jetzt die Lösungen der quadratischen Gleichung finden?

$x^{2}+10x+16=0\qquad x=?$

Um das zu finden, machen wir in den vorherigen Rechnungen zwei Schritte zurück.

$x^{2}+10x+16=0\rightarrow x^{2}+10x+25-9=0\rightarrow (x+5)^{2}-9=0$

Letzteres ist doch eine binomische Formel, die plus-minus Formel:

$a^{2}-b^{2}=(a+b)(a-b)$

Anstatt $a^{2}$ haben wir hier $(x+5)^{2}$, also an der Stelle von $a$ ist $(x+5)$. Anstatt $b^{2}$ haben wir 9, also an der Stelle von $b$ ist 3 . Es gilt daher:

$x^{2}+10x+16=0\rightarrow (x+5)^{2}-9=0\rightarrow ((x+5)+3)((x+5)-3)=0$$\rightarrow (x+8)(x+2)=0\$also $\ x+8=0\rightarrow x=-8$ oder $x+2=0\rightarrow x=-2$

Es gibt hier zwei Lösungen, −8 und −2. Es ist leicht festzustellen: Werden die Klammer ausmultipliziert, ergibt sich den quadratischen Term am Anfang:

$(x+8)(x+2)=x^{2}+2x+8x+16=x^{2}+10x+16$

Um die allgemeine Lösung der abstrakten Gleichung zu finden, werden die hier vorgeführten Schritte durchgeführt, diesmal allerdings mit Symbolen und nicht mit konkreten Zahlen.

$ax^{2}+bx+c=0\qquad x=?$

Im konkreten Beispiel $x^{2}+10x+16=0$ war der erster Schritt, den Ausdruck zu einer Plus-Minus binomischen Formel umzuwandeln. Wir haben 9 addiert und subtrahiert und dadurch ist eine Differenz von zwei Ausdrucken ($(x+5)$ und 9) entstanden: $(x+5)^{2}-9=0$. 5 in $(x+5)$ist die Hälfte von 10 in $x^{2}+10x+16=0$. 10 steht in der allgemeinen Gleichung $ax^{2}+bx+c=0$ für b, wir müssen also die Hälfte von b (wie die Hälfte von 10) benutzen:

$a\,x^{2}+b\,x+c=\left(x+{b \over 2}\right)^{2}+?$

Wir müssen allerdings die linke Seite der Gleichung mit $a$ multiplizieren, damit zumindest die Koeffizient von $x^{2}$ stimmt. Somit bekommen wir auf der linken Seite folgenden Ausdruck:

$a\cdot \left(x+{b \over 2}\right)^{2}$, was gleich mit $a\cdot x^{2}+a\cdot b\cdot x+a\cdot {b^{2} \over 4}\$ist.

Jetzt aber stimmt die zweite Koeffizient (von x ohne Quadrat) der allgemeinen Gleichung $ax^{2}+bx+c=0$ nicht mehr (sie sollte einfach $b$ sein und nicht $a\cdot b$). Damit sie auch stimmt, muss im Klammerausdruck $\textstyle \left(x+{b \over 2}\right)^{2}$ an der Stelle von $\textstyle b \over 2$ der Ausdruck $\textstyle b \over {2a}$ benutzt werden. Somit haben wir insgesamt:

$a\cdot \left(x+{b \over {2a}}\right)^{2}$$=a\cdot \left(x^{2}+2\cdot {b \over {2a}}\cdot x+{b^{2} \over {4a^{2}}}\right)$$=a\cdot x^{2}+a\cdot 2\cdot {b \over {2a}}\cdot x+a\cdot {b^{2} \over {4a^{2}}}$$=a\cdot x^{2}+{b}\cdot x+{b^{2} \over {4a}}$

Bisher haben wir es super geschafft! Wir haben die richtige Koeffizient für $x^{2}$ und für $x$. Der letzte Schritt ist einfach, da wir "nur" noch am Ende c brauchen:

$ax^{2}+bx+c$ $=a\cdot x^{2}+{b}\cdot x+{\color {red}c}+{b^{2} \over {4a}}-{b^{2} \over {4a}}=$

$a\cdot x^{2}+{b}\cdot x+{b^{2} \over {4a}}$$\quad +{\color {red}c}-{b^{2} \over {4a}}=$

$a\cdot \left(x+{b \over {2a}}\right)^{2}$$\quad -{{-4a{\color {red}c}} \over {4a}}-{b^{2} \over {4a}}=$

$a\cdot \left(x+{b \over {2a}}\right)^{2}-\left({b^{2} \over {4a}}-{{4ac} \over {4a}}\right)=$

$a\cdot \left(x+{b \over {2a}}\right)^{2}-{{b^{2}-{4ac}} \over {4a}}=\qquad$

$a\cdot \left(x+{b \over {2a}}\right)^{2}-a\cdot {{b^{2}-{4ac}} \over {4a^{2}}}\$

also ($a$ herausheben)

$ax^{2}+bx+c$$\ \ =\ \$$a\cdot \left[\left(x+{b \over {2a}}\right)^{2}-\left({{b^{2}-{4ac}} \over {4a^{2}}}\right)\right]$

Wir haben schon die plus-minus binomsiche Formel, was eindeutig wird, wenn wir die zweite Klammer rechts als Quadrat einer Wurzel schreiben:

$ax^{2}+bx+c$$=a\cdot \left[\left(x+{b \over {2a}}\right)^{2}-\left({\sqrt {b^{2}-{4ac} \over {4a^{2}}}}\right)^{2}\right]$

Der Vorgang, den wir hier vorgeführt haben, wird quadratische Ergänzung genannt.

Completing the square

Lösungsformel der quadratischen Gleichung

Mit Hilfe der quadratischen Ergänzung kann man zeigen, dass:

$ax^{2}+bx+c=a\cdot \left[\left(x+{b \over {2a}}\right)^{2}-\left({\sqrt {b^{2}-{4ac} \over {4a^{2}}}}\right)^{2}\right]$

Die allgemeine quadratische Gleichung $ax^{2}+bx+c=0\$kann man daher auch als eine plus-minus binomische Formel schreiben:

$a\cdot \left[\left(x+{b \over {2a}}\right)^{2}-\left({\sqrt {b^{2}-{4ac} \over {4a^{2}}}}\right)^{2}\right]=0$

Wenn wir die binomische Formel in ihrer Produktform schreiben, bekommen wir:

$a\cdot \left[\left(x+{b \over {2a}}\right)+\left({\sqrt {b^{2}-{4ac} \over {4a^{2}}}}\right)\right]\cdot$$\left[\left(x+{b \over {2a}}\right)-\left({\sqrt {b^{2}-{4ac} \over {4a^{2}}}}\right)\right]=0$

Ein Produkt ist gleich Null, wenn (zumindest) einer der Faktoren null ist, also hier wenn:

• $a=0$. Das kann aber nicht gelten, da wir in diesem Fall keine quadratische Funktion haben.
• $x+{b \over {2a}}{\color {red}+}{\sqrt {b^{2}-{4ac} \over {4a^{2}}}}=0\quad$also$\quad x={\frac {\ -b{\color {red}-}{\sqrt {b^{2}-{4ac} \over {4a^{2}}}}\ }{2a}}$

oder wenn:

• $x+{b \over {2a}}{\color {red}-}{\sqrt {b^{2}-{4ac} \over {4a^{2}}}}=0\quad$also$\quad x={\frac {\ -b{\color {red}+}{\sqrt {b^{2}-{4ac} \over {4a^{2}}}}\ }{2a}}$

Die zwei Lösungen können wir mit einem Index versehen und sie zusammengefasst schreiben:

$x_{1,2}={\frac {\ -b{\color {red}\pm }{\sqrt {b^{2}-{4ac}\ }}}{2a}}$

Somit können wir die Formel für die Lösungen einer quadratischen Gleichung (und ihrer entsprechenden quadratischen Funktion) mit Hilfe der quadratischen Ergänzung und der plus-minus binomischen Formel finden.

Scheitelpunkt einer quadratischen Funktion

Mit Hilfe der quadratischen Ergänzung kann man zeigen, dass:

$ax^{2}+bx+c=a\cdot \left[\left(x+{b \over {2a}}\right)^{2}-\left({\sqrt {b^{2}-{4ac} \over {4a^{2}}}}\right)^{2}\right]$

Die allgemeine quadratische Funktion $Q(x)=ax^{2}+bx+c\$kann man daher auch als eine plus-minus binomische Formel schreiben:

$Q(x)=a\cdot \left[\left(x+{b \over {2a}}\right)^{2}-\left({\sqrt {b^{2}-{4ac} \over {4a^{2}}}}\right)^{2}\right]$

Nehmen wir an, dass $a$ eine positive Zahl ist. Betrachten wir diese Formel genauer, stellen wir fest, dass sie dann ihren kleinsten Wert annimmt, wenn die erste Klammer null ist. Dass liegt daran, dass die erste Klammer ein Quadrat ist und ihr kleinster Wert nur null sein kann (da das Quadrat einer Zahl nie negativ ist). Die erste Klammer ist auch die einzige, die veränderbar ist, da sie die unabhängige Variable $x$ beinhaltet. Wir können dann leicht finden, an welche Stelle das stattfindet und wie viel der Wert der Funktion dann ist:

$x+{b \over {2a}}=0\Rightarrow x=-{\frac {b}{2a}}$

In diesem Fall ist $\textstyle x+{b \over {2a}}=0$ und daher:

$Q(x)=a\cdot \left[\left(x+{b \over {2a}}\right)^{2}-\left({\sqrt {b^{2}-{4ac} \over {4a^{2}}}}\right)^{2}\right]=a\cdot \left(0-{b^{2}-{4ac} \over {4a^{2}}}\right)={b^{2} \over {4a}}-c$

Somit haben wir den Punkt:

$\left(-{\frac {b}{2a}}\ {\Big |}\ {b^{2} \over {4a}}-c\right)$

So ein Punkt wird Extrempunkt genannt. Wenn $a$ positiv ist, ist er ein Minimum, wenn $a$ negativ ein Maximum. Die entsprechende Stelle $\textstyle x=-{\frac {b}{2a}}$ wird Extremstelle genannt.

Die Extremstelle der quadratischen Funktion können wir viel leichter mit Hilfe der ersten Ableitung finden (ohne die quadratische Ergänzung zu benutzen). Da wo die Funktion eine Extremstelle hat, wird sie ihre Richtung im Diagramm ändern. Wäre sie vorher steigend, wird sie dann fallend sein und umgekehrt. Genau am Punkt der Änderung wird sie weder steigend noch fallend sein. Die Steigung also die Ableitung wird null sein, die Tangente der Funktion wird parallel zur x-Achse sein. Um die Stelle zu finden können wir daher die erste Ableitung gleich null setzen. Die erste Ableitung allgemein ist:

$Q(x)=ax^{2}+bx+c\Rightarrow Q'(x)=2\cdot a\,x+b$

Setzen wir diese Ableitung gleich null, ergibt sich:

$2\cdot a\,x+b=0\Rightarrow x=-{\frac {b}{2a}}$

Wenn wir diesen Wert von $x$ in der Funktion einsetzten, bekommen wir nach ein paar Berechnungen den entsprechenden Wert der Funktion:

$Q(-{\tfrac {b}{2a}})=a\left(-{\frac {b}{2a}}\right)^{2}+b\left(-{\frac {b}{2a}}\right)+c\Rightarrow Q(-{\tfrac {b}{2a}})={b^{2} \over {4a}}-c$

Der Extrempunkt ist daher (wie es zu erwarten war) wieder:

$\left(-{\frac {b}{2a}}\ {\Big |}\ {b^{2} \over {4a}}-c\right)$

Polynomfunktionen Diagramm

$\qquad$A $\qquad \quad$B $\qquad$C $\qquad \qquad$D

$\qquad \qquad$E $\qquad \qquad$F $\qquad \qquad$G

$\qquad \qquad$H $\qquad \qquad$K $\qquad \qquad$L

Eine Polynomfunktion ist eine Funktion von einer Summe von Potenzfunktionen, deren Hochzahlen natürliche Zahlen sind:

$P(x)=a_{n}x^{n}+a_{n-1}x^{n-1}+...+a_{2}x^{2}+a_{1}x+a_{0}$

n ist die größte Hochzahl und bestimmt den sogenannten Grad der Funktion (für a_n≠0), a_n, a_n-1, … , a₀ sind die sogenannten Koeffizienten.

Ist die höchste Hochzahl null, dann haben wir die sogenannten "konstanten" Funktionen (Polynomfunktionen 0. Grades) $y=a_{0}$, wie im Diagramm A. Sie sind Geraden, die parallel zu x-Achse laufen und daher keine "Lösung" haben (keine Nullstelle, also sie treffen die x-Achse nie). Einzige Ausnahme die konstante Funktion $y=0$, die die x-Achse selber ist und daher sozusagen unendlich viele "Lösungen" hat.

Ist die höchste Hochzahl eins, dann haben wir die sogenannten "linearen" Funktionen (Polynomfunktionen 1. Grades) $y=a_{1}x+a_{0}$, wie im Diagramm B. Sie sind Geraden, die die x-Achse genau ein mal treffen und daher genau eine "Lösung" haben (eine Nullstelle, also sie treffen die x-Achse ein mal). $a_{1}\$ist die Steigung der Funktion, $a_{0}\$der y-Achsenabschnitt. Ist $a_{1}\$positiv, läuft die Gerade "nach oben" (also von links unten nach rechts oben), wenn negativ dann nach unten.

Ist die höchste Hochzahl 2, dann haben wir die sogenannten "quadratischen" Funktionen (Polynomfunktionen 2. Grades)$y=a_{2}x^{2}+a_{1}x+a_{0}$, wie im Diagramm C. Ihre Form ist eine sogenannte Parabel. Im Diagramm C können wir zwei solche Funktionen die nach oben gerichtet sind. In diesem Fall ist $a_{2}\$positiv, in der anderen Funktion (nach unten) ist diese Koeffizient negativ. Eine Polynomfunktion kann zwei Lösungen haben (wie beide Funktionen, die nach oben gerichtet sind), eine oder sogar keine (wie die Funktion, die nach unten gerichtet ist).

Ist die höchste Hochzahl 3, dann haben wir die sogenannten "kubischen" Funktionen (Polynomfunktionen 3. Grades)$y=a_{3}x^{3}+a_{2}x^{2}+a_{1}x+a_{0}$, wie im Diagramm D und E. Ist $a_{3}\$positiv, läuft die Funktion "nach oben", sonst "nach unten". An dieser Stelle können wir den Begriff des Monotonieverhaltens erklären als auch, wie wir den Grad der Funktion erkennen können. Wenn die Funktion "nach oben" geht, also von links unten nach rechst oben, dann wird sie als "steigend" bezeichnet, was ihr Monotonieverhalten betrifft. Wenn sie "nach unten" läuft, wird sie als "fallend" bezeichnet. Eine Funktion hat nicht unbedingt (und eher seltener) ein festes Monotonieverhalten. Die Funktion in Diagramm D ist bis zur Stelle ca. −3 fallend, dann bis +3 steigend und dann wieder fallend. Die Funktion in Diagramm E, die auch wie im D 3. Grades ist, ist hingegen überall steigend (wie es auch der Fall bei Geraden ist, die "nach oben" laufen). Das Monotonieverhalten kann uns also nichts über den Grad der Funktion sagen. Man merkt allerdings, dass die Funktion im Diagramm E keine Gerade ist. Was sich da ändert, ist die sogenannte Krümmung der Funktion. Die Funktion biegt einmal in eine Richtung und dann wieder in der anderen. Wir haben also zwei "Abbiegungen". Allgemein gilt:

• Der Grad einer Polynomfunktion ist zumindest um 1 größer, als die Anzahl der "Abbiegungen".

Um den Begriff der Krümmung etwas besser zu verstehen, stellen wir uns vor, dass die Kurve in Diagramm D eine Straße wäre und wir mit einem Fahrzeug von links oben fahren. Wir müssen schon am Anfang ein bisschen nach links abbiegen, um auf der "Straße" zu bleiben und dann immer abrupter, bis ungefähr an der Stelle −3. Dann müssen wir immer weniger abbiegen und ungefähr ab der Stelle null müssen wir anfangen, rechts abzubiegen. Wir haben an diese Stelle eine Krümmungsänderung. Auf einer Gerade hingegen (Diagramm B) brauchen wir (dürfen wir sogar) nicht abbiegen.

Diagramme F und G sind Polynomfunktionen 4. Grades, H 5. Grades, K 6.Grades und L 7.Grades. Wenn wir diese Diagramme betrachten, kommen wir zu weiteren Schlüssen:

• Ist das Monotonieverhalten an den Rändern der Funktion unterschiedlich, dann ist die Hochzahl eine gerade Zahl. Wenn die Funktion am Rand links fallend und am Rand rechts steigend ist (wie in den beide "oberen" Funktionen in Diagramm C, als auch in Diagramm G und Diagramm K), dann ist die Koeffizient der höchsten Potenz positiv, sonst ist sie negativ.

• Ist das Monotonieverhalten an den Rändern der Funktion gleich, dann ist die Hochzahl eine ungerade Zahl. Wenn die Funktion links und rechts steigend ist (wie in den Diagrammen E, H und L), dann ist die Koeffizient der höchsten Potenz positiv, sonst ist sie negativ.

Die Abbiegungen (um 1 erhöht) können uns nur zur Erschließung des minimalen möglichen Grades der Funktion helfen. Wir wissen ja nicht, wie die Funktion außerhalb des sichtbaren Bereiches läuft und auch andere Sachen nicht. Im Diagramm H beispielsweise können wir mit Sicherheit sagen, dass die Funktion zumindest von 5. Grad ist (es gibt 4 sichtbaren Abbiegungen; 4+1=5). Im Diagramm K gibt es 5 sichtbare Abbiegungen, die Funktion ist zumindest 6. Grades. Wenn wir Diagramme H und K vergleichen, stellen wir fest, dass die Änderung des Monotonieverhaltens eine Krümmung voraussetzt (zumindest in den Funktionen, die wir hier behandeln). Das Gegenteil ist allerdings nicht der Fall. Im Diagramm H folgt nach jeder Abbiegung eine Änderung des Monotonieverhaltens (also von fallend zu steigend oder umgekehrt). Im Diagramm K hingegen gibt es in der Umgebung der Lösung III zwei Abbiegungen, die nicht zu einer Änderung des Monotonieverhaltens führt. Das gleiche gilt in Diagramm E, wo wir zwei Abbiegungen haben ohne dass sich das Monotonieverhalten überhaupt ändert (die Funktion ist immer steigend).

Über die Anzahl der Lösungen können wir mit Hilfe der Diagrammen Folgendes schließen:

• Eine Polynomfunktion hat höchstens so viele Lösungen wie ihr Grad. Ist der Grad eine ungerade Zahl, dann hat sie zumindest eine Lösung. Ist der Grad eine Gerade Zahl, dann kann sie doch auch keine Lösung haben.

Wenn der Grad ungerade ist, ist das Monotonieverhalten an den Rändern der Funktion das gleiche, beispielsweise steigend. Das bedeutet dann, dass die Kurve mit Sicherheit zumindest einmal die x-Achse treffen wird. Das ist nicht der Fall beim geraden Grad, wo die ganze Funktion sich unterhalb oder oberhalb der x-Asche befinden kann (wie im Diagramm C für die "untere" Funktion und in Diagramm F).

Noch eine Information zu der Ableitung von Polynomfunktionen:

• Die Ableitung einer Polynomfunktion ist eine neue Polynomfunktion mit einem Grad um 1 reduziert. Einzige Ausnahme die konstante Funktion, deren Ableitung null ist (also der Grad bleibt in diesem Fall null).

Umkehrfunktionen mit Umformen finden

Eine Funktion ist eine Verbindung zwischen zwei (oder mehreren) Sachen. Ein einfaches Beispiel ist die Angabe der Temperatur T in Abhängigkeit von der Zeit t. Es kann sein, dass diese Abhängigkeit in einem gewissen Experiment durch die folgende Formel ausgedrückt wird:

$T(t)=35-2t\$(t in Minuten, T in °C)

Das bedeutet in diesem Fall, dass die Temperatur am Anfang 35°C ist und jede Minute um 2°C fällt. In diesem Fall ist die Zeit die sogenannte unabhängige Variable, die Temperatur die abhängige. Die Frage in diesem Fall ist: "Wie viel ist die Temperatur nach so und so viele Minuten?" Wenn wir die Temperatur nach 195 s messen wollen, müssen wir erst die s in min umrechnen: $195\ s=195:60\ min=3{,}25\ min$. Diese Zahl setzen wir dann in die Formel ein, um die entsprechende Temperatur zu finden:

$T(3{,}25)=35-2\cdot 3{,}25=28{,}5\$

Die Temperatur wird daher 28,5°C sein.

Was ist aber, wenn wir die Frage umkehren? "Wann ist die Temperatur 10°C?"

Um diese Frage zu beantworten, müssen wir die Funktion auf die Variable t (Zeit) umformen. Wir vergessen kurz die Funktionsdarstellung T(t), wir schreiben für die Temperatur einfach T und formen auf diese Variable um:

$\textstyle T=35-2t\ \Rightarrow \ 2t=35-T\ \Rightarrow \ t={\frac {35-T}{2}}$

Jetzt können wir wieder die Funktionsdarstellung benutzen:

$t(T)={\frac {35-T}{2}}\$(t in Minuten, T in °C)

Hier ist die Temperatur die unabhängige Variable und die Zeit die abhängige. Wir wollen wissen, "wie viel" die Zeit, "bei" einer gewissen Temperatur ist. Diese Funktion ist die sogenannte Umkehrfunktion der Funktion am Anfang.

Die Angabe der Einheiten ist immer notwendig, wenn die Variablen Einheiten aufweisen, um Fehler bei den Berechnungen zu vermeiden. In diesem Beispiel hätten wir ein anderes Ergebnis, wenn wir 195 statt 3,25 benutzt hätten. Wenn allerdings die Variablen reine Zahlen sind, dann brauchen wir auch keine Einheiten angeben (es gibt ja dann keine). Hier sind einige Gegenrechnungen, die beim Umformen notwendig sein können. Manche davon haben wir gelernt, manche vielleicht auch noch nicht. Letztere werden wir erst später erklären.

$+\leftrightarrow -\qquad \cdot \leftrightarrow :\qquad {\sqrt[{n}]{\ a\ }}\leftrightarrow a^{n}\qquad \sin \leftrightarrow \arcsin \qquad$

$\cos \leftrightarrow \arccos \qquad \tan \leftrightarrow \arctan \qquad e^{x}\leftrightarrow \ln x$

Funktionserkennung

Funktionserkennung in Diagramm

Diagramm erkennen

Diagramm Eigenschaften

Es gibt unendlich viele Funktionen und es macht daher keinen Sinn, sie alle einzeln zu besprechen. Hier werden wir uns nur mit einer begrenzten Anzahl von Funktionen beschäftigen: Polynomfunktionen, Wurzelfunktionen, trigonometrische Funktionen, indirekte Proportionalität, Logarithmus und Exponentialfunktion. Wir werden manche von denen paarweise vergleichen. Dadurch können wir besondere Merkmale einer Funktion erkennen, die uns zu entscheiden helfen können, ob eine Funktion durch ein bestimmtes Diagramm dargestellt wird (und umgekehrt).

Polynomfunktion höheren Grades und Sinusfunktion.

Sinusfunktion Polynom 9.Grad Polynom 3. Grad Vergleich

Links sehen wir eine Sinusfunktion und zwei Polynomfunktionen. Die Mitte der beiden Polynomfunktionen ist kaum von der Sinusfunktion zu unterscheiden. Das bedeutet nicht, dass jede Polynomfunktion wie eine Sinusfunktion aussieht, aber dass es Polynomfunktionen geben kann, die teilweise stark wie eine Sinusfunktion aussehen. In der Regel sehen allerdings Polynomfunktionen nicht so stark wie eine Sinusfunktion aus (Bilder rechts). Das Merkmal, das diese der Sinusfunktion ähnlichen Polynomfunktionen von der Sinusfunktion selber unterscheidet, ist in den Diagramm leicht erkennbar: ihre Ränder.

Polynomfunktionen, die nicht so stark wie Sinusfunktion aussehen

Wurzel und Logarithmusfunktion

Wurzelfunktion Logarithmusfunktion Vergleich A Vergleich B

Links sehen wir eine Wurzelfunktion und eine (leicht verschobene) Logarithmusfunktion. Beide Funktionen sind nur für positiven Werten von x definierbar (außer wenn sie "verschoben" sind, wie der Fall mit der Logarithmusfunktion hier ist). Wenn wir hier einen bestimmten Bereich vergleichen (Vergleich A), sind die Funktionen wieder kaum voneinander zu unterscheiden, was allerdings bei größeren Bereichen nicht der Fall ist (Vergleich B). Es gibt drei grundsätzliche Unterscheide zwischen den beiden Funktionen: Die Logarihmusfunktion wird beim steigenden x viel schneller "parallel" zur x-Achse. Anders gesagt, ihre (immer positive) Steigung setzt sich schneller herab, allerdings ohne den Wert null zu erreichen. Die Logarithmusfunktion hat eine sogenannte "Asymptote". Betrachten wir das Bild rechts und bewegen wir uns von rechts nach links. An der Stelle 4 ist der Wert der Funktion 2, an der Stelle 2 ist der Wert 1, an der Stelle 1 ist er null. Unterhalb von 1 wird er Wert negativ und zwar immer abrupter. Die Werte ganz nah zur Stelle null können wir nicht mehr sehen. Sie werden immer negativer, sie berühren aber die y-Achse nie. Die y-Achse ist in diesem Fall eine sogenannte "Asymptote". Logarithmus wird für negative Werte oder null ("nicht positive Werte") nicht definiert. Daher beschränkt sich die Funktion auf der rechten Seite der y-Achse. In den Diagrammen links ist die Funktion etwas verschoben (das geht, wenn wir verschiedene sogenannte "Parameter" ändern). Sie hat aber immer noch eine Asymptote (in diesem Fall die Gerade x=−0,12, die allerdings keine Funktion in eigenem Sinn ist). Die (quadratische) Wurzelfunktion "stoppt" bei null. Die Wurzeln mit geradem Wurzelexponent werden nur für nicht negative Werte von x definiert und ihr Wertebereich ist auch nur nicht negative Zahlen. Der Grund für das erstere liegt daran, dass es keine (beispielsweise) quadratische Wurzel einer negativen Zahl gibt (wie ${\sqrt {-3}}$). Dass die Werte der Funktion nur positiv sind, liegt an der Definition einer Funktion allgemein. Teil der Definition einer Funktion ist, dass es für jeden x-Wert genau einen y-Wert gibt. Wir wissen schon, dass die Gleichung $y^{2}=9\$zwei Lösungen hat, y= 3 und y=−3. Wegen der Definition einer Funktion allerdings kann die Funktion $y={\sqrt {x}}\$nur eine Lösung haben. Es wurde vereinbart, dass die positive Lösung gewählt wird (sonst gäbe es für x=9 zwei y-Werte, 3 und −3). Daher sieht die Wurzelfunktion wie das erste Bild oben links ("Wurzelfunktion") und nicht wie das Bild hier rechts. Das Bild hier rechts besteht aus zwei Funktionen (die auf der x-Achse gespiegelt werden): $y={\sqrt {x}}\$und $y=-{\sqrt {x}}$. Wir haben gesehen, dass die beide Funktionen (Logarithmus und Wurzelfunktion) bei einem gewissen Bereich übereinstimmen. Das bedeutet nicht, dass jede Logarithmusfunktion bei einem bestimmten Bereich mit jeder Wurzelfunktion übereinstimmt, sondern dass es eine Logarithmus und eine Wurzelfunktion geben kann, die bei einem bestimmten Intervall übereinstimmen.

Quadratische und Exponentialfunktion

quadratische Funktion Exponentialfunktionen Vergleich A Vergleich B

Links sehen wir eine quadratische und zwei exponentiellen Funktionen (beide im zweiten Diagramm). Die eine exponentielle ist fallend (von links oben nach rechts unten) und die andere steigend. Sie werden auf der y-Achse "gespiegelt". Die quadratische ist links der Achse fallend und rechts steigend. Hier sehen wir wieder, dass die von uns gewählten Funktionen bei einem bestimmten Intervall übereinstimmen (Vergleich A). Allerdings weisen sie auch erhebliche Unterschiede: Die Exponentialfunktionen sind entweder ("streng") fallend oder ("streng") steigend. Die quadratische Funktion ist links fallend und rechts steigend. Die Exponentialfunktionen weisen (wie die Logarithmusfunktion) eine Asymptote auf, allerdings ist sie in diesem Fall nicht die y-Achse (oder eine Parallele zu ihr) sondern die x-Achse. Beispielsweise wird der Wert der fallenden Exponentialfunktion immer kleiner bei steigendem x, allerdings wird sie nie null oder negativ. Das ist also der Sinn einer Asymptote. Die Asymptote einer Funktion ist eine Gerade (in irgendeine Richtung und nicht nur die x- oder y-Achse). Für diese Gerade ist es beweisbar, dass die Werte der Funktion ihr immer näher werden (aber sie nie berühren).

Indirekte Proportionalität und Exponentialfunktion

Exponentialfunktion Indirekte Proportionalität Vergleich A Vergleich B

Links sehen wir eine Exponentialfunktion und eine indirekte Proportionalität. Im zentralen Bereich um die y-Achse gibt es in diesem Fall keine Übereinstimmung (nur 2 Schnittpunkte, Vergleich A). Allerdings verlaufen weiter rechts von der y-Achse beide Funktionen fast parallel zur x-Achse. Daher geht es einfach, mit einer kleinen Verschiebung (einer Änderung von irgendeinem Parameter), dass die Funktionen in einem (sogar großen) Intervall fast übereinstimmen (Vergleich B). Hier wollen wir uns auf die Unterschiede konzentrieren. Die indirekte Proportionalität besteht aus zwei "Zweigen", rechts oben ("erstes Quadrant") und links unten ("drittes Quadrant"). Wir sehen keinen Wert für x=0. Tatsächlich hat diese Funktion keinen Wert an dieser Stelle. $\textstyle f{x}={\frac {a}{x}}\$ist nicht definierbar für x=0 (die Division durch null ist nicht definierbar). Wir sehen auch, dass links von der y-Achse die Funktion extrem negative Werte annimmt (gegen $-\infty$) und rechts extrem positive (gegen $+\infty$). Das macht schon Sinn: je kleiner der Nenner in einem Bruch, desto größer der Bruch selber. Der Bruch wird also Millionen, Milliarden usw. sein, je näher x zu null ist. Die y-Achse ist in diesem Fall eine Asymptote und zwar für beide Zweige. Das gilt für die Exponentialfunktion nicht. Die x-Achse ist eine Asymptote für beide Funktionen, für die Exponentialfunktion hier allerdings nur auf der rechten Seite. Für die indirekte Proportionalität wird die x-Achse auf der rechten Seite von oben angenähert, auf der linken Seite von unten. Es gilt, dass der Wert der Funktion nie Null wird (sonst wäre die Division durch null definierbar).

Tangens und kubische Funktion

Tangensfunktion Polynom 3. Grad Vergleich A Vergleich B

Links sehen wir eine Tangensfunktion und eine Polynomfunktion 3. Grades ("kubische Funktion"). In angezeigtem Bereich ("Intervall") sind sie kaum von einander zu unterscheiden (Vergleich A). Es gibt allerdings wieder eindeutige Unterschiede (Vergleich B): Die Tangensfunktion ist eine periodische Funktion, d.h. sie wird ständig wiederholt. In diesem Fall ist die Länge des wiederholten Intervalls $2\pi$. Für die Tangensfunktion gibt es nicht nur eine, sondern unendlich viele Asymptoten, die sich im gleichen Intervall wie die Periode ($2\pi$) wiederholen. Die Gleichungen für diese Asymptoten lauten: $x=\pi \pm n\cdot 2\pi$, also $x=\dots -5\pi ,\ x=\dots -3\pi ,\ x=\dots -\pi ,\ x=\dots \pi ,\ x=\dots 3\pi ,\ x=\dots -5\pi \dots \$Diese Geraden sind allerdings keine Funktionen, da jedem bestimmten Wert von x sogar unendlich viele Werte von y entsprechen. Für die kubische Funktion gibt es keine Asymptote, auch wenn ihrer Steigung in beiden Richtungen immer abrupter wird.

Umkehrfunktionen in Diagramm erkennen

y-Achse als Spiegel

x-Achse als Spiegel

Indirekte Proportionalität

Im Bild "y-Achse als Spiegel" ist zu erkennen, dass jeder der beiden dargestellten Funktionen das Spiegelbild der anderen auf der y-Achse ist. Die (blaue) Funktion f ist steigend, die (rote) Funktion g ist fallend und ihre Punkte entsprechen genau einander, wenn wir an der y-Achse als Spiegel denken. Beispielsweise entspricht der Punkt (1|2) der Funktion g dem Punkt (−1|2) der Funktion f. Der y-Wert ist genau der gleiche, der Betrag der x-Werte auch und nur das Vorzeichen der x-Werte ist anders. Wenn wir eine Spiegelung auf der y-Achse haben können wir daher schreiben:

$f(x)=g(-x)$

Die Werte der Funktionen sind gleich für die Gegenstellen.

Im Bild "x-Achse als Spiegel" können wir eine ähnliche Situation erkennen, nun jetzt mit der x-Achse als Spiegel. Die Kurve kann nach der Definition der Funktion nicht eine einzige Funktion darstellen, das es (mit der Ausnahme der Stelle 0) jeder Stelle zwei Werte entsprechen (eine oberhalb und einer unterhalb der x-Achse). Wir haben daher zwei Funktionen, die auf der x-Achse gespiegelt werden. Dem Punkt (4|2) der Funktion oben entspricht Beispielsweise der Punkt (4|−2) der Funktion unten. Wenn wir eine Spiegelung auf der x-Achse haben können wir daher schreiben:

$f(x)=-g(x)$

An jeder Stelle hat eine Funktion den Gegenwert der anderen.

Im Bild "Indirekte Proportionalität" können wir zwei Funktionen sehen, die beide eine indirekte Proportionalität darstellen. Jede Funktion ist ihr eigener Spiegel und zwar auf zwei Achsen. Diese Achsen sind auch im Bild dargestellt und sie entsprechen den Funktionen y=x (steigende Diagonale) und y=−x (fallende Diagonale). Wenn wir beispielsweise die (rote) Funktion $\textstyle {\frac {2}{x}}\$beobachten, stellen wir fest, dass der Punkt (2|1) auf der Diagonale y=x gespiegelt wird und dem Punkt (1|2) entspricht. Man sagt in diesem Fall, dass die indirekte Proportionalität ihre eigene Umkehrfunktion ist.

Wenn eine Funktion die Spiegelung einer anderen Funktion über die Achse y=x ist, dann ist sie ihre Umkehrfunktion. Das Umgekehrte gilt auch: Umkehrfunktionen werden auf der Diagonale y=x gespiegelt. Umkehrfunktionen werden oft mit Hochzahl −1 dargestellt. Beispielsweise wird die Umkehrfunktion von $f(x)$ mit $f^{-1}(x)\$dargestellt. Für die Umkehrfunktionen allgemeiner gilt:

Wenn $f(a)=b\$dann $f^{-1}(b)=a$

Um die Umkehrfunktion zu finden, müssen wir auf die unabhängige Variable umformen. Um die Umkehrfunktion darzustellen, müssen wir die Funktion auf der Diagonale y=x spiegeln. In den folgenden Bildern sehen wir jeweils ein Paar von Umkehrfunktionen:

• 
• 
• 
• 

Quadrat und Wurzel

Umkehrung mit drei Zweigen

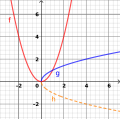
In vielen Fällen kommt es vor, dass die Umkehrfunktion einer Funktion aus mehreren Teilefunktionen besteht, da sie sonst keine Funktion mehr ist. Das gilt z.B. für die zwei Funktionen um die x-Achse im Bild "Quadrat und Wurzel", die wir auch am Anfang dieses Teils gesehen haben. Sie sind die Funktionen $y={\sqrt {x}}\$und $y=-{\sqrt {x}}$. Zusammen sind sie die Umkehrung der Funktion $y=x^{2}$, die im Bild auch zu sehen ist. Man sagt daher, dass die Umkehrung der Funktion $y=x^{2}\$aus zwei "Zweige" besteht, die Funktion $y={\sqrt {x}}\$ und die Funktion $y=-{\sqrt {x}}$. Im Bild "Umkehrung mit drei Zweigen" sehen wir ein ähnliches Beispiel (für eine kubische Funktion und die entsprechende Umkehrung, die einer kubischen Wurzel entspricht und aus drei Zweigen besteht).

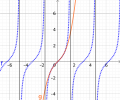
Die Darstellung mit mehreren Zweigen macht allerdings nicht immer Sinn. Die Umkehrfunktionen der trigonometrischen Funktionen beständen in diesem Fall aus unendlich vielen Zweigen. In den folgenden Bildern sehen wir die Umkehrfunktionen von Sinus, Kosinus und Tangens. Der Definitionsbereich für Sinus und Kosinus beschränkt sich auf das Intervall $[-1,\ 1]$, der Wertebereich auf das Intervall $\textstyle [-{\frac {\pi }{2}},\ {\frac {\pi }{2}}]\$bzw. $[0,\ \pi ]$.

• 
  sin und arcsin
• 
  cos und arccos
• 
  arctan

Funktionserkennung in Text

Bei den Textaufgaben ist das Verständnis sowohl der deutschen als auch der mathematischen Sprache notwendig. Wenn es um die Erkennung einer Funktionsart geht, gibt es bestimmte Merkmale im Text, die den entscheidenden Unterschied ausmachen. Als allgemeine Regel gilt allerdings: Wir müssen immer auf die Übereinstimmung der Einheiten aufpassen.

Lineare und Exponentialfunktion

Vergleichen wir zunächst einmal folgende Texte:

1. Ein 40 cm hoher Baum wächst jedes Jahr um 30 cm.
2. Ein 40 cm hoher Baum wächst jedes Jahr um 30%.
3. Die Höhe eines 40 cm hohen Baum wird jedes Jahr das 1,3-fache des vorherigen Jahrs.
4. Ein 40 cm hoher Baum wächst jedes Jahr um 130%.
5. Ein 40 cm hoher Baum wächst jedes Jahr 12 cm.

Es gibt einen entscheidenden Unterschied in den Texten.

• Im ersten und fünften Text wird die Änderung in Einheiten gegeben. Es gibt bei der Änderung keinen Vergleich zum Anfangswert. In diesem Fall haben wir eine lineare Funktion. Jede Änderung der unabhängigen Variablen (hier der Zeit) um eine Einheit, bewirkt die Änderung der abhängigen Variable um immer die gleichen Anzahl ihrer Einheiten. Im ersten Beispiel: Jedes Jahr (eine Einheit der unabhängigen Variable), wird die Höhe (abhängige Variable) genau 30 cm ändern. Diese Änderungsrate (30 cm/Jahr) wird die Steigung der Funktion sein und bleibt vom Jahr zum Jahr gleich. Der Wert am Anfang wird der y-Achsenabschnitt sein.
• Im zweiten, dritten und vierten Text wird die Änderung als Anteil angegeben ("Prozent", "-fach"). Die Änderung in Einheiten bleibt daher vom Jahr zum Jahr nicht die gleiche. Der Anfangswert für den Vergleich wird jedes Jahr ein neuer Wert sein. Beispielsweise sind 30% von 40 cm 12 cm. Der Baum wird daher nach einem Jahr 52 cm sein. Am nächsten Jahr wird er wieder 30% wachsen, das sind aber nicht mehr 12 cm sondern 30% von 52 cm, also 15,6 cm. Der Baum wächst jedes Jahr nicht um den gleichen Wert sondern um den gleichen Anteil. Es gibt keine feste Steigung, wir haben daher sicherlich keine lineare Funktion. In diesem Fall geht es um eine Exponentialfunktion.

Vertiefen wir jetzt etwas mehr in den Eigenschaften dieser beiden Funktionen.

• Bei der linearen Funktion ist die Steigung s durch eine Änderungsrate angegeben. Wenn sie positiv ist, ist die Funktion steigend, wenn negativ fallend. Wenn noch eine Zahl in der Textaufgabe angegeben ist, sollte sie der Wert am Anfang sein, also der y-Achsenabschnitt A_y. Selbstverständlich müssen wir darauf aufpassen, dass die Einheiten übereinstimmen. Die Funktion ist dann:
  $\quad f(x)=s\,x+A_{y}$
  In unserem Beispiel:
  $\quad f(x)=30\,x+40$
• Bei der Exponentialfunktion ist die Sache teilweise etwas komplizierter. Das einfachste ist der y-Achsenabschnitt A_y. Er ist so viel wie der Anfangswert, genauso wie bei der linearen Funktion. In der Exponentialfunktion wird er allerdings addiert, sondern mit der Potenzzahl multipliziert. Die Hochzahl wird die unabhängige Variable sein. Die Basis der Potenz müssen wir erst berechnen. Sie ist der Wachstumsanteil W_A(als Zahl und nicht als Prozent) um 1 erhöht. In unserem Beispiel ist der Jahreswachstum 30% also 0,3. 0,3 um 1 erhöht ist 1,3. Diese Zahl wird die Basis sein:
  $\quad f(x)=A_{y}\ (W_{A}+1)^{x}$
  In unserem Beispiel:
  $\quad f(x)=40\cdot (0{,}3+1)^{x}=40\cdot 1{,}3^{x}$
  Ob die Exponentialfunktion steigend oder fallend ist, hängt sowohl vom Vorzeichen des Anfangswert als auch von der Basis der Potenz ab:
  • Wenn der Anfangswert positiv ist, ist die Darstellung der Funktion im ganzen Diagramm oberhalb der x-Acshe.
    • Ist die Basis mehr als 1, dann ist die Funktion steigend, mit Basis weniger als 1 ist sie fallend.
    • Ist die Basis weniger als 1, dann ist die Funktion fallend, mit Basis mehr als 1 ist sie steigend.
  • Wenn der Anfangswert negativ ist, ist die Darstellung der Funktion im ganzen Diagramm unterhalb der x-Acshe.
    • Ist die Basis mehr als 1, dann ist die Funktion fallend, mit Basis weniger als 1 ist sie steigend.
    • Ist die Basis weniger als 1, dann ist die Funktion steigend, mit Basis mehr als 1 ist sie fallend.
  • Trivialfall: Basis 1, dann ist ja die Funktion eine Konstante...

Noch drei Sachen:

• Im fünften Text ist das Wachstum das erste Jahr 30%. Der Baum wächst das erste Jahr 12 cm und 12 cm sind 30% von 40%. Das zweite Jahr ist allerdings das Wachstum in Prozent doch weniger. Der Baum ist jetzt 52 cm und wächst wieder 12 cm, was ca. 23% ist!
• Im vierten Text ist das Wachstum 130%, also 1,3. Das wird NICHT die Basis der Potenz in der Exponentialfunktion sein. Diese Zahl müssen wir erst um 1 erhöhen. Die Basis wird daher in diesem Fall 2,3 sein.
• Die Funktion im zweiten und dritten Text ist genau die gleiche Exponentialfunktion: $\quad f(x)=40\cdot 1{,}3^{x}$. Wenn der Wert jedes nächste das 1,3-fache des vorherigen Jahres ist, dann ist 0,3 (also 30%) mehr. Wenn die Aufgabe mit einem Vielfachen ausgedrückt wird, ist die Basis dieses Vielfache.

Periodische Funktionen und Polynomfunktionen

Wie der Name schon andeutet, sind periodische Funktionen Funktionen die sich wiederholen. Es gibt viele verschiedene periodische Funktionen, hier werden wir uns mit den trigonometrischen Funktionen Sinus, Kosinus und Tangens beschäftigen. Die allgemeine Formel für die Sinusfunktion ist:

$\ y=A_{0}\,\sin \left(\omega \,x\right)\quad$

$A_{0}\$ist die maximale Ablenkung, Amplitude genannt. $\omega \$ist die sogenannte Winkelfrequenz. Die wird mit Hilfe der Periode T berechnet:

$\omega ={\frac {1}{2\pi \,T}}$

Daher können wir die Formel auch in Bezug auf die Periode schreiben:

$\ \ y=A_{0}\sin {\frac {x}{2\pi \,T}}\quad$

Die Formeln für Kosinus und Sinus entsprechen der Formel für Sinus:

$\ \ y=A_{0}\cos {\frac {x}{2\pi \,T}}\quad$

$\ \ y=A_{0}\tan {\frac {x}{2\pi \,T}}\quad (x\neq {\frac {\pi }{2}}+2n\pi ,n\in \mathbb {N} )$

Teile einer Polynomfunktion können auch wie eine Sinusfunktion aussehen. Bei Textaufgaben ist es allerdings leicht zu erkennen, wann eine trigonometrische Funktion vorkommt. Das Wort Wiederholung oder Periode oder was ähnliches wird vorkommen. Von den Polynomfunktionen kommt die lineare Funktion oft vor, sie ist allerdings sehr leicht im Text von einer periodische Funktion zu erkennen. Die Polynomfunktionen von einem höheren Grad kommen in allen Wissenschaften oft vor. Sie werden in der Regel explizit erwähnt, entweder in der Angabe oder durch eine Formel.

Indirekte Proportionalität

Die indirekte Proportionalität kommt in der Wissenschaft oft in Formeln der Form $\textstyle a={\frac {b}{c}}$. In dieser Formel besteht eine indirekte Proportionalität zwischen a und c. Zwischen a und b wie auch zwischen b und c besteht eine direkte Proportionalität. Hier sind ein paar Beispiele aus der Physik:

• Dichte: $\rho ={\frac {m}{V}}$
  $\qquad$m steht für die Masse und V fürs Volumen. Bei gleicher Masse ist die Dichte desto kleiner, je größer das Volumen ist. Wenn 1 kg Wasser und 1 kg Eisen verglichen werden, wird das Wasser viel mehr Volumen haben, also eine kleine Dichte.
• Druck: $p={\frac {F}{A}}$
  $\qquad$F steht für die Kraft, A für die Fläche. Bei gleicher Kraft ist der Druck desto kleiner, je größer die Fläche ist. Wenn wir einen Nagel mit dem Kopf an die Wand einschlagen, wird er kaum oder gar nicht eindringen.
• Geschwindigkeit: $v={\frac {s}{t}}$
  $\qquad$s steht für die zurückgelegte Strecke, t für die Zeit. Bei gleicher Strecke ist die Geschwindigkeit desto kleiner, je größer die Zeit ist. Wenn wir mehr Zeit brauchen, sind wir langsamer.
• Stromstärke: $I={\frac {U}{R}}$
  $\qquad$U steht für die Spannung, R für den Widerstand. Bei gleicher Spannung ist die Stromstärke desto kleiner, je größer der Widerstand ist. Der elektrische Widerstand wirkt ja gegen den elektrischen Strom.

Logarithmusfunktion

Die Logarithmusfunktion ist die Umkehrfunktion der Exponentialfunktion. Sie wird nur für x>0 definiert. Ihre Wertebereich ist allerdings die ganzen reellen Zahlen. Logarithmus wird bei der Einheiten von verschiedenen Größen benutzt, die sich exponentiell ändern. Solche logarithmische Skalas sind z.B. die "Lautstärke" (logarithmische Einheit: Dezibel, dB), der saure oder basische Charakter einer wässrigen Lösung (logarithmische Größe: pH-Wert), die stärke eines Erdbebens (logarithmische Richterskala), die Helligkeit von Sternen usw.. In der Regel wird es explizit erwähnt, dass es gerade um eine logarithmische Größe geht.