MathemaTriX ⋅ Theorie. Grundniveau 2

Hoch

STOPP PUSHBACKS • FREE ASSANGE • FRIEDEN AUF DER WELT ${\color {white}\mathbf {MATHE} \mu \alpha T\mathbb {R} ix}$ DEINE FESTE BEGLEITERIN FÜR DIE SCHULMATHEMATIK EINFACH UND VERSTÄNDLICH GRATIS!* MIT MEHR ALS 200 THEORIE- UND AUFGABEN-ERKLÄRUNGS VIDEOS! Mathe lernen ist wie Fahrradfahren lernen: Du kannst es dir stundenlang erklären lassen, du wirst nie fahren können, wenn du nicht selber zu fahren probierst.

Inhalt Ein-Aus- klappen

AUFGABEN

Grundniveau 1 Grundniveau 2 Vertiefend 1 Vertiefend 2 Experten 1 Experten 2

Grundrechenarten und Bruchrechnungen

Division

Der Haupt(vor)gang der Division

Dividend mit Nullen am Ende

Wenn der Dividend Nullen am Ende hat, kann man sich ein paar Schritte sparen. Schauen wir ein Beispiel:

Schauen wir jetzt, wie die richtige Regel lautet:

Man kann also die Division aufhören und die restlichen Nullen erst dann schreiben, wenn der Rest zum ersten Mal Null ist!

Wenn der Divisor auch Nullen am Ende hat, kann man vom beiden Divisor und Dividend so viele Nullen streichen, wie die Nullen des Divisors und erst dann die Division durchführen. Beispielsweise ist 7910000:400=79100:4 (in beiden Fällen ist das Ergebnis 19775). Warum das so ist, kann man erst verstehen, wenn man das Kürzen von Brüchen gelernt hat, daher lernen wir es hier zunächst einmal einfach so, als Regel...

Null in der Mitte des Ergebnisses

Null am Anfang des Ergebnisses

Dividend mit Komma (einfach)

Was ist, wenn der Divident schon Nachkommastellen hat? In diesem Fall wird die Division, wie wir sie bisher gelernt haben, mit einer Änderung durchgeführt:   Wenn zur nächsten Ziffer nach dem Komma gesprungen werden muss, dann muss man erst ein Komma im Ergebnis schreiben.   In unserem Fall ist es nicht wenn man die Ziffer 9 im Dividend erreicht. Das Komma muss geschrieben werden, erst bevor man die nächste Ziffer nach dem Komma (hier die Ziffer 2) runter bringen muss. Erst dann schreibt man das Komma und dann macht man die Rechnung (12:3) und dann schreibt man das Ergebnis dieser Rechnung (4) nach dem Komma. Es gibt kein anderes Komma in der Zahl (also auf gar keinen Fall irgendwo ein zweites Komma schreiben). Eine Bemerkung noch: Den letzten Rest haben wird hier mit (R) in Klammern geschrieben. Den Begriff Rest benutzt man eigentlich bei ganzzahligen Divisionen (mit Zahlen ohne Nachkommastellen). 0 ist hier der Teilrest der letzten Teildivision (12:4=3 R 0). Wenn bei einer Division mit Nachkommastellen im Ergebnis Teilrest 0 hat, kann man mit der Division aufhören. Das ist allerdings nur selten der Fall, wie wir gleich lernen werden.

Divisor mit Komma (einfach)

Was ist, wenn der Divisor Nachkommastellen hat, wie zum Beispiel in 236,2875:0,5? In diesem Fall wird das Komma sowohl im Divisor als auch im Dividenden so oft nach rechts verschoben, bis der Divisor keine (notwendige) Kommastelle mehr hat. In unserem Beispiel, wenn das Komma im Divisor (0,5) ein Mal nach rechts verschoben wird, bekommt man die Zahl 5, die keine Nachkommastellen hat. Das Komma wird dann auch im Dividenden (236,2875) ein Mal nach rechts verschoben (also der neue Dividend wird 2362,875 sein). Mit diesen neuen Zahlen kann man die Division ganz normal fortführen, wie im Bild am Rand. Der Prozess ist also:

Komma in Divisor verschieben, bis er keine Nachkommastelle hat:$0{\color {red},}5\ \to \ 0\underbrace {_{\color {red}{\xcancel {,}}}5{,}} _{1\ mal}...\ \to \ 5$ → Komma genauso oft (hier einmal) im Divident verschieben: $236{\color {red},}2875\ \to \ 236\underbrace {_{\color {red}{\xcancel {,}}}2{,}} _{1\ mal}875\ \to \ 2362{,}875\$ → Division mit den neuen Zahlen durchführen (siehe Bild)

Was ist, wenn der Dividend keine Nachkommastellen hat, beispielsweise 205:0,04?

In diesem Fall denkt man, dass ein Komma am Ende des Dividenden steht, und schreibt so viele Nullen wie notwendig nach dem Komma: 205=205,00 (allerdings gilt auch 205=205,00000 und so weiter). Dann wird der Vorgang wie vorher durchgeführt:

Komma im Divisor verschieben: $0{\color {red},}04\to 0\underbrace {_{\color {red}{\xcancel {,}}}04{,}} _{2\ mal}\to 4$ → Komma genauso oft (hier zweimal) im Dividenden verschieben, bis er keine Nachkommastelle hat:$205{\color {red},}00\ \to \ 205\underbrace {_{\color {red}{\xcancel {,}}}00{,}} _{2\ mal}...\ \to \ 20500\$ → Division mit den neuen Zahlen durchführen (siehe Bild)

Ein letztes Beispiel: 205:0,0004. Hier muss man das Komma sogar viermal verschieben:

Komma im Divisor verschieben: $0{\color {red},}0004\ \to \ 0\underbrace {_{\color {red}{\xcancel {,}}}0004{,}} _{4\ mal}...\ \to \ 4$\ → Komma genauso oft (hier zweimal) im Dividenden verschieben, bis er keine Nachkommastelle hat:$205{\color {red},}000000\ \to \ 205\underbrace {_{\color {red}{\xcancel {,}}}0000{,}} _{4\ mal}...\ \to \ 2050000\$ → Division mit den neuen Zahlen durchführen (siehe Bild)

Dividend ohne Komma, Ergebnis mit Komma (mit Null Rest)

Was ist, wenn die Division nicht genau aufgeht. wie zum Beispiel in 935:4?

		In diesem Beispiel ist es klar, dass ein Rest geben wird. Die Division kann man aber doch weiter fortsetzen, wie wir bei Zahlen mit Nachkommastellen schon gelernt haben. In diesem Beispiel können wir 935 als Zahl mit Nachkommastellen schreiben (freilich alle Nullen), wie wir schon gelernt haben: 935=935,00... Dann führen wir die Division in der gewöhnlichen Weise durch (siehe Bild). Allerdings kann man in diesem Fall die Nullen im Dividenden gar nicht schreiben, wie im Bild links unten zu sehen ist. In diesem Fall werden Nullen weiter unten geschrieben, bis der Teilrest irgendwann Null wird. Vorsicht aber: Wenn der Dividend zu Ende ist und die erste Null dazu benutzt wird, muss man ein Komma im Ergebnis schreiben!
			Diesen Prozess (weiter Nullen schreiben) kann man auch benutzen, wenn der Dividend zwar schon Nachkommastellen hat, der Teilrest am Ende aber doch nicht Null ist. In diesem Fall schreibt man Nullen weiter, selbstverständlich ohne ein zweites Komma im Ergebnis zu schreiben!

Dividend ohne Komma, Ergebnis mit Komma (periodisch)

Bisher war es fast immer in den Beispielen so, dass der Teilrest am Ende Null war. Das war kein Zufall, die Beispiele wurden einfach so gewählt, damit sie verständlicher sind. In der Regel ist der Teilrest keine genaue Zahl. Probieren wir es mit dem folgenden Beispiel:

Wie wir schon gelernt haben, wenn man das Ende der Zahl erreicht und keine Ziffer mehr hat, kann man doch die Division weiterführen: erst eine Null im Ergebnis schreiben und dann eine Null jedes Mal dazuschreiben, bis irgendwann der Teilrest Null wird. In unserem Fall hier passiert so etwas aber nicht. Wie man sieht, wiederholen sich die Zahlen 2 und 7 immer wieder und, wie man hoffentlich versteht, das wird immer so bleiben. Wir haben hier diese Wiederholung mit verschiedenen Farben dargestellt. Die wiederholte Zifferreihenfolge nennt man Periode. Man sagt, dass das Ergebnis von 938 durch 11 gleich 85 Komma 27 periodisch ist. Man bezeichnet die Periode mit einem Strich über der Zifferreihenfolge (oder mit einem Punkt, wenn es nur eine Ziffer ist). Man schreibt also: $938:11=85{,}{\overline {27}}$

Man braucht die Division nicht weiterführen. Wann kann man aber genau damit aufhören? Wenn man schon mit Null hinzufügen angefangen hat (passiert hier bei der letzten Ziffer der Zahl 938) und der gleiche Teildividend vorkommt, dann kann man aufhören, wie im Bild hier

Kombinationen

Punktrechnungen mit 10, 100, 1000 und so weiter

• Wenn man eine Zahl mit 10, 100, 1000 und so weiter multipliziert, dann verschiebt sich das Komma der Zahl einfach nach rechts (die Zahl wird größer), so oft, wie es Nullen gibt:

3,45 · 10 = 34,5    (Mal 10; in 10 gibt es eine Null, Komma wird einmal nach rechts verschoben)

54 · 10000 = 54,0000 · 10000 = 540000    (Mal 10000; in 10000 gibt es vier Nullen, Komma wird 4 Mal nach rechts verschoben; Allerdings gibt es kein Komma am Ende der Zahl 54; man schreibt ein Komma am Ende der Zahl und dazu nach dem Komma so viele Nullen, wie man will, und schiebt dann das Komma)

0,008 · 100 = 0,8    (Mal 100; in 100 gibt es 2 Nullen, Komma wird 2 Mal nach rechts verschoben)

• Wenn man eine Zahl mit 10, 100, 1000 und so weiter dividiert, dann verschiebt sich das Komma der Zahl einfach nach links (die Zahl wird kleiner), so oft, wie es Nullen gibt:

3,45:10 = 0,345    (Durch 10; in 10 gibt es eine Null, Komma wird einmal nach links verschoben; allerdings gibt es links vor 3,4 keine Null, man schreibt also links von der Zahl so viele Nullen, wie man will, und schiebt dann das Komma)

54:10000 = 0,0054    (Durch 10000; in 10000 gibt es 4 Nullen, Komma wird 4 Mal nach links verschoben; allerdings gibt es links vor 54 kein Komma, man schreibt also links von der Zahl ein Komma und so viele Nullen, wie man will, und schiebt dann das Komma)

0,008:100 = 0,00008    (Durch 10; in 10 gibt es eine Null, Komma wird 1 Mal nach links verschoben; allerdings muss man zuerst am Ende der Kommazahl weitere Nullen schreiben)

900000:100 = 9000,00 = 9000    (Durch 100; in 100 gibt es 2 Nullen, Komma wird 2 Mal nach links verschoben; da es kein Komma am Ende der Zahl gibt, muss man erst das Komma schreiben)

Vorrang der Rechenarten

Vorrang mit Klammern in Klammern

$5+6\cdot 7-55:$	$(21-4\cdot 8)$	$-3\cdot$	$[7+$	$2\cdot (6\cdot 3-39:3)]$	$-57$	$=$	In der großen Klammer hat die kleine Klammer Vorrang (Klammer vor Punkt vor Strich)
	↓		$7+$	$2\cdot (18-13)$			In der kleinen Klammer erst Punkt und dann Strichrechnung
	↓		7   +   $2\cdot 5$				Kleine Klammer durch ihr Ergebnis in der großen Klammer ersetzen
	$21-32$		$7$   +   $10$				In den verbliebenen Klammern erst Punkt- und dann Strichrechnungen
	$-11$		$17$				Man kann also die Klammer durch das jeweilige Ergebnis ersetzen

${\begin{array}{c}5+6\cdot 7-55:{\cancelto {21-32=-11}{(21-4\cdot 8)}}-3\cdot \underbrace {{\Bigl [}7+{\color {blue}\overbrace {2\cdot {\color {red}({\cancelto {18}{6\cdot 3}}-{\cancelto {13}{39:3)}}}} ^{2\cdot {\color {red}{\cancelto {5}{(18-13)}}}=\ \ 10}{\color {black}{\Bigr ]}}}} _{7+{\color {blue}10}=17}-57=\\\\5+{\cancelto {42}{6\cdot 7}}-{\cancelto {-5}{55:(-11)}}+{\cancelto {51}{3\cdot 17}}-57\\\\5+42+5-51-57=-56\end{array}}$

(an Plus-Minus Regeln halten!)

(an Plus-Minus Regeln halten!)

Bruchrechnungen

Gemischte Zahlen

Eine gemischte Zahl besteht aus einer natürlichen Zahl und einem echten Bruch:  $\textstyle 6{\frac {4}{5}}$

Gemischte Zahl in unechten Bruch umwandeln

Um eine gemischte Zahl in einen Bruch umzuwandeln, multipliziert man die natürliche Zahl mit dem Nenner des Bruches und addiert das Ergebnis zum Zähler. Das neue Ergebnis ist dann der Zähler des neuen Bruches, der Nenner bleibt der gleiche:

$6{\frac {4}{5}}={\frac {6\cdot 5+4}{5}}={\frac {34}{5}}$

Unechten Bruch in gemischte Zahl umwandeln

Um einen unechten Bruch in eine gemischte Zahl umzuwandeln, dividiert man den Zähler mit dem Nenner (ohne Nachkommastellen). Das Ergebnis der Division ist der „Zahlteil“ der gemischten Zahl, der Rest ist der Zähler des „Bruchteils“, der Nenner bleibt der gleiche:

    (siehe Division)

Folgendes Beispiel setzt die Anwendung eines Taschenrechners voraus:

${\frac {1895}{23}}=?\qquad \qquad {\begin{array}{rrl}1895&:{\boldsymbol {2}}3&={\color {red}{\boldsymbol {8}}2}{,}\dots \\\ {\color {red}{\boldsymbol {8}}2}&\cdot \ {\boldsymbol {2}}3&={\color {YellowOrange}1886}\\1895&-{\color {YellowOrange}1886}&={\color {blue}{\boldsymbol {9}}}\end{array}}\qquad \qquad {\text{ also }}\quad {\frac {1895}{23}}={\color {red}{\boldsymbol {8}}2}{\frac {\color {blue}{\boldsymbol {9}}}{{\boldsymbol {2}}3}}$

Eintausend-achthundert-fünfundneunzig Dreiundzwanzigstel sind so viel wie zweiundachtzig Ganzen und neun Zwanzigstel.

Das Ergebnis der Division 1895:23 mit dem Taschenrechner ist 82 Komma einige Nachkommastellen. Dieses Ergebnis ohne Nachkommastellen (82) wird die ganze Zahl in der gemischte Zahl sein. Das Ergebnis ohne Nachkommastellen (82) wird dann mit den Nenner (hier 23) multipliziert: 82·23=1886. Dieses Produkt (1886) wird dann vom Zähler (1895) subtrahiert: 1895-1886=9. Diese Differenz (9) stellt den neuen Zähler in der gemischten Zahl dar, der Nenner bleibt unverändert (23).

Der Prozess also mit Anwendung eines Taschenrechners könnte so aussehen:

${\frac {1895}{23}}=?$

Division mit dem Taschenrechner durchführen (1895:23=82 Komma einige Nachkommastellen). Ergebnis nach dem Gleichzeichen samt Bruchstrich und Nenner (23) schreiben:

${\frac {\color {red}1895}{23}}={\color {red}81}{\frac {?}{\color {red}23}}$

Die Diagonale (hier oben mit roten Zahlen markiert:) Zähler links (1895) minus ganze Zahl (81) mal Nenner rechts (23) wie im folgenden benutzen und Ergebnis in den Zähler rechts schreiben:

$1895-81\cdot 23={\color {red}9}$

also

${\frac {1895}{23}}=81{\frac {\color {red}9}{23}}$

Erweitern und Kürzen

Erweitern

Erweitern ist, wenn man sowohl Zähler als auch Nenner eines Bruches mit der gleichen Zahl multipliziert. Der neue Bruch bleibt dann doch gleich:

${\frac {4}{7}}={\frac {4\cdot 5}{7\cdot 5}}={\frac {20}{35}}$

Bruchkürzen

Kürzen ist, wenn man sowohl Zähler als auch Nenner eines Bruches mit der gleichen Zahl dividiert. Der neue Bruch bleibt dann doch gleich:

${\frac {12}{8}}={\frac {12:4}{8:4}}={\frac {3}{2}}$

In all diesen Fällen arbeitet man mit natürlichen Zahlen (positive Zahlen ohne Komma).

Erklärung des Erweiterns und des Kürzens

7 2         5

Vergleichen wir die beiden Bilder. Im ersten Bild wird das Ganze im $5$ geteilt, zwei Teile davon werden dunkel dargestellt. Das ist also eine Repräsentation des Bruches $\textstyle \ {\frac {2}{5}}$. Im zweiten Bild wird das Ganze nicht nur in $5$ (waagerecht) sondern auch in $7$ (senkrecht) geteilt. Dadurch entstehen im Ganzen $\ 5\cdot 7=35\$ kleine "Quadrate". Jedes kleines Quadrat ist daher $\textstyle \ {\frac {1}{35}}\$ des Ganzen. Die dunkle Region ($\textstyle \ {\frac {2}{5}}$) beinhaltet allerdings $\ 2\cdot 7=14\$ solche "Quadrate" also $\textstyle \ {\frac {14}{35}}$. Man folgt daraus, dass $\textstyle \ {\frac {2}{5}}={\frac {14}{35}}\$ ist. Man hat in diesem Fall sowohl den Zähler als auch den Nenner mit der gleichen Zahl (hier $7$) multipliziert: $\textstyle \ {\frac {2}{5}}={\frac {2\cdot 7}{5\cdot 7}}={\frac {14}{35}}\$. Diesen Prozess nennt man erweitern.

Der Gegenprozess ist dann das Kürzen. Im ersten Bild wird das Ganze in $5$ Zeilen und $7$ Spalten also insgesamt in $\ 7\cdot 5=35\$ kleine "Quadrate" geteilt (das könnte selbstverständlich eine andere Austeilung sein). Die blaue Region ist $\ 3\cdot 5=15\$ solche Teile, also $\textstyle \ {\frac {15}{35}}$. Wenn man jetzt die waagerechte Austeilung (in Fünf Zeilen geteilt) entfernt (zweites Bild), dann ist das ganze nur in $7$ (Spalten) geteilt, wobei jetzt die blaue Region $3$ Spalten davon ist also $\textstyle \ {\frac {3}{7}}$. In diesem Fall haben wir sowohl Zähler als auch Nenner durch die gleichen Zahl (hier $5$) dividiert: $\textstyle \ {\frac {15}{35}}={\frac {15:5}{35:5}}={\frac {3}{7}}$. Diesen Prozess nennt man kürzen.

Arbeiten mit ganzen Zahlen und Brüchen

Die Rechnungen mit ganzen Zahlen und Brüchen sind leicht, wenn man den vorherigen Stoff schon verstanden hat.

Strichrechnungen

Um eine ganze Zahl in einen Bruch umzuwandeln, reicht das Produkt der ganzen Zahl mit dem Nenner des Bruches als Zähler im Bruch zu schreiben:

$3={\frac {5\cdot 3}{5}}={\frac {15}{5}}$

Das sollte schon klar sein, da 15:5=3 ist... Um das zu veranschaulichen reicht es 3 ganzen jeweils in 5 geteilt nebeneinander zu stellen. Dann werden genau 3×5=15 Fünftel aufgezählt!

Hat man einmal die ganze Zahl als (gleichnamigen) Bruch, kann man auch eine entsprechende Strichrechnung durchführen, z.B.:

$3+{\frac {2}{7}}={\frac {3\cdot 7}{7}}+{\frac {2}{7}}={\frac {23}{7}}\qquad \qquad 5-{\frac {5}{9}}={\frac {5\cdot 9}{9}}-{\frac {5}{9}}={\frac {40}{9}}$

Punktrechnungen

Genau so leicht ist die entsprechende Multiplikation. Im ersten Bild werden zwei Fünftel dargestellt und diese werden 4 mal nebeneinander dargestellt. Insgesamt sind es daher 4×2=8 Fünftel.

$4\cdot {\frac {2}{5}}={\frac {4\cdot 2}{5}}={\frac {8}{5}}$

Um das Produkt einer ganzen Zahl mit einem Bruch zu berechnen, reicht es das Produkt der ganzen Zahl mit dem Zähler des Bruches in einem neuen gleichnamigen Bruch zu schreiben.

Die Division ist dann auch leicht:

$4:{\frac {3}{13}}=4\cdot {\frac {13}{3}}={\frac {52}{3}}\ (=17{\frac {1}{3}})$

Um den Quotient einer ganzen Zahl durch einem Bruch zu berechnen, reicht es das Produkt der ganzen Zahl mit dem Kehrwert des Bruches zu berechnen.

Textaufgaben zu den Bruchrechnungen

Die Textaufgaben mit Bruchrechnungen werden i.d.R. leicht in die mathematische Sprache umgewandelt:

In einem Staat mit 8,46 Millionen Einwohner trinkt jeder Einwohner durchschnittlich vier Neuntel Liter Milch täglich.

1. 1. Wie viel Liter werden dann täglich konsumiert?
   2. Der Gewinn für die Eigentümer ist 0,8¢/Liter Milch. Wie viel ist der tägliche Gewinn? Finden Sie ihn gerechtfertigt?
2. Im einem anderen Staat gibt es 4 Supermarktketten. Zusammen gewinnen die Eigentümer 105000€ täglich. Eigentümer A bekommt zwei Fünftel des Gewinns, Eigentümer B ein Drittel und den Rest teilen die anderen zwei Eigentümer C und D. Wie viel gewinnt täglich jeder Eigentümer? Finden Sie den Gewinn gerechtfertigt?

Aufgabe a lässt sich leicht berechnen:

$8{,}46\cdot {\frac {4}{9}}=3,76\ {\text{(Millionen Liter)}}$

Da der Gewinn pro Liter 0,8¢ ist, soll man 0,8 mit 3,76 Mil. multiplizieren (dann hat man ¢) und dann durch 100 dividieren (dann hat man €):

$3{,}76\cdot {\frac {0{,}8\cdot 1000000}{100}}=30080\ {\text{(€)}}$

Ob dieser Gewinn gerechtfertigt ist, soll jeder für sich entscheiden (die Eigentümer werden ihn sicherlich gerechtfertigt finden, sonst würden sie ihn nicht machen...).

Aufgabe b ist ebenfalls nicht besonders schwer:

Eigentümer A: $105000\cdot {\frac {2}{5}}=44000\ {\text{(€)}}$

Eigentümer B: $105000\cdot {\frac {1}{3}}=35000\ {\text{(€)}}$

Eigentümer C und D teilen den Rest: $105000-44000-35000=26000\qquad 26000:2=13000\ {\text{(€ jeweils für Eigentümer C und D)}}$

Primfaktorzerlegung

Was sind Primzahlen

Primzahlen sind die natürlichen Zahlen (Zahlen ohne Komma und Minus), die nur durch 1 und sich selbst geteilt werden können. (teilbar: dividieren, ohne dass eine Kommazahl entsteht)

	2	3	4	5	6	7	8	9	10	11	12	13
geht auch durch			2		2 3		2 4	3	2 5		2 3 4 6
Prim- zahl	✔	✔	✘	✔	✘	✔	✘	✘	✘	✔	✘	✔

Z.B.:

2 ist nur durch 2 und 1 teilbar und daher eine Primzahl.

3 ist nur durch 3 und 1 teilbar und daher eine Primzahl.

4 ist nur durch 4 und 1, aber auch durch 2 teilbar und daher keine Primzahl.

5 ist nur durch 5 und 1 teilbar und daher eine Primzahl.

6 ist nur durch 6 und 1, aber auch durch 2 und 3 teilbar und daher keine Primzahl.

usw.

Was bedeutet in diesen Sätzen "teilbar"? Eine Zahl ist durch eine andere Zahl teilbar, wenn das Ergebnis der Division keine Nachkommastellen enthält.

Nehmen wir die Zahl 5.

$5:1=5$

$5:2=2{,}5$

$5:3=1{,}{\dot {3}}$ 

$5:4=1{,}25$

$5:5=1$

Dividiert man 5 durch jede größere natürliche Zahl (also: 6,7,8…), erhält man als Ergebnis eine Kommazahl kleiner als 1 (also Null-Komma-irgendwas). Beispielsweise:

$5:6=0{,}8{\dot {3}}$

Teilbar ist die Zahl 5 also nur durch eins (5:1=5) und sich selbst (5:5=1). Da bei unserem Beispiel alle anderen Ergebnisse ein Komma enthalten ist die Zahl 5 eine Primzahl.

Für 6 hingegen ist das nicht der Fall. 6 ist selbstverständlich durch 1 und 6 teilbar, aber eben auch durch 2 (6:2=3) und durch 3 (6:3=2). Daher ist 6 KEINE Primzahl.

Die ersten Primzahlen sind also 2, 3, 5, 7, 11, 13, 17, 19, 23 ...

Faktor ist ein Teil einer Multiplikation.

Primfaktorzerlegung (PFZ) bedeutet daher, eine Zahl als Produkt von Primzahlen auszudrücken (die dann Faktoren sind; Primzahlen die auch Faktoren sind, nennt man Primfaktoren; wenn man eine Zahl in Primfaktoren zerlegt, hat man die PFZ).

Vorgangsweise

Nehmen wir die Zahl 7800. Wir versuchen sie durch die Primzahlen der Reihe nach und soweit es jedes Mal geht zu dividieren. Die erste Primzahl ist 2 7800 : 2 = 3900. Geht es weiter durch 2? Ja! 3900 : 2 = 1950. Geht es noch weiter? Ja! 1950:2=975. Weiter durch 2 geht es aber nicht.

Probieren wir dann durch 3. Geht es? Ja! 975:3=325. Geht es weiter durch 3? Nein! (325:3 = 108,33

Probieren wir die nächste Primzahl: 325:5=65. Das geht nochmal: 65:5=13.

Die nächsten Primzahlen sind 7 und 11, da geht es nicht. Es geht wieder durch 13 13:13=1.

Hier sind wir fertig. Wir haben 7800 drei mal durch 2, ein mal durch 3, zwei mal durch 5 und ein mal durch 13 dividiert und dann war das Ergebnis 1. Es gilt daher: 7800:2:2:2:3:5:5:13=1 und umgekehrt (Gegenrechnung) 7800=2·2·2·3·5·5·13.

Schreibweise

Anwendungen

Kürzen mit Primfaktorzerlegung

Wir haben schon das Kürzen von Brüchen gesehen:

${\frac {45}{35}}={\frac {45:5}{35:5}}={\frac {9}{7}}$

Hier sieht man sofort, dass man sowohl den Zähler als auch den Nenner durch 5 teilen kann. Was ist aber, wenn man große Zahlen hat? In diesem Fall ist es besser, die PFZ der Zahlen erst durchzuführen:

${\frac {6664}{8820}}=$?

6664	2
3332	2
1666	2
833	7
119	7
17	17
1

8820	2
4410	2
2205	3
735	3
245	5
49	7
7	7
1

Man schreibt Zähler und Nenner als Produkt von Primzahlen und kürzt den Bruch (also Primzahlen, die oben und unten vorkommen, werden gestrichen)

${\frac {6664}{8820}}={\frac {{\cancel {2}}\cdot {\cancel {2}}\cdot 2\cdot {\cancel {7}}\cdot {\cancel {7}}\cdot 17}{{\cancel {2}}\cdot {\cancel {2}}\cdot 3\cdot 3\cdot 5\cdot {\cancel {7}}\cdot {\cancel {7}}}}={\frac {2\cdot 17}{3\cdot 3\cdot 5}}={\frac {34}{45}}$

Teilbarkeit

Bei der PFZ haben wir immer probiert, eine Zahl durch einer Primzahl zu teilen. Kann man wissen, ob das geht, ohne die Division zu machen? Für viele Primzahlen geht das. Die einfachsten Regel sind für 2, 3 und 5:

Durch 2

Wenn eine Zahl in 0, 2, 4, 6, 8 endet (gerade Zahl), dann ist sie durch 2 teilbar:

2004 und 33338 sind durch 2 teilbar: 2004 endet in 4, 33338 in 8.

2005 oder 486863 sind nicht durch 2 teilbar: 2005 endet in 5 und 486863 in 3.

Durch 3

Wenn eine Zahl auf 0 oder 5 endet, dann ist sie durch 5 teilbar:

409 und 85923 sind nicht durch 5 teilbar (sie enden auf 9 bzw. auf 3).

490 und 89235 hingegen sind durch 5 teilbar (sie enden auf 0 bzw. auf 5)

Durch 3 (oder 9)

Wenn die Summe der Ziffern einer Zahl durch 3 (bzw. 9) teilbar ist, dann ist die Zahl auch durch 3 (bzw. 9) teilbar:

135 ist durch 3 teilbar: 1+3+5=9 (9:3=3, die Summe der Ziffer 9 ist durch 3 teilbar, also auch die Zahl 135). Sie ist auch durch 9 teilbar (9 ist durch 9 teilbar)

3564825 ist durch 3 teilbar: 3+5+6+4+8+2+5=33, 33:3=11. 33 ist durch 3 teilbar, daher auch 3564825. 33 ist aber nicht durch 9 teilbar, also 3564825 auch nicht.

3564824 ist nicht durch 3 oder 9 teilbar: 3+5+6+4+8+2+4=32, 32 ist nicht durch 3 oder 9 teilbar.

35644825 ist sowohl durch 3 als auch durch 9 teilbar: 3+5+6+4+4+8+2+4=32, 32 ist durch 3 und 9 teilbar.

Durch 7

Um zu verstehen, wie man herausfindet, ob eine Zahl durch 7 teilbar ist, machen wir ein Beispiel. Nehmen wir die Zahl 4445. Man teilt sie in Teilen am Ende anfangend und jedes mal zwei Ziffern nehmend: 44 | 45. Wenn die Summe vom doppelten des linken Teils und vom rechten Teil durch 7 teilbar ist, dann ist es auch die ganze Zahl: 2·44+45=133. Wenn man nicht sofort sehen kann, ob 133 durch 7 teilbar ist, kann man den Vorgang wiederholen: 133 in zwei Teilen → 1 | 33 2·1+33=35. 35 ist durch 7 teilbar, daher auch 133 und 4445. Bei größeren Zahlen muss man den Vorgang wiederholen. Probieren wir es mit einer größeren Zahl: 437381 43 | 73 | 81 2·43+73=159 2·159+81=399 → 3 | 99 3·2+99= 105 → 1 | 05 1·2+05=7 7 ist offenbar durch 7 teilbar also auch 105 und 399 und 437381! Man muss sagen: diese Regel kann doch länger dauern, als die eigentliche Division zu machen...

Durch 11

Für die Teilbarkeit durch 11 gibt es eine Regel: wenn die Differenz der alternierenden Summen der Ziffern einer Zahl 0 oder durch 11 teilbar ist, dann ist die Zahl auch durch 11 teilbar. Beispiel: 981607. Man nimmt die Summe der ersten, der dritten und der fünften (alternierend) Ziffer 9+1+0= 10 und die Summe der zweiten, der vierten und der sechsten (alternierend) Ziffer 8+6+7=21. Die Differenz der beiden Summen ist 21-10=11, was durch 11 teilbar ist. Daher ist auch 981607 durch 11 teilbar!

Schluss und Prozentrechnung

Indirekte Proportionalität

In der direkten Proportionalität haben wir gesehen, wie man vorgeht, wenn zwei Größen gleichzeitig größer oder kleiner werden. Wenn man mehr von einer Ware kaufen will, dann muss man auch mehr bezahlen. Wenn man weniger kaufen will, dann zahlt man auch weniger. Wenn man mehr kg von einem Stoff hat, dann hat man auch mehr Liter des Stoffes. Es gibt aber auch Fälle, bei denen die Erhöhung einer Größe die Verminderung einer anderen bedeutet:

• 3 Arbeiter brauchen 15 Stunden, um ein Haus mit Fliesen zu verlegen. Wie viel Zeit brauchen dann 5 Arbeiter?

1 Arbeiter würde in diesem Fall mehr Zeit brauchen. Es gibt für einen Arbeiter viel mehr Boden zu verlegen, wenn er alleine arbeitet. Also weniger Arbeiter brauchen mehr Zeit. Das ist also KEINE direkte sondern eine indirekte Proportionalität.

Wie bei der direkten Proportionalität schreibt man hier auch die gegebenen Größen nebeneinander und gleiche Größen untereinander.

${\begin{matrix}{\text{3 Arbeiter}}\\{\text{5 Arbeiter}}\end{matrix}}\quad {\begin{matrix}\cdots \cdots \\\cdots \cdots \end{matrix}}\quad {\begin{matrix}{\text{15 Stunden}}\\x\end{matrix}}$

In diesem Fall multipliziert man mit der Zahl gerade gegenüber (und NICHT schräg gegenüber, wie in der direkten Proportionalität) und dividiert dann durch die andere Zahl:

${\begin{matrix}{\text{3 Arbeiter}}\\\downarrow :\\{\text{5 Arbeiter}}\end{matrix}}\quad {\begin{matrix}{\dot {\longleftarrow }}\\\\{}\end{matrix}}\quad {\begin{matrix}{\text{15 Stunden}}\\{}\\x\end{matrix}}$      $\left({\frac {15\cdot 3}{5}}\right)\qquad x=9\ {\text{Stunden}}\ \$  (die die Arbeiter in diesem Fall brauchen).

Um zu unterscheiden, ob man eine direkte oder indirekte Proportionalität hat, muss man schon die Sprache und die Zusammenhänge gut verstehen können!

Vergleich direkter und indirekter Proportionalität

Wie wir in den vorherigen Absätzen gesehen haben, muss man sowohl bei der direkten als auch bei der indirekten Proportionalität die Daten, die (in der Regel in einem Satz) in Verbindung gebracht werden, in einer Zeile nebeneinander schreiben (hier bei der direkten Proportionalität 3,5 Liter und 14,7 kg und bei der indirekten 3 Arbeiter und 15 Stunden) und dafür sorgen, dass in jeder Spalte die gleichen Einheiten geschrieben werden.

${\begin{matrix}{\text{3,5 Liter}}\\\\{\text{0,0175 Lit}}\end{matrix}}\quad {\begin{matrix}\cdots \cdots \\{}\\\cdots \cdots \end{matrix}}\quad {\begin{matrix}{\text{14,7 kg}}\\{}\\x\end{matrix}}$

${\begin{matrix}{\text{3 Arbeiter}}\\{}\\{\text{5 Arbeiter}}\end{matrix}}\quad {\begin{matrix}\cdots \cdots \\\\\cdots \cdots \end{matrix}}\quad {\begin{matrix}{\text{15 Stunden}}\\{}\\x\end{matrix}}$

Bei beiden Vorgängen fängt man dann mit der Zahl an, die nur an der gleichen Spalte mit x steht (hier 14,7 kg in der direkten und 15 Stunden in der indirekten Proporionalität). Der Unterschied ist: bei der direkten Proportionalität geht man dann schräg, bei der indirekten gerade gegenüber, und multiplitiert mit dieser Zahl (hier 0,0175 Liter in der direkten und 3 Arbeiter in der indirekten Proporionalität). Am Ende dividiert man in beiden Fällen mit der übriggebliebenen Zahl (hier 3,5 Liter in der direkten und 5 Arbeiter in der indirekten Proporionalität).

${\begin{matrix}{\text{3,5 Liter}}\\\uparrow :\\{\text{0,0175 Lit}}\end{matrix}}\quad {\begin{matrix}\cdots \cdots \\\swarrow \cdot \\\cdots \cdots \end{matrix}}\quad {\begin{matrix}{\text{14,7 kg}}\\{}\\x\end{matrix}}$

${\begin{matrix}{\text{3 Arbeiter}}\\\downarrow :\\{\text{5 Arbeiter}}\end{matrix}}\quad {\begin{matrix}{\dot {\longleftarrow }}\\\\{}\end{matrix}}\quad {\begin{matrix}{\text{15 Stunden}}\\{}\\x\end{matrix}}$

Wie kann man verstehen, ob eine direkte oder eine indirekte Proportionalität vorliegt?

Nehmen wir den folgenden Bruch b:  $\textstyle b={\frac {z}{n}}$,  wobei z der Zähler und n der Nenner ist. Wenn z=20 und n=5 ist, dann ist der Bruch b=4: $\textstyle b={\frac {20}{5}}=4$. Wenn jetzt der Zähler z größer wird (z.B. z=30), dann wird der ganze Bruch b auch größer:  $\textstyle b={\frac {30}{5}}=6$. Wenn der Zählerz kleiner wird (z.B. z=10), dann wird der ganze Bruch auch kleiner:  $\textstyle b={\frac {10}{5}}=2$. Je größer der Zähler, desto größer der Bruch. Je kleiner der Zähler, desto kleiner der Bruch. Diesen Zusammenhang nennt man direkte Proportionalität.

Wenn jetzt der Nenner größer wird (z.B. n=10), dann wird der ganze Bruch das Gegenteil, also kleiner:

Wenn der Zähler z=20 und der Nenner n=5 ist, dann ist der Bruch b=4: $\textstyle b={\frac {20}{5}}=4$. Wird der Nenner n größer, z.B. 10, dann wird der Bruch b kleiner:  $\textstyle b={\frac {20}{10}}=2$. Wenn der Nenner kleiner wird (z.B. n=2), dann wird der ganze Bruch das Gegenteil, also größer:  $\textstyle b={\frac {20}{2}}=10$. Je größer der Nenner, desto kleiner der Bruch. Je kleiner der Nenner, desto größer der Bruch. Diesen Zusammenhang nennt man indirekte Proportionalität.

Wenn zwei Größen (z.B. Volumen und grob gesagt Gewicht) gleichzeitig wachsen oder gleichzeitig weniger werden, dann liegt eine direkte Proportionalität vor (z.B. wenn man mehr Wasser hat, ist sowohl das Volumen als auch das Gewicht mehr). Wenn das Wachstum einer Größe zur Verminderung einer anderen führt, dann liegt eine indirekte Proportionalität vor (z.B. mehr Arbeiter brauchen weniger Zeit, um die gleiche Arbeit zu erledigen). So kann man verstehen, ob man direkte oder indirekte Proportionalität benutzen soll. Beim nächsten Kapitel allerdings (Prozentrechnung) kommt nur die direkte Proportionalität vor!

Vertiefende Aufgaben der Prozentrechnung

Prozentrechnung bei Wachstum oder Zerfall

Exponential und Logarithmus Funktion

Dieses Kapitel fängt mit Grundniveau 3 an.

Arbeiten mit Termen

Umformen Grundwissen Gegenrechnungen

Nachdem Vassili Lisa drei Äpfel gibt, hat er fünf Äpfel. Wie viele Äpfel hatte er vorher?

Wie kann man diese Aufgabe in der mathematischen Sprache schreiben? Für das Gefragte (wie viele Äpfel) wird in Mathematik irgendein Symbol benutzt, als Stellvertreter für die noch unbekannte Zahl. In der Regel wird als Symbol ein Buchstabe verwendet und nicht allzu selten x.
Mit x sind also die Äpfel gemeint, die Vassili am Anfang hatte. Wir wissen noch nicht, wie viele sie waren, daher schreiben wir ein Symbol dafür, ein Buchstabe, also x.

Wenn Vassili drei Äpfel der Lisa gibt, dann hat er weniger Äpfel als zuvor, es geht um eine Subtraktion. Von den x Äpfeln am Anfang sind drei Äpfel zu subtrahieren. Dass dann noch fünf Äpfel bleiben, wird durch den folgenden mathematischen Ausdruck geschrieben:

x−3=5

Man kann für x verschiedene Zahlen ausprobieren, z.B. 2, 3, 7, 8 oder 9. So kann man schon feststellen, dass nur acht minus drei gleich fünf ist. „x“ muss also 8 sein, damit die Rechnung stimmt. Vassili hatte also 8 Äpfel am Anfang.

Die ganze Zeit ausprobieren ist allerdings nicht gerade geschickt. Besonders bei größeren Zahlen wird es sogar ziemlich schwer. Es gibt in der Mathematik einen geschickteren Weg, die Aufgabe zu lösen. Man benutzt die sogenannte Gegenrechnung. Bei allen Gleichungen gibt es zwei Teile, ein Teil links vom „=“ und ein Teil rechts vom „=“. Bringt man einen Term von einer Seite zur anderen, dann muss man die Gegenrechnung benutzen.

Die Gegenrechnung der Subtraktion ist die Addition und umgekehrt.

Wenn x−3=5 ist, dann kann man die 3 auf die andere Seite vom „=“ bringen und statt minus die Gegenrechnung (plus) benutzen:

x=5+3       also x=8

Bei der Aufgabe c+4452 = 341 bringt man 4452 auf die andere Seite und benutzt die Gegenrechnung von minus. Die Lösung ist daher:

c+4452 = 341 → c= 341−4452 → c = −4111

Die Gegenrechnung der Multiplikation ist die Division und umgekehrt.

3f=114

Zwischen 3 und f steht nichts.

Wenn in Mathematik zwischen zwei Ausdrucken (zum Beispiel einer Zahl und einem Symbol, einer Klammer und einer Zahl und so weiter) nichts steht, dann ist Multiplikation gemeint (einzige Ausnahme: die gemischten Zahlen).

Da zwischen 3 und f nichts steht, ist mal gemeint. f ist ein Symbol und steht für irgendeine Zahl. Die Aufgabe ist herauszufinden, wie viel f sein soll, damit die Rechnung stimmt. In diesem fall soll 3 auf die andere Seite gebracht und die Gegenrechnung von mal (also durch) benutzt werden:

3f=114 (nichts zwischen 3 und f, also mal gemeint):

3·f=114 (3 auf die andere Seite von „=“ bringen und Gegenrechnung, also hier Division, benutzen)

f=114:3 und daher

f = 38.

Man kann auch einen Bruch statt einer Division benutzen:

$f={\frac {114}{3}}=38$

Entsprechend ist die Gegenrechnung der Division die Multiplikation:

$\textstyle {\frac {k}{5}}=11$    also k:5 = 11 und daher k = 11 · 5

k = 55

Was ist aber die Gegenrechnung vom Quadrat?

Die Gegenrechnung von Quadrat ist die sogenannte „Wurzel“:

z² = 81 also z = ${\sqrt {81}}$  und daher z=9

9 ist die Zahl, deren Quadrat 81 ist, daher ist die Wurzel von 81 gleich 9. Wenn wir in der Gleichung z² = 81 z durch 9 ersetzen, dann stimmt die Gleichung tatsächlich: 9² = 81

Selbstverständlich ist die Gegenrechnung der Wurzel das Quadrat.

${\sqrt {m}}$ = 13 also m = 13² und daher m=169

Obwohl es für das Niveau dieses Buches nicht absolut notwendig ist, können wir doch auf eine Tatsache aufmerksam machen: Die Gleichung z² = 81 hat noch eine Lösung, wenn z gleich −9 ist. Freilich stimmt die Gleichung (−9)² = 81. (−9)² bedeutet (−9)·(−9). Minus mal minus ist plus und daher:

(−9)² =(−9)·(−9)= + 9·9 = 81 also

(−9)² = 81

Zahlendarstellungen Mengentheorie und Aussagenlogik

Zahlendarstellungen

(Dekadisches oder) Dezimalsystem

Darstellungen einer Zahl im Dezimalssystem

Die römische Zahlendarstellung

Die griechische Zahlendarstellung

Runden

Grundregeln des Rundens

Das Quadrat von 7 ist 49 und daher ist die Wurzel von 49 gleich 7 (sie sind Gegenrechnungen). Was ist aber mit der Wurzel von 7? Wenn man die Rechnung mit einem einfacheren Taschenrechner macht, kommt das folgende Ergebnis vor:

2,6457513110645905905

Das bedeutet, dass das Quadrat von 2,6457513110645905905 (die Gegenrechnung) 7 sein sollte. Wenn man aber mit dem Taschenrechner die Rechnung macht:

2,6457513110645905905² = 2,6457513110645905905 · 2,6457513110645905905

kommt 6,99999999999999999999 als Ergebnis heraus, was zwar fast 7 ist, aber nicht genau 7.

Man spricht in diesem Fall vom Runden. Der Taschenrechner gibt beim Wurzelziehen ein Ergebnis an, das nicht genau ist. Das genaue Ergebnis hat unendlich viele Nachkommastellen. Es ist unmöglich die Wurzel von 7 mit einer Kommazahl ganz genau zu bestimmen. Die einzige Weise die Wurzel von 7 genau anzugeben, ist ${\sqrt {7}}$ zu schreiben!

Wie genau das Ergebnis mit Kommastellen ist, hängt vom Taschenrechner ab. Jeder Taschenrechner kann eine bestimmte Anzahl von Nachkommastellen berechnen. Die Wurzel aus 7 mit einer Kommazahl genau anzugeben ist aber nicht möglich.

Der Taschenrechner gibt ein Ergebnis an, das so nah wie möglich zum tatsächlichen Wert von $\ {\sqrt {7}}\$ ist und so viele Nachkommastellen hat, wie der Taschenrechner berechnen kann. In der Anzeige des Taschenrechners stehen sogar oft weniger Stellen (wieder gerundet) als die Stellen, die der Taschenrechner berechnen kann.

Das Runden ist in solchen Fällen unvermeidbar und oft notwendig und sinnvoll. Stellen wir uns vor, dass ein Produkt 6€ kostet. In einer Sonderaktion wird allerdings ein Rabatt 17% gewährt. In diesem Fall ist der Preis nach dem Rabatt:

6 ⋅ 0,83 = 4,938€

Hier muss man wieder runden. Die Münze mit dem kleinsten Wert ist 1¢ (0,01€). So was wie 0,008€ kann man nicht in Bar bezahlen. Man kann auch nicht genau 4.938€ bezahlen. Man muss auf zwei Nachkommastellen runden:

4,938€ ≈ 4,94€

Warum haben wir hier 4,94 und nicht 4,93 geschrieben?

4,938 liegt näher bei 4,94 als bei 4,93.

Wenn man rundet, rundet man auf (also eins nach oben), wenn die nächste Ziffer 5 oder mehr ist. Man rundet ab (also die Ziffer bleibt die gleiche), wenn die nächste Ziffer weniger als 5 ist:

5,6873729 ≈ 5,69      5,6873729 ≈ 5,687373

5,6873729 ≈ 5,68737     5,6873729 ≈ 5,687     8,785 ≈ 8,79

Im letzten Beispiel sehen wir, dass aufgerundet wird, wenn die nächste Ziffer 5 ist. 8,785 rundet man auf 8,79. Die nächste Ziffer von ist 5, daher wird aufgerundet. Diese Art vom Runden von 5 wird „kaufmännische“ Rundung genannt und wird in der Schule benutzt. Dieser Art der Rundung von 5 kann allerdings zu Probleme führen, besonders in der Statistik. Daher gibt es auch andere Regeln, wie man rundet, wenn die nächste Stelle eine einzige 5 ist.

Wie viele Nachkommastellen muss man schreiben? Das ist vom Problem abhängig.

Die Ziffern ohne die Nullen zu Beginn oder am Ende der Zahl nennt man gültige Ziffern.

Es kann sein, dass bei einer Aufgabe festgelegt wird, auf wie viele Stellen gerundet wird:

Aufgabe: Runden auf drei (gültige) Stellen (oder in diesem Beispiel auf zwei Nachkommastellen)

5,6873729 ≈ 5,69

Aufgabe: Runden auf sieben Stellen (oder in diesem Beispiel auf sechs Nachkommastellen)

5,6873729 ≈ 5,687373

Aufgabe: Runden auf sechs Stellen (oder in diesem Beispiel auf fünf Nachkommastellen)

5,6873729 ≈ 5,68737

Aufgabe: Runden auf vier Stellen (oder in diesem Beispiel auf drei Nachkommastellen)

5,6873729 ≈ 5,687

Aufgabe: Runden auf zwei (gültige) Stellen (oder in diesem Beispiel auf vier Nachkommastellen)

0,002356 ≈ 0,0024

Wenn es keine Angabe über die gültigen Ziffern gibt, schreibt man nicht mehr als 5 oder 6 gültigen Ziffern insgesamt (also samt Ziffer vor dem Komma), beispielsweise:

895,76038≈895,760    0,007854309826≈0,00785   9874086973≈9874100000

In manchen Fällen sollte es von der Aufgabe klar sein, wie vielen gültige Stellen zu erwarten sind. Ein solchen Beispiel haben wir schon mit dem € gesehen.

Ein anderes Beispiel ist, wenn man ein Messband benutzt, um einen Abstand zu messen. Ein Messband kann nur bis mm messen und nichts kleineres. Wenn der gemessene Abstand 145cm ist und ihn in 7 teilt, kann das Ergebnis nur eine Nachkommastelle haben (mm).

Wenn man die Zeit mit einem elektronischen Stoppuhr misst, zeigt diese oft Nachkkommastellen nach der Sekunde, z.B. 6,463s. Das ist wieder völlig daneben, da die Reaktionszeit des Menschen mehr als 0,1s ist. Man kann also mit einer Stoppuhr, die mit der Hand betrieben wird, nicht genauer als eine Nachkommastelle nach der Sekunde messen. Die restlichen Nachkommastellen führen zum falschen Eindruck, dass man doch so genau (mit drei Nachkommastellen) messen kann.

Hier kann man auch erklären: Eine Zahl ändert sich nicht, wenn man eine oder mehrere Nullen vor der ersten Ziffer oder nach der letzten Nachkommastelle hinzufügt:

7,34 = 007,34 = 7,340 = 7,34000 = 000007,34000000

8888 = 8888,0000 = 0008888

Aufrunden von 9

Wenn die Ziffer, die gerundet werden muss, 9 ist, gibt es beim Aufrunden eine gewisse Schwierigkeit. Die Ziffer sollte um 1 erhöht werden, es gibt aber keine Ziffer, die mehr als 9 ist. In diesem Fall wird wie bei der Division, also auch mit der vorherigen Ziffer gearbeitet. Runden wir folgende Beispiele auf drei gültigen Stellen:

• 8,695408

Wir wollen hier drei Stellen benutzen, die letzte Stelle ist 9. Nach der 9 folgt 5, wie müssen also aufrunden. 9 muss um 1 erhöht werden. Das geht nicht. Dann nimmt man zwei Ziffern (also hier die Ziffern nach dem Komma 69) und erhöht sie um 1 (69 wird zu 70). Also:

8,695408 ≈ 8,70

• 0,039995

Wir wollen wieder drei Stellen benutzen, die letzte Stelle ist 9. Nach der 9 folgt 9, wie müssen also aufrunden. 9 muss um 1 erhöht werden. Das geht nicht. Dann nimmt man zwei Ziffern (also hier die Ziffern 99) und versucht sie um 1 zu erhöhen. Das geht auch nicht, 99 ist die größte zweistellige Zahl. In diesem Fall nehmen alle drei Stellen (399) und erhöhen wir sie um 1:

0,039995≈0,0400

Die zwei Nullen nach dem 4 müssen geschrieben werden, um zu zeigen, dass es auf drei gültigen Stellen gerundet wurde.

• 999,73

In diesem Beispiel muss man wieder alle drei Stellen benutzen, das Runden findet aber doch davor statt!

999,73≈1000

Einheiten

Einheiten und physikalische Größen

Unsere Umgebung, die Natur, wir selber haben viele Eigenschaften: ein Wald kann schön sein, ein Berg kann groß oder klein sein, das Meer blau usw. Manche Eigenschaften, die man messen kann, sind für die Physik wichtig. Solche Eigenschaften sind z.B. die Länge (oder der Abstand, der Weg usw.), die Masse (grob gesagt: das Gewicht), die Zeit, die Geschwindigkeit, die Kraft, die elektrische Ladung usw. Alle diese Eigenschaften, die für die Physik wichtig sind und die man messen kann, nennt man physikalische Größen.

Jede Größe kann man mit verschiedenen Einheiten messen. Für den Abstand z.B. benutzt man Meter (oder auch Zolle, Kilometer, Millimeter usw.), für die Zeit Sekunde (oder Stunden, Tagen, Minuten usw.) für die Masse Kilogramm (oder Gramm, Tonne usw.), für die Kraft Newton usw..

Vorsätze von Einheiten

Für jede Einheit gibt es verschiedene Vorsätze, also kleine Wörter, die einen gewissen Anteil der Einheit zeigen:

Milli (m) bedeutet ein Tausendstel, Zenti (c) ein Hundertstel, Deci (d) ein Zehntel, Kilo (k) bedeutet Tausend. Ein Milligramm (mg) bedeutet daher ein Tausendstel eines Gramms, ein Zentimeter (cm) bedeutet ein Hundertstel eines Meters, ein Kilogramm (kg) Tausend Gramms, ein Decivolt (dV) ein Zehntel eines Volts, ein Zentiliter (cL) ein Hundertstel eines Liters, ein Kilowatt (kW) Tausent Watts.

Einheiten Umwandeln

Einheiten ohne Hochzahl

Abstand

Für die Umrechnungen eines Abstandes benutzt man folgendes Schema:

In diesem Bild:

• Wenn ein Abstand z.B. in km gegeben ist und in dm umgerechnet werden soll (von links nach rechts, vom größten zum kleinsten) muss man multiplizieren, in diesem Beispiel einmal mit 1000 und einmal mit 10:

2,35km= 2,35 ·1000 ·10 dm = 23500 dm

• wenn ein Abstand z.B. in cm gegeben ist und in m umgerechnet werden soll (von rechts nach links, vom kleinsten zum größten) muss man dividieren, in diesem Beispiel zwei mal durch 10:

0,054cm= 0,054:10:10 m = 0,00054m

Masse

Für die Umrechnungen einer Masse benutzt man folgendes Schema:

In diesem Bild:

• wenn eine Masse z.B. in kg gegeben ist und in mg umgerechnet werden soll (von links nach rechts, vom größten zum kleinsten) muss man multiplizieren, in diesem Beispiel zwei mal mit 1000:

0,087kg= 0,087 ·1000 ·1000 mg = 87000mg

• wenn eine Masse z.B. in g gegeben ist und in Tonnen (t) umgerechnet werden soll (von rechts nach links, vom kleinsten zum größten) muss man dividieren, in diesem Beispiel zwei mal durch 1000:

36530g= 36530:1000:1000 t = 0,03653t

Zeit

Für die Umrechnungen der Zeit benutzt man folgendes Schema:

In diesem Bild:

• wenn eine Zeit z.B. in Minuten gegeben ist und in Sekunden umgerechnet werden soll (von links nach rechts, vom größten zum kleinsten) muss man multiplizieren, in diesem Beispiel einmal mit 60:

0,08min= 0,08·60 s = 4,8s

• wenn eine Zeit z.B. in Minuten gegeben ist und in Tage umgerechnet werden soll (von rechts nach links, vom kleinsten zum größten) muss man dividieren, in diesem Beispiel einmal durch 60 und einmal durch 24:

36630 min= 36630:60:24 Tage = 25,4375 Tage

Einheiten mit Hochzahl

Flächeninhalt

Für die Umrechnungen einer Fläche benutzt man wieder das Schema des Abstandes:

ABER!!!

Fläche ist immer mit Quadrat: km², m², dm², cm², mm²

Es ist immer hoch 2. Daher muss man jeden Schritt (oder alle Schritte zusammen) 2 mal machen! Daher kann man folgendes bild benutzen:

In diesem Bild:

• Wenn eine Fläche z.B. in km² gegeben ist und in dm² umgerechnet werden soll (von links nach rechts, vom größten zum kleinsten) muss man multiplizieren, in diesem Beispiel einmal mit 1000² und einmal mit 10².

2,35km²= 2,35 ·1000² ·10²dm² = 2,35 ·1000000 ·100 dm² = 235000000dm²

• Wenn eine Fläche z.B. in cm² gegeben ist und in m² umgerechnet werden soll (von rechts nach links, vom kleinsten zum größten) muss man dividieren, in diesem Beispiel zwei mal durch 10², also zwei mal durch 100 dividieren.

0,054cm² = 0,054:10² :10² m² = 0,054:100 :100 m² = 0,0000054m²

Volumen

Für die Umrechnungen eines Volumens benutzt man wieder das Schema des Abstandes:

Volumen ist immer Kubik: km³, m³, dm³, cm³, mm³

Es ist immer hoch 3. Daher muss man jeden Schritt (oder alle Schritte zusammen) hoch 3 machen! Daher kann man folgendes Bild benutzen:

In diesem Bild:

• Wenn das Volumen z.B. in km³ gegeben ist und in dm³ umgerechnet werden soll (von links nach rechts, vom größten zum kleinsten) muss man multiplizieren, in diesem Beispiel einmal mit 1000³ und einmal mit 10³.

2,35 km³ = 2,35 ·1000³ ·10³ dm³ = 2,35 ·1000000000·1000 dm³ = 2350000000000 dm³ (=2,35·10¹² dm³)

• Wenn das Volumen z.B. in cm³ gegeben ist und in m³ umgerechnet werden soll (von rechts nach links, vom kleinsten zum größten) muss man dividieren, in diesem Beispiel zwei mal durch 10³.

0,054cm³ = 0,054:10³:10³ m³ = 0,054:1000 :1000 m³ = 0,000000054 m³ (= 5,4 ·10^-8 m³)

Eine Einheit, die oft am Alltag für das Volumen benutzt wird, ist der Liter. Ein Liter ist genau so viel wie ein dm³. Daher ist ein$\ m\ell \$(Milliliter) so viel wie ein cm³.

Statistik und Wahrscheinlichkeitsrechnung

Lageparameter

Lageparameter Einführung

In der Mathematik, besonders im Bereich der Statistik, gibt es viele sogenannten Mittelwerte. Was ist ein Mittelwert? Wenn man viele Werte (viele Zahlen, die irgendwas messen) hat, dann gibt es eine Zahl, die sich irgendwie in der Mitte dieser Werte befindet. Das ist ein Mittelwert. Es gibt aber verschiedene „Mitten“, also verschiedene Wege um diese Mitte zu berechnen, je nachdem wie das Problem ist. Zwei von diesen Wegen werden wir hier lernen, den Durchschnitt (auch arithmetisches Mittel genannt) und den Median (auch Zentralwert genannt). Wir werden auch den sogenannten Modalwert (Modus) kennenlernen, der zwar kein Mittelwert aber für die Beschreibung von Daten oft hilfreich ist.

Durchschnitt (arithmetisches Mittel)

Fangen wir mit einem Beispiel an:

• Die Familien eines kleinen Dorfes haben Kirschen geerntet. Die Ernte für die verschiedenen Familien war: 54kg, 65kg, 48kg, 76kg, 52kg, 65kg, 45kg. Sie haben allerdings vereinbart, dass jede Familie doch gleich so viele Kirschen bekommt. Wie viel bekommt jede Familie?

Um diese Frage zu beantworten, soll man erst die ganze Ernte berechnen, also die Teilernten addieren. Dann wird die ganze Ernte auf die Anzahl der Familien geteilt. So wird jede Familie gleich so viele Kirschen bekommen. Das Ergebnis nennt man Durchschnitt.

$\mathbf {Durchschnitt} ={\frac {\mathrm {Summe\ der\ Werte} }{\mathrm {Anzahl\ der\ Werte} }}={\frac {54+65+48+76+52+65+45}{7}}\approx 57{,}86$  (das sind kg)

Jede Familie bekommt dann ca. 57,86 kg.

Den Durchschnitt (auch arithmetisches Mittel genannt) mehrerer Werte berechnet man, indem man ihre Summe durch ihre Anzahl (wie viele Werte wir haben) dividiert:

$\mathbf {Durchschnitt} ={\frac {\mathbf {Summe\ der\ Werte} }{\mathbf {Anzahl\ der\ Werte} }}$

Median (Zentralwert)

Den Median (auch Zentralwert genannt) mehrerer Werte findet man, indem man die Werte zuerst der Größe nach ordnet (z.B. vom kleineren zum größeren) und dann den Wert in der Mitte der Reihe wählt.

Ein Beispiel!

• Das Gewicht der Schüler in einer Klasse ist: 54kg, 65kg, 48kg, 76kg, 52kg, 65kg, 45kg. Wie viel ist der Median?

Zuerst der Größe nach ordnen!

45, 48, 52, 54, 65, 65, 76

(ALLE Werte schreiben, also zwei oder mehr mal schreiben, wenn der Wert mehrmals vorkommt; jeden Wert muss man schreiben, so oft wie er vorkommt)

Der Wert in der Mitte ist 54. Es gibt 3 Werte links und 3 Werte rechts. Also 54 ist genau in der Mitte. Daher ist 54kg der Median!

Was ist aber, wenn die Anzahl der Werte eine gerade Zahl ist, wenn wir z.B. 12 Werte haben (12 ist eine gerade Zahl) und nicht 7 wie vorher (7 ist eine ungerade Zahl). Wenn man 7 Werte hat (oder irgendeine andere ungerade Zahl) dann gibt es genau eine Zahl in der Mitte. Bei gerader Anzahl der Werte gibt es doch 2 Zahlen in der Mitte. In diesem Fall wird als Median der Wert definiert, der genau zwischen den beiden Zahlen in der Mitte steht, also der Durchschnitt der beide Zahlen. Schauen wir ein Beispiel an!

• Das Gewicht der Schüler in einer Klasse ist: 52kg, 65kg, 48kg, 76kg, 52kg, 65kg, 45kg, 65kg, 45 kg, 45kg, 78kg, 69kg. Wie viel ist der Median?

Zuerst der Größe nach ordnen!

45, 45, 45, 48, 52, 52, 65, 65, 65, 69, 76, 78

(ALLE Werte schreiben, also jeden Wert schreiben, so oft wie er vorkommt)

Hier gibt es zwei Werte in der Mitte, 52 und 65. Der Median ist genau in der Mitte also die beide Werte addieren und durch 2 dividieren:

$\mathbf {Median} ={\frac {52kg+65kg}{2}}=58{,}5\ kg$

Modus (Modalwert)

Der Modus (auch Modalwert genannt) von mehreren Werten ist der Wert, der am häufigsten vorkommt.

Ein Beispiel!

• Das Gewicht der Schüler in einer Klasse ist: 54kg, 63kg, 48kg, 76kg, 52kg, 63kg, 45kg. Wie viel ist der Modalwert?

Hier kommt 63 zwei mal vor, alle andere Werte kommen nur einmal vor. Daher ist 63kg der Modus.

Was ist aber, wenn mehrere Werte öfters vorkommen? Noch ein Beispiel!

• Das Gewicht der Schüler in einer Klasse ist: 52kg, 65kg, 48kg, 76kg, 52kg, 65kg, 45kg, 65kg, 45 kg, 45kg, 78kg, 69kg.

Hier kommt 45 drei mal vor, 65 drei mal vor, 52 zwei mal vor und die restlichen Werte nur ein mal vor. 45 und 65 kommen am öftesten vor. Daher sind sie beide Modalwerte. 52 hingegen kommt nicht so oft vor wie 45 und 65 (also „nur“ zwei mal), daher ist 52 kein Modalwert. Es gilt also:

Modalwerte (Modi): 45kg und 65kg

Geometrische Konstruktionen

Wird in BRP nicht gefragt! Wenn du doch das lernen willst, hier klicken!

Geometrie der Ebene

Definitionen der ebenen Geometrie

Grundbegriffe der Geometrie

Strecke

Strecke Definition

Strecke ist der kürzeste Weg zwischen zwei Punkten. Z.B von den beiden gezeichneten Möglichkeiten zwischen A und B im Bild "Strecken Definition", welche ist die kürzeste?

Gerade und Strahl

Gerade und Strahl

Wenn ich eine Strecke auf einer Seite unendlich lang verlängere, dann habe ich einen Strahl. Wenn ich das an beiden Seiten tue, dann hab ich eine Gerade.

Winkel

Winkel Darstellung

Zwischen zwei Strahlen, die vom gleichen Punkt ausgehen, entsteht ein Winkel. Mit einem Winkel misst man eine Drehung.

Rechter Winkel

vier rechte Winkel

Wenn sich zwei Geraden einander so schneiden, dass vier gleichen Winkel entstehen, dann ist jeder von diesen Winkeln ein rechter Winkel.

Parallelen

zwei Parallele Geraden

Wenn zwei Geraden so nebeneinander liegen, dass sie nie einander schneiden und immer den Gleichen Abstand haben, dann sind sie parallel zueinander.

Punkt

Um alle Begriffe bisher zu definieren, haben wir den Punkt gebraucht. Was ist aber wieder ein Punkt? Diese ist die schwerste Definition. Wenn man beispielsweise den Abstand zwischen Wien und Linz berechnen will, muss man einen Ort in jeder Stadt wählen, sonst kann der Abstand bis 15km mehr oder weniger sein! Dieser Ort könnte z.B. eine Säule in der Mitte von jeder Stadt sein. Für so einen großen Abstand reicht eine Säule schon. Sie ist sozusagen ein Punkt.

Wenn man aber die Säule selber messen will, geht es nicht mehr. Man nimmt dann zwei winzigen Flächen am Rand der Säule. Je kleiner das Objekt ist, das wir messen wollen, desto kleiner muss der „Punkt“ sein.

Im idealen Fall ist der Punkt gar nichts, hat selber keine Länge, keine Breite und keine Höhe! So kann man sich einen Punkt vorstellen und so wird er auch definiert.

Eckpunkt

Seite und Diagonale

Die Seiten einer ebenen Figur sind die Abgrenzungen der Figur vom Rest der Ebene. Im folgenden Bild eines Quadrats werden alle seine Seiten mit a bezeichnet, im Bild des Rechtecks werden zwei Seiten mit a und zwei mit b bezeichnet. Eine Seite verbindet zwei Punkte die nacheinander liegen. Die Diagonale verbindet hingegen zwei gegenüberliegenden Eckpunkte, die sich nicht am Rand der gleichen Seite befinden. Ein Quadrat und ein Rechteck haben jeweils zwei Diagonalen, die gleich lang sind, in einem Parallelogramm hingegen sind sie nicht gleich lang.

Figuren

Quadrat

Quadrat

Ein Quadrat ist eine viereckige geschlossene Figur, deren Seiten als auch deren Winkel gleich zu einander sind. Formeln: u=4a, A=a² (u ist der Umfang, a die Seite, A die Fläche). Mit d ist hier die sogenannte Diagonale gezeigt (verbindet zwei gegenüberliegende Eckpunkte).

Rechteck

Rechteck

Ein Rechteck ist eine viereckige geschlossene Figur, deren Winkel gleich zueinander sind und deren gegenüberliegenden Seiten auch gleich sind. Formeln: u=2a+2b oder u=2(a+b), A=a·b. Mit d ist wieder die Diagonale bezeichnet, mit a und b die Seiten (in der Figur ist a für die Länge, also die längere Seite und b für die Breite, also die kürzere Seite).

Parallelogramm

Parallelogramm

Ein Parallelogramm ist eine viereckige geschlossene Figur, deren gegenüberliegenden Seiten gleich sind. Daher sind sie auch parallel. Formeln: u=2a+2b oder u=2(a+b), A=a·h_a oder A=b·h_b. In der Figur ist h_a die Höhe zur Seite a und h_b die Höhe zur Seite b. Mit d wird eine der beiden Diagonalen bezeichnet (hier die kürzeste).

Raute (Rhombus)

Rhobus

Eine Raute ist eine viereckige geschlossene Figur, deren Seiten gleich sind. Daher sind auch alle Winkeln gleich. Formeln: u=4a, A=$\textstyle {\frac {e\cdot f}{2}}$. Mit e und f sind die beiden Diagonale bezeichnet, mit a die Seite.

Trapez

Trapez

Ein Trapez ist eine viereckige geschlossene Figur mit zwei gegenüberliegenden parallele Seiten. Formeln: u=a+b+c+d, $\textstyle A={\frac {a+c}{2}}\cdot h$. Mit a, b, c und d werden die vier (nicht unbedingt gleichen) Seiten bezeichnet, mit h die Höhe auf die Basis (Basis ist nicht nur beim Trapez, sondern bei jeder Figur die untere Seite, beim Trapez im Bild hier die Seite a, also die Seite die im Bild unten steht). In der Figur sieht man auch die Diagonalen (ohne Symbol).

Deltoid

Deltoid1

Ein Deltoid ist eine viereckige geschlossene Figur mit zwei Paaren nacheinander liegenden gleichen Seiten.

Vieleck (regelmäßiges)

Siebeneck

Ein Vieleck ist eine Figur mit mehreren Winkeln. Wenn die Figur geschlossen ist und alle Seiten (und Winkel) gleich zueinander, dann ist das Vieleck regelmäßig. Im Bild sieht man ein regelmäßiges Siebeneck, die Seite ist hier mit s bezeichnet.

Dreieck, Besondere Dreiecke

• 
  spitz
• 
  gleichseitiges
• 
  gleichschenkliges
• 
  rechtwinkeliges
• 
  stumpfwinkeliges

Ein Dreieck ist eine geschlossene Figur mit drei Winkel. Ist einer Winkel mehr als 90°, dann heißt das Dreieck stumpfwinkeliges, wenn alle Winkel kleiner als 90° sind, dann spitzwinkeliges.

Bei allen Dreiecken gilt für den Umfang: u=a+b+c, wobei a, b und c die Symbole für die Seiten sind. Die allgemeinen Formeln für die Fläche sind  $\textstyle A={\frac {a\cdot h_{a}}{2}}={\frac {b\cdot h_{b}}{2}}={\frac {c\cdot h_{c}}{2}}$, wobei h_a, h_b und h_c die Höhen zu den entsprechenden Seiten sind (im Bild nicht zu sehen).

Ist einer der Winkeln 90°, dann wird das Dreieck rechtwinkelig genannt. Die Formel für die Fläche ist in diesem Fall  $\textstyle A={\frac {a\cdot b}{2}}$, wobei hier a und b die kleineren Seiten sind (Katheten genannt). Die größte Seite (dem rechten Winkel gegenüber) nennt man Hypotenuse.

Sind zwei der drei Winkel (und auch zwei Seiten) gleich, dann nennt man das Dreieck gleichschenklig. Sind alle Winkel (und Seiten) gleich, dann ist es ein gleichseitiges Dreieck (mit Seite a). Für die Fläche des gleichseitigen Dreiecks gilt:  $\textstyle A={\frac {\sqrt {3}}{4}}\cdot a^{2}$.

Kreis, Kreissektor, Kreisring

• 
  Kreis
• 
  Kreisteile
• 
  Kreisring

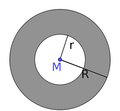
Ein Kreis ist die Menge aller Punkten, die von einem Punkt M (Mittelpunkt genannt) den gleichen Abstand r (Radius genannt) haben. Formeln: u=2πr, A=πr². r ist der Radius. Hier wird mit d der Durchmesser bezeichnet. π ist eine Zahl (wie 2 oder 5,632), mit dem Unterschied, dass man diese Zahl (π) nicht genau angeben kann. π ist ungefähr 3,14159... Sie ist das Verhältnis (also der Bruch) des Umfangs zum Durchmesser $\textstyle ({\boldsymbol {\pi }}={\frac {\boldsymbol {u}}{\boldsymbol {d}}})$.

Schneidet man einen Kreis wie einen Torten-schnitt (also zwei Schnitte von Mittelpunkt aus bis am Rand), dann hat man einen Kreissektor. Schneidet man ein Stück mit einer Strecke von einem zu einem anderen Punkt des Kreises, hat man ein Kreissegment. Im Bild steht für den Bogen das englische Wort "arc". Schneidet man von der Mitte eines Kreises einen kleineren Kreis mit den selben Mittelpunkt ab, dann bekommt man ein Kreisring.

Ellipse

Ellipse

Schneidet man einen Zylinder schief, dann entsteht eine Ellipse. Die sieht wie ein zerquetschter Kreis aus. Die genauere Definition ist kompliziert:

Man nimmt zwei Punkte, die Brennpunkte (im Bild B₁ und B₂). Jeder Punkt der Ellipse (im Bild z.B. X) hat zu jedem Brennpunkt einen gewissen Abstand (im Bild z.B. ist der Abstand zum Brennpunkt B₁ mit s bezeichnet und zum B₂ mit p). In einer Ellipse ist die Summe der beiden Abständen (also s+p) immer gleich (im Bild gleich 2a, wobei a die sogenannte große Halbachse ist). Mit b wird hier die sogenannte kleine Halbachse bezeichnet.

Intuitiver Beweis der Formeln des Flächeninhalts mancher ebenen Figuren

Definition des Quadratzentimeters

1 cm²

Ein Zentimeter Quadrat (1 cm², ein Zentimeter hoch zwei) ist ganz einfach ein Quadrat, dessen Seite ein Zentimeter ist (erstes Bild).

Fläche des Rechtecks

Rechteck

Im zweiten Bild sieht man ein Rechteck, dass aus mehreren Quadrat Zentimeter besteht. Hier haben wir zwei Zeilen, jede mit 3 Quadraten. Insgesamt 2x3=6 (cm²). Man kann offenbar sagen, dass der Flächeninhalt A eines Rechtecks die Länge a der einer Seite mal die Länge b der anderen ist.

A = a · b

Sonderfall: Das Quadrat. Da gilt A = a · a = a², da die Seiten gleich sind.

Fläche des Parallelogramms

Parallelogramm

Im Fall eines Parallelogramms kann man sich vorstellen, dass ein Stück der Figur so wie im Bild geschnitten und auf der anderen Seite wieder hinzugefügt werden kann. Dadurch entsteht wieder ein Rechteck, dessen Seiten jetzt die Basis a und die Höhe h_a des Parallelogramms sind. Die Fläche des dadurch entstandenen Rechtecks ist daher der Flächeninhalt des Parallelogramms:

A= a · h_a

Fläche des Dreiecks

Fläche des Dreiecks

Im Fall eines Dreiecks kann man sich wie im Bild vorstellen, dass ein zweites Dreieck, gleich groß wie das erste, umgedreht und auf das erste zugefügt wird. So entsteht wieder ein Parallelogramm, dessen Flächeninhalt A = b · h_b ist. Weil aber dieses Parallelogramm aus 2 gleiche Dreiecke besteht, muss man für den Flächeninhalt des Dreiecks das ganze mit 2 dividieren:

$A={\frac {b\cdot h_{b}}{2}}$

Entsprechend für die anderen Seiten kann man schreiben:

$A={\frac {a\cdot h_{a}}{2}}$

$A={\frac {c\cdot h_{c}}{2}}$

Sonderfälle: Rechtwinkeliges, gleichschenkeliges und gleichseitiges Dreieck. In den zwei letzten Fällen kann man den Satz des Pythagoras benutzen, um eine Formel zu erzeugen (machen wir aber hier nicht).

Fläche des Trapezes

Fläche des Trapezes

Genauso geht man bei einem Trapez vor. Es entsteht ein Parallelogramm, dessen Basis aber jetzt a+b ist und den Flächeninhalt daher (a+b) · h. Weil, wie vorher beim Dreieck, das Trapez zwei mal vorkommt, muss man wieder für den Flächeninhalt des Trapezes das ganze durch 2 dividieren:

$A={\frac {a+c}{2}}\cdot h$

Anwendung der Formeln

Variablen in der Geometrie

Bei allen Formeln gibt es sogenannten „Variablen“. Es geht in der Regel um ein Buchstabe, der für irgendwas steht. Hier schreiben wir, wofür diese Symbole in der Geometrie stehen.

• Ein großes A, steht in der Regel für die Fläche (genauer für den Flächeninhalt)

• Ein u steht i.d.R. für den Umfang (also wie lang das Rum-herum der Figur ist)

• a, b, c usw. stehen i.d.R. für die Seiten (auch Länge oder Breite) von Figuren

• h (oder H) steht i.d.R. für die Höhe einer Figur. Oft gibt es dann ein Index, z.B. h_b, was dann bedeutet, dass diese die Höhe für die Seite b ist.

• r (oder R) steht i.d.R. für den Radius eines Kreises.

• d steht bei einem Kreis für den Durchmesser des Kreises, bei einem Parallelogramm (oder Rechteck, Quadrat, Trapez, Vieleck) aber für die Diagonale!

• Griechische kleine Buchstaben (α, β, γ, δ, ε, θ, φ) stehen i.d.R. für Winkel.

• Allerdings ist mit dem griechischen Buchstabe π die Kreiszahl bezeichnet (π≈3,1415...).

Formel Einsetzen in der ebenen Geometrie

Bei einer Aufgabe sind immer gewisse Informationen gegeben, z.B.:

• Ein Zimmer ist 4m lang und 2,8m breit. Finden Sie seinen Umfang und seine Fläche heraus!

In solchen Problemen soll man die gegebenen Zahlen in die Formel sinnvoll einsetzen. Das bedeutet, dass man die Buchstaben in der Formel durch Zahlen ersetzt. In diesem Beispiel sucht man in einer Formelsammlung das Rechteck (da ein Zimmer die Form eines Rechtecks hat).

Rechteck

In der Figur, die man in der Formelsammlung finden kann, kann man sehen, dass mit a die Länge und mit b die Breite bezeichnet wird. In der Formelsammlung kann man auch die Formel für den Umfang finden:

u=2a+2b

Die Länge a ist gegeben: 4m. Die Breite b auch: 2,8m. Wenn nichts zwischen einer Zahl und einer Variable steht (hier z.B. 2a), dann ist mal gemeint (2 mal a). Man schreibt also an der Stelle von a und b die Zahlen 4 und 2,8:

$u=2a+2b=2{\cancel {a}}^{=4}+2{\cancel {b}}^{=2{,}8}=2\cdot 4+2\cdot 2,8=13,6\ (m$, da wie m mit m addiert haben)

In der Spalte für die Fläche steht beim Rechteck:

A=a·b   also

$A=a\cdot b={\cancel {a}}^{=4}\cdot {\cancel {b}}^{=2{,}8}=4\cdot 2,8=11,2\ (m^{2}$, da wie m mit m multipliziert haben)

Man soll auch auf die Einheiten aufpassen:

Der Umfang ist eine Strecke, also er wird in Streckeneinheiten gemessen (hier m), die Fläche hingegen in Flächeneinheiten (hier in m²).

Andererseites kann es sein, dass eine Größe in verschiedenen Einheiten gegeben wird, z.B.:

• Die Länge eines Rechtecks ist 5dm und seine Breite 32cm. Finden Sie seinen Umfang und seine Fläche heraus!

Das Einsetzen von Werten in einer Formel setzt voraus, dass die Einheiten übereinstimmen. Man muss z.B. überall in der Formel Werte in Stunden haben und nicht irgendwo Stunden, an einer anderen Stelle Minuten usw. Hier muss man den Wert einer der beiden Seiten umwandeln, z.B.:

32cm=32:10 dm = 3,2 dm

Jetzt sind beide Seiten (Länge und Breite) in dm und es kann weiter berechnet werden:

u=2a+2b und A=a·b

Die Länge a ist gegeben: a=5dm. Die Breite b haben wir jetzt auch in dm umgerechet: b=3,2dm:

$u=2a+2b=2{\cancel {a}}^{=5}+2{\cancel {b}}^{=3{,}2}=2\cdot 5+2\cdot 3{,}2=16{,}4\ (dm$, da wie hier dm mit dm addiert haben)      und

$A=a\cdot b={\cancel {a}}^{=5}\cdot {\cancel {b}}^{=3{,}2}=5\cdot 3{,}2=16\ (dm^{2}$,da wie hier dm mit dm multipliziert haben)

Hätten wir die Einheiten (die 32cm) nicht umgewandelt, hätten wir Probleme mit dem Einheit am Ende oder sogar ein völlig falsche Antwort:

• Bei der Multiplikation hätten wir:

$\textstyle A=a\cdot b={\cancel {a}}^{=5}\cdot {\cancel {b}}^{=32}=5\cdot 32=160\qquad$FALSCH! Wenn man hier dm² oder cm² als Einheit schreibt, ist das Ergebnis völlig falsch, die Einheit, die wir schreiben hätten sollen, wäre dm⋅cm, das wäre zwar richtig, aber diese Einheit wird für die Fläche nie benutzt.

• Bei der Addition hätten wir:

$u=2a+2b=2{\cancel {a}}^{=5}+2{\cancel {b}}^{=32}=2\cdot 5+2\cdot 32=74\qquad$FALSCH! Hier ist sogar der Wert völlig falsch! Der richtige Wert, wie wir gesehen haben, ist 16,4 dm (oder 164 cm). Man kann nicht dm und cm addieren oder subtrahieren, genauso wie man nicht dm und kg addieren kann! Addieren (oder subtrahieren) kann man nur Sachen, die genau die gleichen Einheiten haben!

Nicht nur bei Multiplikation oder Addition müssen die Einheiten übereinstimmen, sondern auch bei Division und allen anderen Rechenarten. Bei Multiplikation und Addition haben wir das Beispiel gerade eben gesehen (Fläche und Umfang des Rechtecks am letzten Beispiel). Ein Beispiel für Division, ist wenn man die Fläche eines Rechtecks durch seine Länge dividiert, um die Breite zu berechnen. Wenn die Fläche 6cm² und die Länge 30mm, dann kann man NICHT die Division so durchführen:  $\textstyle b={\frac {6}{30}}$, da 6 in cm gegeben ist und 30 in mm. Man soll zuerst z.B. die mm in cm umwandeln (30mm=3cm) und dann die Division durchführen:  $\textstyle b={\frac {6}{3}}=2$ (das sind dann cm, da wir cm² durch cm dividiert haben und man die Hochzahl und dann kann man die Einheiten kürzen:  $\textstyle {\frac {cm^{\cancel {2}}}{\cancel {cm}}}=cm$.

Wir können also schreiben:

Bei Rechnungen müssen die Einheiten immer übereinstimmen!

Bei einer Rechnung (oder Gleichung) muss man immer erst kontrollieren, ob die Einheiten übereinstimmen, dann die Einheiten, die nicht übereinstimmen, in übereinstimmenden Einheiten umwandeln und erst am Ende die Rechnung durchführen! Das gilt immer (auch bei der Schluss-und Prozentrechnung)!

In Physik benutzt man sogar Einheitssysteme, das ist aber für dieses Buch ein fortgeschrittenes Thema.

Geometrie des Raums

Dieses Kapitel fängt im mittleren Niveau 1 an.

Diagramme

Was ist ein Diagramm

In Diagrammen kann man verschiedene Daten in einem Bild darstellen, die man dann schnell ablesen kann. Diagramme können helfen, einen schnellen Überblick zu bekommen, werden aber auch oft benutzt, um einen falschen Eindruck zu bewirken. Hier werden das Säulendiagramm, das Liniendiagramm, das Kreisdiagramm und das Boxplotdiagramm präsentiert, es gibt aber auch zahlreiche andere Diagrammarten, wie z.B. Punktdiagramm, Balkendiagramm usw.

Säulendiagramm

Das Diagramm mit den Farben gibt die Anzahl der Steine in einem Kinderspiel, die eine gewisse Farbe haben. 4 Steine sind rot, 1 ist orange, 1 ist gelb, keine ist grün, es gibt 6 türkis usw. So ein Diagramm nennt man Säulendiagramm, weil es aus „Säulen“ besteht, wie in einem alten Tempel (Bild rechts). Die Farben sind sogenannte nominale Variablen. Nominale Variablen können wir zwar voneinander unterscheiden, wir können aber nicht z.B. sagen, dass rot "größer" als blau ist, wie z.B. wir sagen können, dass 4 mehr als 1 ist. Nominalen Variablen können wir also nicht der Größe nach ordnen. In diesem Diagramm können wir allerdings den sogenannten Modus ablesen, also welche Farbe am häufigsten vorkommt (Türkis).

Das folgende Diagramm gibt die Anzahl der Packungen, die eine gewisse Anzahl von Bananen pro Packung beinhalten. Die Anzahl der Bananen pro Packung ist eine sogenannte kardinale Größe (genauer gesagt: Variable einer Verhältnisskala). Wir können die einzelne Werte addieren, wir können auch dadurch einen Durchschnitt finden. Das geht allerdings nicht mit den Werten, die auf der x-Achse stehen (hier Bananen pro Packung), sondern nur mit den einzelnen Werten.

Säulendiagramm

Wenn die Frage z.B. ist, wie viele Packungen 4 Bananen haben, geht man so vor:

Auf der Achse unten (waagerechte Achse, x-Achse, auch Abszissenachse oder einfach Abszisse genannt) kann man die Bananen pro Packung ablesen, also kann man Bananen ablesen. Da wo 4 Bananen stehen (unten am Diagramm) befindet sich eine Säule. Man kann sehen, wie hoch diese Säule ist. Sie ist so hoch wie 5 Packungen. Die Anzahl der Packungen kann man links ablesen (auf der senkrechte Achse, der y-Achse, auch Ordinatenachse oder einfach Ordinate genannt). Also es gibt 5 Packungen mit 4 Bananen.

Wie viele Packungen haben 3 Bananen? Da, wo 3 Bananen stehen (unten, x-Achse), gibt es keine Säule! Die Höhe der Säule ist daher 0. Es gibt also keine (0) Packung, die 3 Bananen hat!

Wie viele Packungen haben keine Banane? Da, wo 0 Bananen stehen (unten, x-Achse), gibt es eine Säule, die 4 Packungen hoch ist. Es gibt also 4 Packungen mit keiner Banane!

Wie viele Packungen haben höchstens 3 Bananen? Höchstens bedeutet bis, also so viel wie 3 Bananen oder weniger (also 2, 1 oder keine Banane). Es gibt keine Packung mit 3 Bananen, 3 Pack. mit 2 Ban., 2 Pack. mit 1 Banane und 4 Pack. mit keiner Banane, also insgesamt 0+3+2+4=9 Pack..

Wie viele Packungen haben mindestens 3 Bananen? Mindestens bedeutet ab, also so viel wie 3 Bananen oder mehr (also 4, 5, 6 oder mehr Bananen). Es gibt keine Packung mit 3 Bananen, 5 Pack. mit 4 Ban. und 1 Pack. mit 5 Ban., also insgesamt 0+5+1=6 Pack..

Liniendiagramm

Die Kurve in einem Liniendiagramm kann irgendeine Form haben (und nicht nur eine Gerade). Das folgende Beispiel zeigt die Körpertemperatur von einer Person (namens Gregor) am 12.3.15. Man kann sich aber vorstellen, was im Diagramm dargestellt wird. Man kann z.B. sehen welche Temperatur Gregor um 6 oder um 22.15 Uhr hatte, oder am welchen Zeitpunkten seine Temperatur z.B. 36,45°C oder 36,6°C war.

Kreisdiagramm

Ein Kreisdiagramm zeigt Anteile des Ganzen. Es kann benutzt werden, um einen schnellen Überblick von statistischen Daten zu bekommen.

Ein Beispiel: In einer Klasse sind 8 Personen aus Österreich, 2 aus Deutschland, 2 aus der Türkei, 2 aus Serbien und 2 aus Tschechien. Diese Information kann man so wie im Bild in einem Kreisdiagramm darstellen. Die Hälfte des Kreises sind die 8 Personen aus Österreich. Die andere Hälfte ist in vier gleichen Teilen geteilt, also jeweils 2 Personen für Türkei, Deutschland, Serbien und Tschechien.