Beweisarchiv: Geometrie: Planimetrie: Kreis: Japanischer Satz für konzyklische Vierecke

Kreis: Mittelpunktswinkel-Umfangswinkel · Satz des Ptolemäus · Sehnensatz · Sehnentangentenwinkel · Sehnenviereck · Sekantensatz · Tangentenviereck · Japanischer Satz für konzyklische Vierecke · Satz des Thales

Rechtwinkliges Dreieck: Satz des Pythagoras

Ellipse: Satz vom Flüstergewölbe · Konjugierte Durchmesser

Regelmäßige Vielecke: Dreieck · Viereck · Fünfeck · Sechseck ·

Dreieck: Satz des Heron · Berechnung des Flächeninhalts des Diagonalendreiecks im Quader · Elementarer Satz zur Charakterisierung des Schwerpunkts im Dreieck via Flächeninhalte

Viereck: Flächenformel von Bretschneider

Inzidenzgeometrie ·

affine Geometrie: einfache Hilfssätze · Homothetien und Translationen · Desarguesche affine Ebenen sind Vektorräume

Trigonometrie

Additionstheoreme: Sinus · Kosinus · Tangens · Kotangens

Trigonometriesätze: Sinussatz · Kosinussatz · Neue Folgerungen aus dem Projektionssatz der Dreiecksgeometrie

Trigonometrie in der komplexen Ebene: Tangens und Kotangens in rechtwinkligen Dreiecken aus komplexen Zahlen

Voraussetzung

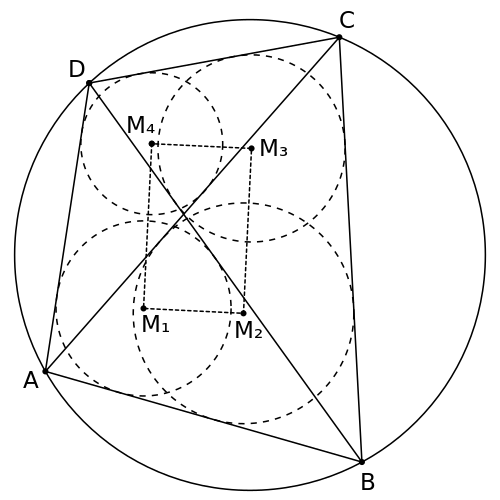
$\square ABCD$ sei ein nicht überschlagenes Sehnenviereck.

Ferner sei

$M_{1}$ der Mittelpunkt des Inkreises von $\triangle ADB{,}$
$M_{2}$ der Mittelpunkt des Inkreises von $\triangle ACB{,}$
$M_{3}$ der Mittelpunkt des Inkreises von $\triangle DCB$ und
$M_{4}$ der Mittelpunkt des Inkreises von $\triangle ADC$ .

Behauptung

$\square M_{1}M_{2}M_{3}M_{4}$ ist ein Rechteck.

Beweis

$\left|\sphericalangle ABD\right|=\left|\sphericalangle ACD\right|$

(im folgenden $\alpha$ -Winkel genannt) weil beide Winkel Umfangswinkel zur Sehne ${\overline {AD}}$ sind. Daraus folgt, dass

$\left|\sphericalangle AM_{1}D\right|=\left|\sphericalangle AM_{4}D\right|=90^{\circ }+{\frac {\left|\alpha \right|}{2}}$

weil

$\left|\sphericalangle AM_{1}D\right|=180^{\circ }-{\frac {\left|\sphericalangle BAD\right|+\left|\sphericalangle BDA\right|}{2}}=180^{\circ }-{\frac {180^{\circ }-\left|\sphericalangle ABD\right|}{2}}={\underline {\underline {90^{\circ }+{\frac {\left|\alpha \right|}{2}}}}}$

Durch die Gleichheit dieser Winkel ist $\square AM_{1}M_{4}D$ ein Sehnenviereck.

Durch die Eigenschaften der Sehnenvierecke gilt jetzt $\left|\sphericalangle M_{1}M_{4}D\right|=180^{\circ }-\left|\sphericalangle DAM_{1}\right|$

Alle Aussagen gelten analog auch für $\square DCM_{4}M_{3}$

Also gilt auch

$\left|\sphericalangle DM_{4}M_{3}\right|=180^{\circ }-\left|\sphericalangle M_{3}CD\right|$

Durch Addition der Winkel kommt folgendes heraus

$\left|\sphericalangle M_{1}M_{4}D\right|+\left|\sphericalangle DM_{4}M_{3}\right|=360^{\circ }-\left|\sphericalangle DAM_{1}\right|-\left|\sphericalangle M_{3}CD\right|=360^{\circ }-{\frac {\left|\sphericalangle DAB\right|+\left|\sphericalangle BCD\right|}{2}}=360^{\circ }-{\frac {180^{\circ }}{2}}={\underline {\underline {270^{\circ }}}}$

Da

$\sphericalangle M_{1}M_{4}M_{3}=270^{\circ }$

gilt

$\sphericalangle M_{3}M_{4}M_{1}=90^{\circ }$

Da alle Aussagen analog für die anderen Winkel zwischen den Mittelpunkten gelten, betragen sie alle $90^{\circ }$ .

Somit ist $\square M_{1}M_{2}M_{3}M_{4}$ ein Rechteck. q.e.d. (quod erat demonstrandum = was zu beweisen war)