Beweisarchiv: Geometrie
- Schwerpunktsätze von Leibniz
- Planimetrie
- Kreis: Mittelpunktswinkel-Umfangswinkel · Satz des Ptolemäus · Sehnensatz · Sehnentangentenwinkel · Sehnenviereck · Sekantensatz · Tangentenviereck · Japanischer Satz für konzyklische Vierecke · Satz des Thales
- Rechtwinkliges Dreieck: Satz des Pythagoras
- Ellipse: Satz vom Flüstergewölbe · Konjugierte Durchmesser
- Regelmäßige Vielecke: Dreieck · Viereck · Fünfeck · Sechseck ·
- Dreieck: Satz des Heron · Berechnung des Flächeninhalts des Diagonalendreiecks im Quader · Elementarer Satz zur Charakterisierung des Schwerpunkts im Dreieck via Flächeninhalte
- Viereck: Flächenformel von Bretschneider
- Inzidenzgeometrie ·
- affine Geometrie: einfache Hilfssätze · Homothetien und Translationen · Desarguesche affine Ebenen sind Vektorräume
- Trigonometrie
- Additionstheoreme: Sinus · Kosinus · Tangens · Kotangens
- Trigonometriesätze: Sinussatz · Kosinussatz · Neue Folgerungen aus dem Projektionssatz der Dreiecksgeometrie
- Trigonometrie in der komplexen Ebene: Tangens und Kotangens in rechtwinkligen Dreiecken aus komplexen Zahlen
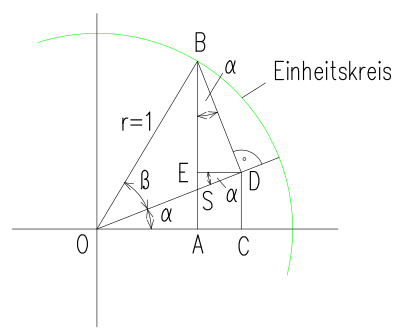
Beweis für:

Im rechtwinkligen Dreieck  ist
ist
(1) 
Im rechtwinkligen Dreieck  ist
ist
(2) 
und
(3) 
Im rechtwinkligen Dreieck  ist
ist
(4.1) 
(2) eingesetzt
(4.2) 
(4.3) 
Zwischenbeweis:
Die Dreiecke  und
und  sind beide rechtwinklig
sind beide rechtwinklig
und deshalb sind  Scheitelwinkel und daher ist auch
Scheitelwinkel und daher ist auch
(5.0) 
Im rechtwinkligen Dreieck  gilt:
gilt:
(5.1) 
(3) eingesetzt
(5.2) 
(5.3) 
(6.1) 
(4.3) und (5.3) eingesetzt
(6.2) 
in (1) eingesetzt
(7) 
Wenn Winkel  negativ:
negativ:
(8) 
(9a) 
und
(9b) 
eingesetzt in (8)
(10) 
(7) und (10) zusammengefasst
(11) 
Daraus ergibt sich auch für den doppelten Winkel
bei 
(12) 
(13) 
oder weil

(14.1) 
(14.2) 
oder
(15.1) 
(15.2) 
Halbwinkelformel
Aus Formel (14.2): 
wenn: 
(16) 
aufgelöst nach: 
(17.1) 
oder
(17.2) 
Beweis für:

Für den Beweis werden die Beziehungen

verwendet.
Es gilt:

Die Umformung zur vorletzten Zeile ist möglich, da entweder  oder
oder  auftritt.
auftritt.
Additionstheoreme













































