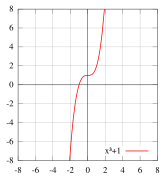
MathemaTriX ⋅ Aufgaben. Funktionen

Hoch

STOPP PUSHBACKS • FREE ASSANGE • FRIEDEN AUF DER WELT ${\color {white}\mathbf {MATHE} \mu \alpha T\mathbb {R} ix}$ DEINE FESTE BEGLEITERIN FÜR DIE SCHULMATHEMATIK EINFACH UND VERSTÄNDLICH GRATIS!* MIT MEHR ALS 200 THEORIE- UND AUFGABEN-ERKLÄRUNGS VIDEOS! Mathe lernen ist wie Fahrradfahren lernen: Du kannst es dir stundenlang erklären lassen, du wirst nie fahren können, wenn du nicht selber zu fahren probierst.

Inhalt Ein-Aus- klappen

AUFGABEN

KAPITEL Grundrechenarten Bruchrechnungen $-{\tfrac {\cdot \ +}{\ :\ }}$ Schlussrechnung Prozentrechnung Exponentialfunktion Logarithmus Arbeiten mit Termen $\mathbb {X} ^{2}$ Zahlendarstellungen Mengentheorie Aussagenlogik ${\begin{matrix}\mathbb {R} :=\\\mathbb {Q} \cup \mathbb {I} \end{matrix}}$ Einheiten $cm^{2}$ Statistik und Wahrscheinlichkeit Geometrische Konstruktionen Geometrie der Ebene Geometrie des Raums Diagramme Funktionen $f(x)$ Lineare Gleichungssysteme ${\begin{smallmatrix}{a_{1}\ b_{2}}\\{a_{2}\ b_{2}}\end{smallmatrix}}$ Trigonometrische Funktionen Vektoren Differentialrechnung $^{dy}/_{dx}$ Integralrechnung $\textstyle \int _{a}^{b}dx$ Folgen $a_{n}$ Beweise $a\rightarrow b$

Funktion allgemein

Lineare Funktion

Steigung und y Achsenabschnitt

Tabelle für eine lineare Funktion erstellen

1. 
   

   Erstellen Sie eine Tabelle mit dem Wert von x und y und den entsprechenden Punkt (x|y) für die lineare Funktion $y=-2x+1$ und für die folgenden x-Werte: $-2,\ -1,\ 0,\ 1,\ 2.$ Für die gleiche Funktion sind folgende y-Werte gegeben: $-4,\ -2,\ 0,\ 2,\ 4.$ Finden Sie die entsprechenden x-Werte.

2. 
   

   Erstellen Sie eine Tabelle mit dem Wert von x und y und den entsprechenden Punkt (x|y) für die lineare Funktion $y=-2x+1$ und für die folgenden x-Werte: $-4,\ -2,\ 0,\ 2,\ 4.$ Für die gleiche Funktion sind folgende y-Werte gegeben: $-2,\ -1,\ 0,\ 1,\ 2.$ Finden Sie die entsprechenden x-Werte.

3. 
   

   Erstellen Sie eine Tabelle mit dem Wert von x und y und den entsprechenden Punkt (x|y) für die lineare Funktion $y=3x-1$ und für die folgenden x-Werte: $-2,\ -1,\ 0,\ 1,\ 2.$ Für die gleiche Funktion sind folgende y-Werte gegeben: $-4,\ -2,\ 0,\ 2,\ 4.$ Finden Sie die entsprechenden x-Werte.

4. 
   

   Erstellen Sie eine Tabelle mit dem Wert von x und y und den entsprechenden Punkt (x|y) für die lineare Funktion $y=3x-1$ und für die folgenden x-Werte: $-4,\ -2,\ 0,\ 2,\ 4.$ Für die gleiche Funktion sind folgende y-Werte gegeben: $-2,\ -1,\ 0,\ 1,\ 2.$ Finden Sie die entsprechenden x-Werte.

5. 
   

   Erstellen Sie eine Tabelle mit dem Wert von x und y und den entsprechenden Punkt (x|y) für die lineare Funktion $y=-0,5x+2$ und für die folgenden x-Werte: $-2,\ -1,\ 0,\ 1,\ 2.$ Für die gleiche Funktion sind folgende y-Werte gegeben: $-4,\ -2,\ 0,\ 2,\ 4.$ Finden Sie die entsprechenden x-Werte.

6. 
   

   Erstellen Sie eine Tabelle mit dem Wert von x und y und den entsprechenden Punkt (x|y) für die lineare Funktion $y=-0,5x+2$ und für die folgenden x-Werte: $-4,\ -2,\ 0,\ 2,\ 4.$ Für die gleiche Funktion sind folgende y-Werte gegeben: $-2,\ -1,\ 0,\ 1,\ 2.$ Finden Sie die entsprechenden x-Werte.

7. 
   

   Erstellen Sie eine Tabelle mit dem Wert von x und y und den entsprechenden Punkt (x|y) für die lineare Funktion $y=1,5x-3$ und für die folgenden x-Werte: $-2,\ -1,\ 0,\ 1,\ 2.$ Für die gleiche Funktion sind folgende y-Werte gegeben: $-4,\ -2,\ 0,\ 2,\ 4.$ Finden Sie die entsprechenden x-Werte.

8. 
   

   Erstellen Sie eine Tabelle mit dem Wert von x und y und den entsprechenden Punkt (x|y) für die lineare Funktion $y=1,5x-3$ und für die folgenden x-Werte: $-4,\ -2,\ 0,\ 2,\ 4.$ Für die gleiche Funktion sind folgende y-Werte gegeben: $-2,\ -1,\ 0,\ 1,\ 2.$ Finden Sie die entsprechenden x-Werte.

Lineare Funktion Alltagsbeispiel

Die Talstation einer Seilbahn befindet sich auf 346 m Höhe, die erste Station auf dem Berg auf 930 m Höhe und in einer horizontalen Abstand von 2,84 km. Nehmen wir an, dass das Seil gerade ist. Fertigen Sie eine Skizze dieses Zusammenhangs in einem Koordinatensystem an. Wie lautet die entsprechende lineare Funktion? Auf welcher Höhe befindet sich das Seil in einem horizontalen Abstand von 490 m von der Talstation entfernt? Bei welchem horizontalen Abstand ist die Höhe 560 m?

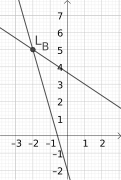
Diagramm einer linearen Funktion mit Hilfe von zwei Punkten erstellen

Eine lineare Funktion mit Hilfe von zwei Punkten ermitteln

Das Diagramm stellt den Gewinn bei der Produktion von Mehl dar.

Einheiten der Steigung

Die Steigung und ihre Zusammenhänge

Zeigen Sie, dass die Steigung s einer linearen Funktion $\textstyle s={\frac {\Delta y}{\Delta x}}\$ist!

Textaufgaben zu den linearen Funktionen

Der 69 Liter Tank eines Generators ist zu zwei drittel voll und verbraucht jede 10 Minuten halbes Liter Brennstoff. Geben Sie zuerst den Zusammenhang zwischen Zeit und Volumen des Brennstoffes als lineare Funktion an! Wie lang dauert es, bis der Tank leer wird? Nach wie viel Zeit hat der Tank noch 25 Liter?

Darstellungen der linearen Funktion

1. Wie lautet die implizite und die Vektorform der
   linearen Funktion $y={\tfrac {2}{3}}x-5$?
2. Wie lautet die explizite und die Vektorform der
   linearen Funktion $5x+2y=13$?
3. Wie lautet die explizite und die implizite Form der
   linearen Funktion ${\tbinom {x}{y}}={\tbinom {3}{4}}t+{\tbinom {0}{3}}$?
4. Berechnen Sie den Winkel zwischen den Geraden der zweiten und der dritten Funktion!

Lösung(en) einer Funktion

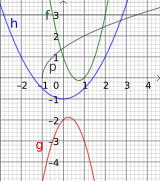
Schnittpunkte von Funktionen

Schnittpunkte von Funktionen in einem Diagramm

Im Bild sehen wir eine Polynomfunktion r(x) (gestrichelt), drei quadratische Funktionen p(x), q(x) und h(x) (zwei Kurven p und h nach oben und eine Kurve q nach unten) und zwei lineare Funktionen g(x) und f(x) (Gerade g nach unten rechts und Gerade f nach oben rechts). Lesen Sie vom Diagramm ab: Die Lösungen (Nullstellen) jeder Funktion. Den y-Achsenabschnitt jeder Funktion. Die Lösungen der Gleischungssysteme, die aus folgenden Funktionen bestehen: i) g und f $\quad$ii) p und r $\quad$iii) p und g iv)f und q $\quad$v) r und f $\quad$vi) g und h

Schnittpunkte von Funktionen in einem Text

Gegeben sind die Funktionen $g(x)=2x-3$$\quad f(x)=-{\frac {7}{3}}x\quad$$q(x)=-0{,}04x^{2}+0{,}64$ $p(x)=-x^{2}-1\quad \ h(x)=0{,}25x^{2}-x+1$ Berechnen Sie die Lösungen (Nullstellen) jeder Funktion! Lesen Sie den y-Achsenabschnitt jeder Funktion ab! Finden Sie, ob der Punkt P:(2|−5) zu mancher der Funktionen gehört! Lesen Sie die Steigung der beiden Geraden ab! Berechnen Sie die Lösungen der folgenden Gleichungssysteme i) g und f, ii) p und q, iii) p und g

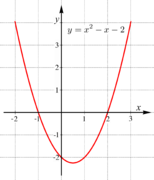
Die quadratische Funktion

Die quadratische Gleichung

Lösen Sie folgende quadratische Gleichungen: $3w^{2}-4w+1=0$ $4c^{2}+1=0$ $4m^{2}+12m+9=0$

Quadratische Gleichung Textaufgaben

Ein PKW fährt von Brüssels ins 212 km entfernte Amsterdam. Nachdem er 145 km zurückgelegt hat, begegnet ihm ein LKW, der 24 Minuten später von Amsterdam nach Brüssels abgefahren ist und in der Stunde 20 km weniger zurücklegt als der PKW. Berechnen Sie die Geschwindigkeit des PKWs. Nach wie viel Zeit treffen die Wagen einander?

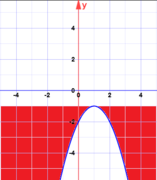
Quadratische Funktion Vertiefung

Ermitteln Sie den Scheitelpunkt der quadratischen Funktion $c(k)=4k^{2}+7k-2$ Mit Hilfe der quadratischen Ergänzung wandeln Sie diese Funktion zu einer Plus-Minus binomsiche Formel!

Polynomfunktionen Diagramm

In den folgenden Diagrammen bestimmen Sie den Grad der dargestellten Polynomfunktion, die Anzahl ihrer Lösungen, ihr Monotonieverhalten in den verschiedenen Intervallen, das Vorzeichen der Koeffizienten der Potenz mit dem höchsten Grad und wenn möglich den Wert des y-Achsenabschnitts! A B C D E F G H I

Umkehrfunktionen mit Umformen finden

Finden Sie die Umkehrfunktion: $\ y=5\ x+{\frac {1}{3}}\quad$

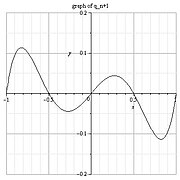
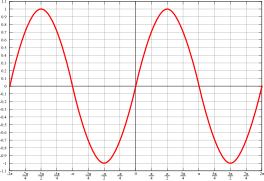
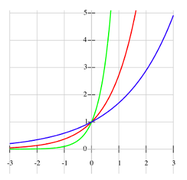
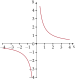
Funktionserkennung in Diagramm und Text

Funktionserkennung in Diagramm

Welches der folgenden Diagrammen stellt was dar? A) lineare Funktion, B) Polynomfunktion 2. Grades C) Wurzelfunktion, D) Polynomfunktion 3. Grades E) Polynomfunktion 4. Grades, F) Sinusfunktion G) Kosinusfunktion, H) quadratische Funktion, K) (natürlichen) Logarithmusfunktion, L) $\textstyle {\frac {a}{x}}$ M) Exponentialfunktion, N) Umkehrfunktionenpaar 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

Funktionsdiagramme Eigenschaften erkennen

Wählen Sie das jeweils richtige Diagramm und beantworten Sie die entsprechende Frage! Wie viel ist der y-Achsenabschnitt bei jedem Diagramm? Wie viel ist die Steigung der linearen Funktionen? $ax^{2}+bx+c\$ist die quadratische Funktion. Bei welcher Funktion ist a negativ bzw. positiv? $ae^{b\ x}\$ist die exponentielle Funktion. ${\frac {a}{x}}\$ist die indirekte Proportionalität. Bei welcher Funktion ist a negativ bzw. positiv? In welchen Intervallen sind die quadratischen und die linearen Funktionen, die Sinusfunktionen bzw die indirekte Proportionalität steigend bzw. fallend? Gibt es in irgendeinem Diagramm eine Funktion und ihre Umkehrfunktion? Gibt es in irgendeinem Diagramm eine Funktion und ihre auf der y-Achse gespeigelte Funktion? Was gilt in diesem Fall für f(x) und ihre Spiegelfunktion fs(x)?

Funktionserkennung in Text

Im Folgenden finden wir verschiedene Diagramme, Formel und Namen von Funktionen als auch Textaufgaben darüber. Welche sind die richtigen Kombinationen für jede Textaufgabe? Mit Hilfe der Textaufgaben finden Sie die Werte der Parameter a und b in der dem Text entsprechenden Formel. Texte TA (Text A) Fanny will feststellen, ob ihre Katze einen freien Fall überlebt und lässt sie aus einem 8 m hohen Turm mit einer 3 m/s² festen Beschleunigung Fallen. TB (Text B) Die Bevölkerung in Deutschland ist ca. 82 Millionen und wird jede Jahrzehnte um 2,3% weniger. TC (Text C) Bei der Schwingung einer Feder ist die maximale Ablenkung 3 cm, eine vollständige Wiederholung braucht 350 ms. TD (Text D) Ein Baum ist 3,5 m groß und wächst pro Woche um 5 cm. TE (Text E) Eine 1,8 dm große Kerze schmilzt jede Stunde um 3 cm. TF (Text F) Wenn wir auf einen Nagel eine Kraft ausüben, ist der Druck desto größer, je kleiner die Fläche A an der Spitze des Nagels ist aber je größer die Kraft F ist. (Hier a und b durch entsprechende Symbole ersetzten) TG (Text G) Ein Bakterienkultur verdreifacht sich jede Stunde. Am Anfang gibt es 5 Bakterien. Diagramme DA (Diagramm A) DB (Diagramm B) DC (Diagramm C) DD (Diagramm D) DE (Diagramm E) DF (Diagramm F) DG (Diagramm G) DH (Diagramm H) DI (Diagramm I) Funktionsnamen NA: (Name A) lineare, NB:(Name B) quadratische, NC: (Name C) exponentielle, ND: (Name D) logarithmische, NE: (Name E) Potenzfunktion 3. Grades, NF: (Name F) Sinusfunktion, NG: (Name G) Wurzelfunktion, NH:(Name H) indirekte Proportionalität. Formeln FA: (Formel A)$\ y=a\ x+b\quad$FB: (Formel B)$\ y=a\ e^{b\ x}\quad$FC: (Formel C)$\ y=a\tan b\ x\quad$ FD: (Formel D)$\textstyle \ y={\frac {a}{b}}\quad$FE: (Formel E)$\ \textstyle \ y=a\sin {\frac {1}{2\pi b}}x\quad$ FF: (Formel F)$\ y=a\ x^{2}+b\quad$FG: (Formel G)$\ y=a\ x^{3{,}2}+b\quad$