MathemaTriX ⋅ Wiederholung

STOPP PUSHBACKS • FREE ASSANGE • FRIEDEN AUF DER WELT

${\color {white}\mathbf {MATHE} \mu \alpha T\mathbb {R} ix}$	DEINE FESTE BEGLEITERIN
	FÜR DIE SCHULMATHEMATIK

EINFACH UND
VERSTÄNDLICH

GRATIS!^*

STARTEN!

MIT MEHR ALS 200 THEORIE- UND AUFGABEN-ERKLÄRUNGS VIDEOS!

Mathe lernen ist wie Fahrradfahren lernen: Du kannst es dir stundenlang erklären lassen, du wirst nie fahren können, wenn du nicht selber zu fahren probierst.

Inhalt
Ein-Aus-
klappen

Links

HAUPTSEITE

\ \

NIVEAU

\ \

TERMINE

\ \

THEMA

\ \

VOLL

Kurzanleitung

Du entscheidest bei jedem Thema, ob du erst ein Video sehen oder die Theorie lesen oder doch die Aufgaben direkt ausprobieren willst.
	Klickst du auf dieses Bild, findest du eine Aufgabensammlung zum entsprechenden Thema
	Klickst du auf dieses Bild, findest du externe Links zu entsprechenden Projekten und Videos im Internet
	Klickst du auf dieses Bild oder , findest du ein entsprechendes Theorie-Video^[1]
	Klickst du auf dieses Bild, findest du ein entsprechendes Video mit gelösten Aufgaben^[1]
	Klickst du auf dieses Bild oder , findest du das entsprechende Theorie-Teil
	Klickst du auf dieses Bild, findest du entsprechende Beispiele aus offiziellen Prüfungen!
	Klickst du auf dieses Bild, kannst du in der entsprechende Seite deine Frage stellen!

↑ ^1,0 ^1,1 Dieses Bild bedeutet allerdings, dass kein solches Projekt-Video zur Zeit vorhanden ist

Probetests

Probetests
•[ Himmel]-Lösung

Maturas Nach Thema

\ \

WH Alle Maturas mit Lösungen

Rechts

{\color {blue}\ell ichtung}

Einheiten und Zahlendarstellung

Grundwissen

Phys. Größe	Einheiten

Zeit (t)	Tag	24	h	60	min	60	s	1000	ms

Masse (m) ("Gewicht")	t	1000	kg	1000	g	1000	mg

Abstand (d, $\ell$ ,...) (Strecke, ...)	km	1000	m	10	dm	10	cm	10	mm

Fläche (A)	km²	1000²	m²	10²	dm²	10²	cm²	10²	mm²

Volumen (V)	km³	1000³	m³	10³	dm³ $(\ell )$	10³	cm³	10³	mm³

Umrechnung	groß	$----\longrightarrow$			mal	$----\longrightarrow$			klein

		$\longleftarrow ----$			durch	$\longleftarrow ----$

Zusammengesetzte Einheiten:

Jeder "Teil"-Einheit müssen wir durch die entsprechende "Ziel"-Einheit ersetzen.

Beispiel:

Rechnen wir 45 in/s in m/min um, wenn wir wissen, dass 5 Zoll (englische Längeneinheit, Symbol "in" von "inch") 127 mm sind. Jeder "Teil"-Einheit wird durch die entsprechende "Ziel"-Einheit ersetzt. Wir haben zwei "Teil"-Einheiten Zoll (in) und Sekunde (s) (für die Umrechnungen kann man notfalls auch Schlussrechnung benutzen).

5 Zoll sind 127 mm, also 0,127 m. Daher ist 1 Zoll (in):

$1\ in={\tfrac {0{,}127}{5}}\ m.$

1 Minute ist 60 Sekunde daher ist 1 s:

$1\ s={\tfrac {1}{60}}\ min\$

Wir ersetzen dann die "Teil"-Einheiten durch die "Ziel"-Einheiten:

$\textstyle 45{\frac {in}{s}}=45{\dfrac {\cancelto {=1\ in}{{\frac {0{,}127}{5}}\ m}}{\cancelto {=1\ s}{{\frac {1}{60}}\ min}}}=45\cdot {\dfrac {\frac {0{,}127}{5}}{\frac {1}{60}}}{\frac {m}{min}}=68{,}58{\frac {m}{min}}$

Wenn wir mehrere Werte der gleichen physikalischen (oder sonst) Größe mit unterschiedlichen Einheiten vergleichen wollen, dann wählen wir eine Einheit und rechnen wir alle andere auf diese Einheit um.

Gleitkommadarstellung

In der Gleitkommadarstellung haben wir eine Zahl z zwischen 1 und $9{,}{\dot {9}}$ (also $1\leq z<10$ und eine Potenz von 10. Die Zahl 340000 ist dann $3{,}4\cdot 10^{5}\$ (Komma 5 mal nach links verschoben, "Zahl kleiner geworden" also Hochzahl +5). Die Zahl 0,00673 ist dann $6{,}73\cdot 10^{-3}\$ (Komma 3 mal nach rechts verschoben, "Zahl größer geworden" also Hochzahl -3).

Präfixe

Die Präfixe stehen in der Formelsammlung!

Die Präfixe im SI:^[1]
Symbol	Name	Ursprung	Wert
T	Tera	gr. τέρας téras = Ungeheuer / gr. τετράκις tetrákis = viermal	10¹²	1.000.000.000.000	Billion
G	Giga	gr. γίγας gígas = Riese	10⁹	1.000.000.000	Milliarde
M	Mega	gr. μέγα méga = groß	10⁶	1.000.000	Million
k	Kilo	gr. χίλιοι chílioi = tausend	10³	1.000	Tausend
h	Hekto	gr. ἑκατόν hekatón = hundert	10²	100	Hundert
da	Deka	gr. δέκα déka = zehn	10¹	10	Zehn
—	—	—	10⁰	1	Eins
d	Dezi	gr. δέκατος dékatos daraus lat. decimus = zehnter	10⁻¹	0,1	Zehntel
c	Zenti	gr. ἑκατοστός hekatostós daraus lat. centesimus = hundertster	10⁻²	0,01	Hundertstel
m	Milli	lat. millesimus = tausendster	10⁻³	0,001	Tausendstel
µ	Mikro	gr. μικρός mikrós = klein	10⁻⁶	0,000 001	Millionstel
n	Nano	gr. νάνος nános = "Zwerg"	10⁻⁹	0,000 000 001	Milliardstel
p	Piko	ital. piccolo = klein	10⁻¹²	0,000 000 000 001	Billionstel

Zahlendarstellungen

Die gleiche Zahl kann in unterschiedlichen Darstellung auftauchen. Beispiel:

${\sqrt {81}}=3^{2}=9=900\%={\tfrac {90}{10}}={\tfrac {45}{5}}\ {\text{usw.}}$

In diesen Fall rechnen wir alles mit einem Hilfsmittel (z.B. GeoGebra) und vergleichen wir die Ergebnisse.

Wenn verschiedene Ausdrücke mit einem Symbol verglichen werden müssen, ersetzen wir dieses Symbol durch eine etwas komplexer Zahl (also nicht 0 oder 1 sondern z.B. 44) und führen wir den vorherigen Schritt aus: wir rechnen alles mit einem Hilfsmittel (z.B. GeoGebra) und wir vergleichen die Ergebnisse. Beispiel:

${\sqrt {a^{3}}}\$ mit $a^{1{,}5}\$ vergleichen. Ersetzen wir a durch 44 und machen wir die Berechnung:

${\sqrt {44^{3}}}\approx 291{,}86$

$44^{1{,}5}\approx 291{,}86$

Also wir können annehmen, dass die Ausdrücke gleichwertig sind.

Das ist selbstverständlich kein genauer Weg, er macht allerdings das Leben einfacher (sonst muss man einige Regeln lernen ).

Einheiten und Zahlendarstellung

Prozentrechnung

Der Wert am Anfang (Grundwert) ist 100%. Das ist der Wert, mit dem verglichen wird ("als", Genitiv oder "von"). Bei zeitlicher Reihenfolge ist das der erste Wert (außer wenn der zweite Wert der Vergleichswert ist).
Prozentberechnungen gehen notfalls (und am Einfachsten) mit Hilfe der Schlussrechnung. Am besten allerdings mit der Umrechnung arbeiten (siehe weiter: "Komma verschieben")
Prozent ist eine Zahl. Prozent bedeutet "Hundertstel".
Daher ist 100%=1
Also: von % zur Zahl Komma zwei mal links, von Zahl zu % zwei mal rechts verschieben.
Bei Wachstum addiert man den "Wachstumsprozent" zu 100%, bei Abnahme wird subtrahiert.

Beispiele: 0,02%=0,0002; 230=23000%; 230%=2,3 also 130% mehr als der Anfangswert; 0,8=80% also 20% weniger als der Anfangswert.

Bei einer Reihenfolge von Prozentänderungen ist das Ergebnis nicht die Summe der Prozentänderungen: Der Grundwert ist nicht der Gleiche!

Beispiel: Eine Pflanze wird 20% größer und dann noch 50% größer. Das Endergebnis ist nicht 70% größer!
Der Grundwert ist nicht der Gleiche!
Um die tatsächliche Gesamtänderung zu berechnen gehen wir so vor:
$100\%+20\%=120\%=1{,}2.\$
$100\%+50\%=150\%=1{,}5.\$
$1{,}2\cdot 1{,}5=1{,}8=180\%.\$
Also 80% Wachstum. Klarer wird es mit konkreten Zahlen.

Prozentrechnung vertiefend

Änderungen

y in Abhängigkeit von x, y in Bezug auf x, je x desto y
Punkt (x|y), also erst x und dann y.
Absolute Änderung: $\Delta y$ also nur die y-Änderung $(\Delta y=y_{2}-y_{1})$ für die zwei angegebenen x-Werte. Also die x-Werte sind angegeben, die y-Werte muss man subtrahieren!
Relative Änderung: ${\tfrac {\Delta y}{y_{1}}}={\tfrac {y_{2}-y_{1}}{y_{1}}}$ keine Einheiten (kann man mit Kommaverschieben als Prozentsatz angeben). Die Differenz der y-Werte durch den ersten y-Wert.
Mittlere Änderungsrate, auch Differenzenquotient.: ${\tfrac {\Delta y}{\Delta x}}={\tfrac {y_{2}-y_{1}}{x_{2}-x_{1}}}$ Einheit: Einheiten der y-Achse pro eine Einheit der x-Achse. → Steigung der Gerade, die zwei Punkte verbindet.

Relative Änderung

Mittlere Änderungsrate

Lineare Funktion und Regression

y in Abhängigkeit von x
Punkt (x|y), also erst x und dann y.

Lineare Funktion, also Gerade.

$y=k\cdot x+d$
$f(x)=k\cdot x+d$
$y=m\cdot x+n$
$y=s\cdot x+A_{y}$

f(x) oder y ist die y-Achse (das y), x die x-Achse (das x).

d (bzw. n oder $A_{y}$ oder was auch immer nicht mit x multipliziert wird) ist der "Anfangswert", also der Wert der Funktion (y-Wert) da, wo x Null ist (y-Achsenabschnitt). Die Einheiten von d sind die Einheiten des y-Achse.

k (bzw. m oder s oder was auch immer mit x multipliziert wird) ist die Steigung der lineare Funktion. Wenn die Gerade eine Verbindung zwischen zwei Punkte in einem Liniendiagramm darstellt, dann sprechen wir von einer mittlere Änderungsrate. Die Steigung (z.B. k) ist positiv, wenn die Funktion nach oben geht, negativ wenn sie nach unten geht und Null wenn sie parallel zur x.Achse ist. y=d (z.B. y=4) bedeutet, dass die Steigung gleich Null ist, also die Gerade ist parallel zur x-Achse. Es gilt:
$k={\tfrac {\Delta y}{\Delta x}}$
Die Einheiten der Steigung sind daher y-Einheiten pro eine x-Einheit.

Für die Funktion selber können wir beliebige Symbole benutzen, z.B.:

$A(h)=d\cdot h+m$

In diesem Beispiel steht A(h) als Ausdruck für die Abhängigkeit, also A (wofür in der Angabe A steht) in Abhängigkeit von h (wofür in der Angabe h steht). A(h) ist daher hier das y, h steht für das x. Mit h (also das Symbol für die x-Achse) wird hier d multipliziert, also ist d hier doch die Steigung. m wird zu diesem Produkt addiert, daher ist es der y-Achsenabschnitt ("Anfangswert").

In einem Punkt schreiben wir erst x und dann y (x|y). Um herauszufinden, ob drei oder mehrere Punkte zu einer und derselben Gerade gehören, können wir ggf. Tabellenkalkulation benutzen. Tabellenkalkulation benutzen wir bei der Regression.

Die lineare Funktion kommt oft als Regressionsgerade vor. Der Korrelationskoeffizient (mit r angegeben) ist NICHT mit der Steigung zu verwechseln. Im ersten Bild sind die Punkte weit entfernt von der Gerade, im zweiten fast auf der Gerade, also im zweiten Fall ist der Koeffizient fast 1 (in diesem Fall allerdings −1, da fallend), im ersten Bild hingegen zwischen 0 und 1, aber näher zu 0,5. Man sagt: "Der lineare Zusammenhang zwischen (was auch immer auf den beiden Achsen steht) ist schwach (falls r nah zu 0) bzw. stark (im Gegenfall)". In Geogebra als r abzulesen, wenn man die Statistik (Symbol $\Sigma$ rechts oben im Diagramm) abruft, dafür ist die Gerade nicht notwendig.

Lineare Funktion und Regression

Exponentialfunktion

$N(t)=N_{0}\cdot a^{t}$

N(t) ist die y-Achse (das y), t die x-Achse (das x). $N_{0}\$ ist der "Anfangswert", also der Wert der Funktion (y-Wert) da, wo x Null ist (y-Achsenabschnitt). Die Basis der Potenzzahl (das ist ein "Änderungsfaktor") kann man auch als "Prozentsatz" interpretieren, z.B. $N(t)=N_{0}\cdot 0{,}964^{t}$ bedeutet, dass bei jeder Änderung der x-Achse (z.B. t Zeit in Jahren) um 1 (z.B. jährlich) bleiben (0,964=) 96,4% des vorherigen Wertes, also 3,6% (100%−96,4%) weniger.

Extra Merkmal der Exponentialfunktion: Halbwertszeit: Nach der gleichen Änderung des x-Wertes wird der Wert der Funktion (y-Wert) immer halbiert. Im Bild: Am Anfang (also an der Stelle 0) ist der Wert der Funktion

N(0)=N_{0}\cdot a^{t}=8000\cdot a^{0}=8000\cdot 1=8000

, nach 3,5 auf der x-Achse (also an der Stelle 3,5) ist N(t) =N(3,5)=4000 (also die Hälfte), nach noch 3,5 auf der x-Achse (also an der Stelle 7) ist N(t) 2000 (also die Hälfte der Hälfte) usw.
Die Halbwertszeit kann man berechnen, indem man am Wert Funktion die Hälfte des Anfangswerts einsetzt, z.B.

2350=4700\cdot 0{,}9^{t}

(2350 ist die Hälfte von 4700) oder

0{,}5=0{,}6^{t}

(hier "fehlt" der Anfangswert, er ist also 1, und die Hälfte von 1 ist ja 0,5). Entsprechend für eine "Verdoppelungszeit" oder ähnliches:

2=0{,}7^{t}

,

7{,}6=3{,}8\cdot 0{,}9^{t}

usw.

Noch dazu: die Exponentialfunktion hat keine "Nullstellen": sie kommt immer näher zur x-Achse aber trifft diese nie!

Exponentialfunktion

Vergleich linearer und exponentieller Funktion

Lineare Funktion

Exponentialfunktion

Formel

f(x)=s\cdot x+A_{y}

N(t)=N_{0}\cdot a^{t}

Im Text erkennen durch

Steigung der Gerade
(in der Formel: s)
Änderungsrate
y-Einheiten PRO eine x-Einheit

Basis der Hochzahl
(in der Formel: a)
Relative Änderung
("Prozent"-Änderung)
des y-Wertes
bei Änderung des x-Wertes um 1

Änderungsrate

Absolut
(genauer Wert)

Relativ
(Anteil,
Prozent, -fach)

steigend ("nach oben")
Wachstum

s>0 (positiv)

a>1

fallend ("nach unten")
Abnahme

s<0 (negativ)

0<a<1

y-Achsenabschnitt
(i.d.R. "Anfangswert")

A_{y}

N_{0}

Diagramme

Funktionen allgemein

y in Abhängigkeit von x, y in Bezug auf x, je x desto y, bei Figuren oder so: y die Höhe und x der horizontale Abstand usw.
Punkt (x|y)→ x und y gegeben
- Punkt (x|y)
- Wert der Funktion → (y) an der Stelle → (x)
- Nullstelle a (a ist x, y ist Null)
- y-Achsenabschnitt b → da, wo die y-Achse abgeschnitten wird, also der Abschnitt b ist y und x wird Null sein. Auch Anfangswert (der Funktion) genannt (nicht mit dem Wert "am Anfang" in Prozentrechnung verwechseln, der ist 100%).

Wenn der Anfangswert (anders gesagt: der y-Achsenabschnitt) gefragt ist, dann an der Stelle von x Null einsetzen. OHNE löse!
Wenn eine Stelle (also x), oder was auch immer auf der x-Asche steht, gegeben ist und der Wert der Funktion, oder was auch immer auf der y-Achse steht, gefragt wird, dann an der Stelle von x diesen Wert einsetzen. OHNE löse!

Umformen

- Wenn der y-Wert (oder was auch immer allein auf der linken Seite einer Formel steht) gefragt wird und all der Rest gegeben ist (z.B. x-Wert gegeben), dann KEINE löse in Geogebra benutzen (sondern einfach als Taschenrechner benutzen).

löse in GeoGebra hat 3 Varianten:

Wenn zwei oder mehrere Sachen gefragt sind (Koeffizienten in einer Polynomfunktion oder allgemein in einer Funktion, Kombination von Eigenschaften), schreiben wir Symbole für die gefragten Sachen (für Polynomfunktionen sind es standardmäßig z.B. a,b,c,d für eine Funktion 3. Grades, muss aber nicht sein, für Textaufgaben können wir frei die Symbole wählen). Dann brauchen wir so viele Gleichungen, wie die gefragten Sachen (die mit Symbolen dargestellt werden). Wir haben in diesem Fall mehrere Symbole und so viele Gleichungen wie die Symbole. → löse mit geschweiften Klammern und Beistriche zwischen den Gleichungen benutzen!
Wenn der y-Wert gegeben ist, dann setzen wir diesen Wert in die Funktion für was auch immer für y da steht ein (z.B. V, H(a), wo a das x ist, f(x), also das ganze f(x) ersetzen). → löse OHNE geschweifte Klammer und OHNE Beistriche!
- es kann auch eine Formel sein, wo das gegeben ist, was auf der linken Seite der Formel ganz allein steht, z.B. das Volumen in der Formel V=a³, wobei V gegeben und a gefragt wird.
Wenn wir NUR eine Gleichung haben aber mehrere Symbole, dann benutzen wir löse OHNE geschweifte Klammern, allerdings mit Beistrich. Nach dem Beistrich steht das Symbol, auf das wir die Gleichung lösen wollen (sonst weiß GeoGebra nicht, auf welches Symbol die Gleichung zu lösen ist).

Umformen

Kurvendiskussion Umkehraufgaben

F ist der y-Achsenabschnitt, die Nullstelle −1,8 sehen wir (knapp) ganz links. Die Steigung der Funktion f (rot) am Punkt C bzw. an der Stelle C_x ist so viel, wie die Steigung der Tangente t (blau), also −0,9 oder auch so viel wie tan(α). Bei A und B (extrema) ist f´(x)=0

GeoGebra: Löse mit geschwungenen Klammern (und Beistriche zwischen den Gleichungen)!

y in Abhängigkeit von x, y in Bezug auf x, je x desto y, bei Figuren oder so: y die Höhe und x der horizontale Abstand usw.

Bei Kurvendiskussion Umkehraufgaben ist:
- entweder ein Punkt gegeben:
  → Funktion selber benutzen
- oder die Steigung (1. Ableitung):
  → 1. Ableitung benutzen

Punkt (x|y)→ x und y gegeben
- Punkt (x|y)
- Wert der Funktion → (y) an der Stelle → (x)
- Nullstelle a (a ist x, y ist Null)
- y-Achsenabschnitt b → da, wo die y-Achse abgeschnitten wird, also der Abschnitt b ist y und x wird Null sein. Auch Anfangswert (der Funktion) genannt (nicht mit dem Wert "am Anfang" in Prozentrechnung verwechseln, der ist 100%).

Steigung (Wenn 1 Punkt gegeben ist) :
- 1. Ableitung = f´(x) (in Geogebra Funktion schreiben und das Symbol f´ benutzen)
- "momentane Änderungsrate an der Stelle a ist c" oder
- f´(a)=c:
  →f´(x) wird durch c ersetzt und x wird durch a (die Stelle a oder was im Klammer bei f´(a) steht) ersetzt
- Winkel (f´(x) durch tan(Winkel) ersetzen)
- Tangente (die Tangente t ist eine Gerade: t(x)= k⋅x+d. f´(x) durch die Steigung k dieser Gerade ersetzen)
- knickfrei (gleiche Steigung)
- Extrempunkt (oder Extremstelle) (und alles was „extrem“ bedeutet, also höchste, tiefste, kleinste usw.)
  → Steigung Null 0: f´(x) durch 0 ersetzen

Steigung (Wenn 2 Punkte gegeben sind) :
- mittlere Änderungsrate
- Steigung einer Gerade
- Differenzenquotient
- $k={\tfrac {\Delta y}{\Delta x}}$ (k oder whatever Buchstabe für die Steigung der Gerade da steht)

Intervall → x-Achse (wenn nichts anderes gesagt wird)

Kurvendiskussion Umkehraufgaben

Kurvendiskussion direkte Anwendung

Textaufgaben 1. Ableitung

Ausdrücke, die für die 1. Ableitung oft vorkommen (besonders bei der direkter Anwendung der Kurvendiskussion), sind diejenigen, die mit einer Änderungsrate zu tun haben, z.B. Geschwindigkeit in einem Weg-Zeit Diagramm. Beispiele:

Bei welcher (was auf die x-Achse steht) hat die Funktion ihren größten Wert (was auf die y-Achse steht)? → Hier muss man die Stelle (x-Wert) mit Hilfe der 1. Ableitung (f'(x)=0, in CAS mit "löse") berechnen, da wo die Funktion ihren größten Wert (y-Wert) hat (also an einem "Gipfel" im Diagramm). Entsprechend wenn der kleinste Wert gefragt wird.
Wie viel ist der größte Wert (was auf die y-Achse steht)? → Hier muss man erst die Stelle (x-Wert) mit Hilfe der 1. Ableitung (f'(x)=0, in CAS mit "löse") berechnen. Dann müssen wir diese Stelle (x-Wert) in der eigentlichen Funktion ("Anfangsfunktion") einsetzten und den y-Wert berechnen (in CAS ohne "löse"). Entsprechend wenn der kleinste Wert gefragt wird.
Wir findet man den größten (bzw. kleinsten) Wert der Funktion? Hier keine GeoGebra! Man braucht "nur" die Beschreibung: " Wir setzen die 1. Ableitung gleich Null und wir berechnen dadurch die Stelle, wo die Funktion ihr Extremwerten hat. Dann setzen wir diese Stelle (x-Wert) an die eigentliche Funktion ein und berechnen wir den entsprechendn Wert der Funktion (y-Wert)."

Textaufgaben 2. Ableitung

Die Ausdrücke für die 2. Ableitung sind etwas schwieriger beim Verständnis, z.B. kann gefragt werden, wo die Änderungsrate der Funktion einen Extremwert (Minimum oder Maximum) hat (an dieser Stelle ist dan die 2.Ableitung gleich NulFoll). In einem s-t (Abstand-Zeit) Diagramm ist die 2. Ableitung die Beschleunigung. Beispiel:

An welcher Stelle steigt die (was auch immer auf der y-Achse steht) am schnellsten (bzw. langsamsten)? 2. Ableitung gleich Null setzten und entsprechende Stelle berechnen.

Positiv oder Negativ

Wert der Funktion: positiv, wenn die Kurve oberhalb der x-Achse ist, negativ unterhalb und Null (Nullstelle) wenn sie die x-Achse schneidet oder berührt.
1. Ableitung: positiv, wenn die Funktion "nach oben" geht, negativ "nach unten". Null bei einem "Gipfel" oder "Talsohle".
2. Ableitung (nur für Nerds): positiv, wenn man auf der Kurve "fährt" und links abbiegen muss, negativ beim Rechstabbiegen (Null: "gerade fahren", in der Regel dazwischen).

Folgende Stichwörter sind in der Regel bei der Textaufgaben der direkten Anwendung der Kurvendiskussion nicht notwendig.

Stichwörter Kurvendiskussion

Anwendung der Funktion selbst
$f(x)\$ allgemein Am Punkt $(x_{wert}\|y_{wert})$ Die Funktion hat an der Stelle c ( $x_{wert}$ ) den Wert d ( $y_{wert}$ ) $y_{wert}\$ in Abhängigkeit von $x_{wert}$ $y_{wert}\$ in Bezug auf $x_{wert}$ je $x_{wert}\$ desto $y_{wert}$
$f(x)=0$ x-Achsenabschnitt Nullstellen
$f(0)=A_{y}$ y-Achsenabschnitt Die Funktion schneidet die y-Achse an ... (oder Ähnliches)

Anwendung der ersten Ableitung
$f'(x)\$ allgemein *(Wert der) Ableitung der Funktion* (an einem Punkt oder Stelle) Steigung der Funktion (an einem Punkt oder Stelle) Steigung der Tangente der Funktion (an einem Punkt oder Stelle) knickfrei (gleiche Steigung) Tangens des Winkels zwischen Tangente der Funktion und x-Achse (an einem Punkt oder Stelle) momentane Änderungsrate
$f'(x)=0$ Die Funktion hat einen Extrempunkt (Maximum: Hochpunkt* oder Minimum: Tiefpunkt)* Die Tangente läuft parallel zur x-Achse (oder senkrecht zur y-Achse, oder "steht normal" auf der y-Achse) Der Tangens ist null Die Funktion hat einen Sattelpunkt

Anwendung der zweiten Ableitung
$f''(x)\$ allgemein Der Wert der zweiten Ableitung (an einem Punkt oder Stelle)
$f''(x)=0$ Die Funktion hat einen Wendepunkt an der Stelle p (an den Punkt $(p\|r)$ ) Die Funktion hat einen Sattelpunkt an der Stelle p (an den Punkt $(p\|r)$ )

Kurvendiskussion

Integrieren

Integral $\leftrightarrow$ Fläche
Geogebra: Integral(Funktion ohne f(x) schreiben, $x_{1},\ x_{2}$ )
Bei entsprechenden Aufgaben entsprechende Fläche schraffieren.

Wenn es um das Integral einer Funktion (und nicht einer Differen)z geht, dann ist das Integral dieser Funktion die Fläche zwischen Kurve und x-Achse und zwischen den Grenzen (Stellen, x-Werte), die im Integral angegeben werden. $\int _{a}^{b}f(x)dx$ (1. Bild). $\ a,\ b\$ sind daher hier Werte von x (Stellen) also ein Intervall [a;b] zwischen a und b auf der x-Achse, das die seitlichen (links und rechts) Grenzen des Integrals angibt. Die Funktion f(x) kann auch eine Zahl sein (!), z.B $\int _{a}^{b}3\ dx\$ ist die Fläche zwischen der Gerade y=3 (parallel zur x-Achse) und zwischen x=a und x=b, also die Fläche eines Rechtecks im Diagramm (ähnlich wie im 2. Bild).
Wenn es um das Integral einer Differenz geht, dann ist das Integral dieser Differenz die Fläche zwischen den beiden Funktionen (3. Bild). Aufpassen! Wenn ein Minus zwischen zwei Sachen da steht, dann haben wir schon zwei Funktionen. Dabei kann die eine nur eine Zahl sein, z.B. $\int _{a}^{b}(f(x)-4)dx.\ a,\ b\$ oder $\int _{a}^{b}(5-f(x))dx.\ a,\ b\$ (4. und 5. Bild).
Sind keine Grenzwerte angegeben, soll das sogenannte unbestimmte Integral berechnet werden (z.B. mit Geogebra), in diesem Fall steht auch eine Konstante immer dabei. Das Integral berechnet die Änderung der Größe, die durch die Fläche berechnet wird, z.B. zurückgelegte Strecke in einem v-t Diagramm (wie im Bild) und Geschwindigkeits-Änderung (und nicht die Geschwindigkeit an einem Zeitpunkt: dafür braucht man auch die Geschwindigkeit am Anfang) in einem a-t Diagramm (a: Beschleunigung).

Integrieren

Mittelwerte und Standardabweichung

Mittelwerte Arithmetisches Mittel (Durchschnitt): $\mathbf {Durchschnitt} ={\frac {\mathrm {Summe\ der\ Werte} }{\mathrm {Anzahl\ der\ Werte} }}={\frac {\sum _{i=1}^{n}a_{n}}{n}}$
Erwartungswert ist etwas wie der Durchschnitt

Zentralwert (Median): Den Median mehrerer Werte findet man, indem man die Werte zuerst der Größe nach ordnet (z.B. vom kleineren zum größeren) und dann den Wert in der Mitte der Reihe wählt.

Modalwert(e) oder Modus (die Modi). Der Modus von mehreren Werten ist der Wert, der am häufigsten vorkommt.

Wenn einer oder mehrerer Werte häufiger vorkommen, dann muss man bei der Berechnung des Durchschnitts den Wert mit der jeweiligen Häufigkeit multiplizieren und die Produkte addieren, wie in folgenden Beispiel mit Diagramm:

Bananen pro Packung	Anzahl der Packungen	Gesamte Bananen in diesen Packungen

0	4	0⋅4=	0
1	2	1⋅2=	2
2	3	2⋅3=	6
3	0	3⋅0=	0
4	5	4⋅5=	20
5	1	5⋅1=	5
	4+2+3+0+5+1=		0+2+6+0+20+5=
Summe	15 Packungen		33 Bananen

Es gibt also 33 Bananen in 15 Packungen. Der Durchschnitt ist daher: $\textstyle {\frac {33}{15}}=2,2$ B/P (Bananen pro Packung) im Durchschnitt.

In der Tabelle sind die Werte schon eingeordnet. Wir haben insgesamt 15 Werte (7+1+7), der Median wird daher der 8. Wert sein. Die erste 4 Werte sind '0', die nächsten 2 sind '1', die nächsten 3 sind '2'. 4+2+3 sind schon 9 Werte, der 8. Wert ist zwischen 7. und 9., also '2'.

Bei manchen Aufgaben ist es günstiger, Geogebra zu benutzen.

Lageparameter

Mittelwerte bei einem Säulendiagramm

Standardabweichung

Die Standardabweichung zeigt, wie "breit" um den Durchschnitt sich die Werte verteilen. Formel:
$s={\sqrt {{\frac {1}{n-1}}\sum \limits _{i=1}^{n}\left(x_{i}-{\overline {x}}\right)^{2}\quad }}$
Wenn wir also ein Formel in einem entsprechenden Thema sehen, die eine Wurzel von einer Summe beinhaltet, dann soll es die Standardabweichung sein, wie z.B.:
${\sqrt {\tfrac {5\cdot (18-21{,}93)^{2}+4\cdot (23-21{,}93)^{2}+1\cdot (21-21{,}93)^{2}+2\cdot (19-21{,}93)^{2}+2\cdot (24-21{,}93)^{2}}{14}}}$
Schauen wir mal, was hier so steht. In jeder Klammer unterhalb der Wurzel steht minus 21,93. Das ist der Durchschnitt (auch arithmetisches Mittel, oft auch einfach Mittelwert genannt).In der ersten Klammer steht davor die Zahl 5 und in der Klammer die Zahl 18. Das bedeutet, dass der Wert 18 5 mal vorkommt. Also, was vor jeder Klammer steht, ist die Häufigkeit des Wertes, der im Klammer steht (im Klammer steht allerdings, wie schon erwähnt, der Durchschnitt, der wird subtrahiert). Jede Klammer wird quadriert. Wenn das nicht der Fall ist, ist die Formel falsch. Was im Nenner steht, ist die gesamte Anzahl der Werte (manchmal um 1 reduziert). Tatsächlich, wenn wir in diesem Beispiel die Zahlen vor den Klammern addieren, bekommen wir $5+4+1+2+2=14.\$

Wenn wir keinen Nenner haben, dann steht vor jeder Klammer die entsprechende Wahrscheinlichkeit (des Wertes in der Klammer, der halt nicht der Durchschnitt ist):
${\sqrt {0{,}2\cdot (18-19{,}75)^{2}+0{,}1\cdot (23-19{,}75)^{2}+0{,}15\cdot (21-19{,}75)^{2}+0{,}5\cdot (19-19{,}75)^{2}+0{,}05\cdot (24-19{,}75)^{2}}}$
Hier ist der Durchschnitt 19,75, die Wahrscheinlichkeiten sind 20% für 18, 10% für 23, 15% für 21, 50% für 19 und 5% für 24.

Streumaßen

Boxplot

Die Daten sind eingeordnet. Die genauen Daten kann man nicht ablesen. Klar ist nur: die ein viertel kleinsten Werte befinden sich zwischen "Antenne" links (oder unten) und Anfang (links oder unten) des Rechtecks das sich irgendwo in der "Mitte" befindet; Diese linke (oder untere) Seite des Rechtecks ist das erste "Quartil". In diesem Rechteck und bis zur "Linie" irgendwo in seiner "Mitte" befindet sich das zweite viertel der eingeordneten Werte. Daher ist diese Linie (die nur in seltenen Fällen genau in der Mitte des Rechtecks ist) der Median (Zentralwert). Das dritte viertel befindet sich dann bis zur rechten (bzw. oberen) Seite des Rechtecks (drittes Quartil) und die größten viertel Werte sind darüber.

(Inter)Quartilabstand (IQR): Die Differenz der Werte an den Seiten des Rechtecks.

Spannweite (allgemein und nicht nur im boxplot): Maximum minus Minimum.

Möglicherweise gibt es "Ausreißer": Oft werden sie mit Hilfe des IQR definiert: ist der Wert links (einer der größten) mehr als das 1,5-fache des IQR als das dritte Quartil (rechte bzw obere Seite des Rechtecks), dann ist es ein Ausreißer.

Boxplot

Binomialverteilung

μ oder E(x)→ Erwartungswert (Durchschnitt, „wie viel ist im Mittel erwartet“, arithmetisches Mittel)
σ→ Standardabweichung

Merkmale:

Zwei mögliche Ergebnisse bei einem Versuch (z.B. schwarz oder nicht schwarz, ein Gegenstand oder eine Person hat eine Eigenschaft oder hat sie nicht)
Wahrscheinlichkeit bei jedem Versuch bleibt konstant

Eingabe in geogebra:

n: Gesamtanzahl der Versuche (Personen, Geräte oder was auch immer)
p: Wahrscheinlichkeit (Prozentsatz) bei einem Versuch (oder Wahrscheinlichkeit von einem Merkmal). Das ist ein Wert zwischen 0 und 1

$P(X=k)={\binom {n}{k}}p^{k}(1-p)^{n-k}:$ Wahrscheinlichkeit, dass unter n Wiederholungen (Versuche, Personen usw.) das Merkmal k mal vorkommt

VORSICHT: zwei Fälle unterscheiden:

(„Sonder“fall) Wir haben eine Anzahl A von Gegenständen. Ein Teilanzahl T davon hat eine Eigenschaft (z.B. Schwarz) der Rest (A minus T) nicht. Wir ziehen dann mit Zurücklegen c mal. In diesem Fall ist das c die gesamte Anzahl der Versuche und NICHT das A. Das A wird benutzt um die Wahrscheinlichkeit p bei einmal Ziehen zu berechnen, nämlich T/A (T durch A), z.B. schwarze Kugeln durch gesamte Kugeln.
(„Normal“fall) Wir haben eine Anzahl A von Gegenständen. Diesmal ist kein Teilanzahl von diesen A Gegenständen gegeben, die eine Eigenschaft haben, sondern eine Wahrscheinlichkeit p, dass sie diese Eigenschaft haben. Dann ist hier doch n=A die Gesamtanzahl und p ganz normal das p.

μ und σ liest man oben links ab!

$\mu =n\cdot p$
$\sigma ={\sqrt {n\cdot p\cdot (1-p)\ }}$

k liest man oben rechts (und weiter darunter), da liest man auch die Wahrscheinlichkeit P(X=k), dass das angegebene Merkmal k von n mal vorkommt:
$P(X=k)={\binom {n}{k}}p^{k}(1-p)^{n-k}$

Wenn es um mindestens bzw. höchstens geht, dann kommt in dieser Formel das Symbol ∑ vor:
$P(min\leq k\leq max)=\sum _{i=min}^{max}{\binom {n}{i}}p^{i}(1-p)^{n-i}$

höchstens a: P ( 0 ≤ X ≤ a) =
Null links, a rechts von X!

mindestens a: P ( a ≤ X ≤ n) =
a links, n rechts von X!

mindestens a und höchstens b: P ( a ≤ X ≤ b) =
a links, b rechts von X!

Nach dem „=“ steht die Wahrscheinlichkeit bei mehreren Versuchen (Personen usw.) also eine Zahl zwischen 0 und 1 (Prozent: zwei mal Komma veschieben)

Binomialverteilung

Normalverteilung

μ oder E(x)→ Erwartungswert (Durchschnitt, „wie viel ist im Mittel erwartet“, arithmetisches Mittel)
σ→ Standardabweichung

Merkmale:
Verteilung einer Eigenschaft, die unendlich viele Werte annehmen kann (z.B. Gewicht, Länge, Zeit usw.)

μ oder E(x) (Erwartungswert) ist der Wert auf der x-Achse genau in der „Mitte“ („Spitze“) des Diagramms.
Wenn f´´=0 oder das Wort „Wendepunkt“ an einem Punkt steht, dass ist der x-Wert 1 mal die Standardabweichung σ mehr als der Erwartungswert μ (rechts von μ, μ+σ) bzw. 1 mal weniger (links von μ, μ−σ).

In Geogebra kann man μ und σ eingeben!

**Bei größerem μ *verschiebt* sich das Diagramm nach rechts, bei kleinerem nach links**

**Bei anderem σ wird das Diagramm „spitzer“ (kleineres σ) bzw. „flächer“ (größeres σ)**

**Beispiel, wenn sich σ *und* μ ändern**

Man kann Grenzwerte a und b angeben:
P( a ≤ X ≤ b) =

Man kann auch eine von drei „Klammermöglichkeiten“ wählen: ] [] [

Aufpassen, welcher Bereich dann im Diagramm markiert ist!:

84,13%
15,87%

Mit der Klammer links: ] → P( a ≤ X) = p
hab ich eine Obergrenze b mit der Wahrscheinlichkeit p
(linker Bereich markiert, egal ob groß oder klein)

15,87%
84,13%

Mit der Klammer rechts: [ → P( X ≤ b) = p
hab ich eine Untergrenze b mit der Wahrscheinlichkeit p
(rechter Bereich markiert, egal ob groß oder klein)

68,27%
38,75%
50%

P( a ≤ X ≤ b) =
Nach dem „=“ steht die Wahrscheinlichkeit, also eine Zahl zwischen 0 und 1 (Prozent: zwei mal Komma veschieben). Das ist die Wahrscheinlichkeit, dass das Merkmal sich zwischen den zwei Grenzwerten a und b (x-Werte) steht (oder unterhalb oder oberhalb der Grenze bei den Klammer [ bzw. ] → achte auf den markierten Bereich!)

Mit [] kann man nicht den Prozentsatz p (mit Komma verschoben) eingeben, dafür braucht man entweder die Klammer [ oder die ]

Wenn ein symmetrisches Bereich in Frage kommt: Prozentsatz aus 100% subtrahieren und der Rest in zwei teilen. Die Grenzwerte für das Ergebnis mit den Klammern ] bzw. [ finden.
BEISPIEL

68,3% symmetrisches Interval:
100%-68,3%= 31,7%
31,7%:2=15,85%
linke Klammer ] wählen, p=0.1585 angeben und unteren Grenzwert markieren
rechte Klammer [ wählen, p=0.1585 angeben und oberen Grenzwert markieren
Somit haben wir die beiden Grenzwerte.

Die Wahrscheinlichkeit kann auch durch ein Bruch angegeben sein!

Normalverteilung bei gegebenen $\mu$ und $\sigma$

Baumdiagramm

Aufpassen! Wenn der Vorgang MIT zurücklegen ist, dann kann es wohl sein, dass KEIN Baumdiagramm notwendig ist (sondern Binomialverteilung).

Sind die Wahrscheinlichkeiten untereinander: multiplizieren. Beispiel: Wahrscheinlichkeit das eine Person Gruppe A und Rhesus positiv ist:
P(A+)=0,31⋅0,82
Gibt es mehrere "Pfade" nebeneinander: die entsprechenden Produkte addieren! Beispiel: Wahrscheinlichkeit das eine Person Rhesus positiv ist:
P(Rhesus +)=0,31⋅0,82+0,14⋅0,8+0,43⋅0,82+0,12⋅0,82
Die Summe der Produkte bei jeder "Zeile" soll immer 1 sein: beim Gegenereignis benutzen!
Die Wahrscheinlichkeit kann auch durch ein Bruch angegeben sein! Gibt es beispielsweise 2 Personen, die rote Kondome benutzen und 7, die andere Verhütungsmittel benutzen, müssen beim ersten Schritt die Brüche ${\tfrac {2}{9}}$ bzw. ${\tfrac {7}{9}}$ benutzt werden (also im Nenner immer die Summe und im Zähler die entsprechende Anzahl). Ist der Versuch ohne Zurücklegen, wird der Nenner bei jedem Schritt um 1 weniger, sonst bleibt er gleich.
Vorsicht "Zumindest 1" deutet auf die Gegenwahrscheinlichkeit an! Wenn dieser Ausdruck vorkommt, dann rechnet man 1 minus die Wahrscheinlichkeit von "keins" (das ist dann nur ein Pfad im Baumdiagramm)

Baumdiagramm

Vektoren

Seien $A={\binom {x_{A}}{y_{A}}}$ , $B={\binom {x_{B}}{y_{B}}}$ zwei Punkte und ${\vec {u}}={\binom {u_{x}}{u_{y}}}$ ein Vektor.

${\vec {AB}}={\binom {x_{B}-x_{A}}{y_{B}-y_{A}}}$
Betrag (Länge): $\left|{\vec {u}}\right|={\sqrt {u_{x}^{\ 2}+u_{y}^{\ 2}}}$ (nach dem Satz von Pythagoras, siehe Bild)

Seien ${\vec {a}}={\binom {a_{1}}{a_{2}}}$ , ${\vec {b}}={\binom {b_{1}}{b_{2}}}$ zwei Vektoren.

Strichrechnungen: ${\vec {a}}\pm {\vec {b}}={\binom {a_{1}}{a_{2}}}\pm {\binom {b_{1}}{b_{2}}}={\binom {a_{1}\pm b_{1}}{a_{2}\pm b_{2}}}$
Zahl mal Vektor: $m\cdot {\binom {b_{1}}{b_{2}}}={\binom {m\cdot b_{1}}{m\cdot b_{2}}}$
Skalarprodukt: ${\vec {a}}\cdot {\vec {b}}={\binom {a_{1}}{a_{2}}}\cdot {\binom {b_{1}}{b_{2}}}=a_{1}\cdot b_{1}+a_{2}\cdot b_{2}$ ${\vec {a}}\cdot {\vec {b}}={\binom {a_{1}}{a_{2}}}\cdot {\binom {b_{1}}{b_{2}}}=a_{1}\cdot b_{1}+a_{2}\cdot b_{2}$
- Wenn das Skalarprodukt null ist, dann ist der Winkel zwischen den Vektoren 90° ("sie stehen normal auf einander") un dumkegehrt, also wenn die Vektoren normal aufeinander stehen, dann ist ihr Skalarprotukt null.

Vektorrechnungen

Folgen

Mit der expliziten Formel wird das n-te Glied der Folge mit Hilfe des ersten berechnet.
Mit der rekursiven Formel wird das nächste Glied mit Hilfe des vorherigen berechnet. Das erste Glied muss angegeben sein.

Arithmetische Folge

Entspricht der linearen Funktion
Jedes nächste Glied ist um eine Zahl d mehr als das vorherige. Diese Zahl d nennt man Differenz (ist sie ja auch).
Explizite Formel: $a_{n}=a_{1}+(n-1)\cdot d\quad n\in \mathbb {N} _{*}$
n zeigt die Reihung des Glieds in der Folge
Rekursive Formel: $a_{1},\ \ a_{n+1}=a_{n}+d\quad n\in \mathbb {N} _{*}$ → Das erste Glied ist $a_{1},\$ das (n+1)-te Glied ist so viel wie das n-te Glied plus die Differenz d.

Geometrische Folge

Entspricht der exponentiellen Funktion
Jedes nächste Glied wird mit einer Zahl q multipliziert. Diese Zahl q nennt man Quotient (ist sie ja auch).
Explizite Formel: $b_{n}=b_{1}\cdot q^{n-1}\quad n\in \mathbb {N} _{*}$
n zeigt die Reihung des Glieds in der Folge
Rekursive Formel: $b_{1},\ \ b_{n+1}=b_{n}\cdot q\quad n\in \mathbb {N} _{*}$ → Das erste Glied ist $b_{1},\$ das (n+1)-te Glied ist so viel wie das n-te Glied mal den Quotient q.

Mengenlehre

S1\bigcup S2\

Vereinigung: Alles zusammen! Ausdruck: z.B. das eine oder das andere

S1\bigcap S2\

Schnitt: was gleichzeitig zu beiden gehört (unter dem Becher)! Ausdruck: Gleichzeitig - sowohl als auch

S1\setminus S2\

Differenz: das Erste ohne das, was dann auch zu zweite gehört! Ausdruck: Ohne

Bei Venn-Diagramm-Aufbau Aufgaben: immer mit der kleinsten Teilmenge anfangen, die angegeben oder zu berechnen ist. Das soll in der Regel entweder die Anzahl der Objekte, die keine der angegebenen Eigenschaften haben, sein, oder die Anzahl der Objekte die alle angegebenen Eigenschaften haben.

Mengenlehre

Geometrie

In Bearbeitung

Trigonometrie

$\sin \theta ={\frac {\text{Gegenkathete}}{\text{Hypotenuse}}}\$ und $\ \cos \theta ={\frac {\text{Ankathete}}{\text{Hypotenuse}}}\$

wobei $\theta$ irgendein nicht rechter Winkel
in einem Rechtwinkeligen Dreieck.

Für ein rechtwinkeliges Dreieck mit Seiten a, b (Katheten), c (Hypotenuse) und entsprechenden gegenüberliegenden Winkel $\alpha ,\ \beta ,\ \gamma$

$\textstyle \sin \beta ={\frac {b}{c}}(=\cos \alpha )\$ und $\textstyle \ \cos \beta ={\frac {a}{c}}(=\sin \alpha )$ ,

da gegenüber von $\beta$ die Seite b ist.

$\tan \alpha ={\frac {\text{Gegenkathete}}{\text{Ankathete}}}\ ={\frac {a}{b}}={\frac {c\ \sin \alpha }{c\ \cos \alpha }}={\frac {\sin \alpha }{\cos \alpha }}$

Umkehrfunktionen:

$\arcsin ,\ \arccos \$ bzw. $\ \arctan \$
oder $\sin ^{-1},\ \cos ^{-1}\$ bzw. $\ \tan ^{-1}\$ (besonders bei Taschenrechnern)

Die Anwendung ist bei jeder Aufgabe unterschiedlich.

Pythagoras Satz in Trigonometrie

$\sin ^{2}\phi +\cos ^{2}\phi =1$

Sinussatz:

${\frac {\sin \alpha }{a}}={\frac {\sin \beta }{b}}={\frac {\sin \gamma }{c}}$

Kosinussatz:

$c^{2}=a^{2}+b^{2}-2\,a\,b\,\cos \gamma \qquad$ (usw.)

Anwendung des Kosinussatzes: Wenn es um zwei Seiten und den Winkel dazwischen geht. In allen anderen Fällen Sinussatz oder sonstiges.

Textaufgaben Schlussbegriff für trigonometrische Funktionen: Wiederholung!

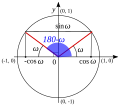
Einheitskreis

Winkel mit gleichen Kosinus
$\omega \ {\text{und }}360^{\circ }-\omega$
Winkel mit gleichen Sinus
$\omega \ {\text{und }}180^{\circ }-\omega$
Winkel mit gleichen Sinus und Kosinus
$\omega \ {\text{und }}360^{\circ }+\omega$

Trigonometrische Funktion

$A_{0}$ ist die Amplitude, $\phi$ die Phase, $f$ die Frequenz. Falls die Frequenz 1 ist, ist der "Berg zu Berg" Abstand $2\pi$ (also $360^{\circ }$ ), falls sie mehr als 1 ist, ist dieser Abstand kleiner. Die Phase ist nach links positiv.

Trigonometrische Aufgaben

Diagramme

In Bearbeitung

Diagramme

Altes Material (wird gelöscht)

Einheiten:
y in Abhängigkeit von x,
y in Bezug auf x
je ...x, desto ... y
horizontal (waagerecht): x
Höhe (senkrecht): y
usw.
Ist y angegeben, wird dieser Wert an der Stelle von f(x) eingesetzt, ist x angegeben, wird x durch diese Zahl ersetzt (GeoGebra: Löse, bei x sogar nicht notwendig)
Ist die Einheit nicht auf der x oder y Achse abzulesen, dann kann es die Ableitung (y-Achse durch x-Achse) oder das Integral (y-Achse mal x-Achse) sein.
Es gibt daher 4 Möglichkeiten, wenn eine Größe oder eine Einheit angegeben sind, nämlich:

die y-Achse,
die x-Achse,
die Steigung (Quotient y durch x Achse, 1. Ableitung oder mittlere Änderungsrate) oder
die Fläche (Produkt y mal x Achse, Integral)

Sowohl x als auch y sind gleichzeitig angegeben, wenn ein Punkt (x|y) angegeben ist.

Die folgenden Aufgaben sollst du an dieser Stelle nicht vollständig lösen Du sollst nur herausfinden, was jeweils auf den Achsen und was mit der 1. Ableitung dargestellt wird.
Lineare Funktion und Regression	Mathematrix: Werkzeuge/ Links

Die 1. Ableitung ist die Steigung der Funktion, ist die Steigung der Tangente, ist der Tangens des Winkels mit der x-Achse, ist die momentane Änderungsrate. Sie ist an einem Punkt zu berechnen. $f'(x)={\tfrac {dy}{dx}}={\tfrac {d\ f(x)}{dx}}={\tfrac {d}{dx}}f(x).\$

Mittlere Änderungsrate: ist die Steigung der verbindende Gerade zwischen zwei Punkten. $s={\tfrac {\Delta y}{\Delta x}}\$ Differenzenquotient. Einheiten wie die 1. Ableitung der Funktion (also y-Achse durch x-Achse). Sie ist das Gleiche wie die 1.Ableitung NUR dann, wenn die Funktion eine Gerade ist, braucht allerdings immer zwei Punkte (im Gegensatz zur 1. Ableitung).

Momentane Änderungsrate: ist die Steigung der Funktion an einem Punkt. Nur bei einer linearen Funktion ist sie gleich zur mittleren Änderungsrate, da bei einer Gerade die Steigung immer gleich bleibt.

Relative Änderung: ist eine reine Zahl (möglicherweise auch in % ausgedrückt). Differenz der Werte durch Wert am Anfang: $\left|{\tfrac {y_{ende}-y_{anfang}}{y_{anfang}}}\right|.\$ Befindet sich also im Nenner einer der beiden Werte des Zählers, ist der Bruch keine Steigung mehr (keine mittlere Änderungsrate) sondern eine relative Änderung. Prozentsatz ist allerdings dieser Bruch, nur wenn er mit 100% (was ja $100\cdot {\tfrac {1}{100}}$ also 1 ist) multipliziert wird.

Absolute Änderung: die Differenz zwei Werte (y-Werte) der Funktion. Auch wenn sie an zwei Stellen (x-Werte) der Funktion gefragt wird, kann es sein, dass wir doch die entsprechenden y-Werte subtrahieren müssen!

Der entscheidende Unterschied zwischen Änderungsrate und relativer Änderung ist daher der Nenner des Bruches. Ist er einer der beiden Werte des Zählers, dann geht es (fast immer) um eine relative Änderung. Ist er eine Differenz von Werten (der x-Achse), dann geht es um eine mittlere Änderungsrate (Steigung). Die absolute Änderung hingegen ist (fast immer) kein Bruch sondern einfach eine Differenz von zwei Werten.

Die Steigung kann daher entweder eine mittlere Änderungsrate sein oder eine momentane (1. Ableitung einer Funktion):
mittlere Änderungsrate, wenn es um zwei Punkte geht (dann ist sie auch die Steigung der verbindenden Gerade),
momentane Änderungsrate, wenn es um einen Punkt geht. Nur bei einer Gerade sind diese gleich (aber doch nicht gleichbedeutend, eben wegen der Punkte).

Eine Tangente "berührt" eine Kurve und schneidet diese nicht ab (zumindest nicht am gefragten Punkt).

Diagramme 1

Diagramme 2

Anwendung der Funktion selbst
$f(x)\$ allgemein Am Punkt $(x_{wert}\|y_{wert})$ Die Funktion hat an der Stelle c ( $x_{wert}$ ) den Wert d ( $y_{wert}$ ) $y_{wert}\$ in Abhängigkeit von $x_{wert}$ $y_{wert}\$ in Bezug auf $x_{wert}$ je $x_{wert}\$ desto $y_{wert}$
$f(x)=0$ x-Achsenabschnitt Nullstellen
$f(0)=A_{y}$ y-Achsenabschnitt Die Funktion schneidet die y-Achse an ... (oder Ähnliches)

Anwendung der ersten Ableitung
$f'(x)\$ allgemein *(Wert der) Ableitung der Funktion* (an einem Punkt oder Stelle) Steigung der Funktion (an einem Punkt oder Stelle) Steigung der Tangente der Funktion (an einem Punkt oder Stelle) knickfrei (gleiche Steigung) Tangens des Winkels zwischen Tangente der Funktion und x-Achse (an einem Punkt oder Stelle) momentane Änderungsrate
$f'(x)=0$ Die Funktion hat einen Extrempunkt (Maximum: Hochpunkt* oder Minimum: Tiefpunkt)* Die Tangente läuft parallel zur x-Achse (oder senkrecht zur y-Achse, oder "steht normal" auf der y-Achse) Der Tangens ist null Die Funktion hat einen Sattelpunkt

Anwendung der zweiten Ableitung
$f''(x)\$ allgemein Der Wert der zweiten Ableitung (an einem Punkt oder Stelle)
$f''(x)=0$ Die Funktion hat einen Wendepunkt an der Stelle p (an den Punkt $(p\|r)$ ) Die Funktion hat einen Sattelpunkt an der Stelle p (an den Punkt $(p\|r)$ )

Ausdrücke, die für die 1. Ableitung oft vorkommen (besonders bei der direkter Anwendung der Kurvendiskussion), sind diejenigen, die mit einer Änderungsrate zu tun haben, z.B. Geschwindigkeit in einem Weg-Zeit Diagramm. Die Ausdrücke für die 2. Ableitung sind etwas schwieriger beim Verständnis, z.B. kann gefragt werden, wo die Änderungsrate der Funktion einen Extremwert (Minimum oder Maximum) hat (an dieser Stelle ist dan die 2.Ableitung gleich Null).

Kurvendiskussion Umkehraufgaben

Kurvendiskussion

Fußnoten

↑ BIPM – SI prefixes (englisch) – „BIPM – SI-Broschüre“, 8. Auflage, März 2006, Abschnitt 3.1: SI-Präfixe

BILDERVERZEICHNIS

ÖFFNE DEIN HORIZONT!
LERNE MIT MATHEMATRIX!

\quad

\quad

\quad

$\mathbf {MATHE} \mu \alpha T\mathbb {R} ix$
LOGO	CH DE AT

SPENDEN
Der Hauptautor ggf. das Team verdient zwar nicht viel, braucht allerdings dein Geld eigentlich nicht. Wenn du aber doch meinst, dass gute Arbeit belohnt werden soll und dieses Projekt gut findest, kannst du immer in diesem Link spenden. Das ist allerdings vielleicht die einzige Einrichtung mit völliger Transparenz, wo du genau weißt, was mit deinem Geld passiert.

[KeinVideo-1] 1,0 ^1,1 Dieses Bild bedeutet allerdings, dass kein solches Projekt-Video zur Zeit vorhanden ist

[BIPM_–_SI_prefixes-2] BIPM – SI prefixes (englisch) – „BIPM – SI-Broschüre“, 8. Auflage, März 2006, Abschnitt 3.1: SI-Präfixe

[1]

[1]