Name
Majuskel
Minuskel
Alpha
Α
α
Beta
Β
β
Gamma
Γ
γ
Delta
Δ
δ
Epsilon
Ε
ε
Zeta
Ζ
ζ
Eta
Η
η
Theta
Θ
θ
Iota
Ι
ι
Kappa
Κ
κ
Lambda
Λ
λ
My
Μ
μ
Ny
Ν
ν
Xi
Ξ
ξ
Omikron
Ο
ο
Pi
Π
π
Rho
Ρ
ρ
Sigma
Σ
σ
Tau
Τ
τ
Ypsilon
Υ
υ
Phi
Φ
φ
Chi
Χ
χ
Psi
Ψ
ψ
Omega
Ω
ω
Majuskel
Minuskel
Majuskel
Minuskel
A
A
{\displaystyle {\mathfrak {A}}}
a
a
{\displaystyle {\mathfrak {a}}}
N
N
{\displaystyle {\mathfrak {N}}}
n
n
{\displaystyle {\mathfrak {n}}}
B
B
{\displaystyle {\mathfrak {B}}}
b
b
{\displaystyle {\mathfrak {b}}}
O
O
{\displaystyle {\mathfrak {O}}}
o
o
{\displaystyle {\mathfrak {o}}}
C
C
{\displaystyle {\mathfrak {C}}}
c
c
{\displaystyle {\mathfrak {c}}}
P
P
{\displaystyle {\mathfrak {P}}}
p
p
{\displaystyle {\mathfrak {p}}}
D
D
{\displaystyle {\mathfrak {D}}}
d
d
{\displaystyle {\mathfrak {d}}}
Q
Q
{\displaystyle {\mathfrak {Q}}}
q
q
{\displaystyle {\mathfrak {q}}}
E
E
{\displaystyle {\mathfrak {E}}}
e
e
{\displaystyle {\mathfrak {e}}}
R
R
{\displaystyle {\mathfrak {R}}}
r
r
{\displaystyle {\mathfrak {r}}}
F
F
{\displaystyle {\mathfrak {F}}}
f
f
{\displaystyle {\mathfrak {f}}}
S
S
{\displaystyle {\mathfrak {S}}}
s
s
{\displaystyle {\mathfrak {s}}}
G
G
{\displaystyle {\mathfrak {G}}}
g
g
{\displaystyle {\mathfrak {g}}}
T
T
{\displaystyle {\mathfrak {T}}}
t
t
{\displaystyle {\mathfrak {t}}}
H
H
{\displaystyle {\mathfrak {H}}}
h
h
{\displaystyle {\mathfrak {h}}}
U
U
{\displaystyle {\mathfrak {U}}}
u
u
{\displaystyle {\mathfrak {u}}}
I
I
{\displaystyle {\mathfrak {I}}}
i
i
{\displaystyle {\mathfrak {i}}}
V
V
{\displaystyle {\mathfrak {V}}}
v
v
{\displaystyle {\mathfrak {v}}}
J
J
{\displaystyle {\mathfrak {J}}}
j
j
{\displaystyle {\mathfrak {j}}}
W
W
{\displaystyle {\mathfrak {W}}}
w
w
{\displaystyle {\mathfrak {w}}}
K
K
{\displaystyle {\mathfrak {K}}}
k
k
{\displaystyle {\mathfrak {k}}}
X
X
{\displaystyle {\mathfrak {X}}}
x
x
{\displaystyle {\mathfrak {x}}}
L
L
{\displaystyle {\mathfrak {L}}}
l
l
{\displaystyle {\mathfrak {l}}}
Y
Y
{\displaystyle {\mathfrak {Y}}}
y
y
{\displaystyle {\mathfrak {y}}}
M
M
{\displaystyle {\mathfrak {M}}}
m
m
{\displaystyle {\mathfrak {m}}}
Z
Z
{\displaystyle {\mathfrak {Z}}}
z
z
{\displaystyle {\mathfrak {z}}}
Symbol
Bedeutung
Verwendung
Bedeutung
¬
{\displaystyle \neg }
Negation
¬
a
{\displaystyle \neg a}
nicht a
∧
{\displaystyle \land }
Konjunktion
a
∧
b
{\displaystyle a\land b}
a und b
∨
{\displaystyle \lor }
Disjunktion
a
∨
b
{\displaystyle a\lor b}
a oder b
⇒
{\displaystyle \Rightarrow }
Implikation
a
⇒
b
{\displaystyle a\Rightarrow b}
a impliziert b
⇔
{\displaystyle \Leftrightarrow }
Äquivalenz
a
⇔
b
{\displaystyle a\Leftrightarrow b}
a genau dann, wenn b
⊕
{\displaystyle \oplus }
Kontravalenz
a
⊕
b
{\displaystyle a\oplus b}
entweder a oder b
∀
{\displaystyle \forall }
Allquantor
∀
x
(
P
(
x
)
)
{\displaystyle \forall x(P(x))}
für alle x gilt: P (x )
∃
{\displaystyle \exists }
Existenzquantor
∃
x
(
P
(
x
)
)
{\displaystyle \exists x(P(x))}
es gibt ein x , für das gilt: P (x )
⊢
{\displaystyle \vdash }
syntaktische Implikation
M
⊢
B
{\displaystyle M\vdash B}
aus der Formelmenge M lässt sich B formal herleiten
⊨
{\displaystyle \models }
semantische Implikation
M
⊨
B
{\displaystyle M\models B}
bei jeder Interpretation, bei der alle Aussagen in M wahr sind, ist auch B wahr
Tautologie
⊨
B
{\displaystyle \models B}
B ist unter jeder Interpretation wahr
Zahlenbereiche
Symbol
Bedeutung
Beschreibung
N
∗
{\displaystyle \mathbb {N} ^{*}}
Menge der natürlichen Zahlen ohne Null
N
∗
=
{
1
,
2
,
3
,
4
,
…
}
{\displaystyle \mathbb {N} ^{*}=\{1,2,3,4,\ldots \}}
N
0
{\displaystyle \mathbb {N} _{0}}
Menge der natürlichen Zahlen mit Null
N
0
=
{
0
,
1
,
2
,
3
,
…
}
{\displaystyle \mathbb {N} _{0}=\{0,1,2,3,\ldots \}}
Z
{\displaystyle \mathbb {Z} }
Menge der ganzen Zahlen
Z
=
{
…
,
−
2
,
−
1
,
0
,
1
,
2
,
…
}
{\displaystyle \mathbb {Z} =\{\ldots ,-2,-1,0,1,2,\ldots \}}
Q
{\displaystyle \mathbb {Q} }
Menge der rationalen Zahlen
I
{\displaystyle \mathbb {I} }
Menge der irrationalen Zahlen
I
=
R
∖
Q
{\displaystyle \mathbb {I} =\mathbb {R} \setminus \mathbb {Q} }
R
{\displaystyle \mathbb {R} }
Menge der reellen Zahlen
C
{\displaystyle \mathbb {C} }
Menge der komplexen Zahlen
A
{\displaystyle \mathbb {A} }
Menge der algebraischen Zahlen
T
{\displaystyle \mathbb {T} }
Menge der transzendenten Zahlen
T
=
C
∖
A
{\displaystyle \mathbb {T} =\mathbb {C} \setminus \mathbb {A} }
H
{\displaystyle \mathbb {H} }
Menge der Quaternionen
Schreibweise
Bedeutung
{
}
{\displaystyle \{\}}
leere Menge
{
a
,
b
,
c
,
d
}
{\displaystyle \{a,b,c,d\}}
die Menge aus den Elementen a , b , c , d
{
x
∈
M
∣
P
(
x
)
}
{\displaystyle \{x\in M\mid P(x)\}}
die Menge der
x
∈
M
{\displaystyle x\in M}
P
(
x
)
{\displaystyle P(x)}
{
x
∈
R
∣
x
>
0
}
{\displaystyle \{x\in \mathbb {R} \mid x>0\}}
Menge der positiven reellen Zahlen
{
x
∈
R
∣
x
≥
0
}
{\displaystyle \{x\in \mathbb {R} \mid x\geq 0\}}
Menge der nichtnegativen reellen Zahlen
2
A
,
P
(
A
)
{\displaystyle 2^{A},\;{\mathcal {P}}(A)}
Potenzmenge von A
B
A
,
A
b
b
(
A
,
B
)
{\displaystyle B^{A},\mathrm {Abb} (A,B)}
Menge der Abbildungen von A nach B
A
n
{\displaystyle A^{n}}
n -faches kartesisches Produkt von A mit sich selbst
A
¯
,
A
C
{\displaystyle {\overline {A}},\;A^{\mathrm {C} }}
Komplementärmenge von A
Symbol
Bedeutung
Verwendung
Bedeutung
∈
{\displaystyle \in }
Element von
x
∈
M
{\displaystyle x\in M}
x ist ein Element von M
⊆
{\displaystyle \subseteq }
Teilmenge von
A
⊆
B
{\displaystyle A\subseteq B}
A ist eine Teilmenge von B
⊂
,
⊊
{\displaystyle \subset ,\subsetneq }
echte Teilmenge von
A
⊂
B
{\displaystyle A\subset B}
A ist eine echte Teilmenge von B
∪
{\displaystyle \cup }
Vereinigungsmenge
A
∪
B
{\displaystyle A\cup B}
Vereinigung von A und B
∩
{\displaystyle \cap }
Schnittmenge
A
∩
B
{\displaystyle A\cap B}
Schnitt von A und B
∖
{\displaystyle \setminus }
Differenzmenge
A
∖
B
{\displaystyle A\setminus B}
A ohne B
△
{\displaystyle \triangle }
symmetrische Differenz
A
△
B
{\displaystyle A\triangle B}
symmetrische Differenz von A und B
⋃
{\displaystyle \bigcup }
Vereinigungsmenge
⋃
i
∈
I
A
i
{\displaystyle \bigcup _{i\in I}A_{i}}
Vereinigung aller
A
i
{\displaystyle A_{i}}
i
∈
I
{\displaystyle i\in I}
⋂
{\displaystyle \bigcap }
Schnittmenge
⋂
i
∈
I
A
i
{\displaystyle \bigcap _{i\in I}A_{i}}
Schnitt aller
A
i
{\displaystyle A_{i}}
i
∈
I
{\displaystyle i\in I}
⨆
{\displaystyle \bigsqcup }
disjunkte Vereinigung
⨆
i
∈
I
A
i
{\displaystyle \bigsqcup _{i\in I}A_{i}}
Vereinigung aller
(
i
,
A
i
)
{\displaystyle (i,A_{i})}
i
∈
I
{\displaystyle i\in I}
×
{\displaystyle \times }
kartesisches Produkt
A
×
B
{\displaystyle A\times B}
kartesisches Produkt von A und B
∏
{\displaystyle \prod }
kartesisches Produkt
∏
i
∈
I
A
i
{\displaystyle \prod _{i\in I}A_{i}}
kartesisches Produkt der
A
i
{\displaystyle A_{i}}
i
∈
I
{\displaystyle i\in I}
Schreibweise
Bedeutung
[
a
,
b
]
{\displaystyle [a,b]}
geschlossenes Intervall
{
x
∈
R
∣
a
≤
x
≤
b
}
{\displaystyle \{x\in \mathbb {R} \mid a\leq x\leq b\}}
(
a
,
b
)
{\displaystyle (a,b)}
offenes Intervall
{
x
∈
R
∣
a
<
x
<
b
}
{\displaystyle \{x\in \mathbb {R} \mid a<x<b\}}
[
a
,
b
)
{\displaystyle [a,b)}
halboffenes Intervall
{
x
∈
R
∣
a
≤
x
<
b
}
{\displaystyle \{x\in \mathbb {R} \mid a\leq x<b\}}
(
a
,
b
]
{\displaystyle (a,b]}
halboffenes Intervall
{
x
∈
R
∣
a
<
x
≤
b
}
{\displaystyle \{x\in \mathbb {R} \mid a<x\leq b\}}
R
+
{\displaystyle \mathbb {R} ^{+}}
positive reelle Zahlen:
{
x
∈
R
∣
x
>
0
}
{\displaystyle \{x\in \mathbb {R} \mid x>0\}}
R
0
+
{\displaystyle \mathbb {R} _{0}^{+}}
nichtnegative reelle Zahlen:
{
x
∈
R
∣
x
≥
0
}
{\displaystyle \{x\in \mathbb {R} \mid x\geq 0\}}
R
−
{\displaystyle \mathbb {R} ^{-}}
negative reelle Zahlen:
{
x
∈
R
∣
x
<
0
}
{\displaystyle \{x\in \mathbb {R} \mid x<0\}}
R
0
−
{\displaystyle \mathbb {R} _{0}^{-}}
nichtpositive reelle Zahlen:
{
x
∈
R
∣
0
≤
x
}
{\displaystyle \{x\in \mathbb {R} \mid 0\leq x\}}
R
2
=
R
×
R
{\displaystyle \mathbb {R} ^{2}=\mathbb {R} \times \mathbb {R} }
die Koordinatenebene
R
×
{
0
}
{\displaystyle \mathbb {R} \times \{0\}}
die x -Achse
{
0
}
×
R
{\displaystyle \{0\}\times \mathbb {R} }
die y -Achse
R
×
R
+
{\displaystyle \mathbb {R} \times \mathbb {R} ^{+}}
die obere Halbebene
R
+
×
R
{\displaystyle \mathbb {R} ^{+}\times \mathbb {R} }
die rechte Halbebene
R
+
×
R
+
{\displaystyle \mathbb {R} ^{+}\times \mathbb {R} ^{+}}
der Quadrant (+,+)
f
|
A
{\displaystyle f|_{A}}
Einschränkung von
f
{\displaystyle f}
A
sup
M
{\displaystyle \sup M}
Supremum der Menge M
inf
M
{\displaystyle \inf M}
Infimum der Menge M
∑
k
=
m
n
a
k
{\displaystyle \sum _{k=m}^{n}a_{k}}
die Summe
a
m
+
a
m
+
1
+
⋯
+
a
n
−
1
+
a
n
{\displaystyle a_{m}+a_{m+1}+\cdots +a_{n-1}+a_{n}}
∏
k
=
m
n
a
k
{\displaystyle \prod _{k=m}^{n}a_{k}}
das Produkt
a
m
⋅
a
m
+
1
⋅
…
⋅
a
n
−
1
⋅
a
n
{\displaystyle a_{m}\cdot a_{m+1}\cdot \ldots \cdot a_{n-1}\cdot a_{n}}
lim
n
→
∞
a
n
{\displaystyle \lim _{n\to \infty }a_{n}}
Grenzwert der Folge
(
a
n
)
{\displaystyle (a_{n})}
lim
x
→
a
f
(
x
)
{\displaystyle \lim _{x\to a}f(x)}
Grenzwert der Funktion
f
{\displaystyle f}
x gegen a
d
f
(
x
)
d
x
|
x
=
a
{\displaystyle {\frac {\mathrm {d} f(x)}{\mathrm {d} x}}{\bigg |}_{x=a}}
Ableitung von
f
{\displaystyle f}
a
f
′
(
a
)
{\displaystyle f'(a)}
(
D
f
)
(
a
)
{\displaystyle (Df)(a)}
d
2
f
(
x
)
d
x
2
,
f
″
,
D
2
f
{\displaystyle {\frac {\mathrm {d} ^{2}f(x)}{\mathrm {d} x^{2}}},f'',D^{2}f}
zweite Ableitung von
f
{\displaystyle f}
d
n
f
(
x
)
d
x
n
,
f
(
n
)
,
D
n
f
{\displaystyle {\frac {\mathrm {d} ^{n}f(x)}{\mathrm {d} x^{n}}},f^{(n)},D^{n}f}
n -te Ableitung von
f
{\displaystyle f}
∫
f
(
x
)
d
x
{\displaystyle \int f(x)\,\mathrm {d} x}
unbestimmtes Integral von
f
{\displaystyle f}
∫
a
b
f
(
x
)
d
x
{\displaystyle \int _{a}^{b}f(x)\,\mathrm {d} x}
bestimmtes Integral von
f
{\displaystyle f}
[
a
,
b
]
{\displaystyle [a,b]}
C
H
∫
a
b
,
−
∫
a
b
{\displaystyle \mathrm {CH} \int _{a}^{b},\;-\!\!\!\!\!\!\int _{a}^{b}}
cauchyscher Hauptwert , engl. PV, CPV (principial value), franz. v.p.
[
F
(
x
)
]
x
=
a
x
=
b
{\displaystyle [F(x)]_{x=a}^{x=b}}
Kurzschreibweise für
F
(
b
)
−
F
(
a
)
{\displaystyle F(b)-F(a)}
Schreibweise
Bedeutung
∂
f
(
x
)
∂
x
k
|
x
=
a
{\displaystyle {\frac {\partial f(x)}{\partial x_{k}}}{\bigg |}_{x=a}}
partielle Ableitung von
f
{\displaystyle f}
a
(
D
k
f
)
(
a
)
{\displaystyle (D_{k}f)(a)}
(
∂
k
f
)
(
a
)
{\displaystyle (\partial _{k}f)(a)}
(
∇
f
)
(
a
)
{\displaystyle (\nabla f)(a)}
Gradient von
f
{\displaystyle f}
a
⟨
∇
,
F
⟩
(
a
)
{\displaystyle \langle \nabla ,\mathbf {F} \rangle (a)}
Divergenz von F an der Stelle a
(
∇
×
F
)
(
a
)
{\displaystyle (\nabla \times \mathbf {F} )(a)}
Rotation von F an der Stelle a
(
D
v
f
)
(
a
)
{\displaystyle (D_{v}f)(a)}
Richtungsableitung (in Richtung v ) von
f
{\displaystyle f}
a
[
(
d
f
)
(
a
)
]
(
v
)
{\displaystyle [(\mathrm {d} f)(a)](v)}
totales Differential von
f
{\displaystyle f}
a , dual gepaart mit dem Vektor v
(
D
f
)
(
a
)
{\displaystyle (Df)(a)}
Jacobi-Matrix von
f
{\displaystyle f}
a ;
x
=
(
x
1
,
…
,
x
n
)
{\displaystyle x=(x_{1},\ldots ,x_{n})}
a
=
(
a
1
,
…
,
a
n
)
{\displaystyle a=(a_{1},\ldots ,a_{n})}
J
[
f
]
(
a
)
{\displaystyle J[f](a)}
∂
f
(
x
)
∂
x
|
x
=
a
{\displaystyle {\frac {\partial f(x)}{\partial x}}{\bigg |}_{x=a}}
∫
γ
f
(
x
)
d
s
{\displaystyle \int _{\gamma }f(\mathbf {x} )\,\mathrm {d} s}
Kurvenintegral erster Art
∫
γ
⟨
F
(
x
)
,
d
x
⟩
{\displaystyle \int _{\gamma }\langle \mathbf {F} (\mathbf {x} ),\mathrm {d} \mathbf {x} \rangle }
Kurvenintegral zweiter Art
∫
γ
f
(
z
)
d
z
{\displaystyle \int _{\gamma }f(z)\,\mathrm {d} z}
komplexes Kurvenintegral
∫
C
{\displaystyle \int _{C}}
Kurvenintegral über einen doppelpunktfreien Weg
C
=
B
i
l
d
(
γ
)
{\displaystyle C=\mathrm {Bild} (\gamma )}
∮
C
{\displaystyle \oint _{C}}
Kurvenintegral über einen geschlossenen doppelpunktfreien Weg
Römische Ziffern
Ziffer
I
V
X
L
C
D
M
Wert
1
5
10
50
100
500
1000
Es gab keine Null.
Regeln:
Die Zeichen werden hintereinander geschrieben (wobei im Allgemeinen links mit dem Symbol der größten Zahl begonnen wird).
Ihre Werte werden addiert.
Die Grundzeichen (I, X, C, M) werden höchstens dreimal, die Hilfszeichen (V,L,D) nur einmal hintereinander geschrieben.
Steht das Symbol einer kleineren Zahl vor dem einer größeren, so wird der kleinere Wert vom größeren subtrahiert.
Es darf höchstens ein Symbol der nächstkleineren Zahl vorangestellt werden.
Römische Zahlen
Zahl
I
II
III
IV
V
VI
VII
VIII
IX
X
Wert
1
2
3
4
5
6
7
8
9
10
Zahl
X
XX
XXX
XL
L
LX
LXX
LXXX
XC
C
Wert
10
20
30
40
50
60
70
80
90
100
Zahl
C
CC
CCC
CD
D
DC
DCC
DCCC
CM
M
Wert
100
200
300
400
500
600
700
800
900
1000
Beispiele:
XVII = 10 + 5 + 1 + 1 = 17
MMIII = 1000 + 1000 + 1 + 1 + 1 = 2003
IX = 10 − 1 = 9 Die höchste Zahl, die damit dargestellt werden kann, ist somit 3999 (MMMCMXCIX).
Software
Microsoft Excel
=RÖMISCH(arabische Zahl)
LibreOffice Calc
=RÖMISCH(arabische Zahl)
Es ist
N
⊂
Z
⊂
Q
⊂
R
⊂
C
⊂
H
⊂
O
⊂
S
.
{\displaystyle \mathbb {N} \subset \mathbb {Z} \subset \mathbb {Q} \subset \mathbb {R} \subset \mathbb {C} \subset \mathbb {H} \subset \mathbb {O} \subset \mathbb {S} .}
N
{\displaystyle \mathbb {N} }
Z
{\displaystyle \mathbb {Z} }
Q
{\displaystyle \mathbb {Q} }
R
{\displaystyle \mathbb {R} }
C
{\displaystyle \mathbb {C} }
H
{\displaystyle \mathbb {H} }
O
{\displaystyle \mathbb {O} }
S
{\displaystyle \mathbb {S} }
C
{\displaystyle \mathbb {C} }
N
{\displaystyle \mathbb {N} }
N
0
{\displaystyle \mathbb {N} _{0}}
N
1
{\displaystyle \mathbb {N} _{1}}
Jede rationale Zahl
r
{\displaystyle r}
r
=
a
b
.
{\displaystyle r={\frac {a}{b}}.}
a
{\displaystyle a}
b
{\displaystyle b}
r
{\displaystyle r}
echt (eigentlich) für
0
<
|
a
|
<
|
b
|
,
0
<
|
r
|
<
1
{\displaystyle 0<|a|<|b|,\ 0<|r|<1}
unecht (uneigentlich) für
0
<
|
b
|
<
|
a
|
,
1
<
|
r
|
{\displaystyle 0<|b|<|a|,\ 1<|r|}
reduziert für
ggT
(
a
,
b
)
=
1
{\displaystyle \operatorname {ggT} (a,b)=1}
Stammbruch für
|
a
|
=
1
{\displaystyle |a|=1}
Zweigbruch für
|
a
|
≠
1
{\displaystyle |a|\neq 1}
Rechenoperationen erster bis dritter Stufe [ Bearbeiten ] [ Bearbeiten ] Addieren oder Zusammenzählen
Summand* + Summand* = Summe
3 + 4 = 7
*Früher wurde für den ersten Summanden auch der Begriff Augend und für die anderen Summanden auch der Begriff Addend verwendet.
Satz: Die Summanden dürfen beliebig vertauscht werden -> Kommutativgesetz
Subtrahieren oder Abziehen
Minuend - Subtrahend = Differenz
8 - 2 = 6
Faktor* x Faktor* = Produkt
8 x 8 = 64
* Früher wurde für den ersten Faktor auch der Begriff Multiplikator und für die anderen Faktoren auch der Begriff Multiplikand verwendet .
Satz: Die Faktoren dürfen beliebig vertauscht werden -> Kommutativgesetz
Dividieren, Teilen oder Bruchrechnen
Zähler
Nenner
{\displaystyle {\frac {\mbox{Zähler}}{\mbox{Nenner}}}}
Dividend
Divisor
=
Quotient
{\displaystyle {\frac {\mbox{Dividend}}{\mbox{Divisor}}}={\mbox{Quotient}}}
Beispiel:
8
2
=
4
{\displaystyle {\frac {8}{2}}=4}
0
,
25
{\displaystyle 0{,}25\ }
2
5
8
=
2
+
5
8
{\displaystyle 2{\frac {5}{8}}=2+{\frac {5}{8}}}
5
8
,
3
8
,
1
8
{\displaystyle {\frac {5}{8}},{\frac {3}{8}},{\frac {1}{8}}}
5
8
,
3
2
,
1
9
{\displaystyle {\frac {5}{8}},{\frac {3}{2}},{\frac {1}{9}}}
[ Bearbeiten ]
5
8
+
3
8
−
1
8
=
5
+
3
−
1
8
=
7
8
{\displaystyle {\frac {5}{8}}+{\frac {3}{8}}-{\frac {1}{8}}={\frac {5+3-1}{8}}={\frac {7}{8}}}
==
[ Bearbeiten ]
1
4
+
1
2
−
1
3
=
3
12
+
6
12
−
4
12
=
5
12
{\displaystyle {\frac {1}{4}}+{\frac {1}{2}}-{\frac {1}{3}}={\frac {3}{12}}+{\frac {6}{12}}-{\frac {4}{12}}={\frac {5}{12}}}
5
8
⋅
3
2
=
5
⋅
3
8
⋅
2
=
15
16
{\displaystyle {\frac {5}{8}}\cdot {\frac {3}{2}}={\frac {5\cdot 3}{8\cdot 2}}={\frac {15}{16}}}
5
8
:
2
3
=
5
⋅
3
8
⋅
2
=
15
16
{\displaystyle {\frac {5}{8}}:{\frac {2}{3}}={\frac {5\cdot 3}{8\cdot 2}}={\frac {15}{16}}}
Folgende Vorrangregeln sind in der Mathematik üblich.
Die Assoziativität ist nur bei Verletzung des Assoziativgesetzes von Bedeutung.
Im Zweifelsfall können Klammern gesetzt werden.
Operationen
Bedeutung
Assoziativität
a
i
{\displaystyle a_{i}}
Indizierung
rechts
f
(
x
)
{\displaystyle f(x)}
Funktionsapplikation
links
a
b
{\displaystyle a^{b}}
Potenzierung
rechts
−
a
{\displaystyle -a}
Negation
rechts
a
b
,
a
/
b
,
{\displaystyle ab,\,a/b,}
M
∩
N
{\displaystyle M\cap N}
Multiplikation, Division,
links
a
+
b
,
a
−
b
,
{\displaystyle a+b,\,a-b,}
M
∪
N
{\displaystyle M\cup N}
Addition, Subtraktion,
links
a
=
b
,
a
≠
b
,
{\displaystyle a=b,\,a\neq b,}
a
<
b
,
a
≤
b
,
{\displaystyle a<b,\,a\leq b,}
M
⊆
N
,
{\displaystyle M\subseteq N,}
a
∈
M
{\displaystyle a\in M}
Gleichheitsrelationen,
keine
¬
A
{\displaystyle \neg A}
logische Negation
rechts
A
∧
B
{\displaystyle A\land B}
Konjunktion
links
A
∨
B
,
A
⊕
B
{\displaystyle A\lor B,\,A\oplus B}
Disjunktion, Kontravalenz
links
A
⇒
B
,
A
→
B
{\displaystyle A\Rightarrow B,\,A\rightarrow B}
Implikation
keine
A
⇔
B
,
A
≡
B
{\displaystyle A\Leftrightarrow B,\,A\equiv B}
Äquivalenz
keine
A
⊢
B
,
A
⊨
B
{\displaystyle A\vdash B,\,A\models B}
syntaktische und semantische
keine
A
impliziert
B
{\displaystyle A\,\,{\text{impliziert}}\,\,B}
metasprachliche Implikation
keine
A
gdw.
B
{\displaystyle A\,\,{\text{gdw.}}\,\,B}
metasprachliche Äquivalenz
keine
Neutrales Element bezüglich der Addition: a + 0 = a .
Neutrales Element bezüglich der Subtraktion: a − 0 = a .
Neutrales Element bezüglich der Multiplikation: a · 1 = a .
Neutrales Element bezüglich der Division: a : 1 = a .
Verhältnis von Umfang eines Kreises zum Durchmesser des Kreises,
π
=
{\displaystyle \pi =}
Reihenentwicklung nach Leibniz:
π
4
=
∑
k
=
0
∞
(
−
1
)
k
2
k
+
1
=
1
−
1
3
+
1
5
−
1
7
+
1
9
−
1
11
+
⋯
{\displaystyle {\frac {\pi }{4}}=\sum _{k=0}^{\infty }{\frac {(-1)^{k}}{2\,k+1}}=1-{\frac {1}{3}}+{\frac {1}{5}}-{\frac {1}{7}}+{\frac {1}{9}}-{\frac {1}{11}}+\cdots }
Basis des natürlichen Logarithmus,
e = 2,71828 18284 59045 23536 02874 71352 66249 77572 47093 69995 95749 66967 …
e
=
∑
k
=
0
∞
1
k
!
=
1
+
1
1
+
1
1
⋅
2
+
1
1
⋅
2
⋅
3
+
1
1
⋅
2
⋅
3
⋅
4
+
⋯
{\displaystyle \mathrm {e} =\sum _{k=0}^{\infty }{\frac {1}{k!}}=1+{\frac {1}{1}}+{\frac {1}{1\cdot 2}}+{\frac {1}{1\cdot 2\cdot 3}}+{\frac {1}{1\cdot 2\cdot 3\cdot 4}}+\cdots }
γ
=
{\displaystyle \gamma =}
Γ
′
(
1
)
=
ψ
(
1
)
=
−
γ
{\displaystyle \Gamma ^{\prime }(1)=\psi (1)=-\gamma }
Die Zahl i ist das Grundelement der imaginären Zahlen,
i
2
=
−
1.
{\displaystyle \mathrm {i} ^{2}=-1.}
Achtung: Die für
x
,
y
≥
0
{\displaystyle x,y\geq 0}
x
y
=
x
y
{\displaystyle {\sqrt {x}}\,{\sqrt {y}}={\sqrt {xy}}}
x
,
y
{\displaystyle x,y}
So ist zum Beispiel
i
2
=
−
1
−
1
≠
(
−
1
)
(
−
1
)
=
1
=
1
{\displaystyle \mathrm {i} ^{2}={\sqrt {-1}}\,{\sqrt {-1}}\neq {\sqrt {(-1)(-1)}}={\sqrt {1}}=1}
2
=
{\displaystyle {\sqrt {2}}=}
3
=
{\displaystyle {\sqrt {3}}=}
5
=
{\displaystyle {\sqrt {5}}=}
Φ
=
1
+
5
2
=
{\displaystyle \Phi ={\frac {1+{\sqrt {5}}}{2}}=}
δ
=
{\displaystyle \delta =}
α
=
{\displaystyle \alpha =}
Sei
R
{\displaystyle R}
R
=
R
{\displaystyle R=\mathbb {R} }
R
=
C
{\displaystyle R=\mathbb {C} }
a
,
b
∈
R
{\displaystyle a,b\in R}
a
b
=
b
a
{\displaystyle ab=ba}
(
a
+
b
)
2
=
a
2
+
2
a
b
+
b
2
{\displaystyle (a+b)^{2}=a^{2}+2ab+b^{2}\,}
(erste binomische Formel)
(
a
−
b
)
2
=
a
2
−
2
a
b
+
b
2
{\displaystyle (a-b)^{2}=a^{2}-2ab+b^{2}\,}
(zweite binomische Formel)
a
2
−
b
2
=
(
a
+
b
)
(
a
−
b
)
{\displaystyle a^{2}-b^{2}=(a+b)(a-b)\,}
(dritte binomische Formel)
und:
(
a
+
b
)
3
=
a
3
+
3
a
2
b
+
3
a
b
2
+
b
3
{\displaystyle (a+b)^{3}=a^{3}+3a^{2}b+3ab^{2}+b^{3}\,}
a
3
+
b
3
=
(
a
+
b
)
(
a
2
−
a
b
+
b
2
)
{\displaystyle a^{3}+b^{3}=(a+b)(a^{2}-ab+b^{2})\,}
(
a
−
b
)
3
=
a
3
−
3
a
2
b
+
3
a
b
2
−
b
3
{\displaystyle (a-b)^{3}=a^{3}-3a^{2}b+3ab^{2}-b^{3}\,}
a
3
−
b
3
=
(
a
−
b
)
(
a
2
+
a
b
+
b
2
)
{\displaystyle a^{3}-b^{3}=(a-b)(a^{2}+ab+b^{2})\,}
Sei
R
{\displaystyle R}
R
=
R
{\displaystyle R=\mathbb {R} }
R
=
C
{\displaystyle R=\mathbb {C} }
a
,
b
∈
R
{\displaystyle a,b\in R}
a
b
=
b
a
{\displaystyle ab=ba}
(
a
+
b
)
n
=
∑
k
=
0
n
(
n
k
)
a
n
−
k
b
k
{\displaystyle (a+b)^{n}=\sum _{k=0}^{n}{\binom {n}{k}}a^{n-k}b^{k}}
(
a
−
b
)
n
=
∑
k
=
0
n
(
−
1
)
k
(
n
k
)
a
n
−
k
b
k
{\displaystyle (a-b)^{n}=\sum _{k=0}^{n}(-1)^{k}{\binom {n}{k}}a^{n-k}b^{k}}
(
a
+
b
)
2
=
a
2
+
2
a
b
+
b
2
{\displaystyle (a+b)^{2}=a^{2}+2ab+b^{2}}
(
a
−
b
)
2
=
a
2
−
2
a
b
+
b
2
{\displaystyle (a-b)^{2}=a^{2}-2ab+b^{2}}
(
a
+
b
)
3
=
a
3
+
3
a
2
b
+
3
a
b
2
+
b
3
{\displaystyle (a+b)^{3}=a^{3}+3a^{2}b+3ab^{2}+b^{3}}
(
a
−
b
)
3
=
a
3
−
3
a
2
b
+
3
a
b
2
−
b
3
{\displaystyle (a-b)^{3}=a^{3}-3a^{2}b+3ab^{2}-b^{3}}
(
a
+
b
)
4
=
a
4
+
4
a
3
b
+
6
a
2
b
2
+
4
a
b
3
+
b
4
{\displaystyle (a+b)^{4}=a^{4}+4a^{3}b+6a^{2}b^{2}+4ab^{3}+b^{4}}
(
a
−
b
)
4
=
a
4
−
4
a
3
b
+
6
a
2
b
2
−
4
a
b
3
+
b
4
{\displaystyle (a-b)^{4}=a^{4}-4a^{3}b+6a^{2}b^{2}-4ab^{3}+b^{4}}
usw.
usw.
Das pascalsche Dreieck ist eine Wertetabelle für die Binomialkoeffizienten
(
n
k
)
=
n
!
k
!
⋅
(
n
−
k
)
!
.
{\displaystyle {\binom {n}{k}}={\frac {n!}{k!\cdot (n-k)!}}.}
k =0k =1k =2k =3k =4k =5k =6k =7k =8
n =0
1
n =1
1
1
n =2
1
2
1
n =3
1
3
3
1
n =4
1
4
6
4
1
n =5
1
5
10
10
5
1
n =6
1
6
15
20
15
6
1
n =7
1
7
21
35
35
21
7
1
n =8
1
8
28
56
70
56
28
8
1
Das Dreieck lässt sich rekursiv durch die Vorschrift
(
n
k
)
+
(
n
k
+
1
)
=
(
n
+
1
k
+
1
)
{\displaystyle {\binom {n}{k}}+{\binom {n}{k+1}}={\binom {n+1}{k+1}}}
erzeugen.
Sei
R
{\displaystyle R}
a
1
,
…
,
a
m
∈
R
{\displaystyle a_{1},\ldots ,a_{m}\in R}
a
i
{\displaystyle a_{i}}
(
a
1
+
…
+
a
m
)
n
=
∑
k
1
+
…
+
k
m
=
n
(
n
k
1
,
…
,
k
m
)
a
1
k
1
⋅
…
⋅
a
m
k
m
.
{\displaystyle (a_{1}+\ldots +a_{m})^{n}=\sum _{k_{1}+\ldots +k_{m}=n}{\binom {n}{k_{1},\ldots ,k_{m}}}a_{1}^{k_{1}}\cdot \ldots \cdot a_{m}^{k_{m}}.}
In Multiindex-Notation:
(
a
1
+
…
+
a
m
)
n
=
∑
|
k
|
=
n
(
n
k
)
a
k
{\displaystyle (a_{1}+\ldots +a_{m})^{n}=\sum _{|k|=n}{\binom {n}{k}}a^{k}}
mit
k
=
(
k
1
,
…
,
k
m
)
,
{\displaystyle k=(k_{1},\ldots ,k_{m}),}
|
k
|
=
k
1
+
…
+
k
m
,
{\displaystyle |k|=k_{1}+\ldots +k_{m},}
(
n
k
)
=
(
n
k
1
,
…
,
k
m
)
:=
n
!
k
1
!
+
…
+
k
m
!
,
{\displaystyle {\binom {n}{k}}={\binom {n}{k_{1},\ldots ,k_{m}}}:={\frac {n!}{k_{1}!+\ldots +k_{m}!}},}
a
k
=
a
1
k
1
⋅
…
⋅
a
m
k
m
.
{\displaystyle a^{k}=a_{1}^{k_{1}}\cdot \ldots \cdot a_{m}^{k_{m}}.}
Die ersten Formeln sind:
n =2
(a+b)2
= a2 + b2 + 2ab
(a+b+c)2
= a2 + b2 + c2 + 2ab + 2ac + 2bc
(a+b+c+d)2
= a2 + b2 + c2 + d2 + 2ab + 2ac + 2ad + 2bc + 2bd + 2cd
n =3
(a+b)3
= a3 + b3 + 3a2 b + 3b2 a
(a+b+c)3
= a3 + b3 + c3 + 3a2 b + 3a2 c + 3b2 a + 3b2 c + 3c2 a + 3c2 b + 6abc
a
0
=
1
{\displaystyle a^{0}=1}
a
1
=
a
{\displaystyle a^{1}=a}
a
2
=
a
⋅
a
{\displaystyle a^{2}=a\cdot a}
a
3
=
a
⋅
a
⋅
a
{\displaystyle a^{3}=a\cdot a\cdot a}
usw.
a
n
=
a
⋅
a
⋅
…
⋅
a
⏟
n
F
a
k
t
o
r
e
n
{\displaystyle a^{n}=\underbrace {a\cdot a\cdot \ldots \cdot a} _{n\,\mathbf {Faktoren} }}
Definition für
a
∈
R
{\displaystyle a\in \mathbb {R} }
n
∈
Z
,
n
≥
0
{\displaystyle n\in \mathbb {Z} ,n\geq 0}
a
0
:=
1
,
0
0
:=
1
,
{\displaystyle a^{0}:=1,\quad 0^{0}:=1,}
a
n
:=
a
n
−
1
⋅
a
.
(
n
≥
1
)
{\displaystyle a^{n}:=a^{n-1}\cdot a.\quad (n\geq 1)}
Für
a
≠
0
{\displaystyle a\neq 0}
a
−
n
:=
1
a
n
.
{\displaystyle a^{-n}:={\frac {1}{a^{n}}}.}
Definition für
a
∈
R
,
a
>
0
{\displaystyle a\in \mathbb {R} ,a>0}
r
∈
R
{\displaystyle r\in \mathbb {R} }
a
r
:=
exp
(
r
⋅
ln
(
a
)
)
.
{\displaystyle a^{r}:=\exp(r\cdot \ln(a)).}
Für
r
≠
0
{\displaystyle r\neq 0}
a
r
:=
exp
(
ln
(
a
)
r
)
=
a
1
/
r
.
{\displaystyle {\sqrt[{r}]{a}}:=\exp \left({\frac {\ln(a)}{r}}\right)=a^{1/r}.}
Für
a
,
b
∈
R
,
a
,
b
>
0
{\displaystyle a,b\in \mathbb {R} ,a,b>0}
r
,
s
∈
R
{\displaystyle r,s\in \mathbb {R} }
a
r
a
s
=
a
r
+
s
{\displaystyle a^{r}a^{s}=a^{r+s}}
a
r
a
s
=
a
r
−
s
{\displaystyle {\frac {a^{r}}{a^{s}}}=a^{r-s}}
(
a
r
)
s
=
a
r
s
{\displaystyle (a^{r})^{s}=a^{rs}}
(
a
b
)
r
=
a
r
b
r
{\displaystyle (a\,b)^{r}=a^{r}b^{r}}
(
a
b
)
r
=
a
r
b
r
{\displaystyle {\Big (}{\frac {a}{b}}{\Big )}^{r}={\frac {a^{r}}{b^{r}}}}
(
1
a
)
r
=
1
a
r
{\displaystyle {\Big (}{\frac {1}{a}}{\Big )}^{r}={\frac {1}{a^{r}}}}
Ist zusätzlich
r
≠
0
{\displaystyle r\neq 0}
(
a
r
)
s
=
a
s
r
{\displaystyle ({\sqrt[{r}]{a}})^{s}={\sqrt[{r}]{a^{s}}}}
(
a
b
r
)
s
=
a
s
r
b
s
r
{\displaystyle ({\sqrt[{r}]{a\,b}})^{s}={\sqrt[{r}]{a^{s}}}{\sqrt[{r}]{b^{s}}}}
(
a
b
r
)
s
=
a
s
r
b
s
r
{\displaystyle \left({\sqrt[{r}]{\frac {a}{b}}}\right)^{s}={\frac {\sqrt[{r}]{a^{s}}}{\sqrt[{r}]{b^{s}}}}}
a
s
r
=
a
s
/
r
{\displaystyle {\sqrt[{r}]{a^{s}}}=a^{s/r}}
a
r
r
=
a
{\displaystyle {\sqrt[{r}]{a^{r}}}=a}
a
−
r
=
1
a
r
=
1
a
r
{\displaystyle {\sqrt[{-r}]{a}}={\frac {1}{\sqrt[{r}]{a}}}={\sqrt[{r}]{\frac {1}{a}}}}
Für
a
,
b
∈
R
{\displaystyle a,b\in \mathbb {R} }
m
,
n
∈
Z
,
m
,
n
≥
0
{\displaystyle m,n\in \mathbb {Z} ,m,n\geq 0}
(
a
b
)
n
=
a
n
b
n
{\displaystyle (a\,b)^{n}=a^{n}b^{n}}
(
a
m
)
n
=
a
m
n
{\displaystyle (a^{m})^{n}=a^{mn}}
b
≠
0
⟹
(
a
b
)
n
=
a
n
b
n
{\displaystyle b\neq 0\implies \left({\frac {a}{b}}\right)^{n}={\frac {a^{n}}{b^{n}}}}
Graph des Logarithmus zur Basis 2, e und 1/2 Für
a
,
x
,
y
∈
R
{\displaystyle a,x,y\in \mathbb {R} }
a
,
x
>
0
{\displaystyle a,x>0}
a
≠
1
{\displaystyle a\neq 1}
x
=
a
y
⟺
y
=
log
a
(
x
)
.
{\displaystyle x=a^{y}\iff y=\log _{a}(x).}
Für
x
,
y
,
a
,
r
∈
R
{\displaystyle x,y,a,r\in \mathbb {R} }
x
,
y
,
a
>
0
{\displaystyle x,y,a>0}
a
≠
1
{\displaystyle a\neq 1}
log
(
x
y
)
=
log
(
x
)
+
log
(
y
)
{\displaystyle \log(x\,y)=\log(x)+\log(y)}
log
(
1
)
=
0
{\displaystyle \log(1)=0\,}
log
a
(
x
)
=
log
(
x
)
log
(
a
)
{\displaystyle \log _{a}(x)={\frac {\log(x)}{\log(a)}}}
log
(
x
y
)
=
log
(
x
)
−
log
(
y
)
{\displaystyle \log \left({\frac {x}{y}}\right)=\log(x)-\log(y)}
log
(
1
x
)
=
−
log
(
x
)
{\displaystyle \log \left({\frac {1}{x}}\right)=-\log(x)}
log
(
x
r
)
=
r
log
(
x
)
{\displaystyle \log(x^{r})=r\,\log(x)}
r
≠
0
⟹
log
(
x
r
)
=
1
r
log
(
x
)
{\displaystyle r\neq 0\implies \log({\sqrt[{r}]{x}})={\frac {1}{r}}\,\log(x)}
Welcher Logarithmus verwendet wird, ist unerheblich. D. h. man setzt
log
:=
log
a
{\displaystyle \log :=\log _{a}}
a
{\displaystyle a}
a
>
0
{\displaystyle a>0}
a
≠
1
{\displaystyle a\neq 1}
log
:=
ln
{\displaystyle \log :=\ln }
log
:=
lg
{\displaystyle \log :=\lg }
Bezeichnung
Definierende
Basis
Natürliche Logarithmen
ln
e
ln
(
x
)
=
x
{\displaystyle \mathrm {e} ^{\ln(x)}=x\,}
e=2,718 281 828 459 045... (eulersche Zahl)
Dekadische Logarithmen
lg
10
lg
(
x
)
=
x
{\displaystyle 10^{\lg(x)}=x\,}
10
Binäre Logarithmen
lb, ld
2
l
b
(
x
)
=
x
{\displaystyle 2^{\mathrm {lb} (x)}=x\,}
2
Sind
f
,
g
{\displaystyle f,g}
G
{\displaystyle G}
f
(
x
)
=
g
(
x
)
{\displaystyle f(x)=g(x)}
eine Bestimmungsgleichung, wenn die Lösungsmenge
L
=
{
x
∈
G
∣
f
(
x
)
=
g
(
x
)
}
{\displaystyle L=\{x\in G\mid f(x)=g(x)\}}
gesucht ist.
Bei
G
{\displaystyle G}
L
=
{
(
x
,
y
)
∈
G
∣
f
(
x
,
y
)
=
g
(
x
,
y
)
}
,
{\displaystyle L=\{(x,y)\in G\mid f(x,y)=g(x,y)\},}
L
=
{
(
x
,
y
,
z
)
∈
G
∣
f
(
x
,
y
,
z
)
=
g
(
x
,
y
,
z
)
}
,
{\displaystyle L=\{(x,y,z)\in G\mid f(x,y,z)=g(x,y,z)\},}
usw. Man schreibt auch
x
=
(
x
1
,
x
2
)
{\displaystyle x=(x_{1},x_{2})}
x
=
(
x
1
,
x
2
,
x
3
)
{\displaystyle x=(x_{1},x_{2},x_{3})}
Äquivalenzumformungen lassen die Lösungsmenge einer Gleichung unverändert.
Seien
A
(
x
)
,
B
(
x
)
{\displaystyle A(x),B(x)}
Äquivalenz
Implikation
Gilt für alle
x
∈
G
{\displaystyle x\in G}
A
(
x
)
⟺
B
(
x
)
,
{\displaystyle A(x)\iff B(x),}
so gilt:
{
x
∈
G
∣
A
(
x
)
}
=
{
x
∈
G
∣
B
(
x
)
}
.
{\displaystyle \{x\in G\mid A(x)\}=\{x\in G\mid B(x)\}.}
Gilt für alle
x
∈
G
{\displaystyle x\in G}
A
(
x
)
⟹
B
(
x
)
,
{\displaystyle A(x)\implies B(x),}
so gilt:
{
x
∈
G
∣
A
(
x
)
}
⊆
{
x
∈
G
∣
B
(
x
)
}
.
{\displaystyle \{x\in G\mid A(x)\}\subseteq \{x\in G\mid B(x)\}.}
Seien
f
,
g
,
h
{\displaystyle f,g,h}
G
{\displaystyle G}
Z
=
R
{\displaystyle Z=\mathbb {R} }
Z
=
C
{\displaystyle Z=\mathbb {C} }
Für alle x gilt:
f
(
x
)
=
g
(
x
)
⟺
f
(
x
)
+
h
(
x
)
=
g
(
x
)
+
h
(
x
)
,
{\displaystyle f(x)=g(x)\iff f(x)+h(x)=g(x)+h(x),}
f
(
x
)
=
g
(
x
)
⟺
f
(
x
)
−
h
(
x
)
=
g
(
x
)
−
h
(
x
)
.
{\displaystyle f(x)=g(x)\iff f(x)-h(x)=g(x)-h(x).}
Besitzt
h
(
x
)
{\displaystyle h(x)}
x :
f
(
x
)
=
g
(
x
)
⟺
f
(
x
)
⋅
h
(
x
)
=
g
(
x
)
⋅
h
(
x
)
,
{\displaystyle f(x)=g(x)\iff f(x)\cdot h(x)=g(x)\cdot h(x),}
f
(
x
)
=
g
(
x
)
⟺
f
(
x
)
h
(
x
)
=
g
(
x
)
h
(
x
)
.
{\displaystyle f(x)=g(x)\iff {\frac {f(x)}{h(x)}}={\frac {g(x)}{h(x)}}.}
Besitzt
h
(
x
)
{\displaystyle h(x)}
x :
f
(
x
)
=
g
(
x
)
⟹
f
(
x
)
⋅
h
(
x
)
=
g
(
x
)
⋅
h
(
x
)
.
{\displaystyle f(x)=g(x)\implies f(x)\cdot h(x)=g(x)\cdot h(x).}
i
{\displaystyle i}
f
(
G
)
∪
g
(
G
)
{\displaystyle f(G)\cup \operatorname {g} (G)}
injektive Funktion, dann gilt für alle x :
f
(
x
)
=
g
(
x
)
⟺
i
(
f
(
x
)
)
=
i
(
g
(
x
)
)
.
{\displaystyle f(x)=g(x)\iff i(f(x))=i(g(x)).}
Jede streng monotone Funktion ist injektiv.
Polynomgleichungen
Geometrische Darstellung einer komplexen Zahl. Kartesische Form
z
=
a
+
b
i
{\displaystyle z=a+b\mathrm {i} }
Polarform (trigonometrische Darstellung)
z
=
r
(
cos
φ
+
i
sin
φ
)
{\displaystyle z=r(\cos \varphi +\mathrm {i} \sin \varphi )}
Polarform (Exponentialdarstellung)
z
=
r
e
i
φ
{\displaystyle z=r\mathrm {e} ^{\mathrm {i} \varphi }}
Name
Operation
Polarform
kartesische Form
Identität
z
{\displaystyle z}
=
r
e
i
φ
{\displaystyle =r\mathrm {e} ^{\mathrm {i} \varphi }}
=
a
+
b
i
{\displaystyle =a+b\mathrm {i} }
Identität
z
1
{\displaystyle z_{1}}
=
r
1
e
i
φ
1
{\displaystyle =r_{1}\mathrm {e} ^{\mathrm {i} \varphi _{1}}}
=
a
1
+
b
1
i
{\displaystyle =a_{1}+b_{1}\mathrm {i} }
Identität
z
2
{\displaystyle z_{2}}
=
r
2
e
i
φ
2
{\displaystyle =r_{2}\mathrm {e} ^{\mathrm {i} \varphi _{2}}}
=
a
2
+
b
2
i
{\displaystyle =a_{2}+b_{2}\mathrm {i} }
Addition
z
1
+
z
2
{\displaystyle z_{1}+z_{2}}
=
(
a
1
+
a
2
)
+
(
b
1
+
b
2
)
i
{\displaystyle =(a_{1}+a_{2})+(b_{1}+b_{2})\mathrm {i} }
Subtraktion
z
1
−
z
2
{\displaystyle z_{1}-z_{2}}
=
(
a
1
−
a
2
)
+
(
b
1
−
b
2
)
i
{\displaystyle =(a_{1}-a_{2})+(b_{1}-b_{2})\mathrm {i} }
Multiplikation
z
1
z
2
{\displaystyle z_{1}z_{2}}
=
r
1
r
2
e
i
(
φ
1
+
φ
2
)
{\displaystyle =r_{1}r_{2}\mathrm {e} ^{\mathrm {i} (\varphi _{1}+\varphi _{2})}}
=
(
a
1
a
2
−
b
1
b
2
)
+
(
a
1
b
2
+
a
2
b
1
)
i
{\displaystyle =(a_{1}a_{2}-b_{1}b_{2})+(a_{1}b_{2}+a_{2}b_{1})\mathrm {i} }
Division
z
1
z
2
{\displaystyle {\frac {z_{1}}{z_{2}}}}
=
r
1
r
2
e
i
(
φ
1
−
φ
2
)
{\displaystyle ={\frac {r_{1}}{r_{2}}}\mathrm {e} ^{\mathrm {i} (\varphi _{1}-\varphi _{2})}}
=
a
1
a
2
+
b
1
b
2
a
2
2
+
b
2
2
+
a
2
b
1
−
a
1
b
2
a
2
2
+
b
2
2
i
{\displaystyle ={\frac {a_{1}a_{2}+b_{1}b_{2}}{a_{2}^{2}+b_{2}^{2}}}+{\frac {a_{2}b_{1}-a_{1}b_{2}}{a_{2}^{2}+b_{2}^{2}}}\mathrm {i} }
Kehrwert
1
z
{\displaystyle {\frac {1}{z}}}
=
1
r
e
−
i
φ
{\displaystyle ={\frac {1}{r}}\mathrm {e} ^{-\mathrm {i} \varphi }}
=
a
a
2
+
b
2
−
b
a
2
+
b
2
i
{\displaystyle ={\frac {a}{a^{2}+b^{2}}}-{\frac {b}{a^{2}+b^{2}}}\mathrm {i} }
Potenzierung
z
n
{\displaystyle z^{n}}
=
r
n
e
n
i
φ
{\displaystyle =r^{n}\mathrm {e} ^{n\mathrm {i} \varphi }}
Konjugation
z
¯
{\displaystyle {\overline {z}}}
=
r
e
−
i
φ
{\displaystyle =r\mathrm {e} ^{-\mathrm {i} \varphi }}
=
a
−
b
i
{\displaystyle =a-b\mathrm {i} }
Realteil
R
e
(
z
)
{\displaystyle \mathrm {Re} (z)}
=
r
cos
φ
{\displaystyle =r\cos \varphi }
=
a
{\displaystyle =a}
Imaginärteil
I
m
(
z
)
{\displaystyle \mathrm {Im} (z)}
=
r
sin
φ
{\displaystyle =r\sin \varphi }
=
b
{\displaystyle =b}
Betrag
|
z
|
{\displaystyle |z|}
=
r
{\displaystyle =r}
=
a
2
+
b
2
{\displaystyle ={\sqrt {a^{2}+b^{2}}}}
Argument
a
r
g
(
z
)
{\displaystyle \mathrm {arg} (z)}
=
φ
{\displaystyle =\varphi }
=
s
(
b
)
arccos
(
a
r
)
{\displaystyle =s(b)\arccos {\Big (}{\frac {a}{r}}{\Big )}}
s
(
b
)
:=
{
+
1
wenn
b
≥
0
,
−
1
wenn
b
<
0
{\displaystyle s(b):={\begin{cases}+1&{\text{wenn}}\;b\geq 0,\\-1&{\text{wenn}}\;b<0\end{cases}}}
Rechenweg zur Division:
z
1
z
2
=
z
1
z
2
¯
z
2
z
2
¯
=
z
1
z
¯
2
|
z
2
|
2
{\displaystyle {\frac {z_{1}}{z_{2}}}={\frac {z_{1}{\overline {z_{2}}}}{z_{2}{\overline {z_{2}}}}}={\frac {z_{1}{\overline {z}}_{2}}{|z_{2}|^{2}}}}
1
z
=
z
¯
z
z
¯
=
z
¯
|
z
|
2
{\displaystyle {\frac {1}{z}}={\frac {\overline {z}}{z\,{\overline {z}}}}={\frac {\overline {z}}{|z|^{2}}}}
Für alle
z
,
z
1
,
z
2
∈
C
{\displaystyle z,z_{1},z_{2}\in \mathbb {C} }
z
1
+
z
2
¯
=
z
¯
1
+
z
¯
2
{\displaystyle {\overline {z_{1}+z_{2}}}={\bar {z}}_{1}+{\bar {z}}_{2}}
z
1
−
z
2
¯
=
z
¯
1
−
z
¯
2
{\displaystyle {\overline {z_{1}-z_{2}}}={\bar {z}}_{1}-{\bar {z}}_{2}}
z
1
z
2
¯
=
z
¯
1
z
¯
2
{\displaystyle {\overline {z_{1}z_{2}}}={\bar {z}}_{1}\,{\bar {z}}_{2}}
z
2
≠
0
⟹
(
z
1
z
2
)
¯
=
z
¯
1
z
¯
2
{\displaystyle z_{2}\neq 0\implies {\overline {{\Big (}{\frac {z_{1}}{z_{2}}}{\Big )}}}={\frac {{\bar {z}}_{1}}{{\bar {z}}_{2}}}}
|
z
¯
|
=
|
z
|
{\displaystyle |{\bar {z}}|=|z|}
z
¯
¯
=
z
{\displaystyle {\bar {\bar {z}}}=z}
z
z
¯
=
|
z
|
2
{\displaystyle z{\bar {z}}=|z|^{2}}
Re
(
z
)
=
z
+
z
¯
2
{\displaystyle \operatorname {Re} (z)={\frac {z+{\bar {z}}}{2}}}
Im
(
z
)
=
z
−
z
¯
2
i
{\displaystyle \operatorname {Im} (z)={\frac {z-{\bar {z}}}{2i}}}
e
z
¯
=
e
z
¯
{\displaystyle {\overline {\mathrm {e} ^{z}}}=\mathrm {e} ^{\bar {z}}}
sin
(
z
)
¯
=
sin
(
z
¯
)
{\displaystyle {\overline {\sin(z)}}=\sin({\bar {z}})}
cos
(
z
)
¯
=
cos
(
z
¯
)
{\displaystyle {\overline {\cos(z)}}=\cos({\bar {z}})}
Für alle
z
∈
C
∖
{
x
∈
R
∣
x
≤
0
}
{\displaystyle z\in \mathbb {C} \setminus \{x\in \mathbb {R} \mid x\leq 0\}}
x
∈
C
{\displaystyle x\in \mathbb {C} }
z
x
¯
=
z
¯
x
¯
{\displaystyle {\overline {z^{x}}}={\bar {z}}^{\bar {x}}}
ln
(
z
)
¯
=
ln
(
z
¯
)
{\displaystyle {\overline {\ln(z)}}=\ln({\bar {z}})}
arg
(
z
¯
)
=
−
arg
(
z
)
{\displaystyle \arg({\bar {z}})=-\arg(z)}
Für alle
r
>
0
{\displaystyle r>0}
z
,
z
1
,
z
2
∈
C
∖
{
0
}
{\displaystyle z,z_{1},z_{2}\in \mathbb {C} \setminus \{0\}}
x
∈
C
{\displaystyle x\in \mathbb {C} }
arg
(
r
z
)
=
arg
(
z
)
{\displaystyle \arg(rz)=\arg(z)}
arg
(
z
1
z
2
)
≡
arg
(
z
1
)
+
arg
(
z
2
)
(
mod
2
π
)
{\displaystyle \arg(z_{1}z_{2})\equiv \arg(z_{1})+\arg(z_{2}){\pmod {2\pi }}}
arg
(
z
1
z
2
)
≡
arg
(
z
1
)
−
arg
(
z
2
)
(
mod
2
π
)
{\displaystyle \arg {\Big (}{\frac {z_{1}}{z_{2}}}{\Big )}\equiv \arg(z_{1})-\arg(z_{2}){\pmod {2\pi }}}
arg
(
1
z
)
≡
−
arg
(
z
)
(
mod
2
π
)
{\displaystyle \arg {\Big (}{\frac {1}{z}}{\Big )}\equiv -\arg(z){\pmod {2\pi }}}
arg
(
z
¯
)
≡
−
arg
(
z
)
(
mod
2
π
)
{\displaystyle \arg({\bar {z}})\equiv -\arg(z){\pmod {2\pi }}}
arg
(
z
x
)
≡
arg
(
z
)
Re
(
x
)
+
ln
(
|
z
|
)
Im
(
x
)
(
mod
2
π
)
{\displaystyle \arg(z^{x})\equiv \arg(z)\operatorname {Re} (x)+\ln(|z|)\operatorname {Im} (x){\pmod {2\pi }}}
Für alle
z
∈
C
∖
{
x
∈
R
∣
x
≤
0
}
{\displaystyle z\in \mathbb {C} \setminus \{x\in \mathbb {R} \mid x\leq 0\}}
arg
(
z
¯
)
=
−
arg
(
z
)
{\displaystyle \arg({\bar {z}})=-\arg(z)}
arg
(
1
z
)
=
−
arg
(
z
)
{\displaystyle \arg {\Big (}{\frac {1}{z}}{\Big )}=-\arg(z)}
Allgemeine Potenzfunktion
f
:
R
2
→
C
,
f
(
x
,
y
)
:=
x
y
{\displaystyle f\colon \mathbb {R} ^{2}\to \mathbb {C} ,\;f(x,y):=x^{y}}
Allgemeine Potenzfunktion
z
=
x
y
{\displaystyle z=x^{y}}
Definitionen:
e
z
:=
e
a
cos
(
b
)
+
i
e
a
sin
(
b
)
(
z
=
a
+
b
i
)
{\displaystyle \mathrm {e} ^{z}:=\mathrm {e} ^{a}\cos(b)+\mathrm {i} \,\mathrm {e} ^{a}\sin(b)\qquad (z=a+b\mathrm {i} )}
ln
(
z
)
:=
ln
(
|
z
|
)
+
arg
(
z
)
i
(
z
≠
0
)
{\displaystyle \ln(z):=\ln(|z|)+\operatorname {arg} (z)\,\mathrm {i} \qquad (z\neq 0)}
z
w
:=
e
w
ln
(
z
)
(
z
≠
0
)
{\displaystyle z^{w}:=\mathrm {e} ^{w\ln(z)}\qquad (z\neq 0)}
Für alle
z
,
z
1
,
z
2
∈
C
{\displaystyle z,z_{1},z_{2}\in \mathbb {C} }
e
z
1
+
z
2
=
e
z
1
e
z
2
{\displaystyle \mathrm {e} ^{z_{1}+z_{2}}=\mathrm {e} ^{z_{1}}\mathrm {e} ^{z_{2}}}
e
−
z
=
1
e
z
{\displaystyle \mathrm {e} ^{-z}={\frac {1}{\mathrm {e^{z}} }}}
e
z
≠
0
{\displaystyle \mathrm {e} ^{z}\neq 0}
e
i
z
=
cos
(
z
)
+
i
sin
(
z
)
{\displaystyle \mathrm {e} ^{\mathrm {i} z}=\cos(z)+\mathrm {i} \sin(z)}
∀
k
∈
Z
:
e
2
k
π
i
=
1
{\displaystyle \forall k\in \mathbb {Z} \colon \;\mathrm {e} ^{2k\pi \mathrm {i} }=1}
∀
k
∈
Z
:
e
(
2
k
+
1
)
π
i
+
1
=
0
{\displaystyle \forall k\in \mathbb {Z} \colon \;\mathrm {e} ^{(2k+1)\pi \mathrm {i} }+1=0}
Für alle
z
∈
C
∖
{
0
}
{\displaystyle z\in \mathbb {C} \setminus \{0\}}
x
,
y
∈
C
{\displaystyle x,y\in \mathbb {C} }
z
x
+
y
=
z
x
z
y
{\displaystyle z^{x+y}=z^{x}z^{y}}
z
x
−
y
=
z
x
z
y
{\displaystyle z^{x-y}={\frac {z^{x}}{z^{y}}}}
z
−
x
=
1
z
x
{\displaystyle z^{-x}={\frac {1}{z^{x}}}}
z
0
=
1
{\displaystyle z^{0}=1}
Für alle
r
>
0
{\displaystyle r>0}
z
∈
C
∖
{
0
}
{\displaystyle z\in \mathbb {C} \setminus \{0\}}
x
∈
C
{\displaystyle x\in \mathbb {C} }
(
r
z
)
x
=
r
x
z
x
{\displaystyle (rz)^{x}=r^{x}z^{x}}
(
z
r
)
x
=
z
x
r
x
{\displaystyle {\Big (}{\frac {z}{r}}{\Big )}^{x}={\frac {z^{x}}{r^{x}}}}
(
1
r
)
x
=
1
r
x
=
r
−
x
{\displaystyle {\Big (}{\frac {1}{r}}{\Big )}^{x}={\frac {1}{r^{x}}}=r^{-x}}
Für alle
r
>
0
{\displaystyle r>0}
z
∈
C
∖
{
x
∈
R
∣
x
≤
0
}
{\displaystyle z\in \mathbb {C} \setminus \{x\in \mathbb {R} \mid x\leq 0\}}
x
∈
C
{\displaystyle x\in \mathbb {C} }
(
r
z
)
x
=
r
x
z
x
{\displaystyle {\Big (}{\frac {r}{z}}{\Big )}^{x}={\frac {r^{x}}{z^{x}}}}
Graph der Funktion f (z ) = z 5 −1. Die Nullstellen von f heißen fünfte Einheitswurzeln . Die n -ten Wurzeln einer komplexen Zahl bilden immer ein regelmäßiges n -Eck, dessen Zentrum im Koordinatenursprung liegt. Sei
φ
:=
arg
(
z
)
{\displaystyle \varphi :=\arg(z)}
n
∈
N
{\displaystyle n\in \mathbb {N} }
z
=
w
n
⟺
w
=
|
z
|
n
exp
(
i
φ
+
2
k
π
i
n
)
,
k
∈
{
0
,
1
,
…
,
n
−
1
}
.
{\displaystyle z=w^{n}\iff w={\sqrt[{n}]{|z|}}\exp {\Big (}{\frac {\mathrm {i} \varphi +2k\pi \mathrm {i} }{n}}{\Big )},\;k\in \{0,1,\ldots ,n-1\}.}
Hauptwert:
z
n
=
|
z
|
n
exp
(
i
φ
n
)
.
{\displaystyle {\sqrt[{n}]{z}}={\sqrt[{n}]{|z|}}\exp {\Big (}{\frac {\mathrm {i} \varphi }{n}}{\Big )}.}
Hauptwert, allgemein für
z
,
x
∈
C
∖
{
0
}
{\displaystyle z,x\in \mathbb {C} \setminus \{0\}}
z
x
:=
exp
(
ln
(
z
)
x
)
.
{\displaystyle {\sqrt[{x}]{z}}:=\exp {\bigg (}{\frac {\ln(z)}{x}}{\bigg )}.}
Definitionen:
ln
(
z
)
:=
ln
(
|
z
|
)
+
arg
(
z
)
i
(
z
≠
0
)
{\displaystyle \ln(z):=\ln(|z|)+\operatorname {arg} (z)\,\mathrm {i} \qquad (z\neq 0)}
log
b
(
a
)
:=
ln
(
a
)
ln
(
b
)
(
a
,
b
∈
C
∖
{
0
}
)
{\displaystyle \log _{b}(a):={\frac {\ln(a)}{\ln(b)}}\qquad (a,b\in \mathbb {C} \setminus \{0\})}
Logarithmus als Urbild der Exponentialfunktion:
Ln
(
z
)
:=
{
w
∣
exp
(
z
)
=
w
}
{\displaystyle \operatorname {Ln} (z):=\{w\mid \exp(z)=w\}}
Ln
(
z
)
=
{
w
∣
w
=
ln
(
z
)
+
2
k
π
i
,
k
∈
Z
}
{\displaystyle \operatorname {Ln} (z)=\{w\mid w=\ln(z)+2k\pi \mathrm {i} ,\;k\in \mathbb {Z} \}}
Für alle
r
>
0
{\displaystyle r>0}
z
∈
C
∖
{
0
}
{\displaystyle z\in \mathbb {C} \setminus \{0\}}
ln
(
r
z
)
=
ln
(
r
)
+
ln
(
z
)
{\displaystyle \ln(rz)=\ln(r)+\ln(z)}
Für alle
z
∈
C
∖
{
x
∈
R
∣
x
≤
0
}
{\displaystyle z\in \mathbb {C} \setminus \{x\in \mathbb {R} \mid x\leq 0\}}
ln
(
1
z
)
=
−
ln
(
z
)
{\displaystyle \ln {\Big (}{\frac {1}{z}}{\Big )}=-\ln(z)}
Für alle
x
,
y
∈
C
∖
{
0
}
{\displaystyle x,y\in \mathbb {C} \setminus \{0\}}
ln
(
x
y
)
≡
ln
(
x
)
+
ln
(
y
)
(
mod
2
π
i
)
{\displaystyle \ln(xy)\equiv \ln(x)+\ln(y)\quad {\pmod {2\pi \mathrm {i} }}}
Für alle
z
∈
C
∖
{
0
}
{\displaystyle z\in \mathbb {C} \setminus \{0\}}
x
∈
C
{\displaystyle x\in \mathbb {C} }
ln
(
z
x
)
≡
x
ln
(
z
)
(
mod
2
π
i
)
{\displaystyle \ln(z^{x})\equiv x\ln(z)\quad {\pmod {2\pi \mathrm {i} }}}
Ist
α
{\displaystyle \alpha \,}
z
{\displaystyle z\,}
|
z
α
|
∈
Θ
(
|
z
|
Re
α
)
{\displaystyle \left|z^{\alpha }\right|\in \Theta \left(|z|^{{\text{Re}}\,\alpha }\right)}
|
z
|
→
∞
{\displaystyle |z|\to \infty \,}
Θ
{\displaystyle \Theta }
Sind
z
1
,
z
2
{\displaystyle z_{1},z_{2}\,}
α
{\displaystyle \alpha \,}
(
z
1
⋅
z
2
)
α
=
z
1
α
⋅
z
2
α
{\displaystyle (z_{1}\cdot z_{2})^{\alpha }=z_{1}^{\alpha }\cdot z_{2}^{\alpha }}
(
z
1
z
2
)
α
=
z
1
α
z
2
α
{\displaystyle \left({\frac {z_{1}}{z_{2}}}\right)^{\alpha }={\frac {z_{1}^{\alpha }}{z_{2}^{\alpha }}}}
Ist
z
{\displaystyle z\,}
0
z
=
{
0
Re
(
z
)
>
0
1
z
=
0
nicht definiert
sonst
{\displaystyle 0^{z}=\left\{{\begin{matrix}0&{\text{Re}}(z)>0\\1&z=0\\{\text{nicht definiert}}&{\text{sonst}}\end{matrix}}\right.}
(
a
2
+
b
2
)
(
c
2
+
d
2
)
=
(
a
c
−
b
d
)
2
+
(
a
d
+
b
c
)
2
{\displaystyle (a^{2}+b^{2})(c^{2}+d^{2})=(ac-bd)^{2}+(ad+bc)^{2}\,}
Beweis (Formel von Fibonacci)
Aus
(
a
+
i
b
)
(
c
+
i
d
)
=
(
a
c
−
b
d
)
+
i
(
a
d
+
b
c
)
{\displaystyle (a+ib)(c+id)=(ac-bd)+i(ad+bc)\,}
folgt
|
a
+
i
b
|
2
⋅
|
c
+
i
d
|
2
=
|
(
a
c
−
b
d
)
+
i
(
a
d
+
b
c
)
|
2
{\displaystyle |a+ib|^{2}\cdot |c+id|^{2}=|(ac-bd)+i(ad+bc)|^{2}}
a
+
i
b
=
a
2
+
b
2
+
a
2
+
i
Θ
(
b
)
a
2
+
b
2
−
a
2
{\displaystyle {\sqrt {a+ib}}={\sqrt {\frac {{\sqrt {a^{2}+b^{2}}}+a}{2}}}+i\,\Theta (b)\,{\sqrt {\frac {{\sqrt {a^{2}+b^{2}}}-a}{2}}}}
Θ
(
b
)
=
{
1
,
b
≥
0
−
1
,
b
<
0
{\displaystyle \Theta (b)=\left\{{\begin{matrix}1&,&b\geq 0\\\\-1&,&b<0\end{matrix}}\right.}
Beweis
Für jede von Null verschiedene komplexe Zahl
a
+
i
b
{\displaystyle a+ib\,}
a
+
i
b
{\displaystyle a+ib\,}
Mit
a
+
i
b
=
x
+
i
y
{\displaystyle {\sqrt {a+ib}}=x+iy}
x
≥
0
{\displaystyle x\geq 0}
x
=
0
{\displaystyle x=0\,}
y
≥
0
{\displaystyle y\geq 0}
Wenn
(
x
+
i
y
)
2
=
a
+
i
b
{\displaystyle (x+iy)^{2}=a+ib\,}
x
2
−
y
2
=
a
,
2
x
y
=
b
{\displaystyle x^{2}-y^{2}=a\,,\,2xy=b}
x
2
+
y
2
=
a
2
+
b
2
{\displaystyle x^{2}+y^{2}={\sqrt {a^{2}+b^{2}}}}
Daher ist
x
2
=
(
x
2
+
y
2
)
+
(
x
2
−
y
2
)
2
=
a
2
+
b
2
+
a
2
⇒
x
=
a
2
+
b
2
+
a
2
≥
0
{\displaystyle x^{2}={\frac {(x^{2}+y^{2})+(x^{2}-y^{2})}{2}}={\frac {{\sqrt {a^{2}+b^{2}}}+a}{2}}\Rightarrow x={\sqrt {\frac {{\sqrt {a^{2}+b^{2}}}+a}{2}}}\geq 0}
und
y
2
=
(
x
2
+
y
2
)
−
(
x
2
−
y
2
)
2
=
a
2
+
b
2
−
a
2
⇒
y
=
Θ
(
b
)
a
2
+
b
2
−
a
2
{\displaystyle y^{2}={\frac {(x^{2}+y^{2})-(x^{2}-y^{2})}{2}}={\frac {{\sqrt {a^{2}+b^{2}}}-a}{2}}\Rightarrow y=\Theta (b)\,{\sqrt {\frac {{\sqrt {a^{2}+b^{2}}}-a}{2}}}}
da im Fall
x
>
0
sgn
(
y
)
=
sgn
(
2
x
y
)
=
sgn
(
b
)
{\displaystyle x>0\quad {\text{sgn}}(y)={\text{sgn}}(2xy)={\text{sgn}}(b)}
x
=
0
{\displaystyle x=0\,}
b
=
0
{\displaystyle b=0\,}
y
≥
0
{\displaystyle y\geq 0}
Punktsymmetrie
Achsensymmetrie
sin
(
−
x
)
=
−
sin
(
x
)
,
tan
(
−
x
)
=
−
tan
(
x
)
,
cot
(
−
x
)
=
−
cot
(
x
)
,
csc
(
−
x
)
=
−
csc
(
x
)
{\displaystyle {\begin{aligned}\sin(-x)&=-\sin(x),\\\tan(-x)&=-\tan(x),\\\cot(-x)&=-\cot(x),\\\csc(-x)&=-\csc(x)\end{aligned}}}
cos
(
−
x
)
=
cos
(
x
)
,
sec
(
−
x
)
=
sec
(
x
)
{\displaystyle {\begin{aligned}\cos(-x)&=\cos(x),\\\sec(-x)&=\sec(x)\end{aligned}}}
Definition der Winkel- und Hyperbelfunktionen durch die e-Funktion [ Bearbeiten ]
sin
(
z
)
=
e
i
z
−
e
−
i
z
2
i
{\displaystyle \sin(z)={\frac {\mathrm {e} ^{\mathrm {i} z}-\mathrm {e} ^{-\mathrm {i} z}}{2\mathrm {i} }}}
sinh
(
z
)
=
e
z
−
e
−
z
2
{\displaystyle \sinh(z)={\frac {\mathrm {e} ^{z}-\mathrm {e} ^{-z}}{2}}}
sin
(
i
z
)
=
i
sinh
(
z
)
{\displaystyle \sin(\mathrm {i} z)=\mathrm {i} \sinh(z)\,}
sinh
(
i
z
)
=
i
sin
(
z
)
{\displaystyle \sinh(\mathrm {i} z)=\mathrm {i} \sin(z)\,}
cos
(
z
)
=
e
i
z
+
e
−
i
z
2
{\displaystyle \cos(z)={\frac {\mathrm {e} ^{\mathrm {i} z}+\mathrm {e} ^{-\mathrm {i} z}}{2}}}
cosh
(
z
)
=
e
z
+
e
−
z
2
{\displaystyle \cosh(z)={\frac {\mathrm {e} ^{z}+\mathrm {e} ^{-z}}{2}}}
cos
(
i
z
)
=
cosh
(
z
)
{\displaystyle \cos(\mathrm {i} z)=\cosh(z)\,}
cosh
(
i
z
)
=
cos
(
z
)
{\displaystyle \cosh(\mathrm {i} z)=\cos(z)\,}
tan
(
z
)
=
1
i
e
i
z
−
e
−
i
z
e
i
z
+
e
−
i
z
{\displaystyle \tan(z)={\frac {1}{\mathrm {i} }}\,{\frac {\mathrm {e} ^{\mathrm {i} z}-\mathrm {e} ^{-\mathrm {i} z}}{\mathrm {e} ^{\mathrm {i} z}+\mathrm {e} ^{-\mathrm {i} z}}}}
tanh
(
z
)
=
e
z
−
e
−
z
e
z
+
e
−
z
{\displaystyle \tanh(z)={\frac {\mathrm {e} ^{z}-\mathrm {e} ^{-z}}{\mathrm {e} ^{z}+\mathrm {e} ^{-z}}}}
tan
(
i
z
)
=
i
tanh
(
z
)
{\displaystyle \tan(\mathrm {i} z)=\mathrm {i} \tanh(z)\,}
tanh
(
i
z
)
=
i
tan
(
z
)
{\displaystyle \tanh(\mathrm {i} z)=\mathrm {i} \tan(z)\,}
cot
(
z
)
=
i
e
i
z
+
e
−
i
z
e
i
z
−
e
−
i
z
{\displaystyle \cot(z)=\mathrm {i} \,{\frac {\mathrm {e} ^{\mathrm {i} z}+\mathrm {e} ^{-\mathrm {i} z}}{\mathrm {e} ^{\mathrm {i} z}-\mathrm {e} ^{-\mathrm {i} z}}}}
coth
(
z
)
=
e
z
+
e
−
z
e
z
−
e
−
z
{\displaystyle \coth(z)={\frac {\mathrm {e} ^{z}+\mathrm {e} ^{-z}}{\mathrm {e} ^{z}-\mathrm {e} ^{-z}}}}
cot
(
i
z
)
=
1
i
coth
(
z
)
{\displaystyle \cot(\mathrm {i} z)={\frac {1}{\mathrm {i} }}\coth(z)\,}
coth
(
i
z
)
=
1
i
cot
(
z
)
{\displaystyle \coth(\mathrm {i} z)={\frac {1}{\mathrm {i} }}\cot(z)\,}
sec
(
z
)
=
2
e
i
z
+
e
−
i
z
{\displaystyle \sec(z)={\frac {2}{\mathrm {e} ^{\mathrm {i} z}+\mathrm {e} ^{-\mathrm {i} z}}}}
sech
(
z
)
=
2
e
z
+
e
−
z
{\displaystyle \operatorname {sech} (z)={\frac {2}{\mathrm {e} ^{z}+\mathrm {e} ^{-z}}}}
sec
(
i
z
)
=
sech
(
z
)
{\displaystyle \sec(\mathrm {i} z)=\operatorname {sech} (z)}
sech
(
i
z
)
=
sec
(
z
)
{\displaystyle \operatorname {sech} (\mathrm {i} z)=\sec(z)}
csc
(
z
)
=
2
i
e
i
z
−
e
−
i
z
{\displaystyle \csc(z)={\frac {2\mathrm {i} }{\mathrm {e} ^{\mathrm {i} z}-\mathrm {e} ^{-\mathrm {i} z}}}}
csch
(
z
)
=
2
e
z
−
e
−
z
{\displaystyle \operatorname {csch} (z)={\frac {2}{\mathrm {e} ^{z}-\mathrm {e} ^{-z}}}}
csc
(
i
z
)
=
1
i
csch
(
z
)
{\displaystyle \csc(\mathrm {i} z)={\frac {1}{\mathrm {i} }}\,\operatorname {csch} (z)}
csch
(
i
z
)
=
1
i
csc
(
z
)
{\displaystyle \operatorname {csch} (\mathrm {i} z)={\frac {1}{\mathrm {i} }}\,\csc(z)}
Gegenseitige Darstellbarkeit von Winkelfunktionen [ Bearbeiten ]
sin
cos
tan
cot
sec
csc
sin2 (x)
sin
2
(
x
)
{\displaystyle \sin ^{2}(x)}
1
−
cos
2
(
x
)
{\displaystyle 1-\cos ^{2}(x)}
tan
2
(
x
)
1
+
tan
2
(
x
)
{\displaystyle {\frac {\tan ^{2}(x)}{1+\tan ^{2}(x)}}}
1
cot
2
(
x
)
+
1
{\displaystyle {\frac {1}{\cot ^{2}(x)+1}}}
sec
2
(
x
)
−
1
sec
2
(
x
)
{\displaystyle {\frac {\sec ^{2}(x)-1}{\sec ^{2}(x)}}}
1
csc
2
(
x
)
{\displaystyle {\frac {1}{\csc ^{2}(x)}}}
cos2 (x)
1
−
sin
2
(
x
)
{\displaystyle 1-\sin ^{2}(x)}
cos
2
(
x
)
{\displaystyle \cos ^{2}(x)}
1
1
+
tan
2
(
x
)
{\displaystyle {\frac {1}{1+\tan ^{2}(x)}}}
cot
2
(
x
)
cot
2
(
x
)
+
1
{\displaystyle {\frac {\cot ^{2}(x)}{\cot ^{2}(x)+1}}}
1
sec
2
(
x
)
{\displaystyle {\frac {1}{\sec ^{2}(x)}}}
csc
2
(
x
)
−
1
csc
2
(
x
)
{\displaystyle {\frac {\csc ^{2}(x)-1}{\csc ^{2}(x)}}}
tan2 (x)
sin
2
(
x
)
1
−
sin
2
(
x
)
{\displaystyle {\frac {\sin ^{2}(x)}{1-\sin ^{2}(x)}}}
1
−
cos
2
(
x
)
cos
2
(
x
)
{\displaystyle {\frac {1-\cos ^{2}(x)}{\cos ^{2}(x)}}}
tan
2
(
x
)
{\displaystyle \tan ^{2}(x)}
1
cot
2
(
x
)
{\displaystyle {\frac {1}{\cot ^{2}(x)}}}
sec
2
(
x
)
−
1
{\displaystyle \sec ^{2}(x)-1}
1
csc
2
(
x
)
−
1
{\displaystyle {\frac {1}{\csc ^{2}(x)-1}}}
cot2 (x)
1
−
sin
2
(
x
)
sin
2
(
x
)
{\displaystyle {\frac {1-\sin ^{2}(x)}{\sin ^{2}(x)}}}
cos
2
(
x
)
1
−
cos
2
(
x
)
{\displaystyle {\frac {\cos ^{2}(x)}{1-\cos ^{2}(x)}}}
1
tan
2
(
x
)
{\displaystyle {\frac {1}{\tan ^{2}(x)}}}
cot
2
(
x
)
{\displaystyle \cot ^{2}(x)}
1
sec
2
(
x
)
−
1
{\displaystyle {\frac {1}{\sec ^{2}(x)-1}}}
csc
2
(
x
)
−
1
{\displaystyle \csc ^{2}(x)-1}
sec2 (x)
1
1
−
sin
2
(
x
)
{\displaystyle {\frac {1}{1-\sin ^{2}(x)}}}
1
cos
2
(
x
)
{\displaystyle {\frac {1}{\cos ^{2}(x)}}}
1
+
tan
2
(
x
)
{\displaystyle 1+\tan ^{2}(x)}
cot
2
(
x
)
+
1
cot
2
(
x
)
{\displaystyle {\frac {\cot ^{2}(x)+1}{\cot ^{2}(x)}}}
sec
2
(
x
)
{\displaystyle \sec ^{2}(x)}
csc
2
(
x
)
csc
2
(
x
)
−
1
{\displaystyle {\frac {\csc ^{2}(x)}{\csc ^{2}(x)-1}}}
csc2 (x)
1
sin
2
(
x
)
{\displaystyle {\frac {1}{\sin ^{2}(x)}}}
1
1
−
cos
2
(
x
)
{\displaystyle {\frac {1}{1-\cos ^{2}(x)}}}
1
+
tan
2
(
x
)
tan
2
(
x
)
{\displaystyle {\frac {1+\tan ^{2}(x)}{\tan ^{2}(x)}}}
cot
2
(
x
)
+
1
{\displaystyle \cot ^{2}(x)+1}
sec
2
(
x
)
sec
2
(
x
)
−
1
{\displaystyle {\frac {\sec ^{2}(x)}{\sec ^{2}(x)-1}}}
csc
2
(
x
)
{\displaystyle \csc ^{2}(x)}
Die Gleichungen gelten für alle
x
∈
R
{\displaystyle x\in \mathbb {R} }
Man beachte, dass die Gleichungen nach dem Wurzelziehen nur betragsmäßig gültig sind, da beim Quadrieren die Vorzeichen verloren gehen.
Winkelfunktionen mit verschobenem Argument [ Bearbeiten ]
±
φ
{\displaystyle \pm \varphi }
π
2
±
φ
{\displaystyle {\frac {\pi }{2}}\pm \varphi }
π
±
φ
{\displaystyle \pi \pm \varphi }
3
π
2
±
φ
{\displaystyle {\frac {3\pi }{2}}\pm \varphi }
sin
{\displaystyle \sin \,}
±
sin
{\displaystyle \pm \sin }
cos
{\displaystyle \cos \!}
∓
sin
{\displaystyle \mp \sin }
−
cos
{\displaystyle -\cos \!}
cos
{\displaystyle \cos \,}
cos
{\displaystyle \cos \!}
∓
sin
{\displaystyle \mp \sin \!}
−
cos
{\displaystyle -\cos \!}
±
sin
{\displaystyle \pm \sin \!}
tan
{\displaystyle \tan \,}
±
tan
{\displaystyle \pm \tan \!}
∓
cot
{\displaystyle \mp \cot \!}
±
tan
{\displaystyle \pm \tan \!}
∓
cot
{\displaystyle \mp \cot \!}
cot
{\displaystyle \cot \,}
±
cot
{\displaystyle \pm \cot \!}
∓
tan
{\displaystyle \mp \tan \!}
±
cot
{\displaystyle \pm \cot \!}
∓
tan
{\displaystyle \mp \tan \!}
sec
{\displaystyle \sec \,}
sec
{\displaystyle \sec \!}
∓
csc
{\displaystyle \mp \csc \!}
−
sec
{\displaystyle -\sec \!}
±
csc
{\displaystyle \pm \csc \!}
csc
{\displaystyle \csc \,}
±
csc
{\displaystyle \pm \csc }
sec
{\displaystyle \sec \!}
∓
csc
{\displaystyle \mp \csc }
−
sec
{\displaystyle -\sec \!}
1
+
tan
(
π
4
−
x
)
=
2
1
+
tan
x
{\displaystyle 1+\tan \left({\frac {\pi }{4}}-x\right)={\frac {2}{1+\tan x}}}
sin
(
x
±
y
)
=
sin
x
cos
y
±
sin
y
cos
x
{\displaystyle \sin(x\pm y)=\sin x\;\cos y\pm \sin y\;\cos x}
cos
(
x
±
y
)
=
cos
x
cos
y
∓
sin
x
sin
y
{\displaystyle \cos(x\pm y)=\cos x\;\cos y\mp \sin x\;\sin y}
tan
(
x
±
y
)
=
tan
x
±
tan
y
1
∓
tan
x
tan
y
{\displaystyle \tan(x\pm y)={\frac {\tan x\pm \tan y}{1\mp \tan x\;\tan y}}}
cot
(
x
±
y
)
=
±
cot
x
cot
y
∓
1
cot
x
±
cot
y
{\displaystyle \cot \left(x\pm y\right)={\frac {\pm \cot x\cot y\mp 1}{\cot x\pm \cot y}}}
sin
(
x
+
y
)
sin
(
x
−
y
)
=
cos
2
y
−
cos
2
x
{\displaystyle \sin(x+y)\,\sin(x-y)=\cos ^{2}y-\cos ^{2}x}
cos
(
x
+
y
)
cos
(
x
−
y
)
=
cos
2
y
−
sin
2
x
{\displaystyle \cos(x+y)\,\cos(x-y)=\cos ^{2}y-\sin ^{2}x}
sin
(
2
x
)
=
2
sin
x
cos
x
=
2
tan
x
1
+
tan
2
x
{\displaystyle \sin(2x)=2\,\sin x\,\cos x={\frac {2\tan x}{1+\tan ^{2}x}}}
cos
(
2
x
)
=
cos
2
x
−
sin
2
x
=
1
−
2
sin
2
x
=
2
cos
2
x
−
1
=
1
−
tan
2
x
1
+
tan
2
x
{\displaystyle \cos(2x)=\cos ^{2}x-\sin ^{2}x=1-2\sin ^{2}x=2\cos ^{2}x-1={\frac {1-\tan ^{2}x}{1+\tan ^{2}x}}}
tan
(
2
x
)
=
2
tan
x
1
−
tan
2
x
=
2
cot
x
−
tan
x
{\displaystyle \tan(2x)={\frac {2\tan x}{1-\tan ^{2}x}}={\frac {2}{\cot x-\tan x}}}
cot
(
2
x
)
=
cot
2
x
−
1
2
cot
x
=
cot
x
−
tan
x
2
{\displaystyle \cot(2x)={\frac {\cot ^{2}x-1}{2\cot x}}={\frac {\cot x-\tan x}{2}}}
[ Bearbeiten ]
sin
(
3
x
)
=
3
sin
x
−
4
sin
3
x
{\displaystyle \sin(3x)=3\sin x-4\sin ^{3}x\!}
sin
(
4
x
)
=
8
sin
x
cos
3
x
−
4
sin
x
cos
x
{\displaystyle \sin(4x)=8\sin x\;\cos ^{3}x-4\sin x\;\cos x}
sin
(
5
x
)
=
16
sin
x
cos
4
x
−
12
sin
x
cos
2
x
+
sin
x
{\displaystyle \sin(5x)=16\sin x\;\cos ^{4}x-12\sin x\;\cos ^{2}x+\sin x}
sin
(
n
x
)
=
n
sin
x
cos
n
−
1
x
−
(
n
3
)
sin
3
x
cos
n
−
3
x
+
(
n
5
)
sin
5
x
cos
n
−
5
x
−
+
…
{\displaystyle \sin(nx)=n\;\sin x\;\cos ^{n-1}x-{n \choose 3}\sin ^{3}x\;\cos ^{n-3}x+{n \choose 5}\sin ^{5}x\;\cos ^{n-5}x\;-\;+\;\dots }
cos
(
3
x
)
=
4
cos
3
x
−
3
cos
x
{\displaystyle \cos(3x)=4\cos ^{3}x-3\cos x\!}
cos
(
4
x
)
=
8
cos
4
x
−
8
cos
2
x
+
1
{\displaystyle \cos(4x)=8\cos ^{4}x-8\cos ^{2}x+1\!}
cos
(
5
x
)
=
16
cos
5
x
−
20
cos
3
x
+
5
cos
x
{\displaystyle \cos(5x)=16\cos ^{5}x-20\cos ^{3}x+5\cos x\!}
cos
(
n
x
)
=
cos
n
x
−
(
n
2
)
sin
2
x
cos
n
−
2
x
+
(
n
4
)
sin
4
x
cos
n
−
4
x
−
+
…
{\displaystyle \cos(nx)=\cos ^{n}x-{n \choose 2}\sin ^{2}x\;\cos ^{n-2}x+{n \choose 4}\sin ^{4}x\;\cos ^{n-4}x\;-\;+\;\dots }
tan
(
n
x
)
=
∑
k
=
0
∞
(
−
1
)
k
(
n
2
k
+
1
)
tan
2
k
+
1
∑
k
=
0
∞
(
−
1
)
k
(
n
2
k
)
tan
2
k
{\displaystyle \tan(nx)={\frac {\sum _{k=0}^{\infty }(-1)^{k}\,{n \choose 2k+1}\,\tan ^{2k+1}}{\sum _{k=0}^{\infty }(-1)^{k}\,{n \choose 2k}\,\tan ^{2k}}}}
cot
(
n
x
)
=
(
−
1
)
n
−
1
(
∑
k
=
0
∞
(
−
1
)
k
(
n
2
k
+
1
)
cot
2
k
+
1
∑
k
=
0
∞
(
−
1
)
k
(
n
2
k
)
cot
2
k
)
(
−
1
)
n
−
1
{\displaystyle \cot(nx)=(-1)^{n-1}\,\left({\frac {\sum _{k=0}^{\infty }(-1)^{k}\,{n \choose 2k+1}\,\cot ^{2k+1}}{\sum _{k=0}^{\infty }(-1)^{k}\,{n \choose 2k}\,\cot ^{2k}}}\right)^{(-1)^{n-1}}}
Rekursionsformeln mit
n
,
x
∈
C
{\displaystyle n,x\in \mathbb {C} }
cos
(
n
x
)
=
2
cos
(
x
)
cos
(
(
n
−
1
)
x
)
+
cos
(
(
n
−
2
)
x
)
,
sin
(
n
x
)
=
2
cos
(
x
)
sin
(
(
n
−
1
)
x
)
+
sin
(
(
n
−
2
)
x
)
.
{\displaystyle {\begin{aligned}\cos(nx)&=2\cos(x)\cos((n-1)x)+\cos((n-2)x),\\\sin(nx)&=2\cos(x)\sin((n-1)x)+\sin((n-2)x).\end{aligned}}}
sin
x
2
=
1
−
cos
x
2
{\displaystyle \sin {\frac {x}{2}}={\sqrt {\frac {1-\cos x}{2}}}}
x
∈
[
0
,
2
π
]
{\displaystyle x\in [0,2\pi ]}
cos
x
2
=
1
+
cos
x
2
{\displaystyle \cos {\frac {x}{2}}={\sqrt {\frac {1+\cos x}{2}}}}
x
∈
[
−
π
,
π
]
{\displaystyle x\in [-\pi ,\pi ]}
tan
x
2
=
1
−
cos
x
1
+
cos
x
=
1
−
cos
x
sin
(
x
)
=
sin
x
1
+
cos
x
{\displaystyle \tan {\frac {x}{2}}={\sqrt {\frac {1-\cos x}{1+\cos x}}}={\frac {1-\cos x}{\sin(x)}}={\frac {\sin x}{1+\cos x}}}
x
∈
]
−
π
,
π
[
{\displaystyle x\in ]-\pi ,\pi [}
cot
x
2
=
1
+
cos
x
1
−
cos
x
=
1
+
cos
x
sin
x
=
sin
x
1
−
cos
x
{\displaystyle \cot {\frac {x}{2}}={\sqrt {\frac {1+\cos x}{1-\cos x}}}={\frac {1+\cos x}{\sin x}}={\frac {\sin x}{1-\cos x}}}
x
∈
]
−
π
,
π
[
{\displaystyle x\in ]-\pi ,\pi [}
Aus den Additionstheoremen lassen sich Identitäten ableiten:
sin
x
±
sin
y
=
2
sin
x
±
y
2
cos
x
∓
y
2
{\displaystyle \sin x\pm \sin y=2\sin {\frac {x\pm y}{2}}\,\cos {\frac {x\mp y}{2}}}
cos
x
±
cos
y
=
±
2
cos
sin
(
x
+
y
2
)
cos
sin
(
x
−
y
2
)
{\displaystyle \cos x\pm \cos y=\pm 2\;{\begin{matrix}\cos \\\sin \end{matrix}}\left({\frac {x+y}{2}}\right){\begin{matrix}\cos \\\sin \end{matrix}}\left({\frac {x-y}{2}}\right)}
tan
x
±
tan
y
=
sin
(
x
±
y
)
cos
(
x
)
cos
(
y
)
,
cot
x
±
cot
y
=
sin
(
y
±
x
)
sin
(
x
)
sin
(
y
)
{\displaystyle \tan x\pm \tan y={\frac {\sin(x\pm y)}{\cos(x)\,\cos(y)}}\quad ,\quad \cot x\pm \cot y={\frac {\sin(y\pm x)}{\sin(x)\,\sin(y)}}}
cos
x
cos
y
=
cos
(
x
−
y
)
+
cos
(
x
+
y
)
2
{\displaystyle \cos x\;\cos y={\frac {\cos(x-y)+\cos(x+y)}{2}}}
sin
x
sin
y
=
cos
(
x
−
y
)
−
cos
(
x
+
y
)
2
{\displaystyle \sin x\;\sin y={\frac {\cos(x-y)-\cos(x+y)}{2}}}
sin
x
cos
y
=
sin
(
x
−
y
)
+
sin
(
x
+
y
)
2
{\displaystyle \sin x\;\cos y={\frac {\sin(x-y)+\sin(x+y)}{2}}}
tan
x
tan
y
=
tan
x
+
tan
y
cot
x
+
cot
y
=
−
tan
x
−
tan
y
cot
x
−
cot
y
{\displaystyle \tan x\;\tan y={\frac {\tan x+\tan y}{\cot x+\cot y}}=-{\frac {\tan x-\tan y}{\cot x-\cot y}}}
cot
x
cot
y
=
cot
x
+
cot
y
tan
x
+
tan
y
=
−
cot
x
−
cot
y
tan
x
−
tan
y
{\displaystyle \cot x\;\cot y={\frac {\cot x+\cot y}{\tan x+\tan y}}=-{\frac {\cot x-\cot y}{\tan x-\tan y}}}
tan
x
cot
y
=
tan
x
+
cot
y
cot
x
+
tan
y
=
−
tan
x
−
cot
y
cot
x
−
tan
y
{\displaystyle \tan x\;\cot y={\frac {\tan x+\cot y}{\cot x+\tan y}}=-{\frac {\tan x-\cot y}{\cot x-\tan y}}}
sin
x
sin
y
sin
z
=
1
4
[
sin
(
x
+
y
−
z
)
+
sin
(
y
+
z
−
x
)
+
sin
(
z
+
x
−
y
)
−
sin
(
x
+
y
+
z
)
]
{\displaystyle \sin x\;\sin y\;\sin z={\frac {1}{4}}\left[\sin(x+y-z)+\sin(y+z-x)+\sin(z+x-y)-\sin(x+y+z)\right]}
cos
x
cos
y
cos
z
=
1
4
[
cos
(
x
+
y
−
z
)
+
cos
(
y
+
z
−
x
)
+
cos
(
z
+
x
−
y
)
+
cos
(
x
+
y
+
z
)
]
{\displaystyle \cos x\;\cos y\;\cos z={\frac {1}{4}}\left[\cos(x+y-z)+\cos(y+z-x)+\cos(z+x-y)+\cos(x+y+z)\right]}
sin
x
sin
y
cos
z
=
1
4
[
−
cos
(
x
+
y
−
z
)
+
cos
(
y
+
z
−
x
)
+
cos
(
z
+
x
−
y
)
−
cos
(
x
+
y
+
z
)
]
{\displaystyle \sin x\;\sin y\;\cos z={\frac {1}{4}}\left[-\cos(x+y-z)+\cos(y+z-x)+\cos(z+x-y)-\cos(x+y+z)\right]}
sin
x
cos
y
cos
z
=
1
4
[
sin
(
x
+
y
−
z
)
−
sin
(
y
+
z
−
x
)
+
sin
(
z
+
x
−
y
)
+
sin
(
x
+
y
+
z
)
]
{\displaystyle \sin x\;\cos y\;\cos z={\frac {1}{4}}\left[\sin(x+y-z)-\sin(y+z-x)+\sin(z+x-y)+\sin(x+y+z)\right]}
(
2
cos
x
)
2
n
=
∑
k
=
−
n
n
(
2
n
n
−
k
)
cos
2
k
x
{\displaystyle (2\cos x)^{2n}=\sum _{k=-n}^{n}{2n \choose n-k}\cos 2kx}
(
2
sin
x
)
2
n
=
∑
k
=
−
n
n
(
−
1
)
k
(
2
n
n
−
k
)
cos
2
k
x
{\displaystyle (2\sin x)^{2n}=\sum _{k=-n}^{n}(-1)^{k}\,{2n \choose n-k}\cos 2kx}
(
2
cos
x
)
2
n
+
1
=
2
∑
k
=
0
n
(
2
n
+
1
n
−
k
)
cos
(
2
k
+
1
)
x
{\displaystyle (2\cos x)^{2n+1}=2\sum _{k=0}^{n}{2n+1 \choose n-k}\cos(2k+1)x}
(
2
sin
x
)
2
n
+
1
=
2
∑
k
=
0
n
(
−
1
)
k
(
2
n
+
1
n
−
k
)
sin
(
2
k
+
1
)
x
{\displaystyle (2\sin x)^{2n+1}=2\sum _{k=0}^{n}(-1)^{k}\,{2n+1 \choose n-k}\sin(2k+1)x}
Zurück zur Formelsammlung Mathematik
Definition der Arkusfunktionen durch den Logarithmus [ Bearbeiten ]
arcsin
z
=
−
i
log
(
1
−
z
2
+
i
z
)
{\displaystyle \arcsin z=-\mathrm {i} \,\log \left({\sqrt {1-z^{2}}}+\mathrm {i} z\right)}
arccos
z
=
−
i
log
(
z
+
i
1
−
z
2
)
{\displaystyle \arccos z=-\mathrm {i} \,\log \left(z+\mathrm {i} \,{\sqrt {1-z^{2}}}\right)}
arctan
z
=
i
2
(
log
(
1
−
i
z
)
−
log
(
1
+
i
z
)
)
{\displaystyle \arctan z={\frac {\mathrm {i} }{2}}{\Big (}\log(1-\mathrm {i} z)-\log(1+\mathrm {i} z){\Big )}}
z
≠
±
i
{\displaystyle z\neq \pm \mathrm {i} \,}
arccot
z
=
{
arctan
(
1
z
)
z
≠
0
π
2
z
=
0
{\displaystyle \operatorname {arccot} z=\left\{{\begin{matrix}\arctan \left({\frac {1}{z}}\right)&&z\neq 0\\{\frac {\pi }{2}}&&z=0\end{matrix}}\right.}
arcsec
z
=
arccos
(
1
z
)
{\displaystyle \operatorname {arcsec} z=\arccos \left({\frac {1}{z}}\right)}
z
≠
0
{\displaystyle z\neq 0\,}
arccsc
z
=
arcsin
(
1
z
)
{\displaystyle \operatorname {arccsc} z=\arcsin \left({\frac {1}{z}}\right)}
z
≠
0
{\displaystyle z\neq 0\,}
arcsin
(
i
z
)
=
i
arsinh
z
arsinh
(
i
z
)
=
i
arcsin
z
arctan
(
i
z
)
=
i
artanh
z
artanh
(
i
z
)
=
i
arctan
z
arccot
(
i
z
)
=
−
i
arcoth
z
arcoth
(
i
z
)
=
−
i
arccot
z
arccsc
(
i
z
)
=
−
i
arcsch
z
arcsch
(
i
z
)
=
−
i
arccsc
z
{\displaystyle {\begin{matrix}\arcsin(\mathrm {i} z)&=&\;\;\,\mathrm {i} \;\operatorname {arsinh} \,z&\qquad &\operatorname {arsinh} (\mathrm {i} z)&=&\;\;\mathrm {i} \;\arcsin z\\\arctan(\mathrm {i} z)&=&\;\;\,\,\mathrm {i} \;\operatorname {artanh} \,z&\qquad &\operatorname {artanh} (\mathrm {i} z)&=&\;\;\;\mathrm {i} \;\arctan z\\\operatorname {arccot}(\mathrm {i} z)&=&-\mathrm {i} \;\operatorname {arcoth} \,z&\qquad &\operatorname {arcoth} (\mathrm {i} z)&=&-\mathrm {i} \;\operatorname {arccot} z\\\operatorname {arccsc}(\mathrm {i} z)&=&-\mathrm {i} \;\operatorname {arcsch} \,z&\qquad &\operatorname {arcsch} (\mathrm {i} z)&=&-\mathrm {i} \;\operatorname {arccsc} z\\\end{matrix}}}
Verkettung einer Winkelfunktion mit einer Arkusfunktion [ Bearbeiten ]
f
∘
g
{\displaystyle f\circ g}
arcsin
{\displaystyle \arcsin \!}
arccos
{\displaystyle \arccos \!}
arctan
{\displaystyle \arctan \!}
arccot
{\displaystyle \operatorname {arccot} \!}
arcsec
{\displaystyle \operatorname {arcsec} \!}
arccsc
{\displaystyle \operatorname {arccsc} \!}
sin
{\displaystyle \sin \!}
z
{\displaystyle z\!}
1
−
z
2
{\displaystyle {\sqrt {1-z^{2}}}}
z
1
+
z
2
{\displaystyle {\frac {z}{\sqrt {1+z^{2}}}}}
1
z
1
+
1
z
2
{\displaystyle {\frac {1}{z\,{\sqrt {1+{\frac {1}{z^{2}}}}}}}}
1
−
1
z
2
{\displaystyle {\sqrt {1-{\frac {1}{z^{2}}}}}}
1
z
{\displaystyle {\frac {1}{z}}}
cos
{\displaystyle \cos \!}
1
−
z
2
{\displaystyle {\sqrt {1-z^{2}}}}
z
{\displaystyle z\!}
1
1
+
z
2
{\displaystyle {\frac {1}{\sqrt {1+z^{2}}}}}
1
1
+
1
z
2
{\displaystyle {\frac {1}{\sqrt {1+{\frac {1}{z^{2}}}}}}}
1
z
{\displaystyle {\frac {1}{z}}}
1
−
1
z
2
{\displaystyle {\sqrt {1-{\frac {1}{z^{2}}}}}}
tan
{\displaystyle \tan \!}
z
1
−
z
2
{\displaystyle {\frac {z}{\sqrt {1-z^{2}}}}}
1
−
z
2
z
{\displaystyle {\frac {\sqrt {1-z^{2}}}{z}}}
z
{\displaystyle z\!}
1
z
{\displaystyle {\frac {1}{z}}}
z
1
−
1
z
2
{\displaystyle z\,{\sqrt {1-{\frac {1}{z^{2}}}}}}
1
z
1
−
1
z
2
{\displaystyle {\frac {1}{z\,{\sqrt {1-{\frac {1}{z^{2}}}}}}}}
cot
{\displaystyle \cot \!}
1
−
z
2
z
{\displaystyle {\frac {\sqrt {1-z^{2}}}{z}}}
z
1
−
z
2
{\displaystyle {\frac {z}{\sqrt {1-z^{2}}}}}
1
z
{\displaystyle {\frac {1}{z}}}
z
{\displaystyle z\!}
1
z
1
−
1
z
2
{\displaystyle {\frac {1}{z\,{\sqrt {1-{\frac {1}{z^{2}}}}}}}}
z
1
−
1
z
2
{\displaystyle z\,{\sqrt {1-{\frac {1}{z^{2}}}}}}
sec
{\displaystyle \sec \!}
1
1
−
z
2
{\displaystyle {\frac {1}{\sqrt {1-z^{2}}}}}
1
z
{\displaystyle {\frac {1}{z}}}
1
+
z
2
{\displaystyle {\sqrt {1+z^{2}}}}
1
+
1
z
2
{\displaystyle {\sqrt {1+{\frac {1}{z^{2}}}}}}
z
{\displaystyle z\!}
1
1
−
1
z
2
{\displaystyle {\frac {1}{\sqrt {1-{\frac {1}{z^{2}}}}}}}
csc
{\displaystyle \csc \!}
1
z
{\displaystyle {\frac {1}{z}}}
1
1
−
z
2
{\displaystyle {\frac {1}{\sqrt {1-z^{2}}}}}
1
+
z
2
z
{\displaystyle {\frac {\sqrt {1+z^{2}}}{z}}}
z
1
+
1
z
2
{\displaystyle z\,{\sqrt {1+{\frac {1}{z^{2}}}}}}
1
1
−
1
z
2
{\displaystyle {\frac {1}{\sqrt {1-{\frac {1}{z^{2}}}}}}}
z
{\displaystyle z\!}
arcsin
(
z
)
+
arccos
(
z
)
=
π
2
{\displaystyle \arcsin(z)+\arccos(z)={\frac {\pi }{2}}}
arctan
(
z
)
+
arccot
(
z
)
=
{
π
2
Re
(
z
)
>
0
z
∈
i
]
−
1
,
0
]
z
∈
i
]
1
,
∞
[
−
π
2
Re
(
z
)
<
0
z
∈
i
]
−
∞
,
−
1
[
z
∈
i
]
0
,
1
[
{\displaystyle \arctan(z)+\operatorname {arccot}(z)=\left\{{\begin{matrix}{\frac {\pi }{2}}&&\operatorname {Re} (z)>0&&z\in \mathrm {i} \,]-1,0]&&z\in \mathrm {i} \,]1,\infty [\\\\-{\frac {\pi }{2}}&&\operatorname {Re} (z)<0&&z\in \mathrm {i} \,]-\infty ,-1[&&z\in \mathrm {i} \,]0,1[\end{matrix}}\right.}
arcsec
(
z
)
+
arccsc
(
z
)
=
π
2
{\displaystyle \operatorname {arcsec}(z)+\operatorname {arccsc}(z)={\frac {\pi }{2}}}
z
≠
0
{\displaystyle z\neq 0\,}
Zurück zur Formelsammlung Mathematik
Definition von Hyperbel- und Winkelfunktionen durch die e-Funktion [ Bearbeiten ]
sin
(
z
)
=
e
i
z
−
e
−
i
z
2
i
{\displaystyle \sin(z)={\frac {e^{\mathrm {i} z}-e^{-\mathrm {i} z}}{2\mathrm {i} }}}
sinh
(
z
)
=
e
z
−
e
−
z
2
{\displaystyle \sinh(z)={\frac {e^{z}-e^{-z}}{2}}}
sin
(
i
z
)
=
i
sinh
(
z
)
{\displaystyle \sin(\mathrm {i} z)=\mathrm {i} \sinh(z)\,}
sinh
(
i
z
)
=
i
sin
(
z
)
{\displaystyle \sinh(\mathrm {i} z)=\mathrm {i} \sin(z)\,}
cos
(
z
)
=
e
i
z
+
e
−
i
z
2
{\displaystyle \cos(z)={\frac {e^{\mathrm {i} z}+e^{-\mathrm {i} z}}{2}}}
cosh
(
z
)
=
e
z
+
e
−
z
2
{\displaystyle \cosh(z)={\frac {e^{z}+e^{-z}}{2}}}
cos
(
i
z
)
=
cosh
(
z
)
{\displaystyle \cos(\mathrm {i} z)=\cosh(z)\,}
cosh
(
i
z
)
=
cos
(
z
)
{\displaystyle \cosh(\mathrm {i} z)=\cos(z)\,}
tan
(
z
)
=
1
i
e
i
z
−
e
−
i
z
e
i
z
+
e
−
i
z
{\displaystyle \tan(z)={\frac {1}{\mathrm {i} }}\,{\frac {e^{\mathrm {i} z}-e^{-\mathrm {i} z}}{e^{\mathrm {i} z}+e^{-\mathrm {i} z}}}}
tanh
(
z
)
=
e
z
−
e
−
z
e
z
+
e
−
z
{\displaystyle \tanh(z)={\frac {e^{z}-e^{-z}}{e^{z}+e^{-z}}}}
tan
(
i
z
)
=
i
tanh
(
z
)
{\displaystyle \tan(\mathrm {i} z)=\mathrm {i} \tanh(z)\,}
tanh
(
i
z
)
=
i
tan
(
z
)
{\displaystyle \tanh(\mathrm {i} z)=\mathrm {i} \tan(z)\,}
cot
(
z
)
=
i
e
i
z
+
e
−
i
z
e
i
z
−
e
−
i
z
{\displaystyle \cot(z)=\mathrm {i} \,{\frac {e^{iz}+e^{-iz}}{e^{iz}-e^{-iz}}}}
coth
(
z
)
=
e
z
+
e
−
z
e
z
−
e
−
z
{\displaystyle \coth(z)={\frac {e^{z}+e^{-z}}{e^{z}-e^{-z}}}}
cot
(
i
z
)
=
1
i
coth
(
z
)
{\displaystyle \cot(\mathrm {i} z)={\frac {1}{\mathrm {i} }}\coth(z)\,}
coth
(
i
z
)
=
1
i
cot
(
z
)
{\displaystyle \coth(\mathrm {i} z)={\frac {1}{\mathrm {i} }}\cot(z)\,}
sec
(
z
)
=
2
e
i
z
+
e
−
i
z
{\displaystyle \sec(z)={\frac {2}{e^{\mathrm {i} z}+e^{-\mathrm {i} z}}}}
sech
(
z
)
=
2
e
z
+
e
−
z
{\displaystyle \operatorname {sech} (z)={\frac {2}{e^{z}+e^{-z}}}}
sec
(
i
z
)
=
sech
(
z
)
{\displaystyle \sec(\mathrm {i} z)=\operatorname {sech} (z)}
sech
(
i
z
)
=
sec
(
z
)
{\displaystyle \operatorname {sech} (\mathrm {i} z)=\sec(z)}
csc
(
z
)
=
2
i
e
i
z
−
e
−
i
z
{\displaystyle \csc(z)={\frac {2\mathrm {i} }{e^{\mathrm {i} z}-e^{-\mathrm {i} z}}}}
csch
(
z
)
=
2
e
z
−
e
−
z
{\displaystyle \operatorname {csch} (z)={\frac {2}{e^{z}-e^{-z}}}}
csc
(
i
z
)
=
1
i
csch
(
z
)
{\displaystyle \csc(\mathrm {i} z)={\frac {1}{\mathrm {i} }}\,\operatorname {csch} (z)}
csch
(
i
z
)
=
1
i
csc
(
z
)
{\displaystyle \operatorname {csch} (\mathrm {i} z)={\frac {1}{\mathrm {i} }}\,\csc(z)}
[ Bearbeiten ]
csch
(
2
z
)
=
coth
(
z
)
−
coth
(
2
z
)
{\displaystyle \operatorname {csch} (2z)=\coth(z)-\coth(2z)}
Zurück zur Formelsammlung Mathematik
Definition der Areafunktionen durch den Logarithmus [ Bearbeiten ]
arsinh
(
z
)
=
ln
(
z
+
z
2
+
1
)
{\displaystyle \operatorname {arsinh} (z)=\ln \left(z+{\sqrt {z^{2}+1}}\right)}
arcosh
(
z
)
=
ln
(
z
+
z
−
1
z
+
1
)
{\displaystyle \operatorname {arcosh} (z)=\ln \left(z+{\sqrt {z-1}}\,{\sqrt {z+1}}\right)}
artanh
(
z
)
=
1
2
(
ln
(
1
+
z
)
−
ln
(
1
−
z
)
)
{\displaystyle \operatorname {artanh} (z)={\frac {1}{2}}{\Big (}\ln(1+z)-\ln(1-z){\Big )}}
z
≠
±
1
{\displaystyle z\neq \pm 1\,}
arcoth
(
z
)
=
{
artanh
(
1
z
)
z
≠
0
i
π
2
z
=
0
{\displaystyle \operatorname {arcoth} (z)=\left\{{\begin{matrix}\operatorname {artanh} \left({\frac {1}{z}}\right)&&z\neq 0\\{\frac {\mathrm {i} \pi }{2}}&&z=0\end{matrix}}\right.}
arsech
(
z
)
=
ln
(
1
+
1
−
z
2
z
)
{\displaystyle \operatorname {arsech} (z)=\ln \left({\frac {1+{\sqrt {1-z^{2}}}}{z}}\right)}
arcsch
(
z
)
=
ln
(
1
+
1
+
z
2
z
)
{\displaystyle \operatorname {arcsch} (z)=\ln \left({\frac {1+{\sqrt {1+z^{2}}}}{z}}\right)}
arcsin
(
i
z
)
=
i
arsinh
z
arsinh
(
i
z
)
=
i
arcsin
z
arctan
(
i
z
)
=
i
artanh
z
artanh
(
i
z
)
=
i
arctan
z
arccot
(
i
z
)
=
−
i
arcoth
z
arcoth
(
i
z
)
=
−
i
arccot
z
arccsc
(
i
z
)
=
−
i
arcsch
z
arcsch
(
i
z
)
=
−
i
arccsc
z
{\displaystyle {\begin{matrix}\arcsin(\mathrm {i} z)&=&\;\;\,\mathrm {i} \;\operatorname {arsinh} \,z&\qquad &\operatorname {arsinh} (\mathrm {i} z)&=&\;\;\mathrm {i} \;\arcsin z\\\arctan(\mathrm {i} z)&=&\;\;\,\,\mathrm {i} \;\operatorname {artanh} \,z&\qquad &\operatorname {artanh} (\mathrm {i} z)&=&\;\;\;\mathrm {i} \;\arctan z\\\operatorname {arccot}(\mathrm {i} z)&=&-\mathrm {i} \;\operatorname {arcoth} \,z&\qquad &\operatorname {arcoth} (\mathrm {i} z)&=&-\mathrm {i} \;\operatorname {arccot} z\\\operatorname {arccsc}(\mathrm {i} z)&=&-\mathrm {i} \;\operatorname {arcsch} \,z&\qquad &\operatorname {arcsch} (\mathrm {i} z)&=&-\mathrm {i} \;\operatorname {arccsc} z\\\end{matrix}}}
Verkettung einer Hyperbelfunktion mit einer Areafunktion [ Bearbeiten ]
arsinh
{\displaystyle \operatorname {arsinh} \!}
arcosh
{\displaystyle \operatorname {arcosh} \!}
artanh
{\displaystyle \operatorname {artanh} \!}
arcoth
{\displaystyle \operatorname {arcoth} \!}
arsech
{\displaystyle \operatorname {arsech} \!}
arcsch
{\displaystyle \operatorname {arcsch} \!}
sinh
{\displaystyle \sinh \!}
z
{\displaystyle z\!}
z
−
1
z
+
1
{\displaystyle {\sqrt {z-1}}\;{\sqrt {z+1}}}
z
1
−
z
2
{\displaystyle {\frac {z}{\sqrt {1-z^{2}}}}}
1
z
1
−
1
z
2
{\displaystyle {\frac {1}{z\,{\sqrt {1-{\frac {1}{z^{2}}}}}}}}
1
z
−
1
1
z
+
1
{\displaystyle {\sqrt {{\frac {1}{z}}-1}}\;{\sqrt {{\frac {1}{z}}+1}}}
1
z
{\displaystyle {\frac {1}{z}}}
cosh
{\displaystyle \cosh \!}
1
+
z
2
{\displaystyle {\sqrt {1+z^{2}}}}
z
{\displaystyle z\!}
1
1
−
z
2
{\displaystyle {\frac {1}{\sqrt {1-z^{2}}}}}
1
1
−
1
z
2
{\displaystyle {\frac {1}{\sqrt {1-{\frac {1}{z^{2}}}}}}}
1
z
{\displaystyle {\frac {1}{z}}}
1
+
1
z
2
{\displaystyle {\sqrt {1+{\frac {1}{z^{2}}}}}}
tanh
{\displaystyle \tanh \!}
z
1
+
z
2
{\displaystyle {\frac {z}{\sqrt {1+z^{2}}}}}
z
−
1
z
+
1
z
{\displaystyle {\frac {{\sqrt {z-1}}\;{\sqrt {z+1}}}{z}}}
z
{\displaystyle z\!}
1
z
{\displaystyle {\frac {1}{z}}}
z
1
z
−
1
1
z
+
1
{\displaystyle z\,{\sqrt {{\frac {1}{z}}-1}}\;{\sqrt {{\frac {1}{z}}+1}}}
1
z
1
+
1
z
2
{\displaystyle {\frac {1}{z\,{\sqrt {1+{\frac {1}{z^{2}}}}}}}}
coth
{\displaystyle \coth \!}
1
+
z
2
z
{\displaystyle {\frac {\sqrt {1+z^{2}}}{z}}}
z
z
−
1
z
+
1
{\displaystyle {\frac {z}{{\sqrt {z-1}}\;{\sqrt {z+1}}}}}
1
z
{\displaystyle {\frac {1}{z}}}
z
{\displaystyle z\!}
1
z
1
1
z
−
1
1
z
+
1
{\displaystyle {\frac {1}{z}}{\frac {1}{{\sqrt {{\frac {1}{z}}-1}}\;{\sqrt {{\frac {1}{z}}+1}}}}}
z
1
+
1
z
2
{\displaystyle z\,{\sqrt {1+{\frac {1}{z^{2}}}}}}
sech
{\displaystyle \operatorname {sech} \!}
1
1
+
z
2
{\displaystyle {\frac {1}{\sqrt {1+z^{2}}}}}
1
z
{\displaystyle {\frac {1}{z}}}
1
−
z
2
{\displaystyle {\sqrt {1-z^{2}}}}
1
−
1
z
2
{\displaystyle {\sqrt {1-{\frac {1}{z^{2}}}}}}
z
{\displaystyle z\!}
1
1
+
1
z
2
{\displaystyle {\frac {1}{\sqrt {1+{\frac {1}{z^{2}}}}}}}
csch
{\displaystyle \operatorname {csch} \!}
1
z
{\displaystyle {\frac {1}{z}}}
1
z
−
1
z
+
1
{\displaystyle {\frac {1}{{\sqrt {z-1}}\;{\sqrt {z+1}}}}}
1
−
z
2
z
{\displaystyle {\frac {\sqrt {1-z^{2}}}{z}}}
z
1
−
1
z
2
{\displaystyle z\,{\sqrt {1-{\frac {1}{z^{2}}}}}}
1
1
z
−
1
1
z
+
1
{\displaystyle {\frac {1}{{\sqrt {{\frac {1}{z}}-1}}\;{\sqrt {{\frac {1}{z}}+1}}}}}
z
{\displaystyle z\!}
Zurück zur Formelsammlung Mathematik
lim
|
ξ
|
→
∞
(
1
+
z
ξ
)
ξ
=
e
z
∀
z
∈
C
{\displaystyle \lim _{|\xi |\to \infty }\left(1+{\frac {z}{\xi }}\right)^{\xi }=e^{z}\qquad \forall z\in \mathbb {C} }
lim
n
→
∞
n
!
n
z
z
(
z
+
1
)
⋯
(
z
+
n
)
=
Γ
(
z
)
∀
z
∉
Z
≤
0
{\displaystyle \lim _{n\to \infty }{\frac {n!\,n^{z}}{z\,(z+1)\cdots (z+n)}}=\Gamma (z)\qquad \forall z\notin \mathbb {Z} _{\leq 0}}
ohne Beweis (Gaußsche Definition der Gammafunktion)
lim
n
→
∞
1
n
y
∏
k
=
0
n
(
1
+
y
k
+
x
)
=
Γ
(
x
)
Γ
(
x
+
y
)
{\displaystyle \lim _{n\to \infty }{\frac {1}{n^{y}}}\,\prod _{k=0}^{n}\left(1+{\frac {y}{k+x}}\right)={\frac {\Gamma (x)}{\Gamma (x+y)}}}
lim
ε
→
0
+
(
|
Γ
(
−
n
+
ε
e
i
ϱ
1
)
|
−
|
Γ
(
−
n
+
ε
e
i
ϱ
2
)
|
)
=
ψ
(
n
+
1
)
Γ
(
n
+
1
)
(
cos
ϱ
1
−
cos
ϱ
2
)
{\displaystyle \lim _{\varepsilon \to 0^{+}}\left(\left|\Gamma \left(-n+\varepsilon \,e^{i\varrho _{1}}\right)\right|-\left|\Gamma \left(-n+\varepsilon \,e^{i\varrho _{2}}\right)\right|\right)={\frac {\psi (n+1)}{\Gamma (n+1)}}{\Big (}\cos \varrho _{1}-\cos \varrho _{2}{\Big )}}
f
{\displaystyle f\,}
lim
z
1
,
z
2
→
0
z
1
f
(
z
1
)
−
z
2
f
(
z
2
)
z
1
−
z
2
{\displaystyle \lim _{z_{1},z_{2}\to 0}{\frac {z_{1}\,f(z_{1})-z_{2}\,f(z_{2})}{z_{1}-z_{2}}}}
Γ
(
−
n
+
z
)
{\displaystyle \Gamma (-n+z)\,}
(
−
1
)
n
Ψ
(
n
+
1
)
Γ
(
n
+
1
)
{\displaystyle (-1)^{n}{\frac {\Psi (n+1)}{\Gamma (n+1)}}}
Γ
(
−
n
+
z
)
z
{\displaystyle \Gamma (-n+z)\,z\,}
(
−
1
)
n
1
Γ
(
n
+
1
)
{\displaystyle (-1)^{n}{\frac {1}{\Gamma (n+1)}}}
Ψ
(
−
n
+
z
)
{\displaystyle \Psi (-n+z)\,}
Ψ
(
n
+
1
)
{\displaystyle \Psi (n+1)\,}
Ψ
(
−
n
+
z
)
z
{\displaystyle \Psi (-n+z)\,z}
−
1
{\displaystyle -1\,}
ζ
(
1
+
z
)
(
1
+
z
)
α
{\displaystyle \zeta (1+z)\,(1+z)^{\alpha }}
α
+
γ
{\displaystyle \alpha +\gamma \,}
lim
n
→
∞
n
!
e
n
n
n
2
π
n
=
1
{\displaystyle \lim _{n\to \infty }{\frac {n!\,e^{n}}{n^{n}\,{\sqrt {2\pi n}}}}=1}
Beweis (Stirlingsche Formel)
Mit
z
=
ϱ
e
i
φ
{\displaystyle z=\varrho e^{i\varphi }}
Γ
(
z
)
∼
2
π
z
(
z
e
)
z
{
1
−
π
<
φ
<
π
1
e
2
π
i
z
−
1
φ
=
π
{\displaystyle \Gamma (z)\sim {\sqrt {\frac {2\pi }{z}}}\left({\frac {z}{e}}\right)^{z}\left\{{\begin{matrix}1&-\pi <\varphi <\pi \\{\frac {1}{e^{2\pi iz}-1}}&\varphi =\pi \end{matrix}}\right.}
ϱ
→
∞
{\displaystyle \varrho \to \infty }
lim
n
→
∞
n
n
!
n
=
e
{\displaystyle \lim _{n\to \infty }{\frac {n}{\sqrt[{n}]{n!}}}=e}
1. Beweis
Die Stirlingformel besagt, dass die Folge
a
n
=
n
!
e
n
n
n
2
π
n
{\displaystyle a_{n}={\frac {n!\,e^{n}}{n^{n}\,{\sqrt {2\pi n}}}}}
1
{\displaystyle 1\,}
a
n
n
=
n
!
n
e
n
2
π
n
2
n
{\displaystyle {\sqrt[{n}]{a_{n}}}={\frac {{\sqrt[{n}]{n!}}\,\,e}{n\,{\sqrt[{2n}]{2\pi n}}}}}
1
{\displaystyle 1\,}
lim
n
→
∞
2
π
n
2
n
=
1
{\displaystyle \lim _{n\to \infty }{\sqrt[{2n}]{2\pi n}}=1}
lim
n
→
∞
n
!
n
n
e
=
1
{\displaystyle \lim _{n\to \infty }{\frac {\sqrt[{n}]{n!}}{n}}\,e=1}
lim
n
→
∞
n
n
!
n
=
e
{\displaystyle \lim _{n\to \infty }{\frac {n}{\sqrt[{n}]{n!}}}=e}
lim
n
→
∞
n
π
2
2
n
(
2
n
n
)
=
1
{\displaystyle \lim _{n\to \infty }{\frac {\sqrt {n\pi }}{2^{2n}}}{2n \choose n}=1}
Beweis
∏
k
=
1
n
4
k
2
−
1
4
k
2
=
∏
k
=
1
n
(
2
k
−
1
)
⋅
(
2
k
+
1
)
2
k
⋅
2
k
=
(
2
n
)
!
2
n
n
!
⋅
(
2
n
)
!
2
n
n
!
(
2
n
+
1
)
2
n
n
!
⋅
2
n
n
!
=
(
2
n
+
1
)
[
(
2
n
)
!
2
2
n
n
!
2
]
2
=
(
2
n
+
1
)
[
1
2
2
n
(
2
n
n
)
]
2
{\displaystyle \prod _{k=1}^{n}{\frac {4k^{2}-1}{4k^{2}}}=\prod _{k=1}^{n}{\frac {(2k-1)\cdot (2k+1)}{2k\cdot 2k}}={\frac {{\frac {(2n)!}{2^{n}\,n!}}\,\cdot \,{\frac {(2n)!}{2^{n}\,n!}}\,(2n+1)}{2^{n}\,n!\,\cdot \,2^{n}\,n!}}=(2n+1)\left[{\frac {(2n)!}{2^{2n}\,n!^{2}}}\right]^{2}=(2n+1)\left[{\frac {1}{2^{2n}}}{2n \choose n}\right]^{2}}
lim
n
→
∞
(
2
n
+
1
)
[
1
2
2
n
(
2
n
n
)
]
2
=
∏
k
=
1
∞
4
k
2
−
1
4
k
2
=
2
π
(Wallis Produkt)
{\displaystyle \lim _{n\to \infty }(2n+1)\left[{\frac {1}{2^{2n}}}{2n \choose n}\right]^{2}=\prod _{k=1}^{\infty }{\frac {4k^{2}-1}{4k^{2}}}={\frac {2}{\pi }}\qquad {\text{(Wallis Produkt)}}}
lim
n
→
∞
2
n
+
1
2
2
n
(
2
n
n
)
=
2
π
{\displaystyle \lim _{n\to \infty }{\frac {\sqrt {2n+1}}{2^{2n}}}{2n \choose n}={\sqrt {\frac {2}{\pi }}}}
lim
n
→
∞
(
n
+
1
2
)
π
2
2
n
(
2
n
n
)
=
1
{\displaystyle \lim _{n\to \infty }{\frac {\sqrt {\left(n+{\frac {1}{2}}\right)\pi }}{2^{2n}}}{2n \choose n}=1}
lim
n
→
∞
n
π
(
n
+
1
2
)
π
=
1
{\displaystyle \lim _{n\to \infty }{\frac {\sqrt {n\pi }}{\sqrt {\left(n+{\frac {1}{2}}\right)\pi }}}=1}
lim
n
→
∞
n
π
2
2
n
(
2
n
n
)
=
1
{\displaystyle \lim _{n\to \infty }{\frac {\sqrt {n\pi }}{2^{2n}}}{2n \choose n}=1}
B
(
α
n
,
β
n
)
∼
2
π
n
α
+
β
α
β
(
α
α
β
β
(
α
+
β
)
α
+
β
)
n
{\displaystyle B(\alpha n,\beta n)\sim {\sqrt {\frac {2\pi }{n}}}\,{\sqrt {\frac {\alpha +\beta }{\alpha \,\beta }}}\left({\frac {\alpha ^{\alpha }\,\beta ^{\beta }}{(\alpha +\beta )^{\alpha +\beta }}}\right)^{n}}
lim
n
→
∞
(
α
n
+
β
n
)
!
(
α
n
)
!
(
β
n
)
!
n
=
(
α
+
β
)
α
+
β
α
α
β
β
{\displaystyle \lim _{n\to \infty }{\sqrt[{n}]{\frac {(\alpha n+\beta n)!}{(\alpha n)!\,(\beta n)!}}}={\frac {(\alpha +\beta )^{\alpha +\beta }}{\alpha ^{\alpha }\,\beta ^{\beta }}}}
lim
y
→
∞
|
Γ
(
x
+
i
y
)
|
2
π
y
y
x
e
−
π
2
y
=
1
x
∈
R
{\displaystyle \lim _{y\to \infty }{\frac {|\Gamma (x+iy)|}{{\sqrt {\frac {2\pi }{y}}}\,y^{x}\,e^{-{\frac {\pi }{2}}y}}}=1\qquad x\in \mathbb {R} }
A
:=
lim
n
→
∞
e
n
2
4
∏
k
=
1
n
k
k
n
n
2
2
+
n
2
+
1
12
=
e
1
12
−
ζ
′
(
−
1
)
{\displaystyle A:=\lim _{n\to \infty }{\frac {e^{\frac {n^{2}}{4}}\,\prod _{k=1}^{n}k^{k}}{n^{{\frac {n^{2}}{2}}+{\frac {n}{2}}+{\frac {1}{12}}}}}=e^{{\frac {1}{12}}-\zeta '(-1)}}
Beweis (Glaisher-Kinkelin-Konstante)
Betrachte die asymptotische Entwicklung
∑
k
=
1
n
k
p
=
ζ
(
−
p
)
+
n
p
+
1
p
+
1
+
n
p
2
+
p
12
n
p
−
1
+
O
(
n
p
−
3
)
{\displaystyle \sum _{k=1}^{n}k^{p}=\zeta (-p)+{\frac {n^{p+1}}{p+1}}+{\frac {n^{p}}{2}}+{\frac {p}{12}}\,n^{p-1}+O\left(n^{p-3}\right)}
p
{\displaystyle p\,}
∑
k
=
1
n
k
p
log
k
=
−
ζ
′
(
−
p
)
+
n
p
+
1
log
n
p
+
1
−
n
p
+
1
(
p
+
1
)
2
+
n
p
log
n
2
+
p
12
n
p
−
1
log
n
+
n
p
−
1
12
+
O
(
n
p
−
3
log
n
)
{\displaystyle \sum _{k=1}^{n}k^{p}\,\log k=-\zeta '(-p)+{\frac {n^{p+1}\,\log n}{p+1}}-{\frac {n^{p+1}}{(p+1)^{2}}}+{\frac {n^{p}\,\log n}{2}}+{\frac {p}{12}}\,n^{p-1}\,\log n+{\frac {n^{p-1}}{12}}+O\left(n^{p-3}\,\log n\right)}
p
=
1
{\displaystyle p=1\,}
∑
k
=
1
n
k
log
k
=
−
ζ
′
(
−
1
)
+
n
2
2
log
n
−
n
2
4
+
n
2
log
n
+
1
12
log
n
+
1
12
+
O
(
log
n
n
2
)
{\displaystyle \sum _{k=1}^{n}k\,\log k=-\zeta '(-1)+{\frac {n^{2}}{2}}\,\log n-{\frac {n^{2}}{4}}+{\frac {n}{2}}\,\log n+{\frac {1}{12}}\,\log n+{\frac {1}{12}}+O\left({\frac {\log n}{n^{2}}}\right)}
a
n
:=
n
2
4
+
∑
k
=
1
n
k
log
k
−
(
n
2
2
+
n
2
+
1
12
)
log
n
→
1
12
−
ζ
′
(
−
1
)
{\displaystyle a_{n}:={\frac {n^{2}}{4}}+\sum _{k=1}^{n}k\,\log k-\left({\frac {n^{2}}{2}}+{\frac {n}{2}}+{\frac {1}{12}}\right)\log n\to {\frac {1}{12}}-\zeta '(-1)}
⇒
A
=
lim
n
→
∞
e
a
n
=
e
1
12
−
ζ
′
(
−
1
)
{\displaystyle \Rightarrow \,A=\lim _{n\to \infty }e^{a_{n}}=e^{{\frac {1}{12}}-\zeta '(-1)}}
lim
n
→
∞
[
(
n
+
1
)
n
+
1
n
n
−
n
n
(
n
−
1
)
n
−
1
]
=
e
{\displaystyle \lim _{n\to \infty }\left[{\frac {(n+1)^{n+1}}{n^{n}}}-{\frac {n^{n}}{(n-1)^{n-1}}}\right]=e}
Beweis (Kellersche Darstellung von e)
lim
m
→
∞
(
∑
k
=
1
m
(
log
k
)
n
k
−
(
log
m
)
n
+
1
n
+
1
)
=
γ
n
{\displaystyle \lim _{m\to \infty }\left(\sum _{k=1}^{m}{\frac {(\log k)^{n}}{k}}-{\frac {(\log m)^{n+1}}{n+1}}\right)=\gamma _{n}}
ohne Beweis (Stieltjes Konstanten)
lim
n
→
∞
(
H
n
−
log
n
)
=
γ
{\displaystyle \lim _{n\to \infty }\left(H_{n}-\log n\right)=\gamma }
Beweis, dass der Grenzwert existiert (Eulersche Konstante)
Für
x
>
0
{\displaystyle x>0\,}
x
−
1
≥
log
x
{\displaystyle x-1\geq \log x}
x
≥
log
(
1
+
x
)
{\displaystyle x\geq \log(1+x)}
x
>
−
1
{\displaystyle x>-1\,}
x
=
−
1
k
+
1
{\displaystyle x={\frac {-1}{k+1}}}
−
1
k
+
1
≥
log
k
−
log
(
k
+
1
)
{\displaystyle {\frac {-1}{k+1}}\geq \log k-\log(k+1)}
log
(
k
+
1
)
−
log
k
≥
1
k
+
1
{\displaystyle \log(k+1)-\log k\geq {\frac {1}{k+1}}}
x
=
1
k
{\displaystyle x={\frac {1}{k}}}
1
k
≥
log
(
k
+
1
)
−
log
k
{\displaystyle {\frac {1}{k}}\geq \log(k+1)-\log k}
Napierschen Ungleichung
1
a
<
2
a
+
b
<
log
a
−
log
b
a
−
b
<
1
a
b
<
1
b
a
=
k
+
1
{\displaystyle {\frac {1}{a}}<{\frac {2}{a+b}}<{\frac {\log a-\log b}{a-b}}<{\frac {1}{\sqrt {ab}}}<{\frac {1}{b}}\qquad a=k+1}
b
=
k
{\displaystyle b=k\,}
log
(
k
+
1
)
−
log
k
≥
H
k
+
1
−
H
k
{\displaystyle \log(k+1)-\log k\geq H_{k+1}-H_{k}}
H
k
−
log
k
≥
H
k
+
1
−
log
(
k
+
1
)
{\displaystyle H_{k}-\log k\geq H_{k+1}-\log(k+1)}
(
H
n
−
log
n
)
n
≥
1
{\displaystyle (H_{n}-\log n)_{n\geq 1}}
H
n
≥
∑
k
=
1
n
(
log
(
k
+
1
)
−
log
k
)
=
log
(
n
+
1
)
>
log
n
{\displaystyle H_{n}\geq \sum _{k=1}^{n}{\big (}\log(k+1)-\log k{\big )}=\log(n+1)>\log n}
H
n
−
log
n
{\displaystyle H_{n}-\log n\,}
lim
n
→
∞
(
H
n
−
log
n
)
{\displaystyle \lim _{n\to \infty }\left(H_{n}-\log n\right)}
lim
n
→
∞
(
log
n
−
∑
k
=
0
n
1
k
+
x
)
=
ψ
(
x
)
{\displaystyle \lim _{n\to \infty }\left(\log n-\sum _{k=0}^{n}{\frac {1}{k+x}}\right)=\psi (x)}
lim
z
→
1
(
ζ
(
z
)
−
1
z
−
1
)
=
γ
{\displaystyle \lim _{z\to 1}\left(\zeta (z)-{\frac {1}{z-1}}\right)=\gamma }
lim
n
→
∞
1
n
!
∫
n
+
a
n
n
+
b
n
x
n
e
x
d
x
=
1
2
π
∫
a
b
e
−
x
2
2
d
x
a
,
b
∈
C
{\displaystyle \lim _{n\to \infty }{\frac {1}{n!}}\int _{n+a{\sqrt {n}}}^{n+b{\sqrt {n}}}{\frac {x^{n}}{e^{x}}}\,dx={\frac {1}{\sqrt {2\pi }}}\,\int _{a}^{b}e^{-{\frac {x^{2}}{2}}}\,dx\qquad a,b\in \mathbb {C} }
ohne Beweis (Grenzwert, der sich aus der
χ
2
{\displaystyle \chi ^{2}}
-Verteilung ergibt)
(
z
α
)
′
=
α
z
α
−
1
α
∈
C
,
z
∈
C
∖
{
z
∈
R
:
z
≤
0
}
{\displaystyle (z^{\alpha })'=\alpha \,z^{\alpha -1}\qquad \alpha \in \mathbb {C} \;,\;z\in \mathbb {C} \setminus \left\{z\in \mathbb {R} \,:\,z\leq 0\right\}}
(
e
z
)
′
=
e
z
z
∈
C
{\displaystyle (\mathrm {e} ^{z})'=\mathrm {e} ^{z}\qquad z\in \mathbb {C} }
(
a
z
)
′
=
a
z
log
a
a
≠
0
,
z
∈
C
{\displaystyle (a^{z})'=a^{z}\,\log a\qquad a\neq 0\,,\,z\in \mathbb {C} }
(
log
z
)
′
=
1
z
z
∈
C
∖
{
z
∈
R
:
z
≤
0
}
{\displaystyle (\log z)'={\frac {1}{z}}\qquad z\in \mathbb {C} \setminus \left\{z\in \mathbb {R} \,:\,z\leq 0\right\}}
∼
{\displaystyle \sim }
∼
h
{\displaystyle \operatorname {\sim \!h} }
a
r
c
∼
{\displaystyle \operatorname {arc\!\sim } }
a
r
∼
h
{\displaystyle \operatorname {ar\!\sim \!h} }
sin
{\displaystyle \sin \!}
cos
{\displaystyle \cos \!}
cosh
{\displaystyle \cosh \!}
1
1
−
z
2
{\displaystyle {\frac {1}{\sqrt {1-z^{2}}}}}
1
1
+
z
2
{\displaystyle {\frac {1}{\sqrt {1+z^{2}}}}}
cos
{\displaystyle \cos \!}
−
sin
{\displaystyle -\sin \!}
sinh
{\displaystyle \sinh \!}
−
1
1
−
z
2
{\displaystyle {\frac {-1}{\sqrt {1-z^{2}}}}}
1
z
−
1
z
+
1
{\displaystyle {\frac {1}{{\sqrt {z-1}}\,{\sqrt {z+1}}}}}
tan
{\displaystyle \tan \!}
1
+
tan
2
{\displaystyle 1+\tan ^{2}\!}
1
−
tanh
2
{\displaystyle 1-\tanh ^{2}\!}
1
1
+
z
2
{\displaystyle {\frac {1}{1+z^{2}}}}
1
1
−
z
2
{\displaystyle {\frac {1}{1-z^{2}}}}
cot
{\displaystyle \cot \!}
−
1
−
cot
2
{\displaystyle -1-\cot ^{2}\!}
1
−
coth
2
{\displaystyle 1-\operatorname {coth} ^{2}\!}
−
1
1
+
z
2
{\displaystyle {\frac {-1}{1+z^{2}}}}
1
1
−
z
2
{\displaystyle {\frac {1}{1-z^{2}}}}
sec
{\displaystyle \sec \!}
sec
⋅
tan
{\displaystyle \sec \cdot \tan }
−
sech
⋅
tanh
{\displaystyle -\operatorname {sech} \cdot \operatorname {tanh} }
1
z
2
1
−
1
z
2
{\displaystyle {\frac {1}{z^{2}\,{\sqrt {1-{\frac {1}{z^{2}}}}}}}}
−
1
z
2
1
z
−
1
1
z
+
1
{\displaystyle {\frac {-1}{z^{2}\,{\sqrt {{\frac {1}{z}}-1}}\,{\sqrt {{\frac {1}{z}}+1}}}}}
csc
{\displaystyle \csc \!}
−
csc
⋅
cot
{\displaystyle -\csc \cdot \cot }
−
csch
{\displaystyle -\operatorname {csch} }
−
1
z
2
1
−
1
z
2
{\displaystyle {\frac {-1}{z^{2}\,{\sqrt {1-{\frac {1}{z^{2}}}}}}}}
−
1
z
2
1
+
1
z
2
{\displaystyle {\frac {-1}{z^{2}\,{\sqrt {1+{\frac {1}{z^{2}}}}}}}}
Γ
′
(
z
)
=
Γ
(
z
)
ψ
(
z
)
z
∉
Z
≤
0
{\displaystyle \Gamma '(z)=\Gamma (z)\,\psi (z)\qquad z\notin \mathbb {Z} _{\leq 0}}
1
2
(
d
d
x
)
n
log
(
x
2
+
y
2
)
=
(
−
1
)
n
−
1
(
n
−
1
)
!
x
2
+
y
2
n
cos
(
n
arctan
y
x
)
{\displaystyle {\frac {1}{2}}\left({\frac {\mathrm {d} }{\mathrm {d} x}}\right)^{n}\log(x^{2}+y^{2})={\frac {(-1)^{n-1}\,(n-1)!}{{\sqrt {x^{2}+y^{2}}}^{n}}}\,\cos \left(n\,\arctan {\frac {y}{x}}\right)}
(
d
d
x
)
n
arctan
x
y
=
(
−
1
)
n
−
1
(
n
−
1
)
!
x
2
+
y
2
n
sin
(
n
arctan
y
x
)
{\displaystyle \left({\frac {\mathrm {d} }{\mathrm {d} x}}\right)^{n}\arctan {\frac {x}{y}}={\frac {(-1)^{n-1}\,(n-1)!}{{\sqrt {x^{2}+y^{2}}}^{n}}}\,\sin \left(n\,\arctan {\frac {y}{x}}\right)}
(
d
d
x
)
n
1
1
−
x
2
=
∑
k
=
0
⌊
n
2
⌋
n
!
(
2
n
−
2
k
)
!
2
n
k
!
(
n
−
k
)
!
(
n
−
2
k
)
!
x
n
−
2
k
1
−
x
2
2
n
−
2
k
+
1
=
∑
k
=
0
⌊
n
2
⌋
1
2
2
k
n
!
2
k
!
2
x
n
−
2
k
(
n
−
2
k
)
!
1
1
−
x
2
2
n
+
1
{\displaystyle \left({\frac {\mathrm {d} }{\mathrm {d} x}}\right)^{n}{\frac {1}{\sqrt {1-x^{2}}}}=\sum _{k=0}^{\lfloor {\frac {n}{2}}\rfloor }{\frac {n!\,(2n-2k)!}{2^{n}\,k!\,(n-k)!\,(n-2k)!}}\,{\frac {x^{n-2k}}{{\sqrt {1-x^{2}}}^{\,2n-2k+1}}}=\sum _{k=0}^{\lfloor {\frac {n}{2}}\rfloor }{\frac {1}{2^{2k}}}\,{\frac {n!^{2}}{k!^{2}}}\,{\frac {x^{n-2k}}{(n-2k)!}}\,{\frac {1}{{\sqrt {1-x^{2}}}^{\,2n+1}}}}
(
d
d
x
)
n
1
(
1
−
x
2
)
m
=
∑
k
=
0
⌊
n
2
⌋
Γ
(
m
+
k
)
Γ
(
m
)
Γ
(
2
m
+
n
)
Γ
(
2
m
+
2
k
)
n
!
k
!
x
n
−
2
k
(
n
−
2
k
)
!
1
(
1
−
x
2
)
n
+
m
{\displaystyle \left({\frac {\mathrm {d} }{\mathrm {d} x}}\right)^{n}{\frac {1}{(1-x^{2})^{m}}}=\sum _{k=0}^{\lfloor {\frac {n}{2}}\rfloor }{\frac {\Gamma (m+k)}{\Gamma (m)}}\,{\frac {\Gamma (2m+n)}{\Gamma (2m+2k)}}\,{\frac {n!}{k!}}\,{\frac {x^{n-2k}}{(n-2k)!}}\,{\frac {1}{(1-x^{2})^{n+m}}}}
(
x
d
d
x
)
n
f
(
x
)
=
∑
k
=
0
n
{
n
k
}
x
k
f
(
k
)
(
x
)
{\displaystyle \left(x\,{\frac {\mathrm {d} }{\mathrm {d} x}}\right)^{n}f(x)=\sum _{k=0}^{n}\left\{{\begin{matrix}n\\k\end{matrix}}\right\}\,x^{k}\,f^{(k)}(x)}
Beweis
Der Induktionsanfang für
n
=
0
{\displaystyle n=0\,}
(
x
d
d
x
)
n
+
1
f
(
x
)
=
∑
k
=
0
n
{
n
k
}
x
d
d
x
(
x
k
f
(
k
)
(
x
)
)
=
∑
k
=
0
n
{
n
k
}
k
x
k
f
(
k
)
(
x
)
⏟
1. Summe
+
∑
k
=
0
n
{
n
k
}
x
k
+
1
f
(
k
+
1
)
(
x
)
⏟
2. Summe
{\displaystyle \left(x{\frac {\mathrm {d} }{\mathrm {d} x}}\right)^{n+1}f(x)=\sum _{k=0}^{n}\left\{{\begin{matrix}n\\k\end{matrix}}\right\}\,x\,{\frac {\mathrm {d} }{\mathrm {d} x}}\left(x^{k}f^{(k)}(x)\right)=\underbrace {\sum _{k=0}^{n}\left\{{\begin{matrix}n\\k\end{matrix}}\right\}\,k\,x^{k}\,f^{(k)}(x)} _{\text{1. Summe}}+\underbrace {\sum _{k=0}^{n}\left\{{\begin{matrix}n\\k\end{matrix}}\right\}\,x^{k+1}\,f^{(k+1)}(x)} _{\text{2. Summe}}}
{
n
k
}
=
0
{\displaystyle \left\{{\begin{matrix}n\\k\end{matrix}}\right\}=0}
∑
k
=
1
n
+
1
{
n
k
−
1
}
x
k
f
(
k
)
(
x
)
{\displaystyle \sum _{k=1}^{n+1}\left\{{\begin{matrix}n\\k-1\end{matrix}}\right\}\,x^{k}\,f^{(k)}(x)}
{
n
k
}
=
0
{\displaystyle \left\{{\begin{matrix}n\\k\end{matrix}}\right\}=0}
(
x
d
d
x
)
n
+
1
f
(
x
)
=
∑
k
=
0
n
+
1
(
{
n
k
}
k
+
{
n
k
−
1
}
)
x
k
f
(
k
)
(
x
)
{\displaystyle \left(x\,{\frac {\mathrm {d} }{\mathrm {d} x}}\right)^{n+1}f(x)=\sum _{k=0}^{n+1}\left(\left\{{\begin{matrix}n\\k\end{matrix}}\right\}\,k+\left\{{\begin{matrix}n\\k-1\end{matrix}}\right\}\right)\,x^{k}f^{(k)}(x)}
{
n
k
}
k
+
{
n
k
−
1
}
=
{
n
+
1
k
}
{\displaystyle \left\{{\begin{matrix}n\\k\end{matrix}}\right\}\,k+\left\{{\begin{matrix}n\\k-1\end{matrix}}\right\}=\left\{{\begin{matrix}n+1\\k\end{matrix}}\right\}}
∑
k
=
0
n
+
1
{
n
+
1
k
}
x
k
f
(
k
)
(
x
)
{\displaystyle \sum _{k=0}^{n+1}\left\{{\begin{matrix}n+1\\k\end{matrix}}\right\}\,x^{k}\,f^{(k)}(x)}
∑
k
=
1
n
k
=
n
(
n
+
1
)
2
{\displaystyle \sum _{k=1}^{n}k={\frac {n(n+1)}{2}}}
∑
k
=
1
n
(
2
k
−
1
)
=
n
2
{\displaystyle \sum _{k=1}^{n}(2k-1)=n^{2}}
Beweis
Auf Wikipedia unter Induktionsbeweis ist der Beweis zu finden.
Es ist
∑
k
=
1
n
(
2
k
−
1
)
=
∑
k
=
1
n
2
k
−
∑
k
=
1
n
1
=
2
∑
k
=
1
n
k
−
n
=
2
n
(
n
+
1
)
2
−
n
=
n
2
{\displaystyle \sum _{k=1}^{n}(2k-1)=\sum _{k=1}^{n}2k-\sum _{k=1}^{n}1=2\sum _{k=1}^{n}k-n=2{\frac {n(n+1)}{2}}-n=n^{2}}
∑
k
=
1
n
k
2
=
n
(
n
+
1
)
(
2
n
+
1
)
6
{\displaystyle \sum _{k=1}^{n}k^{2}={\frac {n(n+1)(2n+1)}{6}}}
Beweis
Beweismethode: Induktionsbeweis
Oder direkt wie folgt:
Mit
∑
k
=
1
n
(
2
k
−
1
)
=
n
2
{\displaystyle \sum _{k=1}^{n}(2k-1)=n^{2}}
∑
k
=
1
n
k
2
=
∑
k
=
1
n
∑
l
=
1
k
(
2
l
−
1
)
=
1
+
(
1
+
3
)
+
(
1
+
3
+
5
)
+
(
1
+
3
+
5
+
7
)
+
⋯
+
(
1
+
3
+
5
+
7
+
⋯
+
(
2
n
−
1
)
)
{\displaystyle \sum _{k=1}^{n}k^{2}=\sum _{k=1}^{n}\sum _{l=1}^{k}(2l-1)=1+(1+3)+(1+3+5)+(1+3+5+7)+\cdots +(1+3+5+7+\cdots +(2n-1))}
Es existieren
n
{\displaystyle n}
(
1
,
3
,
5
,
⋯
,
2
n
−
1
)
{\displaystyle (1,3,5,\cdots ,2n-1)}
n
{\displaystyle n}
1
{\displaystyle 1}
(
n
−
1
)
{\displaystyle (n-1)}
3
{\displaystyle 3}
(
2
n
−
1
)
{\displaystyle (2n-1)}
∑
k
=
1
n
∑
l
=
1
k
(
2
l
−
1
)
=
n
⋅
1
+
(
n
−
1
)
⋅
3
+
(
n
−
2
)
⋅
5
+
⋯
+
1
⋅
(
2
n
−
1
)
=
∑
k
=
1
n
(
n
−
k
+
1
)
⋅
(
2
k
−
1
)
{\displaystyle \sum _{k=1}^{n}\sum _{l=1}^{k}(2l-1)=n\cdot 1+(n-1)\cdot 3+(n-2)\cdot 5+\cdots +1\cdot (2n-1)=\sum _{k=1}^{n}(n-k+1)\cdot (2k-1)}
Damit ergibt sich:
∑
k
=
1
n
k
2
=
∑
k
=
1
n
(
2
k
−
1
)
⋅
(
n
−
k
+
1
)
=
∑
k
=
1
n
(
k
(
2
n
+
3
)
−
2
k
2
−
n
−
1
)
=
(
2
n
+
3
)
∑
k
=
1
n
k
−
2
∑
k
=
1
n
k
2
−
∑
k
=
1
n
n
−
∑
k
=
1
n
1
{\displaystyle \sum _{k=1}^{n}k^{2}=\sum _{k=1}^{n}(2k-1)\cdot (n-k+1)=\sum _{k=1}^{n}(k(2n+3)-2k^{2}-n-1)=(2n+3)\sum _{k=1}^{n}k-2\sum _{k=1}^{n}k^{2}-\sum _{k=1}^{n}n-\sum _{k=1}^{n}1}
Daraus folgt:
3
∑
k
=
1
n
k
2
=
(
2
n
+
3
)
n
(
n
+
1
)
2
−
n
2
−
n
=
(
2
n
+
3
)
n
(
n
+
1
)
−
2
n
(
n
+
1
)
2
=
(
2
n
+
1
)
n
(
n
+
1
)
2
{\displaystyle 3\sum _{k=1}^{n}k^{2}=(2n+3){\frac {n(n+1)}{2}}-n^{2}-n={\frac {(2n+3)n(n+1)-2n(n+1)}{2}}={\frac {(2n+1)n(n+1)}{2}}}
Womit schließlich folgt:
∑
k
=
1
n
k
2
=
(
2
n
+
1
)
n
(
n
+
1
)
6
{\displaystyle \sum _{k=1}^{n}k^{2}={\frac {(2n+1)n(n+1)}{6}}}
Sind
a
,
b
{\displaystyle a,b\,}
a
<
b
{\displaystyle a<b\,}
f
:
[
a
,
b
]
→
R
{\displaystyle f:[a,b]\to \mathbb {R} }
n
{\displaystyle n\,}
∑
a
<
k
≤
b
f
(
k
)
=
∫
a
b
f
(
x
)
d
x
+
∑
k
=
0
n
−
1
(
−
1
)
k
+
1
B
k
+
1
(
k
+
1
)
!
(
f
(
k
)
(
b
)
−
f
(
k
)
(
a
)
)
+
(
−
1
)
n
−
1
n
!
∫
a
b
B
n
(
x
)
f
(
n
)
(
x
)
d
x
{\displaystyle \sum _{a<k\leq b}f(k)=\int _{a}^{b}f(x)\,dx+\sum _{k=0}^{n-1}{\frac {(-1)^{k+1}\,B_{k+1}}{(k+1)!}}\left(f^{(k)}(b)-f^{(k)}(a)\right)+{\frac {(-1)^{n-1}}{n!}}\int _{a}^{b}B_{n}(x)\,f^{(n)}(x)\,dx}
Hierbei steht
B
k
(
x
)
{\displaystyle B_{k}(x)\,}
k
{\displaystyle k}
B
k
{\displaystyle B_{k}\,}
k
{\displaystyle k}
Beweis
∫
k
−
1
k
f
(
x
)
d
x
=
[
(
x
−
k
+
1
2
)
f
(
x
)
]
k
−
1
k
−
∫
k
−
1
k
(
x
−
k
+
1
2
)
f
′
(
x
)
d
x
=
f
(
k
)
2
+
f
(
k
−
1
)
2
−
∫
k
−
1
k
B
1
(
x
)
f
′
(
x
)
d
x
{\displaystyle \int _{k-1}^{k}f(x)\,dx=\left[\left(x-k+{\frac {1}{2}}\right)f(x)\right]_{k-1}^{k}-\int _{k-1}^{k}\left(x-k+{\frac {1}{2}}\right)f'(x)\,dx={\frac {f(k)}{2}}+{\frac {f(k-1)}{2}}-\int _{k-1}^{k}B_{1}(x)\,f'(x)\,dx}
⇒
∫
a
b
f
(
x
)
d
x
=
∑
a
<
k
≤
b
∫
k
−
1
k
f
(
x
)
d
x
=
∑
a
<
k
≤
b
f
(
k
)
−
1
2
(
f
(
b
)
−
f
(
a
)
)
−
∫
a
b
B
1
(
x
)
f
′
(
x
)
d
x
{\displaystyle \Rightarrow \int _{a}^{b}f(x)\,dx=\sum _{a<k\leq b}\int _{k-1}^{k}f(x)\,dx=\sum _{a<k\leq b}f(k)-{\frac {1}{2}}\left(f(b)-f(a)\right)-\int _{a}^{b}B_{1}(x)\,f'(x)\,dx}
⇒
∑
a
<
k
≤
b
f
(
k
)
=
∫
a
b
f
(
x
)
d
x
+
1
2
(
f
(
b
)
−
f
(
a
)
)
+
∫
a
b
B
1
(
x
)
f
′
(
x
)
d
x
{\displaystyle \Rightarrow \sum _{a<k\leq b}f(k)=\int _{a}^{b}f(x)\,dx+{\frac {1}{2}}\left(f(b)-f(a)\right)+\int _{a}^{b}B_{1}(x)\,f'(x)\,dx}
n
=
1
{\displaystyle n=1\,}
B
n
+
1
′
(
x
)
=
(
n
+
1
)
B
n
(
x
)
{\displaystyle B_{n+1}'(x)=(n+1)B_{n}(x)\,}
∫
a
b
B
n
(
x
)
f
(
n
)
(
x
)
d
x
=
∫
a
b
B
n
+
1
′
(
x
)
n
+
1
f
(
n
)
(
x
)
d
x
{\displaystyle \int _{a}^{b}B_{n}(x)\,f^{(n)}(x)\,dx=\int _{a}^{b}{\frac {B_{n+1}'(x)}{n+1}}\,f^{(n)}(x)\,dx}
=
[
B
n
+
1
(
x
)
n
+
1
f
(
n
)
(
x
)
]
a
b
−
∫
a
b
B
n
+
1
(
x
)
n
+
1
f
(
n
+
1
)
(
x
)
d
x
=
B
n
+
1
n
+
1
(
f
(
n
)
(
b
)
−
f
(
n
)
(
a
)
)
−
1
n
+
1
∫
a
b
B
n
+
1
(
x
)
f
(
n
+
1
)
(
x
)
d
x
{\displaystyle =\left[{\frac {B_{n+1}(x)}{n+1}}\,f^{(n)}(x)\right]_{a}^{b}-\int _{a}^{b}{\frac {B_{n+1}(x)}{n+1}}\,f^{(n+1)}(x)\,dx={\frac {B_{n+1}}{n+1}}\left(f^{(n)}(b)-f^{(n)}(a)\right)-{\frac {1}{n+1}}\int _{a}^{b}B_{n+1}(x)\,f^{(n+1)}(x)\,dx}
⇒
(
−
1
)
n
−
1
n
!
∫
a
b
B
n
(
x
)
f
(
n
)
(
x
)
d
x
=
(
−
1
)
n
+
1
B
n
+
1
(
n
+
1
)
!
(
f
(
n
)
(
b
)
−
f
(
n
)
(
a
)
)
+
(
−
1
)
n
(
n
+
1
)
!
∫
a
b
B
n
+
1
(
x
)
f
(
n
+
1
)
(
x
)
d
x
{\displaystyle \Rightarrow {\frac {(-1)^{n-1}}{n!}}\int _{a}^{b}B_{n}(x)\,f^{(n)}(x)\,dx={\frac {(-1)^{n+1}\,B_{n+1}}{(n+1)!}}\left(f^{(n)}(b)-f^{(n)}(a)\right)+{\frac {(-1)^{n}}{(n+1)!}}\int _{a}^{b}B_{n+1}(x)\,f^{(n+1)}(x)\,dx}
∑
k
=
1
n
k
p
=
∑
k
=
0
n
k
!
(
n
+
1
k
+
1
)
{
p
k
}
p
∈
C
{\displaystyle \sum _{k=1}^{n}k^{p}=\sum _{k=0}^{n}k!\,{n+1 \choose k+1}{\begin{Bmatrix}p\\k\end{Bmatrix}}\qquad p\in \mathbb {C} }
∑
k
=
1
n
k
p
=
1
p
+
1
∑
k
=
0
p
(
−
1
)
k
(
p
+
1
k
)
B
k
n
p
+
1
−
k
p
∈
Z
≥
0
{\displaystyle \sum _{k=1}^{n}k^{p}={\frac {1}{p+1}}\,\sum _{k=0}^{p}(-1)^{k}\,{p+1 \choose k}\,B_{k}\,\,n^{p+1-k}\qquad p\in \mathbb {Z} ^{\geq 0}}
1. Beweis
Einerseits ist
∑
k
=
0
n
−
1
e
k
x
=
∑
k
=
0
n
−
1
∑
p
=
0
∞
(
k
x
)
p
p
!
=
∑
p
=
0
∞
∑
k
=
0
n
−
1
k
p
x
p
p
!
{\displaystyle \sum _{k=0}^{n-1}e^{kx}=\sum _{k=0}^{n-1}\sum _{p=0}^{\infty }{\frac {(kx)^{p}}{p!}}=\sum _{p=0}^{\infty }\sum _{k=0}^{n-1}k^{p}\,{\frac {x^{p}}{p!}}}
∑
k
=
0
n
−
1
e
k
x
=
e
n
x
−
1
e
x
−
1
=
x
e
x
−
1
e
n
x
−
1
x
{\displaystyle \sum _{k=0}^{n-1}e^{kx}={\frac {e^{nx}-1}{e^{x}-1}}={\frac {x}{e^{x}-1}}\,{\frac {e^{nx}-1}{x}}}
∑
k
=
0
∞
B
k
k
!
x
k
∑
k
=
0
∞
n
k
+
1
(
k
+
1
)
!
x
k
=
∑
p
=
0
∞
∑
k
=
0
p
B
k
k
!
n
p
−
k
+
1
(
p
−
k
+
1
)
!
x
p
(Cauchy-Produkt)
{\displaystyle \sum _{k=0}^{\infty }{\frac {B_{k}}{k!}}\,x^{k}\,\,\sum _{k=0}^{\infty }{\frac {n^{k+1}}{(k+1)!}}\,x^{k}=\sum _{p=0}^{\infty }\sum _{k=0}^{p}{\frac {B_{k}}{k!}}\,{\frac {n^{p-k+1}}{(p-k+1)!}}\,x^{p}\qquad {\text{(Cauchy-Produkt)}}}
=
∑
p
=
0
∞
∑
k
=
0
p
p
!
k
!
(
p
+
1
−
k
)
!
B
k
n
p
+
1
−
k
x
p
p
!
{\displaystyle =\sum _{p=0}^{\infty }\sum _{k=0}^{p}{\frac {p!}{k!\,(p+1-k)!}}\,B_{k}\,n^{p+1-k}\,{\frac {x^{p}}{p!}}}
∑
k
=
1
n
−
1
k
p
=
1
p
+
1
∑
k
=
0
p
(
p
+
1
k
)
B
k
n
p
+
1
−
k
{\displaystyle \sum _{k=1}^{n-1}k^{p}={\frac {1}{p+1}}\,\sum _{k=0}^{p}{p+1 \choose k}\,B_{k}\,\,n^{p+1-k}}
(
−
1
)
k
{\displaystyle (-1)^{k}\,}
B
1
n
p
=
−
1
2
n
p
{\displaystyle B_{1}\,n^{p}=-{\frac {1}{2}}\,n^{p}}
−
B
1
n
p
=
1
2
n
p
{\displaystyle -B_{1}\,n^{p}={\frac {1}{2}}\,n^{p}}
∑
k
=
1
n
k
p
=
1
p
+
1
∑
k
=
0
p
(
−
1
)
k
(
p
+
1
k
)
B
k
n
p
+
1
−
k
{\displaystyle \sum _{k=1}^{n}k^{p}={\frac {1}{p+1}}\,\sum _{k=0}^{p}(-1)^{k}\,{p+1 \choose k}\,B_{k}\,\,n^{p+1-k}}
2. Beweis
In der Euler-Maclaurinschen Summenformel
∑
a
<
k
≤
b
f
(
k
)
=
∫
a
b
f
(
x
)
d
x
+
∑
k
=
0
n
−
1
(
−
1
)
k
+
1
B
k
+
1
(
k
+
1
)
!
(
f
(
k
)
(
b
)
−
f
(
k
)
(
a
)
)
+
(
−
1
)
n
−
1
n
!
∫
a
b
B
n
(
x
)
f
(
n
)
(
x
)
d
x
{\displaystyle \sum _{a<k\leq b}f(k)=\int _{a}^{b}f(x)\,dx+\sum _{k=0}^{n-1}{\frac {(-1)^{k+1}\,B_{k+1}}{(k+1)!}}\left(f^{(k)}(b)-f^{(k)}(a)\right)+{\frac {(-1)^{n-1}}{n!}}\int _{a}^{b}B_{n}(x)\,f^{(n)}(x)\,dx}
a
=
0
,
b
=
m
,
f
(
x
)
=
x
p
{\displaystyle a=0\,,\,b=m\,,\,f(x)=x^{p}}
n
=
p
+
1
{\displaystyle n=p+1\,}
f
(
n
)
(
x
)
=
0
{\displaystyle f^{(n)}(x)=0\,}
∑
k
=
1
m
k
p
=
∫
0
m
x
p
d
x
+
∑
k
=
0
p
(
−
1
)
k
+
1
B
k
+
1
(
k
+
1
)
!
(
p
!
(
p
−
k
)
!
m
p
−
k
−
p
!
(
p
−
k
)
!
0
p
−
k
)
{\displaystyle \sum _{k=1}^{m}k^{p}=\int _{0}^{m}x^{p}\,dx+\sum _{k=0}^{p}{\frac {(-1)^{k+1}\,B_{k+1}}{(k+1)!}}\left({\frac {p!}{(p-k)!}}m^{p-k}-{\frac {p!}{(p-k)!}}0^{p-k}\right)}
k
=
p
{\displaystyle k=p}
m
0
{\displaystyle m^{0}}
0
0
{\displaystyle 0^{0}}
1
{\displaystyle 1}
∑
k
=
1
m
k
p
=
m
p
+
1
p
+
1
+
∑
k
=
0
p
−
1
(
−
1
)
k
+
1
B
k
+
1
(
k
+
1
)
!
p
!
(
p
−
k
)
!
m
p
−
k
{\displaystyle \sum _{k=1}^{m}k^{p}={\frac {m^{p+1}}{p+1}}+\sum _{k=0}^{p-1}{\frac {(-1)^{k+1}\,B_{k+1}}{(k+1)!}}\,{\frac {p!}{(p-k)!}}\,m^{p-k}}
=
m
p
+
1
p
+
1
+
∑
k
=
1
p
(
−
1
)
k
B
k
k
!
p
!
(
p
+
1
−
k
)
!
m
p
+
1
−
k
=
1
p
+
1
∑
k
=
0
p
(
−
1
)
k
(
p
+
1
)
!
k
!
(
p
+
1
−
k
)
!
B
k
m
p
+
1
−
k
{\displaystyle ={\frac {m^{p+1}}{p+1}}+\sum _{k=1}^{p}{\frac {(-1)^{k}\,B_{k}}{k!}}\,{\frac {p!}{(p+1-k)!}}\,m^{p+1-k}={\frac {1}{p+1}}\sum _{k=0}^{p}(-1)^{k}\,{\frac {(p+1)!}{k!\,(p+1-k)!}}\,B_{k}\,m^{p+1-k}}
∑
k
=
1
n
k
p
=
ζ
(
−
p
)
+
1
p
+
1
∑
k
=
0
m
(
−
1
)
k
(
p
+
1
k
)
B
k
n
p
+
1
−
k
+
o
(
n
p
+
1
−
m
)
p
∈
C
∖
{
−
1
}
{\displaystyle \sum _{k=1}^{n}k^{p}=\zeta (-p)+{\frac {1}{p+1}}\,\sum _{k=0}^{m}(-1)^{k}\,{p+1 \choose k}\,B_{k}\,\,n^{p+1-k}+o(n^{p+1-m})\qquad p\in \mathbb {C} \setminus \{-1\}}
H
n
=
γ
+
log
n
−
∑
k
=
1
m
B
k
k
1
n
k
+
o
(
n
−
m
)
{\displaystyle H_{n}=\gamma +\log n-\sum _{k=1}^{m}{\frac {B_{k}}{k}}\,{\frac {1}{n^{k}}}+o(n^{-m})}
B
n
=
∑
k
=
0
n
(
−
1
)
k
k
+
1
k
!
{
n
k
}
{\displaystyle B_{n}=\sum _{k=0}^{n}{\frac {(-1)^{k}}{k+1}}\,k!\,{\begin{Bmatrix}n\\k\end{Bmatrix}}}
∑
k
=
0
n
z
k
=
1
−
z
n
+
1
1
−
z
{\displaystyle \sum _{k=0}^{n}z^{k}={\frac {1-z^{n+1}}{1-z}}}
|
z
|
<
1
{\displaystyle |z|<1}
Korollar zu den Partialsummen der geometrischen Reihe [ Bearbeiten ]
∑
k
=
a
b
−
1
k
m
z
k
=
(
z
d
d
z
)
m
(
z
b
−
z
a
z
−
1
)
(
z
≠
1
)
{\displaystyle \sum _{k=a}^{b-1}k^{m}z^{k}={\Big (}z{\frac {\mathrm {d} }{\mathrm {d} z}}{\Big )}^{m}{\Big (}{\frac {z^{b}-z^{a}}{z-1}}{\Big )}\qquad (z\neq 1)}
(
x
+
y
)
n
=
∑
k
=
0
n
(
n
k
)
x
n
−
k
y
k
{\displaystyle (x+y)^{n}=\sum _{k=0}^{n}{n \choose k}x^{n-k}\,y^{k}}
Beweis
Der Induktionsanfang
n
=
0
{\displaystyle n=0\,}
(
x
+
y
)
n
+
1
=
(
x
+
y
)
(
x
+
y
)
n
=
(
x
+
y
)
∑
k
=
0
n
(
n
k
)
x
n
−
k
y
k
{\displaystyle (x+y)^{n+1}=(x+y)\,(x+y)^{n}=(x+y)\sum _{k=0}^{n}{n \choose k}\,x^{n-k}\,y^{k}}
∑
k
=
0
n
(
n
k
)
x
n
+
1
−
k
y
k
+
∑
k
=
0
n
(
n
k
)
x
n
−
k
y
k
+
1
{\displaystyle \sum _{k=0}^{n}{n \choose k}\,x^{n+1-k}\,y^{k}+\sum _{k=0}^{n}{n \choose k}\,x^{n-k}\,y^{k+1}}
(
n
k
)
=
0
{\displaystyle {n \choose k}=0}
k
=
n
+
1
{\displaystyle k=n+1\,}
k
{\displaystyle k\,}
n
+
1
{\displaystyle n+1\,}
k
↦
k
−
1
{\displaystyle k\mapsto k-1}
∑
k
=
1
n
+
1
(
n
k
−
1
)
x
n
+
1
−
k
y
k
{\displaystyle \sum _{k=1}^{n+1}{n \choose k-1}\,x^{n+1-k}\,y^{k}}
(
n
k
−
1
)
=
0
{\displaystyle {n \choose k-1}=0}
k
=
0
{\displaystyle k=0\,}
k
=
0
{\displaystyle k=0\,}
(
x
+
y
)
n
+
1
=
∑
k
=
0
n
+
1
(
n
k
)
x
n
+
1
−
k
y
k
+
∑
k
=
0
n
+
1
(
n
k
−
1
)
x
n
+
1
−
k
y
k
{\displaystyle (x+y)^{n+1}=\sum _{k=0}^{n+1}\,{n \choose k}\,x^{n+1-k}\,y^{k}+\sum _{k=0}^{n+1}\,{n \choose k-1}x^{n+1-k}\,y^{k}}
(
n
k
)
+
(
n
k
−
1
)
=
(
n
+
1
k
)
{\displaystyle {n \choose k}+{n \choose k-1}={n+1 \choose k}}
∑
k
=
0
n
+
1
(
n
+
1
k
)
x
n
+
1
−
k
y
k
{\displaystyle \sum _{k=0}^{n+1}\,{n+1 \choose k}\,x^{n+1-k}\,y^{k}}
∑
k
=
0
n
(
n
k
)
=
2
n
{\displaystyle \sum _{k=0}^{n}{n \choose k}=2^{n}}
Beweis
Das Ergebnis ergibt sich sofort aus dem Binomischen Lehrsatz für
x
=
y
=
1
{\displaystyle x=y=1}
∑
k
=
0
n
(
−
1
)
k
(
n
k
)
=
0
{\displaystyle \sum _{k=0}^{n}(-1)^{k}{n \choose k}=0}
Beweis
Das Ergebnis ergibt sich sofort aus dem Binomischen Lehrsatz für
x
=
1
{\displaystyle x=1}
y
=
−
1
{\displaystyle y=-1}
∑
k
=
0
n
k
(
n
k
)
=
n
⋅
2
n
−
1
{\displaystyle \sum _{k=0}^{n}k{n \choose k}=n\cdot 2^{n-1}}
Beweis
Es gilt:
k
⋅
(
n
k
)
=
n
⋅
(
n
−
1
k
−
1
)
{\displaystyle k\cdot {n \choose k}=n\cdot {n-1 \choose k-1}}
∑
k
=
0
n
k
⋅
(
n
k
)
=
∑
k
=
0
n
n
⋅
(
n
−
1
k
−
1
)
=
n
⋅
∑
k
=
0
n
(
n
−
1
k
−
1
)
=
n
⋅
∑
k
=
0
n
−
1
(
n
−
1
k
)
=
n
⋅
2
n
−
1
{\displaystyle \sum _{k=0}^{n}k\cdot {n \choose k}=\sum _{k=0}^{n}n\cdot {n-1 \choose k-1}=n\cdot \sum _{k=0}^{n}{n-1 \choose k-1}=n\cdot \sum _{k=0}^{n-1}{n-1 \choose k}=n\cdot 2^{n-1}}
(
f
g
)
(
n
)
(
x
)
=
∑
k
=
0
n
(
n
k
)
f
(
n
−
k
)
(
x
)
g
(
k
)
(
x
)
{\displaystyle (fg)^{(n)}(x)=\sum _{k=0}^{n}{n \choose k}f^{(n-k)}(x)\,g^{(k)}(x)}
Beweis
Der Induktionsbeweis ist analog zum Induktionsbeweis des Binomisches Lehrsatzes.
n
!
z
(
z
+
1
)
⋯
(
z
+
n
)
=
∑
k
=
0
n
(
−
1
)
k
(
n
k
)
1
k
+
z
{\displaystyle {\frac {n!}{z\,(z+1)\cdots (z+n)}}=\sum _{k=0}^{n}(-1)^{k}\,{n \choose k}\,{\frac {1}{k+z}}}
Beweis
n
!
z
(
z
+
1
)
⋯
(
z
+
n
)
=
n
!
Γ
(
z
)
Γ
(
n
+
1
+
z
)
=
B
(
n
+
1
,
z
)
{\displaystyle {\frac {n!}{z\,(z+1)\cdots (z+n)}}={\frac {n!\,\,\Gamma (z)}{\Gamma (n+1+z)}}=B(n+1,z)}
=
∫
0
1
(
1
−
t
)
n
t
z
−
1
d
t
=
∑
k
=
0
n
(
−
1
)
k
(
n
k
)
∫
0
1
t
k
+
z
−
1
d
t
=
∑
k
=
0
n
(
−
1
)
k
(
n
k
)
1
k
+
z
{\displaystyle =\int _{0}^{1}(1-t)^{n}\,t^{z-1}\,dt=\sum _{k=0}^{n}(-1)^{k}\,{n \choose k}\,\int _{0}^{1}t^{k+z-1}\,dt=\sum _{k=0}^{n}(-1)^{k}\,{n \choose k}\,{\frac {1}{k+z}}}
Steht
Δ
{\displaystyle \Delta \,}
Δ
f
(
x
)
=
f
(
x
)
−
f
(
x
−
1
)
{\displaystyle \Delta f(x)=f(x)-f(x-1)\,}
so gilt
Δ
n
f
(
x
)
=
∑
k
=
0
n
(
−
1
)
k
(
n
k
)
f
(
x
−
k
)
{\displaystyle \Delta ^{n}f(x)=\sum _{k=0}^{n}(-1)^{k}\,{n \choose k}\,f(x-k)}
Beweis
Der Induktionsbeweis hierzu ist analog zum Beweis des Binomischen Lehrsatzes.
∑
k
=
0
n
(
−
1
)
k
(
n
k
)
(
x
−
k
)
n
=
n
!
n
∈
N
,
x
∈
R
{\displaystyle \sum _{k=0}^{n}(-1)^{k}{n \choose k}(x-k)^{n}=n!\qquad n\in \mathbb {N} \,,\,x\in \mathbb {R} }
Beweis
Ist
Δ
{\displaystyle \Delta \,}
Δ
f
(
x
)
=
f
(
x
)
−
f
(
x
−
1
)
{\displaystyle \Delta f(x)=f(x)-f(x-1)\,}
Δ
x
n
=
x
n
−
(
x
−
1
)
n
=
n
x
n
−
1
+
.
.
.
{\displaystyle \Delta x^{n}=x^{n}-(x-1)^{n}=n\,x^{n-1}+...}
Δ
m
x
n
=
(
n
)
m
x
n
−
m
{\displaystyle \Delta ^{m}\,x^{n}=(n)_{m}\,x^{n-m}}
m
=
n
{\displaystyle m=n\,}
Δ
n
x
n
=
n
!
{\displaystyle \Delta ^{n}x^{n}=n!\,}
Δ
n
f
(
x
)
=
∑
k
=
0
n
(
−
1
)
k
(
n
k
)
f
(
x
−
k
)
{\displaystyle \Delta ^{n}f(x)=\sum _{k=0}^{n}(-1)^{k}\,{n \choose k}\,f(x-k)}
f
(
x
)
=
x
n
{\displaystyle f(x)=x^{n}\,}
∑
k
=
0
n
cos
(
k
x
)
=
sin
(
n
+
1
2
x
)
cos
(
n
2
x
)
sin
x
2
{\displaystyle \sum _{k=0}^{n}\cos(kx)={\frac {\sin \left({\frac {n+1}{2}}\,x\right)\,\cos \left({\frac {n}{2}}\,x\right)}{\sin {\frac {x}{2}}}}}
1. Beweis
∑
k
=
0
n
e
i
k
x
=
e
i
(
n
+
1
)
x
−
1
e
i
x
−
1
=
e
i
(
n
+
1
2
)
x
−
e
−
i
x
2
e
i
x
2
−
e
−
i
x
2
{\displaystyle \sum _{k=0}^{n}e^{ikx}={\frac {e^{i(n+1)x}-1}{e^{ix}-1}}={\frac {e^{i\left(n+{\frac {1}{2}}\right)x}-e^{-i{\frac {x}{2}}}}{e^{i{\frac {x}{2}}}-e^{-i{\frac {x}{2}}}}}}
=
cos
(
n
+
1
2
)
x
−
cos
x
2
2
i
sin
x
2
+
i
sin
(
n
+
1
2
)
x
−
sin
x
2
2
i
sin
x
2
=
i
sin
(
n
+
1
2
x
)
sin
(
n
2
x
)
sin
x
2
+
sin
(
n
+
1
2
x
)
cos
(
n
2
x
)
sin
x
2
{\displaystyle ={\frac {\cos \left(n+{\frac {1}{2}}\right)x-\cos {\frac {x}{2}}}{2i\,\sin {\frac {x}{2}}}}+i\,{\frac {\sin \left(n+{\frac {1}{2}}\right)x-\sin {\frac {x}{2}}}{2i\,\sin {\frac {x}{2}}}}=i\,{\frac {\sin \left({\frac {n+1}{2}}\,x\right)\,\sin \left({\frac {n}{2}}\,x\right)}{\sin {\frac {x}{2}}}}+{\frac {\sin \left({\frac {n+1}{2}}\,x\right)\,\cos \left({\frac {n}{2}}\,x\right)}{\sin {\frac {x}{2}}}}}
∑
k
=
0
n
sin
(
k
x
)
=
sin
(
n
+
1
2
x
)
sin
(
n
2
x
)
sin
x
2
{\displaystyle \sum _{k=0}^{n}\sin(kx)={\frac {\sin \left({\frac {n+1}{2}}\,x\right)\,\sin \left({\frac {n}{2}}\,x\right)}{\sin {\frac {x}{2}}}}}
1. Beweis
∑
k
=
0
n
e
i
k
x
=
e
i
(
n
+
1
)
x
−
1
e
i
x
−
1
=
e
i
(
n
+
1
2
)
x
−
e
−
i
x
2
e
i
x
2
−
e
−
i
x
2
{\displaystyle \sum _{k=0}^{n}e^{ikx}={\frac {e^{i(n+1)x}-1}{e^{ix}-1}}={\frac {e^{i\left(n+{\frac {1}{2}}\right)x}-e^{-i{\frac {x}{2}}}}{e^{i{\frac {x}{2}}}-e^{-i{\frac {x}{2}}}}}}
=
cos
(
n
+
1
2
)
x
−
cos
x
2
2
i
sin
x
2
+
i
sin
(
n
+
1
2
)
x
−
sin
x
2
2
i
sin
x
2
=
i
sin
(
n
+
1
2
x
)
sin
(
n
2
x
)
sin
x
2
+
sin
(
n
+
1
2
x
)
cos
(
n
2
x
)
sin
x
2
{\displaystyle ={\frac {\cos \left(n+{\frac {1}{2}}\right)x-\cos {\frac {x}{2}}}{2i\,\sin {\frac {x}{2}}}}+i\,{\frac {\sin \left(n+{\frac {1}{2}}\right)x-\sin {\frac {x}{2}}}{2i\,\sin {\frac {x}{2}}}}=i\,{\frac {\sin \left({\frac {n+1}{2}}\,x\right)\,\sin \left({\frac {n}{2}}\,x\right)}{\sin {\frac {x}{2}}}}+{\frac {\sin \left({\frac {n+1}{2}}\,x\right)\,\cos \left({\frac {n}{2}}\,x\right)}{\sin {\frac {x}{2}}}}}
[ Bearbeiten ]
∑
k
=
0
n
(
n
k
)
k
m
x
k
=
∑
k
=
0
m
{
m
k
}
n
!
(
n
−
k
)
!
x
k
(
1
+
x
)
n
−
k
{\displaystyle \sum _{k=0}^{n}{n \choose k}\,k^{m}\,x^{k}=\sum _{k=0}^{m}\left\{{\begin{matrix}m\\k\end{matrix}}\right\}{\frac {n!}{(n-k)!}}\,x^{k}\,(1+x)^{n-k}}
Beweis
Wende die Formel
(
x
d
d
x
)
m
f
(
x
)
=
∑
k
=
0
m
{
m
k
}
x
k
f
(
k
)
(
x
)
{\displaystyle \left(x\,{\frac {d}{dx}}\right)^{m}f(x)=\sum _{k=0}^{m}\left\{{\begin{matrix}m\\k\end{matrix}}\right\}\,x^{k}\,f^{(k)}(x)}
f
(
x
)
=
(
1
+
x
)
n
{\displaystyle f(x)=(1+x)^{n}\,}
∑
k
=
0
m
{
m
k
}
n
!
(
n
−
k
)
!
=
n
m
{\displaystyle \sum _{k=0}^{m}{\begin{Bmatrix}m\\k\end{Bmatrix}}\,{\frac {n!}{(n-k)!}}=n^{m}}
[ Bearbeiten ]
∑
k
=
0
n
{
n
k
}
k
m
x
k
=
∑
k
=
0
m
(
m
k
)
ϕ
m
−
k
(
−
x
)
ϕ
n
+
k
(
x
)
ϕ
n
(
x
)
=
∑
k
=
0
∞
k
n
k
!
x
k
e
x
{\displaystyle \sum _{k=0}^{n}{\begin{Bmatrix}n\\k\end{Bmatrix}}\,k^{m}\,x^{k}=\sum _{k=0}^{m}{m \choose k}\phi _{m-k}(-x)\,\phi _{n+k}(x)\quad \qquad \phi _{n}(x)=\sum _{k=0}^{\infty }{\frac {k^{n}}{k!}}\,{\frac {x^{k}}{e^{x}}}}
∑
k
=
1
n
−
1
ζ
(
2
k
)
ζ
(
2
n
−
2
k
)
=
2
n
+
1
2
ζ
(
2
n
)
{\displaystyle \sum _{k=1}^{n-1}\zeta (2k)\,\zeta (2n-2k)={\frac {2n+1}{2}}\,\zeta (2n)}
n
∈
Z
≥
2
{\displaystyle n\in \mathbb {Z} ^{\geq 2}}
Beweis
Ist
f
(
z
)
=
∑
n
=
0
∞
ζ
(
2
n
)
z
2
n
−
1
{\displaystyle f(z)=\sum _{n=0}^{\infty }\zeta (2n)\,z^{2n-1}}
(
1
)
f
′
(
z
)
z
2
2
=
∑
n
=
0
∞
2
n
−
1
2
ζ
(
2
n
)
z
2
n
{\displaystyle (1)\quad f'(z)\,{\frac {z^{2}}{2}}=\sum _{n=0}^{\infty }{\frac {2n-1}{2}}\,\zeta (2n)\,z^{2n}}
(
2
)
(
f
(
z
)
z
)
2
=
∑
k
=
0
∞
ζ
(
2
k
)
z
2
k
∑
k
=
0
∞
ζ
(
2
k
)
z
2
k
=
∑
n
=
0
∞
∑
k
=
0
n
ζ
(
2
k
)
ζ
(
2
n
−
2
k
)
z
2
n
{\displaystyle (2)\quad (f(z)\,z)^{2}=\sum _{k=0}^{\infty }\zeta (2k)\,z^{2k}\,\sum _{k=0}^{\infty }\zeta (2k)\,z^{2k}=\sum _{n=0}^{\infty }\sum _{k=0}^{n}\zeta (2k)\,\zeta (2n-2k)\,z^{2n}}
f
(
z
)
=
−
π
2
cot
π
z
{\displaystyle f(z)=-{\frac {\pi }{2}}\cot \pi z}
f
′
(
z
)
z
2
2
=
π
2
(
1
+
cot
2
π
z
)
π
z
2
2
=
π
2
4
z
2
+
(
f
(
z
)
z
)
2
{\displaystyle f'(z)\,{\frac {z^{2}}{2}}={\frac {\pi }{2}}\,\left(1+\cot ^{2}\pi z\right)\,\pi \,{\frac {z^{2}}{2}}={\frac {\pi ^{2}}{4}}z^{2}+(f(z)\,z)^{2}}
2
n
−
1
2
ζ
(
2
n
)
=
∑
k
=
0
n
ζ
(
2
k
)
ζ
(
2
n
−
2
k
)
{\displaystyle {\frac {2n-1}{2}}\,\zeta (2n)=\sum _{k=0}^{n}\zeta (2k)\,\zeta (2n-2k)}
n
>
1
{\displaystyle n>1\,}
ζ
(
0
)
=
−
1
2
{\displaystyle \zeta (0)=-{\frac {1}{2}}}
−
1
2
ζ
(
2
n
)
{\displaystyle -{\frac {1}{2}}\zeta (2n)}
∑
k
=
1
n
−
1
ζ
(
2
k
)
ζ
(
2
n
−
2
k
)
=
2
n
+
1
2
ζ
(
2
n
)
{\displaystyle \sum _{k=1}^{n-1}\zeta (2k)\,\zeta (2n-2k)={\frac {2n+1}{2}}\,\zeta (2n)}
[ Bearbeiten ]
∑
k
=
1
n
cot
2
(
k
π
2
n
+
1
)
=
2
n
(
2
n
−
1
)
6
{\displaystyle \sum _{k=1}^{n}\cot ^{2}\left({\frac {k\pi }{2n+1}}\right)={\frac {2n(2n-1)}{6}}}
∑
k
=
1
n
cot
4
(
k
π
2
n
+
1
)
=
2
n
(
2
n
−
1
)
6
4
n
2
+
10
n
−
9
15
{\displaystyle \sum _{k=1}^{n}\cot ^{4}\left({\frac {k\pi }{2n+1}}\right)={\frac {2n(2n-1)}{6}}\,{\frac {4n^{2}+10n-9}{15}}}
∑
k
=
1
n
cot
6
(
k
π
2
n
+
1
)
=
2
n
(
2
n
−
1
)
6
32
n
4
+
112
n
3
+
8
n
2
−
252
n
+
135
315
{\displaystyle \sum _{k=1}^{n}\cot ^{6}\left({\frac {k\pi }{2n+1}}\right)={\frac {2n(2n-1)}{6}}\,{\frac {32n^{4}+112n^{3}+8n^{2}-252n+135}{315}}}
∑
k
=
1
n
cot
8
(
k
π
2
n
+
1
)
=
2
n
(
2
n
−
1
)
6
192
n
6
+
864
n
5
+
496
n
4
−
2248
n
3
−
1388
n
2
+
3834
n
−
1575
4725
{\displaystyle \sum _{k=1}^{n}\cot ^{8}\left({\frac {k\pi }{2n+1}}\right)={\frac {2n(2n-1)}{6}}\,{\frac {192n^{6}+864n^{5}+496n^{4}-2248n^{3}-1388n^{2}+3834n-1575}{4725}}}
∑
k
=
0
n
−
1
e
i
π
m
k
2
+
ℓ
k
n
=
e
−
i
π
ℓ
2
4
n
m
i
n
m
∑
k
=
0
m
−
1
e
−
i
π
n
k
2
+
ℓ
k
m
m
n
+
ℓ
{\displaystyle \sum _{k=0}^{n-1}e^{i\pi {\frac {mk^{2}+\ell k}{n}}}=e^{-i\pi {\frac {\ell ^{2}}{4nm}}}\,\,{\sqrt {i{\frac {n}{m}}}}\,\,\sum _{k=0}^{m-1}e^{-i\pi {\frac {nk^{2}+\ell k}{m}}}\qquad mn+\ell }
Beweis
m
,
n
∈
Z
>
0
{\displaystyle m,n\in \mathbb {Z} ^{>0}}
ℓ
∈
Z
{\displaystyle \ell \in \mathbb {Z} }
m
n
+
ℓ
{\displaystyle mn+\ell }
f
(
z
)
=
e
i
π
m
z
2
+
ℓ
z
n
e
2
π
i
z
−
1
{\displaystyle f(z)={\frac {e^{i\pi {\frac {mz^{2}+\ell z}{n}}}}{e^{2\pi iz}-1}}}
R
>
1
{\displaystyle R>1\,}
ε
∈
]
0
,
1
[
{\displaystyle \varepsilon \in ]0,1[}
∮
f
d
z
=
2
π
i
∑
k
=
0
n
−
1
res
(
f
,
k
)
=
∑
k
=
0
n
−
1
e
i
π
m
k
2
+
ℓ
k
n
{\displaystyle \oint f\,dz=2\pi i\sum _{k=0}^{n-1}{\text{res}}(f,k)=\sum _{k=0}^{n-1}e^{i\pi {\frac {mk^{2}+\ell k}{n}}}}
f
(
x
+
i
y
)
=
e
i
π
m
(
x
2
−
y
2
)
+
ℓ
x
n
e
−
π
m
⋅
2
x
y
+
ℓ
y
n
e
2
π
i
x
e
−
2
π
y
−
1
{\displaystyle f(x+iy)={\frac {e^{i\pi {\frac {m(x^{2}-y^{2})+\ell x}{n}}}\,e^{-\pi {\frac {m\cdot 2xy+\ell y}{n}}}}{e^{2\pi ix}\,e^{-2\pi y}-1}}}
∫
B
R
f
d
z
{\displaystyle \int _{B_{R}}f\,dz}
∫
D
R
f
d
z
{\displaystyle \int _{D_{R}}f\,dz}
R
→
∞
{\displaystyle R\to \infty \,}
f
(
n
+
z
)
=
f
(
z
)
e
i
π
2
m
z
e
i
π
(
m
n
+
ℓ
)
⏟
=
1
=
f
(
z
)
(
e
2
π
i
z
)
m
{\displaystyle f(n+z)=f(z)\,e^{i\pi \,2mz}\,\underbrace {e^{i\pi (mn+\ell )}} _{=1}=f(z)\,\,(e^{2\pi iz})^{m}}
f
(
n
+
z
)
−
f
(
z
)
=
(
e
2
π
i
z
)
m
−
1
e
2
π
i
z
−
1
e
i
π
m
z
2
+
ℓ
z
n
=
∑
k
=
0
m
−
1
e
2
π
i
k
z
e
i
π
m
z
2
+
ℓ
z
n
{\displaystyle f(n+z)-f(z)={\frac {(e^{2\pi iz})^{m}-1}{e^{2\pi iz}-1}}\,e^{i\pi {\frac {mz^{2}+\ell z}{n}}}=\sum _{k=0}^{m-1}e^{2\pi ikz}\,e^{i\pi {\frac {mz^{2}+\ell z}{n}}}}
C
∖
Z
{\displaystyle \mathbb {C} \setminus \mathbb {Z} }
Z
{\displaystyle \mathbb {Z} }
lim
R
→
∞
∮
f
d
z
=
∫
A
∞
,
ε
f
d
z
+
∫
C
∞
,
ε
f
d
z
=
∫
C
∞
,
ε
[
f
(
z
)
−
f
(
n
+
z
)
]
d
z
{\displaystyle \lim _{R\to \infty }\oint f\,dz=\int _{A_{\infty ,\varepsilon }}f\,dz+\int _{C_{\infty ,\varepsilon }}f\,dz=\int _{C_{\infty ,\varepsilon }}\left[f(z)-f(n+z)\right]\,dz}
ε
→
0
+
{\displaystyle \varepsilon \to 0+}
∫
−
∞
∞
[
f
(
n
+
(
1
+
i
)
t
)
−
f
(
(
1
+
i
)
t
)
]
(
1
+
i
)
d
t
{\displaystyle \int _{-\infty }^{\infty }\left[f{\Big (}n+(1+i)t{\Big )}-f{\Big (}(1+i)t{\Big )}\right]\,(1+i)\,dt}
=
(
1
+
i
)
∑
k
=
0
m
−
1
∫
−
∞
∞
e
2
π
i
k
t
e
−
2
π
k
t
e
i
π
2
i
m
t
2
+
ℓ
t
+
i
ℓ
t
n
d
t
=
e
−
i
π
ℓ
2
4
n
m
i
n
m
∑
k
=
0
m
−
1
e
−
i
π
n
k
2
+
ℓ
k
m
{\displaystyle =(1+i)\sum _{k=0}^{m-1}\int _{-\infty }^{\infty }e^{2\pi ikt}\,e^{-2\pi kt}\,e^{i\pi {\frac {2imt^{2}+\ell t+i\ell t}{n}}}\,dt=e^{-i\pi {\frac {\ell ^{2}}{4nm}}}\,\,{\sqrt {i{\frac {n}{m}}}}\,\,\sum _{k=0}^{m-1}e^{-i\pi {\frac {nk^{2}+\ell k}{m}}}}
∑
k
=
0
n
−
1
e
i
π
k
2
m
n
=
i
n
m
∑
k
=
0
m
−
1
e
−
i
π
k
2
n
m
m
{\displaystyle \sum _{k=0}^{n-1}e^{i\pi k^{2}{\frac {m}{n}}}={\sqrt {i{\frac {n}{m}}}}\,\,\sum \limits _{k=0}^{m-1}e^{-i\pi k^{2}{\frac {n}{m}}}\qquad m}
n
{\displaystyle n\,}
∑
k
=
0
n
−
1
e
i
π
k
2
m
n
=
1
=
∑
k
=
0
m
−
1
e
i
π
k
2
n
m
m
{\displaystyle \sum _{k=0}^{n-1}e^{i\pi k^{2}{\frac {m}{n}}}=1=\sum _{k=0}^{m-1}e^{i\pi k^{2}{\frac {n}{m}}}\qquad m}
n
{\displaystyle n\,}
Beweis
Für
m
,
n
∈
Z
>
0
{\displaystyle m,n\in \mathbb {Z} ^{>0}}
m
⋅
n
{\displaystyle m\cdot n}
f
(
z
)
=
e
i
π
z
2
m
n
e
2
π
i
z
−
1
{\displaystyle f(z)={\frac {e^{i\pi z^{2}{\frac {m}{n}}}}{e^{2\pi iz}-1}}}
R
>
1
{\displaystyle R>1\,}
ε
∈
]
0
,
1
[
{\displaystyle \varepsilon \in ]0,1[}
∮
f
d
z
=
2
π
i
∑
k
=
0
n
−
1
res
(
f
,
k
)
=
∑
k
=
0
n
−
1
e
i
π
k
2
m
n
{\displaystyle \oint f\,dz=2\pi i\sum _{k=0}^{n-1}{\text{res}}(f,k)=\sum _{k=0}^{n-1}e^{i\pi k^{2}\,{\frac {m}{n}}}}
x
>
0
{\displaystyle x>0\,}
f
(
x
+
i
y
)
=
e
i
π
(
x
2
−
y
2
)
m
n
e
−
2
π
x
y
m
n
e
2
π
i
x
e
−
2
π
y
−
1
→
0
{\displaystyle f(x+iy)={\frac {e^{i\pi (x^{2}-y^{2}){\frac {m}{n}}}\,e^{-2\pi xy\,{\frac {m}{n}}}}{e^{2\pi ix}\,e^{-2\pi y}-1}}\to 0}
y
→
±
∞
{\displaystyle y\to \pm \infty \,}
∫
B
R
f
d
z
{\displaystyle \int _{B_{R}}f\,dz}
∫
D
R
f
d
z
{\displaystyle \int _{D_{R}}f\,dz}
R
→
∞
{\displaystyle R\to \infty \,}
f
(
n
+
z
)
=
f
(
z
)
e
i
π
2
n
z
m
n
e
i
π
n
2
m
n
⏟
=
1
=
f
(
z
)
(
e
2
π
i
z
)
m
{\displaystyle f(n+z)=f(z)\,e^{i\pi \,2nz\,{\frac {m}{n}}}\,\underbrace {e^{i\pi n^{2}\,{\frac {m}{n}}}} _{=1}=f(z)\,\,(e^{2\pi iz})^{m}}
f
(
n
+
z
)
−
f
(
z
)
=
(
e
2
π
i
z
)
m
−
1
e
2
π
i
z
−
1
e
i
π
z
2
m
n
=
∑
k
=
0
m
−
1
e
2
π
i
k
z
e
i
π
z
2
m
n
{\displaystyle f(n+z)-f(z)={\frac {(e^{2\pi iz})^{m}-1}{e^{2\pi iz}-1}}\,e^{i\pi z^{2}{\frac {m}{n}}}=\sum _{k=0}^{m-1}e^{2\pi ikz}\,e^{i\pi z^{2}{\frac {m}{n}}}}
C
∖
Z
{\displaystyle \mathbb {C} \setminus \mathbb {Z} }
Z
{\displaystyle \mathbb {Z} }
lim
R
→
∞
∮
f
d
z
=
∫
A
∞
,
ε
f
d
z
+
∫
C
∞
,
ε
f
d
z
=
∫
C
∞
,
ε
[
f
(
z
)
−
f
(
n
+
z
)
]
d
z
{\displaystyle \lim _{R\to \infty }\oint f\,dz=\int _{A_{\infty ,\varepsilon }}f\,dz+\int _{C_{\infty ,\varepsilon }}f\,dz=\int _{C_{\infty ,\varepsilon }}\left[f(z)-f(n+z)\right]\,dz}
ε
→
0
+
{\displaystyle \varepsilon \to 0+}
∫
i
R
[
f
(
n
+
z
)
−
f
(
z
)
]
d
z
=
∫
−
∞
∞
[
f
(
n
+
i
t
)
−
f
(
i
t
)
]
i
d
t
{\displaystyle \int _{i\mathbb {R} }\left[f(n+z)-f(z)\right]\,dz=\int _{-\infty }^{\infty }\left[f(n+it)-f(it)\right]\,i\,dt}
=
i
∑
k
=
0
m
−
1
∫
−
∞
∞
e
−
2
π
k
t
e
−
i
π
m
n
t
2
d
t
=
i
n
m
∑
k
=
0
m
−
1
e
−
i
π
k
2
n
m
{\displaystyle =i\sum _{k=0}^{m-1}\int _{-\infty }^{\infty }e^{-2\pi kt}\,e^{-i\pi {\frac {m}{n}}t^{2}}\,dt={\sqrt {i{\frac {n}{m}}}}\,\,\sum _{k=0}^{m-1}e^{-i\pi k^{2}{\frac {n}{m}}}}
∑
k
=
0
n
−
1
e
2
π
i
n
k
2
=
i
n
2
(
1
+
e
−
i
π
n
2
)
{\displaystyle \sum _{k=0}^{n-1}e^{{\frac {2\pi i}{n}}k^{2}}={\sqrt {\frac {in}{2}}}\,\left(1+e^{-i\pi {\frac {n}{2}}}\right)}
Beweis
In der Landsberg-Schaar Relation
∑
k
=
0
n
−
1
e
i
π
k
2
m
n
=
i
n
m
∑
k
=
0
m
−
1
e
−
i
π
k
2
n
m
{\displaystyle \sum _{k=0}^{n-1}e^{i\pi k^{2}{\frac {m}{n}}}={\sqrt {i{\frac {n}{m}}}}\,\,\sum \limits _{k=0}^{m-1}e^{-i\pi k^{2}{\frac {n}{m}}}}
m
=
2
{\displaystyle m=2\,}
[ Bearbeiten ]
∑
k
=
0
n
−
1
csc
2
(
z
+
k
π
n
)
=
n
2
csc
2
z
{\displaystyle \sum _{k=0}^{n-1}\csc ^{2}\left({\frac {z+k\pi }{n}}\right)=n^{2}\,\csc ^{2}z}
[ Bearbeiten ]
∑
k
=
0
n
−
1
tan
2
(
(
2
k
+
1
)
π
4
n
)
=
n
⋅
(
2
n
−
1
)
{\displaystyle \sum _{k=0}^{n-1}\tan ^{2}\left({\frac {(2k+1)\pi }{4n}}\right)=n\cdot (2n-1)}
Beweis
e
i
2
n
x
=
(
cos
x
+
i
sin
x
)
2
n
=
∑
k
=
0
2
n
(
2
n
k
)
i
k
(
sin
x
)
k
(
cos
x
)
2
n
−
k
{\displaystyle e^{i\,2nx}=(\cos x+i\sin x)^{2n}=\sum _{k=0}^{2n}{2n \choose k}\,i^{k}\,(\sin x)^{k}\,(\cos x)^{2n-k}}
cos
(
2
n
x
)
=
∑
k
=
0
n
(
2
n
2
k
)
(
−
1
)
k
(
sin
x
)
2
k
(
cos
x
)
2
n
−
2
k
{\displaystyle \cos(2nx)=\sum _{k=0}^{n}{2n \choose 2k}\,(-1)^{k}\,(\sin x)^{2k}\,(\cos x)^{2n-2k}}
cos
(
2
n
x
)
(
cos
x
)
2
n
=
∑
k
=
0
n
(
2
n
2
k
)
(
−
tan
2
x
)
k
{\displaystyle {\frac {\cos(2nx)}{(\cos x)^{2n}}}=\sum _{k=0}^{n}{2n \choose 2k}\left(-\tan ^{2}x\right)^{k}}
x
=
(
2
k
+
1
)
π
4
n
k
=
0
,
.
.
.
,
n
−
1
{\displaystyle x={\frac {(2k+1)\pi }{4n}}\quad k=0,...,n-1}
P
(
X
)
=
∑
k
=
0
n
(
2
n
2
k
)
X
k
{\displaystyle P(X)=\sum _{k=0}^{n}{2n \choose 2k}X^{k}}
X
=
−
tan
2
(
(
2
k
+
1
)
π
4
n
)
{\displaystyle X=-\tan ^{2}\left({\frac {(2k+1)\pi }{4n}}\right)}
X
n
−
1
{\displaystyle X^{n-1}}
(
2
n
2
(
n
−
1
)
)
=
n
⋅
(
2
n
−
1
)
{\displaystyle {2n \choose 2(n-1)}=n\cdot (2n-1)}
[ Bearbeiten ]
∑
k
=
0
n
−
1
(
−
1
)
k
csc
(
2
k
+
1
2
n
+
1
⋅
π
2
)
=
n
+
1
−
(
−
1
)
n
2
{\displaystyle \sum _{k=0}^{n-1}(-1)^{k}\,\csc \left({\frac {2k+1}{2n+1}}\cdot {\frac {\pi }{2}}\right)=n+{\frac {1-(-1)^{n}}{2}}}
Beweis
∏
k
=
0
n
−
1
[
X
+
(
−
1
)
k
sin
(
2
k
+
1
2
n
+
1
⋅
π
2
)
]
=
U
n
(
X
)
−
(
−
1
)
n
U
n
−
1
(
X
)
2
n
=:
P
n
(
X
)
{\displaystyle \prod _{k=0}^{n-1}\left[X+(-1)^{k}\,\sin \left({\frac {2k+1}{2n+1}}\cdot {\frac {\pi }{2}}\right)\right]={\frac {U_{n}(X)-(-1)^{n}\,U_{n-1}(X)}{2^{n}}}=:P_{n}(X)}
U
n
{\displaystyle U_{n}\,}
P
n
(
0
)
=
∏
k
=
0
n
−
1
[
(
−
1
)
k
sin
(
2
k
+
1
2
n
+
1
⋅
π
2
)
]
=
(
−
1
)
n
⋅
(
n
−
1
)
2
2
n
{\displaystyle P_{n}(0)=\prod _{k=0}^{n-1}\left[(-1)^{k}\,\sin \left({\frac {2k+1}{2n+1}}\cdot {\frac {\pi }{2}}\right)\right]={\frac {(-1)^{\frac {n\cdot (n-1)}{2}}}{2^{n}}}}
Q
n
(
X
)
:=
(
−
1
)
n
⋅
(
n
−
1
)
2
⋅
2
n
⋅
X
n
⋅
P
n
(
1
X
)
=
∏
k
=
0
n
−
1
(
X
+
(
−
1
)
k
sin
(
2
k
+
1
2
n
+
1
⋅
π
2
)
)
{\displaystyle Q_{n}(X):=(-1)^{\frac {n\cdot (n-1)}{2}}\cdot 2^{n}\cdot X^{n}\cdot P_{n}\left({\frac {1}{X}}\right)=\prod _{k=0}^{n-1}\left(X+{\frac {(-1)^{k}}{\sin \left({\frac {2k+1}{2n+1}}\cdot {\frac {\pi }{2}}\right)}}\right)}
∑
k
=
0
n
−
1
(
−
1
)
k
sin
(
2
k
+
1
2
n
+
1
⋅
π
2
)
=
coeff
n
−
1
Q
n
{\displaystyle \sum _{k=0}^{n-1}{\frac {(-1)^{k}}{\sin \left({\frac {2k+1}{2n+1}}\cdot {\frac {\pi }{2}}\right)}}={\text{coeff}}_{n-1}Q_{n}}
(
−
1
)
n
⋅
(
n
−
1
)
2
⋅
2
n
⋅
coeff
1
P
n
=
(
−
1
)
n
⋅
(
n
−
1
)
2
coeff
1
(
U
n
−
(
−
1
)
n
U
n
−
1
)
{\displaystyle (-1)^{\frac {n\cdot (n-1)}{2}}\cdot 2^{n}\cdot {\text{coeff}}_{1}P_{n}=(-1)^{\frac {n\cdot (n-1)}{2}}\,{\text{coeff}}_{1}{\Big (}U_{n}-(-1)^{n}\,U_{n-1}{\Big )}}
=
(
−
1
)
n
⋅
(
n
−
1
)
2
(
(
n
+
1
)
⋅
sin
n
π
2
+
(
−
1
)
n
⋅
n
⋅
cos
n
π
2
)
=
{
n
n
gerade
n
+
1
n
ungerade
{\displaystyle =(-1)^{\frac {n\cdot (n-1)}{2}}\,{\Big (}(n+1)\cdot \sin {\frac {n\pi }{2}}+(-1)^{n}\cdot n\cdot \cos {\frac {n\pi }{2}}{\Big )}=\left\{{\begin{matrix}n&n\,{\text{gerade}}\\\\n+1&n\,{\text{ungerade}}\end{matrix}}\right.}
∑
k
=
m
n
a
k
Δ
b
k
=
[
a
k
b
k
]
m
n
+
1
−
∑
k
=
m
n
Δ
a
k
b
k
+
1
{\displaystyle \sum _{k=m}^{n}a_{k}\,\Delta b_{k}={\Big [}a_{k}\,b_{k}{\Big ]}_{m}^{n+1}-\sum _{k=m}^{n}\Delta a_{k}\,b_{k+1}}
Beweis
a
k
Δ
b
k
+
Δ
a
k
b
k
+
1
=
a
k
(
b
k
+
1
−
b
k
)
+
(
a
k
+
1
−
a
k
)
b
k
+
1
=
a
k
+
1
b
k
+
1
−
a
k
b
k
{\displaystyle a_{k}\,\Delta b_{k}+\Delta a_{k}\,b_{k+1}=a_{k}\,(b_{k+1}-b_{k})+(a_{k+1}-a_{k})\,b_{k+1}=a_{k+1}\,b_{k+1}-a_{k}\,b_{k}}
∑
k
=
m
n
(
a
k
Δ
b
k
+
Δ
a
k
b
k
+
1
)
=
[
a
k
b
k
]
m
n
+
1
{\displaystyle \sum _{k=m}^{n}\left(a_{k}\,\Delta b_{k}+\Delta a_{k}\,b_{k+1}\right)={\Big [}a_{k}\,b_{k}{\Big ]}_{m}^{n+1}}
[ Bearbeiten ]
∑
k
=
1
n
⌊
k
⌋
=
n
⋅
N
−
N
⋅
(
N
−
1
)
⋅
(
2
N
+
5
)
6
,
N
:=
⌊
n
⌋
{\displaystyle \sum _{k=1}^{n}\left\lfloor {\sqrt {k}}\,\right\rfloor =n\cdot N-{\frac {N\cdot (N-1)\cdot (2N+5)}{6}}\qquad ,\qquad N:=\left\lfloor {\sqrt {n}}\,\right\rfloor }
∑
k
=
0
n
−
1
sin
(
2
⌊
k
n
⌋
+
1
)
π
2
n
=
csc
(
π
2
n
)
{\displaystyle \sum _{k=0}^{n-1}\sin {\frac {\left(2\left\lfloor {\sqrt {kn}}\,\right\rfloor +1\right)\pi }{2n}}=\csc \left({\frac {\pi }{2n}}\right)}
Beweis
⌊
k
n
⌋
=
j
⟺
j
≤
k
n
<
j
+
1
⟺
j
2
n
≤
k
<
(
j
+
1
)
2
n
⟺
k
∈
[
j
2
n
,
(
j
+
1
)
2
n
[
{\displaystyle \left\lfloor {\sqrt {kn}}\,\right\rfloor =j\iff j\leq {\sqrt {kn}}<j+1\iff {\frac {j^{2}}{n}}\leq k<{\frac {(j+1)^{2}}{n}}\iff k\in \left[{\frac {j^{2}}{n}},{\frac {(j+1)^{2}}{n}}\right[}
⌋
x
⌊
:=
{
⌊
x
⌋
x
∉
Z
x
−
1
x
∈
Z
{\displaystyle \rfloor x\lfloor :=\left\{{\begin{matrix}\lfloor x\rfloor &x\notin \mathbb {Z} \\x-1&x\in \mathbb {Z} \end{matrix}}\right.}
card
(
Z
∩
[
a
j
,
a
j
+
1
[
)
=
⌋
a
j
+
1
⌊
−
⌋
a
j
⌊
=
Δ
⌋
a
j
⌊
{\displaystyle {\text{card}}{\big (}\mathbb {Z} \cap [a_{j},a_{j+1}[{\big )}=\rfloor a_{j+1}\lfloor -\rfloor a_{j}\lfloor =\Delta \rfloor a_{j}\lfloor }
S
:=
∑
k
=
0
n
−
1
sin
(
2
⌊
k
n
⌋
+
1
)
π
2
n
=
∑
j
=
0
n
−
1
sin
(
2
j
+
1
)
π
2
n
⋅
Δ
⌋
j
2
n
⌊
{\displaystyle S:=\sum _{k=0}^{n-1}\sin {\frac {\left(2\left\lfloor {\sqrt {kn}}\,\right\rfloor +1\right)\pi }{2n}}=\sum _{j=0}^{n-1}\sin {\frac {(2j+1)\pi }{2n}}\cdot \Delta \left\rfloor {\frac {j^{2}}{n}}\right\lfloor }
partieller Summation ist
S
=
[
sin
(
2
j
+
1
)
π
2
n
⋅
⌋
j
2
n
⌊
]
0
n
−
∑
j
=
0
n
−
1
Δ
sin
(
2
j
+
1
)
π
2
n
⋅
⌋
(
j
+
1
)
2
n
⌊
{\displaystyle S=\left[\sin {\frac {(2j+1)\pi }{2n}}\cdot \left\rfloor {\frac {j^{2}}{n}}\right\lfloor \,\,\,\right]_{0}^{n}-\sum _{j=0}^{n-1}\Delta \sin {\frac {(2j+1)\pi }{2n}}\cdot \left\rfloor {\frac {(j+1)^{2}}{n}}\right\lfloor }
=
sin
(
2
n
+
1
)
π
2
n
⋅
(
n
−
1
)
−
sin
π
2
n
⋅
(
−
1
)
−
∑
j
=
1
n
Δ
sin
(
2
j
−
1
)
π
2
n
⋅
⌋
j
2
n
⌊
{\displaystyle =\sin {\frac {(2n+1)\pi }{2n}}\cdot (n-1)-\sin {\frac {\pi }{2n}}\cdot (-1)-\sum _{j=1}^{n}\Delta \sin {\frac {(2j-1)\pi }{2n}}\cdot \left\rfloor {\frac {j^{2}}{n}}\right\lfloor }
Δ
sin
(
2
j
−
1
)
π
2
n
=
sin
(
2
j
+
1
)
π
2
n
−
sin
(
2
j
−
1
)
π
2
n
=
2
⋅
sin
π
2
n
⋅
cos
j
π
n
{\displaystyle \Delta \sin {\frac {(2j-1)\pi }{2n}}=\sin {\frac {(2j+1)\pi }{2n}}-\sin {\frac {(2j-1)\pi }{2n}}=2\cdot \sin {\frac {\pi }{2n}}\cdot \cos {\frac {j\pi }{n}}}
S
=
−
n
sin
π
2
n
+
2
sin
π
2
n
−
2
sin
π
2
n
⋅
∑
j
=
1
n
cos
j
π
n
⋅
⌋
j
2
n
⌊
=
−
n
sin
π
2
n
−
2
sin
π
2
n
⋅
∑
j
=
0
n
cos
j
π
n
⋅
⌋
j
2
n
⌊
⏟
=:
A
{\displaystyle S=-n\sin {\frac {\pi }{2n}}+2\sin {\frac {\pi }{2n}}-2\sin {\frac {\pi }{2n}}\cdot \sum _{j=1}^{n}\cos {\frac {j\pi }{n}}\cdot \left\rfloor {\frac {j^{2}}{n}}\right\lfloor =-n\sin {\frac {\pi }{2n}}-2\sin {\frac {\pi }{2n}}\cdot \underbrace {\sum _{j=0}^{n}\cos {\frac {j\pi }{n}}\cdot \left\rfloor {\frac {j^{2}}{n}}\right\lfloor } _{=:A}}
A
=
∑
j
=
0
n
cos
(
n
−
j
)
π
n
⋅
⌋
(
n
−
j
)
2
n
⌊
=
−
∑
j
=
0
n
cos
j
π
n
⋅
⌋
n
−
2
j
+
j
2
n
⌊
{\displaystyle A=\sum _{j=0}^{n}\cos {\frac {(n-j)\pi }{n}}\cdot \left\rfloor {\frac {(n-j)^{2}}{n}}\right\lfloor =-\sum _{j=0}^{n}\cos {\frac {j\pi }{n}}\cdot \left\rfloor n-2j+{\frac {j^{2}}{n}}\right\lfloor }
⌋
n
−
2
j
+
j
2
n
⌊
=
(
n
−
2
j
)
+
⌋
j
2
n
⌊
{\displaystyle \left\rfloor n-2j+{\frac {j^{2}}{n}}\right\lfloor =(n-2j)+\left\rfloor {\frac {j^{2}}{n}}\right\lfloor }
2
A
=
∑
j
=
0
n
(
2
j
−
n
)
cos
j
π
n
=
∑
j
=
0
n
2
j
⋅
cos
j
π
n
{\displaystyle 2A=\sum _{j=0}^{n}(2j-n)\cos {\frac {j\pi }{n}}=\sum _{j=0}^{n}2j\cdot \cos {\frac {j\pi }{n}}}
⇒
2
sin
π
2
n
⋅
A
=
∑
j
=
0
n
j
⋅
2
sin
π
2
n
cos
j
π
n
=
∑
j
=
0
n
j
⋅
Δ
sin
(
2
j
−
1
)
π
2
n
{\displaystyle \Rightarrow \,2\sin {\frac {\pi }{2n}}\cdot A=\sum _{j=0}^{n}j\cdot 2\sin {\frac {\pi }{2n}}\,\cos {\frac {j\pi }{n}}=\sum _{j=0}^{n}j\cdot \Delta \sin {\frac {(2j-1)\pi }{2n}}}
=
[
j
⋅
sin
(
2
j
−
1
)
π
2
n
]
0
n
+
1
−
∑
j
=
0
n
sin
(
2
j
+
1
)
π
2
n
=
−
(
n
+
1
)
sin
π
2
n
−
∑
j
=
0
n
sin
(
2
j
+
1
)
π
2
n
=
−
n
sin
π
2
n
−
∑
j
=
0
n
−
1
sin
(
2
j
+
1
)
π
2
n
{\displaystyle =\left[j\cdot \sin {\frac {(2j-1)\pi }{2n}}\right]_{0}^{n+1}-\sum _{j=0}^{n}\sin {\frac {(2j+1)\pi }{2n}}=-(n+1)\sin {\frac {\pi }{2n}}-\sum _{j=0}^{n}\sin {\frac {(2j+1)\pi }{2n}}=-n\sin {\frac {\pi }{2n}}-\sum _{j=0}^{n-1}\sin {\frac {(2j+1)\pi }{2n}}}
S
=
∑
j
=
0
n
−
1
sin
(
2
j
+
1
)
π
2
n
=
csc
(
π
2
n
)
{\displaystyle S=\sum _{j=0}^{n-1}\sin {\frac {(2j+1)\pi }{2n}}=\csc \left({\frac {\pi }{2n}}\right)}
∑
k
=
1
n
1
k
=
∑
k
=
1
n
(
−
1
)
k
+
1
(
n
k
)
1
k
{\displaystyle \sum _{k=1}^{n}{\frac {1}{k}}=\sum _{k=1}^{n}(-1)^{k+1}{n \choose k}{\frac {1}{k}}}
Zurück zur Formelsammlung Mathematik
Zurück zur Formelsammlung Mathematik
∏
k
=
0
n
−
1
Γ
(
z
+
k
n
)
=
2
π
n
−
1
n
1
2
−
n
z
Γ
(
n
z
)
{\displaystyle \prod _{k=0}^{n-1}\Gamma \left(z+{\frac {k}{n}}\right)={\sqrt {2\pi }}^{\,n-1}\,n^{{\frac {1}{2}}-nz}\,\Gamma (nz)}
1. Beweis (Gaußsche Multiplikationsformel)
Nach der Gaußschen Definition der Gammafunktion ist
Γ
(
z
+
k
n
)
=
lim
m
→
∞
m
!
m
z
+
k
n
−
1
(
z
+
k
n
)
(
z
+
k
n
+
1
)
⋯
(
z
+
k
n
+
m
−
1
)
{\displaystyle \Gamma \left(z+{\frac {k}{n}}\right)=\lim _{m\to \infty }{\frac {m!\,\,m^{z+{\frac {k}{n}}-1}}{\left(z+{\frac {k}{n}}\right)\left(z+{\frac {k}{n}}+1\right)\cdots \left(z+{\frac {k}{n}}+m-1\right)}}}
m
!
{\displaystyle m!\,}
2
π
m
(
m
e
)
m
{\displaystyle {\sqrt {2\pi m}}\left({\frac {m}{e}}\right)^{m}}
n
m
{\displaystyle n^{m}\,}
Γ
(
z
+
k
n
)
=
lim
m
→
∞
2
π
(
m
n
e
)
m
m
z
+
k
n
−
1
2
(
n
z
+
k
)
(
n
z
+
k
+
n
)
⋯
(
n
z
+
k
+
n
(
m
−
1
)
)
{\displaystyle \Gamma \left(z+{\frac {k}{n}}\right)=\lim _{m\to \infty }{\frac {{\sqrt {2\pi }}\,\left({\frac {mn}{e}}\right)^{m}\,m^{z+{\frac {k}{n}}-{\frac {1}{2}}}}{(nz+k)(nz+k+n)\cdots (nz+k+n(m-1))}}}
n
n
z
−
1
2
∏
k
=
0
n
−
1
Γ
(
z
+
k
n
)
=
lim
m
→
∞
2
π
n
(
m
n
e
)
m
n
(
m
n
)
n
z
−
1
2
n
z
(
n
z
+
1
)
⋯
(
n
z
+
m
n
−
1
)
{\displaystyle n^{nz-{\frac {1}{2}}}\prod _{k=0}^{n-1}\Gamma \left(z+{\frac {k}{n}}\right)=\lim _{m\to \infty }{\frac {{\sqrt {2\pi }}^{\,n}\,\left({\frac {mn}{e}}\right)^{mn}\,(mn)^{nz-{\frac {1}{2}}}}{nz\,(nz+1)\cdots (nz+mn-1)}}}
m
n
{\displaystyle mn\,}
m
{\displaystyle m\,}
lim
m
→
∞
2
π
n
(
m
e
)
m
m
n
z
−
1
2
n
z
(
n
z
+
1
)
⋯
(
n
z
+
m
−
1
)
=
2
π
n
−
1
Γ
(
n
z
)
{\displaystyle \lim _{m\to \infty }{\frac {{\sqrt {2\pi }}^{\,n}\,\left({\frac {m}{e}}\right)^{m}\,m^{nz-{\frac {1}{2}}}}{nz\,(nz+1)\cdots (nz+m-1)}}={\sqrt {2\pi }}^{\,n-1}\,\Gamma (nz)}
2. Beweis
Setzt man
F
n
(
z
)
=
n
n
z
∏
k
=
0
n
−
1
Γ
(
z
+
k
n
)
Γ
(
n
z
)
{\displaystyle F_{n}(z)={\frac {n^{nz}\,\prod \limits _{k=0}^{n-1}\Gamma \left(z+{\frac {k}{n}}\right)}{\Gamma (nz)}}}
F
n
(
z
+
1
)
=
n
n
z
n
n
∏
k
=
0
n
−
1
[
(
z
+
k
n
)
Γ
(
z
+
k
n
)
]
∏
k
=
0
n
−
1
(
n
z
+
k
)
Γ
(
n
z
)
=
F
n
(
z
)
{\displaystyle F_{n}(z+1)={\frac {n^{nz}\,n^{n}\,\prod \limits _{k=0}^{n-1}\left[\left(z+{\frac {k}{n}}\right)\,\Gamma \left(z+{\frac {k}{n}}\right)\right]}{\prod \limits _{k=0}^{n-1}(nz+k)\,\Gamma (nz)}}=F_{n}(z)}
z
{\displaystyle z\,}
Γ
(
z
+
k
n
)
∼
Γ
(
z
)
z
k
n
{\displaystyle \Gamma \left(z+{\frac {k}{n}}\right)\sim \Gamma (z)\,z^{\frac {k}{n}}}
F
n
(
z
)
∼
n
n
z
Γ
n
(
z
)
z
n
−
1
2
Γ
(
n
z
)
{\displaystyle F_{n}(z)\sim {\frac {n^{nz}\,\Gamma ^{n}(z)\,z^{\frac {n-1}{2}}}{\Gamma (nz)}}}
Γ
(
z
)
∼
2
π
z
(
z
e
)
z
{\displaystyle \Gamma (z)\sim {\sqrt {\frac {2\pi }{z}}}\,\left({\frac {z}{e}}\right)^{z}}
F
n
(
z
)
∼
n
n
z
2
π
z
n
(
z
e
)
n
z
z
n
−
1
2
2
π
n
z
(
n
z
e
)
n
z
=
n
2
π
n
−
1
{\displaystyle F_{n}(z)\sim {\frac {n^{nz}\,{\sqrt {\frac {2\pi }{z}}}^{\,n}\,\left({\frac {z}{e}}\right)^{nz}\,z^{\frac {n-1}{2}}}{{\sqrt {\frac {2\pi }{nz}}}\,\left({\frac {nz}{e}}\right)^{nz}}}={\sqrt {n}}\,{\sqrt {2\pi }}^{\,n-1}}
F
n
(
z
)
{\displaystyle F_{n}(z)\,}
z
{\displaystyle z\,}
F
n
(
z
)
=
n
2
π
n
−
1
{\displaystyle F_{n}(z)={\sqrt {n}}\,{\sqrt {2\pi }}^{\,n-1}}
3. Beweis
Nach der Formel
ψ
(
z
)
+
γ
=
∫
0
1
1
−
t
z
−
1
1
−
t
d
t
=
n
∫
0
1
t
n
−
1
−
t
n
z
−
1
1
−
t
n
d
t
{\displaystyle \psi (z)+\gamma =\int _{0}^{1}{\frac {1-t^{z-1}}{1-t}}\,dt=n\int _{0}^{1}{\frac {t^{n-1}-t^{nz-1}}{1-t^{n}}}\,dt}
ψ
(
z
+
k
n
)
+
γ
=
n
∫
0
1
[
t
n
−
1
1
−
t
n
−
t
n
z
+
k
−
1
1
−
t
n
]
d
t
{\displaystyle \psi \left(z+{\frac {k}{n}}\right)+\gamma =n\int _{0}^{1}\left[{\frac {t^{n-1}}{1-t^{n}}}-{\frac {t^{nz+k-1}}{1-t^{n}}}\right]dt}
∑
k
=
0
n
−
1
ψ
(
z
+
k
n
)
+
n
γ
=
n
∫
0
1
[
n
t
n
−
1
1
−
t
n
−
t
n
z
−
1
1
−
t
]
d
t
{\displaystyle \sum _{k=0}^{n-1}\psi \left(z+{\frac {k}{n}}\right)+n\gamma =n\int _{0}^{1}\left[{\frac {nt^{n-1}}{1-t^{n}}}-{\frac {t^{nz-1}}{1-t}}\right]dt}
n
ψ
(
n
z
)
+
n
γ
=
n
∫
0
1
1
−
t
n
z
−
1
1
−
t
d
t
{\displaystyle n\psi (nz)+n\gamma =n\int _{0}^{1}{\frac {1-t^{nz-1}}{1-t}}\,dt}
∑
k
=
0
n
−
1
ψ
(
z
+
k
n
)
−
n
ψ
(
n
z
)
=
n
∫
0
1
[
n
t
n
−
1
1
−
t
n
−
1
1
−
t
]
d
t
=
n
[
log
(
1
−
t
n
)
−
log
(
1
−
t
)
]
0
1
=
−
n
log
n
{\displaystyle \sum _{k=0}^{n-1}\psi \left(z+{\frac {k}{n}}\right)-n\psi (nz)=n\int _{0}^{1}\left[{\frac {n\,t^{n-1}}{1-t^{n}}}-{\frac {1}{1-t}}\right]dt=n{\Big [}\log(1-t^{n})-\log(1-t){\Big ]}_{0}^{1}=-n\log n}
z
{\displaystyle z\,}
∑
k
=
0
n
−
1
log
Γ
(
z
+
k
n
)
=
C
n
−
n
z
log
n
+
log
Γ
(
n
z
)
{\displaystyle \sum _{k=0}^{n-1}\log \Gamma \left(z+{\frac {k}{n}}\right)=C_{n}-nz\log n+\log \Gamma (nz)}
∏
k
=
0
n
−
1
Γ
(
z
+
k
n
)
=
e
C
n
n
−
n
z
Γ
(
n
z
)
{\displaystyle \prod _{k=0}^{n-1}\Gamma \left(z+{\frac {k}{n}}\right)=e^{C_{n}}\,n^{-nz}\,\Gamma (nz)}
z
=
1
n
{\displaystyle z={\frac {1}{n}}}
e
C
n
=
∏
k
=
1
n
Γ
(
z
+
k
n
)
n
=
2
π
n
−
1
n
1
2
{\displaystyle e^{C_{n}}=\prod _{k=1}^{n}\Gamma \left(z+{\frac {k}{n}}\right)\,n={\sqrt {2\pi }}^{\,n-1}\,n^{\frac {1}{2}}}
4. Beweis
Betrachte die Formel von Liouville :
∫
0
∞
⋯
∫
0
∞
e
−
(
x
1
+
x
2
+
.
.
.
+
x
n
−
1
+
z
n
x
1
x
2
⋯
x
n
−
1
)
x
1
1
n
−
1
x
2
2
n
−
1
⋯
x
n
−
1
n
−
1
n
−
1
d
x
1
d
x
2
⋯
d
x
n
−
1
=
1
n
2
π
n
−
1
e
−
n
z
{\displaystyle \int _{0}^{\infty }\cdots \int _{0}^{\infty }e^{-\left(x_{1}+x_{2}+...+x_{n-1}+{\frac {z^{n}}{x_{1}\,x_{2}\cdots x_{n-1}}}\right)}\,x_{1}^{{\frac {1}{n}}-1}\,x_{2}^{{\frac {2}{n}}-1}\cdots x_{n-1}^{{\frac {n-1}{n}}-1}\,dx_{1}\,dx_{2}\cdots dx_{n-1}={\frac {1}{\sqrt {n}}}\,{\sqrt {2\pi }}^{\,n-1}\,e^{-nz}}
z
α
−
1
{\displaystyle z^{\alpha -1}}
z
{\displaystyle z\,}
0
{\displaystyle 0\,}
∞
{\displaystyle \infty }
∫
0
∞
⋯
∫
0
∞
e
−
(
x
1
+
x
2
+
.
.
.
+
x
n
−
1
)
∫
0
∞
e
−
z
n
x
1
x
2
⋯
x
n
−
1
z
α
−
1
d
z
⏟
=
1
n
Γ
(
α
n
)
(
x
1
x
2
⋅
x
n
−
1
)
α
n
x
1
1
n
−
1
x
2
2
n
−
1
⋯
x
n
−
1
n
−
1
n
−
1
d
x
1
d
x
2
⋯
d
x
n
−
1
=
1
n
2
π
n
−
1
∫
0
∞
e
−
n
z
z
α
−
1
d
z
{\displaystyle \int _{0}^{\infty }\cdots \int _{0}^{\infty }e^{-(x_{1}+x_{2}+...+x_{n-1})}\underbrace {\int _{0}^{\infty }e^{-{\frac {z^{n}}{x_{1}\,x_{2}\cdots x_{n-1}}}}\,z^{\alpha -1}\,dz} _{={\frac {1}{n}}\,\Gamma \left({\frac {\alpha }{n}}\right)\,(x_{1}x_{2}\cdot x_{n-1})^{\frac {\alpha }{n}}}\,\,x_{1}^{{\frac {1}{n}}-1}\,x_{2}^{{\frac {2}{n}}-1}\cdots x_{n-1}^{{\frac {n-1}{n}}-1}\,dx_{1}\,dx_{2}\cdots dx_{n-1}={\frac {1}{\sqrt {n}}}\,{\sqrt {2\pi }}^{\,n-1}\,\int _{0}^{\infty }e^{-nz}\,z^{\alpha -1}\,dz}
⇒
1
n
Γ
(
α
n
)
∫
0
∞
⋯
∫
0
∞
e
−
(
x
1
+
x
2
+
.
.
.
+
x
n
−
1
)
x
1
α
+
1
n
−
1
x
2
α
+
2
n
−
1
⋯
x
n
−
1
α
+
n
−
1
n
−
1
d
x
1
d
x
2
⋯
d
x
n
−
1
=
1
n
2
π
n
−
1
Γ
(
α
)
n
α
{\displaystyle \Rightarrow \,{\frac {1}{n}}\,\Gamma \left({\frac {\alpha }{n}}\right)\int _{0}^{\infty }\cdots \int _{0}^{\infty }e^{-(x_{1}+x_{2}+...+x_{n-1})}\,x_{1}^{{\frac {\alpha +1}{n}}-1}\,x_{2}^{{\frac {\alpha +2}{n}}-1}\cdots x_{n-1}^{{\frac {\alpha +n-1}{n}}-1}\,dx_{1}\,dx_{2}\cdots dx_{n-1}={\frac {1}{\sqrt {n}}}\,{\sqrt {2\pi }}^{\,n-1}\,{\frac {\Gamma (\alpha )}{n^{\alpha }}}}
⇒
1
n
Γ
(
α
n
)
Γ
(
α
+
1
n
)
Γ
(
α
+
2
n
)
⋯
Γ
(
α
+
n
−
1
n
)
=
1
n
2
π
n
−
1
Γ
(
α
)
n
α
{\displaystyle \Rightarrow \,{\frac {1}{n}}\,\Gamma \left({\frac {\alpha }{n}}\right)\,\Gamma \left({\frac {\alpha +1}{n}}\right)\,\Gamma \left({\frac {\alpha +2}{n}}\right)\cdots \Gamma \left({\frac {\alpha +n-1}{n}}\right)={\frac {1}{\sqrt {n}}}\,{\sqrt {2\pi }}^{\,n-1}\,{\frac {\Gamma (\alpha )}{n^{\alpha }}}}
⇒
∏
k
=
0
n
−
1
Γ
(
α
n
+
k
n
)
=
2
π
n
−
1
n
1
2
−
α
Γ
(
α
)
{\displaystyle \Rightarrow \,\prod _{k=0}^{n-1}\Gamma \left({\frac {\alpha }{n}}+{\frac {k}{n}}\right)={\sqrt {2\pi }}^{\,n-1}\,n^{{\frac {1}{2}}-\alpha }\,\Gamma (\alpha )}
∏
k
=
1
n
−
1
Γ
(
k
n
)
=
(
2
π
)
n
−
1
2
n
{\displaystyle \prod _{k=1}^{n-1}\Gamma \left({\frac {k}{n}}\right)={\frac {(2\pi )^{\frac {n-1}{2}}}{\sqrt {n}}}}
∏
k
=
1
n
−
1
(
1
−
ξ
k
)
=
n
ξ
=
e
2
π
i
n
{\displaystyle \prod _{k=1}^{n-1}\left(1-\xi ^{k}\right)=n\qquad \xi =e^{\frac {2\pi i}{n}}}
α
2
n
−
2
α
n
β
n
cos
(
n
θ
)
+
β
2
n
=
∏
k
=
0
n
−
1
(
α
2
−
2
α
β
cos
(
θ
+
2
π
k
n
)
+
β
2
)
{\displaystyle \alpha ^{2n}-2\alpha ^{n}\beta ^{n}\cos(n\theta )+\beta ^{2n}=\prod _{k=0}^{n-1}\left(\alpha ^{2}-2\alpha \beta \,\cos \left(\theta +{\frac {2\pi k}{n}}\right)+\beta ^{2}\right)}
∏
k
=
0
n
−
1
(
1
+
z
2
k
)
=
1
−
z
2
n
1
−
z
z
≠
1
{\displaystyle \prod _{k=0}^{n-1}\left(1+z^{2^{k}}\right)={\frac {1-z^{2^{n}}}{1-z}}\qquad z\neq 1}
Beweis
Der Induktionsanfang für
n
=
0
{\displaystyle n=0\,}
∏
k
=
0
n
(
1
+
z
2
k
)
=
1
−
z
2
n
1
−
z
(
1
+
z
2
n
)
=
1
−
z
2
n
+
1
1
−
z
{\displaystyle \prod _{k=0}^{n}\left(1+z^{2^{k}}\right)={\frac {1-z^{2^{n}}}{1-z}}\,\left(1+z^{2^{n}}\right)={\frac {1-z^{2^{n+1}}}{1-z}}}
∏
k
=
1
n
2
z
1
/
2
k
+
z
−
1
/
2
k
=
2
n
z
1
/
2
n
−
z
−
1
/
2
n
z
−
z
−
1
z
≠
±
1
{\displaystyle \prod _{k=1}^{n}{\frac {2}{z^{1/2^{k}}+z^{-1/2^{k}}}}=2^{n}\,{\frac {z^{1/2^{n}}-z^{-1/2^{n}}}{z-z^{-1}}}\qquad z\neq \pm 1}
∏
k
=
0
n
−
1
sin
(
z
+
k
π
n
)
=
sin
n
z
2
n
−
1
{\displaystyle \prod _{k=0}^{n-1}\sin \left(z+{\frac {k\pi }{n}}\right)={\frac {\sin nz}{2^{n-1}}}}
Beweis
2
i
sin
(
z
+
k
π
n
)
=
e
i
(
z
+
k
π
n
)
−
e
−
i
(
z
+
k
π
n
)
=
e
i
(
z
+
k
π
n
)
⋅
(
1
−
e
−
i
(
2
z
+
2
k
π
n
)
)
{\displaystyle 2i\sin \left(z+{\frac {k\pi }{n}}\right)=e^{i\left(z+{\frac {k\pi }{n}}\right)}-e^{-i\left(z+{\frac {k\pi }{n}}\right)}=e^{i\left(z+{\frac {k\pi }{n}}\right)}\cdot \left(1-e^{-i\left(2z+{\frac {2k\pi }{n}}\right)}\right)}
2
n
i
n
∏
k
=
0
n
−
1
sin
(
z
+
k
π
n
)
=
e
i
∑
k
=
0
n
−
1
(
z
+
k
π
n
)
⋅
∏
k
=
0
n
−
1
(
1
−
e
−
i
(
2
z
+
2
k
π
n
)
)
=
e
i
n
z
⋅
e
i
(
n
−
1
)
π
2
(
1
−
e
−
i
⋅
2
n
z
)
=
i
n
−
1
(
e
i
n
z
−
e
−
i
n
z
)
{\displaystyle 2^{n}\,i^{n}\,\prod _{k=0}^{n-1}\sin \left(z+{\frac {k\pi }{n}}\right)=e^{i\sum \limits _{k=0}^{n-1}\left(z+{\frac {k\pi }{n}}\right)}\cdot \prod _{k=0}^{n-1}\left(1-e^{-i\left(2z+{\frac {2k\pi }{n}}\right)}\right)=e^{inz}\cdot e^{i(n-1){\frac {\pi }{2}}}\,\left(1-e^{-i\cdot 2nz}\right)=i^{n-1}\,\left(e^{inz}-e^{-inz}\right)}
∏
k
=
1
n
−
1
sin
(
k
π
n
)
=
n
2
n
−
1
{\displaystyle \prod _{k=1}^{n-1}\sin \left({\frac {k\pi }{n}}\right)={\frac {n}{2^{n-1}}}}
∏
k
=
1
⌊
n
−
1
2
⌋
tan
(
k
π
n
)
=
{
n
,
n
ungerade
1
,
n
gerade
{\displaystyle \prod _{k=1}^{\lfloor {\frac {n-1}{2}}\rfloor }\tan \left({\frac {k\pi }{n}}\right)=\left\{{\begin{matrix}{\sqrt {n}}&,&n&{\text{ungerade}}\\\\1&,&n&{\text{gerade}}\end{matrix}}\right.}
Beweis
Ist
n
{\displaystyle n\,}
n
=
2
m
{\displaystyle n=2m\,}
∏
k
=
1
m
−
1
tan
(
k
π
2
m
)
=
∏
k
=
1
m
−
1
tan
(
(
m
−
k
)
π
2
m
)
=
∏
k
=
1
m
−
1
tan
(
π
2
−
k
π
2
m
)
=
∏
k
=
1
m
−
1
cot
(
k
π
2
m
)
=
[
∏
k
=
1
m
−
1
tan
(
k
π
2
m
)
]
−
1
{\displaystyle \prod _{k=1}^{m-1}\tan \left({\frac {k\pi }{2m}}\right)=\prod _{k=1}^{m-1}\tan \left({\frac {(m-k)\pi }{2m}}\right)=\prod _{k=1}^{m-1}\tan \left({\frac {\pi }{2}}-{\frac {k\pi }{2m}}\right)=\prod _{k=1}^{m-1}\cot \left({\frac {k\pi }{2m}}\right)=\left[\prod _{k=1}^{m-1}\tan \left({\frac {k\pi }{2m}}\right)\right]^{-1}}
∏
k
=
1
m
−
1
tan
(
k
π
2
m
)
=
+
1
{\displaystyle \prod _{k=1}^{m-1}\tan \left({\frac {k\pi }{2m}}\right)=+1}
n
{\displaystyle n\,}
n
=
2
m
+
1
{\displaystyle n=2m+1\,}
∏
k
=
1
m
tan
(
k
π
2
m
+
1
)
=
(
−
1
)
m
∏
k
=
1
m
tan
(
(
2
m
+
1
−
k
)
π
2
m
+
1
)
=
(
−
1
)
m
∏
k
=
m
+
1
2
m
tan
(
k
π
2
m
+
1
)
{\displaystyle \prod _{k=1}^{m}\tan \left({\frac {k\pi }{2m+1}}\right)=(-1)^{m}\prod _{k=1}^{m}\tan \left({\frac {(2m+1-k)\pi }{2m+1}}\right)=(-1)^{m}\prod _{k=m+1}^{2m}\tan \left({\frac {k\pi }{2m+1}}\right)}
∏
k
=
1
2
m
tan
(
k
π
2
m
+
1
)
=
(
−
1
)
m
∏
k
=
1
m
tan
2
(
k
π
2
m
+
1
)
{\displaystyle \prod _{k=1}^{2m}\tan \left({\frac {k\pi }{2m+1}}\right)=(-1)^{m}\prod _{k=1}^{m}\tan ^{2}\left({\frac {k\pi }{2m+1}}\right)}
tan
x
=
sin
x
cos
x
=
1
i
e
i
x
−
e
−
i
x
e
i
x
+
e
−
i
x
=
1
i
e
2
i
x
−
1
e
2
i
x
+
1
=
i
1
−
e
2
i
x
1
+
e
2
i
x
{\displaystyle \tan x={\frac {\sin x}{\cos x}}={\frac {1}{i}}\,{\frac {e^{ix}-e^{-ix}}{e^{ix}+e^{-ix}}}={\frac {1}{i}}\,{\frac {e^{2ix}-1}{e^{2ix}+1}}=i\,{\frac {1-e^{2ix}}{1+e^{2ix}}}}
tan
(
k
π
2
m
+
1
)
=
i
1
−
e
2
π
i
k
2
m
+
1
1
+
e
2
π
i
k
2
m
+
1
{\displaystyle \tan \left({\frac {k\pi }{2m+1}}\right)=i\,{\frac {1-e^{2\pi i\,{\frac {k}{2m+1}}}}{1+e^{2\pi i\,{\frac {k}{2m+1}}}}}}
∏
k
=
1
2
m
tan
(
k
π
2
m
+
1
)
=
(
−
1
)
m
∏
k
=
1
2
m
(
1
−
ξ
k
2
m
+
1
)
∏
k
=
1
2
m
(
1
+
ξ
k
2
m
+
1
)
=
(
−
1
)
m
f
(
1
)
f
(
−
1
)
{\displaystyle \prod _{k=1}^{2m}\tan \left({\frac {k\pi }{2m+1}}\right)=(-1)^{m}\,{\frac {\prod _{k=1}^{2m}\left(1-\xi ^{\frac {k}{2m+1}}\right)}{\prod _{k=1}^{2m}\left(1+\xi ^{\frac {k}{2m+1}}\right)}}=(-1)^{m}\,{\frac {f(1)}{f(-1)}}}
f
(
X
)
=
∏
k
=
1
2
m
(
X
−
ξ
k
2
m
+
1
)
=
X
2
m
+
1
−
1
X
−
1
{\displaystyle f(X)=\prod _{k=1}^{2m}\left(X-\xi ^{\frac {k}{2m+1}}\right)={\frac {X^{2m+1}-1}{X-1}}}
∏
k
=
1
m
tan
2
(
k
π
2
m
+
1
)
=
f
(
1
)
f
(
−
1
)
=
2
m
+
1
1
=
n
{\displaystyle \prod _{k=1}^{m}\tan ^{2}\left({\frac {k\pi }{2m+1}}\right)={\frac {f(1)}{f(-1)}}={\frac {2m+1}{1}}=n}
tan
(
k
π
2
m
+
1
)
{\displaystyle \tan \left({\frac {k\pi }{2m+1}}\right)}
k
=
1
,
.
.
.
,
m
{\displaystyle k=1,...,m\,}
∏
k
=
1
m
tan
(
k
π
2
m
+
1
)
=
+
n
{\displaystyle \prod _{k=1}^{m}\tan \left({\frac {k\pi }{2m+1}}\right)=+{\sqrt {n}}}
|
Γ
(
n
+
i
x
)
|
2
=
∏
k
=
0
n
−
1
(
k
2
+
x
2
)
π
x
sinh
π
x
n
∈
Z
≥
0
,
x
∈
R
{\displaystyle |\Gamma (n+ix)|^{2}=\prod _{k=0}^{n-1}(k^{2}+x^{2})\,{\frac {\pi x}{\sinh \pi x}}\qquad n\in \mathbb {Z} ^{\geq 0}\,,\,x\in \mathbb {R} }
|
Γ
(
n
+
1
2
+
i
x
)
|
2
=
∏
k
=
0
n
−
1
(
x
2
+
(
k
+
1
2
)
2
)
π
cosh
π
x
n
∈
Z
≥
0
,
x
∈
R
{\displaystyle \left|\Gamma \left(n+{\frac {1}{2}}+ix\right)\right|^{2}=\prod _{k=0}^{n-1}\left(x^{2}+\left(k+{\frac {1}{2}}\right)^{2}\right)\,{\frac {\pi }{\cosh \pi x}}\qquad n\in \mathbb {Z} ^{\geq 0}\,,\,x\in \mathbb {R} }
Zurück zur Formelsammlung Mathematik
∏
k
=
1
∞
4
k
2
4
k
2
−
1
=
π
2
{\displaystyle \prod _{k=1}^{\infty }{\frac {4k^{2}}{4k^{2}-1}}={\frac {\pi }{2}}}
1. Beweis (Wallis Produkt)
Setzt man
a
k
=
∫
0
π
2
(
sin
x
)
k
d
x
{\displaystyle a_{k}=\int _{0}^{\frac {\pi }{2}}(\sin x)^{k}\,dx}
a
k
+
1
=
k
k
+
1
a
k
−
1
{\displaystyle a_{k+1}={\frac {k}{k+1}}\,a_{k-1}}
a
k
+
1
≤
a
k
≤
a
k
−
1
{\displaystyle a_{k+1}\leq a_{k}\leq a_{k-1}}
a
k
+
1
∼
a
k
−
1
{\displaystyle a_{k+1}\sim a_{k-1}\,}
w
k
:=
a
2
k
+
1
a
2
k
{\displaystyle w_{k}:={\frac {a_{2k+1}}{a_{2k}}}}
k
{\displaystyle k\,}
1
{\displaystyle 1\,}
w
k
/
w
k
−
1
=
a
2
k
+
1
/
a
2
k
−
1
a
2
k
/
a
2
k
−
2
=
2
k
2
k
+
1
2
k
−
1
2
k
=
4
k
2
4
k
2
−
1
{\displaystyle w_{k}/w_{k-1}={\frac {a_{2k+1}/a_{2k-1}}{a_{2k}/a_{2k-2}}}={\frac {\,\,\,{\frac {2k}{2k+1}}\,\,\,}{\frac {2k-1}{2k}}}={\frac {4k^{2}}{4k^{2}-1}}}
∏
k
=
1
n
4
k
2
4
k
2
−
1
=
w
n
w
0
→
1
w
0
=
a
0
a
1
=
π
2
{\displaystyle \prod _{k=1}^{n}{\frac {4k^{2}}{4k^{2}-1}}={\frac {w_{n}}{w_{0}}}\to {\frac {1}{w_{0}}}={\frac {a_{0}}{a_{1}}}={\frac {\pi }{2}}}
2. Beweis
Setzt man in der Produktdarstellung
sin
π
z
=
π
z
∏
k
=
1
∞
(
1
−
z
2
k
2
)
z
=
1
2
{\displaystyle \sin \pi z=\pi z\,\prod _{k=1}^{\infty }\left(1-{\frac {z^{2}}{k^{2}}}\right)\quad z={\frac {1}{2}}}
1
=
π
2
∏
k
=
1
∞
(
1
−
1
4
k
2
)
{\displaystyle 1={\frac {\pi }{2}}\,\prod _{k=1}^{\infty }\left(1-{\frac {1}{4k^{2}}}\right)}
∏
n
=
1
∞
(
(
1
−
x
2
n
)
(
1
+
x
2
n
−
1
z
2
)
(
1
+
x
2
n
−
1
z
2
)
)
=
∑
n
∈
Z
x
n
2
z
2
n
|
x
|
<
1
,
z
≠
0
{\displaystyle \prod _{n=1}^{\infty }\left(\left(1-x^{2n}\right)\left(1+x^{2n-1}z^{2}\right)\left(1+{\frac {x^{2n-1}}{z^{2}}}\right)\right)=\sum _{n\in \mathbb {Z} }x^{n^{2}}\,z^{2n}\qquad |x|<1\;,\;z\neq 0}
Beweis (Jacobisches Tripelprodukt)
Für
0
<
|
x
|
<
1
{\displaystyle 0<|x|<1\,}
F
(
z
)
:=
∏
n
=
1
∞
(
1
+
x
2
n
−
1
z
2
)
∏
n
=
1
∞
(
1
+
x
2
n
−
1
z
2
)
{\displaystyle F(z):=\prod _{n=1}^{\infty }\left(1+x^{2n-1}z^{2}\right)\,\prod _{n=1}^{\infty }\left(1+{\frac {x^{2n-1}}{z^{2}}}\right)}
F
(
x
z
)
=
∏
n
=
1
∞
(
1
+
x
2
n
+
1
z
2
)
∏
n
=
1
∞
(
1
+
x
2
n
−
3
z
2
)
=
∏
n
=
2
∞
(
1
+
x
2
n
−
1
z
2
)
∏
n
=
0
∞
(
1
+
x
2
n
−
1
z
2
)
{\displaystyle F(xz)=\prod _{n=1}^{\infty }\left(1+x^{2n+1}z^{2}\right)\,\prod _{n=1}^{\infty }\left(1+{\frac {x^{2n-3}}{z^{2}}}\right)=\prod _{n=2}^{\infty }\left(1+x^{2n-1}z^{2}\right)\,\prod _{n=0}^{\infty }\left(1+{\frac {x^{2n-1}}{z^{2}}}\right)}
x
z
2
F
(
x
z
)
=
x
z
2
(
1
+
1
x
z
2
)
∏
n
=
2
∞
(
1
+
x
2
n
−
1
z
2
)
∏
n
=
1
∞
(
1
+
x
2
n
−
1
z
2
)
=
F
(
z
)
{\displaystyle xz^{2}\,F(xz)=xz^{2}\left(1+{\frac {1}{xz^{2}}}\right)\,\prod _{n=2}^{\infty }\left(1+x^{2n-1}z^{2}\right)\,\prod _{n=1}^{\infty }\left(1+{\frac {x^{2n-1}}{z^{2}}}\right)=F(z)}
G
(
z
)
:=
∏
n
=
1
∞
(
1
−
x
2
n
)
F
(
z
)
{\displaystyle G(z):=\prod _{n=1}^{\infty }\left(1-x^{2n}\right)\,F(z)}
G
{\displaystyle G\,}
x
z
2
G
(
x
z
)
=
G
(
z
)
{\displaystyle xz^{2}\,G(xz)=G(z)}
G
{\displaystyle G\,}
G
(
z
)
=
∑
m
∈
Z
a
m
z
2
m
{\displaystyle G(z)=\sum _{m\in \mathbb {Z} }a_{m}z^{2m}}
G
(
1
z
)
=
G
(
z
)
{\displaystyle G\left({\frac {1}{z}}\right)=G(z)\,}
a
−
m
=
a
m
{\displaystyle a_{-m}=a_{m}\,}
x
z
2
G
(
x
z
)
=
∑
m
∈
Z
a
m
x
2
m
+
1
z
2
m
+
2
=
∑
m
∈
Z
a
m
−
1
x
2
m
−
1
z
2
m
{\displaystyle xz^{2}G(xz)=\sum _{m\in \mathbb {Z} }a_{m}\,x^{2m+1}\,z^{2m+2}=\sum _{m\in \mathbb {Z} }a_{m-1}\,x^{2m-1}\,z^{2m}}
a
m
=
a
m
−
1
x
2
m
−
1
{\displaystyle a_{m}=a_{m-1}\,x^{2m-1}\,}
a
n
=
a
0
x
n
2
{\displaystyle a_{n}=a_{0}\,x^{n^{2}}}
G
(
z
)
=
a
0
∑
n
∈
Z
x
n
2
z
2
n
{\displaystyle G(z)=a_{0}\sum _{n\in \mathbb {Z} }x^{n^{2}}\,z^{2n}}
G
(
1
)
=
a
0
∑
n
∈
Z
x
n
2
=
∏
n
=
1
∞
[
(
1
−
x
2
n
)
(
1
+
x
2
n
−
1
)
2
]
{\displaystyle G(1)=a_{0}\,\sum _{n\in \mathbb {Z} }x^{n^{2}}=\prod _{n=1}^{\infty }\left[\left(1-x^{2n}\right)\left(1+x^{2n-1}\right)^{2}\right]}
1
{\displaystyle 1\,}
a
0
=
1
{\displaystyle a_{0}=1\,}
∏
n
=
1
∞
(
1
−
q
n
)
3
=
∑
n
=
0
∞
(
−
1
)
n
(
2
n
+
1
)
q
n
(
n
+
1
)
2
|
q
|
<
1
{\displaystyle \prod _{n=1}^{\infty }\left(1-q^{n}\right)^{3}=\sum _{n=0}^{\infty }(-1)^{n}\,(2n+1)\,q^{\frac {n(n+1)}{2}}\qquad |q|<1}
Beweis (Jacobische Formel)
Im Jacobischen Tripelprodukt
∏
n
=
1
∞
(
(
1
−
x
2
n
)
(
1
+
x
2
n
−
1
z
2
)
(
1
+
x
2
n
−
1
z
2
)
)
=
∑
n
∈
Z
x
n
2
z
2
n
{\displaystyle \prod _{n=1}^{\infty }\left(\left(1-x^{2n}\right)\left(1+x^{2n-1}z^{2}\right)\left(1+{\frac {x^{2n-1}}{z^{2}}}\right)\right)=\sum _{n\in \mathbb {Z} }x^{n^{2}}\,z^{2n}}
x
=
q
1
2
{\displaystyle x=q^{\frac {1}{2}}}
z
2
=
−
a
q
−
1
2
:
{\displaystyle z^{2}=-aq^{-{\frac {1}{2}}}\;:}
∏
n
=
1
∞
(
(
1
−
q
n
)
(
1
−
a
q
n
−
1
)
(
1
−
a
−
1
q
n
)
)
=
∑
n
∈
Z
q
n
2
2
(
−
a
q
−
1
2
)
n
{\displaystyle \prod _{n=1}^{\infty }\left(\left(1-q^{n}\right)\left(1-aq^{n-1}\right)\left(1-a^{-1}q^{n}\right)\right)=\sum _{n\in \mathbb {Z} }q^{\frac {n^{2}}{2}}\,\left(-aq^{-{\frac {1}{2}}}\right)^{n}}
(
1
−
a
)
∏
n
=
1
∞
(
(
1
−
q
n
)
(
1
−
a
q
n
)
(
1
−
a
−
1
q
n
)
)
{\displaystyle (1-a)\prod _{n=1}^{\infty }\left((1-q^{n})(1-aq^{n})(1-a^{-1}q^{n})\right)}
=
∑
n
∈
Z
(
−
1
)
n
a
n
q
n
(
n
−
1
)
2
=
∑
n
=
1
∞
(
−
1
)
n
a
n
q
n
(
n
−
1
)
2
+
∑
n
=
0
∞
(
−
1
)
−
n
a
−
n
q
−
n
(
−
n
−
1
)
2
{\displaystyle =\sum _{n\in \mathbb {Z} }(-1)^{n}\,a^{n}\,q^{\frac {n(n-1)}{2}}=\sum _{n=1}^{\infty }(-1)^{n}\,a^{n}\,q^{\frac {n(n-1)}{2}}+\sum _{n=0}^{\infty }(-1)^{-n}\,a^{-n}\,q^{\frac {-n(-n-1)}{2}}}
=
∑
n
=
0
∞
(
−
1
)
n
+
1
a
n
+
1
q
n
(
n
+
1
)
2
+
∑
n
=
0
∞
(
−
1
)
n
a
−
n
q
n
(
n
+
1
)
2
=
∑
n
=
0
∞
(
−
1
)
n
(
a
−
n
−
a
n
+
1
)
q
n
(
n
+
1
)
2
{\displaystyle =\sum _{n=0}^{\infty }(-1)^{n+1}\,a^{n+1}\,q^{\frac {n(n+1)}{2}}+\sum _{n=0}^{\infty }(-1)^{n}\,a^{-n}\,q^{\frac {n(n+1)}{2}}=\sum _{n=0}^{\infty }(-1)^{n}\,\left(a^{-n}-a^{n+1}\right)\,q^{\frac {n(n+1)}{2}}}
1
−
a
:
{\displaystyle 1-a\,:}
∏
n
=
1
∞
(
(
1
−
q
n
)
(
1
−
a
q
n
)
(
1
−
a
−
1
q
n
)
)
=
∑
n
=
0
∞
(
−
1
)
n
1
a
n
1
−
a
2
n
+
1
1
−
a
q
n
(
n
+
1
)
2
{\displaystyle \prod _{n=1}^{\infty }\left((1-q^{n})(1-aq^{n})(1-a^{-1}q^{n})\right)=\sum _{n=0}^{\infty }(-1)^{n}\,{\frac {1}{a^{n}}}\,{\frac {1-a^{2n+1}}{1-a}}\,q^{\frac {n(n+1)}{2}}}
a
→
1
{\displaystyle a\to 1\,}
∏
n
=
1
∞
(
1
−
q
n
)
3
=
∑
n
=
0
∞
(
−
1
)
n
(
2
n
+
1
)
q
n
(
n
+
1
)
2
{\displaystyle \prod _{n=1}^{\infty }\left(1-q^{n}\right)^{3}=\sum _{n=0}^{\infty }(-1)^{n}\,(2n+1)\,q^{\frac {n(n+1)}{2}}}
∏
n
=
1
∞
(
1
−
q
n
)
=
∑
n
∈
Z
(
−
1
)
n
q
n
(
3
n
+
1
)
2
|
q
|
<
1
{\displaystyle \prod _{n=1}^{\infty }\left(1-q^{n}\right)=\sum _{n\in \mathbb {Z} }(-1)^{n}\,q^{\frac {n\,(3n+1)}{2}}\qquad |q|<1}
Beweis (Pentagonalzahlensatz)
∏
k
=
1
∞
(
1
+
z
k
)
=
∏
k
=
1
∞
(
1
−
z
2
k
−
1
)
−
1
|
z
|
<
1
{\displaystyle \prod _{k=1}^{\infty }(1+z^{k})=\prod _{k=1}^{\infty }(1-z^{2k-1})^{-1}\qquad |z|<1}
Beweis (Eulersche Identität)
Es sei
a
n
=
∏
k
=
1
n
(
1
−
z
k
)
{\displaystyle a_{n}=\prod _{k=1}^{n}(1-z^{k})}
a
2
n
{\displaystyle a_{2n}\,}
∏
k
=
1
n
(
1
−
z
2
k
)
∏
k
=
1
n
(
1
−
z
2
k
−
1
)
=
a
2
n
{\displaystyle \prod _{k=1}^{n}(1-z^{2k})\,\prod _{k=1}^{n}(1-z^{2k-1})=a_{2n}}
1
−
z
2
k
=
(
1
+
z
k
)
(
1
−
z
k
)
{\displaystyle 1-z^{2k}=(1+z^{k})(1-z^{k})\,}
∏
k
=
1
n
(
1
+
z
k
)
a
n
{\displaystyle \prod _{k=1}^{n}(1+z^{k})\,\,a_{n}}
a
n
{\displaystyle a_{n}\,}
∏
k
=
1
n
(
1
+
z
k
)
=
a
2
n
a
n
∏
k
=
1
n
(
1
−
z
2
k
−
1
)
−
1
{\displaystyle \prod _{k=1}^{n}(1+z^{k})={\frac {a_{2n}}{a_{n}}}\,\prod _{k=1}^{n}(1-z^{2k-1})^{-1}}
n
{\displaystyle n\,}
a
2
n
a
n
{\displaystyle {\frac {a_{2n}}{a_{n}}}}
1
{\displaystyle 1\,}
e
2
=
(
4
3
)
1
2
⋅
(
6
⋅
8
5
⋅
7
)
1
4
⋅
(
10
⋅
12
⋅
14
⋅
16
9
⋅
11
⋅
13
⋅
15
)
1
8
⋯
{\displaystyle {\frac {e}{2}}=\left({\frac {4}{3}}\right)^{\frac {1}{2}}\cdot \left({\frac {6\cdot 8}{5\cdot 7}}\right)^{\frac {1}{4}}\cdot \left({\frac {10\cdot 12\cdot 14\cdot 16}{9\cdot 11\cdot 13\cdot 15}}\right)^{\frac {1}{8}}\cdots }
Beweis (Catalansche Darstellung)
e
2
=
(
2
1
)
1
2
⋅
(
2
⋅
4
3
⋅
3
)
1
4
⋅
(
4
⋅
6
⋅
6
⋅
8
5
⋅
5
⋅
7
⋅
7
)
1
8
⋯
{\displaystyle {\frac {e}{2}}=\left({\frac {2}{1}}\right)^{\frac {1}{2}}\cdot \left({\frac {2\cdot 4}{3\cdot 3}}\right)^{\frac {1}{4}}\cdot \left({\frac {4\cdot 6\cdot 6\cdot 8}{5\cdot 5\cdot 7\cdot 7}}\right)^{\frac {1}{8}}\cdots }
Beweis (Pippenger Produkt)
sinc
z
=
∏
k
=
1
∞
cos
(
z
2
k
)
=
1
2
+
cos
z
2
⋅
1
2
+
1
2
1
2
+
cos
z
2
⋅
1
2
+
1
2
1
2
+
1
2
1
2
+
cos
z
2
⋯
{\displaystyle {\text{sinc}}\,z=\prod _{k=1}^{\infty }\cos \left({\frac {z}{2^{k}}}\right)={\sqrt {{\frac {1}{2}}+{\frac {\cos z}{2}}}}\cdot {\sqrt {{\frac {1}{2}}+{\frac {1}{2}}{\sqrt {{\frac {1}{2}}+{\frac {\cos z}{2}}}}}}\cdot {\sqrt {{\frac {1}{2}}+{\frac {1}{2}}{\sqrt {{\frac {1}{2}}+{\frac {1}{2}}{\sqrt {{\frac {1}{2}}+{\frac {\cos z}{2}}}}}}}}\cdots }
Beweis
sin
2
z
=
2
sin
z
cos
z
⇒
cos
z
=
sin
2
z
2
sin
z
=
sin
2
z
2
z
sin
z
z
=
sinc
2
z
sinc
z
⇒
cos
(
z
2
k
)
=
sinc
(
z
2
k
−
1
)
sinc
(
z
2
k
)
{\displaystyle \sin 2z=2\,\sin z\,\cos z\,\Rightarrow \,\cos z={\frac {\sin 2z}{2\,\sin z}}={\frac {\frac {\sin 2z}{2z}}{\frac {\sin z}{z}}}={\frac {{\text{sinc}}\,2z}{{\text{sinc}}\,z}}\,\Rightarrow \,\cos \left({\frac {z}{2^{k}}}\right)={{\text{sinc}}\left({\frac {z}{2^{k-1}}}\right) \over {\text{sinc}}\left({\frac {z}{2^{k}}}\right)}}
∏
k
=
1
n
cos
(
z
2
k
)
{\displaystyle \prod _{k=1}^{n}\cos \left({\frac {z}{2^{k}}}\right)}
∏
k
=
1
n
sinc
(
z
2
k
−
1
)
sinc
(
z
2
k
)
=
sinc
z
sinc
(
z
2
n
)
{\displaystyle \prod _{k=1}^{n}{{\text{sinc}}\left({\frac {z}{2^{k-1}}}\right) \over {\text{sinc}}\left({\frac {z}{2^{k}}}\right)}={\frac {{\text{sinc}}\,z}{{\text{sinc}}\left({\frac {z}{2^{n}}}\right)}}}
n
→
∞
{\displaystyle n\to \infty \,}
sinc
z
{\displaystyle {\text{sinc}}\,z}
2
π
=
1
2
⋅
1
2
+
1
2
1
2
⋅
1
2
+
1
2
1
2
+
1
2
1
2
⋯
=
2
2
⋅
2
+
2
2
⋅
2
+
2
+
2
2
⋯
{\displaystyle {\frac {2}{\pi }}={\sqrt {\frac {1}{2}}}\cdot {\sqrt {{\frac {1}{2}}+{\frac {1}{2}}{\sqrt {\frac {1}{2}}}}}\cdot {\sqrt {{\frac {1}{2}}+{\frac {1}{2}}{\sqrt {{\frac {1}{2}}+{\frac {1}{2}}{\sqrt {\frac {1}{2}}}}}}}\cdots ={\frac {\sqrt {2}}{2}}\cdot {\frac {\sqrt {2+{\sqrt {2}}}}{2}}\cdot {\frac {\sqrt {2+{\sqrt {2+{\sqrt {2}}}}}}{2}}\cdots }
Beweis (Vietasche Produktdarstellung)
sin
π
z
=
π
z
∏
k
=
1
∞
(
1
−
z
2
k
2
)
z
∈
C
{\displaystyle \sin \pi z=\pi z\,\prod _{k=1}^{\infty }\left(1-{\frac {z^{2}}{k^{2}}}\right)\qquad z\in \mathbb {C} }
Beweis für
|
z
|
<
1
{\displaystyle |z|<1\,}
sinh
π
z
=
π
z
∏
k
=
1
∞
(
1
+
z
2
k
2
)
z
∈
C
{\displaystyle \sinh \pi z=\pi z\,\prod _{k=1}^{\infty }\left(1+{\frac {z^{2}}{k^{2}}}\right)\qquad z\in \mathbb {C} }
cos
π
z
=
∏
k
=
1
∞
(
1
−
z
2
(
k
−
1
2
)
2
)
z
∈
C
{\displaystyle \cos \pi z=\prod _{k=1}^{\infty }\left(1-{\frac {z^{2}}{\left(k-{\frac {1}{2}}\right)^{2}}}\right)\qquad z\in \mathbb {C} }
cosh
π
z
=
∏
k
=
1
∞
(
1
+
z
2
(
k
−
1
2
)
2
)
z
∈
C
{\displaystyle \cosh \pi z=\prod _{k=1}^{\infty }\left(1+{\frac {z^{2}}{\left(k-{\frac {1}{2}}\right)^{2}}}\right)\qquad z\in \mathbb {C} }
∏
k
=
1
∞
(
1
−
z
n
k
n
)
=
[
∏
k
=
0
n
−
1
Γ
(
1
−
ξ
k
z
)
]
−
1
ξ
=
e
2
π
i
n
{\displaystyle \prod _{k=1}^{\infty }\left(1-{\frac {z^{n}}{k^{n}}}\right)=\left[\prod _{k=0}^{n-1}\Gamma (1-\xi ^{k}z)\right]^{-1}\qquad \xi =e^{\frac {2\pi i}{n}}}
Γ
(
z
)
=
1
z
∏
k
=
1
∞
(
1
+
1
k
)
z
1
+
z
k
z
∉
Z
≤
0
{\displaystyle \Gamma (z)={\frac {1}{z}}\,\prod _{k=1}^{\infty }{\frac {\left(1+{\frac {1}{k}}\right)^{z}}{1+{\frac {z}{k}}}}\qquad z\notin \mathbb {Z} _{\leq 0}}
Beweis (Eulersche Produktdarstellung)
Γ
(
z
)
=
1
z
e
−
γ
z
∏
k
=
1
∞
e
z
k
1
+
z
k
z
∉
Z
≤
0
{\displaystyle \Gamma (z)={\frac {1}{z}}\,e^{-\gamma z}\,\prod _{k=1}^{\infty }{\frac {e^{\frac {z}{k}}}{1+{\frac {z}{k}}}}\qquad z\notin \mathbb {Z} _{\leq 0}}
Beweis (Weierstraßsche Produktdarstellung)
∏
k
=
1
∞
[
1
π
Γ
(
1
2
+
z
2
k
)
]
=
2
−
2
z
Γ
(
1
+
z
)
z
∉
Z
<
0
{\displaystyle \prod _{k=1}^{\infty }\left[{\frac {1}{\sqrt {\pi }}}\,\Gamma \left({\frac {1}{2}}+{\frac {z}{2^{k}}}\right)\right]=2^{-2z}\,\Gamma (1+z)\qquad z\notin \mathbb {Z} _{<0}}
∏
k
=
0
∞
[
(
1
+
y
k
+
x
)
e
−
y
k
+
x
]
=
Γ
(
x
)
e
y
ψ
(
x
)
Γ
(
x
+
y
)
{\displaystyle \prod _{k=0}^{\infty }\left[\left(1+{\frac {y}{k+x}}\right)e^{-{\frac {y}{k+x}}}\right]={\frac {\Gamma (x)\,e^{y\,\psi (x)}}{\Gamma (x+y)}}}
Beweis (Mellinsche Formel)
Γ
(
x
)
|
Γ
(
x
+
i
y
)
|
=
∏
k
=
0
∞
1
+
(
y
x
+
k
)
2
{\displaystyle {\frac {\Gamma (x)}{|\Gamma (x+iy)|}}=\prod _{k=0}^{\infty }{\sqrt {1+\left({\frac {y}{x+k}}\right)^{2}}}}
∏
k
=
0
∞
(
1
+
(
−
1
)
k
a
k
+
b
)
=
Γ
(
b
2
a
)
Γ
(
a
+
b
2
a
)
Γ
(
b
+
1
2
a
)
Γ
(
a
+
b
−
1
2
a
)
a
∈
C
∖
{
0
}
,
b
a
∈
C
∖
Z
≤
0
{\displaystyle \prod _{k=0}^{\infty }\left(1+{\frac {(-1)^{k}}{ak+b}}\right)={\frac {\Gamma \!\left({\frac {b}{2a}}\right)\,\Gamma \!\left({\frac {a+b}{2a}}\right)}{\Gamma \!\left({\frac {b+1}{2a}}\right)\,\Gamma \!\left({\frac {a+b-1}{2a}}\right)}}\qquad a\in \mathbb {C} \setminus \{0\}\quad ,\quad {\frac {b}{a}}\in \mathbb {C} \setminus \mathbb {Z} ^{\leq 0}}
∏
k
=
1
∞
1
−
e
−
2
π
k
z
1
−
e
−
2
π
k
/
z
=
e
π
12
(
z
−
1
z
)
z
Re
(
z
)
>
0
{\displaystyle \prod _{k=1}^{\infty }{\frac {1-e^{-2\pi kz}}{1-e^{-2\pi k/z}}}={\frac {e^{{\frac {\pi }{12}}\left(z-{\frac {1}{z}}\right)}}{\sqrt {z}}}\qquad {\text{Re}}(z)>0}
∏
n
=
0
∞
(
∏
k
=
0
n
(
k
+
1
)
(
−
1
)
k
+
1
(
n
k
)
)
n
⋅
(
n
+
1
)
2
n
+
3
=
e
7
ζ
(
3
)
24
ζ
(
2
)
{\displaystyle \prod _{n=0}^{\infty }\left(\prod _{k=0}^{n}(k+1)^{(-1)^{k+1}\,{n \choose k}}\right)^{\frac {n\cdot (n+1)}{2^{n+3}}}=e^{\frac {7\,\zeta (3)}{24\,\zeta (2)}}}
Beweis
η
(
s
)
=
∑
k
=
1
∞
(
−
1
)
k
−
1
k
s
{\displaystyle \eta (s)=\sum _{k=1}^{\infty }{\frac {(-1)^{k-1}}{k^{s}}}}
η
′
(
s
)
=
∑
k
=
1
∞
(
−
1
)
k
k
s
log
k
{\displaystyle \eta '(s)=\sum _{k=1}^{\infty }{\frac {(-1)^{k}}{k^{s}}}\,\log k}
S
:=
∑
k
=
1
∞
(
−
1
)
k
k
2
log
k
{\displaystyle S:=\sum _{k=1}^{\infty }(-1)^{k}\,k^{2}\,\log k}
η
′
(
−
2
)
=
7
ζ
(
3
)
24
ζ
(
2
)
{\displaystyle \eta '(-2)={\frac {7\,\zeta (3)}{24\,\zeta (2)}}}
S
=
∑
k
=
0
∞
(
−
1
)
k
+
1
(
k
+
1
)
2
log
(
k
+
1
)
{\displaystyle S=\sum _{k=0}^{\infty }(-1)^{k+1}\,(k+1)^{2}\,\log(k+1)}
(
k
+
1
)
2
=
∑
n
≥
k
(
n
k
)
n
⋅
(
n
+
1
)
2
n
+
3
{\displaystyle (k+1)^{2}=\sum _{n\geq k}{n \choose k}{\frac {n\cdot (n+1)}{2^{n+3}}}}
S
=
∑
n
=
0
∞
∑
k
=
0
n
(
−
1
)
k
+
1
(
n
k
)
log
(
k
+
1
)
⋅
n
⋅
(
n
+
1
)
2
n
+
3
{\displaystyle S=\sum _{n=0}^{\infty }\sum _{k=0}^{n}(-1)^{k+1}{n \choose k}\,\log(k+1)\cdot {\frac {n\cdot (n+1)}{2^{n+3}}}}
exp
{\displaystyle {\text{exp}}}
Zurück zu Formelsammlung Mathematik Formelsammlung Mathematik: Analysis
…Funktionen
Integrale der Form
R(x) ,
R(x,exp) ,
R(x,log) ,
R(x,sin) ,
R(x,cos) ,
R(x,tan) ,
R(x,sec) ,
R(x,sinh) ,
R(x,cosh) ,
R(x,arcsin) ,
R(x,arctan) ,
R(x,arccot) ,
R(x,Gamma) ,
R(x,BesselJ) ,
R(x,Ci) ,
R(x,LambertW) ,
R(x,exp,sin) ,
R(x,exp,cos) ,
R(x,exp,arctan) ,
R(x,exp,Gamma) ,
R(x,exp,erf) ,
R(x,log,sin) ,
R(x,log,cos) ,
R(x,log,tan) ,
R(x,log,cosh) ,
R(x,log,artanh) ,
R(x,log,Gamma) ,
R(x,sin,cos) ,
R(x,sin,tan) ,
R(x,sin,sinh) ,
R(x,sin,cosh) ,
R(x,sin,tanh) ,
R(x,sin,coth) ,
R(x,sin,BesselJ) ,
R(x,cos,cosh) ,
R(x,cos,arccos) ,
R(x,cos,BesselJ) ,
R(x,sinh,cosh) ,
R(x,exp,sin,cos) ,
R(x,exp,cosh,arctan) ,
R(x,log,sin,Gamma) ,
R(x,log,cos,Gamma) ,
R(x,sin,cos,cosh) ,
R(x,cos,sinh,cosh) ,
R(x,exp,sin,cot,coth)
Allgemeine Integralformeln
Mehrfachintegrale
Zurück zur Formelsammlung Mathematik
F
(
s
)
=
F
[
f
(
t
)
]
(
s
)
=
1
2
π
∫
−
∞
∞
f
(
t
)
e
−
i
s
t
d
t
{\displaystyle F(s)={\mathcal {F}}[f(t)](s)={\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{\infty }f(t)e^{-ist}\,dt}
ohne Beweis (Fourier-Transformation)
f
(
t
)
=
F
−
1
[
F
(
s
)
]
(
t
)
=
1
2
π
∫
−
∞
∞
F
(
s
)
e
i
s
t
d
s
{\displaystyle f(t)={\mathcal {F}}^{-1}[F(s)](t)={\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{\infty }F(s)e^{ist}\,ds}
ohne Beweis (Rücktransformation)
F
[
(
f
∗
g
)
(
t
)
]
(
s
)
=
2
π
⋅
F
[
f
(
t
)
]
(
s
)
⋅
F
[
g
(
t
)
]
(
s
)
{\displaystyle {\mathcal {F}}[(f*g)(t)](s)={\sqrt {2\pi }}\cdot {\mathcal {F}}[f(t)](s)\cdot {\mathcal {F}}[g(t)](s)}
Beweis (Faltung)
F
[
(
f
∗
g
)
(
t
)
]
(
s
)
=
1
2
π
∫
−
∞
∞
∫
−
∞
∞
f
(
u
)
g
(
t
−
u
)
d
u
e
−
i
s
t
d
t
{\displaystyle {\mathcal {F}}[(f*g)(t)](s)={\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }f(u)\,g(t-u)\,du\,\,e^{-ist}\,dt}
=
1
2
π
∫
−
∞
∞
∫
−
∞
∞
f
(
u
)
e
−
i
s
u
g
(
t
−
u
)
e
−
i
s
(
t
−
u
)
d
t
d
u
{\displaystyle ={\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }f(u)\,e^{-isu}\,g(t-u)\,e^{-is(t-u)}\,dt\,du}
=
1
2
π
∫
−
∞
∞
∫
−
∞
∞
f
(
u
)
e
−
i
s
u
g
(
v
)
e
−
i
s
v
d
v
d
u
{\displaystyle ={\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }f(u)\,e^{-isu}\,g(v)\,e^{-isv}\,dv\,du}
=
1
2
π
∫
−
∞
∞
f
(
u
)
e
−
i
s
u
d
u
⋅
∫
−
∞
∞
g
(
v
)
e
−
i
s
v
d
v
=
2
π
⋅
F
[
f
(
t
)
]
(
s
)
⋅
F
[
g
(
t
)
]
(
s
)
{\displaystyle ={\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{\infty }f(u)\,e^{-isu}\,du\cdot \int _{-\infty }^{\infty }g(v)\,e^{-isv}\,dv={\sqrt {2\pi }}\cdot {\mathcal {F}}[f(t)](s)\cdot {\mathcal {F}}[g(t)](s)}
F
(
s
)
=
L
[
f
(
t
)
]
(
s
)
=
∫
0
∞
f
(
t
)
e
−
s
t
d
t
{\displaystyle F(s)={\mathcal {L}}[f(t)](s)=\int _{0}^{\infty }f(t)e^{-st}\,dt}
ohne Beweis (Laplace-Transformation)
f
(
t
)
=
L
−
1
[
F
(
s
)
]
(
t
)
=
1
2
π
i
∫
a
−
i
∞
a
+
i
∞
F
(
s
)
e
s
t
d
s
{\displaystyle f(t)={\mathcal {L}}^{-1}[F(s)](t)={\frac {1}{2\pi i}}\int _{a-i\infty }^{a+i\infty }F(s)e^{st}\,ds}
Beweis (Rücktransformation, Bromwich-Integral)
Im Folgenden sei
f
(
t
)
=
0
{\displaystyle f(t)=0\,}
t
<
0
{\displaystyle t<0\,}
f
(
t
)
e
−
a
t
=
F
−
1
[
F
[
f
(
τ
)
e
−
a
τ
]
(
ω
)
]
(
t
)
{\displaystyle f(t)e^{-at}={\mathcal {F}}^{-1}\left[{\mathcal {F}}[f(\tau )\,e^{-a\tau }](\omega )\right](t)}
=
1
2
π
∫
−
∞
∞
∫
−
∞
∞
f
(
τ
)
e
−
a
τ
e
−
i
ω
τ
d
τ
e
i
ω
t
d
ω
{\displaystyle ={\frac {1}{2\pi }}\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }f(\tau )\,e^{-a\tau }\,e^{-i\omega \tau }\,d\tau \,e^{i\omega t}\,d\omega }
⇒
f
(
t
)
=
1
2
π
∫
−
∞
∞
∫
0
∞
f
(
τ
)
e
−
(
a
+
i
ω
)
τ
d
τ
e
(
a
+
i
ω
)
t
d
ω
{\displaystyle \Rightarrow f(t)={\frac {1}{2\pi }}\int _{-\infty }^{\infty }\int _{0}^{\infty }f(\tau )\,e^{-(a+i\omega )\tau }\,d\tau \,e^{(a+i\omega )t}d\omega }
s
=
a
+
i
ω
(
d
s
=
i
d
ω
)
{\displaystyle s=a+i\omega \,\,(ds=i\,d\omega )}
f
(
t
)
=
1
2
π
i
∫
a
−
i
∞
a
+
i
∞
∫
0
∞
f
(
τ
)
e
−
s
τ
d
τ
⏟
F
(
s
)
e
s
t
d
s
{\displaystyle f(t)={\frac {1}{2\pi i}}\int _{a-i\infty }^{a+i\infty }\underbrace {\int _{0}^{\infty }f(\tau )e^{-s\tau }\,d\tau } _{F(s)}\,e^{st}\,ds}
L
[
(
f
∗
g
)
(
t
)
]
(
s
)
=
F
(
s
)
⋅
G
(
s
)
{\displaystyle {\mathcal {L}}[(f*g)(t)](s)=F(s)\cdot G(s)}
Beweis (Faltung)
F
(
s
)
⋅
G
(
s
)
=
∫
0
∞
f
(
σ
)
e
−
s
σ
d
σ
⋅
∫
0
∞
g
(
τ
)
e
−
s
τ
d
τ
=
∫
0
∞
∫
0
∞
f
(
σ
)
e
−
s
(
σ
+
τ
)
d
σ
g
(
τ
)
d
τ
{\displaystyle F(s)\cdot G(s)=\int _{0}^{\infty }f(\sigma )\,e^{-s\sigma }\,d\sigma \cdot \int _{0}^{\infty }g(\tau )\,e^{-s\tau }\,d\tau =\int _{0}^{\infty }\int _{0}^{\infty }f(\sigma )\,e^{-s(\sigma +\tau )}\,d\sigma \,g(\tau )\,d\tau }
t
=
σ
+
τ
(
d
t
=
d
σ
)
{\displaystyle t=\sigma +\tau \,(dt=d\sigma )}
∫
0
∞
∫
τ
∞
f
(
t
−
τ
)
e
−
s
t
d
t
g
(
τ
)
d
τ
{\displaystyle \int _{0}^{\infty }\int _{\tau }^{\infty }f(t-\tau )\,e^{-st}\,dt\,g(\tau )\,d\tau }
∫
0
∞
∫
0
t
f
(
t
−
τ
)
g
(
τ
)
d
τ
e
−
s
t
d
t
=
∫
0
∞
(
f
∗
g
)
(
t
)
e
−
s
t
d
t
=
L
[
(
f
∗
g
)
(
t
)
]
(
s
)
{\displaystyle \int _{0}^{\infty }\int _{0}^{t}f(t-\tau )\,g(\tau )\,d\tau \,e^{-st}\,dt=\int _{0}^{\infty }(f*g)(t)\,e^{-st}\,dt={\mathcal {L}}[(f*g)(t)](s)}
F
(
s
)
=
M
[
f
(
t
)
]
(
s
)
=
∫
0
∞
f
(
t
)
t
s
−
1
d
t
{\displaystyle F(s)={\mathcal {M}}[f(t)](s)=\int _{0}^{\infty }f(t)\,t^{s-1}\,dt}
ohne Beweis (Mellin-Transformation)
f
(
t
)
=
M
−
1
[
F
(
s
)
]
(
t
)
=
1
2
π
i
∫
a
−
i
∞
a
+
i
∞
F
(
s
)
t
−
s
d
s
{\displaystyle f(t)={\mathcal {M}}^{-1}[F(s)](t)={\frac {1}{2\pi i}}\int _{a-i\infty }^{a+i\infty }F(s)\,t^{-s}\,ds}
Beweis (Rücktransformation)
f
(
e
t
)
e
a
t
=
F
[
F
−
1
[
f
(
e
τ
)
e
a
τ
]
(
ω
)
]
(
t
)
{\displaystyle f(e^{t})\,e^{at}={\mathcal {F}}\left[{\mathcal {F}}^{-1}[f(e^{\tau })\,e^{a\tau }](\omega )\right](t)}
=
1
2
π
∫
−
∞
∞
∫
−
∞
∞
f
(
e
τ
)
e
a
τ
e
i
ω
τ
d
τ
e
−
i
ω
t
d
ω
{\displaystyle ={\frac {1}{2\pi }}\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }f(e^{\tau })\,e^{a\tau }\,e^{i\omega \tau }\,d\tau \,e^{-i\omega t}\,d\omega }
⇒
f
(
e
t
)
=
1
2
π
∫
−
∞
∞
∫
−
∞
∞
f
(
e
τ
)
e
(
a
+
i
ω
)
τ
d
τ
e
−
(
a
+
i
ω
)
t
d
ω
{\displaystyle \Rightarrow f(e^{t})={\frac {1}{2\pi }}\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }f(e^{\tau })\,e^{(a+i\omega )\tau }\,d\tau \,e^{-(a+i\omega )t}\,d\omega }
s
=
a
+
i
ω
(
d
s
=
i
d
ω
)
{\displaystyle s=a+i\omega \,\,(ds=i\,d\omega )}
f
(
e
t
)
=
1
2
π
i
∫
a
−
i
∞
a
+
i
∞
∫
−
∞
∞
f
(
e
τ
)
e
s
τ
d
τ
e
−
s
t
d
s
{\displaystyle f(e^{t})={\frac {1}{2\pi i}}\int _{a-i\infty }^{a+i\infty }\int _{-\infty }^{\infty }f(e^{\tau })\,e^{s\tau }\,d\tau \,e^{-st}\,ds}
u
=
e
τ
{\displaystyle u=e^{\tau }\,}
f
(
e
t
)
=
1
2
π
i
∫
a
−
i
∞
a
+
i
∞
∫
0
∞
f
(
u
)
u
s
−
1
d
u
⏟
F
(
s
)
e
−
s
t
d
s
{\displaystyle f(e^{t})={\frac {1}{2\pi i}}\int _{a-i\infty }^{a+i\infty }\underbrace {\int _{0}^{\infty }f(u)\,u^{s-1}\,du} _{F(s)}\,e^{-st}\,ds}
e
t
{\displaystyle e^{t}\,}
t
{\displaystyle t\,}
M
[
(
f
∗
g
)
(
t
)
]
(
s
)
=
F
(
s
)
⋅
G
(
s
)
{\displaystyle {\mathcal {M}}\left[(f*g)(t)\right](s)=F(s)\cdot G(s)}
Beweis (Faltung)
M
[
(
f
∗
g
)
(
t
)
]
(
s
)
=
∫
0
∞
∫
0
∞
f
(
t
u
)
g
(
u
)
d
u
u
⋅
t
s
−
1
d
t
{\displaystyle {\mathcal {M}}\left[(f*g)(t)\right](s)=\int _{0}^{\infty }\int _{0}^{\infty }f\left({\frac {t}{u}}\right)g(u)\,{\frac {du}{u}}\cdot t^{s-1}\,dt}
=
∫
0
∞
∫
0
∞
f
(
t
u
)
t
s
−
1
d
t
⋅
g
(
u
)
d
u
u
=
∫
0
∞
∫
0
∞
f
(
t
)
(
u
t
)
s
−
1
u
d
t
⋅
g
(
u
)
d
u
u
{\displaystyle =\int _{0}^{\infty }\int _{0}^{\infty }f\left({\frac {t}{u}}\right)t^{s-1}\,dt\cdot g(u)\,{\frac {du}{u}}=\int _{0}^{\infty }\int _{0}^{\infty }f(t)\,(ut)^{s-1}\,u\,dt\cdot g(u)\,{\frac {du}{u}}}
=
∫
0
∞
∫
0
∞
f
(
t
)
t
s
−
1
d
t
⋅
g
(
u
)
u
s
−
1
d
u
=
F
(
s
)
⋅
G
(
s
)
{\displaystyle =\int _{0}^{\infty }\int _{0}^{\infty }f(t)\,t^{s-1}\,dt\cdot g(u)\,u^{s-1}\,du=F(s)\cdot G(s)}
y
′
+
P
(
x
)
y
=
Q
(
x
)
{\displaystyle y'+P(x)\,y=Q(x)\,}
Lösung
Bestimme erst eine Lösung
y
h
{\displaystyle y_{h}\,}
y
′
+
P
(
x
)
y
=
0
{\displaystyle y'+P(x)y=0}
y
′
=
−
P
(
x
)
y
⇒
y
′
y
=
−
P
(
x
)
⇒
log
y
=
−
∫
P
(
x
)
d
x
⇒
y
=
e
−
∫
P
(
x
)
d
x
{\displaystyle y'=-P(x)y\,\Rightarrow \,{\frac {y'}{y}}=-P(x)\,\Rightarrow \,\log y=-\int P(x)\,dx\,\Rightarrow \,y=e^{-\int P(x)\,dx}}
μ
=
e
∫
P
(
x
)
d
x
{\displaystyle \mu =e^{\int P(x)\,dx}}
y
h
=
1
μ
{\displaystyle y_{h}={\frac {1}{\mu }}}
y
′
+
P
(
x
)
y
=
Q
(
x
)
{\displaystyle y'+P(x)\,y=Q(x)}
y
=
c
⋅
y
h
{\displaystyle y=c\cdot y_{h}}
Q
(
x
)
=
y
′
+
P
(
x
)
y
=
c
′
⋅
y
h
+
c
⋅
y
h
′
+
P
(
x
)
⋅
c
⋅
y
h
⏟
=
0
{\displaystyle Q(x)=y'+P(x)\,y=c'\cdot y_{h}+\underbrace {c\cdot y_{h}'+P(x)\cdot c\cdot y_{h}} _{=0}}
⇒
c
′
=
1
y
h
⋅
Q
(
x
)
=
μ
⋅
Q
(
x
)
⇒
c
=
∫
μ
⋅
Q
(
x
)
d
x
{\displaystyle \Rightarrow \,c'={\frac {1}{y_{h}}}\cdot Q(x)=\mu \cdot Q(x)\,\Rightarrow \,c=\int \mu \cdot Q(x)\,dx}
y
=
1
μ
∫
μ
⋅
Q
(
x
)
d
x
=
e
−
∫
P
(
x
)
d
x
∫
e
∫
P
(
x
)
d
x
Q
(
x
)
d
x
{\displaystyle y={\frac {1}{\mu }}\,\int \mu \cdot Q(x)\,dx=e^{-\int P(x)\,dx}\,\int e^{\int P(x)\,dx}\,Q(x)\,dx}
x
2
y
″
+
x
y
′
+
(
x
2
−
n
2
)
y
=
0
{\displaystyle x^{2}\,y''+x\,y'+(x^{2}-n^{2})\,y=0}
(
1
−
x
2
)
y
″
−
2
x
y
′
+
n
(
n
+
1
)
y
=
0
{\displaystyle (1-x^{2})\,y''-2xy'+n(n+1)\,y=0}
x
(
1
−
x
)
y
″
+
(
γ
−
(
α
+
β
+
1
)
x
)
y
′
−
α
β
y
=
0
{\displaystyle x\,(1-x)\,y''+\left(\gamma -(\alpha +\beta +1)x\right)\,y'-\alpha \beta \,y=0}
x
y
″
+
(
α
+
1
−
x
)
y
′
+
n
y
=
0
{\displaystyle x\,y''+(\alpha +1-x)\,y'+n\,y=0}
y
″
−
x
y
′
+
n
y
=
0
{\displaystyle y''-x\,y'+n\,y=0}
(
1
−
x
2
)
y
″
−
x
y
′
+
n
2
y
=
0
{\displaystyle (1-x^{2})\,y''-x\,y'+n^{2}\,y=0}
y
″
−
λ
x
y
=
0
{\displaystyle y''-\lambda \,x\,y=0}
Homogene lineare Dgl. mit konstanten Koeffizienten [ Bearbeiten ]
∑
k
=
0
n
a
k
y
(
k
)
=
0
,
a
k
∈
C
{\displaystyle \sum _{k=0}^{n}a_{k}\,y^{(k)}=0\quad ,\quad a_{k}\in \mathbb {C} }
Lösung
Die Funktion
y
=
e
λ
x
{\displaystyle y=e^{\lambda x}}
λ
{\displaystyle \lambda }
P
(
λ
)
=
∑
k
=
0
n
a
k
λ
k
{\displaystyle P(\lambda )=\sum _{k=0}^{n}a_{k}\,\lambda ^{k}}
λ
{\displaystyle \lambda \,}
ν
{\displaystyle \nu }
y
=
x
m
e
λ
x
{\displaystyle y=x^{m}\,e^{\lambda x}}
m
=
0
,
.
.
.
,
ν
−
1
{\displaystyle m=0,...,\nu -1}
D
k
(
x
m
e
λ
x
)
=
∑
j
=
0
k
(
k
j
)
D
j
x
m
D
k
−
j
e
λ
x
{\displaystyle D^{k}\left(x^{m}\,e^{\lambda x}\right)=\sum _{j=0}^{k}{k \choose j}\,\,D^{j}\,x^{m}\,\,D^{k-j}\,e^{\lambda x}}
D
j
x
m
{\displaystyle D^{j}\,x^{m}}
j
>
m
{\displaystyle j>m}
D
k
(
x
m
e
λ
x
)
=
∑
k
=
0
min
(
k
,
m
)
k
!
(
k
−
j
)
!
j
!
m
!
(
m
−
j
)
!
x
m
−
j
λ
k
−
j
e
λ
x
{\displaystyle D^{k}\left(x^{m}\,e^{\lambda x}\right)=\sum _{k=0}^{{\text{min}}(k,m)}{\frac {k!}{(k-j)!\,j!}}\,{\frac {m!}{(m-j)!}}\,x^{m-j}\,\lambda ^{k-j}\,e^{\lambda x}}
∑
k
=
0
n
a
k
D
k
(
x
m
e
λ
x
)
=
∑
k
=
0
n
a
k
∑
j
=
0
min
(
k
,
m
)
(
m
j
)
k
!
(
k
−
j
)
!
λ
k
−
j
x
m
−
j
e
λ
x
{\displaystyle \sum _{k=0}^{n}a_{k}\,D^{k}\left(x^{m}e^{\lambda x}\right)=\sum _{k=0}^{n}a_{k}\,\sum _{j=0}^{{\text{min}}(k,m)}{m \choose j}\,{\frac {k!}{(k-j)!}}\,\lambda ^{k-j}\,x^{m-j}\,e^{\lambda x}}
=
∑
j
=
0
m
∑
k
=
j
n
a
k
(
m
j
)
k
!
(
k
−
j
)
!
λ
k
−
j
x
m
−
j
e
λ
x
=
∑
j
=
0
m
(
m
j
)
[
∑
k
=
j
n
a
k
k
!
(
k
−
j
)
!
λ
k
−
j
]
x
m
−
j
e
λ
x
{\displaystyle =\sum _{j=0}^{m}\sum _{k=j}^{n}a_{k}\,{m \choose j}\,{\frac {k!}{(k-j)!}}\,\lambda ^{k-j}\,x^{m-j}\,e^{\lambda x}=\sum _{j=0}^{m}{m \choose j}\,\left[\sum _{k=j}^{n}a_{k}\,{\frac {k!}{(k-j)!}}\,\lambda ^{k-j}\right]\,x^{m-j}\,e^{\lambda x}}
=
∑
j
=
0
m
(
m
j
)
P
(
j
)
(
λ
)
x
m
−
j
e
λ
x
=
0
{\displaystyle =\sum _{j=0}^{m}{m \choose j}\,P^{(j)}(\lambda )\,x^{m-j}\,e^{\lambda x}=0}
P
{\displaystyle P\,}
λ
1
,
.
.
.
,
λ
r
{\displaystyle \lambda _{1},...,\lambda _{r}}
ν
1
,
.
.
.
,
ν
r
{\displaystyle \nu _{1},...,\nu _{r}}
y
=
∑
k
=
1
r
∑
ℓ
=
0
ν
k
−
1
c
k
,
ℓ
x
ℓ
e
λ
k
x
{\displaystyle y=\sum _{k=1}^{r}\sum _{\ell =0}^{\nu _{k}-1}c_{k,\ell }\,x^{\ell }\,e^{\lambda _{k}x}}
∑
k
=
0
n
a
k
(
c
x
+
d
)
k
y
(
k
)
=
F
(
x
)
{\displaystyle \sum _{k=0}^{n}a_{k}\,(c\,x+d)^{k}\,y^{(k)}=F(x)}
M
(
x
,
y
)
d
x
+
N
(
x
,
y
)
d
y
=
0
{\displaystyle M(x,y)\,dx+N(x,y)\,dy=0}
y
′
+
P
(
x
)
y
=
Q
(
x
)
y
n
(
n
≠
1
)
{\displaystyle y'+P(x)\,y=Q(x)\,y^{n}\qquad (n\neq 1)}
y
′
=
P
(
x
)
y
2
+
Q
(
x
)
y
+
R
(
x
)
{\displaystyle y'=P(x)\,y^{2}+Q(x)\,y+R(x)}
Lösung
Ist bereits eine partikuläre Lösung
y
p
{\displaystyle y_{p}\,}
[
y
′
=
P
(
x
)
y
2
+
Q
(
x
)
y
+
R
(
x
)
y
p
′
=
P
(
x
)
y
p
2
+
Q
(
x
)
y
p
+
R
(
x
)
]
{\displaystyle \left[{\begin{matrix}y'=P(x)\,y^{2}+Q(x)\,y+R(x)\\y'_{p}=P(x)\,y_{p}^{2}+Q(x)\,y_{p}+R(x)\end{matrix}}\right]}
y
′
−
y
p
′
=
P
(
x
)
(
y
2
−
y
p
2
)
+
Q
(
x
)
(
y
−
y
p
)
{\displaystyle y'-y'_{p}=P(x)\,(y^{2}-y_{p}^{2})+Q(x)\,(y-y_{p})}
u
=
y
−
y
p
{\displaystyle u=y-y_{p}}
y
2
−
y
p
2
=
(
y
+
y
p
)
(
y
−
y
p
)
=
(
u
+
2
y
p
)
u
{\displaystyle y^{2}-y_{p}^{2}=(y+y_{p})(y-y_{p})=(u+2y_{p})\,u}
u
′
=
P
(
x
)
(
u
+
2
y
p
)
u
+
Q
(
x
)
u
{\displaystyle u'=P(x)\,(u+2y_{p})\,u+Q(x)\,u}
⇒
u
′
=
P
(
x
)
u
2
+
(
2
y
p
P
(
x
)
+
Q
(
x
)
)
u
⇒
u
′
+
(
−
2
y
p
P
(
x
)
−
Q
(
x
)
)
u
=
P
(
x
)
u
2
{\displaystyle \Rightarrow \,u'=P(x)\,u^{2}+{\Big (}2y_{p}\,P(x)+Q(x){\Big )}\,u\,\Rightarrow \,u'+{\Big (}-2y_{p}P(x)-Q(x){\Big )}\,u=P(x)\,u^{2}}
Bernoullischen Dgl. zurückgeführt.
a
(
y
′
)
x
+
b
(
y
′
)
y
+
c
(
y
′
)
=
0
{\displaystyle a(y')\,x+b(y')\,y+c(y')=0}
y
=
x
y
′
+
f
(
y
′
)
=
0
{\displaystyle y=x\,y'+f(y')=0}
y
=
x
f
(
y
′
)
+
g
(
y
′
)
{\displaystyle y=x\,f(y')+g(y')}
exp
z
=
∑
k
=
0
∞
z
k
k
!
z
∈
C
{\displaystyle \exp z=\sum _{k=0}^{\infty }{\frac {z^{k}}{k!}}\qquad z\in \mathbb {C} }
ln
(
1
−
z
)
=
−
∑
k
=
1
∞
z
k
k
|
z
|
≤
1
,
z
≠
1
{\displaystyle \ln(1-z)=-\sum _{k=1}^{\infty }{\frac {z^{k}}{k}}\qquad |z|\leq 1\,,\,z\neq 1}
sin
z
=
∑
k
=
0
∞
(
−
1
)
k
z
2
k
+
1
(
2
k
+
1
)
!
z
∈
C
{\displaystyle \sin z=\sum _{k=0}^{\infty }(-1)^{k}{\frac {z^{2k+1}}{(2k+1)!}}\qquad z\in \mathbb {C} }
cos
z
=
∑
k
=
0
∞
(
−
1
)
k
z
2
k
(
2
k
)
!
z
∈
C
{\displaystyle \cos z=\sum _{k=0}^{\infty }(-1)^{k}{\frac {z^{2k}}{(2k)!}}\qquad z\in \mathbb {C} }
tan
z
=
∑
k
=
1
∞
(
−
1
)
k
B
2
k
2
2
k
(
1
−
2
2
k
)
(
2
k
)
!
z
2
k
−
1
=
∑
k
=
1
∞
2
⋅
λ
(
2
k
)
(
π
2
)
2
k
z
2
k
−
1
|
z
|
<
π
2
{\displaystyle \tan z=\sum _{k=1}^{\infty }(-1)^{k}\,{\frac {B_{2k}\,2^{2k}\,(1-2^{2k})}{(2k)!}}\,z^{2k-1}=\sum _{k=1}^{\infty }{\frac {2\cdot \lambda (2k)}{\left({\frac {\pi }{2}}\right)^{2k}}}\,z^{2k-1}\qquad |z|<{\frac {\pi }{2}}}
Beweis
Ersetzt man in der Reihenentwicklung
z
tanh
z
=
∑
k
=
1
∞
B
2
k
2
2
k
(
2
2
k
−
1
)
(
2
k
)
!
z
2
k
{\displaystyle z\tanh z=\sum _{k=1}^{\infty }{\frac {B_{2k}\,2^{2k}\,(2^{2k}-1)}{(2k)!}}\,z^{2k}}
z
{\displaystyle z\,}
i
z
{\displaystyle iz\,}
−
z
tan
z
=
∑
k
=
0
∞
(
−
1
)
k
B
2
k
2
2
k
(
2
2
k
−
1
)
(
2
k
)
!
z
2
k
{\displaystyle -z\tan z=\sum _{k=0}^{\infty }(-1)^{k}\,{\frac {B_{2k}\,2^{2k}\,(2^{2k}-1)}{(2k)!}}\,z^{2k}}
cot
z
=
∑
k
=
0
∞
(
−
1
)
k
B
2
k
(
2
2
k
−
1
)
(
2
k
)
!
z
2
k
−
1
=
∑
k
=
0
∞
−
2
ζ
(
2
k
)
π
2
k
z
2
k
−
1
0
<
|
z
|
<
π
{\displaystyle \cot z=\sum _{k=0}^{\infty }(-1)^{k}{\frac {B_{2k}\,(2^{2k}-1)}{(2k)!}}\,z^{2k-1}=\sum _{k=0}^{\infty }{\frac {-2\,\zeta (2k)}{\pi ^{2k}}}\,z^{2k-1}\qquad 0<|z|<\pi }
sec
z
=
∑
k
=
0
∞
|
E
k
|
z
k
k
!
=
∑
k
=
0
∞
2
⋅
β
(
2
k
+
1
)
(
π
2
)
2
k
+
1
z
2
k
|
z
|
<
π
2
{\displaystyle \sec z=\sum _{k=0}^{\infty }|E_{k}|\,{\frac {z^{k}}{k!}}=\sum _{k=0}^{\infty }{\frac {2\cdot \beta (2k+1)}{\left({\frac {\pi }{2}}\right)^{2k+1}}}\,z^{2k}\qquad |z|<{\frac {\pi }{2}}}
csc
z
=
∑
k
=
0
∞
(
−
1
)
k
(
2
−
2
2
k
)
B
2
k
(
2
k
)
!
z
2
k
−
1
=
∑
k
=
0
∞
2
⋅
η
(
2
k
)
π
2
k
z
2
k
−
1
0
<
|
z
|
<
π
{\displaystyle \csc z=\sum _{k=0}^{\infty }(-1)^{k}\,{\frac {(2-2^{2k})\,B_{2k}}{(2k)!}}\,z^{2k-1}=\sum _{k=0}^{\infty }{\frac {2\cdot \eta (2k)}{\pi ^{2k}}}\,z^{2k-1}\qquad 0<|z|<\pi }
Beweis
Ersetzt man in der Reihenentwicklung
z
csch
z
=
∑
k
=
0
∞
(
2
−
2
2
k
)
B
2
k
(
2
k
)
!
z
2
k
{\displaystyle z\,{\text{csch}}\,z=\sum _{k=0}^{\infty }{\frac {(2-2^{2k})\,B_{2k}}{(2k)!}}\,z^{2k}}
z
{\displaystyle z\,}
i
z
{\displaystyle iz\,}
z
csc
z
=
∑
k
=
0
∞
(
−
1
)
k
(
2
−
2
2
k
)
B
2
k
(
2
k
)
!
z
2
k
{\displaystyle z\csc z=\sum _{k=0}^{\infty }(-1)^{k}\,{\frac {(2-2^{2k})\,B_{2k}}{(2k)!}}\,z^{2k}}
sinh
z
=
∑
k
=
0
∞
z
2
k
+
1
(
2
k
+
1
)
!
z
∈
C
{\displaystyle \sinh z=\sum _{k=0}^{\infty }{\frac {z^{2k+1}}{(2k+1)!}}\qquad z\in \mathbb {C} }
cosh
z
=
∑
k
=
0
∞
z
2
k
(
2
k
)
!
z
∈
C
{\displaystyle \cosh z=\sum _{k=0}^{\infty }{\frac {z^{2k}}{(2k)!}}\qquad z\in \mathbb {C} }
tanh
z
=
∑
k
=
1
∞
B
2
k
2
2
k
(
2
2
k
−
1
)
(
2
k
)
!
z
2
k
−
1
|
z
|
<
π
2
{\displaystyle \tanh z=\sum _{k=1}^{\infty }{\frac {B_{2k}\,2^{2k}\,(2^{2k}-1)}{(2k)!}}\,z^{2k-1}\qquad |z|<{\frac {\pi }{2}}}
coth
z
=
∑
k
=
0
∞
B
2
k
2
2
k
(
2
k
)
!
z
2
k
−
1
0
<
|
z
|
<
π
{\displaystyle \coth z=\sum _{k=0}^{\infty }{\frac {B_{2k}\,2^{2k}}{(2k)!}}\,z^{2k-1}\qquad 0<|z|<\pi }
Beweis
Für
0
<
|
z
|
<
2
π
{\displaystyle 0<|z|<2\pi \,}
coth
z
2
=
e
z
2
+
e
−
z
2
e
z
2
−
e
−
z
2
=
e
z
+
1
e
z
−
1
=
1
+
2
e
z
−
1
{\displaystyle \coth {\frac {z}{2}}={\frac {e^{\frac {z}{2}}+e^{-{\frac {z}{2}}}}{e^{\frac {z}{2}}-e^{-{\frac {z}{2}}}}}={\frac {e^{z}+1}{e^{z}-1}}=1+{\frac {2}{e^{z}-1}}}
z
2
coth
z
2
=
z
2
+
z
e
z
−
1
{\displaystyle {\frac {z}{2}}\,\coth {\frac {z}{2}}={\frac {z}{2}}+{\frac {z}{e^{z}-1}}}
−
B
1
z
+
∑
k
=
0
∞
B
k
k
!
z
k
=
∑
k
=
0
∞
B
2
k
(
2
k
)
!
z
2
k
{\displaystyle -B_{1}z+\sum _{k=0}^{\infty }{\frac {B_{k}}{k!}}\,z^{k}=\sum _{k=0}^{\infty }{\frac {B_{2k}}{(2k)!}}\,z^{2k}}
z
{\displaystyle z\,}
2
z
{\displaystyle 2z\,}
z
coth
z
=
∑
k
=
0
∞
B
2
k
2
2
k
(
2
k
)
!
z
2
k
{\displaystyle z\,\coth z=\sum _{k=0}^{\infty }{\frac {B_{2k}\,2^{2k}}{(2k)!}}\,z^{2k}}
0
<
|
z
|
<
π
{\displaystyle 0<|z|<\pi \,}
sech
z
=
∑
k
=
0
∞
E
k
z
k
k
!
|
z
|
<
π
2
{\displaystyle {\text{sech}}\,z=\sum _{k=0}^{\infty }E_{k}\,{\frac {z^{k}}{k!}}\qquad |z|<{\frac {\pi }{2}}}
csch
z
=
∑
k
=
0
∞
(
2
−
2
2
k
)
B
2
k
(
2
k
)
!
z
2
k
−
1
0
<
|
z
|
<
π
{\displaystyle {\text{csch}}\,z=\sum _{k=0}^{\infty }{\frac {(2-2^{2k})\,B_{2k}}{(2k)!}}\,z^{2k-1}\qquad 0<|z|<\pi }
Beweis
Aus der Reihenentwicklung
z
coth
z
=
∑
k
=
0
∞
B
2
k
2
2
k
(
2
k
)
!
z
2
k
{\displaystyle z\coth z=\sum _{k=0}^{\infty }{\frac {B_{2k}\,2^{2k}}{(2k)!}}\,z^{2k}}
0
<
|
z
|
<
π
{\displaystyle 0<|z|<\pi \,}
z
csch
z
=
2
⋅
z
2
coth
z
2
−
z
coth
z
{\displaystyle z\,{\text{csch}}\,z=2\cdot {\frac {z}{2}}\coth {\frac {z}{2}}-z\coth z\,}
z
csch
z
=
∑
k
=
0
∞
(
2
−
2
2
k
)
B
2
k
(
2
k
)
!
z
2
k
{\displaystyle z\,{\text{csch}}\,z=\sum _{k=0}^{\infty }{\frac {(2-2^{2k})\,B_{2k}}{(2k)!}}\,z^{2k}}
arcsin
z
=
∑
k
=
0
∞
(
−
1
)
k
(
−
1
2
k
)
z
2
k
+
1
2
k
+
1
=
∑
k
=
0
∞
1
2
2
k
(
2
k
k
)
z
2
k
+
1
2
k
+
1
|
z
|
≤
1
{\displaystyle \arcsin z=\sum _{k=0}^{\infty }(-1)^{k}{-{\frac {1}{2}} \choose k}{\frac {z^{2k+1}}{2k+1}}=\sum _{k=0}^{\infty }{\frac {1}{2^{2k}}}{2k \choose k}{\frac {z^{2k+1}}{2k+1}}\qquad |z|\leq 1}
arcsin
z
1
−
z
2
=
∑
k
=
1
∞
(
2
z
)
2
k
−
1
k
(
2
k
k
)
|
z
|
<
1
{\displaystyle {\frac {\arcsin z}{\sqrt {1-z^{2}}}}=\sum _{k=1}^{\infty }{\frac {(2z)^{2k-1}}{k\,{2k \choose k}}}\qquad |z|<1}
1. Beweis
Aus
∫
0
π
2
sin
2
n
−
1
θ
d
θ
=
2
2
n
−
1
n
(
2
n
n
)
{\displaystyle \int _{0}^{\frac {\pi }{2}}\sin ^{2n-1}\theta \,d\theta ={\frac {2^{2n-1}}{n\,{2n \choose n}}}}
∫
0
π
2
(
z
sin
θ
)
2
n
−
1
d
θ
=
(
2
z
)
2
n
−
1
n
(
2
n
n
)
{\displaystyle \int _{0}^{\frac {\pi }{2}}(z\,\sin \theta )^{2n-1}\,d\theta ={\frac {(2z)^{2n-1}}{n\,{2n \choose n}}}}
∑
n
=
1
∞
(
2
z
)
2
n
−
1
n
(
2
n
n
)
=
∫
0
π
2
z
sin
θ
1
−
(
z
sin
θ
)
2
d
θ
=
[
−
arctan
(
z
cos
θ
1
−
z
2
)
1
−
z
2
]
0
π
2
=
arctan
(
z
1
−
z
2
)
1
−
z
2
=
arcsin
z
1
−
z
2
{\displaystyle \sum _{n=1}^{\infty }{\frac {(2z)^{2n-1}}{n\,{2n \choose n}}}=\int _{0}^{\frac {\pi }{2}}{\frac {z\,\sin \theta }{1-(z\,\sin \theta )^{2}}}\,d\theta =\left[-{\frac {\arctan \left({\frac {z\,\cos \theta }{\sqrt {1-z^{2}}}}\right)}{\sqrt {1-z^{2}}}}\right]_{0}^{\frac {\pi }{2}}={\frac {\arctan \left({\frac {z}{\sqrt {1-z^{2}}}}\right)}{\sqrt {1-z^{2}}}}={\frac {\arcsin z}{\sqrt {1-z^{2}}}}}
2. Beweis
Die analytische Funktion
y
:
B
1
(
0
)
→
C
,
x
↦
arcsin
x
1
−
x
2
{\displaystyle y:B_{1}(0)\to \mathbb {C} \;,\;x\mapsto {\frac {\arcsin x}{\sqrt {1-x^{2}}}}}
∑
n
=
1
∞
a
n
x
2
n
−
1
{\displaystyle \sum _{n=1}^{\infty }a_{n}\,x^{2n-1}}
y
′
=
1
−
x
2
1
1
−
x
2
−
arcsin
x
1
2
1
−
x
2
(
−
2
x
)
1
−
x
2
{\displaystyle y'={\frac {{\sqrt {1-x^{2}}}\,{\frac {1}{\sqrt {1-x^{2}}}}-\arcsin x\,{\frac {1}{2{\sqrt {1-x^{2}}}}}\,(-2x)}{1-x^{2}}}}
(
1
−
x
2
)
y
′
=
1
+
x
y
{\displaystyle (1-x^{2})\,y'=1+xy}
y
{\displaystyle y\,}
a
n
{\displaystyle a_{n}\,}
y
′
=
∑
n
=
1
∞
(
2
n
−
1
)
a
n
x
2
n
−
2
{\displaystyle y'=\sum _{n=1}^{\infty }(2n-1)\,a_{n}\,x^{2n-2}}
x
2
y
′
=
∑
n
=
1
∞
(
2
n
−
1
)
a
n
x
2
n
{\displaystyle x^{2}y'=\sum _{n=1}^{\infty }(2n-1)\,a_{n}\,x^{2n}}
y
′
=
a
1
+
∑
n
=
2
∞
(
2
n
−
1
)
a
n
x
2
n
−
2
{\displaystyle y'=a_{1}+\sum _{n=2}^{\infty }(2n-1)\,a_{n}\,x^{2n-2}}
y
′
=
a
1
+
∑
n
=
1
∞
(
2
n
+
1
)
a
n
+
1
x
2
n
{\displaystyle y'=a_{1}+\sum _{n=1}^{\infty }(2n+1)\,a_{n+1}\,x^{2n}}
(
1
−
x
2
)
y
′
=
a
1
+
∑
n
=
1
∞
(
(
2
n
+
1
)
a
n
+
1
−
(
2
n
−
1
)
a
n
)
x
2
n
{\displaystyle (1-x^{2})y'=a_{1}+\sum _{n=1}^{\infty }{\Big (}(2n+1)\,a_{n+1}-(2n-1)\,a_{n}{\Big )}x^{2n}}
1
+
∑
n
=
1
∞
a
n
x
2
n
{\displaystyle 1+\sum _{n=1}^{\infty }a_{n}x^{2n}}
a
n
=
1
{\displaystyle a_{n}=1\,}
(
2
n
+
1
)
a
n
+
1
=
2
n
a
n
{\displaystyle (2n+1)\,a_{n+1}=2n\,a_{n}\,}
a
n
+
1
a
n
=
2
n
2
n
+
1
{\displaystyle {\frac {a_{n+1}}{a_{n}}}={\frac {2n}{2n+1}}}
a
n
{\displaystyle a_{n}\,}
∏
k
=
1
n
−
1
2
k
2
k
+
1
{\displaystyle \prod _{k=1}^{n-1}{\frac {2k}{2k+1}}}
2
2
n
2
n
(
2
n
n
)
{\displaystyle {\frac {2^{2n}}{2n\,{2n \choose n}}}}
arcsin
x
1
−
x
2
=
∑
n
=
1
∞
2
2
n
2
n
(
2
n
n
)
x
2
n
−
1
{\displaystyle {\frac {\arcsin x}{\sqrt {1-x^{2}}}}=\sum _{n=1}^{\infty }{\frac {2^{2n}}{2n\,{2n \choose n}}}\,x^{2n-1}}
arcsin
2
z
=
1
2
∑
k
=
1
∞
(
2
z
)
2
k
k
2
(
2
k
k
)
|
z
|
≤
1
{\displaystyle \arcsin ^{2}z={\frac {1}{2}}\sum _{k=1}^{\infty }{\frac {(2z)^{2k}}{k^{2}\,{2k \choose k}}}\qquad |z|\leq 1}
1. Beweis
Integriert man die Formel
arcsin
z
1
−
z
2
=
∑
k
=
1
∞
(
2
z
)
2
k
−
1
k
(
2
k
k
)
{\displaystyle {\frac {\arcsin z}{\sqrt {1-z^{2}}}}=\sum _{k=1}^{\infty }{\frac {(2z)^{2k-1}}{k\,{2k \choose k}}}}
1
2
arcsin
2
z
=
∑
k
=
1
∞
(
2
z
)
2
k
(
2
k
)
2
(
2
k
k
)
{\displaystyle {\frac {1}{2}}\arcsin ^{2}z=\sum _{k=1}^{\infty }{\frac {(2z)^{2k}}{(2k)^{2}\,{2k \choose k}}}}
2. Beweis
Aus der Formel
cos
p
x
=
1
−
p
2
sin
2
x
2
!
+
p
2
(
p
2
−
2
2
)
sin
4
x
4
!
−
p
2
(
p
2
−
2
2
)
(
p
2
−
4
2
)
sin
6
x
6
!
+
.
.
.
{\displaystyle \cos px=1-p^{2}\,{\frac {\sin ^{2}x}{2!}}+p^{2}(p^{2}-2^{2})\,{\frac {\sin ^{4}x}{4!}}-p^{2}(p^{2}-2^{2})(p^{2}-4^{2})\,{\frac {\sin ^{6}x}{6!}}+...}
p
∈
C
{\displaystyle p\in \mathbb {C} }
x
∈
[
−
π
2
,
π
2
]
{\displaystyle x\in \left[-{\frac {\pi }{2}},{\frac {\pi }{2}}\right]}
1
−
cos
p
x
p
2
=
sin
2
x
2
!
−
(
p
2
−
2
2
)
sin
4
x
4
!
+
(
p
2
−
2
2
)
(
p
2
−
4
2
)
sin
6
x
6
!
−
(
p
2
−
2
2
)
(
p
2
−
4
2
)
(
p
2
−
6
2
)
sin
8
x
8
!
+
.
.
.
{\displaystyle {\frac {1-\cos px}{p^{2}}}={\frac {\sin ^{2}x}{2!}}-(p^{2}-2^{2})\,{\frac {\sin ^{4}x}{4!}}+(p^{2}-2^{2})(p^{2}-4^{2})\,{\frac {\sin ^{6}x}{6!}}-(p^{2}-2^{2})(p^{2}-4^{2})(p^{2}-6^{2})\,{\frac {\sin ^{8}x}{8!}}+...}
p
→
0
{\displaystyle p\to 0\,}
x
2
2
=
1
2
!
sin
2
x
+
2
2
4
!
sin
4
x
+
2
2
⋅
4
2
6
!
sin
6
x
+
2
2
⋅
4
2
⋅
6
2
8
!
sin
8
x
+
.
.
.
{\displaystyle {\frac {x^{2}}{2}}={\frac {1}{2!}}\,\sin ^{2}x+{\frac {2^{2}}{4!}}\,\sin ^{4}x+{\frac {2^{2}\cdot 4^{2}}{6!}}\sin ^{6}x+{\frac {2^{2}\cdot 4^{2}\cdot 6^{2}}{8!}}\sin ^{8}x+...}
2
2
⋅
4
2
⋯
(
2
n
−
2
)
2
(
2
n
)
!
=
(
2
n
−
1
(
n
−
1
)
!
)
2
(
2
n
)
!
=
2
2
n
−
2
n
!
2
n
2
(
2
n
)
!
=
1
4
2
2
n
n
2
(
2
n
n
)
{\displaystyle {\frac {2^{2}\cdot 4^{2}\cdots (2n-2)^{2}}{(2n)!}}={\frac {\left(2^{n-1}\,(n-1)!\right)^{2}}{(2n)!}}={\frac {2^{2n-2}\,n!^{2}}{n^{2}\,(2n)!}}={\frac {1}{4}}\,{\frac {2^{2n}}{n^{2}\,{2n \choose n}}}}
x
2
=
1
2
∑
n
=
1
∞
2
2
n
n
2
(
2
n
n
)
sin
2
n
x
{\displaystyle x^{2}={\frac {1}{2}}\sum _{n=1}^{\infty }{\frac {2^{2n}}{n^{2}\,{2n \choose n}}}\,\sin ^{2n}x}
x
{\displaystyle x\,}
arcsin
x
{\displaystyle \arcsin x\,}
arcsin
3
z
=
6
∑
k
=
0
∞
[
∑
m
=
0
k
−
1
1
(
2
m
+
1
)
2
]
1
2
2
k
(
2
k
k
)
z
2
k
+
1
2
k
+
1
|
z
|
<
1
{\displaystyle \arcsin ^{3}z=6\sum _{k=0}^{\infty }\left[\sum _{m=0}^{k-1}{\frac {1}{(2m+1)^{2}}}\right]\,{\frac {1}{2^{2k}}}\,{2k \choose k}\,{\frac {z^{2k+1}}{2k+1}}\qquad |z|<1}
Beweis
Setzt man
f
n
(
x
)
=
(
sin
x
)
2
n
+
1
(
2
n
+
1
)
!
{\displaystyle f_{n}(x)={\frac {(\sin x)^{2n+1}}{(2n+1)!}}}
f
n
″
(
x
)
=
f
n
−
1
(
x
)
−
(
2
n
+
1
)
2
f
n
(
x
)
{\displaystyle f_{n}''(x)=f_{n-1}(x)-(2n+1)^{2}f_{n}(x)\,}
x
=
∑
n
=
0
∞
1
2
2
n
(
2
n
n
)
(
sin
x
)
2
n
+
1
2
n
+
1
=
∑
n
=
0
∞
b
n
2
f
n
(
x
)
{\displaystyle x=\sum _{n=0}^{\infty }{\frac {1}{2^{2n}}}\,{2n \choose n}\,{\frac {(\sin x)^{2n+1}}{2n+1}}=\sum _{n=0}^{\infty }b_{n}^{2}f_{n}(x)}
b
n
=
(
2
n
)
!
2
n
n
!
{\displaystyle b_{n}={\frac {(2n)!}{2^{n}\,n!}}}
b
n
+
1
=
b
n
(
2
n
+
1
)
{\displaystyle b_{n+1}=b_{n}(2n+1)\,}
x
3
=
∑
n
=
0
∞
a
n
b
n
2
f
n
(
x
)
{\displaystyle x^{3}=\sum _{n=0}^{\infty }a_{n}b_{n}^{2}f_{n}(x)}
a
0
=
0
{\displaystyle a_{0}=0\,}
6
x
=
∑
n
=
1
∞
a
n
b
n
2
(
f
n
−
1
(
x
)
−
(
2
n
+
1
)
2
f
n
(
x
)
)
=
∑
n
=
0
∞
a
n
+
1
b
n
+
1
2
f
n
(
x
)
−
∑
n
=
1
∞
a
n
b
n
2
(
2
n
+
1
)
2
f
n
(
x
)
{\displaystyle 6x=\sum _{n=1}^{\infty }a_{n}b_{n}^{2}\left(f_{n-1}(x)-(2n+1)^{2}f_{n}(x)\right)=\sum _{n=0}^{\infty }a_{n+1}b_{n+1}^{2}f_{n}(x)-\sum _{n=1}^{\infty }a_{n}b_{n}^{2}(2n+1)^{2}f_{n}(x)}
(
a
n
+
1
−
a
n
)
b
n
2
(
2
n
+
1
)
2
=
6
b
n
2
⇒
a
n
+
1
−
a
n
=
6
1
(
2
n
+
1
)
2
⇒
a
n
=
6
∑
k
=
0
n
−
1
1
(
2
k
+
1
)
2
{\displaystyle (a_{n+1}-a_{n})b_{n}^{2}(2n+1)^{2}=6b_{n}^{2}\,\Rightarrow \,a_{n+1}-a_{n}=6\,{\frac {1}{(2n+1)^{2}}}\,\Rightarrow \,a_{n}=6\sum _{k=0}^{n-1}{\frac {1}{(2k+1)^{2}}}}
arcsin
4
z
=
6
∑
k
=
0
∞
[
∑
m
=
1
k
−
1
1
(
2
m
)
2
]
(
2
z
)
2
k
k
2
(
2
k
k
)
|
z
|
<
1
{\displaystyle \arcsin ^{4}z=6\sum _{k=0}^{\infty }\left[\sum _{m=1}^{k-1}{\frac {1}{(2m)^{2}}}\right]\,{\frac {(2z)^{2k}}{k^{2}\,{2k \choose k}}}\qquad |z|<1}
Beweis
Setzt man
f
n
(
x
)
=
(
sin
x
)
2
n
(
2
n
)
!
{\displaystyle f_{n}(x)={\frac {(\sin x)^{2n}}{(2n)!}}}
f
n
″
(
x
)
=
f
n
−
1
(
x
)
−
(
2
n
)
2
f
n
(
x
)
{\displaystyle f_{n}''(x)=f_{n-1}(x)-(2n)^{2}f_{n}(x)\,}
x
2
=
1
2
∑
n
=
1
∞
2
2
n
n
2
(
2
n
n
)
(
sin
x
)
2
n
=
1
2
∑
n
=
1
∞
b
n
2
f
n
(
x
)
{\displaystyle x^{2}={\frac {1}{2}}\sum _{n=1}^{\infty }{\frac {2^{2n}}{n^{2}\,{2n \choose n}}}\,(\sin x)^{2n}={\frac {1}{2}}\sum _{n=1}^{\infty }b_{n}^{2}f_{n}(x)}
b
n
=
2
n
(
n
−
1
)
!
{\displaystyle b_{n}=2^{n}\,(n-1)!\,}
b
n
+
1
=
b
n
⋅
2
n
{\displaystyle b_{n+1}=b_{n}\cdot 2n}
x
4
=
1
2
∑
n
=
1
∞
a
n
b
n
2
f
n
(
x
)
{\displaystyle x^{4}={\frac {1}{2}}\sum _{n=1}^{\infty }a_{n}b_{n}^{2}f_{n}(x)}
a
1
=
0
{\displaystyle a_{1}=0\,}
12
x
2
=
1
2
∑
n
=
1
∞
a
n
b
n
2
(
f
n
−
1
(
x
)
−
(
2
n
)
2
f
n
(
x
)
)
=
1
2
∑
n
=
0
∞
a
n
+
1
b
n
+
1
2
f
n
(
x
)
−
1
2
∑
n
=
1
∞
a
n
b
n
2
(
2
n
)
2
f
n
(
x
)
{\displaystyle 12x^{2}={\frac {1}{2}}\sum _{n=1}^{\infty }a_{n}b_{n}^{2}\left(f_{n-1}(x)-(2n)^{2}f_{n}(x)\right)={\frac {1}{2}}\sum _{n=0}^{\infty }a_{n+1}b_{n+1}^{2}\,f_{n}(x)-{\frac {1}{2}}\sum _{n=1}^{\infty }a_{n}\,b_{n}^{2}\,(2n)^{2}\,f_{n}(x)}
(
a
n
+
1
−
a
n
)
b
n
2
(
2
n
)
2
=
12
b
n
2
⇒
a
n
+
1
−
a
n
=
12
1
(
2
n
)
2
⇒
a
n
=
12
∑
k
=
1
n
−
1
1
(
2
k
)
2
{\displaystyle (a_{n+1}-a_{n})\,b_{n}^{2}\,(2n)^{2}=12b_{n}^{2}\,\Rightarrow \,a_{n+1}-a_{n}=12\,{\frac {1}{(2n)^{2}}}\,\Rightarrow \,a_{n}=12\sum _{k=1}^{n-1}{\frac {1}{(2k)^{2}}}}
arccos
z
=
π
2
−
∑
k
=
0
∞
(
−
1
)
k
(
−
1
2
k
)
z
2
k
+
1
2
k
+
1
=
π
2
−
∑
k
=
0
∞
1
2
2
k
(
2
k
k
)
z
2
k
+
1
2
k
+
1
|
z
|
≤
1
{\displaystyle \arccos z={\frac {\pi }{2}}-\sum _{k=0}^{\infty }(-1)^{k}{-{\frac {1}{2}} \choose k}{\frac {z^{2k+1}}{2k+1}}={\frac {\pi }{2}}-\sum _{k=0}^{\infty }{\frac {1}{2^{2k}}}{2k \choose k}{\frac {z^{2k+1}}{2k+1}}\qquad |z|\leq 1}
arctan
z
=
∑
k
=
0
∞
(
−
1
)
k
z
2
k
+
1
2
k
+
1
|
z
|
≤
1
,
z
≠
±
i
{\displaystyle \arctan z=\sum _{k=0}^{\infty }(-1)^{k}{\frac {z^{2k+1}}{2k+1}}\qquad |z|\leq 1,z\neq \pm i}
arsinh
z
=
∑
k
=
0
∞
(
−
1
2
k
)
z
2
k
+
1
2
k
+
1
|
z
|
≤
1
{\displaystyle {\text{arsinh}}\,z=\sum _{k=0}^{\infty }{-{\frac {1}{2}} \choose k}{\frac {z^{2k+1}}{2k+1}}\qquad |z|\leq 1}
arsinh
2
z
=
1
2
∑
k
=
1
∞
(
−
1
)
k
−
1
(
2
z
)
2
k
k
2
(
2
k
k
)
|
z
|
≤
1
{\displaystyle {\text{arsinh}}^{2}z={\frac {1}{2}}\sum _{k=1}^{\infty }{\frac {(-1)^{k-1}\,(2z)^{2k}}{k^{2}\,{2k \choose k}}}\qquad |z|\leq 1}
artanh
z
=
∑
k
=
0
∞
z
2
k
+
1
2
k
+
1
|
z
|
≤
1
,
z
≠
±
1
{\displaystyle {\text{artanh}}\,z=\sum _{k=0}^{\infty }{\frac {z^{2k+1}}{2k+1}}\qquad |z|\leq 1,z\neq \pm 1}
ζ
(
z
)
=
1
z
−
1
+
∑
k
=
0
∞
(
−
1
)
k
k
!
γ
k
(
z
−
1
)
k
{\displaystyle \zeta (z)={\frac {1}{z-1}}+\sum _{k=0}^{\infty }{\frac {(-1)^{k}}{k!}}\,\gamma _{k}\,(z-1)^{k}}
Beweis
∫
1
N
{
t
}
d
d
t
1
t
s
d
t
=
∑
n
=
2
N
∫
n
−
1
n
(
t
−
(
n
−
1
)
)
d
d
t
1
t
s
d
t
{\displaystyle \int _{1}^{N}\{t\}\,{\frac {d}{dt}}{\frac {1}{t^{s}}}\,dt=\sum _{n=2}^{N}\int _{n-1}^{n}{\big (}t-(n-1){\big )}\,{\frac {d}{dt}}{\frac {1}{t^{s}}}\,dt}
=
∑
n
=
2
N
(
[
(
t
−
(
n
−
1
)
)
1
t
s
]
n
−
1
n
−
∫
n
−
1
n
1
t
s
d
t
)
=
∑
n
=
2
N
1
n
s
−
∫
1
N
1
t
s
d
t
{\displaystyle =\sum _{n=2}^{N}\left(\left[{\big (}t-(n-1){\big )}\,{\frac {1}{t^{s}}}\right]_{n-1}^{n}-\int _{n-1}^{n}{\frac {1}{t^{s}}}\,dt\right)=\sum _{n=2}^{N}{\frac {1}{n^{s}}}-\int _{1}^{N}{\frac {1}{t^{s}}}\,dt}
∑
n
=
2
N
1
n
s
−
∫
1
N
1
t
s
d
t
=
∫
1
N
{
t
}
d
d
t
1
t
s
d
t
(
G
1
)
{\displaystyle \sum _{n=2}^{N}{\frac {1}{n^{s}}}-\int _{1}^{N}{\frac {1}{t^{s}}}\,dt=\int _{1}^{N}\{t\}\,{\frac {d}{dt}}{\frac {1}{t^{s}}}\,dt\qquad (G1)}
(
−
d
d
s
)
m
{\displaystyle \left(-{\frac {d}{ds}}\right)^{m}}
(
G
1
)
{\displaystyle (G1)\,}
∑
n
=
2
N
(
log
n
)
m
n
s
−
∫
1
N
(
log
t
)
m
t
s
d
t
=
∫
1
N
{
t
}
d
d
t
(
log
t
)
m
t
s
d
t
{\displaystyle \sum _{n=2}^{N}{\frac {(\log n)^{m}}{n^{s}}}-\int _{1}^{N}{\frac {(\log t)^{m}}{t^{s}}}\,dt=\int _{1}^{N}\{t\}\,{\frac {d}{dt}}{\frac {(\log t)^{m}}{t^{s}}}\,dt}
s
=
1
{\displaystyle s=1\,}
∑
n
=
2
N
(
log
n
)
m
n
−
(
log
N
)
m
+
1
m
+
1
=
∫
1
N
{
t
}
d
d
t
(
log
t
)
m
t
d
t
{\displaystyle \sum _{n=2}^{N}{\frac {(\log n)^{m}}{n}}-{\frac {(\log N)^{m+1}}{m+1}}=\int _{1}^{N}\{t\}\,{\frac {d}{dt}}{\frac {(\log t)^{m}}{t}}\,dt}
N
→
∞
{\displaystyle N\to \infty \,}
lim
N
→
∞
(
∑
n
=
2
N
(
log
n
)
m
n
−
(
log
N
)
m
+
1
m
+
1
)
=
∫
1
∞
{
t
}
d
d
t
(
log
t
)
m
t
d
t
(
G
2
)
{\displaystyle \lim _{N\to \infty }\left(\sum _{n=2}^{N}{\frac {(\log n)^{m}}{n}}-{\frac {(\log N)^{m+1}}{m+1}}\right)=\int _{1}^{\infty }\{t\}\,{\frac {d}{dt}}{\frac {(\log t)^{m}}{t}}\,dt\qquad (G2)}
(
G
1
)
{\displaystyle (G1)\,}
s
>
1
{\displaystyle s>1\,}
N
→
∞
{\displaystyle N\to \infty \,}
ζ
(
s
)
−
1
−
1
s
−
1
=
∫
1
∞
{
t
}
d
d
t
1
t
s
d
t
{\displaystyle \zeta (s)-1-{\frac {1}{s-1}}=\int _{1}^{\infty }\{t\}\,{\frac {d}{dt}}{\frac {1}{t^{s}}}\,dt}
(
−
d
d
s
)
m
{\displaystyle \left(-{\frac {d}{ds}}\right)^{m}}
(
−
d
d
s
)
m
(
ζ
(
s
)
−
1
−
1
s
−
1
)
=
∫
1
∞
{
t
}
d
d
t
(
log
t
)
m
t
s
d
t
{\displaystyle \left(-{\frac {d}{ds}}\right)^{m}\left(\zeta (s)-1-{\frac {1}{s-1}}\right)=\int _{1}^{\infty }\{t\}\,{\frac {d}{dt}}{\frac {(\log t)^{m}}{t^{s}}}\,dt}
s
→
1
+
{\displaystyle s\to 1+\,}
(
−
1
)
m
lim
s
→
1
+
(
d
d
s
)
m
(
ζ
(
s
)
−
1
−
1
s
−
1
)
=
∫
1
∞
{
t
}
d
d
t
(
log
t
)
m
t
d
t
(
G
3
)
{\displaystyle (-1)^{m}\lim _{s\to 1+}\left({\frac {d}{ds}}\right)^{m}\left(\zeta (s)-1-{\frac {1}{s-1}}\right)=\int _{1}^{\infty }\{t\}\,{\frac {d}{dt}}{\frac {(\log t)^{m}}{t}}\,dt\qquad (G3)}
(
G
2
)
{\displaystyle (G2)\,}
(
G
3
)
{\displaystyle (G3)\,}
γ
m
:=
lim
N
→
∞
(
∑
n
=
1
N
(
log
n
)
m
n
−
(
log
N
)
m
+
1
m
+
1
)
=
(
−
1
)
m
lim
s
→
1
+
(
d
d
s
)
m
(
ζ
(
s
)
−
1
s
−
1
)
{\displaystyle \gamma _{m}:=\lim _{N\to \infty }\left(\sum _{n=1}^{N}{\frac {(\log n)^{m}}{n}}-{\frac {(\log N)^{m+1}}{m+1}}\right)=(-1)^{m}\,\lim _{s\to 1+}\left({\frac {d}{ds}}\right)^{m}\left(\zeta (s)-{\frac {1}{s-1}}\right)}
ζ
(
s
)
{\displaystyle \zeta (s)\,}
s
=
1
{\displaystyle s=1\,}
1
s
−
1
+
∑
m
=
0
∞
(
−
1
)
m
m
!
γ
m
(
s
−
1
)
m
{\displaystyle {\frac {1}{s-1}}+\sum _{m=0}^{\infty }{\frac {(-1)^{m}}{m!}}\,\gamma _{m}\,(s-1)^{m}}
Γ
(
1
+
z
)
=
∑
n
=
0
∞
∑
k
1
+
2
k
2
+
.
.
.
+
n
k
n
=
n
(
−
γ
)
k
1
k
1
!
∏
m
=
2
n
(
(
−
1
)
m
ζ
(
m
)
m
)
k
m
k
m
!
z
n
{\displaystyle \Gamma (1+z)=\sum _{n=0}^{\infty }\;\;\sum _{k_{1}+2k_{2}+...+nk_{n}=n}\!\!{\frac {(-\gamma )^{k_{1}}}{k_{1}!}}\prod _{m=2}^{n}{\frac {\left((-1)^{m}\,{\frac {\zeta (m)}{m}}\right)^{k_{m}}}{k_{m}!}}\;\;z^{n}}
ψ
(
1
+
z
)
=
−
γ
+
∑
k
=
1
∞
(
−
1
)
k
+
1
ζ
(
k
+
1
)
z
k
{\displaystyle \psi (1+z)=-\gamma +\sum _{k=1}^{\infty }(-1)^{k+1}\,\zeta (k+1)\,z^{k}}
J
ν
(
z
)
=
∑
k
=
0
∞
(
−
1
)
k
k
!
Γ
(
ν
+
k
+
1
)
(
z
2
)
ν
+
2
k
{\displaystyle J_{\nu }(z)=\sum _{k=0}^{\infty }{\frac {(-1)^{k}}{k!\,\Gamma (\nu +k+1)}}\left({\frac {z}{2}}\right)^{\nu +2k}}
W
(
z
)
=
∑
n
=
1
∞
(
−
1
)
n
−
1
n
n
−
1
n
!
z
n
|
z
|
<
1
e
{\displaystyle W(z)=\sum _{n=1}^{\infty }{\frac {(-1)^{n-1}\,n^{n-1}}{n!}}\,z^{n}\qquad |z|<{\frac {1}{e}}}
Beweis
Die holomorphe Funktion
f
(
z
)
=
z
e
z
=
∑
n
=
1
∞
1
(
n
−
1
)
!
z
n
{\displaystyle f(z)=z\,e^{z}=\sum _{n=1}^{\infty }{\frac {1}{(n-1)!}}\,z^{n}}
f
′
(
0
)
=
1
{\displaystyle f'(0)=1\,}
z
=
0
{\displaystyle z=0\,}
U
(
0
)
{\displaystyle U(0)\,}
V
(
0
)
{\displaystyle V(0)\,}
f
:
U
(
0
)
→
V
(
0
)
{\displaystyle f:U(0)\to V(0)\,}
a
n
{\displaystyle a_{n}\,}
W
(
z
)
=
∑
n
=
1
∞
a
n
z
n
{\displaystyle W(z)=\sum _{n=1}^{\infty }a_{n}z^{n}}
a
n
=
1
n
!
lim
x
→
0
(
d
d
x
)
n
−
1
(
x
f
(
x
)
)
n
{\displaystyle a_{n}={\frac {1}{n!}}\,\lim _{x\to 0}\left({\frac {d}{dx}}\right)^{n-1}\left({\frac {x}{f(x)}}\right)^{n}}
(
x
f
(
x
)
)
n
=
e
−
n
x
{\displaystyle \left({\frac {x}{f(x)}}\right)^{n}=e^{-nx}}
(
d
d
x
)
n
−
1
(
x
f
(
x
)
)
n
=
(
−
n
)
n
−
1
e
−
n
x
{\displaystyle \left({\frac {d}{dx}}\right)^{n-1}\left({\frac {x}{f(x)}}\right)^{n}=(-n)^{n-1}\,e^{-nx}}
a
n
=
(
−
n
)
n
−
1
n
!
{\displaystyle a_{n}={\frac {(-n)^{n-1}}{n!}}}
e
z
2
(
t
−
1
t
)
=
∑
n
∈
Z
J
n
(
z
)
t
n
{\displaystyle e^{{\frac {z}{2}}\left(t-{\frac {1}{t}}\right)}=\sum _{n\in \mathbb {Z} }J_{n}(z)\,t^{n}}
1. Beweis
e
z
2
(
t
−
1
t
)
=
e
z
2
t
⋅
e
−
z
2
1
t
=
∑
n
=
0
∞
1
n
!
(
z
2
)
n
t
n
⋅
∑
k
=
0
∞
(
−
1
)
k
k
!
(
z
2
)
k
1
t
k
{\displaystyle e^{{\frac {z}{2}}\left(t-{\frac {1}{t}}\right)}=e^{{\frac {z}{2}}t}\cdot e^{-{\frac {z}{2}}{\frac {1}{t}}}=\sum _{n=0}^{\infty }{\frac {1}{n!}}\left({\frac {z}{2}}\right)^{n}\,t^{n}\cdot \sum _{k=0}^{\infty }{\frac {(-1)^{k}}{k!}}\left({\frac {z}{2}}\right)^{k}\,{\frac {1}{t^{k}}}}
=
∑
k
=
0
∞
∑
n
=
0
∞
(
−
1
)
k
k
!
n
!
(
z
2
)
n
+
k
t
n
−
k
=
∑
k
=
0
∞
∑
n
=
−
k
∞
(
−
1
)
k
k
!
(
n
+
k
)
!
(
z
2
)
n
+
2
k
t
n
{\displaystyle =\sum _{k=0}^{\infty }\sum _{n=0}^{\infty }{\frac {(-1)^{k}}{k!\,n!}}\left({\frac {z}{2}}\right)^{n+k}\,t^{n-k}=\sum _{k=0}^{\infty }\sum _{n=-k}^{\infty }{\frac {(-1)^{k}}{k!\,(n+k)!}}\left({\frac {z}{2}}\right)^{n+2k}\,t^{n}}
1
(
n
+
k
)
!
{\displaystyle {\frac {1}{(n+k)!}}}
n
<
−
k
{\displaystyle n<-k\,}
n
{\displaystyle n\,}
e
z
2
(
t
−
1
t
)
=
∑
n
∈
Z
∑
k
=
0
∞
(
−
1
)
k
k
!
(
n
+
k
)
!
(
z
2
)
n
+
2
k
t
n
=
∑
n
∈
Z
J
n
(
z
)
t
n
{\displaystyle e^{{\frac {z}{2}}\left(t-{\frac {1}{t}}\right)}=\sum _{n\in \mathbb {Z} }\sum _{k=0}^{\infty }{\frac {(-1)^{k}}{k!\,(n+k)!}}\left({\frac {z}{2}}\right)^{n+2k}\,t^{n}=\sum _{n\in \mathbb {Z} }J_{n}(z)\,t^{n}}
π
cos
α
x
sin
α
π
=
∑
k
∈
Z
(
−
1
)
k
cos
k
x
k
+
α
−
π
<
x
<
π
,
α
∉
Z
{\displaystyle \pi \,{\frac {\cos \alpha x}{\sin \alpha \pi }}=\sum _{k\in \mathbb {Z} }{\frac {(-1)^{k}\,\cos kx}{k+\alpha }}\qquad -\pi <x<\pi \,,\,\alpha \notin \mathbb {Z} }
−
π
sin
α
x
sin
α
π
=
∑
k
∈
Z
(
−
1
)
k
sin
k
x
k
+
α
−
π
<
x
<
π
,
α
∉
Z
{\displaystyle -\pi \,{\frac {\sin \alpha x}{\sin \alpha \pi }}=\sum _{k\in \mathbb {Z} }{\frac {(-1)^{k}\,\sin kx}{k+\alpha }}\qquad -\pi <x<\pi \,,\,\alpha \notin \mathbb {Z} }
Beweis
Es sei
f
(
z
)
=
e
i
x
z
π
sin
π
z
1
z
+
α
{\displaystyle f(z)=e^{ixz}\,{\frac {\pi }{\sin \pi z}}\,{\frac {1}{z+\alpha }}}
γ
N
{\displaystyle \gamma _{N}\,}
(
±
1
±
i
)
(
N
+
1
2
)
{\displaystyle (\pm 1\pm i)\left(N+{\frac {1}{2}}\right)}
z
=
u
+
i
v
{\displaystyle z=u+iv\,}
|
e
i
x
z
|
=
e
−
x
v
{\displaystyle |e^{ixz}|=e^{-xv}\,}
sin
(
π
(
u
+
i
v
)
)
=
sin
π
u
cosh
π
v
+
i
cos
π
u
sinh
π
v
{\displaystyle \sin {\big (}\pi (u+iv){\big )}=\sin \pi u\,\cosh \pi v+i\cos \pi u\,\sinh \pi v}
|
sin
π
z
|
2
=
sin
2
π
u
cosh
2
π
v
⏟
1
+
sinh
2
π
v
+
cos
2
π
u
sinh
2
π
v
=
sin
2
π
u
+
sinh
2
π
v
∼
(
e
π
|
v
|
2
)
2
{\displaystyle |\sin \pi z|^{2}=\sin ^{2}\pi u\,\underbrace {\cosh ^{2}\pi v} _{1+\sinh ^{2}\pi v}+\cos ^{2}\pi u\,\sinh ^{2}\pi v=\sin ^{2}\pi u+\sinh ^{2}\pi v\sim \left({\frac {e^{\pi |v|}}{2}}\right)^{2}}
|
v
|
→
∞
{\displaystyle |v|\to \infty \,}
|
f
(
u
+
i
v
)
|
=
O
(
e
−
x
v
e
−
π
|
v
|
)
{\displaystyle |f(u+iv)|=O\left(e^{-xv}\,e^{-\pi |v|}\right)}
|
v
|
→
∞
{\displaystyle |v|\to \infty \,}
lim
N
→
∞
∮
γ
N
f
d
z
=
0
{\displaystyle \lim _{N\to \infty }\oint _{\gamma _{N}}f\,dz=0}
f
{\displaystyle f\,}
∀
n
∈
Z
{\displaystyle \forall n\in \mathbb {Z} }
res
(
f
,
n
)
=
e
i
n
x
1
cos
n
π
1
n
+
α
{\displaystyle {\text{res}}(f,n)=e^{inx}\,{\frac {1}{\cos n\pi }}\,{\frac {1}{n+\alpha }}}
res
(
f
,
−
α
)
=
e
−
i
α
x
1
−
sin
π
α
{\displaystyle {\text{res}}(f,-\alpha )=e^{-i\alpha x}\,{\frac {1}{-\sin \pi \alpha }}}
∑
n
∈
Z
(
−
1
)
n
e
i
n
x
n
+
α
=
e
−
i
α
x
sin
π
α
{\displaystyle \sum _{n\in \mathbb {Z} }{\frac {(-1)^{n}\,e^{inx}}{n+\alpha }}={\frac {e^{-i\alpha x}}{\sin \pi \alpha }}}
π
cot
π
z
=
∑
k
=
−
∞
∞
1
k
+
z
z
∈
C
∖
Z
{\displaystyle \pi \,\cot \pi z=\sum _{k=-\infty }^{\infty }{\frac {1}{k+z}}\qquad z\in \mathbb {C} \setminus \mathbb {Z} }
π
csc
π
z
=
∑
k
=
−
∞
∞
(
−
1
)
k
k
+
z
z
∈
C
∖
Z
{\displaystyle \pi \,\csc \pi z=\sum _{k=-\infty }^{\infty }{\frac {(-1)^{k}}{k+z}}\qquad z\in \mathbb {C} \setminus \mathbb {Z} }
π
tan
π
z
=
∑
k
=
−
∞
∞
1
k
+
1
2
−
z
z
∈
C
∖
{
k
+
1
2
:
k
∈
Z
}
{\displaystyle \pi \,\tan \pi z=\sum _{k=-\infty }^{\infty }{\frac {1}{k+{\frac {1}{2}}-z}}\qquad z\in \mathbb {C} \setminus \left\{k+{\frac {1}{2}}\,:\,k\in \mathbb {Z} \right\}}
π
sec
π
z
=
∑
k
=
−
∞
∞
(
−
1
)
k
k
+
1
2
−
z
z
∈
C
∖
{
k
+
1
2
:
k
∈
Z
}
{\displaystyle \pi \,\sec \pi z=\sum _{k=-\infty }^{\infty }{\frac {(-1)^{k}}{k+{\frac {1}{2}}-z}}\qquad z\in \mathbb {C} \setminus \left\{k+{\frac {1}{2}}\,:\,k\in \mathbb {Z} \right\}}
sin
(
α
arcsin
z
)
α
=
∑
n
=
0
∞
∏
k
=
1
n
[
(
2
k
−
1
)
2
−
α
2
]
z
2
n
+
1
(
2
n
+
1
)
!
{\displaystyle {\frac {\sin(\alpha \arcsin z)}{\alpha }}=\sum _{n=0}^{\infty }\prod _{k=1}^{n}\left[(2k-1)^{2}-\alpha ^{2}\right]{\frac {z^{2n+1}}{(2n+1)!}}}
1
2
[
(
1
+
z
2
+
z
)
2
α
+
(
1
+
z
2
−
z
)
2
α
]
=
∑
n
=
0
∞
α
(
α
+
n
−
1
)
!
(
α
−
n
)
!
(
2
z
)
2
n
(
2
n
)
!
{\displaystyle {\frac {1}{2}}\left[\left({\sqrt {1+z^{2}}}+z\right)^{2\alpha }+\left({\sqrt {1+z^{2}}}-z\right)^{2\alpha }\right]=\sum _{n=0}^{\infty }\alpha \,{\frac {(\alpha +n-1)!}{(\alpha -n)!}}\,{\frac {(2z)^{2n}}{(2n)!}}}
Beweis
f
(
z
)
=
(
1
+
z
2
+
z
)
2
α
=
1
+
z
2
2
α
(
1
+
z
1
+
z
2
)
2
α
=
1
+
z
2
2
α
∑
k
=
0
∞
(
2
α
k
)
z
k
1
+
z
2
k
{\displaystyle f(z)=\left({\sqrt {1+z^{2}}}+z\right)^{2\alpha }={\sqrt {1+z^{2}}}^{\,2\alpha }\,\left(1+{\frac {z}{\sqrt {1+z^{2}}}}\right)^{2\alpha }={\sqrt {1+z^{2}}}^{\,2\alpha }\,\sum _{k=0}^{\infty }{2\alpha \choose k}\,{\frac {z^{k}}{{\sqrt {1+z^{2}}}^{\,k}}}}
1
2
[
f
(
z
)
−
f
(
−
z
)
]
=
1
+
z
2
2
α
∑
k
=
0
∞
(
2
α
2
k
)
z
2
k
1
+
z
2
2
k
=
∑
k
=
0
∞
(
2
α
2
k
)
z
2
k
(
1
+
z
2
)
α
−
k
{\displaystyle {\frac {1}{2}}{\Big [}f(z)-f(-z){\Big ]}={\sqrt {1+z^{2}}}^{\,2\alpha }\sum _{k=0}^{\infty }{2\alpha \choose 2k}\,{\frac {z^{2k}}{{\sqrt {1+z^{2}}}^{\,2k}}}=\sum _{k=0}^{\infty }{2\alpha \choose 2k}\,z^{2k}\,(1+z^{2})^{\alpha -k}}
=
∑
k
=
0
∞
(
2
α
2
k
)
z
2
k
∑
j
=
0
∞
(
α
−
k
j
)
z
2
j
=
∑
k
,
j
=
0
∞
(
2
α
2
k
)
(
α
−
k
j
)
z
2
k
+
2
j
=
∑
n
=
0
∞
∑
k
=
0
n
(
2
α
2
k
)
(
α
−
k
n
−
k
)
⏟
=
A
2
n
z
2
n
{\displaystyle =\sum _{k=0}^{\infty }{2\alpha \choose 2k}\,z^{2k}\,\sum _{j=0}^{\infty }{\alpha -k \choose j}\,z^{2j}=\sum _{k,j=0}^{\infty }{2\alpha \choose 2k}{\alpha -k \choose j}\,z^{2k+2j}=\sum _{n=0}^{\infty }\underbrace {\sum _{k=0}^{n}{2\alpha \choose 2k}{\alpha -k \choose n-k}} _{=A_{2n}}\,z^{2n}}
A
2
n
=
∑
k
=
0
∞
(
2
α
)
!
(
2
k
)
!
(
2
α
−
2
k
)
!
(
α
−
k
)
!
(
n
−
k
)
!
(
α
−
n
)
!
{\displaystyle A_{2n}=\sum _{k=0}^{\infty }{\frac {(2\alpha )!}{(2k)!\,(2\alpha -2k)!}}\,{\frac {(\alpha -k)!}{(n-k)!\,(\alpha -n)!}}}
=
(
2
α
)
!
(
α
−
n
)
!
∑
k
=
0
∞
(
α
−
k
)
!
2
2
k
π
k
!
(
k
−
1
2
)
!
2
2
α
−
2
k
π
(
α
−
k
)
!
(
α
−
1
2
−
k
)
!
(
n
−
k
)
!
{\displaystyle ={\frac {(2\alpha )!}{(\alpha -n)!}}\sum _{k=0}^{\infty }{\frac {(\alpha -k)!}{{\frac {2^{2k}}{\sqrt {\pi }}}\,k!\,\left(k-{\frac {1}{2}}\right)!\,{\frac {2^{2\alpha -2k}}{\sqrt {\pi }}}\,(\alpha -k)!\,\left(\alpha -{\frac {1}{2}}-k\right)!\,(n-k)!}}}
=
π
(
2
α
)
!
2
2
α
(
α
−
n
)
!
∑
k
=
0
∞
1
k
!
(
k
−
1
2
)
!
(
α
−
1
2
−
k
)
!
(
n
−
k
)
!
{\displaystyle ={\frac {\pi \,(2\alpha )!}{2^{2\alpha }\,(\alpha -n)!}}\,\sum _{k=0}^{\infty }{\frac {1}{k!\,\left(k-{\frac {1}{2}}\right)!\,\left(\alpha -{\frac {1}{2}}-k\right)!\,(n-k)!}}}
=
π
(
2
α
)
!
2
2
α
(
α
−
n
)
!
(
α
+
n
−
1
)
!
(
α
−
1
2
)
!
n
!
(
α
−
1
)
!
(
n
−
1
2
)
!
{\displaystyle ={\frac {\pi \,(2\alpha )!}{2^{2\alpha }\,(\alpha -n)!}}\,{\frac {(\alpha +n-1)!}{\left(\alpha -{\frac {1}{2}}\right)!\,n!\,(\alpha -1)!\,\left(n-{\frac {1}{2}}\right)!}}}
=
π
(
2
α
)
!
2
2
α
(
α
−
n
)
!
(
α
+
n
−
1
)
!
π
2
2
α
−
1
(
2
α
−
1
)
!
π
2
2
n
(
2
n
)
!
=
α
(
α
+
n
−
1
)
!
(
α
−
n
)
!
2
2
n
(
2
n
)
!
{\displaystyle ={\frac {\pi \,(2\alpha )!}{2^{2\alpha }\,(\alpha -n)!}}\,{\frac {(\alpha +n-1)!}{{\frac {\sqrt {\pi }}{2^{2\alpha -1}}}\,(2\alpha -1)!\,{\frac {\sqrt {\pi }}{2^{2n}}}\,(2n)!}}=\alpha \,{\frac {(\alpha +n-1)!}{(\alpha -n)!}}\,{\frac {2^{2n}}{(2n)!}}}
1
2
[
(
1
+
z
2
+
z
)
2
α
+
1
−
(
1
+
z
2
−
z
)
2
α
+
1
]
=
∑
n
=
0
∞
2
α
+
1
2
(
α
+
n
)
!
(
α
−
n
)
!
(
2
z
)
2
n
+
1
(
2
n
+
1
)
!
{\displaystyle {\frac {1}{2}}\left[\left({\sqrt {1+z^{2}}}+z\right)^{2\alpha +1}-\left({\sqrt {1+z^{2}}}-z\right)^{2\alpha +1}\right]=\sum _{n=0}^{\infty }{\frac {2\alpha +1}{2}}\,{\frac {(\alpha +n)!}{(\alpha -n)!}}\,{\frac {(2z)^{2n+1}}{(2n+1)!}}}
Beweis
f
(
z
)
=
(
1
+
z
2
+
z
)
2
α
+
1
=
1
+
z
2
2
α
+
1
(
1
+
z
1
+
z
2
)
2
α
+
1
=
1
+
z
2
2
α
+
1
∑
k
=
0
∞
(
2
α
+
1
k
)
z
k
1
+
z
2
k
{\displaystyle f(z)=\left({\sqrt {1+z^{2}}}+z\right)^{2\alpha +1}={\sqrt {1+z^{2}}}^{\,2\alpha +1}\,\left(1+{\frac {z}{\sqrt {1+z^{2}}}}\right)^{2\alpha +1}={\sqrt {1+z^{2}}}^{\,2\alpha +1}\,\sum _{k=0}^{\infty }{2\alpha +1 \choose k}\,{\frac {z^{k}}{{\sqrt {1+z^{2}}}^{\,k}}}}
1
2
[
f
(
z
)
−
f
(
−
z
)
]
=
1
+
z
2
2
α
+
1
∑
k
=
0
∞
(
2
α
+
1
2
k
+
1
)
z
2
k
+
1
1
+
z
2
2
k
+
1
=
∑
k
=
0
∞
(
2
α
+
1
2
k
+
1
)
z
2
k
+
1
(
1
+
z
2
)
α
−
k
{\displaystyle {\frac {1}{2}}{\Big [}f(z)-f(-z){\Big ]}={\sqrt {1+z^{2}}}^{\,2\alpha +1}\sum _{k=0}^{\infty }{2\alpha +1 \choose 2k+1}\,{\frac {z^{2k+1}}{{\sqrt {1+z^{2}}}^{\,2k+1}}}=\sum _{k=0}^{\infty }{2\alpha +1 \choose 2k+1}\,z^{2k+1}\,(1+z^{2})^{\alpha -k}}
=
∑
k
=
0
∞
(
2
α
+
1
2
k
+
1
)
z
2
k
+
1
∑
j
=
0
∞
(
α
−
k
j
)
z
2
j
=
∑
k
,
j
=
0
∞
(
2
α
+
1
2
k
+
1
)
(
α
−
k
j
)
z
2
k
+
2
j
+
1
=
∑
n
=
0
∞
∑
k
=
0
n
(
2
α
+
1
2
k
+
1
)
(
α
−
k
n
−
k
)
⏟
=
A
2
n
+
1
z
2
n
+
1
{\displaystyle =\sum _{k=0}^{\infty }{2\alpha +1 \choose 2k+1}\,z^{2k+1}\,\sum _{j=0}^{\infty }{\alpha -k \choose j}\,z^{2j}=\sum _{k,j=0}^{\infty }{2\alpha +1 \choose 2k+1}{\alpha -k \choose j}\,z^{2k+2j+1}=\sum _{n=0}^{\infty }\underbrace {\sum _{k=0}^{n}{2\alpha +1 \choose 2k+1}{\alpha -k \choose n-k}} _{=A_{2n+1}}\,z^{2n+1}}
A
2
n
+
1
=
∑
k
=
0
∞
(
2
α
+
1
)
!
(
2
k
+
1
)
!
(
2
α
−
2
k
)
!
(
α
−
k
)
!
(
n
−
k
)
!
(
α
−
n
)
!
{\displaystyle A_{2n+1}=\sum _{k=0}^{\infty }{\frac {(2\alpha +1)!}{(2k+1)!\,(2\alpha -2k)!}}\,{\frac {(\alpha -k)!}{(n-k)!\,(\alpha -n)!}}}
=
(
2
α
+
1
)
!
(
α
−
n
)
!
∑
k
=
0
∞
(
α
−
k
)
!
2
2
k
+
1
π
(
k
+
1
2
)
!
k
!
2
2
α
−
2
k
π
(
α
−
k
)
!
(
α
−
1
2
−
k
)
!
(
n
−
k
)
!
{\displaystyle ={\frac {(2\alpha +1)!}{(\alpha -n)!}}\sum _{k=0}^{\infty }{\frac {(\alpha -k)!}{{\frac {2^{2k+1}}{\sqrt {\pi }}}\,\left(k+{\frac {1}{2}}\right)!\,k!\,{\frac {2^{2\alpha -2k}}{\sqrt {\pi }}}\,(\alpha -k)!\,\left(\alpha -{\frac {1}{2}}-k\right)!\,(n-k)!}}}
=
π
(
2
α
+
1
)
!
2
2
α
+
1
(
α
−
n
)
!
∑
k
=
0
∞
1
k
!
(
k
+
1
2
)
!
(
α
−
1
2
−
k
)
!
(
n
−
k
)
!
{\displaystyle ={\frac {\pi \,(2\alpha +1)!}{2^{2\alpha +1}\,(\alpha -n)!}}\,\sum _{k=0}^{\infty }{\frac {1}{k!\,\left(k+{\frac {1}{2}}\right)!\,\left(\alpha -{\frac {1}{2}}-k\right)!\,(n-k)!}}}
=
π
(
2
α
+
1
)
!
2
2
α
+
1
(
α
−
n
)
!
(
α
+
n
)
!
(
α
−
1
2
)
!
n
!
α
!
(
n
+
1
2
)
!
{\displaystyle ={\frac {\pi \,(2\alpha +1)!}{2^{2\alpha +1}\,(\alpha -n)!}}\,{\frac {(\alpha +n)!}{\left(\alpha -{\frac {1}{2}}\right)!\,n!\,\alpha !\,\left(n+{\frac {1}{2}}\right)!}}}
=
π
(
2
α
+
1
)
!
2
2
α
+
1
(
α
−
n
)
!
(
α
+
n
)
!
π
2
2
α
(
2
α
)
!
π
2
2
n
+
1
(
2
n
+
1
)
!
=
2
α
+
1
2
(
α
+
n
)
!
(
α
−
n
)
!
2
2
n
+
1
(
2
n
+
1
)
!
{\displaystyle ={\frac {\pi \,(2\alpha +1)!}{2^{2\alpha +1}\,(\alpha -n)!}}\,{\frac {(\alpha +n)!}{{\frac {\sqrt {\pi }}{2^{2\alpha }}}\,(2\alpha )!\,{\frac {\sqrt {\pi }}{2^{2n+1}}}\,(2n+1)!}}={\frac {2\alpha +1}{2}}\,{\frac {(\alpha +n)!}{(\alpha -n)!}}\,{\frac {2^{2n+1}}{(2n+1)!}}}
(
1
+
z
2
+
z
)
2
α
=
∑
k
=
0
∞
α
(
α
+
k
2
−
1
)
!
(
α
−
k
2
)
!
(
2
z
)
k
k
!
{\displaystyle \left({\sqrt {1+z^{2}}}+z\right)^{2\alpha }=\sum _{k=0}^{\infty }{\frac {\alpha \,\left(\alpha +{\frac {k}{2}}-1\right)!}{\left(\alpha -{\frac {k}{2}}\right)!}}\,{\frac {(2z)^{k}}{k!}}}
π
z
e
π
z
cosh
π
z
−
cos
π
z
=
1
π
z
3
+
1
z
2
+
π
2
z
+
4
∑
k
=
1
∞
1
z
2
+
(
z
−
2
k
)
2
+
8
z
∑
k
=
1
∞
k
e
2
π
k
−
1
1
z
4
+
4
k
4
{\displaystyle {\frac {\pi }{z}}\,{\frac {e^{\pi z}}{\cosh \pi z-\cos \pi z}}={\frac {1}{\pi z^{3}}}+{\frac {1}{z^{2}}}+{\frac {\pi }{2z}}+4\sum _{k=1}^{\infty }{\frac {1}{z^{2}+(z-2k)^{2}}}+8z\sum _{k=1}^{\infty }{\frac {k}{e^{2\pi k}-1}}\,{\frac {1}{z^{4}+4k^{4}}}}
Beweis
Die Funktion
f
(
z
)
=
π
z
⋅
e
π
z
cosh
π
z
−
cos
π
z
{\displaystyle f(z)={\frac {\pi }{z}}\cdot {\frac {e^{\pi z}}{\cosh \pi z-\cos \pi z}}}
z
=
0
{\displaystyle z=0}
f
{\displaystyle f\,}
z
=
0
{\displaystyle z=0}
1
π
z
3
+
1
z
2
+
π
2
z
{\displaystyle {\frac {1}{\pi z^{3}}}+{\frac {1}{z^{2}}}+{\frac {\pi }{2z}}}
f
{\displaystyle f\,}
z
=
k
⋅
(
±
1
±
i
)
k
=
1
,
2
,
3
,
.
.
.
{\displaystyle z=k\cdot (\pm 1\pm i)\quad k=1,2,3,...}
g
(
z
)
:=
∑
z
0
∈
N
(
±
1
±
i
)
res
(
f
,
z
0
)
z
−
z
0
{\displaystyle g(z):=\sum _{z_{0}\in \mathbb {N} (\pm 1\pm i)}{\frac {{\text{res}}(f,z_{0})}{z-z_{0}}}}
=
∑
k
=
1
∞
res
(
f
,
k
(
1
+
i
)
)
z
−
k
(
1
+
i
)
+
∑
k
=
1
∞
res
(
f
,
k
(
1
−
i
)
)
z
−
k
(
1
−
i
)
+
∑
k
=
1
∞
res
(
f
,
−
k
(
1
+
i
)
)
z
+
k
(
1
+
i
)
+
∑
k
=
1
∞
res
(
f
,
−
k
(
1
−
i
)
)
z
+
k
(
1
−
i
)
{\displaystyle =\sum _{k=1}^{\infty }{\frac {{\text{res}}{\Big (}f,k(1+i){\Big )}}{z-k(1+i)}}+\sum _{k=1}^{\infty }{\frac {{\text{res}}{\Big (}f,k(1-i){\Big )}}{z-k(1-i)}}+\sum _{k=1}^{\infty }{\frac {{\text{res}}{\Big (}f,-k(1+i){\Big )}}{z+k(1+i)}}+\sum _{k=1}^{\infty }{\frac {{\text{res}}{\Big (}f,-k(1-i){\Big )}}{z+k(1-i)}}}
res
(
f
,
k
(
1
+
i
)
)
=
1
i
k
e
2
π
k
e
2
π
k
−
1
res
(
f
,
−
k
(
1
+
i
)
)
=
1
i
k
1
e
2
π
k
−
1
{\displaystyle {\text{res}}{\Big (}f,k(1+i){\Big )}={\frac {1}{ik}}{\frac {e^{2\pi k}}{e^{2\pi k}-1}}\qquad {\text{res}}{\Big (}f,-k(1+i){\Big )}={\frac {1}{ik}}{\frac {1}{e^{2\pi k}-1}}}
res
(
f
,
k
(
1
−
i
)
)
=
−
1
i
k
e
2
π
k
e
2
π
k
−
1
res
(
f
,
−
k
(
1
−
i
)
)
=
−
1
i
k
1
e
2
π
k
−
1
{\displaystyle {\text{res}}{\Big (}f,k(1-i){\Big )}=-{\frac {1}{ik}}{\frac {e^{2\pi k}}{e^{2\pi k}-1}}\qquad {\text{res}}{\Big (}f,-k(1-i){\Big )}=-{\frac {1}{ik}}{\frac {1}{e^{2\pi k}-1}}}
g
(
z
)
=
∑
k
=
1
∞
1
i
k
+
1
i
k
1
e
2
π
k
−
1
z
−
k
(
1
+
i
)
−
∑
k
=
1
∞
1
i
k
+
1
i
k
1
e
2
π
k
−
1
z
−
k
(
1
−
i
)
+
∑
k
=
1
∞
1
i
k
1
e
2
π
k
−
1
z
+
k
(
1
+
i
)
−
∑
k
=
1
∞
1
i
k
1
e
2
π
k
−
1
z
+
k
(
1
−
i
)
{\displaystyle g(z)=\sum _{k=1}^{\infty }{\frac {{\frac {1}{ik}}+{\frac {1}{ik}}{\frac {1}{e^{2\pi k}-1}}}{z-k(1+i)}}-\sum _{k=1}^{\infty }{\frac {{\frac {1}{ik}}+{\frac {1}{ik}}{\frac {1}{e^{2\pi k}-1}}}{z-k(1-i)}}+\sum _{k=1}^{\infty }{\frac {{\frac {1}{ik}}{\frac {1}{e^{2\pi k}-1}}}{z+k(1+i)}}-\sum _{k=1}^{\infty }{\frac {{\frac {1}{ik}}{\frac {1}{e^{2\pi k}-1}}}{z+k(1-i)}}}
=
∑
k
=
1
∞
1
i
k
(
1
z
−
k
(
1
+
i
)
−
1
z
−
k
(
1
−
i
)
)
+
∑
k
=
1
∞
1
i
k
1
e
2
π
k
−
1
(
1
z
−
k
(
1
+
i
)
−
1
z
−
k
(
1
−
i
)
+
1
z
+
k
(
1
+
i
)
−
1
z
+
k
(
1
−
i
)
)
{\displaystyle =\sum _{k=1}^{\infty }{\frac {1}{ik}}\left({\frac {1}{z-k(1+i)}}-{\frac {1}{z-k(1-i)}}\right)+\sum _{k=1}^{\infty }{\frac {1}{ik}}\,{\frac {1}{e^{2\pi k}-1}}\left({\frac {1}{z-k(1+i)}}-{\frac {1}{z-k(1-i)}}+{\frac {1}{z+k(1+i)}}-{\frac {1}{z+k(1-i)}}\right)}
=
4
∑
k
=
1
∞
1
z
2
+
(
z
−
2
k
)
2
+
8
z
∑
k
=
1
∞
k
e
2
π
k
−
1
1
z
4
+
4
k
4
{\displaystyle =4\,\sum _{k=1}^{\infty }{\frac {1}{z^{2}+(z-2k)^{2}}}+8z\,\sum _{k=1}^{\infty }{\frac {k}{e^{2\pi k}-1}}\,{\frac {1}{z^{4}+4k^{4}}}}
h
(
z
)
:=
f
(
z
)
−
1
π
z
3
−
1
z
2
−
π
2
z
−
g
(
z
)
{\displaystyle h(z):=f(z)-{\frac {1}{\pi z^{3}}}-{\frac {1}{z^{2}}}-{\frac {\pi }{2z}}-g(z)}
C
{\displaystyle \mathbb {C} }
h
(
z
)
→
0
{\displaystyle h(z)\to 0}
|
z
|
→
∞
{\displaystyle |z|\to \infty }
h
{\displaystyle h}
h
(
0
)
=
0
{\displaystyle h(0)=0}
f
(
z
)
=
1
π
z
3
+
1
z
2
+
π
2
z
+
g
(
z
)
{\displaystyle f(z)={\frac {1}{\pi z^{3}}}+{\frac {1}{z^{2}}}+{\frac {\pi }{2z}}+g(z)}
π
2
sinh
π
z
cosh
π
z
−
cos
π
z
=
1
2
z
+
∑
k
=
1
∞
z
z
2
+
(
z
−
2
k
)
2
+
∑
k
=
1
∞
z
z
2
+
(
z
+
2
k
)
2
{\displaystyle {\frac {\pi }{2}}\,{\frac {\sinh \pi z}{\cosh \pi z-\cos \pi z}}={\frac {1}{2z}}+\sum _{k=1}^{\infty }{\frac {z}{z^{2}+(z-2k)^{2}}}+\sum _{k=1}^{\infty }{\frac {z}{z^{2}+(z+2k)^{2}}}}
Beweis
Betrachte folgende Formel:
π
z
e
π
z
cosh
π
z
−
cos
π
z
=
1
π
z
3
+
1
z
2
+
π
2
z
+
4
∑
k
=
1
∞
1
z
2
+
(
z
−
2
k
)
2
+
8
z
∑
k
=
1
∞
k
e
2
π
k
−
1
1
z
4
+
4
k
4
{\displaystyle {\frac {\pi }{z}}\,{\frac {e^{\pi z}}{\cosh \pi z-\cos \pi z}}={\frac {1}{\pi z^{3}}}+{\frac {1}{z^{2}}}+{\frac {\pi }{2z}}+4\,\sum _{k=1}^{\infty }{\frac {1}{z^{2}+(z-2k)^{2}}}+8z\,\sum _{k=1}^{\infty }{\frac {k}{e^{2\pi k}-1}}\,{\frac {1}{z^{4}+4k^{4}}}}
z
{\displaystyle z\,}
−
z
{\displaystyle -z\,}
−
π
z
e
−
π
z
cosh
π
z
−
cos
π
z
=
−
1
π
z
3
+
1
z
2
−
π
2
z
+
4
∑
k
=
1
∞
1
z
2
+
(
z
+
2
k
)
2
−
8
z
∑
k
=
1
∞
k
e
2
π
k
−
1
1
z
4
+
4
k
4
{\displaystyle -{\frac {\pi }{z}}\,{\frac {e^{-\pi z}}{\cosh \pi z-\cos \pi z}}=-{\frac {1}{\pi z^{3}}}+{\frac {1}{z^{2}}}-{\frac {\pi }{2z}}+4\,\sum _{k=1}^{\infty }{\frac {1}{z^{2}+(z+2k)^{2}}}-8z\,\sum _{k=1}^{\infty }{\frac {k}{e^{2\pi k}-1}}\,{\frac {1}{z^{4}+4k^{4}}}}
π
z
2
sinh
π
z
cosh
π
z
−
cos
π
z
=
2
z
2
+
4
∑
k
=
1
∞
1
z
2
+
(
z
−
2
k
)
2
+
4
∑
k
=
1
∞
1
z
2
+
(
z
+
2
k
)
2
{\displaystyle {\frac {\pi }{z}}\,{\frac {2\sinh \pi z}{\cosh \pi z-\cos \pi z}}={\frac {2}{z^{2}}}+4\,\sum _{k=1}^{\infty }{\frac {1}{z^{2}+(z-2k)^{2}}}+4\,\sum _{k=1}^{\infty }{\frac {1}{z^{2}+(z+2k)^{2}}}}
z
4
{\displaystyle {\frac {z}{4}}}
π
2
sinh
π
z
cosh
π
z
−
cos
π
z
=
1
2
z
+
∑
k
=
1
∞
z
z
2
+
(
z
−
2
k
)
2
+
∑
k
=
1
∞
z
z
2
+
(
z
+
2
k
)
2
{\displaystyle {\frac {\pi }{2}}\,{\frac {\sinh \pi z}{\cosh \pi z-\cos \pi z}}={\frac {1}{2z}}+\sum _{k=1}^{\infty }{\frac {z}{z^{2}+(z-2k)^{2}}}+\sum _{k=1}^{\infty }{\frac {z}{z^{2}+(z+2k)^{2}}}}
(
1
+
z
)
1
/
z
=
∑
n
=
0
∞
∑
k
=
n
∞
1
k
!
[
k
k
−
n
]
z
n
|
z
|
≤
1
,
z
≠
0
,
1
{\displaystyle (1+z)^{1/z}=\sum _{n=0}^{\infty }\sum _{k=n}^{\infty }{\frac {1}{k!}}{\begin{bmatrix}k\\k-n\end{bmatrix}}\,z^{n}\qquad |z|\leq 1\;,\;z\neq 0,1}
Zu
x
0
,
y
0
∈
C
{\displaystyle x_{0},y_{0}\in \mathbb {C} }
U
(
x
0
)
,
V
(
y
0
)
{\displaystyle U(x_{0}),V(y_{0})\,}
f
:
U
(
x
0
)
→
V
(
y
0
)
,
x
↦
y
0
+
∑
k
=
1
∞
y
k
(
x
−
x
0
)
k
{\displaystyle f:U(x_{0})\to V(y_{0})\;,\;x\mapsto y_{0}+\sum _{k=1}^{\infty }y_{k}(x-x_{0})^{k}}
Für die Koeffizienten
x
n
(
n
≥
1
)
{\displaystyle x_{n}\,(n\geq 1)}
f
−
1
:
V
(
y
0
)
→
U
(
x
0
)
,
y
↦
x
0
+
∑
k
=
1
∞
x
k
(
y
−
y
0
)
k
{\displaystyle f^{-1}:V(y_{0})\to U(x_{0})\,,\,y\mapsto x_{0}+\sum _{k=1}^{\infty }x_{k}(y-y_{0})^{k}}
gibt es die Formel
x
n
=
1
n
!
[
d
n
−
1
d
x
n
−
1
(
x
−
x
0
f
(
x
)
−
f
(
x
0
)
)
n
]
x
→
x
0
{\displaystyle x_{n}={\frac {1}{n!}}\,\left[{\frac {\mathrm {d} ^{n-1}}{\mathrm {d} x^{n-1}}}\left({\frac {x-x_{0}}{f(x)-f(x_{0})}}\right)^{n}\,\right]_{x\to x_{0}}}
Beweis
Setzt man
g
:=
f
−
1
{\displaystyle g:=f^{-1}\,}
f
(
x
0
)
=
y
0
{\displaystyle f(x_{0})=y_{0}\,}
g
(
y
0
)
=
x
0
{\displaystyle g(y_{0})=x_{0}\,}
g
′
(
y
)
=
∑
k
=
1
∞
k
x
k
(
y
−
y
0
)
k
−
1
{\displaystyle g'(y)=\sum _{k=1}^{\infty }k\,x_{k}\,(y-y_{0})^{k-1}}
g
′
(
y
0
)
=
x
1
≠
0
{\displaystyle g'(y_{0})=x_{1}\neq 0\,}
n
x
n
=
res
(
g
′
(
y
)
(
y
−
y
0
)
n
,
y
=
y
0
)
{\displaystyle n\,x_{n}={\text{res}}\left({\frac {g'(y)}{(y-y_{0})^{n}}}\,,\,y=y_{0}\right)}
1
2
π
i
∮
γ
g
′
(
y
)
(
y
−
y
0
)
n
d
y
{\displaystyle {\frac {1}{2\pi i}}\oint _{\gamma }{\frac {g'(y)}{(y-y_{0})^{n}}}\,\mathrm {d} y}
γ
{\displaystyle \gamma \,}
x
0
{\displaystyle x_{0}\,}
y
=
f
(
x
)
{\displaystyle y=f(x)\,}
n
x
n
=
1
2
π
i
∮
g
(
γ
)
g
′
(
f
(
x
)
)
(
f
(
x
)
−
f
(
x
0
)
)
n
f
′
(
x
)
d
x
{\displaystyle n\,x_{n}={\frac {1}{2\pi i}}\oint _{g(\gamma )}{\frac {g'(f(x))}{{\big (}f(x)-f(x_{0}){\big )}^{n}}}\,f'(x)\,\mathrm {d} x}
=
1
2
π
i
∮
g
(
γ
)
1
(
f
(
x
)
−
f
(
x
0
)
)
n
d
x
=
res
(
1
(
f
(
x
)
−
f
(
x
0
)
)
n
,
x
=
x
0
)
{\displaystyle ={\frac {1}{2\pi i}}\oint _{g(\gamma )}{\frac {1}{{\big (}f(x)-f(x_{0}){\big )}^{n}}}\,\mathrm {d} x={\text{res}}\left({\frac {1}{(f(x)-f(x_{0}))^{n}}}\,,\,x=x_{0}\right)}
f
′
(
x
0
)
≠
0
{\displaystyle f'(x_{0})\neq 0\,}
n
{\displaystyle n\,}
n
x
n
=
1
(
n
−
1
)
!
lim
x
→
x
0
d
n
−
1
d
x
n
−
1
(
x
−
x
0
)
n
(
f
(
x
)
−
f
(
x
0
)
)
n
{\displaystyle n\,x_{n}={\frac {1}{(n-1)!}}\,\lim _{x\to x_{0}}{\frac {\mathrm {d} ^{n-1}}{\mathrm {d} x^{n-1}}}{\frac {(x-x_{0})^{n}}{(f(x)-f(x_{0}))^{n}}}}
(
1
+
x
)
n
≥
1
+
n
x
n
∈
N
,
x
≥
−
1
{\displaystyle (1+x)^{n}\geq 1+nx\qquad n\in \mathbb {N} ,\,x\geq -1}
Beweis
Induktionsanfang:
(
1
+
x
)
0
≥
1
{\displaystyle (1+x)^{0}\geq 1}
(
1
+
x
)
n
+
1
=
(
1
+
x
)
n
(
1
+
x
)
≥
(
1
+
n
x
)
(
1
+
x
)
=
1
+
(
n
+
1
)
x
+
n
x
2
≥
1
+
(
n
+
1
)
x
{\displaystyle (1+x)^{n+1}=(1+x)^{n}\,(1+x)\geq (1+nx)(1+x)=1+(n+1)x+nx^{2}\geq 1+(n+1)x}
|
z
1
+
z
2
|
≤
|
z
1
|
+
|
z
2
|
z
1
,
z
2
∈
C
{\displaystyle |z_{1}+z_{2}|\leq |z_{1}|+|z_{2}|\qquad z_{1},z_{2}\in \mathbb {C} }
|
∑
k
=
1
n
z
k
|
≤
∑
k
=
1
n
|
z
k
|
z
1
,
.
.
.
,
z
n
∈
C
{\displaystyle \left|\sum _{k=1}^{n}z_{k}\right|\leq \sum _{k=1}^{n}|z_{k}|\qquad z_{1},...,z_{n}\in \mathbb {C} }
Beweis
Die Dreiecksungleichung
|
z
1
+
z
2
|
≤
|
z
1
|
+
|
z
2
|
{\displaystyle |z_{1}+z_{2}|\leq |z_{1}|+|z_{2}|}
|
∑
k
=
1
n
+
1
z
k
|
≤
|
∑
k
=
1
n
z
k
|
+
|
z
n
+
1
|
≤
∑
k
=
1
n
|
z
k
|
+
|
z
n
+
1
|
{\displaystyle \left|\sum _{k=1}^{n+1}z_{k}\right|\leq \left|\sum _{k=1}^{n}z_{k}\right|+|z_{n+1}|\leq \sum _{k=1}^{n}|z_{k}|+|z_{n+1}|}
Sind
x
=
(
x
1
,
.
.
.
,
x
n
)
{\displaystyle {\boldsymbol {x}}=(x_{1},...,x_{n})}
y
=
(
y
1
,
.
.
.
,
y
n
)
{\displaystyle {\boldsymbol {y}}=(y_{1},...,y_{n})}
(
∑
k
=
1
n
x
k
y
k
)
2
≤
(
∑
k
=
1
n
x
k
2
)
(
∑
k
=
1
n
y
k
2
)
.
{\displaystyle \left(\sum _{k=1}^{n}x_{k}y_{k}\right)^{2}\leq \left(\sum _{k=1}^{n}x_{k}^{2}\right)\left(\sum _{k=1}^{n}y_{k}^{2}\right).}
|
⟨
x
,
y
⟩
|
≤
‖
x
‖
⋅
‖
y
‖
{\displaystyle |\langle {\boldsymbol {x}},{\boldsymbol {y}}\rangle |\leq \|{\boldsymbol {x}}\|\cdot \|{\boldsymbol {y}}\|}
Beweis
0
≤
‖
x
−
λ
y
‖
2
=
⟨
x
−
λ
y
,
x
−
λ
y
⟩
=
‖
x
‖
2
−
2
λ
⟨
x
,
y
⟩
+
λ
2
‖
y
‖
2
{\displaystyle 0\leq \|{\boldsymbol {x}}-\lambda {\boldsymbol {y}}\|^{2}=\langle {\boldsymbol {x}}-\lambda {\boldsymbol {y}},{\boldsymbol {x}}-\lambda {\boldsymbol {y}}\rangle =\|{\boldsymbol {x}}\|^{2}-2\lambda \langle {\boldsymbol {x}},{\boldsymbol {y}}\rangle +\lambda ^{2}\|{\boldsymbol {y}}\|^{2}}
λ
=
⟨
x
,
y
⟩
‖
y
‖
2
:
0
≤
‖
x
‖
2
−
2
⟨
x
,
y
⟩
2
‖
y
‖
2
+
⟨
x
,
y
⟩
2
‖
y
‖
2
⇒
⟨
x
,
y
⟩
2
‖
y
‖
2
≤
‖
x
‖
2
⇒
⟨
x
,
y
⟩
2
≤
‖
x
‖
2
⋅
‖
y
‖
2
{\displaystyle \lambda ={\frac {\langle {\boldsymbol {x}},{\boldsymbol {y}}\rangle }{\|{\boldsymbol {y}}\|^{2}}}\,:\quad 0\leq \|{\boldsymbol {x}}\|^{2}-2\,{\frac {\langle {\boldsymbol {x}},{\boldsymbol {y}}\rangle ^{2}}{\|{\boldsymbol {y}}\|^{2}}}+{\frac {\langle {\boldsymbol {x}},{\boldsymbol {y}}\rangle ^{2}}{\|{\boldsymbol {y}}\|^{2}}}\,\Rightarrow \,{\frac {\langle {\boldsymbol {x}},{\boldsymbol {y}}\rangle ^{2}}{\|{\boldsymbol {y}}\|^{2}}}\leq \|{\boldsymbol {x}}\|^{2}\,\Rightarrow \,\langle {\boldsymbol {x}},{\boldsymbol {y}}\rangle ^{2}\leq \|{\boldsymbol {x}}\|^{2}\cdot \|{\boldsymbol {y}}\|^{2}}
Für
x
1
,
.
.
.
,
x
n
>
0
{\displaystyle x_{1},...,x_{n}>0}
w
=
(
w
1
,
.
.
.
,
w
n
)
{\displaystyle w=(w_{1},...,w_{n})}
∑
k
=
1
n
w
k
=
1
{\displaystyle \sum _{k=1}^{n}w_{k}=1}
und ein
p
∈
R
∖
{
0
}
{\displaystyle p\in \mathbb {R} \setminus \{0\}}
M
w
p
:=
(
∑
k
=
1
n
w
k
x
k
p
)
1
p
{\displaystyle M_{w}^{p}:=\left(\sum _{k=1}^{n}w_{k}x_{k}^{p}\right)^{\frac {1}{p}}}
Es gilt
M
w
0
:=
lim
p
→
0
M
w
p
=
∏
k
=
1
n
x
k
w
k
{\displaystyle M_{w}^{0}:=\lim _{p\to 0}M_{w}^{p}=\prod _{k=1}^{n}x_{k}^{w_{k}}}
r
<
s
{\displaystyle r<s\,}
M
w
r
≤
M
w
s
{\displaystyle M_{w}^{r}\leq M_{w}^{s}}
Beweis
lim
p
→
0
log
(
M
w
p
)
=
lim
p
→
0
1
p
log
(
∑
k
=
1
n
w
k
x
k
p
)
{\displaystyle \lim _{p\to 0}\log(M_{w}^{p})=\lim _{p\to 0}{\frac {1}{p}}\log \left(\sum _{k=1}^{n}w_{k}\,x_{k}^{p}\right)}
=
L.H.
lim
p
→
0
∑
k
=
1
n
w
k
x
k
p
log
x
k
∑
k
=
1
n
w
k
x
k
p
=
∑
k
=
1
n
w
k
log
x
k
=
log
∏
k
=
1
n
x
k
w
k
{\displaystyle {\stackrel {\text{L.H.}}{=}}\lim _{p\to 0}{\frac {\sum \limits _{k=1}^{n}w_{k}\,x_{k}^{p}\,\log x_{k}}{\sum \limits _{k=1}^{n}w_{k}\,x_{k}^{p}}}=\sum _{k=1}^{n}w_{k}\log x_{k}=\log \prod _{k=1}^{n}x_{k}^{w_{k}}}
0
<
r
<
s
{\displaystyle 0<r<s\,}
f
:
R
+
→
R
+
,
x
↦
x
s
r
{\displaystyle f:\mathbb {R} ^{+}\to \mathbb {R} ^{+}\,,\,x\mapsto x^{\frac {s}{r}}}
(
∑
k
=
1
n
w
k
x
k
r
)
s
r
≤
∑
k
=
1
n
w
k
(
x
k
r
)
s
r
⇒
(
∑
k
=
1
n
w
k
x
k
r
)
1
r
≤
(
∑
k
=
1
n
w
k
x
k
s
)
1
s
{\displaystyle \left(\sum _{k=1}^{n}w_{k}\,x_{k}^{r}\right)^{\frac {s}{r}}\leq \sum _{k=1}^{n}w_{k}\,\left(x_{k}^{r}\right)^{\frac {s}{r}}\,\Rightarrow \,\left(\sum _{k=1}^{n}w_{k}\,x_{k}^{r}\right)^{\frac {1}{r}}\leq \left(\sum _{k=1}^{n}w_{k}\,x_{k}^{s}\right)^{\frac {1}{s}}}
r
<
s
<
0
{\displaystyle r<s<0\,}
0
<
−
s
<
−
r
{\displaystyle 0<-s<-r}
(
∑
k
=
1
n
w
k
x
k
−
s
)
1
−
s
≤
(
∑
k
=
1
n
w
k
x
k
−
r
)
1
−
r
{\displaystyle \left(\sum _{k=1}^{n}w_{k}\,x_{k}^{-s}\right)^{\frac {1}{-s}}\leq \left(\sum _{k=1}^{n}w_{k}\,x_{k}^{-r}\right)^{\frac {1}{-r}}}
(
∑
k
=
1
n
w
k
x
k
−
r
)
1
r
≤
(
∑
k
=
1
n
w
k
x
k
−
s
)
1
s
{\displaystyle \left(\sum _{k=1}^{n}w_{k}\,x_{k}^{-r}\right)^{\frac {1}{r}}\leq \left(\sum _{k=1}^{n}w_{k}\,x_{k}^{-s}\right)^{\frac {1}{s}}}
x
1
,
.
.
.
,
x
n
>
0
{\displaystyle x_{1},...,x_{n}>0\,}
x
k
{\displaystyle x_{k}\,}
1
x
k
{\displaystyle {\frac {1}{x_{k}}}\,}
(
∑
k
=
1
n
w
k
x
k
r
)
1
r
≤
(
∑
k
=
1
n
w
k
x
k
s
)
1
s
{\displaystyle \left(\sum _{k=1}^{n}w_{k}\,x_{k}^{r}\right)^{\frac {1}{r}}\leq \left(\sum _{k=1}^{n}w_{k}\,x_{k}^{s}\right)^{\frac {1}{s}}}
lim
s
→
0
M
w
s
=
M
w
0
=
lim
r
→
0
M
w
r
{\displaystyle \lim _{s\to 0}M_{w}^{s}=M_{w}^{0}=\lim _{r\to 0}M_{w}^{r}}
M
w
r
≤
M
w
s
{\displaystyle M_{w}^{r}\leq M_{w}^{s}}
0
≤
r
<
s
{\displaystyle 0\leq r<s}
r
<
s
≤
0
{\displaystyle r<s\leq 0}
r
<
0
<
s
{\displaystyle r<0<s\,}
M
w
r
≤
M
w
s
{\displaystyle M_{w}^{r}\leq M_{w}^{s}}
M
w
r
≤
M
w
0
≤
M
w
s
{\displaystyle M_{w}^{r}\leq M_{w}^{0}\leq M_{w}^{s}}
Insbesondere ergibt sich daraus die Ungleichungskette
1
w
1
x
1
+
.
.
.
+
w
n
x
n
⏟
harmonisches
Mittel
≤
x
1
w
1
⋯
x
n
w
n
⏟
geometrisches
Mittel
≤
w
1
x
1
+
.
.
.
+
w
n
x
n
⏟
arithmetisches
Mittel
≤
w
1
x
1
2
+
.
.
.
+
w
n
x
n
2
⏟
quadratisches
Mittel
≤
w
1
x
1
3
+
.
.
.
+
w
n
x
n
3
3
⏟
kubisches
Mittel
{\displaystyle \underbrace {\frac {1}{{\frac {w_{1}}{x_{1}}}+...+{\frac {w_{n}}{x_{n}}}}} _{\begin{matrix}{\text{harmonisches}}\\{\text{Mittel}}\end{matrix}}\leq \underbrace {x_{1}^{w_{1}}\cdots x_{n}^{w_{n}}} _{\begin{matrix}{\text{geometrisches}}\\{\text{Mittel}}\end{matrix}}\leq \underbrace {w_{1}x_{1}+...+w_{n}x_{n}} _{\begin{matrix}{\text{arithmetisches}}\\{\text{Mittel}}\end{matrix}}\leq \underbrace {\sqrt {w_{1}x_{1}^{2}+...+w_{n}x_{n}^{2}}} _{\begin{matrix}{\text{quadratisches}}\\{\text{Mittel}}\end{matrix}}\leq \underbrace {\sqrt[{3}]{w_{1}x_{1}^{3}+...+w_{n}x_{n}^{3}}} _{\begin{matrix}{\text{kubisches}}\\{\text{Mittel}}\end{matrix}}}
Und daraus wiederum ergibt sich im ungewichteten/gleichgewichteten Fall
w
=
(
1
/
n
,
.
.
.
,
1
/
n
)
{\displaystyle w=\left(1/n,...,1/n\right)}
n
1
x
1
+
.
.
.
+
1
x
n
⏟
harmonisches
Mittel
≤
x
1
⋯
x
n
n
⏟
geometrisches
Mittel
≤
x
1
+
.
.
.
+
x
n
n
⏟
arithmetisches
Mittel
≤
x
1
2
+
.
.
.
+
x
n
2
n
⏟
quadratisches
Mittel
≤
x
1
3
+
.
.
.
+
x
n
3
n
3
⏟
kubisches
Mittel
{\displaystyle \underbrace {\frac {n}{{\frac {1}{x_{1}}}+...+{\frac {1}{x_{n}}}}} _{\begin{matrix}{\text{harmonisches}}\\{\text{Mittel}}\end{matrix}}\leq \underbrace {\sqrt[{n}]{x_{1}\cdots x_{n}}} _{\begin{matrix}{\text{geometrisches}}\\{\text{Mittel}}\end{matrix}}\leq \underbrace {\frac {x_{1}+...+x_{n}}{n}} _{\begin{matrix}{\text{arithmetisches}}\\{\text{Mittel}}\end{matrix}}\leq \underbrace {\sqrt {\frac {x_{1}^{2}+...+x_{n}^{2}}{n}}} _{\begin{matrix}{\text{quadratisches}}\\{\text{Mittel}}\end{matrix}}\leq \underbrace {\sqrt[{3}]{\frac {x_{1}^{3}+...+x_{n}^{3}}{n}}} _{\begin{matrix}{\text{kubisches}}\\{\text{Mittel}}\end{matrix}}}
Für die nichtnegativen Variablen
a
1
,
.
.
.
,
a
n
{\displaystyle a_{1},...,a_{n}}
sei
σ
k
(
a
)
=
∑
1
≤
i
1
<
.
.
.
<
i
k
≤
n
a
i
1
⋯
a
i
k
{\displaystyle \sigma _{k}({\boldsymbol {a}})=\sum _{1\leq i_{1}<...<i_{k}\leq n}a_{i_{1}}\cdots a_{i_{k}}}
und
S
k
(
a
)
=
σ
k
(
a
)
(
n
k
)
{\displaystyle S_{k}({\boldsymbol {a}})={\frac {\sigma _{k}({\boldsymbol {a}})}{n \choose k}}}
Es gilt
S
1
(
a
)
≥
S
2
(
a
)
≥
S
3
(
a
)
3
≥
.
.
.
≥
S
n
(
a
)
n
{\displaystyle S_{1}({\boldsymbol {a}})\geq {\sqrt {S_{2}({\boldsymbol {a}})}}\geq {\sqrt[{3}]{S_{3}({\boldsymbol {a}})}}\geq ...\geq {\sqrt[{n}]{S_{n}({\boldsymbol {a}})}}}
Beweis
F
(
X
)
:=
(
X
+
a
1
)
⋯
(
X
+
a
n
)
{\displaystyle F(X):=(X+a_{1})\cdots (X+a_{n})}
∑
k
=
0
n
σ
k
(
a
)
⋅
X
n
−
k
=
∑
k
=
0
n
(
n
k
)
⋅
S
k
(
a
)
⋅
X
n
−
k
{\displaystyle \sum _{k=0}^{n}\sigma _{k}({\boldsymbol {a}})\cdot X^{n-k}=\sum _{k=0}^{n}{n \choose k}\cdot S_{k}({\boldsymbol {a}})\cdot X^{n-k}}
a
k
<
a
k
+
1
{\displaystyle a_{k}<a_{k+1}\,}
b
k
∈
]
a
k
,
a
k
+
1
[
{\displaystyle b_{k}\in \,\,]a_{k},a_{k+1}[}
F
′
(
b
k
)
=
0
{\displaystyle F'(b_{k})=0}
a
k
=
a
k
+
1
{\displaystyle a_{k}=a_{k+1}}
b
k
=
a
k
{\displaystyle b_{k}=a_{k}}
F
′
(
b
k
)
=
0
{\displaystyle F'(b_{k})=0}
F
′
{\displaystyle F'\,}
F
′
(
X
)
=
n
⋅
(
X
+
b
1
)
⋯
(
X
+
b
n
−
1
)
{\displaystyle F'(X)=n\cdot (X+b_{1})\cdots (X+b_{n-1})}
b
1
≤
.
.
.
≤
b
n
−
1
{\displaystyle b_{1}\leq ...\leq b_{n-1}}
F
′
(
X
)
=
d
d
x
∑
k
=
0
n
(
n
k
)
⋅
S
k
(
a
)
⋅
X
n
−
k
=
∑
k
=
0
n
n
!
(
n
−
k
)
!
k
!
⋅
S
k
(
a
)
⋅
(
n
−
k
)
⋅
X
n
−
1
−
k
=
n
∑
k
=
0
n
−
1
(
n
−
1
k
)
⋅
S
k
(
a
)
⋅
X
n
−
1
−
k
{\displaystyle F'(X)={\frac {d}{dx}}\sum _{k=0}^{n}{n \choose k}\cdot S_{k}({\boldsymbol {a}})\cdot X^{n-k}=\sum _{k=0}^{n}{\frac {n!}{(n-k)!\,k!}}\cdot S_{k}({\boldsymbol {a}})\cdot (n-k)\cdot X^{n-1-k}=n\sum _{k=0}^{n-1}{n-1 \choose k}\cdot S_{k}({\boldsymbol {a}})\cdot X^{n-1-k}}
F
′
(
X
)
=
n
∑
k
=
0
n
−
1
σ
k
(
b
)
⋅
X
n
−
1
−
k
=
n
∑
k
=
0
n
−
1
(
n
−
1
k
)
⋅
S
k
(
b
)
⋅
X
n
−
1
−
k
{\displaystyle F'(X)=n\sum _{k=0}^{n-1}\sigma _{k}({\boldsymbol {b}})\cdot X^{n-1-k}=n\sum _{k=0}^{n-1}{n-1 \choose k}\cdot S_{k}({\boldsymbol {b}})\cdot X^{n-1-k}}
a
{\displaystyle {\boldsymbol {a}}\,}
b
{\displaystyle {\boldsymbol {b}}\,}
S
k
(
a
)
=
S
k
(
b
)
{\displaystyle S_{k}({\boldsymbol {a}})=S_{k}({\boldsymbol {b}})}
F
{\displaystyle F\,}
≤
0
{\displaystyle \leq 0}
F
(
n
−
m
)
(
X
)
=
n
!
m
!
(
X
+
r
1
)
⋯
(
X
+
r
m
)
=
(
d
d
x
)
n
−
m
∑
k
=
0
n
(
n
k
)
⋅
S
k
(
a
)
⋅
X
n
−
k
{\displaystyle F^{(n-m)}(X)={\frac {n!}{m!}}(X+r_{1})\cdots (X+r_{m})=\left({\frac {d}{dx}}\right)^{\!\!n-m}\sum _{k=0}^{n}{n \choose k}\cdot S_{k}({\boldsymbol {a}})\cdot X^{n-k}}
=
∑
k
=
0
m
n
!
(
n
−
k
)
!
k
!
⋅
S
k
(
a
)
⋅
(
n
−
k
)
!
(
m
−
k
)
!
⋅
X
m
−
k
=
n
!
m
!
⋅
∑
k
=
0
m
(
m
k
)
⋅
S
k
(
a
)
⋅
X
m
−
k
{\displaystyle =\sum _{k=0}^{m}{\frac {n!}{(n-k)!\,k!}}\cdot S_{k}({\boldsymbol {a}})\cdot {\frac {(n-k)!}{(m-k)!}}\cdot X^{m-k}={\frac {n!}{m!}}\cdot \sum _{k=0}^{m}{m \choose k}\cdot S_{k}({\boldsymbol {a}})\cdot X^{m-k}}
F
(
n
−
m
)
(
X
)
{\displaystyle F^{(n-m)}(X)\,}
n
!
m
!
⋅
∑
k
=
0
m
(
m
k
)
⋅
S
k
(
r
)
⋅
X
m
−
k
{\displaystyle {\frac {n!}{m!}}\cdot \sum _{k=0}^{m}{m \choose k}\cdot S_{k}({\boldsymbol {r}})\cdot X^{m-k}}
S
k
(
r
)
{\displaystyle S_{k}({\boldsymbol {r}})\,}
S
k
(
a
)
{\displaystyle S_{k}({\boldsymbol {a}})\,}
r
1
⋯
r
m
=
S
m
(
a
)
{\displaystyle r_{1}\cdots r_{m}=S_{m}({\boldsymbol {a}})}
r
1
^
r
2
⋯
r
m
+
r
1
r
2
^
⋯
r
m
+
.
.
.
+
r
1
r
2
⋯
r
m
^
=
r
1
⋯
r
m
⋅
(
1
r
1
+
.
.
.
+
1
r
m
)
=
m
⋅
S
m
−
1
(
a
)
{\displaystyle {\widehat {r_{1}}}\,r_{2}\cdots r_{m}+r_{1}\,{\widehat {r_{2}}}\cdots r_{m}+...+r_{1}\,r_{2}\cdots {\widehat {r_{m}}}=r_{1}\cdots r_{m}\cdot \left({\frac {1}{r_{1}}}+...+{\frac {1}{r_{m}}}\right)=m\cdot S_{m-1}({\boldsymbol {a}})}
r
1
^
r
2
⋯
r
m
+
r
1
r
2
^
⋯
r
m
+
.
.
.
+
r
1
r
2
⋯
r
m
^
m
≥
(
r
1
r
2
⋯
r
m
)
m
r
1
r
2
⋯
r
m
m
{\displaystyle {\frac {{\widehat {r_{1}}}\,r_{2}\cdots r_{m}+r_{1}\,{\widehat {r_{2}}}\cdots r_{m}+...+r_{1}\,r_{2}\cdots {\widehat {r_{m}}}}{m}}\geq {\sqrt[{m}]{\frac {(r_{1}\,r_{2}\cdots r_{m})^{m}}{r_{1}\,r_{2}\cdots r_{m}}}}}
m
⋅
S
m
−
1
(
a
)
m
≥
S
m
(
a
)
m
−
1
m
⇒
S
m
−
1
(
a
)
m
−
1
≥
S
m
(
a
)
m
{\displaystyle {\frac {m\cdot S_{m-1}({\boldsymbol {a}})}{m}}\geq {\sqrt[{m}]{S_{m}({\boldsymbol {a}})^{m-1}}}\,\Rightarrow \,{\sqrt[{m-1}]{S_{m-1}({\boldsymbol {a}})}}\geq {\sqrt[{m}]{S_{m}({\boldsymbol {a}})}}}
Und es gilt
S
m
(
a
)
2
≥
S
m
+
1
(
a
)
⋅
S
m
−
1
(
a
)
{\displaystyle S_{m}({\boldsymbol {a}})^{2}\geq S_{m+1}({\boldsymbol {a}})\cdot S_{m-1}({\boldsymbol {a}})}
m
=
1
,
.
.
.
,
n
−
1
{\displaystyle m=1,...,n-1}
Beweis (Newton Ungleichung)
Für
n
{\displaystyle n\,}
ν
≥
0
,
x
>
0
{\displaystyle {\boldsymbol {\nu }}\geq {\boldsymbol {0}},\,{\boldsymbol {x}}>{\boldsymbol {0}}}
S
{
ν
}
(
x
)
:=
1
n
!
∑
sym
x
1
ν
1
⋯
x
n
ν
n
:=
1
n
!
∑
σ
∈
S
n
x
σ
1
ν
1
⋯
x
σ
n
ν
n
{\displaystyle {\mathcal {S}}\{{\boldsymbol {\nu }}\}({\boldsymbol {x}}):={\frac {1}{n!}}\sum _{\text{sym}}x_{1}^{\nu _{1}}\cdots x_{n}^{\nu _{n}}:={\frac {1}{n!}}\sum _{{\boldsymbol {\sigma }}\in S_{n}}x_{\sigma _{1}}^{\nu _{1}}\cdots x_{\sigma _{n}}^{\nu _{n}}}
Sind
α
,
β
≥
0
{\displaystyle {\boldsymbol {\alpha }},{\boldsymbol {\beta }}\geq {\boldsymbol {0}}}
α
≺
β
⟺
S
{
α
}
(
x
)
≤
S
{
β
}
(
x
)
∀
x
>
0
{\displaystyle {\boldsymbol {\alpha }}\prec {\boldsymbol {\beta }}\iff {\mathcal {S}}\{{\boldsymbol {\alpha }}\}({\boldsymbol {x}})\leq {\mathcal {S}}\{{\boldsymbol {\beta }}\}({\boldsymbol {x}})\;\,\forall {\boldsymbol {x}}>{\boldsymbol {0}}}
x
y
z
3
≤
1
2
(
x
−
y
)
(
y
−
z
)
(
z
−
x
)
(
x
−
y
)
log
z
+
(
y
−
z
)
log
x
+
(
z
−
x
)
log
y
≤
x
+
y
+
z
3
x
>
y
>
z
>
0
{\displaystyle {\sqrt[{3}]{xyz}}\leq {\sqrt {{\frac {1}{2}}\,{\frac {(x-y)(y-z)(z-x)}{(x-y)\log z+(y-z)\log x+(z-x)\log y}}}}\leq {\frac {x+y+z}{3}}\qquad x>y>z>0}
(
1
+
1
n
)
n
<
e
<
(
1
+
1
n
)
n
+
1
2
{\displaystyle \left(1+{\frac {1}{n}}\right)^{n}<e<\left(1+{\frac {1}{n}}\right)^{n+{\frac {1}{2}}}}
Monotoniebetrachtung:
Die Folge
(
1
+
1
n
)
n
{\displaystyle \left(1+{\frac {1}{n}}\right)^{n}}
(
1
+
1
n
)
n
+
1
{\displaystyle \left(1+{\frac {1}{n}}\right)^{n+1}}
(
e
+
x
)
e
−
x
>
(
e
−
x
)
e
+
x
0
<
x
<
e
{\displaystyle (e+x)^{e-x}>(e-x)^{e+x}\qquad 0<x<e}
1
a
<
2
a
+
b
<
log
(
a
)
−
log
(
b
)
a
−
b
<
1
a
b
<
1
b
a
>
b
>
0
{\displaystyle {\frac {1}{a}}<{\frac {2}{a+b}}<{\frac {\log(a)-\log(b)}{a-b}}<{\frac {1}{\sqrt {ab}}}<{\frac {1}{b}}\qquad a>b>0}
Beweis
Für
t
>
1
{\displaystyle t>1\,}
2
<
t
+
1
t
{\displaystyle 2<t+{\frac {1}{t}}}
2
t
<
1
+
1
t
2
{\displaystyle {\frac {2}{t}}<1+{\frac {1}{t^{2}}}}
x
>
1
{\displaystyle x>1\,}
log
(
x
2
)
=
2
log
x
=
2
∫
1
x
1
t
d
t
<
∫
1
x
(
1
+
1
t
2
)
d
t
=
x
−
1
x
{\displaystyle \log(x^{2})=2\log x=2\int _{1}^{x}{\frac {1}{t}}\,dt<\int _{1}^{x}\left(1+{\frac {1}{t^{2}}}\right)\,dt=x-{\frac {1}{x}}}
log
x
<
x
−
1
x
{\displaystyle \log x<{\sqrt {x}}-{\frac {1}{\sqrt {x}}}}
log
x
=
∑
k
=
0
∞
2
2
k
+
1
(
x
−
1
x
+
1
)
2
k
+
1
>
2
x
−
1
x
+
1
{\displaystyle \log x=\sum _{k=0}^{\infty }{\frac {2}{2k+1}}\,\left({\frac {x-1}{x+1}}\right)^{2k+1}>2\,{\frac {x-1}{x+1}}}
2
x
−
1
x
+
1
<
log
x
<
x
−
1
x
{\displaystyle 2\,{\frac {x-1}{x+1}}<\log x<{\sqrt {x}}-{\frac {1}{\sqrt {x}}}}
x
>
1
{\displaystyle x>1\,}
x
=
a
b
{\displaystyle x={\frac {a}{b}}}
2
a
b
−
1
a
b
+
1
<
log
(
a
b
)
<
a
b
−
b
a
{\displaystyle 2\,{\frac {{\frac {a}{b}}-1}{{\frac {a}{b}}+1}}<\log \left({\frac {a}{b}}\right)<{\sqrt {\frac {a}{b}}}-{\sqrt {\frac {b}{a}}}}
2
a
−
b
a
+
b
<
log
(
a
)
−
log
(
b
)
<
a
−
b
a
b
{\displaystyle 2\,{\frac {a-b}{a+b}}<\log(a)-\log(b)<{\frac {a-b}{\sqrt {ab}}}}
a
b
+
c
+
b
c
+
a
+
c
a
+
b
≥
3
2
a
,
b
,
c
>
0
{\displaystyle {\frac {a}{b+c}}+{\frac {b}{c+a}}+{\frac {c}{a+b}}\geq {\frac {3}{2}}\qquad a,b,c>0}
Sind
x
=
(
x
1
,
.
.
.
,
x
n
)
,
y
=
(
y
1
,
.
.
.
,
y
n
)
{\displaystyle {\boldsymbol {x}}=(x_{1},...,x_{n}),{\boldsymbol {y}}=(y_{1},...,y_{n})}
∏
k
=
1
n
(
x
k
+
y
k
)
1
/
n
≥
∏
k
=
1
n
x
k
1
/
n
+
∏
k
=
1
n
y
k
1
/
n
{\displaystyle \prod _{k=1}^{n}(x_{k}+y_{k})^{1/n}\geq \prod _{k=1}^{n}x_{k}^{1/n}+\prod _{k=1}^{n}y_{k}^{1/n}}
Sind
a
1
,
.
.
.
,
a
n
{\displaystyle a_{1},...,a_{n}\,}
b
1
,
.
.
.
,
b
n
{\displaystyle b_{1},...,b_{n}\,}
1
n
∑
k
=
1
n
a
k
b
k
≥
(
1
n
∑
k
=
1
n
a
k
)
(
1
n
∑
k
=
1
n
b
k
)
{\displaystyle {\frac {1}{n}}\sum _{k=1}^{n}a_{k}\,b_{k}\geq \left({\frac {1}{n}}\sum _{k=1}^{n}a_{k}\right)\left({\frac {1}{n}}\sum _{k=1}^{n}b_{k}\right)}
Sind
f
,
g
:
[
0
,
1
]
→
R
{\displaystyle f,g:[0,1]\to \mathbb {R} }
∫
0
1
f
(
x
)
g
(
x
)
d
x
≥
∫
0
1
f
(
x
)
d
x
∫
0
1
g
(
x
)
d
x
{\displaystyle \int _{0}^{1}f(x)\,g(x)\,dx\geq \int _{0}^{1}f(x)\,dx\int _{0}^{1}g(x)\,dx}
1. Beweis
Aus
(
f
(
x
)
−
f
(
y
)
)
(
g
(
x
)
−
g
(
y
)
)
≥
0
{\displaystyle {\Big (}f(x)-f(y){\Big )}{\Big (}g(x)-g(y){\Big )}\geq 0}
f
(
x
)
g
(
x
)
+
f
(
y
)
g
(
y
)
≥
f
(
x
)
g
(
y
)
+
f
(
y
)
g
(
x
)
{\displaystyle f(x)\,g(x)+f(y)\,g(y)\geq f(x)\,g(y)+f(y)\,g(x)}
∫
0
1
f
(
x
)
g
(
x
)
d
x
+
∫
0
1
f
(
y
)
g
(
y
)
d
y
≥
∫
0
1
f
(
x
)
d
x
∫
0
1
g
(
y
)
d
y
+
∫
0
1
f
(
y
)
d
y
∫
0
1
g
(
x
)
d
x
{\displaystyle \int _{0}^{1}f(x)\,g(x)\,dx+\int _{0}^{1}f(y)\,g(y)\,dy\geq \int _{0}^{1}f(x)\,dx\,\int _{0}^{1}g(y)\,dy+\int _{0}^{1}f(y)\,dy\,\int _{0}^{1}g(x)\,dx}
⇒
2
∫
0
1
f
(
x
)
g
(
x
)
d
x
≥
2
∫
0
1
f
(
x
)
d
x
∫
0
1
g
(
x
)
d
x
{\displaystyle \Rightarrow 2\int _{0}^{1}f(x)\,g(x)\,dx\geq 2\int _{0}^{1}f(x)\,dx\,\int _{0}^{1}g(x)\,dx}
2. Beweis
Nach der Tschebyscheff Summen-Ungleichung ist
∑
k
=
1
n
f
(
k
n
)
1
n
∑
k
=
1
n
g
(
k
n
)
1
n
≤
∑
k
=
1
n
f
(
k
n
)
g
(
k
n
)
1
n
{\displaystyle \sum _{k=1}^{n}f\left({\frac {k}{n}}\right){\frac {1}{n}}\;\;\sum _{k=1}^{n}g\left({\frac {k}{n}}\right){\frac {1}{n}}\leq \sum _{k=1}^{n}f\left({\frac {k}{n}}\right)g\left({\frac {k}{n}}\right){\frac {1}{n}}}
n
→
∞
{\displaystyle n\to \infty \,}
Sind
f
1
,
.
.
.
,
f
n
:
[
0
,
1
]
→
R
{\displaystyle f_{1},...,f_{n}:[0,1]\to \mathbb {R} }
f
1
(
0
)
=
.
.
.
=
f
n
(
0
)
=
0
{\displaystyle f_{1}(0)=...=f_{n}(0)=0\,}
∫
0
1
∏
k
=
1
n
f
k
(
x
)
d
x
≥
2
n
n
+
1
∏
k
=
1
n
∫
0
1
f
k
(
x
)
d
x
{\displaystyle \int _{0}^{1}\prod _{k=1}^{n}f_{k}(x)dx\geq {\frac {2^{n}}{n+1}}\prod _{k=1}^{n}\int _{0}^{1}f_{k}(x)dx}
Beweis
Es sei
M
{\displaystyle M\,}
f
:
[
0
,
1
]
→
R
{\displaystyle f:[0,1]\to \mathbb {R} }
f
(
0
)
=
0
{\displaystyle f(0)=0\,}
(
1
)
{\displaystyle (1)\,}
f
∈
M
{\displaystyle f\in M}
0
≤
x
1
<
x
2
≤
1
{\displaystyle 0\leq x_{1}<x_{2}\leq 1}
f
(
x
1
)
>
f
(
x
2
)
{\displaystyle f(x_{1})>f(x_{2})\,}
(
x
1
,
f
(
x
1
)
)
{\displaystyle {\big (}x_{1},f(x_{1}){\big )}}
ℓ
(
x
)
=
f
(
x
2
)
x
2
⋅
x
{\displaystyle \ell (x)={\frac {f(x_{2})}{x_{2}}}\cdot x}
(
2
)
{\displaystyle (2)\,}
M
{\displaystyle M\,}
f
,
g
∈
M
{\displaystyle f,g\in M}
f
⋅
g
∈
M
{\displaystyle f\cdot g\in M}
f
{\displaystyle f\,}
g
{\displaystyle g\,}
[
f
(
x
)
−
f
(
y
)
]
[
g
(
x
)
−
g
(
y
)
]
≥
0
{\displaystyle [f(x)-f(y)]\,[g(x)-g(y)]\geq 0}
f
(
x
)
g
(
x
)
+
f
(
y
)
g
(
y
)
≥
f
(
x
)
g
(
y
)
+
f
(
y
)
g
(
x
)
{\displaystyle f(x)g(x)+f(y)g(y)\geq f(x)g(y)+f(y)g(x)}
α
,
β
≥
0
{\displaystyle \alpha ,\beta \geq 0}
α
+
β
=
1
{\displaystyle \alpha +\beta =1\,}
(
f
g
)
(
α
x
+
β
y
)
=
f
(
α
x
+
β
y
)
g
(
α
x
+
β
y
)
{\displaystyle (fg)(\alpha x+\beta y)=f(\alpha x+\beta y)\,g(\alpha x+\beta y)}
≤
[
α
f
(
x
)
+
β
f
(
y
)
]
[
α
g
(
x
)
+
β
g
(
y
)
]
{\displaystyle \leq [\alpha f(x)+\beta f(y)]\,[\alpha g(x)+\beta g(y)]}
f
{\displaystyle f\,}
g
{\displaystyle g\,}
α
2
f
(
x
)
g
(
x
)
+
α
β
[
f
(
x
)
g
(
y
)
+
f
(
y
)
g
(
x
)
]
+
β
2
f
(
y
)
g
(
y
)
{\displaystyle \alpha ^{2}f(x)g(x)+\alpha \beta [f(x)g(y)+f(y)g(x)]+\beta ^{2}f(y)g(y)\,}
≤
α
2
f
(
x
)
g
(
x
)
+
α
β
[
f
(
x
)
g
(
x
)
+
f
(
y
)
g
(
y
)
]
+
β
2
f
(
y
)
g
(
y
)
{\displaystyle \leq \alpha ^{2}f(x)g(x)+\alpha \beta [f(x)g(x)+f(y)g(y)]+\beta ^{2}f(y)g(y)}
=
(
α
2
+
α
β
)
⏟
=
α
f
(
x
)
g
(
x
)
+
(
α
β
+
β
2
)
⏟
=
β
f
(
y
)
g
(
y
)
=
α
(
f
g
)
(
x
)
+
β
(
f
g
)
(
y
)
{\displaystyle =\underbrace {(\alpha ^{2}+\alpha \beta )} _{=\alpha }f(x)g(x)+\underbrace {(\alpha \beta +\beta ^{2})} _{=\beta }f(y)g(y)=\alpha \,(fg)(x)+\beta \,(fg)(y)}
(
3
)
{\displaystyle (3)\,}
f
^
(
x
)
=
2
x
∫
0
1
f
(
t
)
d
t
{\displaystyle {\widehat {f}}(x)=2x\int _{0}^{1}f(t)\,dt}
f
∈
M
⇒
f
^
∈
M
{\displaystyle f\in M\Rightarrow {\widehat {f}}\in M}
(
4
)
{\displaystyle (4)\,}
f
,
g
∈
M
{\displaystyle f,g\in M}
∫
0
1
g
(
x
)
f
(
x
)
d
x
≥
∫
0
1
g
(
x
)
f
^
(
x
)
d
x
{\displaystyle \int _{0}^{1}g(x)\,f(x)\,dx\geq \int _{0}^{1}g(x)\,{\widehat {f}}(x)\,dx}
∫
0
1
f
^
(
x
)
d
x
{\displaystyle \int _{0}^{1}{\widehat {f}}(x)\,dx}
∫
0
1
f
(
x
)
d
x
{\displaystyle \int _{0}^{1}f(x)\,dx}
0
<
s
<
1
{\displaystyle 0<s<1\,}
f
(
x
)
≤
f
^
(
x
)
{\displaystyle f(x)\leq {\widehat {f}}(x)}
x
≤
s
{\displaystyle x\leq s\,}
f
(
x
)
≥
f
^
(
x
)
{\displaystyle f(x)\geq {\widehat {f}}(x)}
x
≥
s
{\displaystyle x\geq s\,}
∫
0
s
f
^
(
x
)
d
x
+
∫
s
1
f
^
(
x
)
d
x
=
∫
0
s
f
(
x
)
d
x
+
∫
s
1
f
(
x
)
d
x
{\displaystyle \int _{0}^{s}{\widehat {f}}(x)\,dx+\int _{s}^{1}{\widehat {f}}(x)\,dx=\int _{0}^{s}f(x)\,dx+\int _{s}^{1}f(x)\,dx}
⇒
∫
0
s
(
f
^
(
x
)
−
f
(
x
)
)
d
x
=
∫
s
1
(
f
(
x
)
−
f
^
(
x
)
)
d
x
{\displaystyle \Rightarrow \int _{0}^{s}\left({\widehat {f}}(x)-f(x)\right)dx=\int _{s}^{1}\left(f(x)-{\widehat {f}}(x)\right)dx}
g
{\displaystyle g\,}
∫
0
s
g
(
x
)
(
f
^
(
x
)
−
f
(
x
)
)
d
x
{\displaystyle \int _{0}^{s}g(x)\left({\widehat {f}}(x)-f(x)\right)dx}
≤
g
(
s
)
∫
0
s
(
f
^
(
x
)
−
f
(
x
)
)
d
x
=
g
(
s
)
∫
s
1
(
f
(
x
)
−
f
^
(
x
)
)
d
x
{\displaystyle \leq g(s)\int _{0}^{s}\left({\widehat {f}}(x)-f(x)\right)dx=g(s)\int _{s}^{1}\left(f(x)-{\widehat {f}}(x)\right)dx}
≤
∫
s
1
g
(
x
)
(
f
(
x
)
−
f
^
(
x
)
)
d
x
=
−
∫
s
1
g
(
x
)
(
f
^
(
x
)
−
f
(
x
)
)
d
x
{\displaystyle \leq \int _{s}^{1}g(x)\left(f(x)-{\widehat {f}}(x)\right)dx=-\int _{s}^{1}g(x)\left({\widehat {f}}(x)-f(x)\right)dx}
∫
0
1
g
(
x
)
(
f
^
(
x
)
−
f
(
x
)
)
d
x
≤
0
⇒
∫
0
1
g
(
x
)
f
^
(
x
)
d
x
≤
∫
0
1
g
(
x
)
f
(
x
)
d
x
{\displaystyle \int _{0}^{1}g(x)\left({\widehat {f}}(x)-f(x)\right)dx\leq 0\Rightarrow \int _{0}^{1}g(x)\,{\widehat {f}}(x)\,dx\leq \int _{0}^{1}g(x)\,f(x)\,dx}
f
1
,
.
.
.
,
f
n
∈
M
{\displaystyle f_{1},...,f_{n}\in M}
∫
0
1
f
1
(
x
)
⋯
f
n
(
x
)
d
x
≥
∫
0
1
f
^
1
(
x
)
⋯
f
^
n
(
x
)
d
x
=
∫
0
1
2
x
∫
0
1
f
1
(
t
)
d
t
⋯
2
x
∫
0
1
f
n
(
t
)
d
t
d
x
{\displaystyle \int _{0}^{1}f_{1}(x)\cdots f_{n}(x)\,dx\geq \int _{0}^{1}{\widehat {f}}_{1}(x)\cdots {\widehat {f}}_{n}(x)\,dx=\int _{0}^{1}2x\int _{0}^{1}f_{1}(t)\,dt\cdots 2x\int _{0}^{1}f_{n}(t)\,dt\,\,dx}
=
∫
0
1
2
n
x
n
d
x
∫
0
1
f
1
(
t
)
d
t
⋯
∫
0
1
f
n
(
t
)
d
t
=
2
n
n
+
1
∏
i
=
1
n
∫
0
1
f
i
(
x
)
d
x
{\displaystyle =\int _{0}^{1}2^{n}x^{n}\,dx\int _{0}^{1}f_{1}(t)\,dt\cdots \int _{0}^{1}f_{n}(t)\,dt={\frac {2^{n}}{n+1}}\prod _{i=1}^{n}\int _{0}^{1}f_{i}(x)\,dx}
[ Bearbeiten ]
∀
x
≥
0
{\displaystyle \forall x\geq 0}
∑
k
=
0
n
[
x
k
+
1
k
+
1
,
x
2
k
(
2
k
)
!
,
x
2
k
+
1
(
2
k
+
1
)
!
]
{\displaystyle \sum _{k=0}^{n}\left[{\frac {x^{k+1}}{k+1}},{\frac {x^{2k}}{(2k)!}},{\frac {x^{2k+1}}{(2k+1)!}}\right]}
{
>
,
n
=
2
m
<
,
n
=
2
m
+
1
}
[
log
(
1
+
x
)
,
cos
(
x
)
,
sin
(
x
)
]
{\displaystyle \left\{{\begin{matrix}>&,&n=2m\quad \;\;\,\\<&,&n=2m+1\end{matrix}}\right\}\;{\Big [}\log(1+x),\cos(x),\sin(x){\Big ]}}
(
n
−
1
)
!
<
n
n
e
n
e
<
n
!
n
∈
Z
>
1
{\displaystyle (n-1)!<{\frac {n^{n}}{e^{n}}}\,e<n!\qquad n\in \mathbb {Z} ^{>1}}
1. Beweis
n
n
n
!
=
∏
k
=
1
n
−
1
(
1
+
1
k
)
k
<
e
n
−
1
<
∏
k
=
1
n
−
1
(
1
+
1
k
)
k
+
1
=
n
n
(
n
−
1
)
!
{\displaystyle {\frac {n^{n}}{n!}}=\prod _{k=1}^{n-1}\left(1+{\frac {1}{k}}\right)^{k}<e^{n-1}<\prod _{k=1}^{n-1}\left(1+{\frac {1}{k}}\right)^{k+1}={\frac {n^{n}}{(n-1)!}}}
2. Beweis
Da der natürliche Logarithmus streng monoton wächst ist
log
(
k
)
<
∫
k
k
+
1
log
(
x
)
d
x
<
log
(
k
+
1
)
{\displaystyle \log(k)<\int _{k}^{k+1}\log(x)\,dx<\log(k+1)}
k
{\displaystyle k\,}
1
{\displaystyle 1\,}
n
−
1
{\displaystyle n-1\,}
log
(
n
−
1
)
!
<
∫
1
n
log
(
x
)
d
x
<
log
n
!
{\displaystyle \log(n-1)!<\int _{1}^{n}\log(x)\,dx<\log n!}
∫
1
n
log
(
x
)
d
x
=
[
x
log
(
x
)
−
x
]
1
n
=
n
log
(
n
)
−
n
+
1
=
log
(
n
n
e
n
e
)
{\displaystyle \int _{1}^{n}\log(x)\,dx=\left[x\,\log(x)-x\right]_{1}^{n}=n\,\log(n)-n+1=\log \left({\frac {n^{n}}{e^{n}}}\,e\right)}
(
n
−
1
)
!
<
n
n
e
n
e
<
n
!
{\displaystyle (n-1)!<{\frac {n^{n}}{e^{n}}}\,e<n!}
Γ
(
x
α
+
(
1
−
x
)
β
)
≤
Γ
(
α
)
x
Γ
(
β
)
1
−
x
α
,
β
>
0
0
≤
x
≤
1
{\displaystyle \Gamma {\Big (}x\alpha +(1-x)\beta {\Big )}\leq \Gamma (\alpha )^{x}\,\Gamma (\beta )^{1-x}\qquad \alpha ,\beta >0\qquad 0\leq x\leq 1}
Beweis
Γ
(
x
α
+
(
1
−
x
)
β
)
=
∫
0
∞
t
x
α
+
(
1
−
x
)
β
−
1
e
−
t
d
t
=
∫
0
∞
t
(
α
−
1
)
x
+
(
β
−
1
)
(
1
−
x
)
e
−
t
d
t
{\displaystyle \Gamma {\Big (}x\alpha +(1-x)\beta {\Big )}=\int _{0}^{\infty }t^{x\alpha +(1-x)\beta -1}\,e^{-t}\,dt=\int _{0}^{\infty }t^{(\alpha -1)x+(\beta -1)(1-x)}\,e^{-t}\,dt}
=
∫
0
∞
(
t
α
−
1
e
−
t
)
x
(
t
β
−
1
e
−
t
)
1
−
x
d
t
{\displaystyle =\int _{0}^{\infty }(t^{\alpha -1}\,e^{-t})^{x}\,(t^{\beta -1}\,e^{-t})^{1-x}dt}
≤
(
∫
0
∞
t
α
−
1
e
−
t
d
t
)
x
(
∫
0
∞
t
β
−
1
e
−
t
d
t
)
1
−
x
=
Γ
(
α
)
x
Γ
(
β
)
1
−
x
{\displaystyle \leq \left(\int _{0}^{\infty }t^{\alpha -1}\,e^{-t}\,dt\right)^{x}\,\left(\int _{0}^{\infty }t^{\beta -1}\,e^{-t}\,dt\right)^{1-x}=\Gamma (\alpha )^{x}\,\Gamma (\beta )^{1-x}}
n
!
(
n
+
x
)
x
−
1
≤
Γ
(
n
+
x
)
≤
Γ
(
n
)
n
x
0
≤
x
≤
1
1
≤
n
{\displaystyle n!\,(n+x)^{x-1}\leq \Gamma (n+x)\leq \Gamma (n)\,n^{x}\qquad 0\leq x\leq 1\qquad 1\leq n}
Beweis
In der Ungleichung
Γ
(
x
α
+
(
1
−
x
)
β
)
≤
Γ
(
α
)
x
Γ
(
β
)
1
−
x
{\displaystyle \Gamma {\Big (}x\alpha +(1-x)\beta {\Big )}\leq \Gamma (\alpha )^{x}\,\Gamma (\beta )^{1-x}}
α
,
β
>
0
{\displaystyle \alpha ,\beta >0\,}
0
≤
x
≤
1
{\displaystyle 0\leq x\leq 1}
α
=
n
+
1
{\displaystyle \alpha =n+1\,}
β
=
n
{\displaystyle \beta =n\,}
Γ
(
n
+
x
)
≤
Γ
(
n
+
1
)
x
Γ
(
n
)
1
−
x
=
Γ
(
n
)
n
x
{\displaystyle \Gamma (n+x)\leq \Gamma (n+1)^{x}\,\Gamma (n)^{1-x}=\Gamma (n)\,n^{x}}
α
=
n
+
x
{\displaystyle \alpha =n+x\,}
β
=
n
+
1
+
x
{\displaystyle \beta =n+1+x\,}
Γ
(
n
+
1
)
≤
Γ
(
n
+
x
)
x
Γ
(
n
+
1
+
x
)
1
−
x
=
Γ
(
n
+
x
)
(
n
+
x
)
1
−
x
{\displaystyle \Gamma (n+1)\leq \Gamma (n+x)^{x}\,\Gamma (n+1+x)^{1-x}=\Gamma (n+x)\,(n+x)^{1-x}}
n
!
(
n
+
x
)
x
−
1
≤
Γ
(
n
+
x
)
{\displaystyle n!\,(n+x)^{x-1}\leq \Gamma (n+x)}
x
1
−
s
<
Γ
(
x
+
1
)
Γ
(
x
+
s
)
<
(
x
+
1
)
1
−
s
0
<
s
<
1
{\displaystyle x^{1-s}<{\frac {\Gamma (x+1)}{\Gamma (x+s)}}<(x+1)^{1-s}\qquad 0<s<1}
Ist
a
1
,
a
2
,
a
3
,
.
.
.
{\displaystyle a_{1},a_{2},a_{3},...}
(
∑
k
=
1
∞
a
k
)
4
<
π
2
∑
k
=
1
∞
a
k
2
⋅
∑
k
=
1
∞
k
2
a
k
2
{\displaystyle \left(\sum _{k=1}^{\infty }a_{k}\right)^{4}<\pi ^{2}\,\sum _{k=1}^{\infty }a_{k}^{2}\cdot \sum _{k=1}^{\infty }k^{2}a_{k}^{2}}
Hardys erster Beweis der Carlson-Ungleichung
Hardys zweiter Beweis der Carlson-Ungleichung
Betrachte die Fourierreihe
f
(
x
)
=
∑
k
=
1
∞
a
k
cos
k
x
{\displaystyle f(x)=\sum _{k=1}^{\infty }a_{k}\,\cos kx}
f
′
(
x
)
=
∑
k
=
1
∞
−
k
a
k
sin
k
x
{\displaystyle f'(x)=\sum _{k=1}^{\infty }-ka_{k}\,\sin kx}
Parsevalschen Gleichung ist
2
π
∫
0
π
f
2
(
x
)
d
x
=
∑
k
=
1
∞
a
k
2
=:
S
{\displaystyle {\frac {2}{\pi }}\int _{0}^{\pi }f^{2}(x)\,dx=\sum _{k=1}^{\infty }a_{k}^{2}=:S}
2
π
∫
0
π
f
′
2
(
x
)
d
x
=
∑
k
=
1
∞
k
2
a
k
2
=:
T
{\displaystyle {\frac {2}{\pi }}\int _{0}^{\pi }f'^{2}(x)\,dx=\sum _{k=1}^{\infty }k^{2}a_{k}^{2}=:T}
∫
0
π
f
(
x
)
d
x
=
∑
k
=
1
∞
a
k
[
sin
k
x
k
]
0
π
=
0
{\displaystyle \int _{0}^{\pi }f(x)\,dx=\sum _{k=1}^{\infty }a_{k}\left[{\frac {\sin kx}{k}}\right]_{0}^{\pi }=0}
0
<
ξ
<
π
{\displaystyle 0<\xi <\pi }
f
(
ξ
)
=
0
{\displaystyle f(\xi )=0}
(
∑
k
=
1
∞
a
k
)
2
=
f
2
(
0
)
=
f
2
(
0
)
−
f
2
(
ξ
)
=
2
∫
ξ
0
f
(
x
)
f
′
(
x
)
d
x
{\displaystyle \left(\sum _{k=1}^{\infty }a_{k}\right)^{2}=f^{2}(0)=f^{2}(0)-f^{2}(\xi )=2\int _{\xi }^{0}f(x)\,f'(x)\,dx}
Cauchy-Schwarzscher-Ungleichung
<
2
⋅
∫
0
π
f
2
(
x
)
d
x
⋅
∫
0
π
f
′
2
(
x
)
d
x
=
2
⋅
π
2
S
⋅
π
2
T
=
π
S
T
{\displaystyle <2\cdot {\sqrt {\int _{0}^{\pi }f^{2}(x)\,dx}}\cdot {\sqrt {\int _{0}^{\pi }f'^{2}(x)\,dx}}=2\cdot {\sqrt {{\frac {\pi }{2}}\,S}}\cdot {\sqrt {{\frac {\pi }{2}}\,T}}=\pi \,{\sqrt {ST}}}
Sind
(
a
n
)
,
(
b
m
)
{\displaystyle (a_{n}),(b_{m})}
p
,
q
{\displaystyle p,q\,}
so dass
1
<
p
,
q
<
∞
{\displaystyle 1<p,q<\infty }
1
p
+
1
q
=
1
{\displaystyle {\frac {1}{p}}+{\frac {1}{q}}=1}
∑
n
=
1
∞
∑
m
=
1
∞
a
n
b
m
n
+
m
<
π
sin
π
p
⋅
(
∑
n
=
1
∞
a
n
p
)
1
p
⋅
(
∑
m
=
1
∞
b
m
q
)
1
q
{\displaystyle \sum _{n=1}^{\infty }\sum _{m=1}^{\infty }{\frac {a_{n}\,b_{m}}{n+m}}<{\frac {\pi }{\sin {\frac {\pi }{p}}}}\cdot \left(\sum _{n=1}^{\infty }a_{n}^{p}\right)^{\frac {1}{p}}\cdot \left(\sum _{m=1}^{\infty }b_{m}^{q}\right)^{\frac {1}{q}}}
Beweis
Für ein
0
<
α
<
1
{\displaystyle 0<\alpha <1}
∑
m
=
1
∞
1
(
1
+
m
n
)
⋅
(
m
n
)
α
1
n
{\displaystyle \sum _{m=1}^{\infty }{\frac {1}{\left(1+{\frac {m}{n}}\right)\cdot \left({\frac {m}{n}}\right)^{\alpha }}}\,{\frac {1}{n}}}
∫
0
∞
1
(
1
+
x
)
x
α
d
x
=
π
sin
π
α
{\displaystyle \int _{0}^{\infty }{\frac {1}{(1+x)\,x^{\alpha }}}\,dx={\frac {\pi }{\sin \pi \alpha }}}
f
(
x
)
=
1
(
1
+
x
)
x
α
{\displaystyle f(x)={\frac {1}{(1+x)\,x^{\alpha }}}}
∑
n
,
m
=
1
∞
a
n
b
m
n
+
m
=
∑
n
,
m
=
1
∞
a
n
(
n
+
m
)
1
p
(
m
n
)
1
p
q
⋅
b
m
(
n
+
m
)
1
q
(
n
m
)
1
p
q
{\displaystyle \sum _{n,m=1}^{\infty }{\frac {a_{n}\,b_{m}}{n+m}}=\sum _{n,m=1}^{\infty }{\frac {a_{n}}{(n+m)^{\frac {1}{p}}\,\left({\frac {m}{n}}\right)^{\frac {1}{pq}}}}\cdot {\frac {b_{m}}{(n+m)^{\frac {1}{q}}\,\left({\frac {n}{m}}\right)^{\frac {1}{pq}}}}}
<
(
∑
n
,
m
=
1
∞
a
n
p
(
n
+
m
)
(
m
n
)
1
q
)
1
p
⋅
(
∑
n
,
m
=
1
∞
b
m
q
(
n
+
m
)
(
n
m
)
1
p
)
1
q
{\displaystyle <\left(\sum _{n,m=1}^{\infty }{\frac {a_{n}^{p}}{(n+m)\,\left({\frac {m}{n}}\right)^{\frac {1}{q}}}}\right)^{\frac {1}{p}}\cdot \left(\sum _{n,m=1}^{\infty }{\frac {b_{m}^{q}}{(n+m)\,\left({\frac {n}{m}}\right)^{\frac {1}{p}}}}\right)^{\frac {1}{q}}}
=
(
∑
n
=
1
∞
a
n
p
⋅
∑
m
=
1
∞
1
(
n
+
m
)
(
m
n
)
1
q
)
1
p
⋅
(
∑
m
=
1
∞
b
m
q
⋅
∑
n
=
1
∞
1
(
n
+
m
)
(
n
m
)
1
p
)
1
q
{\displaystyle =\left(\sum _{n=1}^{\infty }a_{n}^{p}\cdot \sum _{m=1}^{\infty }{\frac {1}{(n+m)\,\left({\frac {m}{n}}\right)^{\frac {1}{q}}}}\right)^{\frac {1}{p}}\cdot \left(\sum _{m=1}^{\infty }b_{m}^{q}\cdot \sum _{n=1}^{\infty }{\frac {1}{(n+m)\,\left({\frac {n}{m}}\right)^{\frac {1}{p}}}}\right)^{\frac {1}{q}}}
<
(
∑
n
=
1
∞
a
n
p
)
1
p
⋅
(
π
sin
π
q
)
1
p
⋅
(
∑
m
=
1
∞
b
m
q
)
1
q
⋅
(
π
sin
π
p
)
1
q
=
π
sin
π
p
⋅
(
∑
n
=
1
∞
a
n
p
)
1
p
⋅
(
∑
m
=
1
∞
b
m
q
)
1
q
{\displaystyle <\left(\sum _{n=1}^{\infty }a_{n}^{p}\right)^{\frac {1}{p}}\cdot \left({\frac {\pi }{\sin {\frac {\pi }{q}}}}\right)^{\frac {1}{p}}\cdot \left(\sum _{m=1}^{\infty }b_{m}^{q}\right)^{\frac {1}{q}}\cdot \left({\frac {\pi }{\sin {\frac {\pi }{p}}}}\right)^{\frac {1}{q}}={\frac {\pi }{\sin {\frac {\pi }{p}}}}\cdot \left(\sum _{n=1}^{\infty }a_{n}^{p}\right)^{\frac {1}{p}}\cdot \left(\sum _{m=1}^{\infty }b_{m}^{q}\right)^{\frac {1}{q}}}
Sind
f
,
g
:
R
≥
0
→
R
≥
0
{\displaystyle f,g:\mathbb {R} _{\geq 0}\to \mathbb {R} _{\geq 0}}
∫
0
∞
∫
0
∞
f
(
x
)
g
(
y
)
x
+
y
d
x
d
y
<
π
sin
π
p
⋅
(
∫
0
∞
[
f
(
x
)
]
p
d
x
)
1
p
⋅
(
∫
0
∞
[
g
(
y
)
]
q
d
y
)
1
q
{\displaystyle \int _{0}^{\infty }\int _{0}^{\infty }{\frac {f(x)\,g(y)}{x+y}}\,dx\,dy<{\frac {\pi }{\sin {\frac {\pi }{p}}}}\cdot \left(\int _{0}^{\infty }[f(x)]^{p}\,dx\right)^{\frac {1}{p}}\cdot \left(\int _{0}^{\infty }[g(y)]^{q}\,dy\right)^{\frac {1}{q}}}
Ist
f
:
R
≥
0
→
R
≥
0
{\displaystyle f:\mathbb {R} _{\geq 0}\to \mathbb {R} _{\geq 0}}
p
>
1
{\displaystyle p>1}
∫
0
∞
(
1
x
∫
0
x
f
(
t
)
d
t
)
p
d
x
≤
(
p
p
−
1
)
p
⋅
∫
0
∞
[
f
(
x
)
]
p
d
x
{\displaystyle \int _{0}^{\infty }\left({\frac {1}{x}}\int _{0}^{x}f(t)\,dt\right)^{p}dx\leq \left({\frac {p}{p-1}}\right)^{p}\cdot \int _{0}^{\infty }[f(x)]^{p}\,dx}
Beweis
Setze
F
(
x
)
:=
∫
0
x
f
(
t
)
d
t
{\displaystyle F(x):=\int _{0}^{x}f(t)\,dt}
t
=
x
⋅
u
p
r
⇒
d
t
=
x
⋅
p
r
⋅
u
p
r
−
1
d
u
{\displaystyle t=x\cdot u^{\frac {p}{r}}\,\Rightarrow \,dt=x\cdot {\frac {p}{r}}\cdot u^{{\frac {p}{r}}-1}\,du}
F
(
x
)
=
x
⋅
p
r
⋅
∫
0
1
f
(
x
⋅
u
p
r
)
⋅
u
p
r
−
1
d
u
⇒
[
F
(
x
)
]
p
=
x
p
⋅
(
p
r
)
p
⋅
(
∫
0
1
f
(
x
⋅
u
p
r
)
⋅
u
p
r
−
1
d
u
)
p
{\displaystyle F(x)=x\cdot {\frac {p}{r}}\cdot \int _{0}^{1}f\left(x\cdot u^{\frac {p}{r}}\right)\cdot u^{{\frac {p}{r}}-1}\,du\Rightarrow [F(x)]^{p}=x^{p}\cdot \left({\frac {p}{r}}\right)^{p}\cdot \left(\int _{0}^{1}f\left(x\cdot u^{\frac {p}{r}}\right)\cdot u^{{\frac {p}{r}}-1}\,du\right)^{p}}
u
↦
u
p
{\displaystyle u\mapsto u^{p}}
(
∫
0
1
f
(
x
⋅
u
p
r
)
⋅
u
p
r
−
1
d
u
)
p
≤
∫
0
1
[
f
(
x
⋅
u
p
r
)
]
p
⋅
u
p
⋅
(
p
r
−
1
)
⋅
d
u
{\displaystyle \left(\int _{0}^{1}f\left(x\cdot u^{\frac {p}{r}}\right)\cdot u^{{\frac {p}{r}}-1}\,du\right)^{p}\leq \int _{0}^{1}\left[f\left(x\cdot u^{\frac {p}{r}}\right)\right]^{p}\cdot u^{p\cdot \left({\frac {p}{r}}-1\right)}\cdot du}
t
=
x
⋅
u
p
r
{\displaystyle t=x\cdot u^{\frac {p}{r}}}
(
u
p
=
t
r
x
r
⇒
u
=
t
r
p
x
r
p
⇒
d
u
=
r
p
⋅
t
r
p
−
1
x
r
p
d
t
)
{\displaystyle \left(u^{p}={\frac {t^{r}}{x^{r}}}\,\Rightarrow \,u={\frac {t^{\frac {r}{p}}}{x^{\frac {r}{p}}}}\,\Rightarrow \,du={\frac {r}{p}}\cdot {\frac {t^{{\frac {r}{p}}-1}}{x^{\frac {r}{p}}}}\,dt\right)}
∫
0
x
[
f
(
t
)
]
p
⋅
t
p
−
r
x
p
−
r
⋅
r
p
⋅
t
r
p
−
1
x
r
p
d
t
=
x
r
−
r
p
x
p
⋅
r
p
⋅
∫
0
x
[
f
(
t
)
]
p
⋅
t
p
−
r
+
r
p
−
1
d
t
{\displaystyle \int _{0}^{x}[f(t)]^{p}\cdot {\frac {t^{p-r}}{x^{p-r}}}\cdot {\frac {r}{p}}\cdot {\frac {t^{{\frac {r}{p}}-1}}{x^{\frac {r}{p}}}}\,dt={\frac {x^{r-{\frac {r}{p}}}}{x^{p}}}\cdot {\frac {r}{p}}\cdot \int _{0}^{x}\left[f(t)\right]^{p}\cdot t^{p-r+{\frac {r}{p}}-1}\,dt}
[
F
(
x
)
]
p
≤
x
r
−
r
p
⋅
(
p
r
)
p
−
1
⋅
∫
0
x
[
f
(
t
)
]
p
⋅
t
p
−
r
+
r
p
−
1
d
t
{\displaystyle [F(x)]^{p}\leq x^{r-{\frac {r}{p}}}\cdot \left({\frac {p}{r}}\right)^{p-1}\cdot \int _{0}^{x}[f(t)]^{p}\cdot t^{p-r+{\frac {r}{p}}-1}\,dt}
∫
0
∞
[
F
(
x
)
]
p
⋅
x
−
r
−
1
d
x
≤
∫
0
∞
x
r
−
r
p
⋅
(
p
r
)
p
−
1
⋅
∫
0
x
[
f
(
t
)
]
p
⋅
t
p
−
r
+
r
p
−
1
d
t
⋅
x
−
r
−
1
d
x
{\displaystyle \int _{0}^{\infty }[F(x)]^{p}\cdot x^{-r-1}\,dx\leq \int _{0}^{\infty }x^{r-{\frac {r}{p}}}\cdot \left({\frac {p}{r}}\right)^{p-1}\cdot \int _{0}^{x}[f(t)]^{p}\cdot t^{p-r+{\frac {r}{p}}-1}\,dt\cdot x^{-r-1}\,dx}
=
(
p
r
)
p
−
1
⋅
∫
0
∞
∫
0
x
[
f
(
t
)
]
p
⋅
t
p
−
r
+
r
p
−
1
⋅
x
−
r
p
−
1
d
t
d
x
=
(
p
r
)
p
−
1
⋅
∫
0
∞
[
f
(
t
)
]
p
⋅
t
p
−
r
+
r
p
−
1
⋅
∫
t
∞
x
−
r
p
−
1
d
x
⋅
d
t
{\displaystyle =\left({\frac {p}{r}}\right)^{p-1}\cdot \int _{0}^{\infty }\int _{0}^{x}[f(t)]^{p}\cdot t^{p-r+{\frac {r}{p}}-1}\cdot x^{-{\frac {r}{p}}-1}\,dt\,dx=\left({\frac {p}{r}}\right)^{p-1}\cdot \int _{0}^{\infty }[f(t)]^{p}\cdot t^{p-r+{\frac {r}{p}}-1}\cdot \int _{t}^{\infty }x^{-{\frac {r}{p}}-1}\,dx\cdot dt}
=
(
p
r
)
p
⋅
∫
0
∞
[
f
(
t
)
]
p
⋅
t
p
−
r
−
1
d
t
{\displaystyle =\left({\frac {p}{r}}\right)^{p}\cdot \int _{0}^{\infty }[f(t)]^{p}\cdot t^{p-r-1}\,dt}
r
=
p
−
1
{\displaystyle r=p-1}
∫
0
∞
(
F
(
x
)
x
)
p
d
x
≤
(
p
p
−
1
)
p
⋅
∫
0
∞
[
f
(
t
)
]
p
d
t
{\displaystyle \int _{0}^{\infty }\left({\frac {F(x)}{x}}\right)^{p}dx\leq \left({\frac {p}{p-1}}\right)^{p}\cdot \int _{0}^{\infty }[f(t)]^{p}\,dt}
Ist
(
a
n
)
{\displaystyle (a_{n})}
p
>
1
{\displaystyle p>1\,}
∑
n
=
1
∞
(
1
n
∑
k
=
1
n
a
k
)
p
≤
(
p
p
−
1
)
p
⋅
∑
k
=
1
∞
a
k
p
{\displaystyle \sum _{n=1}^{\infty }\left({\frac {1}{n}}\sum _{k=1}^{n}a_{k}\right)^{p}\leq \left({\frac {p}{p-1}}\right)^{p}\cdot \sum _{k=1}^{\infty }a_{k}^{p}}
Sind
p
=
(
p
1
,
.
.
.
,
p
n
)
{\displaystyle {\boldsymbol {p}}=(p_{1},...,p_{n})}
q
=
(
q
1
,
.
.
.
,
q
n
)
{\displaystyle {\boldsymbol {q}}=(q_{1},...,q_{n})}
mit
p
1
≥
.
.
.
≥
p
n
>
0
,
q
1
≥
.
.
.
≥
q
n
>
0
{\displaystyle p_{1}\geq ...\geq p_{n}>0\,\,,\,\,q_{1}\geq ...\geq q_{n}>0}
∑
k
=
1
n
p
k
=
∑
k
=
1
n
q
k
=
1
{\displaystyle \sum _{k=1}^{n}p_{k}=\sum _{k=1}^{n}q_{k}=1}
−
∑
k
=
1
n
p
k
log
(
p
k
)
≤
−
∑
k
=
1
n
p
k
log
(
q
k
)
{\displaystyle -\sum _{k=1}^{n}p_{k}\log(p_{k})\leq -\sum _{k=1}^{n}p_{k}\log(q_{k})}
p
=
q
{\displaystyle {\boldsymbol {p}}={\boldsymbol {q}}}
Ist
f
:
[
a
,
b
]
→
R
{\displaystyle f:[a,b]\to \mathbb {R} }
λ
1
,
.
.
.
,
λ
n
{\displaystyle \lambda _{1},...,\lambda _{n}}
∑
k
=
1
n
λ
k
=
1
{\displaystyle \sum _{k=1}^{n}\lambda _{k}=1}
dann gilt für beliebige
x
1
,
.
.
.
,
x
n
∈
[
a
,
b
]
{\displaystyle x_{1},...,x_{n}\in [a,b]}
f
(
∑
k
=
1
n
λ
k
x
k
)
≤
∑
k
=
1
n
λ
k
f
(
x
k
)
{\displaystyle f\left(\sum _{k=1}^{n}\lambda _{k}\,x_{k}\right)\leq \sum _{k=1}^{n}\lambda _{k}\,f(x_{k})}
Ist
g
:
[
a
,
b
]
→
R
{\displaystyle g:[a,b]\to \mathbb {R} }
f
{\displaystyle f\,}
g
{\displaystyle g\,}
dann gilt
f
(
1
b
−
a
∫
a
b
g
(
x
)
d
x
)
≤
1
b
−
a
∫
a
b
f
(
g
(
x
)
)
d
x
{\displaystyle f\left({\frac {1}{b-a}}\int _{a}^{b}g(x)\,dx\right)\leq {\frac {1}{b-a}}\int _{a}^{b}f\left(g(x)\right)dx}
Beweis
Sei zunächst
φ
:
[
0
,
1
]
→
R
{\displaystyle \varphi :[0,1]\to \mathbb {R} }
f
{\displaystyle f\,}
φ
{\displaystyle \varphi \,}
f
(
∑
k
=
1
n
λ
k
x
k
)
≤
∑
k
=
1
n
λ
k
f
(
x
k
)
{\displaystyle f\left(\sum _{k=1}^{n}\lambda _{k}\,x_{k}\right)\leq \sum _{k=1}^{n}\lambda _{k}\,f(x_{k})}
λ
k
=
1
n
{\displaystyle \lambda _{k}={\frac {1}{n}}}
x
k
=
φ
(
k
n
)
{\displaystyle x_{k}=\varphi \left({\frac {k}{n}}\right)}
f
(
∑
k
=
1
n
φ
(
k
n
)
⋅
1
n
)
≤
∑
k
=
1
n
f
(
φ
(
k
n
)
)
⋅
1
n
{\displaystyle f\left(\sum _{k=1}^{n}\varphi \left({\frac {k}{n}}\right)\cdot {\frac {1}{n}}\right)\leq \sum _{k=1}^{n}f\left(\varphi \left({\frac {k}{n}}\right)\right)\cdot {\frac {1}{n}}}
n
→
∞
{\displaystyle n\to \infty }
f
(
∫
0
1
φ
(
u
)
d
u
)
≤
∫
0
1
f
(
φ
(
u
)
)
d
u
{\displaystyle f\left(\int _{0}^{1}\varphi (u)\,du\right)\leq \int _{0}^{1}f(\varphi (u))\,du}
u
=
x
−
a
b
−
a
⇒
d
u
=
d
x
b
−
a
{\displaystyle u={\frac {x-a}{b-a}}\,\Rightarrow \,du={\frac {dx}{b-a}}}
f
(
∫
a
b
φ
(
x
−
a
b
−
a
)
d
x
b
−
a
)
≤
∫
a
b
f
(
φ
(
x
−
a
b
−
a
)
)
d
x
b
−
a
{\displaystyle f\left(\int _{a}^{b}\varphi \left({\frac {x-a}{b-a}}\right){\frac {dx}{b-a}}\right)\leq \int _{a}^{b}f\left(\varphi \left({\frac {x-a}{b-a}}\right)\right){\frac {dx}{b-a}}}
g
(
x
)
:=
φ
(
x
−
a
b
−
a
)
{\displaystyle g(x):=\varphi \left({\frac {x-a}{b-a}}\right)}
f
(
1
b
−
a
∫
a
b
g
(
x
)
d
x
)
≤
1
b
−
a
∫
a
b
f
(
g
(
x
)
)
d
x
{\displaystyle f\left({\frac {1}{b-a}}\int _{a}^{b}g(x)\,dx\right)\leq {\frac {1}{b-a}}\int _{a}^{b}f(g(x))\,dx}
‖
x
+
y
‖
+
‖
y
+
z
‖
+
‖
z
+
x
‖
≤
‖
x
‖
+
‖
y
‖
+
‖
z
‖
+
‖
x
+
y
+
z
‖
x
,
y
,
z
∈
C
n
{\displaystyle \|\mathbf {x} +\mathbf {y} \|+\|\mathbf {y} +\mathbf {z} \|+\|\mathbf {z} +\mathbf {x} \|\leq \|\mathbf {x} \|+\|\mathbf {y} \|+\|\mathbf {z} \|+\|\mathbf {x} +\mathbf {y} +\mathbf {z} \|\qquad \mathbf {x} ,\mathbf {y} ,\mathbf {z} \in \mathbb {C} ^{n}}
Zurück zur Formelsammlung Mathematik
det
(
A
B
)
=
det
(
A
)
det
(
B
)
{\displaystyle \det(AB)=\det(A)\,\det(B)}
Beweis (Multiplikationssatz)
det
(
A
B
)
=
det
(
A
(
b
1
,
.
.
.
,
b
n
)
)
=
det
(
A
∑
j
=
1
n
b
1
j
e
j
,
.
.
.
,
A
∑
j
=
1
n
b
n
j
e
j
)
{\displaystyle \det(AB)=\det {\Big (}A(b_{1},...,b_{n}){\Big )}=\det \left(A\sum _{j=1}^{n}b_{1j}\,e_{j},...,A\sum _{j=1}^{n}b_{nj}\,e_{j}\right)\,}
=
det
(
∑
j
=
1
n
b
1
j
a
j
,
.
.
.
,
∑
j
=
1
n
b
n
j
a
j
)
=
∑
j
1
=
1
n
⋯
∑
j
n
=
1
n
b
1
j
1
⋯
b
n
j
n
det
(
a
j
1
,
.
.
.
,
a
j
n
)
{\displaystyle =\det \left(\sum _{j=1}^{n}b_{1j}a_{j},...,\sum _{j=1}^{n}b_{nj}a_{j}\right)=\sum _{j_{1}=1}^{n}\cdots \sum _{j_{n}=1}^{n}b_{1j_{1}}\cdots b_{nj_{n}}\,\det(a_{j_{1}},...,a_{j_{n}})}
=
∑
(
j
1
,
.
.
.
,
j
n
)
∈
S
n
b
1
j
1
⋯
b
n
j
n
det
(
a
j
1
,
.
.
.
,
a
j
n
)
=
∑
(
j
1
,
.
.
.
,
j
n
)
∈
S
n
(
−
1
)
sgn
(
j
1
,
.
.
.
,
j
n
)
b
1
j
1
⋯
b
n
j
n
⏟
=
det
(
B
)
det
(
A
)
{\displaystyle =\sum _{(j_{1},...,j_{n})\in S_{n}}b_{1j_{1}}\cdots b_{nj_{n}}\,\det(a_{j_{1}},...,a_{j_{n}})=\underbrace {\sum _{(j_{1},...,j_{n})\in S_{n}}(-1)^{{\text{sgn}}(j_{1},...,j_{n})}\,b_{1j_{1}}\cdots b_{nj_{n}}} _{=\det(B)}\,\det(A)}
det
(
e
A
)
=
e
tr
(
A
)
{\displaystyle \det(\mathrm {e} ^{A})=\mathrm {e} ^{{\text{tr}}(A)}\,}
[ Bearbeiten ]
Beweis
Hat
A
{\displaystyle A\,}
λ
1
,
.
.
.
,
λ
n
{\displaystyle \lambda _{1},...,\lambda _{n}\,}
e
A
{\displaystyle \mathrm {e} ^{A}\,}
e
λ
1
,
.
.
.
,
e
λ
n
{\displaystyle \mathrm {e} ^{\lambda _{1}},...,\mathrm {e} ^{\lambda _{n}}}
det
(
e
A
)
=
e
λ
1
⋯
e
λ
n
=
e
λ
1
+
.
.
.
+
λ
n
=
e
tr
(
A
)
{\displaystyle \det(\mathrm {e} ^{A})=\mathrm {e} ^{\lambda _{1}}\cdots \mathrm {e} ^{\lambda _{n}}=\mathrm {e} ^{\lambda _{1}+...+\lambda _{n}}=\mathrm {e} ^{{\text{tr}}(A)}}
det
(
A
+
x
y
T
)
=
det
(
A
)
+
y
T
adj
(
A
)
x
{\displaystyle \det(A+xy^{T})=\det(A)+y^{T}\,{\text{adj}}(A)\,x}
det
(
1
x
1
x
1
2
⋯
x
1
n
−
1
1
x
2
x
2
2
⋯
x
2
n
−
1
⋮
⋮
⋮
⋱
⋮
1
x
n
x
n
2
⋯
x
n
n
−
1
)
=
∏
i
<
j
(
x
j
−
x
i
)
{\displaystyle \det {\begin{pmatrix}1&x_{1}&x_{1}^{2}&\cdots &x_{1}^{n-1}\\1&x_{2}&x_{2}^{2}&\cdots &x_{2}^{n-1}\\\vdots &\vdots &\vdots &\ddots &\vdots \\1&x_{n}&x_{n}^{2}&\cdots &x_{n}^{n-1}\end{pmatrix}}=\prod _{i<j}(x_{j}-x_{i})}
Beweis (Vandermondesche Determinante)
Es sei
V
n
(
x
1
,
.
.
.
,
x
n
)
=
det
(
1
x
1
x
1
2
⋯
x
1
n
−
1
1
x
2
x
2
2
⋯
x
2
n
−
1
⋮
⋮
⋮
⋱
⋮
1
x
n
x
n
2
⋯
x
n
n
−
1
)
{\displaystyle V_{n}(x_{1},...,x_{n})=\det {\begin{pmatrix}1&x_{1}&x_{1}^{2}&\cdots &x_{1}^{n-1}\\1&x_{2}&x_{2}^{2}&\cdots &x_{2}^{n-1}\\\vdots &\vdots &\vdots &\ddots &\vdots \\1&x_{n}&x_{n}^{2}&\cdots &x_{n}^{n-1}\end{pmatrix}}}
x
1
{\displaystyle x_{1}\,}
V
n
(
x
1
,
.
.
.
,
x
n
)
=
det
(
1
0
0
⋯
0
1
x
2
−
x
1
(
x
2
−
x
1
)
x
2
⋯
(
x
2
−
x
1
)
x
2
n
−
2
⋮
⋮
⋮
⋱
⋮
1
x
n
−
x
1
(
x
n
−
x
1
)
x
n
⋯
(
x
n
−
x
1
)
x
n
n
−
2
)
{\displaystyle V_{n}(x_{1},...,x_{n})=\det {\begin{pmatrix}1&0&0&\cdots &0\\1&x_{2}-x_{1}&(x_{2}-x_{1})x_{2}&\cdots &(x_{2}-x_{1})x_{2}^{n-2}\\\vdots &\vdots &\vdots &\ddots &\vdots \\1&x_{n}-x_{1}&(x_{n}-x_{1})x_{n}&\cdots &(x_{n}-x_{1})x_{n}^{n-2}\end{pmatrix}}}
V
n
(
x
1
,
.
.
.
,
x
n
)
=
(
x
2
−
x
1
)
⋯
(
x
n
−
x
1
)
V
n
−
1
(
x
2
,
.
.
.
,
x
n
)
{\displaystyle V_{n}(x_{1},...,x_{n})=(x_{2}-x_{1})\cdots (x_{n}-x_{1})\,V_{n-1}(x_{2},...,x_{n})}
V
n
−
1
(
x
2
,
.
.
.
,
x
n
)
=
∏
2
≤
i
<
j
(
x
j
−
x
i
)
{\displaystyle V_{n-1}(x_{2},...,x_{n})=\prod _{2\leq i<j}(x_{j}-x_{i})}
V
n
(
x
1
,
.
.
.
,
x
n
)
=
∏
i
<
j
(
x
j
−
x
i
)
{\displaystyle V_{n}(x_{1},...,x_{n})=\prod _{i<j}(x_{j}-x_{i})\,}
det
(
1
x
1
+
y
1
1
x
1
+
y
2
⋯
1
x
1
+
y
n
1
x
2
+
y
1
1
x
2
+
y
2
⋯
1
x
2
+
y
n
⋮
⋮
⋱
⋮
1
x
n
+
y
1
1
x
n
+
y
2
⋯
1
x
n
+
y
n
)
=
∏
i
<
j
(
x
i
−
x
j
)
∏
i
<
j
(
y
i
−
y
j
)
∏
i
,
j
=
1
n
(
x
i
+
y
j
)
{\displaystyle \det {\begin{pmatrix}{\frac {1}{x_{1}+y_{1}}}&{\frac {1}{x_{1}+y_{2}}}&\cdots &{\frac {1}{x_{1}+y_{n}}}\\\\{\frac {1}{x_{2}+y_{1}}}&{\frac {1}{x_{2}+y_{2}}}&\cdots &{\frac {1}{x_{2}+y_{n}}}\\\vdots &\vdots &\ddots &\vdots \\{\frac {1}{x_{n}+y_{1}}}&{\frac {1}{x_{n}+y_{2}}}&\cdots &{\frac {1}{x_{n}+y_{n}}}\end{pmatrix}}={\frac {\prod \limits _{i<j}(x_{i}-x_{j})\,\prod \limits _{i<j}(y_{i}-y_{j})}{\prod \limits _{i,j=1}^{n}(x_{i}+y_{j})}}}
Beweis (Cauchy-Determinante)
Es sei
A
n
=
(
a
i
j
)
{\displaystyle A_{n}=(a_{ij})\,}
n
×
n
{\displaystyle n\times n\,}
a
i
j
=
1
x
i
+
y
j
{\displaystyle a_{ij}={\frac {1}{x_{i}+y_{j}}}}
i
{\displaystyle i\,}
(
i
=
1
,
.
.
.
,
n
−
1
)
{\displaystyle (i=1,...,n-1)\,}
x
n
+
y
n
x
i
+
y
n
{\displaystyle {\frac {x_{n}+y_{n}}{x_{i}+y_{n}}}}
n
{\displaystyle n\,}
A
n
′
=
(
B
n
−
1
0
⋮
0
1
x
n
+
y
1
1
x
n
+
y
2
⋯
1
x
n
+
y
n
)
{\displaystyle A_{n}'=\left({\begin{array}{c|c}{\begin{matrix}&B_{n-1}&\\\end{matrix}}&{\begin{matrix}0\\\vdots \\0\\\end{matrix}}\\\hline {\begin{matrix}{\frac {1}{x_{n}+y_{1}}}&{\frac {1}{x_{n}+y_{2}}}&\cdots \end{matrix}}&{\frac {1}{x_{n}+y_{n}}}\end{array}}\right)}
(
n
−
1
)
×
(
n
−
1
)
{\displaystyle (n-1)\times (n-1)\,}
B
n
−
1
=
(
b
i
j
)
{\displaystyle B_{n-1}=(b_{ij})\,}
b
i
j
=
1
x
i
+
y
j
−
x
n
+
y
n
x
i
+
y
n
⋅
1
x
n
+
y
j
{\displaystyle b_{ij}={\frac {1}{x_{i}+y_{j}}}-{\frac {x_{n}+y_{n}}{x_{i}+y_{n}}}\cdot {\frac {1}{x_{n}+y_{j}}}}
=
(
x
i
+
y
n
)
(
x
n
+
y
j
)
−
(
x
n
+
y
n
)
(
x
i
+
y
j
)
(
x
i
+
y
j
)
(
x
i
+
y
n
)
(
x
n
+
y
j
)
=
1
x
i
+
y
j
⋅
x
i
−
x
n
x
i
+
y
n
⋅
y
j
−
y
n
x
n
+
y
j
{\displaystyle ={\frac {(x_{i}+y_{n})(x_{n}+y_{j})-(x_{n}+y_{n})(x_{i}+y_{j})}{(x_{i}+y_{j})(x_{i}+y_{n})(x_{n}+y_{j})}}={\frac {1}{x_{i}+y_{j}}}\cdot {\frac {x_{i}-x_{n}}{x_{i}+y_{n}}}\cdot {\frac {y_{j}-y_{n}}{x_{n}+y_{j}}}}
B
n
−
1
{\displaystyle B_{n-1}\,}
x
i
−
x
n
x
i
+
y
n
{\displaystyle {\frac {x_{i}-x_{n}}{x_{i}+y_{n}}}}
y
j
−
y
n
x
n
+
y
j
{\displaystyle {\frac {y_{j}-y_{n}}{x_{n}+y_{j}}}}
det
B
n
−
1
{\displaystyle \det B_{n-1}\,}
det
B
n
−
1
=
∏
i
=
1
n
−
1
x
i
−
x
n
x
i
+
y
n
⋅
∏
j
=
1
n
−
1
y
j
−
y
n
x
n
+
y
j
det
A
n
−
1
{\displaystyle \det B_{n-1}=\prod _{i=1}^{n-1}{\frac {x_{i}-x_{n}}{x_{i}+y_{n}}}\cdot \prod _{j=1}^{n-1}{\frac {y_{j}-y_{n}}{x_{n}+y_{j}}}\,\det A_{n-1}}
det
A
n
−
1
=
∏
i
<
j
<
n
(
x
i
−
x
j
)
⋅
∏
i
<
j
<
n
(
y
i
−
y
j
)
∏
i
,
j
=
1
n
−
1
(
x
i
+
y
j
)
{\displaystyle \det A_{n-1}={\frac {\prod \limits _{i<j<n}(x_{i}-x_{j})\cdot \prod \limits _{i<j<n}(y_{i}-y_{j})}{\prod \limits _{i,j=1}^{n-1}(x_{i}+y_{j})}}}
det
A
n
=
det
A
n
′
=
det
B
n
−
1
⋅
1
x
n
+
y
n
{\displaystyle \det A_{n}=\det A_{n}'=\det B_{n-1}\cdot {\frac {1}{x_{n}+y_{n}}}}
∏
i
<
j
=
n
(
x
i
−
x
j
)
∏
i
<
j
=
n
(
y
i
−
y
j
)
∏
i
=
1
n
−
1
(
x
i
+
y
n
)
⋅
∏
j
=
1
n
−
1
(
x
n
+
y
j
)
⋅
(
x
n
+
y
n
)
⋅
det
A
n
−
1
=
∏
i
<
j
(
x
i
−
x
j
)
∏
i
<
j
(
y
i
−
y
j
)
∏
i
,
j
=
1
n
(
x
i
+
y
j
)
{\displaystyle {\frac {\prod \limits _{i<j=n}(x_{i}-x_{j})\,\prod \limits _{i<j=n}(y_{i}-y_{j})}{\prod \limits _{i=1}^{n-1}(x_{i}+y_{n})\cdot \prod \limits _{j=1}^{n-1}(x_{n}+y_{j})\cdot (x_{n}+y_{n})}}\cdot \det A_{n-1}={\frac {\prod \limits _{i<j}(x_{i}-x_{j})\,\prod \limits _{i<j}(y_{i}-y_{j})}{\prod \limits _{i,j=1}^{n}(x_{i}+y_{j})}}}
a
p
−
1
≡
1
mod
p
p
⧸
|
a
{\displaystyle a^{p-1}\equiv 1\,{\text{mod}}\,p\qquad p\!\!\not |a}
ohne Beweis (Kleiner fermatscher Satz)
a
φ
(
n
)
≡
1
mod
n
a
⊥
n
{\displaystyle a^{\varphi (n)}\equiv 1\,{\text{mod}}\,n\qquad a\perp n}
ohne Beweis (Satz von Euler-Fermat)
(
p
−
1
)
!
≡
−
1
mod
p
⟺
p
∈
P
{\displaystyle (p-1)!\equiv -1\,{\text{mod}}\,p\iff p\in \mathbb {P} }
1. Beweis der Rückrichtung (Satz von Wilson)
2. Beweis der Rückrichtung
Im Körper
F
p
{\displaystyle \mathbb {F} _{p}}
1
,
2
,
.
.
.
,
p
−
1
{\displaystyle 1,2,...,p-1\,}
X
2
−
1
=
0
{\displaystyle X^{2}-1=0\,}
1
{\displaystyle 1\,}
p
−
1
{\displaystyle p-1\,}
2
⋅
3
⋯
(
p
−
2
)
{\displaystyle 2\cdot 3\cdots (p-2)}
(
p
−
2
)
!
≡
1
mod
p
{\displaystyle (p-2)!\equiv 1\,{\text{mod}}\,p}
(
p
−
1
)
!
≡
−
1
mod
p
{\displaystyle (p-1)!\equiv -1\,{\text{mod}}\,p}
3. Beweis der Rückrichtung
Das Polynom
X
p
−
1
−
1
{\displaystyle X^{p-1}-1\,}
F
p
{\displaystyle \mathbb {F} _{p}}
1
,
2
,
.
.
.
,
p
−
1
{\displaystyle 1,2,...,p-1\,}
X
p
−
1
−
1
=
(
X
−
1
)
(
X
−
2
)
⋯
(
X
−
(
p
−
1
)
)
{\displaystyle X^{p-1}-1=(X-1)(X-2)\cdots (X-(p-1))}
X
=
0
{\displaystyle X=0\,}
−
1
=
(
−
1
)
(
−
2
)
⋯
(
−
(
p
−
1
)
)
=
(
−
1
)
p
−
1
(
p
−
1
)
!
{\displaystyle -1=(-1)(-2)\cdots (-(p-1))=(-1)^{p-1}\,(p-1)!}
[ Bearbeiten ] Es sei
P
(
n
)
:=
∏
1
<
k
<
n
(
k
,
n
)
=
1
k
{\displaystyle P(n):=\prod \limits _{1<k<n \atop (k,n)=1}k}
Ist
n
{\displaystyle n\,}
4
{\displaystyle 4\,}
p
k
,
2
p
k
{\displaystyle p^{k},2p^{k}\,}
p
{\displaystyle p\,}
P
(
n
)
≡
−
1
mod
n
{\displaystyle P(n)\equiv -1\,{\text{mod}}\,n}
In allen anderen Fällen ist
P
(
n
)
≡
1
mod
n
{\displaystyle P(n)\equiv 1\,{\text{mod}}\,n}
ohne Beweis (Verallgemeinerung des Satzes von Wilson durch Gauß)
[ Bearbeiten ]
∑
k
=
1
(
p
−
1
)
/
2
1
k
≡
−
2
q
p
(
2
)
mod
p
{\displaystyle \sum _{k=1}^{(p-1)/2}{\frac {1}{k}}\equiv -2q_{p}(2)\;{\text{mod}}\;p}
1. Beweis (Eisensteins Kongruenz über den Fermat-Quotienten
q
p
(
2
)
=
2
p
−
1
−
1
p
{\displaystyle q_{p}(2)={\frac {2^{p-1}-1}{p}}}
)
(
2
p
−
1
p
−
1
)
≡
1
mod
p
2
p
∈
P
≥
3
{\displaystyle {2p-1 \choose p-1}\equiv 1\,{\text{mod}}\,p^{2}\qquad p\in \mathbb {P} ^{\geq 3}}
ohne Beweis (Kongruenz von Babbage)
2
∑
k
=
1
(
p
−
1
)
/
2
1
k
2
≡
∑
k
=
1
p
−
1
1
k
2
≡
0
mod
p
p
∈
P
≥
5
{\displaystyle 2\sum _{k=1}^{(p-1)/2}{\frac {1}{k^{2}}}\equiv \sum _{k=1}^{p-1}{\frac {1}{k^{2}}}\equiv 0\;{\text{mod}}\;p\qquad p\in \mathbb {P} ^{\geq 5}}
Beweis (Kongruenzen von Wolstenholme)
∑
k
=
1
p
−
1
1
k
≡
0
mod
p
2
p
∈
P
≥
5
{\displaystyle \sum _{k=1}^{p-1}{\frac {1}{k}}\equiv 0\;{\text{mod}}\;p^{2}\qquad p\in \mathbb {P} ^{\geq 5}}
[ Bearbeiten ]
(
2
p
−
1
p
−
1
)
≡
1
mod
p
3
p
∈
P
≥
5
{\displaystyle {2p-1 \choose p-1}\equiv 1\,{\text{mod}}\,p^{3}\qquad p\in \mathbb {P} ^{\geq 5}}
(
n
p
m
p
)
≡
(
n
m
)
mod
p
3
p
∈
P
≥
5
{\displaystyle {np \choose mp}\equiv {n \choose m}\,{\text{mod}}\,p^{3}\qquad p\in \mathbb {P} ^{\geq 5}}
ohne Beweis (Kongruenz von Ljunggren)
Für eine Primzahl
p
{\displaystyle p\,}
4
n
+
1
{\displaystyle 4n+1\,}
p
=
a
2
+
b
2
{\displaystyle p=a^{2}+b^{2}\,}
a
≡
1
mod
4
{\displaystyle a\equiv 1\,{\text{mod}}\,4}
(
(
p
−
1
)
/
2
(
p
−
1
)
/
4
)
≡
2
a
p
(
(
p
−
1
)
/
2
(
p
−
1
)
/
4
)
≡
(
1
+
2
p
−
1
−
1
2
)
(
2
a
−
p
2
a
)
mod
p
2
{\displaystyle {(p-1)/2 \choose (p-1)/4}\equiv 2a\,\,p\qquad {(p-1)/2 \choose (p-1)/4}\equiv \left(1+{\frac {2^{p-1}-1}{2}}\right)\left(2a-{\frac {p}{2a}}\right)\,{\text{mod}}\,p^{2}}
ohne Beweis (Kongruenz von Gauß und Beukers)
(
−
1
)
p
−
1
2
(
p
−
1
(
p
−
1
)
/
2
)
≡
4
p
−
1
mod
p
3
p
∈
P
≥
5
{\displaystyle (-1)^{\frac {p-1}{2}}{p-1 \choose (p-1)/2}\equiv 4^{p-1}\,{\text{mod}}\,p^{3}\qquad p\in \mathbb {P} ^{\geq 5}}
Beweis (Kongruenz von Morley)
Ist
p
≡
1
mod
3
{\displaystyle p\equiv 1\,{\text{mod}}\,3}
4
p
=
Λ
2
+
27
B
2
{\displaystyle 4p=\Lambda ^{2}+27B^{2}\,}
Λ
≡
1
mod
3
{\displaystyle \Lambda \equiv 1\,{\text{mod}}\,3}
(
2
(
p
−
1
)
/
3
(
p
−
1
)
/
3
)
≡
−
Λ
mod
p
{\displaystyle {2(p-1)/3 \choose (p-1)/3}\equiv -\Lambda \,{\text{mod}}\,p}
ohne Beweis (Kongruenz von Jacobi)
3
1
2
(
F
n
−
1
)
≡
−
1
mod
F
n
⟺
F
n
∈
P
,
F
n
=
2
2
n
+
1
{\displaystyle 3^{{\frac {1}{2}}(F_{n}-1)}\equiv -1\,{\text{mod}}\,F_{n}\iff F_{n}\in \mathbb {P} \quad ,\quad F_{n}=2^{2^{n}}+1}
2
n
≡
2
m
mod
2
k
⟹
E
2
n
−
E
2
m
≡
−
(
2
n
−
2
m
)
mod
2
k
+
1
{\displaystyle 2n\equiv 2m\,{\text{mod}}\,2^{k}\implies E_{2n}-E_{2m}\equiv -(2n-2m)\,{\text{mod}}\,2^{k+1}}
B
n
+
p
m
≡
m
B
n
+
B
n
+
1
mod
p
{\displaystyle B_{n+p^{m}}\equiv mB_{n}+B_{n+1}\;{\text{mod}}\;p}
ohne Beweis (Touchards Kongruenz)
Ist
p
{\displaystyle p\,}
k
,
ℓ
{\displaystyle k,\ell }
k
≡
ℓ
≢
0
mod
p
−
1
{\displaystyle k\equiv \ell \not \equiv 0\,{\text{mod}}\,p-1}
B
k
k
≡
B
ℓ
ℓ
mod
p
{\displaystyle {\frac {B_{k}}{k}}\equiv {\frac {B_{\ell }}{\ell }}\;{\text{mod}}\;p}
ohne Beweis (Kummersche Kongruenz)
Ist
k
{\displaystyle k\,}
B
k
≡
−
∑
p
−
1
|
k
1
p
mod
Z
{\displaystyle B_{k}\equiv -\sum _{p-1|k}{\frac {1}{p}}\;{\text{mod}}\;\mathbb {Z} }
ohne Beweis (Von Staudt-Clausen-Theorem)
[ Bearbeiten ] Ist p eine Primzahl und sind
a
=
(
a
0
,
.
.
.
,
a
r
)
,
b
=
(
b
0
,
.
.
.
,
b
r
)
{\displaystyle {\boldsymbol {a}}=(a_{0},...,a_{r})\,,\,{\boldsymbol {b}}=(b_{0},...,b_{r})}
α
=
a
0
+
a
1
p
+
a
2
p
2
+
.
.
.
+
a
r
p
r
{\displaystyle \alpha =a_{0}+a_{1}p+a_{2}p^{2}+...+a_{r}p^{r}\,}
β
=
b
0
+
b
1
p
+
b
2
p
2
+
.
.
.
+
b
r
p
r
{\displaystyle \beta =b_{0}+b_{1}p+b_{2}p^{2}+...+b_{r}p^{r}\,}
p -adischen Zifferndarstellungen
der natürlichen Zahlen
α
{\displaystyle \alpha \,}
β
{\displaystyle \beta \,}
(
α
β
)
≡
(
a
b
)
mod
p
{\displaystyle {\alpha \choose \beta }\equiv {{\boldsymbol {a}} \choose {\boldsymbol {b}}}\;{\text{mod}}\;p}
(
a
b
)
=
(
a
0
b
0
)
(
a
1
b
1
)
⋯
(
a
r
b
r
)
{\displaystyle {{\boldsymbol {a}} \choose {\boldsymbol {b}}}={a_{0} \choose b_{0}}{a_{1} \choose b_{1}}\cdots {a_{r} \choose b_{r}}}
Beweis
In Anbetracht der Gleichung
(
1
)
β
(
α
β
)
=
α
(
α
−
1
β
−
1
)
{\displaystyle (1)\quad \beta \,{\alpha \choose \beta }=\alpha {\alpha -1 \choose \beta -1}}
(
2
)
b
0
(
α
β
)
≡
β
(
α
β
)
=
1
α
(
α
−
1
β
−
1
)
≡
a
0
(
α
−
1
β
−
1
)
mod
p
{\displaystyle (2)\quad b_{0}{\alpha \choose \beta }\equiv \beta {\alpha \choose \beta }\,{\stackrel {1}{=}}\,\alpha {\alpha -1 \choose \beta -1}\equiv a_{0}{\alpha -1 \choose \beta -1}\;{\text{mod}}\;p}
a
0
,
b
0
≠
0
{\displaystyle a_{0},b_{0}\neq 0\,}
(
α
−
1
β
−
1
)
=
(
a
0
−
1
b
0
−
1
)
(
a
1
b
1
)
⋯
(
a
r
b
r
)
mod
p
{\displaystyle {\alpha -1 \choose \beta -1}={a_{0}-1 \choose b_{0}-1}{a_{1} \choose b_{1}}\cdots {a_{r} \choose b_{r}}\;{\text{mod}}\;p}
b
0
(
α
β
)
≡
2
a
0
(
α
−
1
β
−
1
)
=
a
0
(
a
0
−
1
b
0
−
1
)
(
a
1
b
1
)
⋯
(
a
r
b
r
)
=
1
b
0
(
a
0
b
0
)
(
a
1
b
1
)
⋯
(
a
r
b
r
)
mod
p
{\displaystyle b_{0}{\alpha \choose \beta }\,{\stackrel {2}{\equiv }}\,a_{0}{\alpha -1 \choose \beta -1}=a_{0}{a_{0}-1 \choose b_{0}-1}{a_{1} \choose b_{1}}\cdots {a_{r} \choose b_{r}}\,{\stackrel {1}{=}}\,b_{0}{a_{0} \choose b_{0}}{a_{1} \choose b_{1}}\cdots {a_{r} \choose b_{r}}\;{\text{mod}}\;p}
b
0
{\displaystyle b_{0}\,}
(
α
β
)
≡
(
a
b
)
mod
p
{\displaystyle {\alpha \choose \beta }\equiv {{\boldsymbol {a}} \choose {\boldsymbol {b}}}\;{\text{mod}}\;p}
a
0
=
0
,
b
0
≠
0
{\displaystyle a_{0}=0,b_{0}\neq 0\,}
b
0
(
α
β
)
≡
2
a
0
(
α
−
1
β
−
1
)
=
0
mod
p
{\displaystyle b_{0}{\alpha \choose \beta }\,{\stackrel {2}{\equiv }}\,a_{0}{\alpha -1 \choose \beta -1}=0\;{\text{mod}}\;p}
(
α
β
)
≡
0
mod
p
{\displaystyle {\alpha \choose \beta }\equiv 0\;{\text{mod}}\;p}
(
a
0
b
0
)
=
0
{\displaystyle {a_{0} \choose b_{0}}=0}
(
a
b
)
=
(
a
0
b
0
)
(
a
1
b
1
)
⋯
(
a
r
b
r
)
≡
0
mod
p
{\displaystyle {{\boldsymbol {a}} \choose {\boldsymbol {b}}}={a_{0} \choose b_{0}}{a_{1} \choose b_{1}}\cdots {a_{r} \choose b_{r}}\equiv 0\;{\text{mod}}\;p}
a
0
=
b
0
=
0
{\displaystyle a_{0}=b_{0}=0\,}
α
=
n
p
{\displaystyle \alpha =np\,}
β
=
m
p
{\displaystyle \beta =mp\,}
n
=
a
1
+
a
2
p
+
.
.
.
+
a
r
p
r
−
1
{\displaystyle n=a_{1}+a_{2}p+...+a_{r}p^{r-1}\,}
m
=
b
1
+
b
2
p
+
.
.
.
+
b
r
p
r
−
1
{\displaystyle m=b_{1}+b_{2}p+...+b_{r}p^{r-1}\,}
(
n
p
)
!
=
n
!
p
n
A
n
{\displaystyle (np)!=n!\,p^{n}\,A_{n}}
A
n
=
(
n
p
)
!
n
!
p
n
≡
(
(
p
−
1
)
!
)
n
≡
(
−
1
)
n
mod
p
{\displaystyle A_{n}={\frac {(np)!}{n!\,p^{n}}}\equiv ((p-1)!)^{n}\equiv (-1)^{n}\;{\text{mod}}\;p}
(
α
β
)
=
(
n
p
m
p
)
=
(
n
p
)
!
(
m
p
)
!
(
(
n
−
m
)
p
)
!
=
n
!
p
n
A
n
m
!
p
m
A
m
(
n
−
m
)
!
p
n
−
m
A
n
−
m
{\displaystyle {\alpha \choose \beta }={np \choose mp}={\frac {(np)!}{(mp)!\,((n-m)p)!}}={\frac {n!\,p^{n}\,A_{n}}{m!\,p^{m}\,A_{m}\,\,(n-m)!\,p^{n-m}\,A_{n-m}}}}
=
(
n
m
)
A
n
A
m
A
n
−
m
≡
(
n
m
)
mod
p
{\displaystyle ={n \choose m}{\frac {A_{n}}{A_{m}\,A_{n-m}}}\equiv {n \choose m}\;{\text{mod}}\;p}
≡
(
a
1
b
1
)
⋯
(
a
r
b
r
)
mod
p
{\displaystyle \equiv {a_{1} \choose b_{1}}\cdots {a_{r} \choose b_{r}}\;{\text{mod}}\;p}
(
a
0
b
0
)
=
(
0
0
)
=
1
{\displaystyle {a_{0} \choose b_{0}}={0 \choose 0}=1}
(
α
β
)
≡
(
a
b
)
mod
p
{\displaystyle {\alpha \choose \beta }\equiv {{\boldsymbol {a}} \choose {\boldsymbol {b}}}\;{\text{mod}}\;p}
a
0
≠
0
,
b
0
=
0
{\displaystyle a_{0}\neq 0,b_{0}=0\;}
(
α
−
β
)
(
α
−
β
−
1
)
⋯
(
α
−
β
−
a
0
+
1
)
(
α
β
)
=
α
(
α
−
1
)
⋯
(
α
−
a
0
+
1
)
(
α
−
a
0
β
)
{\displaystyle (\alpha -\beta )(\alpha -\beta -1)\cdots (\alpha -\beta -a_{0}+1){\alpha \choose \beta }=\alpha (\alpha -1)\cdots (\alpha -a_{0}+1){\alpha -a_{0} \choose \beta }}
β
≡
b
0
=
0
mod
p
{\displaystyle \beta \equiv b_{0}=0\;{\text{mod}}\;p}
(
α
−
β
)
(
α
−
β
−
1
)
⋯
(
α
−
β
−
a
0
+
1
)
{\displaystyle (\alpha -\beta )(\alpha -\beta -1)\cdots (\alpha -\beta -a_{0}+1)}
≡
α
(
α
−
1
)
⋯
(
α
−
a
0
+
1
)
≡
a
0
(
a
0
−
1
)
⋯
1
=
a
0
!
≢
0
mod
p
{\displaystyle \equiv \alpha (\alpha -1)\cdots (\alpha -a_{0}+1)\equiv a_{0}(a_{0}-1)\cdots 1=a_{0}!\not \equiv 0\;{\text{mod}}\;p}
a
0
!
(
α
β
)
≡
a
0
!
(
α
−
a
0
β
)
mod
p
{\displaystyle a_{0}!\,{\alpha \choose \beta }\equiv a_{0}!\,{\alpha -a_{0} \choose \beta }\;{\text{mod}}\;p}
a
0
!
{\displaystyle a_{0}!\,}
(
α
β
)
≡
(
α
−
a
0
β
)
mod
p
{\displaystyle {\alpha \choose \beta }\equiv {\alpha -a_{0} \choose \beta }\;{\text{mod}}\;p}
(
α
−
a
0
β
)
≡
(
(
α
−
a
0
)
/
p
(
β
−
b
0
)
/
p
)
mod
p
{\displaystyle {\alpha -a_{0} \choose \beta }\equiv {(\alpha -a_{0})/p \choose (\beta -b_{0})/p}\;{\text{mod}}\;p}
≡
(
a
1
b
1
)
⋯
(
a
r
b
r
)
mod
p
{\displaystyle \equiv {a_{1} \choose b_{1}}\cdots {a_{r} \choose b_{r}}\;{\text{mod}}\;p}
(
a
0
b
0
)
=
1
{\displaystyle {a_{0} \choose b_{0}}=1}
(
α
β
)
≡
(
a
b
)
mod
p
{\displaystyle {\alpha \choose \beta }\equiv {{\boldsymbol {a}} \choose {\boldsymbol {b}}}\;{\text{mod}}\;p}
Zurück zur Formelsammlung Mathematik
a
0
+
1
a
1
+
1
a
2
+
1
a
3
+
⋯
{\displaystyle a_{0}+{\frac {1}{\displaystyle a_{1}+{\frac {1}{\displaystyle a_{2}+{\frac {1}{a_{3}+\cdots }}}}}}}
wobei
a
0
∈
Z
{\displaystyle a_{0}\in \mathbb {Z} }
a
1
,
a
2
,
a
3
,
.
.
.
∈
Z
>
0
{\displaystyle a_{1},a_{2},a_{3},...\in \mathbb {Z} ^{>0}}
[
a
0
,
a
1
,
a
2
,
a
3
,
.
.
.
]
{\displaystyle [a_{0},a_{1},a_{2},a_{3},...]\,}
−
[
a
0
,
a
1
,
a
2
,
a
3
,
a
4
,
…
]
=
{
[
−
(
a
0
+
1
)
,
a
2
+
1
,
a
3
,
a
4
,
a
5
,
…
]
,
a
1
=
1
[
−
(
a
0
+
1
)
,
1
,
a
1
−
1
,
a
2
,
a
3
,
a
4
,
…
]
,
a
1
>
1
{\displaystyle -\left[a_{0},a_{1},a_{2},a_{3},a_{4},\ldots \right]=\left\{{\begin{matrix}\left[-(a_{0}+1),a_{2}+1,a_{3},a_{4},a_{5},\ldots \right]&,&a_{1}=1\\\\\left[-(a_{0}+1),1,a_{1}-1,a_{2},a_{3},a_{4},\ldots \right]&,&a_{1}>1\end{matrix}}\right.}
[
a
0
,
a
1
,
a
2
,
.
.
.
]
−
1
=
{
[
0
,
a
0
,
a
1
,
.
.
.
]
,
a
0
>
0
[
a
1
,
a
2
,
a
3
.
.
.
]
,
a
0
=
0
{\displaystyle \left[a_{0},a_{1},a_{2},...\right]^{-1}=\left\{{\begin{matrix}\left[0,a_{0},a_{1},...\right]&,&a_{0}>0\\\\\left[a_{1},a_{2},a_{3}...\right]&,&a_{0}=0\end{matrix}}\right.}
φ
=
1
+
5
2
=
[
1
¯
]
{\displaystyle \varphi ={\frac {1+{\sqrt {5}}}{2}}=\left[{\overline {1}}\right]}
e
=
[
2
,
1
,
2
k
,
1
¯
]
k
≥
1
{\displaystyle e=\left[2,{\overline {1,2k,1}}\right]_{k\geq 1}}
Beweis
Sei
ϱ
{\displaystyle \varrho \,}
[
a
0
;
a
1
,
a
2
,
a
3
,
.
.
.
]
{\displaystyle [a_{0};a_{1},a_{2},a_{3},...]\,}
a
0
=
2
,
a
3
n
−
2
=
1
,
a
3
n
−
1
=
2
n
,
a
3
n
=
1
{\displaystyle a_{0}=2,a_{3n-2}=1,a_{3n-1}=2n,a_{3n}=1\,}
n
∈
Z
>
0
{\displaystyle n\in \mathbb {Z} ^{>0}}
ϱ
=
[
2
;
1
,
2
,
1
,
1
,
4
,
1
,
1
,
6
,
1
,
1
,
8
,
1
,
.
.
.
]
=
[
2
,
1
,
2
n
,
1
¯
]
n
≥
1
{\displaystyle \varrho =[2;1,2,1,1,4,1,1,6,1,1,8,1,...]=\left[2,{\overline {1,2n,1}}\right]_{n\geq 1}}
p
n
q
n
{\displaystyle {\frac {p_{n}}{q_{n}}}}
{
p
n
=
a
n
p
n
−
1
+
p
n
−
2
q
n
=
a
n
q
n
−
1
+
q
n
−
2
}
{\displaystyle {\begin{Bmatrix}p_{n}=a_{n}p_{n-1}+p_{n-2}\\q_{n}=a_{n}q_{n-1}+q_{n-2}\end{Bmatrix}}}
{
p
−
2
=
0
,
p
−
1
=
1
q
−
2
=
1
,
q
−
1
=
0
}
{\displaystyle {\begin{Bmatrix}p_{-2}=0\;,\;p_{-1}=1\\q_{-2}=1\;,\;q_{-1}=0\end{Bmatrix}}}
(
p
n
q
n
)
n
≥
0
=
(
2
1
,
3
1
,
8
3
,
11
4
,
19
7
,
.
.
.
)
{\displaystyle \left({\frac {p_{n}}{q_{n}}}\right)_{n\geq 0}=\left({\frac {2}{1}},{\frac {3}{1}},{\frac {8}{3}},{\frac {11}{4}},{\frac {19}{7}},...\right)}
ϱ
{\displaystyle \varrho \,}
n
≥
1
{\displaystyle n\geq 1\,}
{
p
3
n
−
1
=
2
n
p
3
n
−
2
+
p
3
n
−
3
p
3
n
=
p
3
n
−
1
+
p
3
n
−
2
p
3
n
+
1
=
p
3
n
+
p
3
n
−
1
}
{
q
3
n
−
1
=
2
n
q
3
n
−
2
+
q
3
n
−
3
q
3
n
=
q
3
n
−
1
+
q
3
n
−
2
q
3
n
+
1
=
q
3
n
+
q
3
n
−
1
}
(
∗
)
{\displaystyle {\begin{Bmatrix}p_{3n-1}&=&2n&p_{3n-2}&+&p_{3n-3}\\p_{3n}&=&&p_{3n-1}&+&p_{3n-2}\\p_{3n+1}&=&&p_{3n}&+&p_{3n-1}\end{Bmatrix}}\quad \quad {\begin{Bmatrix}q_{3n-1}&=&2n&q_{3n-2}&+&q_{3n-3}\\q_{3n}&=&&q_{3n-1}&+&q_{3n-2}\\q_{3n+1}&=&&q_{3n}&+&q_{3n-1}\end{Bmatrix}}\qquad (*)}
[
a
n
(
x
)
=
x
n
+
1
(
x
−
1
)
n
n
!
e
x
,
b
n
(
x
)
=
x
n
(
x
−
1
)
n
+
1
n
!
e
x
,
c
n
(
x
)
=
−
x
n
+
1
(
x
−
1
)
n
+
1
(
n
+
1
)
!
e
x
A
n
=
∫
0
1
a
n
(
x
)
d
x
,
B
n
=
∫
0
1
b
n
(
x
)
d
x
,
C
n
=
∫
0
1
c
n
(
x
)
d
x
]
{\displaystyle {\begin{bmatrix}a_{n}(x)={\frac {x^{n+1}\,(x-1)^{n}}{n!}}\,e^{x}&,&b_{n}(x)={\frac {x^{n}\,(x-1)^{n+1}}{n!}}\,e^{x}&,&c_{n}(x)=-{\frac {x^{n+1}\,(x-1)^{n+1}}{(n+1)!}}\,e^{x}\\\\A_{n}=\int _{0}^{1}a_{n}(x)dx&,&B_{n}=\int _{0}^{1}b_{n}(x)dx&,&C_{n}=\int _{0}^{1}c_{n}(x)dx\end{bmatrix}}}
Behauptung: Für alle
n
≥
0
{\displaystyle n\geq 0\,}
{
A
n
=
p
3
n
−
1
−
q
3
n
−
1
⋅
e
B
n
=
p
3
n
−
q
3
n
⋅
e
C
n
=
p
3
n
+
1
−
q
3
n
+
1
⋅
e
}
{\displaystyle {\begin{Bmatrix}A_{n}&=&p_{3n-1}-q_{3n-1}\cdot e\\B_{n}&=&p_{3n}-q_{3n}\cdot e\\C_{n}&=&p_{3n+1}-q_{3n+1}\cdot e\end{Bmatrix}}}
A
0
=
1
,
B
0
=
2
−
e
,
C
0
=
3
−
e
{\displaystyle A_{0}=1\;,\;B_{0}=2-e\;,\;C_{0}=3-e\,}
n
≥
1
{\displaystyle n\geq 1\,}
{
a
n
(
x
)
=
2
n
c
n
−
1
(
x
)
+
b
n
−
1
(
x
)
+
b
n
′
(
x
)
b
n
(
x
)
=
a
n
(
x
)
+
c
n
−
1
(
x
)
c
n
(
x
)
=
b
n
(
x
)
+
a
n
(
x
)
+
c
n
′
(
x
)
}
{\displaystyle {\begin{Bmatrix}a_{n}(x)&=&2n&c_{n-1}(x)&+&b_{n-1}(x)&+&b_{n}'(x)\\b_{n}(x)&=&&a_{n}(x)&+&c_{n-1}(x)\\c_{n}(x)&=&&b_{n}(x)&+&a_{n}(x)&+&c_{n}'(x)\end{Bmatrix}}}
{
A
n
=
2
n
C
n
−
1
+
B
n
−
1
B
n
=
A
n
+
C
n
−
1
C
n
=
B
n
+
A
n
}
{\displaystyle {\begin{Bmatrix}A_{n}&=&2n&C_{n-1}&+&B_{n-1}\\B_{n}&=&&A_{n}&+&C_{n-1}\\C_{n}&=&&B_{n}&+&A_{n}\end{Bmatrix}}}
A
n
,
B
n
,
C
n
{\displaystyle A_{n}\,,\;B_{n}\,,\;C_{n}}
(
∗
)
{\displaystyle (*)\,}
A
n
,
B
n
,
C
n
{\displaystyle A_{n}\,,\;B_{n}\,,\;C_{n}}
n
→
∞
{\displaystyle n\to \infty \,}
ϱ
:=
lim
n
→
∞
p
n
q
n
=
e
{\displaystyle \varrho :=\lim _{n\to \infty }{\frac {p_{n}}{q_{n}}}=e}
e
1
/
n
=
[
1
,
(
2
k
−
1
)
n
−
1
,
1
¯
]
k
≥
1
n
∈
Z
>
1
{\displaystyle e^{1/n}=\left[{\overline {1,(2k-1)n-1,1}}\right]_{k\geq 1}\qquad n\in \mathbb {Z} ^{>1}}
Beweis
Für
m
∈
Z
>
1
{\displaystyle m\in \mathbb {Z} ^{>1}}
ϱ
m
{\displaystyle \varrho _{m}\,}
[
a
0
;
a
1
,
a
2
,
a
3
,
.
.
.
]
{\displaystyle [a_{0};a_{1},a_{2},a_{3},...]\,}
a
3
n
=
1
,
a
3
n
+
1
=
(
2
n
+
1
)
m
−
1
,
a
3
n
+
2
=
1
{\displaystyle a_{3n}=1\,,\,a_{3n+1}=(2n+1)m-1\,,\,a_{3n+2}=1}
n
∈
Z
≥
0
{\displaystyle n\in \mathbb {Z} ^{\geq 0}}
ϱ
m
=
[
1
,
m
−
1
,
1
,
1
,
3
m
−
1
,
1
,
1
,
5
m
−
1
,
1
,
.
.
.
]
=
[
1
,
(
2
n
+
1
)
m
−
1
,
1
¯
]
n
≥
0
{\displaystyle \varrho _{m}=[1,m-1,1,1,3m-1,1,1,5m-1,1,...]=\left[{\overline {1,(2n+1)m-1,1}}\right]_{n\geq 0}}
p
n
q
n
{\displaystyle {\frac {p_{n}}{q_{n}}}}
{
p
n
=
a
n
p
n
−
1
+
p
n
−
2
q
n
=
a
n
q
n
−
1
+
q
n
−
2
}
{\displaystyle {\begin{Bmatrix}p_{n}=a_{n}p_{n-1}+p_{n-2}\\q_{n}=a_{n}q_{n-1}+q_{n-2}\end{Bmatrix}}}
{
p
−
2
=
0
,
p
−
1
=
1
q
−
2
=
1
,
q
−
1
=
0
}
{\displaystyle {\begin{Bmatrix}p_{-2}=0\;,\;p_{-1}=1\\q_{-2}=1\;,\;q_{-1}=0\end{Bmatrix}}}
(
p
n
q
n
)
n
≥
0
=
(
1
,
m
m
−
1
,
m
+
1
m
,
2
m
+
1
2
m
−
1
,
.
.
.
)
{\displaystyle \left({\frac {p_{n}}{q_{n}}}\right)_{n\geq 0}=\left(1,{\frac {m}{m-1}},{\frac {m+1}{m}},{\frac {2m+1}{2m-1}},...\right)}
ϱ
m
{\displaystyle \varrho _{m}\,}
n
≥
0
{\displaystyle n\geq 0\,}
{
p
3
n
=
p
3
n
−
1
+
p
3
n
−
2
p
3
n
+
1
=
(
(
2
n
+
1
)
m
−
1
)
p
3
n
+
p
3
n
−
1
p
3
n
+
2
=
p
3
n
+
1
+
p
3
n
}
{
q
3
n
=
q
3
n
−
1
+
q
3
n
−
2
q
3
n
+
1
=
(
(
2
n
+
1
)
m
−
1
)
q
3
n
+
q
3
n
−
1
q
3
n
+
2
=
q
3
n
+
1
+
q
3
n
}
(
∗
)
{\displaystyle {\begin{Bmatrix}p_{3n}&=&&p_{3n-1}&+&p_{3n-2}\\p_{3n+1}&=&{\big (}(2n+1)m-1{\big )}&p_{3n}&+&p_{3n-1}\\p_{3n+2}&=&&p_{3n+1}&+&p_{3n}\end{Bmatrix}}\quad {\begin{Bmatrix}q_{3n}&=&&q_{3n-1}&+&q_{3n-2}\\q_{3n+1}&=&{\big (}(2n+1)m-1{\big )}&q_{3n}&+&q_{3n-1}\\q_{3n+2}&=&&q_{3n+1}&+&q_{3n}\end{Bmatrix}}\quad (*)}
[
a
n
(
x
)
=
−
1
m
n
+
1
x
n
(
x
−
1
)
n
n
!
e
x
/
m
,
b
n
(
x
)
=
1
m
n
+
1
x
n
+
1
(
x
−
1
)
n
n
!
e
x
/
m
,
c
n
(
x
)
=
1
m
n
+
1
x
n
(
x
−
1
)
n
+
1
n
!
e
x
/
m
A
n
=
∫
0
1
a
n
(
x
)
d
x
,
B
n
=
∫
0
1
b
n
(
x
)
d
x
,
C
n
=
∫
0
1
c
n
(
x
)
d
x
]
{\displaystyle {\begin{bmatrix}a_{n}(x)=-{\frac {1}{m^{n+1}}}\,{\frac {x^{n}\,(x-1)^{n}}{n!}}\,e^{x/m}&,&b_{n}(x)={\frac {1}{m^{n+1}}}\,{\frac {x^{n+1}\,(x-1)^{n}}{n!}}\,e^{x/m}&,&c_{n}(x)={\frac {1}{m^{n+1}}}\,{\frac {x^{n}\,(x-1)^{n+1}}{n!}}\,e^{x/m}\\\\A_{n}=\int _{0}^{1}a_{n}(x)dx&,&B_{n}=\int _{0}^{1}b_{n}(x)dx&,&C_{n}=\int _{0}^{1}c_{n}(x)dx\end{bmatrix}}}
Behauptung: Für alle
n
≥
0
{\displaystyle n\geq 0\,}
{
A
n
=
p
3
n
−
q
3
n
⋅
e
1
/
m
B
n
=
p
3
n
+
1
−
q
3
n
+
1
⋅
e
1
/
m
C
n
=
p
3
n
+
2
−
q
3
n
+
2
⋅
e
1
/
m
}
{\displaystyle {\begin{Bmatrix}A_{n}&=&p_{3n}-q_{3n}\cdot e^{1/m}\\B_{n}&=&p_{3n+1}-q_{3n+1}\cdot e^{1/m}\\C_{n}&=&p_{3n+2}-q_{3n+2}\cdot e^{1/m}\end{Bmatrix}}}
A
0
=
1
−
e
1
/
m
,
B
0
=
m
−
(
m
−
1
)
⋅
e
1
/
m
,
C
0
=
(
m
+
1
)
−
m
⋅
e
1
/
m
{\displaystyle A_{0}=1-e^{1/m}\;,\;B_{0}=m-(m-1)\cdot e^{1/m}\;,\;C_{0}=(m+1)-m\cdot e^{1/m}\,}
n
≥
1
{\displaystyle n\geq 1\,}
{
a
n
(
x
)
=
c
n
−
1
(
x
)
+
b
n
−
1
(
x
)
+
m
⋅
a
n
′
(
x
)
b
n
(
x
)
=
(
(
2
n
+
1
)
m
−
1
)
a
n
(
x
)
+
c
n
−
1
(
x
)
+
m
⋅
c
n
′
(
x
)
c
n
(
x
)
=
b
n
(
x
)
+
a
n
(
x
)
}
{\displaystyle {\begin{Bmatrix}a_{n}(x)&=&&c_{n-1}(x)&+&b_{n-1}(x)&+&m\cdot a_{n}'(x)\\b_{n}(x)&=&{\big (}(2n+1)m-1{\big )}&a_{n}(x)&+&c_{n-1}(x)&+&m\cdot c_{n}'(x)\\c_{n}(x)&=&&b_{n}(x)&+&a_{n}(x)\end{Bmatrix}}}
{
A
n
=
C
n
−
1
+
B
n
−
1
B
n
=
(
(
2
n
+
1
)
m
−
1
)
A
n
+
C
n
−
1
C
n
=
B
n
+
A
n
}
{\displaystyle {\begin{Bmatrix}A_{n}&=&&C_{n-1}&+&B_{n-1}\\B_{n}&=&{\big (}(2n+1)m-1{\big )}&A_{n}&+&C_{n-1}\\C_{n}&=&&B_{n}&+&A_{n}\end{Bmatrix}}}
A
n
,
B
n
,
C
n
{\displaystyle A_{n}\,,\;B_{n}\,,\;C_{n}}
(
∗
)
{\displaystyle (*)\,}
A
n
,
B
n
,
C
n
{\displaystyle A_{n}\,,\;B_{n}\,,\;C_{n}}
n
→
∞
{\displaystyle n\to \infty \,}
ϱ
m
:=
lim
n
→
∞
p
n
q
n
=
e
1
/
m
{\displaystyle \varrho _{m}:=\lim _{n\to \infty }{\frac {p_{n}}{q_{n}}}=e^{1/m}}
e
2
=
[
7
,
3
k
−
1
,
1
,
1
,
3
k
,
6
(
2
k
+
1
)
¯
]
k
≥
1
{\displaystyle e^{2}=\left[7,{\overline {3k-1,1,1,3k,6(2k+1)}}\right]_{k\geq 1}}
Beweis
Sei
ϱ
{\displaystyle \varrho \,}
[
a
0
;
a
1
,
a
2
,
a
3
,
.
.
.
]
{\displaystyle [a_{0};a_{1},a_{2},a_{3},...]\,}
a
0
=
7
,
{\displaystyle a_{0}=7,\,}
a
5
n
−
4
=
3
n
−
1
,
a
5
n
−
3
=
1
,
a
5
n
−
2
=
1
,
a
5
n
−
1
=
3
n
,
a
5
n
=
6
(
2
n
+
1
)
{\displaystyle a_{5n-4}=3n-1,a_{5n-3}=1,a_{5n-2}=1,a_{5n-1}=3n,a_{5n}=6(2n+1)\,}
n
∈
Z
>
0
{\displaystyle n\in \mathbb {Z} ^{>0}}
ϱ
=
[
7
;
2
,
1
,
1
,
3
,
18
,
5
,
1
,
1
,
6
,
30
,
8
,
1
,
1
,
9
,
42
,
.
.
.
]
=
[
7
,
3
n
−
1
,
1
,
1
,
3
n
,
6
(
2
n
+
1
)
¯
]
n
≥
1
{\displaystyle \varrho =[7;2,1,1,3,18,5,1,1,6,30,8,1,1,9,42,...]=\left[7,{\overline {3n-1,1,1,3n,6(2n+1)}}\right]_{n\geq 1}}
p
n
q
n
{\displaystyle {\frac {p_{n}}{q_{n}}}}
{
p
n
=
a
n
p
n
−
1
+
p
n
−
2
q
n
=
a
n
q
n
−
1
+
q
n
−
2
}
{\displaystyle {\begin{Bmatrix}p_{n}=a_{n}p_{n-1}+p_{n-2}\\q_{n}=a_{n}q_{n-1}+q_{n-2}\end{Bmatrix}}}
{
p
−
2
=
0
,
p
−
1
=
1
q
−
2
=
1
,
q
−
1
=
0
}
{\displaystyle {\begin{Bmatrix}p_{-2}=0\;,\;p_{-1}=1\\q_{-2}=1\;,\;q_{-1}=0\end{Bmatrix}}}
(
p
n
q
n
)
n
≥
0
=
(
7
1
,
15
2
,
22
3
,
37
5
,
133
18
,
2431
329
,
.
.
.
)
{\displaystyle \left({\frac {p_{n}}{q_{n}}}\right)_{n\geq 0}=\left({\frac {7}{1}},{\frac {15}{2}},{\frac {22}{3}},{\frac {37}{5}},{\frac {133}{18}},{\frac {2431}{329}},...\right)}
ϱ
{\displaystyle \varrho \,}
n
≥
1
{\displaystyle n\geq 1\,}
{
p
5
n
−
4
=
(
3
n
−
1
)
p
5
n
−
5
+
p
5
n
−
6
p
5
n
−
3
=
p
5
n
−
4
+
p
5
n
−
5
p
5
n
−
2
=
p
5
n
−
3
+
p
5
n
−
4
p
5
n
−
1
=
3
n
p
5
n
−
2
+
p
5
n
−
3
p
5
n
=
6
(
2
n
+
1
)
p
5
n
−
1
+
p
5
n
−
2
}
{
q
5
n
−
4
=
(
3
n
−
1
)
q
5
n
−
5
+
q
5
n
−
6
q
5
n
−
3
=
q
5
n
−
4
+
q
5
n
−
5
q
5
n
−
2
=
q
5
n
−
3
+
q
5
n
−
4
q
5
n
−
1
=
3
n
q
5
n
−
2
+
q
5
n
−
3
q
5
n
=
6
(
2
n
+
1
)
q
5
n
−
1
+
q
5
n
−
2
}
(
∗
)
{\displaystyle {\begin{Bmatrix}p_{5n-4}&=&(3n-1)&p_{5n-5}&+&p_{5n-6}\\p_{5n-3}&=&&p_{5n-4}&+&p_{5n-5}\\p_{5n-2}&=&&p_{5n-3}&+&p_{5n-4}\\p_{5n-1}&=&3n&p_{5n-2}&+&p_{5n-3}\\p_{5n}&=&6(2n+1)&p_{5n-1}&+&p_{5n-2}\end{Bmatrix}}\quad \quad {\begin{Bmatrix}q_{5n-4}&=&(3n-1)&q_{5n-5}&+&q_{5n-6}\\q_{5n-3}&=&&q_{5n-4}&+&q_{5n-5}\\q_{5n-2}&=&&q_{5n-3}&+&q_{5n-4}\\q_{5n-1}&=&3n&q_{5n-2}&+&q_{5n-3}\\q_{5n}&=&6(2n+1)&q_{5n-1}&+&q_{5n-2}\end{Bmatrix}}\qquad (*)}
[
a
n
(
x
)
=
−
2
n
+
1
x
n
(
x
−
1
)
n
n
!
e
2
x
,
b
n
(
x
)
=
2
n
+
1
x
n
+
1
(
x
−
1
)
n
n
!
e
2
x
,
c
n
(
x
)
=
2
n
+
1
x
n
(
x
−
1
)
n
+
1
n
!
e
2
x
A
n
=
∫
0
1
a
n
(
x
)
d
x
,
B
n
=
∫
0
1
b
n
(
x
)
d
x
,
C
n
=
∫
0
1
c
n
(
x
)
d
x
]
{\displaystyle {\begin{bmatrix}a_{n}(x)=-2^{n+1}\,{\frac {x^{n}\,(x-1)^{n}}{n!}}\,e^{2x}&,&b_{n}(x)=2^{n+1}\,{\frac {x^{n+1}\,(x-1)^{n}}{n!}}\,e^{2x}&,&c_{n}(x)=2^{n+1}\,{\frac {x^{n}\,(x-1)^{n+1}}{n!}}\,e^{2x}\\\\A_{n}=\int _{0}^{1}a_{n}(x)dx&,&B_{n}=\int _{0}^{1}b_{n}(x)dx&,&C_{n}=\int _{0}^{1}c_{n}(x)dx\end{bmatrix}}}
Behauptung: Für alle
n
≥
1
{\displaystyle n\geq 1\,}
{
B
3
n
−
1
=
p
5
n
−
4
−
q
5
n
−
4
⋅
e
2
C
3
n
−
1
=
p
5
n
−
3
−
q
5
n
−
3
⋅
e
2
A
3
n
=
p
5
n
−
2
−
q
5
n
−
2
⋅
e
2
1
2
A
3
n
+
1
=
p
5
n
−
1
−
q
5
n
−
1
⋅
e
2
A
3
n
+
2
=
p
5
n
−
q
5
n
⋅
e
2
}
{\displaystyle {\begin{Bmatrix}B_{3n-1}&=&p_{5n-4}-q_{5n-4}\cdot e^{2}\\C_{3n-1}&=&p_{5n-3}-q_{5n-3}\cdot e^{2}\\A_{3n}&=&p_{5n-2}-q_{5n-2}\cdot e^{2}\\{\frac {1}{2}}A_{3n+1}&=&p_{5n-1}-q_{5n-1}\cdot e^{2}\\A_{3n+2}&=&p_{5n}-q_{5n}\cdot e^{2}\\\end{Bmatrix}}}
B
2
=
15
−
2
e
2
,
C
2
=
22
−
3
e
2
,
A
3
=
37
−
5
e
2
,
1
2
A
4
=
133
−
18
e
2
,
A
5
=
2431
−
329
e
2
{\displaystyle B_{2}=15-2e^{2}\;,\;C_{2}=22-3e^{2}\;,\;A_{3}=37-5e^{2}\;,\;{\frac {1}{2}}A_{4}=133-18e^{2}\;,\;A_{5}=2431-329e^{2}}
n
≥
1
{\displaystyle n\geq 1\,}
{
b
3
n
−
1
(
x
)
=
(
3
n
−
1
)
a
3
n
−
1
(
x
)
+
1
2
a
3
n
−
2
(
x
)
+
1
4
a
3
n
−
1
′
(
x
)
+
1
2
b
3
n
−
1
′
(
x
)
c
3
n
−
1
(
x
)
=
b
3
n
−
1
(
x
)
+
a
3
n
−
1
(
x
)
a
3
n
(
x
)
=
c
3
n
−
1
(
x
)
+
b
3
n
−
1
(
x
)
+
1
2
a
3
n
′
(
x
)
1
2
a
3
n
+
1
(
x
)
=
3
n
a
3
n
(
x
)
+
c
3
n
−
1
(
x
)
+
1
4
a
3
n
+
1
′
(
x
)
+
1
2
c
3
n
′
(
x
)
a
3
n
+
2
(
x
)
=
6
(
2
n
+
1
)
1
2
a
3
n
+
1
(
x
)
+
a
3
n
(
x
)
+
1
2
a
3
n
+
1
′
(
x
)
+
1
2
a
3
n
+
2
′
(
x
)
+
b
3
n
+
1
′
(
x
)
}
{\displaystyle {\begin{Bmatrix}b_{3n-1}(x)&=&(3n-1)&a_{3n-1}(x)&+&{\frac {1}{2}}a_{3n-2}(x)&+&{\frac {1}{4}}a_{3n-1}'(x)+{\frac {1}{2}}b_{3n-1}'(x)\\c_{3n-1}(x)&=&&b_{3n-1}(x)&+&a_{3n-1}(x)\\a_{3n}(x)&=&&c_{3n-1}(x)&+&b_{3n-1}(x)&+&{\frac {1}{2}}a_{3n}'(x)\\{\frac {1}{2}}a_{3n+1}(x)&=&3n&a_{3n}(x)&+&c_{3n-1}(x)&+&{\frac {1}{4}}a_{3n+1}'(x)+{\frac {1}{2}}c_{3n}'(x)\\a_{3n+2}(x)&=&6(2n+1)&{\frac {1}{2}}a_{3n+1}(x)&+&a_{3n}(x)&+&{\frac {1}{2}}a_{3n+1}'(x)+{\frac {1}{2}}a_{3n+2}'(x)+b_{3n+1}'(x)\end{Bmatrix}}}
{
B
3
n
−
1
=
(
3
n
−
1
)
A
3
n
−
1
+
1
2
A
3
n
−
2
C
3
n
−
1
=
B
3
n
−
1
+
A
3
n
−
1
A
3
n
=
C
3
n
−
1
+
B
3
n
−
1
1
2
A
3
n
+
1
=
3
n
A
3
n
+
C
3
n
−
1
A
3
n
+
2
=
6
(
2
n
+
1
)
1
2
A
3
n
+
1
+
A
3
n
}
{\displaystyle {\begin{Bmatrix}B_{3n-1}&=&(3n-1)&A_{3n-1}&+&{\frac {1}{2}}A_{3n-2}\\C_{3n-1}&=&&B_{3n-1}&+&A_{3n-1}\\A_{3n}&=&&C_{3n-1}&+&B_{3n-1}\\{\frac {1}{2}}A_{3n+1}&=&3n&A_{3n}&+&C_{3n-1}\\A_{3n+2}&=&6(2n+1)&{\frac {1}{2}}A_{3n+1}&+&A_{3n}\end{Bmatrix}}}
A
n
,
B
n
,
C
n
{\displaystyle A_{n}\,,\;B_{n}\,,\;C_{n}}
(
∗
)
{\displaystyle (*)\,}
A
n
,
B
n
,
C
n
{\displaystyle A_{n}\,,\;B_{n}\,,\;C_{n}}
n
→
∞
{\displaystyle n\to \infty \,}
ϱ
:=
lim
n
→
∞
p
n
q
n
=
e
2
{\displaystyle \varrho :=\lim _{n\to \infty }{\frac {p_{n}}{q_{n}}}=e^{2}}
e
2
/
n
=
[
1
,
(
6
k
−
5
)
n
−
1
2
,
6
(
2
k
−
1
)
n
,
(
6
k
−
1
)
n
−
1
2
,
1
¯
]
k
≥
1
n
∈
Z
>
1
u
n
g
e
r
a
d
e
{\displaystyle e^{2/n}=\left[\,{\overline {1,{\frac {(6k-5)n-1}{2}},6(2k-1)n,{\frac {(6k-1)n-1}{2}},1}}\,\right]_{k\geq 1}\qquad n\in \mathbb {Z} ^{>1}\;\mathrm {ungerade} }
Beweis
Für eine ungerade Zahl
m
≥
3
{\displaystyle m\geq 3}
ϱ
m
{\displaystyle \varrho _{m}\,}
[
a
0
;
a
1
,
a
2
,
a
3
,
.
.
.
]
{\displaystyle [a_{0};a_{1},a_{2},a_{3},...]\,}
a
5
n
=
1
,
a
5
n
+
1
=
(
6
n
+
1
)
m
−
1
2
,
a
5
n
+
2
=
6
(
2
n
+
1
)
m
,
a
5
n
+
3
=
(
6
n
+
5
)
m
−
1
2
,
a
5
n
+
4
=
1
{\displaystyle a_{5n}=1\,,\,a_{5n+1}={\frac {(6n+1)m-1}{2}}\,,\,a_{5n+2}=6(2n+1)m\,,\,a_{5n+3}={\frac {(6n+5)m-1}{2}}\,,\,a_{5n+4}=1}
n
∈
Z
≥
0
{\displaystyle n\in \mathbb {Z} ^{\geq 0}}
ϱ
m
=
[
1
,
m
−
1
2
,
6
m
,
5
m
−
1
2
,
1
,
1
,
7
m
−
1
2
,
18
m
,
11
m
−
1
2
,
1
,
.
.
.
]
{\displaystyle \varrho _{m}=\left[1,{\frac {m-1}{2}},6m,{\frac {5m-1}{2}},1,1,{\frac {7m-1}{2}},18m,{\frac {11m-1}{2}},1,...\right]}
=
[
1
,
(
6
n
+
1
)
m
−
1
2
,
6
(
2
n
+
1
)
m
,
(
6
n
+
5
)
m
−
1
2
,
1
¯
]
n
≥
0
{\displaystyle =\left[\,{\overline {1,{\frac {(6n+1)m-1}{2}},6(2n+1)m,{\frac {(6n+5)m-1}{2}},1}}\,\right]_{n\geq 0}}
p
n
q
n
{\displaystyle {\frac {p_{n}}{q_{n}}}}
{
p
n
=
a
n
p
n
−
1
+
p
n
−
2
q
n
=
a
n
q
n
−
1
+
q
n
−
2
}
{\displaystyle {\begin{Bmatrix}p_{n}=a_{n}p_{n-1}+p_{n-2}\\q_{n}=a_{n}q_{n-1}+q_{n-2}\end{Bmatrix}}}
{
p
−
2
=
0
,
p
−
1
=
1
q
−
2
=
1
,
q
−
1
=
0
}
{\displaystyle {\begin{Bmatrix}p_{-2}=0\;,\;p_{-1}=1\\q_{-2}=1\;,\;q_{-1}=0\end{Bmatrix}}}
(
p
n
q
n
)
n
≥
0
=
(
1
1
,
(
m
+
1
)
/
2
(
m
−
1
)
/
2
,
3
m
2
+
3
m
+
1
3
m
2
−
3
m
+
1
,
.
.
.
)
{\displaystyle \left({\frac {p_{n}}{q_{n}}}\right)_{n\geq 0}=\left({\frac {1}{1}},{\frac {(m+1)/2}{(m-1)/2}},{\frac {3m^{2}+3m+1}{3m^{2}-3m+1}},...\right)}
ϱ
m
{\displaystyle \varrho _{m}\,}
n
≥
0
{\displaystyle n\geq 0\,}
{
p
5
n
=
p
5
n
−
1
+
p
5
n
−
2
p
5
n
+
1
=
(
6
n
+
1
)
m
−
1
2
p
5
n
+
p
5
n
−
1
p
5
n
+
2
=
6
(
2
n
+
1
)
m
p
5
n
+
1
+
p
5
n
p
5
n
+
3
=
(
6
n
+
5
)
m
−
1
2
p
5
n
+
2
+
p
5
n
+
1
p
5
n
+
4
=
p
5
n
+
3
+
p
5
n
+
2
}
{
q
5
n
=
q
5
n
−
1
+
q
5
n
−
2
q
5
n
+
1
=
(
6
n
+
1
)
m
−
1
2
q
5
n
+
q
5
n
−
1
q
5
n
+
2
=
6
(
2
n
+
1
)
m
q
5
n
+
1
+
q
5
n
q
5
n
+
3
=
(
6
n
+
5
)
m
−
1
2
q
5
n
+
2
+
q
5
n
+
1
q
5
n
+
4
=
q
5
n
+
3
+
q
5
n
+
2
}
(
∗
)
{\displaystyle {\begin{Bmatrix}p_{5n}&=&&p_{5n-1}&+&p_{5n-2}\\p_{5n+1}&=&{\frac {(6n+1)m-1}{2}}&p_{5n}&+&p_{5n-1}\\p_{5n+2}&=&6(2n+1)m&p_{5n+1}&+&p_{5n}\\p_{5n+3}&=&{\frac {(6n+5)m-1}{2}}&p_{5n+2}&+&p_{5n+1}\\p_{5n+4}&=&&p_{5n+3}&+&p_{5n+2}\end{Bmatrix}}\quad {\begin{Bmatrix}q_{5n}&=&&q_{5n-1}&+&q_{5n-2}\\q_{5n+1}&=&{\frac {(6n+1)m-1}{2}}&q_{5n}&+&q_{5n-1}\\q_{5n+2}&=&6(2n+1)m&q_{5n+1}&+&q_{5n}\\q_{5n+3}&=&{\frac {(6n+5)m-1}{2}}&q_{5n+2}&+&q_{5n+1}\\q_{5n+4}&=&&q_{5n+3}&+&q_{5n+2}\end{Bmatrix}}\quad (*)}
[
a
n
(
x
)
=
−
2
n
+
1
m
n
+
1
x
n
(
x
−
1
)
n
n
!
e
2
x
/
m
,
b
n
(
x
)
=
2
n
+
1
m
n
+
1
x
n
+
1
(
x
−
1
)
n
n
!
e
2
x
/
m
,
c
n
(
x
)
=
2
n
+
1
m
n
+
1
x
n
(
x
−
1
)
n
+
1
n
!
e
2
x
/
m
A
n
=
∫
0
1
a
n
(
x
)
d
x
,
B
n
=
∫
0
1
b
n
(
x
)
d
x
,
C
n
=
∫
0
1
c
n
(
x
)
d
x
]
{\displaystyle {\begin{bmatrix}a_{n}(x)=-{\frac {2^{n+1}}{m^{n+1}}}\,{\frac {x^{n}\,(x-1)^{n}}{n!}}\,e^{2x/m}&,&b_{n}(x)={\frac {2^{n+1}}{m^{n+1}}}\,{\frac {x^{n+1}\,(x-1)^{n}}{n!}}\,e^{2x/m}&,&c_{n}(x)={\frac {2^{n+1}}{m^{n+1}}}\,{\frac {x^{n}\,(x-1)^{n+1}}{n!}}\,e^{2x/m}\\\\A_{n}=\int _{0}^{1}a_{n}(x)dx&,&B_{n}=\int _{0}^{1}b_{n}(x)dx&,&C_{n}=\int _{0}^{1}c_{n}(x)dx\end{bmatrix}}}
Behauptung: Für alle
n
≥
0
{\displaystyle n\geq 0\,}
{
A
3
n
=
p
5
n
−
q
5
n
⋅
e
2
/
m
1
2
A
3
n
+
1
=
p
5
n
+
1
−
q
5
n
+
1
⋅
e
2
/
m
A
3
n
+
2
=
p
5
n
+
2
−
q
5
n
+
2
⋅
e
2
/
m
B
3
n
+
2
=
p
5
n
+
3
−
q
5
n
+
3
⋅
e
2
/
m
C
3
n
+
2
=
p
5
n
+
4
−
q
5
n
+
4
⋅
e
2
/
m
}
{\displaystyle {\begin{Bmatrix}A_{3n}&=&p_{5n}-q_{5n}\cdot e^{2/m}\\{\frac {1}{2}}A_{3n+1}&=&p_{5n+1}-q_{5n+1}\cdot e^{2/m}\\A_{3n+2}&=&p_{5n+2}-q_{5n+2}\cdot e^{2/m}\\B_{3n+2}&=&p_{5n+3}-q_{5n+3}\cdot e^{2/m}\\C_{3n+2}&=&p_{5n+4}-q_{5n+4}\cdot e^{2/m}\end{Bmatrix}}}
A
0
=
1
−
e
2
/
m
,
1
2
A
1
=
m
+
1
2
−
m
−
1
2
⋅
e
2
/
m
,
A
2
=
(
3
m
2
+
3
m
+
1
)
−
(
3
m
2
−
3
m
+
1
)
⋅
e
2
/
m
,
{\displaystyle A_{0}=1-e^{2/m}\;,\;{\frac {1}{2}}A_{1}={\frac {m+1}{2}}-{\frac {m-1}{2}}\cdot e^{2/m}\;,\;A_{2}=(3m^{2}+3m+1)-(3m^{2}-3m+1)\cdot e^{2/m}\;,}
B
2
=
15
m
3
+
12
m
2
+
3
m
2
−
15
m
3
−
18
m
2
+
9
m
−
2
2
⋅
e
2
/
m
,
C
2
=
15
m
3
+
18
m
2
+
9
m
+
2
2
−
15
m
3
−
18
m
2
+
3
m
2
⋅
e
2
/
m
{\displaystyle B_{2}={\frac {15m^{3}+12m^{2}+3m}{2}}-{\frac {15m^{3}-18m^{2}+9m-2}{2}}\cdot e^{2/m}\;,\;C_{2}={\frac {15m^{3}+18m^{2}+9m+2}{2}}-{\frac {15m^{3}-18m^{2}+3m}{2}}\cdot e^{2/m}}
n
≥
1
{\displaystyle n\geq 1\,}
{
a
3
n
(
x
)
=
c
3
n
−
1
(
x
)
+
b
3
n
−
1
(
x
)
+
m
2
⋅
a
3
n
′
(
x
)
1
2
a
3
n
+
1
(
x
)
=
(
6
n
+
1
)
m
−
1
2
a
3
n
(
x
)
+
c
3
n
−
1
(
x
)
+
m
4
⋅
a
3
n
+
1
′
(
x
)
+
m
2
⋅
c
3
n
′
(
x
)
a
3
n
+
2
(
x
)
=
6
(
2
n
+
1
)
m
1
2
a
3
n
+
1
(
x
)
+
a
3
n
(
x
)
+
m
2
⋅
a
3
n
+
1
′
(
x
)
+
m
2
⋅
a
3
n
+
2
′
(
x
)
+
m
⋅
b
3
n
+
1
′
(
x
)
b
3
n
+
2
(
x
)
=
(
6
n
+
1
)
m
−
1
2
a
3
n
+
2
(
x
)
+
1
2
a
3
n
+
1
(
x
)
+
m
2
⋅
c
3
n
+
2
′
(
x
)
−
m
4
⋅
a
3
n
+
2
′
(
x
)
c
3
n
+
2
(
x
)
=
b
3
n
+
2
(
x
)
+
a
3
n
+
2
(
x
)
}
{\displaystyle {\begin{Bmatrix}a_{3n}(x)&=&&c_{3n-1}(x)&+&b_{3n-1}(x)&+&{\frac {m}{2}}\cdot a_{3n}'(x)\\{\frac {1}{2}}a_{3n+1}(x)&=&{\frac {(6n+1)m-1}{2}}&a_{3n}(x)&+&c_{3n-1}(x)&+&{\frac {m}{4}}\cdot a_{3n+1}'(x)+{\frac {m}{2}}\cdot c_{3n}'(x)\\a_{3n+2}(x)&=&6(2n+1)m&{\frac {1}{2}}a_{3n+1}(x)&+&a_{3n}(x)&+&{\frac {m}{2}}\cdot a_{3n+1}'(x)+{\frac {m}{2}}\cdot a_{3n+2}'(x)+m\cdot b_{3n+1}'(x)\\b_{3n+2}(x)&=&{\frac {(6n+1)m-1}{2}}&a_{3n+2}(x)&+&{\frac {1}{2}}a_{3n+1}(x)&+&{\frac {m}{2}}\cdot c_{3n+2}'(x)-{\frac {m}{4}}\cdot a_{3n+2}'(x)\\c_{3n+2}(x)&=&&b_{3n+2}(x)&+&a_{3n+2}(x)\end{Bmatrix}}}
{
A
3
n
=
C
3
n
−
1
+
B
3
n
−
1
1
2
A
3
n
+
1
=
(
6
n
+
1
)
m
−
1
2
A
3
n
+
C
3
n
−
1
A
3
n
+
2
=
6
(
2
n
+
1
)
m
1
2
A
3
n
+
1
+
A
3
n
B
3
n
+
2
=
(
6
n
+
5
)
m
−
1
2
A
3
n
+
2
+
1
2
A
3
n
+
1
C
3
n
+
2
=
B
3
n
+
2
+
A
3
n
+
2
}
{\displaystyle {\begin{Bmatrix}A_{3n}&=&&C_{3n-1}&+&B_{3n-1}\\{\frac {1}{2}}A_{3n+1}&=&{\frac {(6n+1)m-1}{2}}&A_{3n}&+&C_{3n-1}\\A_{3n+2}&=&6(2n+1)m&{\frac {1}{2}}A_{3n+1}&+&A_{3n}\\B_{3n+2}&=&{\frac {(6n+5)m-1}{2}}&A_{3n+2}&+&{\frac {1}{2}}A_{3n+1}\\C_{3n+2}&=&&B_{3n+2}&+&A_{3n+2}\end{Bmatrix}}}
A
n
,
B
n
,
C
n
{\displaystyle A_{n}\,,\;B_{n}\,,\;C_{n}}
(
∗
)
{\displaystyle (*)\,}
A
n
,
B
n
,
C
n
{\displaystyle A_{n}\,,\;B_{n}\,,\;C_{n}}
n
→
∞
{\displaystyle n\to \infty \,}
ϱ
m
:=
lim
n
→
∞
p
n
q
n
=
e
2
/
m
{\displaystyle \varrho _{m}:=\lim _{n\to \infty }{\frac {p_{n}}{q_{n}}}=e^{2/m}}
e
−
1
2
=
[
0
,
1
,
4
k
+
2
¯
]
k
≥
1
{\displaystyle {\frac {e-1}{2}}=\left[0,1,{\overline {4k+2}}\right]_{k\geq 1}}
1
e
−
1
=
[
4
k
+
1
,
1
,
1
¯
]
k
≥
0
{\displaystyle {\frac {1}{{\sqrt {e}}-1}}=\left[{\overline {4k+1,1,1}}\right]_{k\geq 0}}
1
e
+
1
=
[
0
,
2
,
4
k
+
1
,
1
,
1
¯
]
k
≥
0
{\displaystyle {\frac {1}{{\sqrt {e}}+1}}=\left[0,2,{\overline {4k+1,1,1}}\right]_{k\geq 0}}
tan
(
1
)
=
[
1
,
2
k
−
1
¯
]
k
≥
1
,
cot
(
1
)
=
[
0
,
1
,
2
k
−
1
¯
]
k
≥
1
{\displaystyle \tan(1)=\left[{\overline {1,2k-1}}\right]_{k\geq 1}\quad ,\quad \cot(1)=\left[0,{\overline {1,2k-1}}\right]_{k\geq 1}}
cot
(
1
n
)
=
[
n
−
1
,
1
,
(
2
k
+
1
)
n
−
2
¯
]
k
≥
1
,
tan
(
1
n
)
=
[
0
,
n
−
1
,
1
,
(
2
k
+
1
)
n
−
2
¯
]
k
≥
1
n
∈
Z
>
1
{\displaystyle \cot \left({\frac {1}{n}}\right)=\left[n-1,{\overline {1,(2k+1)n-2}}\right]_{k\geq 1}\quad ,\quad \tan \left({\frac {1}{n}}\right)=\left[0,n-1,{\overline {1,(2k+1)n-2}}\right]_{k\geq 1}\qquad n\in \mathbb {Z} ^{>1}}
coth
(
1
n
)
=
[
(
2
k
−
1
)
n
¯
]
k
≥
1
,
tanh
(
1
n
)
=
[
0
,
(
2
k
−
1
)
n
¯
]
k
≥
1
n
∈
Z
>
0
{\displaystyle \coth \left({\frac {1}{n}}\right)=\left[{\overline {(2k-1)n}}\right]_{k\geq 1}\qquad ,\qquad \tanh \left({\frac {1}{n}}\right)=\left[0,{\overline {(2k-1)n}}\right]_{k\geq 1}\qquad n\in \mathbb {Z} ^{>0}}
n
tan
(
1
n
)
=
[
1
,
(
4
k
−
1
)
n
−
2
,
1
,
4
k
−
1
¯
]
k
≥
1
n
∈
Z
>
0
{\displaystyle {\sqrt {n}}\,\tan \left({\frac {1}{\sqrt {n}}}\right)=\left[{\overline {1,(4k-1)n-2,1,4k-1}}\right]_{k\geq 1}\qquad n\in \mathbb {Z} ^{>0}}
n
cot
(
1
n
)
=
[
n
−
1
,
1
,
4
k
−
3
,
1
,
(
4
k
+
1
)
n
−
2
¯
]
k
≥
1
n
∈
Z
>
0
{\displaystyle {\sqrt {n}}\,\cot \left({\frac {1}{\sqrt {n}}}\right)=\left[n-1,{\overline {1,4k-3,1,(4k+1)n-2}}\right]_{k\geq 1}\quad n\in \mathbb {Z} ^{>0}}
n
tanh
(
1
n
)
=
[
0
,
4
k
−
3
,
(
4
k
−
1
)
n
¯
]
k
≥
1
n
∈
Z
>
0
{\displaystyle {\sqrt {n}}\,\tanh \left({\frac {1}{\sqrt {n}}}\right)=\left[0,{\overline {4k-3,(4k-1)n}}\right]_{k\geq 1}\qquad n\in \mathbb {Z} ^{>0}}
n
coth
(
1
n
)
=
[
(
4
k
−
3
)
n
,
4
k
−
1
¯
]
k
≥
1
n
∈
Z
>
0
{\displaystyle {\sqrt {n}}\,\coth \left({\frac {1}{\sqrt {n}}}\right)=\left[{\overline {(4k-3)n,4k-1}}\right]_{k\geq 1}\quad n\in \mathbb {Z} ^{>0}}
2
=
[
1
,
2
¯
]
{\displaystyle {\sqrt {2}}=\left[1,{\overline {2}}\right]}
3
=
[
1
,
1
,
2
¯
]
{\displaystyle {\sqrt {3}}=\left[1,{\overline {1,2}}\right]}
4
=
[
2
]
{\displaystyle {\sqrt {4}}=\left[2\right]}
5
=
[
2
,
4
¯
]
{\displaystyle {\sqrt {5}}=\left[2,{\overline {4}}\right]}
6
=
[
2
,
2
,
4
¯
]
{\displaystyle {\sqrt {6}}=\left[2,{\overline {2,4}}\right]}
7
=
[
2
,
1
,
1
,
1
,
4
¯
]
{\displaystyle {\sqrt {7}}=\left[2,{\overline {1,1,1,4}}\right]}
8
=
[
2
,
1
,
4
¯
]
{\displaystyle {\sqrt {8}}=\left[2,{\overline {1,4}}\right]}
9
=
[
3
]
{\displaystyle {\sqrt {9}}=\left[3\right]}
10
=
[
3
,
6
¯
]
{\displaystyle {\sqrt {10}}=\left[3,{\overline {6}}\right]}
Ist
d
∈
Z
>
0
{\displaystyle d\in \mathbb {Z} ^{>0}\,}
d
{\displaystyle {\sqrt {d}}}
[
a
0
,
a
1
,
.
.
.
,
a
n
,
2
a
0
¯
]
{\displaystyle \left[a_{0},{\overline {a_{1},...,a_{n},2a_{0}}}\right]}
a
2
+
1
=
[
a
,
2
a
¯
]
{\displaystyle {\sqrt {a^{2}+1}}=\left[a,{\overline {2a}}\right]}
a
2
+
2
=
[
a
,
a
,
2
a
¯
]
{\displaystyle {\sqrt {a^{2}+2}}=\left[a,{\overline {a,2a}}\right]}
a
2
+
a
=
[
a
,
2
,
2
a
¯
]
{\displaystyle {\sqrt {a^{2}+a}}=\left[a,{\overline {2,2a}}\right]}
a
2
+
2
a
=
[
a
,
1
,
2
a
¯
]
{\displaystyle {\sqrt {a^{2}+2a}}=\left[a,{\overline {1,2a}}\right]}
9
a
2
+
3
=
[
3
a
,
2
a
,
6
a
¯
]
{\displaystyle {\sqrt {9a^{2}+3}}=\left[3a,{\overline {2a,6a}}\right]}
Eine ausführlichere Einteilung stellen die Bernstein Familien und die Levesque-Rhin Familien dar.
[ Bearbeiten ]
Ein regulärer Kettenbruch ist genau dann irrational, wenn er nicht abbricht.
Ein regulärer Kettenbruch ist genau dann periodisch, wenn er die Form
a
+
b
c
d
{\displaystyle {\frac {a+b{\sqrt {c}}}{d}}}
a
∈
Z
,
b
,
c
,
d
∈
Z
≠
0
{\displaystyle a\in \mathbb {Z} ,b,c,d\in \mathbb {Z} ^{\neq 0}}
c
{\displaystyle c\,}
Sind
a
0
,
.
.
.
,
a
n
∈
Z
>
0
{\displaystyle a_{0},...,a_{n}\in \mathbb {Z} ^{>0}}
α
=
[
a
0
,
.
.
.
,
a
n
¯
]
{\displaystyle \alpha =[{\overline {a_{0},...,a_{n}}}]}
P
+
D
Q
{\displaystyle {\frac {P+{\sqrt {D}}}{Q}}}
wobei
P
,
Q
,
D
∈
Z
>
0
{\displaystyle P,Q,D\in \mathbb {Z} ^{>0}}
D
{\displaystyle D\,}
Ist
β
=
[
a
n
,
.
.
.
,
a
0
¯
]
{\displaystyle \beta =[{\overline {a_{n},...,a_{0}}}]}
α
{\displaystyle \alpha \,}
−
1
β
{\displaystyle {\frac {-1}{\beta }}}
P
−
D
Q
{\displaystyle {\frac {P-{\sqrt {D}}}{Q}}}
b
0
+
a
1
b
1
+
a
2
b
2
+
a
3
b
3
+
⋯
{\displaystyle b_{0}+{\frac {a_{1}}{\displaystyle b_{1}+{\frac {a_{2}}{\displaystyle b_{2}+{\frac {a_{3}}{b_{3}+\cdots }}}}}}}
zu betrachten, wobei
b
0
∈
Z
{\displaystyle b_{0}\in \mathbb {Z} }
b
1
,
b
2
,
.
.
.
{\displaystyle b_{1},b_{2},...\,}
a
1
,
a
2
.
.
.
{\displaystyle a_{1},a_{2}...\,}
b
0
,
b
1
,
b
2
,
.
.
.
{\displaystyle b_{0},b_{1},b_{2},...\,}
a
1
,
a
2
,
a
3
,
.
.
.
{\displaystyle a_{1},a_{2},a_{3},...\,}
b
0
+
a
1
|
|
b
1
+
a
2
|
|
b
2
+
a
3
|
|
b
3
+
.
.
.
{\displaystyle b_{0}+{\frac {a_{1}|}{|b_{1}}}+{\frac {a_{2}|}{|b_{2}}}+{\frac {a_{3}|}{|b_{3}}}+...}
b
0
+
K
∞
k
=
1
a
k
b
k
{\displaystyle b_{0}+{\underset {k=1}{\overset {\infty }{K}}}{\frac {a_{k}}{b_{k}}}}
Ist
z
=
x
+
y
{\displaystyle {\sqrt {z}}=x+y}
z
=
x
2
+
2
x
y
+
y
2
⇒
z
−
x
2
2
x
+
y
=
y
⇒
y
=
K
∞
k
=
1
z
−
x
2
2
x
⇒
z
=
x
+
K
∞
k
=
1
z
−
x
2
2
x
{\displaystyle z=x^{2}+2xy+y^{2}\Rightarrow {\frac {z-x^{2}}{2x+y}}=y\Rightarrow y={\underset {k=1}{\overset {\infty }{K}}}{\frac {z-x^{2}}{2x}}\Rightarrow {\sqrt {z}}=x+{\underset {k=1}{\overset {\infty }{K}}}{\frac {z-x^{2}}{2x}}}
e
=
2
+
K
∞
k
=
2
k
k
=
2
+
2
|
|
2
+
3
|
|
3
+
4
|
|
4
+
.
.
.
{\displaystyle e=2+{\underset {k=2}{\overset {\infty }{K}}}{\frac {k}{k}}=2+{\frac {2|}{|2}}+{\frac {3|}{|3}}+{\frac {4|}{|4}}+...}
e
=
2
+
1
|
|
1
+
K
∞
k
=
1
k
k
+
1
=
2
+
1
|
|
1
+
1
|
|
2
+
2
|
|
3
+
3
|
|
4
+
.
.
.
{\displaystyle e=2+{\frac {1|}{|1}}+{\underset {k=1}{\overset {\infty }{K}}}{\frac {k}{k+1}}=2+{\frac {1|}{|1}}+{\frac {1|}{|2}}+{\frac {2|}{|3}}+{\frac {3|}{|4}}+...}
1
e
−
1
=
1
+
K
∞
k
=
1
2
k
2
k
+
1
=
1
+
2
|
|
3
+
4
|
|
5
+
.
.
.
{\displaystyle {\frac {1}{{\sqrt {e}}-1}}=1+{\underset {k=1}{\overset {\infty }{K}}}{\frac {2k}{2k+1}}=1+{\frac {2|}{|3}}+{\frac {4|}{|5}}+...}
π
2
=
1
+
K
∞
k
=
1
1
1
k
=
1
+
1
|
|
1
+
1
|
|
1
2
+
1
|
|
1
3
+
.
.
.
{\displaystyle {\frac {\pi }{2}}=1+{\underset {k=1}{\overset {\infty }{K}}}{\frac {1}{\frac {1}{k}}}=1+{\frac {1|}{|1}}+{\frac {1|}{|{\frac {1}{2}}}}+{\frac {1|}{|{\frac {1}{3}}}}+...}
4
π
=
1
+
K
∞
k
=
1
k
2
2
k
+
1
=
1
+
1
|
|
3
+
4
|
|
5
+
9
|
|
7
+
.
.
.
{\displaystyle {\frac {4}{\pi }}=1+{\underset {k=1}{\overset {\infty }{K}}}{\frac {k^{2}}{2k+1}}=1+{\frac {1|}{|3}}+{\frac {4|}{|5}}+{\frac {9|}{|7}}+...}
π
=
3
+
K
∞
k
=
1
(
2
k
−
1
)
2
6
=
3
+
1
|
|
6
+
9
|
|
6
+
25
|
|
6
+
.
.
.
{\displaystyle \pi =3+{\underset {k=1}{\overset {\infty }{K}}}{\frac {(2k-1)^{2}}{6}}=3+{\frac {1|}{|6}}+{\frac {9|}{|6}}+{\frac {25|}{|6}}+...}
Formel von Brouncker
4
π
=
1
+
K
∞
k
=
1
(
2
k
−
1
)
2
2
=
1
+
1
|
|
2
+
9
|
|
2
+
25
|
|
2
+
.
.
.
{\displaystyle {\frac {4}{\pi }}=1+{\underset {k=1}{\overset {\infty }{K}}}{\frac {(2k-1)^{2}}{2}}=1+{\frac {1|}{|2}}+{\frac {9|}{|2}}+{\frac {25|}{|2}}+...}
2
π
=
1
−
1
|
|
2
+
K
∞
k
=
1
k
(
k
+
1
)
1
=
1
−
1
|
|
2
+
1
⋅
2
|
|
1
+
2
⋅
3
|
|
1
+
3
⋅
4
|
|
1
+
4
⋅
5
|
|
1
+
.
.
.
{\displaystyle {\frac {2}{\pi }}=1-{\frac {1|}{|2}}+{\underset {k=1}{\overset {\infty }{K}}}{\frac {k\,(k+1)}{1}}=1-{\frac {1|}{|2}}+{\frac {1\cdot 2|}{|1}}+{\frac {2\cdot 3|}{|1}}+{\frac {3\cdot 4|}{|1}}+{\frac {4\cdot 5|}{|1}}+...}
π
2
=
1
−
1
|
|
3
−
2
⋅
3
|
|
1
−
2
⋅
1
|
|
3
−
4
⋅
5
|
|
1
−
4
⋅
3
|
|
3
−
6
⋅
7
|
|
1
−
6
⋅
5
|
|
3
+
.
.
.
{\displaystyle {\frac {\pi }{2}}=1-{\frac {1|}{|3}}-{\frac {2\cdot 3|}{|1}}-{\frac {2\cdot 1|}{|3}}-{\frac {4\cdot 5|}{|1}}-{\frac {4\cdot 3|}{|3}}-{\frac {6\cdot 7|}{|1}}-{\frac {6\cdot 5|}{|3}}+...}
12
π
2
=
1
+
K
∞
k
=
1
k
4
2
k
+
1
=
1
+
1
|
|
3
+
16
|
|
5
+
81
|
|
7
+
.
.
.
{\displaystyle {\frac {12}{\pi ^{2}}}=1+{\underset {k=1}{\overset {\infty }{K}}}{\frac {k^{4}}{2k+1}}=1+{\frac {1|}{|3}}+{\frac {16|}{|5}}+{\frac {81|}{|7}}+...}
6
π
2
−
6
=
1
+
1
⋅
1
|
|
1
+
1
⋅
2
|
|
1
+
2
⋅
2
|
|
1
+
2
⋅
3
|
|
1
+
3
⋅
3
|
|
1
+
3
⋅
4
|
|
1
.
.
.
{\displaystyle {\frac {6}{\pi ^{2}-6}}=1+{\frac {1\cdot 1|}{|1}}+{\frac {1\cdot 2|}{|1}}+{\frac {2\cdot 2|}{|1}}+{\frac {2\cdot 3|}{|1}}+{\frac {3\cdot 3|}{|1}}+{\frac {3\cdot 4|}{|1}}...}
1
2
K
−
1
=
1
2
+
1
⋅
1
|
|
1
2
+
1
⋅
2
|
|
1
2
+
2
⋅
2
|
|
1
2
+
2
⋅
3
|
|
1
2
+
3
⋅
3
|
|
1
2
+
3
⋅
4
|
|
1
2
.
.
.
{\displaystyle {\frac {1}{2K-1}}={\frac {1}{2}}+{\frac {1\cdot 1|}{|{\frac {1}{2}}}}+{\frac {1\cdot 2|}{|{\frac {1}{2}}}}+{\frac {2\cdot 2|}{|{\frac {1}{2}}}}+{\frac {2\cdot 3|}{|{\frac {1}{2}}}}+{\frac {3\cdot 3|}{|{\frac {1}{2}}}}+{\frac {3\cdot 4|}{|{\frac {1}{2}}}}...}
e
z
=
1
+
z
|
|
1
+
K
∞
k
=
2
−
z
k
1
+
z
k
=
1
+
z
|
|
1
−
z
2
|
|
1
+
z
2
−
z
3
|
|
1
+
z
3
−
z
4
|
|
1
+
z
4
−
.
.
.
{\displaystyle e^{z}=1+{\frac {z|}{|1}}+{\underset {k=2}{\overset {\infty }{K}}}{\frac {-{\frac {z}{k}}}{1+{\frac {z}{k}}}}=1+{\frac {z|}{|1}}-{\frac {{\frac {z}{2}}|}{|1+{\frac {z}{2}}}}-{\frac {{\frac {z}{3}}|}{|1+{\frac {z}{3}}}}-{\frac {{\frac {z}{4}}|}{|1+{\frac {z}{4}}}}-...}
sin
z
=
z
|
|
1
+
z
2
|
|
2
⋅
3
−
z
2
+
K
∞
k
=
2
(
2
k
−
2
)
(
2
k
−
1
)
z
2
2
k
(
2
k
+
1
)
−
z
2
=
z
|
|
1
+
z
2
|
|
2
⋅
3
−
z
2
+
2
⋅
3
z
2
|
|
4
⋅
5
−
z
2
+
4
⋅
5
z
2
|
|
6
⋅
7
−
z
2
+
.
.
.
{\displaystyle \sin z={\frac {z|}{|1}}+{\frac {z^{2}|}{|2\cdot 3-z^{2}}}+{\underset {k=2}{\overset {\infty }{K}}}{\frac {(2k-2)(2k-1)z^{2}}{2k\,(2k+1)-z^{2}}}={\frac {z|}{|1}}+{\frac {z^{2}|}{|2\cdot 3-z^{2}}}+{\frac {2\cdot 3\,z^{2}|}{|4\cdot 5-z^{2}}}+{\frac {4\cdot 5\,z^{2}|}{|6\cdot 7-z^{2}}}+...}
sinh
z
=
z
|
|
1
−
z
2
|
|
2
⋅
3
−
z
2
+
K
∞
k
=
2
−
(
2
k
−
2
)
(
2
k
−
1
)
z
2
2
k
(
2
k
+
1
)
+
z
2
=
z
|
|
1
−
z
2
|
|
2
⋅
3
+
z
2
−
2
⋅
3
z
2
|
|
4
⋅
5
+
z
2
−
4
⋅
5
z
2
|
|
6
⋅
7
+
z
2
−
.
.
.
{\displaystyle \sinh z={\frac {z|}{|1}}-{\frac {z^{2}|}{|2\cdot 3-z^{2}}}+{\underset {k=2}{\overset {\infty }{K}}}{\frac {-(2k-2)(2k-1)z^{2}}{2k\,(2k+1)+z^{2}}}={\frac {z|}{|1}}-{\frac {z^{2}|}{|2\cdot 3+z^{2}}}-{\frac {2\cdot 3\,z^{2}|}{|4\cdot 5+z^{2}}}-{\frac {4\cdot 5\,z^{2}|}{|6\cdot 7+z^{2}}}-...}
tanh
tan
(
x
y
)
=
x
|
|
y
+
K
∞
k
=
1
±
x
2
(
2
k
+
1
)
y
=
x
|
|
y
±
x
2
|
|
3
y
±
x
2
|
|
5
y
+
.
.
.
{\displaystyle {\begin{matrix}\tanh \\\tan \end{matrix}}\left({\frac {x}{y}}\right)={\frac {x|}{|y}}+{\underset {k=1}{\overset {\infty }{K}}}{\frac {\pm x^{2}}{(2k+1)y}}={\frac {x|}{|y}}\pm {\frac {x^{2}|}{|3y}}\pm {\frac {x^{2}|}{|5y}}+...}
tanh
tan
(
π
z
4
)
=
z
|
|
1
+
K
∞
k
=
1
(
2
k
−
1
)
2
±
z
2
2
=
z
|
|
1
+
1
2
±
z
2
|
|
2
+
3
2
±
z
2
|
|
2
+
5
2
±
z
2
|
|
2
+
.
.
.
{\displaystyle {\begin{matrix}\tanh \\\tan \end{matrix}}\left({\frac {\pi z}{4}}\right)={\frac {z|}{|1}}+{\underset {k=1}{\overset {\infty }{K}}}{\frac {(2k-1)^{2}\pm z^{2}}{2}}={\frac {z|}{|1}}+{\frac {1^{2}\pm z^{2}|}{|2}}+{\frac {3^{2}\pm z^{2}|}{|2}}+{\frac {5^{2}\pm z^{2}|}{|2}}+...}
tanh
tan
(
n
z
)
=
n
tan
(
z
)
|
|
1
+
K
n
−
1
k
=
1
(
k
2
±
n
2
)
tan
2
(
z
)
2
k
+
1
{\displaystyle {\begin{matrix}\tanh \\\tan \end{matrix}}{\Big (}nz{\Big )}={\frac {n\,\tan(z)|}{|1}}+{\underset {k=1}{\overset {n-1}{K}}}{\frac {(k^{2}\pm n^{2})\,\tan ^{2}(z)}{2k+1}}}
tanh
tan
(
α
z
)
=
α
tan
(
z
)
|
|
1
+
K
∞
k
=
1
(
k
2
±
α
2
)
tan
2
(
z
)
2
k
+
1
{\displaystyle {\begin{matrix}\tanh \\\tan \end{matrix}}{\Big (}\alpha z{\Big )}={\frac {\alpha \,\tan(z)|}{|1}}+{\underset {k=1}{\overset {\infty }{K}}}{\frac {(k^{2}\pm \alpha ^{2})\,\tan ^{2}(z)}{2k+1}}}
z
coth
(
z
2
)
=
2
+
K
∞
k
=
1
z
2
4
k
+
2
=
2
+
z
2
|
|
6
+
z
2
|
|
10
+
z
2
|
|
14
+
.
.
.
{\displaystyle z\,\coth \left({\frac {z}{2}}\right)=2+{\underset {k=1}{\overset {\infty }{K}}}{\frac {z^{2}}{4k+2}}=2+{\frac {z^{2}|}{|6}}+{\frac {z^{2}|}{|10}}+{\frac {z^{2}|}{|14}}+...}
z
coth
z
=
1
+
K
∞
k
=
1
z
2
|
|
2
k
+
1
=
1
+
z
2
|
|
3
+
z
2
|
|
5
+
z
2
|
|
7
+
.
.
.
{\displaystyle z\,\coth z=1+{\underset {k=1}{\overset {\infty }{K}}}{\frac {z^{2}|}{|2k+1}}=1+{\frac {z^{2}|}{|3}}+{\frac {z^{2}|}{|5}}+{\frac {z^{2}|}{|7}}+...}
arsinh
z
=
z
1
+
z
2
|
|
1
+
1
⋅
2
z
2
|
|
3
+
1
⋅
2
z
2
|
|
5
+
3
⋅
4
z
2
|
|
7
+
3
⋅
4
z
2
|
|
9
+
5
⋅
6
z
2
|
|
11
+
5
⋅
6
z
2
|
|
13
+
.
.
.
{\displaystyle {\text{arsinh}}\,z={\frac {z{\sqrt {1+z^{2}}}|}{|1}}+{\frac {1\cdot 2\,z^{2}|}{|3}}+{\frac {1\cdot 2\,z^{2}|}{|5}}+{\frac {3\cdot 4\,z^{2}|}{|7}}+{\frac {3\cdot 4\,z^{2}|}{|9}}+{\frac {5\cdot 6\,z^{2}|}{|11}}+{\frac {5\cdot 6\,z^{2}|}{|13}}+...}
arcsin
z
=
z
1
−
z
2
|
|
1
−
1
⋅
2
z
2
|
|
3
−
1
⋅
2
z
2
|
|
5
−
3
⋅
4
z
2
|
|
7
−
3
⋅
4
z
2
|
|
9
−
5
⋅
6
z
2
|
|
11
−
5
⋅
6
z
2
|
|
13
−
.
.
.
{\displaystyle \arcsin z={\frac {z{\sqrt {1-z^{2}}}|}{|1}}-{\frac {1\cdot 2\,z^{2}|}{|3}}-{\frac {1\cdot 2\,z^{2}|}{|5}}-{\frac {3\cdot 4\,z^{2}|}{|7}}-{\frac {3\cdot 4\,z^{2}|}{|9}}-{\frac {5\cdot 6\,z^{2}|}{|11}}-{\frac {5\cdot 6\,z^{2}|}{|13}}-...}
Arkustangens und Areatangens Hyperbolicus [ Bearbeiten ]
arctan
z
=
z
|
|
1
+
K
∞
k
=
1
k
2
z
2
2
k
+
1
=
z
|
|
1
+
z
2
|
|
3
+
4
z
2
|
|
5
+
9
z
2
|
|
7
+
.
.
.
{\displaystyle \arctan z={\frac {z|}{|1}}+{\underset {k=1}{\overset {\infty }{K}}}{\frac {k^{2}z^{2}}{2k+1}}={\frac {z|}{|1}}+{\frac {z^{2}|}{|3}}+{\frac {4z^{2}|}{|5}}+{\frac {9z^{2}|}{|7}}+...}
artanh
z
=
z
|
|
1
+
K
∞
k
=
1
−
k
2
z
2
2
k
+
1
=
z
|
|
1
−
z
2
|
|
3
−
4
z
2
|
|
5
−
9
z
2
|
|
7
−
.
.
.
{\displaystyle {\text{artanh}}\,z={\frac {z|}{|1}}+{\underset {k=1}{\overset {\infty }{K}}}{\frac {-k^{2}z^{2}}{2k+1}}={\frac {z|}{|1}}-{\frac {z^{2}|}{|3}}-{\frac {4z^{2}|}{|5}}-{\frac {9z^{2}|}{|7}}-...}
arctan
artanh
(
z
)
=
z
|
|
1
+
K
∞
k
=
1
±
(
2
k
−
1
)
2
z
2
2
k
+
1
∓
(
2
k
−
1
)
z
2
=
z
|
|
1
±
z
2
|
|
3
∓
z
2
±
9
z
2
|
|
5
∓
3
z
2
±
25
z
2
|
|
7
∓
5
z
2
±
.
.
.
{\displaystyle {\begin{matrix}\arctan \\\operatorname {artanh} \end{matrix}}(z)={\frac {z|}{|1}}+{\underset {k=1}{\overset {\infty }{K}}}{\frac {\pm (2k-1)^{2}z^{2}}{2k+1\mp (2k-1)z^{2}}}={\frac {z|}{|1}}\pm {\frac {z^{2}|}{|3\mp z^{2}}}\pm {\frac {9z^{2}|}{|5\mp 3z^{2}}}\pm {\frac {25z^{2}|}{|7\mp 5z^{2}}}\pm ...}
artanh
(
z
)
=
±
i
π
2
+
1
|
|
z
+
K
∞
k
=
2
−
k
−
1
k
2
k
−
1
k
z
=
±
i
π
2
+
1
|
|
z
−
1
2
|
|
3
2
z
−
2
3
|
|
5
3
z
−
3
4
|
|
7
4
z
−
.
.
.
Im
(
z
)
>
0
Im
(
z
)
<
0
{\displaystyle \operatorname {artanh} (z)=\pm {\frac {i\pi }{2}}+{\frac {1|}{|z}}+{\underset {k=2}{\overset {\infty }{K}}}{\frac {-{\frac {k-1}{k}}}{{\frac {2k-1}{k}}z}}=\pm {\frac {i\pi }{2}}+{\frac {1|}{|z}}-{\frac {{\frac {1}{2}}|}{|{\frac {3}{2}}z}}-{\frac {{\frac {2}{3}}|}{|{\frac {5}{3}}z}}-{\frac {{\frac {3}{4}}|}{|{\frac {7}{4}}z}}-...\qquad {\begin{matrix}{\textrm {Im}}(z)>0\\{\textrm {Im}}(z)<0\end{matrix}}}
e
2
μ
arctan
(
1
z
)
=
1
+
2
μ
|
|
z
−
μ
+
K
∞
k
=
1
μ
2
+
k
2
(
2
k
+
1
)
z
=
1
+
2
μ
|
|
z
−
μ
+
μ
2
+
1
|
|
3
z
+
μ
2
+
4
|
|
5
z
+
μ
2
+
9
|
|
7
z
+
.
.
.
{\displaystyle e^{2\mu \arctan \left({\frac {1}{z}}\right)}=1+{\frac {2\mu |}{|z-\mu }}+{\underset {k=1}{\overset {\infty }{K}}}{\frac {\mu ^{2}+k^{2}}{(2k+1)z}}=1+{\frac {2\mu |}{|z-\mu }}+{\frac {\mu ^{2}+1|}{|3z}}+{\frac {\mu ^{2}+4|}{|5z}}+{\frac {\mu ^{2}+9|}{|7z}}+...}
log
(
1
+
z
)
=
z
|
|
1
+
1
2
z
|
|
2
+
1
2
z
|
|
3
+
2
2
z
|
|
4
+
2
2
z
|
|
5
+
3
2
z
|
|
6
+
3
2
z
|
|
7
+
4
2
z
|
|
8
+
4
2
z
|
|
9
+
.
.
.
{\displaystyle \log(1+z)={\frac {z|}{|1}}+{\frac {1^{2}z|}{|2}}+{\frac {1^{2}z|}{|3}}+{\frac {2^{2}z|}{|4}}+{\frac {2^{2}z|}{|5}}+{\frac {3^{2}z|}{|6}}+{\frac {3^{2}z|}{|7}}+{\frac {4^{2}z|}{|8}}+{\frac {4^{2}z|}{|9}}+...}
log
(
1
+
z
)
=
1
|
|
1
z
+
1
|
|
2
1
+
1
|
|
3
z
+
1
|
|
2
2
+
1
|
|
5
z
+
1
|
|
2
3
+
1
|
|
7
z
+
1
|
|
2
4
+
1
|
|
9
z
+
1
|
|
2
5
+
.
.
.
{\displaystyle \log(1+z)={\frac {1|}{|{\frac {1}{z}}}}+{\frac {1|}{|{\frac {2}{1}}}}+{\frac {1|}{|{\frac {3}{z}}}}+{\frac {1|}{|{\frac {2}{2}}}}+{\frac {1|}{|{\frac {5}{z}}}}+{\frac {1|}{|{\frac {2}{3}}}}+{\frac {1|}{|{\frac {7}{z}}}}+{\frac {1|}{|{\frac {2}{4}}}}+{\frac {1|}{|{\frac {9}{z}}}}+{\frac {1|}{|{\frac {2}{5}}}}+...}
log
(
1
+
z
)
=
z
|
|
1
+
K
∞
k
=
1
k
2
z
k
+
1
−
k
z
=
z
|
|
1
+
z
|
|
2
−
z
+
4
z
|
|
3
−
2
z
+
9
z
|
|
4
−
3
z
+
16
z
|
|
5
−
4
z
+
.
.
.
{\displaystyle \log(1+z)={\frac {z|}{|1}}+{\underset {k=1}{\overset {\infty }{K}}}{\frac {k^{2}z}{k+1-kz}}={\frac {z|}{|1}}+{\frac {z|}{|2-z}}+{\frac {4z|}{|3-2z}}+{\frac {9z|}{|4-3z}}+{\frac {16z|}{|5-4z}}+...}
erf
(
z
)
=
±
1
−
1
π
e
−
z
2
|
|
z
+
1
|
|
2
z
+
2
|
|
z
+
3
|
|
2
z
+
4
|
|
z
+
5
|
|
2
z
+
6
|
|
z
+
7
|
|
2
z
+
8
|
|
z
+
.
.
.
Re
(
z
)
>
0
Re
(
z
)
<
0
{\displaystyle \operatorname {erf} (z)=\pm 1-{\frac {{\frac {1}{\sqrt {\pi }}}e^{-z^{2}}|}{|z}}+{\frac {1|}{|2z}}+{\frac {2|}{|z}}+{\frac {3|}{|2z}}+{\frac {4|}{|z}}+{\frac {5|}{|2z}}+{\frac {6|}{|z}}+{\frac {7|}{|2z}}+{\frac {8|}{|z}}+...\qquad {\begin{matrix}\operatorname {Re} (z)>0\\\operatorname {Re} (z)<0\end{matrix}}}
erf
(
z
)
=
z
π
e
−
z
2
|
|
1
2
+
K
∞
k
=
1
(
−
1
)
k
k
2
z
2
2
k
+
1
2
=
z
π
e
−
z
2
|
|
1
2
−
1
2
z
2
|
|
3
2
+
2
2
z
2
|
|
5
2
−
3
2
z
2
|
|
7
2
+
4
2
z
2
|
|
9
2
−
5
2
z
2
|
|
11
2
+
6
2
z
2
|
|
13
2
−
.
.
.
{\displaystyle \operatorname {erf} (z)={\frac {{\frac {z}{\sqrt {\pi }}}e^{-z^{2}}|}{|{\frac {1}{2}}}}+{\underset {k=1}{\overset {\infty }{K}}}{\frac {(-1)^{k}{\frac {k}{2}}z^{2}}{\frac {2k+1}{2}}}={\frac {{\frac {z}{\sqrt {\pi }}}e^{-z^{2}}|}{|{\frac {1}{2}}}}-{\frac {{\frac {1}{2}}z^{2}|}{|{\frac {3}{2}}}}+{\frac {{\frac {2}{2}}z^{2}|}{|{\frac {5}{2}}}}-{\frac {{\frac {3}{2}}z^{2}|}{|{\frac {7}{2}}}}+{\frac {{\frac {4}{2}}z^{2}|}{|{\frac {9}{2}}}}-{\frac {{\frac {5}{2}}z^{2}|}{|{\frac {11}{2}}}}+{\frac {{\frac {6}{2}}z^{2}|}{|{\frac {13}{2}}}}-...}
Γ
(
z
+
α
+
1
4
)
Γ
(
z
−
α
+
1
4
)
Γ
(
z
+
α
+
3
4
)
Γ
(
z
−
α
+
3
4
)
=
4
|
|
z
+
K
∞
k
=
1
(
2
k
−
1
)
2
−
α
2
2
z
=
4
|
|
z
+
1
2
−
α
2
|
|
2
z
+
3
2
−
α
2
|
|
2
z
+
5
2
−
α
2
|
|
2
z
+
7
2
−
α
2
|
|
2
z
+
.
.
.
{\displaystyle {\frac {\Gamma \left({\frac {z+\alpha +1}{4}}\right)\,\Gamma \left({\frac {z-\alpha +1}{4}}\right)}{\Gamma \left({\frac {z+\alpha +3}{4}}\right)\,\Gamma \left({\frac {z-\alpha +3}{4}}\right)}}={\frac {4|}{|z}}+{\underset {k=1}{\overset {\infty }{K}}}{\frac {(2k-1)^{2}-\alpha ^{2}}{2z}}={\frac {4|}{|z}}+{\frac {1^{2}-\alpha ^{2}|}{|2z}}+{\frac {3^{2}-\alpha ^{2}|}{|2z}}+{\frac {5^{2}-\alpha ^{2}|}{|2z}}+{\frac {7^{2}-\alpha ^{2}|}{|2z}}+...}
BesselI
(
1
+
a
d
,
2
x
d
)
BesselI
(
a
d
,
2
x
d
)
⋅
x
=
K
∞
k
=
1
x
2
a
+
k
d
{\displaystyle {\frac {{\text{BesselI}}\left(1+{\frac {a}{d}},{\frac {2x}{d}}\right)}{{\text{BesselI}}\left({\frac {a}{d}},{\frac {2x}{d}}\right)}}\cdot x={\underset {k=1}{\overset {\infty }{K}}}{\frac {x^{2}}{a+kd}}}
Beweis
Setze
c
k
=
BesselI
(
k
+
a
d
,
2
x
d
)
x
k
=
∑
n
=
0
∞
x
2
n
+
2
k
+
a
d
n
!
d
n
(
a
+
k
+
a
d
)
!
d
n
+
k
+
a
d
{\displaystyle c_{k}={\text{BesselI}}\left(k+{\frac {a}{d}},{\frac {2x}{d}}\right)x^{k}=\sum _{n=0}^{\infty }{\frac {x^{2n+2k+{\frac {a}{d}}}}{n!\,d^{n}\,\left(a+k+{\frac {a}{d}}\right)!\,d^{\,n+k+{\frac {a}{d}}}}}}
(
n
+
k
+
a
d
)
x
2
n
+
2
k
+
a
d
n
!
d
n
(
n
+
k
+
a
d
)
!
d
n
+
k
+
a
d
−
(
k
+
a
d
)
x
2
n
+
2
k
+
a
d
n
!
d
n
(
n
+
k
+
a
d
)
!
d
n
+
k
+
a
d
=
n
x
2
n
+
2
k
+
a
d
n
!
d
n
(
n
+
k
+
a
d
)
!
d
n
+
k
+
a
d
{\displaystyle {\frac {\left(n+k+{\frac {a}{d}}\right)\,x^{2n+2k+{\frac {a}{d}}}}{n!\,d^{n}\,\left(n+k+{\frac {a}{d}}\right)!\,d^{\,n+k+{\frac {a}{d}}}}}-{\frac {\left(k+{\frac {a}{d}}\right)\,x^{2n+2k+{\frac {a}{d}}}}{n!\,d^{n}\,\left(n+k+{\frac {a}{d}}\right)!\,d^{\,n+k+{\frac {a}{d}}}}}={\frac {n\,x^{2n+2k+{\frac {a}{d}}}}{n!\,d^{n}\,\left(n+k+{\frac {a}{d}}\right)!\,d^{\,n+k+{\frac {a}{d}}}}}}
x
2
1
d
x
2
n
+
2
k
−
2
+
a
d
n
!
d
n
(
n
+
k
−
1
+
a
d
)
!
d
n
+
k
−
1
+
a
d
−
(
a
+
k
d
)
⋅
1
d
x
2
n
+
2
k
+
a
d
n
!
d
n
(
n
+
k
+
a
d
)
!
d
n
+
k
+
a
d
=
1
d
x
2
n
+
2
k
+
a
d
(
n
−
1
)
!
d
n
−
1
(
n
+
k
+
a
d
)
!
d
n
+
k
+
a
d
{\displaystyle {\frac {x^{2}\,{\frac {1}{d}}\,x^{2n+2k-2+{\frac {a}{d}}}}{n!\,d^{n}\,\left(n+k-1+{\frac {a}{d}}\right)!\,d^{\,n+k-1+{\frac {a}{d}}}}}-(a+kd)\cdot {\frac {{\frac {1}{d}}\,x^{2n+2k+{\frac {a}{d}}}}{n!\,d^{n}\,\left(n+k+{\frac {a}{d}}\right)!\,d^{\,n+k+{\frac {a}{d}}}}}={\frac {{\frac {1}{d}}\,x^{2n+2k+{\frac {a}{d}}}}{(n-1)!\,d^{n-1}\,\left(n+k+{\frac {a}{d}}\right)!\,d^{\,n+k+{\frac {a}{d}}}}}}
d
{\displaystyle d\,}
n
{\displaystyle n\,}
x
2
c
k
−
1
−
(
a
+
k
d
)
c
k
=
c
k
+
1
{\displaystyle x^{2}\,c_{k-1}-(a+kd)c_{k}=c_{k+1}}
x
2
c
k
−
1
c
k
=
(
a
+
k
d
)
+
c
k
+
1
c
k
{\displaystyle x^{2}\,{\frac {c_{k-1}}{c_{k}}}=(a+kd)+{\frac {c_{k+1}}{c_{k}}}}
c
k
c
k
−
1
=
x
2
(
a
+
k
d
)
+
c
k
+
1
c
k
{\displaystyle {\frac {c_{k}}{c_{k-1}}}={\frac {x^{2}}{(a+kd)+{\frac {c_{k+1}}{c_{k}}}}}}
c
1
c
0
=
x
2
a
+
d
+
c
2
c
1
=
x
2
a
+
d
+
x
2
a
+
2
d
+
c
3
c
2
=
x
2
a
+
d
+
x
2
a
+
2
d
+
x
2
a
+
3
d
+
c
4
c
3
=
.
.
.
{\displaystyle {\frac {c_{1}}{c_{0}}}={\frac {x^{2}}{a+d+{\frac {c_{2}}{c_{1}}}}}={\frac {x^{2}}{a+d+{\frac {x^{2}}{a+2d+{\frac {c_{3}}{c_{2}}}}}}}={\frac {x^{2}}{a+d+{\frac {x^{2}}{a+2d+{\frac {x^{2}}{a+3d+{\frac {c_{4}}{c_{3}}}}}}}}}=...}
(
5
+
5
5
−
5
+
1
2
)
e
2
π
/
5
=
K
∞
k
=
0
e
−
2
k
π
1
=
1
|
|
1
+
e
−
2
π
|
|
1
+
e
−
4
π
|
|
1
+
e
−
6
π
|
|
1
+
e
−
8
π
|
|
1
+
.
.
.
{\displaystyle \left({\sqrt {\frac {5+{\sqrt {5}}}{5}}}-{\frac {{\sqrt {5}}+1}{2}}\right)\,e^{2\pi /5}={\underset {k=0}{\overset {\infty }{K}}}{\frac {e^{-2k\pi }}{1}}={\frac {1|}{|1}}+{\frac {e^{-2\pi }|}{|1}}+{\frac {e^{-4\pi }|}{|1}}+{\frac {e^{-6\pi }|}{|1}}+{\frac {e^{-8\pi }|}{|1}}+...}
(
5
1
+
5
4
3
⋅
5
−
1
2
5
−
1
5
−
5
+
1
2
)
e
2
π
/
5
=
K
∞
k
=
0
e
−
2
k
π
5
1
=
1
|
|
1
+
e
−
2
π
5
|
|
1
+
e
−
4
π
5
|
|
1
+
e
−
6
π
5
|
|
1
+
e
−
8
π
5
|
|
1
+
.
.
.
{\displaystyle \left({\frac {\sqrt {5}}{1+{\sqrt[{5}]{{\sqrt[{4}]{5}}^{\,3}\cdot {\sqrt {\frac {{\sqrt {5}}-1}{2}}}^{\,5}-1}}}}-{\frac {{\sqrt {5}}+1}{2}}\right)\,e^{2\pi /{\sqrt {5}}}={\underset {k=0}{\overset {\infty }{K}}}{\frac {e^{-2k\pi {\sqrt {5}}}}{1}}={\frac {1|}{|1}}+{\frac {e^{-2\pi {\sqrt {5}}}|}{|1}}+{\frac {e^{-4\pi {\sqrt {5}}}|}{|1}}+{\frac {e^{-6\pi {\sqrt {5}}}|}{|1}}+{\frac {e^{-8\pi {\sqrt {5}}}|}{|1}}+...}
π
e
x
2
x
=
∑
k
=
0
∞
k
!
(
2
x
)
k
(
2
k
+
1
)
!
+
1
|
|
x
+
1
|
|
1
+
2
|
|
x
+
3
|
|
1
+
4
|
|
x
+
5
|
|
1
+
6
|
|
x
+
.
.
.
{\displaystyle {\sqrt {\frac {\pi \,e^{x}}{2x}}}=\sum _{k=0}^{\infty }{\frac {k!\,(2x)^{k}}{(2k+1)!}}+{\frac {1|}{|x}}+{\frac {1|}{|1}}+{\frac {2|}{|x}}+{\frac {3|}{|1}}+{\frac {4|}{|x}}+{\frac {5|}{|1}}+{\frac {6|}{|x}}+...}
Zurück zur Formelsammlung Mathematik
Formeln aus der Trigonometrie der Ebene .
Allgemeingültige Formeln befinden sich in den Abschnitten Winkelfunktionen Arkusfunktionen
Es werden die folgenden Bezeichnungen verwendet: Das Dreieck ABC habe die Seiten
a
=
B
C
¯
,
b
=
C
A
¯
,
c
=
A
B
¯
{\displaystyle a={\overline {BC}}\,,\,b={\overline {CA}}\,,\,c={\overline {AB}}}
Winkel
α
,
β
,
γ
{\displaystyle \alpha ,\beta ,\gamma \,}
Ecken A , B und C . Seien
s
a
,
s
b
,
s
c
{\displaystyle s_{a},s_{b},s_{c}}
w
a
,
w
b
,
w
c
{\displaystyle w_{a},w_{b},w_{c}}
h
a
,
h
b
,
h
c
{\displaystyle h_{a},h_{b},h_{c}}
R der Umkreisradius ,
ρ
{\displaystyle \rho }
Inkreisradius und
ρ
a
,
ρ
b
,
ρ
c
{\displaystyle \rho _{a},\rho _{b},\rho _{c}}
Ankreisradien (und zwar die Radien der Ankreise, die den Ecken A , B bzw. C gegenüberliegen) des Dreiecks ABC . Die Variable s steht für den halben Umfang des Dreiecks:
s
=
(
a
+
b
+
c
)
/
2
{\displaystyle s=(a+b+c)/2}
ABC mit A bezeichnet.
α
+
β
+
γ
=
π
(
=
180
∘
)
{\displaystyle \alpha +\beta +\gamma =\pi \quad (=180^{\circ })}
a
b
=
sin
α
sin
β
,
a
sin
α
=
b
sin
β
=
c
sin
γ
=
2
R
,
a
:
b
:
c
=
sin
α
:
sin
β
:
sin
γ
{\displaystyle {\frac {a}{b}}={\frac {\sin \alpha }{\sin \beta }}\quad ,\quad {\frac {a}{\sin \alpha }}={\frac {b}{\sin \beta }}={\frac {c}{\sin \gamma }}=2R\quad ,\quad a:b:c=\sin \alpha :\sin \beta :\sin \gamma \,}
Siehe auch: Sinussatz
a
2
=
b
2
+
c
2
−
2
b
c
cos
α
,
cos
α
=
b
2
+
c
2
−
a
2
2
b
c
,
a
2
+
b
c
cos
α
=
a
2
+
b
2
+
c
2
2
{\displaystyle a^{2}=b^{2}+c^{2}-2bc\ \cos \alpha \quad ,\quad \cos \alpha ={\frac {b^{2}+c^{2}-a^{2}}{2bc}}\quad ,\quad a^{2}+bc\,\cos \alpha ={\frac {a^{2}+b^{2}+c^{2}}{2}}}
Siehe auch: Kosinussatz
a
=
b
cos
γ
+
c
cos
β
{\displaystyle a=b\;\cos \gamma +c\;\cos \beta }
b
+
c
a
=
cos
β
−
γ
2
sin
α
2
,
b
−
c
a
=
sin
β
−
γ
2
cos
α
2
{\displaystyle {\frac {b+c}{a}}={\frac {\cos {\frac {\beta -\gamma }{2}}}{\sin {\frac {\alpha }{2}}}}\quad ,\quad {\frac {b-c}{a}}={\frac {\sin {\frac {\beta -\gamma }{2}}}{\cos {\frac {\alpha }{2}}}}}
a
+
b
a
−
b
=
tan
α
+
β
2
tan
α
−
β
2
=
cot
γ
2
tan
α
−
β
2
{\displaystyle {\frac {a+b}{a-b}}={\frac {\tan {\frac {\alpha +\beta }{2}}}{\tan {\frac {\alpha -\beta }{2}}}}={\frac {\cot {\frac {\gamma }{2}}}{\tan {\frac {\alpha -\beta }{2}}}}}
Siehe auch: Tangenssatz
s
−
a
=
b
+
c
−
a
2
,
(
s
−
b
)
+
(
s
−
c
)
=
a
,
(
s
−
a
)
+
(
s
−
b
)
+
(
s
−
c
)
=
s
{\displaystyle s-a={\frac {b+c-a}{2}}\quad ,\quad \left(s-b\right)+\left(s-c\right)=a\quad ,\quad \left(s-a\right)+\left(s-b\right)+\left(s-c\right)=s}
sin
α
2
=
(
s
−
b
)
(
s
−
c
)
b
c
,
cos
α
2
=
s
(
s
−
a
)
b
c
,
tan
α
2
=
(
s
−
b
)
(
s
−
c
)
s
(
s
−
a
)
{\displaystyle \sin {\frac {\alpha }{2}}={\sqrt {\frac {\left(s-b\right)\left(s-c\right)}{bc}}}\quad ,\quad \cos {\frac {\alpha }{2}}={\sqrt {\frac {s\left(s-a\right)}{bc}}}\quad ,\quad \tan {\frac {\alpha }{2}}={\sqrt {\frac {\left(s-b\right)\left(s-c\right)}{s\left(s-a\right)}}}}
s
=
4
R
cos
α
2
cos
β
2
cos
γ
2
,
s
−
a
=
4
R
cos
α
2
sin
β
2
sin
γ
2
{\displaystyle s=4R\cos \,{\frac {\alpha }{2}}\,\cos {\frac {\beta }{2}}\,\cos {\frac {\gamma }{2}}\quad ,\quad s-a=4R\,\cos {\frac {\alpha }{2}}\,\sin {\frac {\beta }{2}}\,\sin {\frac {\gamma }{2}}}
Heronsche Formel:
A
=
s
(
s
−
a
)
(
s
−
b
)
(
s
−
c
)
=
1
4
(
a
+
b
+
c
)
(
b
+
c
−
a
)
(
c
+
a
−
b
)
(
a
+
b
−
c
)
{\displaystyle A={\sqrt {s\left(s-a\right)\left(s-b\right)\left(s-c\right)}}={\frac {1}{4}}{\sqrt {\left(a+b+c\right)\left(b+c-a\right)\left(c+a-b\right)\left(a+b-c\right)}}}
A
=
1
4
2
(
b
2
c
2
+
c
2
a
2
+
a
2
b
2
)
−
(
a
4
+
b
4
+
c
4
)
{\displaystyle A={\frac {1}{4}}{\sqrt {2\left(b^{2}c^{2}+c^{2}a^{2}+a^{2}b^{2}\right)-\left(a^{4}+b^{4}+c^{4}\right)}}}
A
=
1
2
b
c
sin
α
{\displaystyle A={\frac {1}{2}}bc\sin \alpha }
A
=
1
2
a
h
a
{\displaystyle A={\frac {1}{2}}ah_{a}}
ha die Höhe auf der Seite BC ist.
A
=
2
R
2
sin
α
sin
β
sin
γ
{\displaystyle A=2R^{2}\sin \alpha \sin \beta \sin \gamma \,}
A
=
a
b
c
4
R
{\displaystyle A={\frac {abc}{4R}}}
A
=
ρ
s
=
ρ
a
(
s
−
a
)
{\displaystyle A=\rho \,s=\rho _{a}\left(s-a\right)}
A
=
ρ
ρ
a
ρ
b
ρ
c
{\displaystyle A={\sqrt {\rho \rho _{a}\rho _{b}\rho _{c}}}}
a
=
2
R
sin
α
{\displaystyle a=2R\sin \alpha \,}
R
=
a
b
c
4
A
{\displaystyle R={\frac {abc}{4A}}}
ρ
=
(
s
−
a
)
tan
α
2
=
(
s
−
b
)
tan
β
2
=
(
s
−
c
)
tan
γ
2
{\displaystyle \rho =\left(s-a\right)\tan {\frac {\alpha }{2}}=\left(s-b\right)\tan {\frac {\beta }{2}}=\left(s-c\right)\tan {\frac {\gamma }{2}}}
ρ
=
4
R
sin
α
2
sin
β
2
sin
γ
2
=
s
tan
α
2
tan
β
2
tan
γ
2
{\displaystyle \rho =4R\,\sin {\frac {\alpha }{2}}\,\sin {\frac {\beta }{2}}\,\sin {\frac {\gamma }{2}}=s\tan {\frac {\alpha }{2}}\tan {\frac {\beta }{2}}\tan {\frac {\gamma }{2}}}
ρ
=
R
(
cos
α
+
cos
β
+
cos
γ
−
1
)
{\displaystyle \rho =R\left(\cos \alpha +\cos \beta +\cos \gamma -1\right)}
ρ
=
A
s
=
a
b
c
4
R
s
{\displaystyle \rho ={\frac {A}{s}}={\frac {abc}{4Rs}}}
ρ
=
(
s
−
a
)
(
s
−
b
)
(
s
−
c
)
s
=
1
2
(
b
+
c
−
a
)
(
c
+
a
−
b
)
(
a
+
b
−
c
)
a
+
b
+
c
{\displaystyle \rho ={\sqrt {\frac {\left(s-a\right)\left(s-b\right)\left(s-c\right)}{s}}}={\frac {1}{2}}{\sqrt {\frac {\left(b+c-a\right)\left(c+a-b\right)\left(a+b-c\right)}{a+b+c}}}}
ρ
=
a
cot
β
2
+
cot
γ
2
{\displaystyle \rho ={\frac {a}{\cot {\frac {\beta }{2}}+\cot {\frac {\gamma }{2}}}}}
Chapple-Euler-Ungleichung:
2
ρ
≤
R
{\displaystyle 2\rho \leq R}
ABC gleichseitig ist.
ρ
a
=
s
tan
α
2
{\displaystyle \rho _{a}=s\tan {\frac {\alpha }{2}}}
ρ
a
=
4
R
sin
α
2
cos
β
2
cos
γ
2
=
(
s
−
a
)
tan
α
2
cot
β
2
cot
γ
2
{\displaystyle \rho _{a}=4R\sin {\frac {\alpha }{2}}\cos {\frac {\beta }{2}}\cos {\frac {\gamma }{2}}=\left(s-a\right)\tan {\frac {\alpha }{2}}\cot {\frac {\beta }{2}}\cot {\frac {\gamma }{2}}}
ρ
a
=
R
(
−
cos
α
+
cos
β
+
cos
γ
+
1
)
{\displaystyle \rho _{a}=R\left(-\cos \alpha +\cos \beta +\cos \gamma +1\right)}
ρ
a
=
A
s
−
a
=
a
b
c
4
R
(
s
−
a
)
{\displaystyle \rho _{a}={\frac {A}{s-a}}={\frac {abc}{4R\left(s-a\right)}}}
ρ
a
=
s
(
s
−
b
)
(
s
−
c
)
s
−
a
=
1
2
(
a
+
b
+
c
)
(
c
+
a
−
b
)
(
a
+
b
−
c
)
b
+
c
−
a
{\displaystyle \rho _{a}={\sqrt {\frac {s\left(s-b\right)\left(s-c\right)}{s-a}}}={\frac {1}{2}}{\sqrt {\frac {\left(a+b+c\right)\left(c+a-b\right)\left(a+b-c\right)}{b+c-a}}}}
1
ρ
=
1
ρ
a
+
1
ρ
b
+
1
ρ
c
{\displaystyle {\frac {1}{\rho }}={\frac {1}{\rho _{a}}}+{\frac {1}{\rho _{b}}}+{\frac {1}{\rho _{c}}}}
h
a
=
b
sin
γ
=
c
sin
β
=
2
A
a
=
2
R
sin
β
sin
γ
{\displaystyle h_{a}=b\sin \gamma =c\sin \beta ={\frac {2A}{a}}=2R\sin \beta \sin \gamma }
h
a
=
a
cot
β
+
cot
γ
{\displaystyle h_{a}={\frac {a}{\cot \beta +\cot \gamma }}}
1
h
a
+
1
h
b
+
1
h
c
=
1
ρ
=
1
ρ
a
+
1
ρ
b
+
1
ρ
c
{\displaystyle {\frac {1}{h_{a}}}+{\frac {1}{h_{b}}}+{\frac {1}{h_{c}}}={\frac {1}{\rho }}={\frac {1}{\rho _{a}}}+{\frac {1}{\rho _{b}}}+{\frac {1}{\rho _{c}}}}
Ist
α
=
π
2
(
=
90
∘
)
{\displaystyle \alpha ={\frac {\pi }{2}}\;(=90^{\circ })}
h
a
=
b
c
a
{\displaystyle h_{a}={\frac {b\,c}{a}}}
s
a
=
1
2
2
b
2
+
2
c
2
−
a
2
=
1
2
b
2
+
c
2
+
2
b
c
cos
α
=
a
2
4
+
b
c
cos
α
{\displaystyle s_{a}={\frac {1}{2}}{\sqrt {2b^{2}+2c^{2}-a^{2}}}={\frac {1}{2}}{\sqrt {b^{2}+c^{2}+2bc\cos \alpha }}={\sqrt {{\frac {a^{2}}{4}}+bc\cos \alpha }}}
s
a
2
+
s
b
2
+
s
c
2
=
3
4
(
a
2
+
b
2
+
c
2
)
{\displaystyle s_{a}^{2}+s_{b}^{2}+s_{c}^{2}={\frac {3}{4}}\left(a^{2}+b^{2}+c^{2}\right)}
w
α
=
2
b
c
cos
α
2
b
+
c
=
2
A
a
cos
β
−
γ
2
{\displaystyle w_{\alpha }={\frac {2bc\cos {\frac {\alpha }{2}}}{b+c}}={\frac {2A}{a\cos {\frac {\beta -\gamma }{2}}}}}
Die folgenden Formeln folgen nach längeren Termumformungen aus α + β + γ = 180°, gelten also allgemein für drei beliebige Winkel α, β und γ mit der Eigenschaft α + β + γ = 180°, solange die in den Formeln vorkommenden Funktionen wohldefiniert sind (letzteres betrifft nur die Formeln, in denen Tangens und Kotangens vorkommen).
tan
α
+
tan
β
+
tan
γ
=
tan
α
⋅
tan
β
⋅
tan
γ
{\displaystyle \tan \alpha +\tan \beta +\tan \gamma =\tan \alpha \cdot \tan \beta \cdot \tan \gamma \,}
cot
β
⋅
cot
γ
+
cot
γ
⋅
cot
α
+
cot
α
⋅
cot
β
=
1
{\displaystyle \cot \beta \cdot \cot \gamma +\cot \gamma \cdot \cot \alpha +\cot \alpha \cdot \cot \beta =1}
cot
α
2
+
cot
β
2
+
cot
γ
2
=
cot
α
2
⋅
cot
β
2
⋅
cot
γ
2
{\displaystyle \cot {\frac {\alpha }{2}}+\cot {\frac {\beta }{2}}+\cot {\frac {\gamma }{2}}=\cot {\frac {\alpha }{2}}\cdot \cot {\frac {\beta }{2}}\cdot \cot {\frac {\gamma }{2}}}
tan
β
2
tan
γ
2
+
tan
γ
2
tan
α
2
+
tan
α
2
tan
β
2
=
1
{\displaystyle \tan {\frac {\beta }{2}}\tan {\frac {\gamma }{2}}+\tan {\frac {\gamma }{2}}\tan {\frac {\alpha }{2}}+\tan {\frac {\alpha }{2}}\tan {\frac {\beta }{2}}=1}
sin
α
+
sin
β
+
sin
γ
=
4
cos
α
2
cos
β
2
cos
γ
2
{\displaystyle \sin \alpha +\sin \beta +\sin \gamma =4\cos {\frac {\alpha }{2}}\cos {\frac {\beta }{2}}\cos {\frac {\gamma }{2}}}
−
sin
α
+
sin
β
+
sin
γ
=
4
cos
α
2
sin
β
2
sin
γ
2
{\displaystyle -\sin \alpha +\sin \beta +\sin \gamma =4\cos {\frac {\alpha }{2}}\sin {\frac {\beta }{2}}\sin {\frac {\gamma }{2}}}
cos
α
+
cos
β
+
cos
γ
=
4
sin
α
2
sin
β
2
sin
γ
2
+
1
{\displaystyle \cos \alpha +\cos \beta +\cos \gamma =4\sin {\frac {\alpha }{2}}\sin {\frac {\beta }{2}}\sin {\frac {\gamma }{2}}+1}
−
cos
α
+
cos
β
+
cos
γ
=
4
sin
α
2
cos
β
2
cos
γ
2
−
1
{\displaystyle -\cos \alpha +\cos \beta +\cos \gamma =4\sin {\frac {\alpha }{2}}\cos {\frac {\beta }{2}}\cos {\frac {\gamma }{2}}-1}
sin
(
2
α
)
+
sin
(
2
β
)
+
sin
(
2
γ
)
=
4
sin
α
sin
β
sin
γ
{\displaystyle \sin \left(2\alpha \right)+\sin \left(2\beta \right)+\sin \left(2\gamma \right)=4\sin \alpha \sin \beta \sin \gamma }
−
sin
(
2
α
)
+
sin
(
2
β
)
+
sin
(
2
γ
)
=
4
sin
α
cos
β
cos
γ
{\displaystyle -\sin \left(2\alpha \right)+\sin \left(2\beta \right)+\sin \left(2\gamma \right)=4\sin \alpha \cos \beta \cos \gamma }
cos
(
2
α
)
+
cos
(
2
β
)
+
cos
(
2
γ
)
=
−
4
cos
α
cos
β
cos
γ
−
1
{\displaystyle \cos \left(2\alpha \right)+\cos \left(2\beta \right)+\cos \left(2\gamma \right)=-4\cos \alpha \cos \beta \cos \gamma -1}
−
cos
(
2
α
)
+
cos
(
2
β
)
+
cos
(
2
γ
)
=
−
4
cos
α
sin
β
sin
γ
+
1
{\displaystyle -\cos \left(2\alpha \right)+\cos \left(2\beta \right)+\cos \left(2\gamma \right)=-4\cos \alpha \sin \beta \sin \gamma +1}
sin
2
α
+
sin
2
β
+
sin
2
γ
=
2
⋅
cos
α
⋅
cos
β
⋅
cos
γ
+
2
{\displaystyle \sin ^{2}\alpha +\sin ^{2}\beta +\sin ^{2}\gamma =2\cdot \cos \alpha \cdot \cos \beta \cdot \cos \gamma +2}
−
sin
2
α
+
sin
2
β
+
sin
2
γ
=
2
⋅
cos
α
⋅
sin
β
⋅
sin
γ
{\displaystyle -\sin ^{2}\alpha +\sin ^{2}\beta +\sin ^{2}\gamma =2\cdot \cos \alpha \cdot \sin \beta \cdot \sin \gamma }
cos
2
α
+
cos
2
β
+
cos
2
γ
=
−
2
⋅
cos
α
⋅
cos
β
⋅
cos
γ
+
1
{\displaystyle \cos ^{2}\alpha +\cos ^{2}\beta +\cos ^{2}\gamma =-2\cdot \cos \alpha \cdot \cos \beta \cdot \cos \gamma +1}
−
cos
2
α
+
cos
2
β
+
cos
2
γ
=
−
2
⋅
cos
α
⋅
sin
β
⋅
sin
γ
+
1
{\displaystyle -\cos ^{2}\alpha +\cos ^{2}\beta +\cos ^{2}\gamma =-2\cdot \cos \alpha \cdot \sin \beta \cdot \sin \gamma +1}
−
sin
2
(
2
α
)
+
sin
2
(
2
β
)
+
sin
2
(
2
γ
)
=
−
2
cos
(
2
α
)
sin
(
2
β
)
sin
(
2
γ
)
{\displaystyle -\sin ^{2}\left(2\alpha \right)+\sin ^{2}\left(2\beta \right)+\sin ^{2}\left(2\gamma \right)=-2\cos \left(2\alpha \right)\sin \left(2\beta \right)\sin \left(2\gamma \right)}
−
cos
2
(
2
α
)
+
cos
2
(
2
β
)
+
cos
2
(
2
γ
)
=
2
cos
(
2
α
)
sin
(
2
β
)
sin
(
2
γ
)
+
1
{\displaystyle -\cos ^{2}\left(2\alpha \right)+\cos ^{2}\left(2\beta \right)+\cos ^{2}\left(2\gamma \right)=2\cos \left(2\alpha \right)\sin \left(2\beta \right)\sin \left(2\gamma \right)+1}
Zurück zu Formelsammlung_Mathematik
Die allgemeine Aussage des Satzes des Pythagoras lautet:
In einem rechtwinkligen Dreieck ist das Quadrat über der Hypotenuse gleich der Summe der Quadrate über den beiden Katheten.
c
2
=
a
2
+
b
2
{\displaystyle {\color {Red}c^{2}}={\color {Blue}a^{2}}+{\color {Green}b^{2}}}
Satz: Die Summe der Quadrate über den Katheten ist gleich dem Quadrat über der Hypotenuse.
Daraus folgt:
Im rechtwinkligen Dreieck gilt
a
2
=
p
⋅
c
{\displaystyle a^{2}=p\cdot c}
b
2
=
q
⋅
c
{\displaystyle b^{2}=q\cdot c}
Rechtwinkliges Dreieck mit Höhe h
Im rechtwinkligen Dreieck gilt
h
2
=
p
⋅
q
{\displaystyle h^{2}=p\cdot q}
a
sin
α
=
b
sin
β
=
c
sin
γ
{\displaystyle {\frac {a}{\sin {\alpha }}}={\frac {b}{\sin {\beta }}}={\frac {c}{\sin {\gamma }}}\,}
a
2
=
b
2
+
c
2
−
2
⋅
b
⋅
c
⋅
cos
α
{\displaystyle a^{2}=b^{2}+c^{2}-2\cdot b\cdot c\cdot {\cos {\alpha }}\,}
cos
α
=
b
2
+
c
2
−
a
2
2
⋅
b
⋅
c
{\displaystyle {\cos {\alpha }}={\frac {b^{2}+c^{2}-a^{2}}{2\cdot b\cdot c}}\,}
Die Winkelsumme im Dreieck beträgt 180°. Für ein gleichseitiges Dreieck der Seitenlänge a gilt:
Alle Innenwinkel sind gleich 60°.
Die Höhe = Mittelsenkrechte = Winkelhalbierende
Länge der Höhe
h
=
a
2
3
{\displaystyle h={\frac {a}{2}}\,{\sqrt {3}}}
Fläche
A
=
a
h
2
=
a
2
3
4
{\displaystyle A={\frac {a\,h}{2}}={\frac {a^{2}\,{\sqrt {3}}}{4}}}
Umfang
U
=
3
a
{\displaystyle U=3a\!}
Für ein gleichschenkliges Dreieck der Schenkellänge a und der Länge b der dritten Seite gilt:
Fläche:
A
=
1
2
⋅
b
⋅
h
=
1
2
⋅
b
⋅
a
2
−
b
2
4
{\displaystyle A={\frac {1}{2}}\cdot b\cdot h={\frac {1}{2}}\cdot b\cdot {\sqrt {a^{2}-{\frac {b^{2}}{4}}}}}
Umfang:
U
=
2
a
+
b
{\displaystyle U=2a+b\ }
Die Höhe auf b ist gleichzeitig die Seitenhalbierende von b.
Man kann h also mit dem Pythagoras berechnen:
a
2
=
h
2
+
(
b
2
)
2
{\displaystyle a^{2}=h^{2}+\left({\frac {b}{2}}\right)^{2}}
h
=
a
2
−
b
2
4
{\displaystyle h={\sqrt {a^{2}-{\frac {b^{2}}{4}}}}}
Ist der Winkel
α
{\displaystyle \alpha }
b
=
2
h
tan
α
2
{\displaystyle b=2h\tan {\frac {\alpha }{2}}}
a
=
h
cos
α
2
{\displaystyle a={\frac {h}{\cos {\frac {\alpha }{2}}}}}
b
=
2
a
sin
α
2
{\displaystyle b=2a\sin {\frac {\alpha }{2}}}
Für ein rechtwinkliges Dreieck mit den Seitenlängen a,b,c gilt
a
2
+
b
2
=
c
2
{\displaystyle a^{2}+b^{2}=c^{2}\ }
Dabei liegt die Seite c dem rechten Winkel gegenüber.
Fläche
A
=
a
b
2
{\displaystyle A={\frac {a\,b}{2}}}
Für ein beliebiges Dreieck der Seitenlängen a,b,c , den Ecken A,B,C und dem Schwerpunkt S gilt:
C
S
¯
S
M
¯
=
2
:
1
{\displaystyle {\frac {\overline {CS}}{\overline {SM}}}=2:1}
Verhältnis 2 zu 1
Dabei ist:
C die Ecke C
S der Schwerpunkt = Schnittpunkt der Seitenhalbierenden
M der Mittelpunkt der Seite c Höhenverhältnis:
h
a
:
h
b
:
h
c
=
1
a
:
1
b
:
1
c
{\displaystyle h_{a}:h_{b}:h_{c}={\frac {1}{a}}:{\frac {1}{b}}:{\frac {1}{c}}}
Winkelhalbierende:
A
W
¯
W
B
¯
=
b
a
{\displaystyle {\frac {\overline {AW}}{\overline {WB}}}={\frac {b}{a}}}
Dabei ist W der Schnittpunkt der Winkelhalbierenden des Innenwinkels der Ecke C ( Winkel ACB) mit der Seite c.
Quadrat mit In- und Umkreis Fläche:
A
=
a
2
{\displaystyle A=a^{2}\!}
Umfang:
U
=
4
a
{\displaystyle U=4a\!}
Länge der Diagonalen:
d
=
a
2
{\displaystyle d=a\,{\sqrt {2}}}
Umkreisradius:
r
=
a
2
2
{\displaystyle r={\frac {a}{2}}\,{\sqrt {2}}}
Inkreisradius:
r
=
a
2
{\displaystyle r={\frac {a}{2}}}
Rechteck mit Umkreis Fläche:
A
=
a
⋅
b
{\displaystyle A=a\cdot b}
Umfang:
U
=
2
⋅
(
a
+
b
)
{\displaystyle U=2\cdot (a+b)}
Länge der Diagonalen:
d
=
a
2
+
b
2
{\displaystyle d={\sqrt {a^{2}+b^{2}}}}
Umkreisradius:
r
=
1
2
⋅
a
2
+
b
2
{\displaystyle r\,=\,{\frac {1}{2}}\cdot {\sqrt {a^{2}+b^{2}}}}
Sätze:
Gegenüberliegende Seiten sind gleich lang und parallel.
Die beiden Raumdiagonalen sind gleich lang und halbieren einander.
Der Schnittpunkt der Diagonalen ist Mittelpunkt des Umkreises. Aus diesem Grund ist jedes Rechteck auch ein Sehnenviereck.
Es ist achsensymmetrisch bezüglich der Mittelsenkrechten (Seitensymmetralen) der Rechteckseiten. Die beiden Symmetrieachsen stehen also senkrecht aufeinander.
Es ist punktsymmetrisch (zweizählig symmetrisch) bezüglich des Diagonalenschnittpunkts.
Es ist konvex. Fläche:
A
=
a
⋅
a
⋅
sin
α
=
a
⋅
a
⋅
sin
β
⇔
F
=
a
2
⋅
sin
α
=
a
2
⋅
sin
β
{\displaystyle A=a\cdot a\cdot \sin \alpha =a\cdot a\cdot \sin \beta \Leftrightarrow F\,=\,a^{2}\cdot \sin \alpha =a^{2}\cdot \sin \beta }
Umfang:
U
=
4
⋅
a
{\displaystyle U=4\cdot a}
Diagonale 1
e
=
2
⋅
a
⋅
cos
α
2
=
2
⋅
a
⋅
sin
β
2
{\displaystyle e\,=\,2\cdot a\cdot \cos {\frac {\alpha }{2}}=2\cdot a\cdot \sin {\frac {\beta }{2}}}
Diagonale 2
f
=
2
⋅
a
⋅
sin
α
2
=
2
⋅
a
⋅
cos
β
2
{\displaystyle f\,=\,2\cdot a\cdot \sin {\frac {\alpha }{2}}=2\cdot a\cdot \cos {\frac {\beta }{2}}}
Sätze:
Benachbarte Innenwinkel ergeben als Summe 180 Grad. Alpha + Beta = 180° Grundlegende Begriffe am Parallelogramm Fläche:
A
=
a
⋅
h
a
=
b
⋅
h
b
=
a
⋅
b
⋅
sin
α
{\displaystyle A=a\cdot h_{a}=b\cdot h_{b}=a\cdot b\cdot \sin \alpha }
Umfang:
U
=
2
⋅
(
a
+
b
)
{\displaystyle U=2\cdot (a+b)}
Diagonale e: e²=ha²+(a+x)²Diagonale 2: Strecke x: x²=b²-ha²Sätze:
Gegenüberliegende Seiten sind gleich lang.
Gegenüberliegende Winkel sind gleich groß.
Je zwei benachbarte Winkel sind supplementär (ergeben zusammen 180°).
Die Diagonalen halbieren sich gegenseitig.
Jede Diagonale teilt es in zwei (gleich orientierte) kongruente Dreiecke. Fläche:
A
=
1
2
⋅
(
a
+
c
)
⋅
h
{\displaystyle A\,=\,{\frac {1}{2}}\cdot (a+c)\cdot h}
Umfang:
U
=
a
+
c
+
2
⋅
b
{\displaystyle U=a+c+2\cdot b}
Sätze:
Die Schenkel sind gleich lang.
b
=
d
{\displaystyle b=d\ }
Trapez Fläche:
A
=
1
2
⋅
(
a
+
c
)
⋅
h
{\displaystyle A\,=\,{\frac {1}{2}}\cdot (a+c)\cdot h}
Umfang:
U
=
a
+
b
+
c
+
d
{\displaystyle U=a+b+c+d\ }
Diagonale 1
d
1
=
a
2
+
b
2
−
2
a
b
cos
β
=
c
2
+
d
2
−
2
c
d
cos
δ
{\displaystyle d_{1}={\sqrt {a^{2}+b^{2}-2ab\cos \beta }}={\sqrt {c^{2}+d^{2}-2cd\cos \delta }}}
Diagonale 2
d
2
=
a
2
+
d
2
−
2
a
d
cos
α
=
b
2
+
c
2
−
2
b
c
cos
γ
{\displaystyle d_{2}={\sqrt {a^{2}+d^{2}-2ad\cos \alpha }}={\sqrt {b^{2}+c^{2}-2bc\cos \gamma }}}
Drachenviereck Sätze über das Drachenviereck:
Das Drachenviereck besteht aus zwei gleichschenkligen Dreiecken mit gemeinsamer Basis.
Das Drachenviereck ist in sich einfach achsensymmetrisch; die Symmetrieachse ist die durch die Spitzen der gleichschenkligen Teildreiecke verlaufende Diagonale.
Das Drachenviereck ist nicht zentralsymmetrisch.
Die Diagonalen im Drachenviereck stehen aufeinander senkrecht
e
⊥
f
{\displaystyle e\perp f}
Die Diagonalen im Drachenviereck sind ungleich lang
e
≠
f
{\displaystyle e\not =f}
Im Drachenviereck ist ein Gegenwinkel-Paar gleich groß:
β
=
δ
{\displaystyle \beta =\delta }
Im Drachenviereck werden die ungleich großen Gegenwinkel durch die Diagonale halbiert. Die Summe der Innenwinkel eines n-Ecks beträgt
(
n
−
2
)
⋅
180
∘
{\displaystyle (n-2)\cdot 180^{\circ }}
Die Summe der Außenwinkel eines n-Ecks beträgt
(
n
+
2
)
⋅
180
∘
{\displaystyle (n+2)\cdot 180^{\circ }}
Ein Innenwinkel und sein zugehöriger Außenwinkel betragen als Nebenwinkel zusammen
180
∘
{\displaystyle 180^{\circ }}
Die Winkelhalbierende eines Innenwinkels und die des zugehörigen Außenwinkels stehen senkrecht aufeinander. Jedes regelmäßige n-Eck ist n-fach zentralsymmetrisch.
Um jedes regelmäßige Vieleck lässt sich ein Kreis beschreiben, der durch alle Ecken geht. (Umkreis)
In jedes regelmäßige Vieleck lässt sich ein Kreis beschreiben, der jede Seite in der Seitenmitte von innen berührt. (Inkreis)
Das gemeinsame Zentrum von Um- und Inkreis heißt der Mittelpunkt M des Vielecks.
Durch Verbinden des Mittelpunktes mit den Ecken wird das regelmäßige Vieleck in n kongruente gleichschenklige Dreiecke zerlegt.(Bestimmungsdreiecke des Vielecks)
Jeder Innenwinkel im regelmäßigen n-Eck beträgt
n
−
2
n
⋅
180
∘
{\displaystyle {\frac {n-2}{n}}\cdot 180^{\circ }}
Jeder Außenwinkel im regelmäßigen n-Eck beträgt
360
∘
n
{\displaystyle {\frac {360^{\circ }}{n}}}
Grundlegende Begriffe am Kreis Kreiszahl:
π
{\displaystyle \pi \ }
Radius =
r
{\displaystyle r\ }
Durchmesser =
d
{\displaystyle d\ }
Kreisbogen =
b
{\displaystyle b\ }
Durchmesser eines Kreises:
d
=
2
⋅
r
{\displaystyle d=2\cdot r}
Fläche eines Kreises:
A
=
r
2
⋅
π
{\displaystyle A=r^{2}\cdot \pi }
Umfang eines Kreises:
U
=
d
⋅
π
=
2
⋅
r
⋅
π
{\displaystyle U=d\cdot \pi =2\cdot r\cdot \pi }
Flächeninhalt eines Kreisrings:
A
=
(
r
1
2
−
r
2
2
)
⋅
π
{\displaystyle A=(r_{1}^{2}-r_{2}^{2})\cdot \pi }
Länge eines Kreisbogens:
b
=
α
360
∘
⋅
d
⋅
π
{\displaystyle b={\frac {\alpha }{360^{\circ }}}\cdot d\cdot \pi }
b
=
α
180
∘
⋅
r
⋅
π
{\displaystyle b={\frac {\alpha }{180^{\circ }}}\cdot r\cdot \pi }
Flächeninhalt von Kreissektoren:
A
S
=
α
360
∘
⋅
r
2
⋅
π
{\displaystyle A_{S}={\frac {\alpha }{360^{\circ }}}\cdot r^{2}\cdot \pi }
A
S
=
α
180
∘
⋅
d
2
4
⋅
π
{\displaystyle A_{S}={\frac {\alpha }{180^{\circ }}}\cdot {\frac {d^{2}}{4}}\cdot \pi }
A
S
=
1
2
⋅
b
⋅
r
=
1
4
⋅
b
⋅
d
{\displaystyle A_{S}={\frac {1}{2}}\cdot b\cdot r={\frac {1}{4}}\cdot b\cdot d}
Flächeninhalt eines Kreissegments:
A
=
r
2
⋅
π
⋅
α
360
∘
−
r
2
⋅
sin
α
2
{\displaystyle A={\frac {r^{2}\cdot \pi \cdot {\alpha }}{360^{\circ }}}-{\frac {r^{2}\cdot \sin {\alpha }}{2}}}
A
=
r
2
2
⋅
(
π
⋅
α
180
∘
−
sin
α
)
{\displaystyle A={\frac {r^{2}}{2}}\cdot \left({\frac {\pi \cdot \alpha }{180^{\circ }}}-\sin \alpha \right)}
Kugel mit dem Radius r:Oberfläche:
O
=
4
π
r
2
{\displaystyle O=4\pi r^{2}\!}
Volumen:
V
=
4
3
π
r
3
{\displaystyle V={\frac {4}{3}}\pi r^{3}}
Siehe auch Wikipedia: Kugel
Für einen Würfel mit der Seitenlänge a gilt:
Oberfläche:
O
=
6
a
2
{\displaystyle O=6a^{2}\ }
Volumen:
V
=
a
3
{\displaystyle V=a^{3}\ }
Länge der Raumdiagonalen:
d
=
3
a
2
{\displaystyle d={\sqrt {3a^{2}}}}
Skizze eines Quaders Für einen Quader mit den Seitenlängen a , b , c gilt:
Oberfläche:
O
=
2
(
a
b
+
a
c
+
b
c
)
{\displaystyle O=2\,(ab+ac+bc)}
Volumen:
V
=
a
b
c
{\displaystyle V=abc\!}
Länge der Flächendiagonalen:
d
1
=
a
2
+
b
2
{\displaystyle d_{1}={\sqrt {a^{2}+b^{2}}}}
d
2
=
b
2
+
c
2
{\displaystyle d_{2}={\sqrt {b^{2}+c^{2}}}}
d
3
=
c
2
+
a
2
{\displaystyle d_{3}={\sqrt {c^{2}+a^{2}}}}
Länge der Raumdiagonalen:
D
=
a
2
+
b
2
+
c
2
{\displaystyle D={\sqrt {a^{2}+b^{2}+c^{2}}}}
Für eine Pyramide der Höhe h mit der quadratischen Grundfläche der Seitenlänge a gilt:
Mantelfläche einer quadratischen Pyramide:
A
M
=
4
⋅
S
e
i
t
e
n
f
l
a
¨
c
h
e
=
4
⋅
1
2
⋅
S
e
i
t
e
n
l
a
¨
n
g
e
⋅
H
o
¨
h
e
der Pyramidenseite
=
2
a
⋅
1
4
a
2
+
h
2
{\displaystyle {\begin{alignedat}{2}A_{M}&=4\cdot \mathrm {Seitenfl{\ddot {a}}che} \\&=4\cdot {\frac {1}{2}}\cdot \mathrm {Seitenl{\ddot {a}}nge} \cdot \mathrm {H{\ddot {o}}he} \ {\text{der Pyramidenseite}}\\&=2a\cdot {\sqrt {{\frac {1}{4}}a^{2}+h^{2}}}\end{alignedat}}}
Oberfläche einer quadratischen Pyramide:
A
O
=
G
r
u
n
d
f
l
a
¨
c
h
e
+
4
⋅
S
e
i
t
e
n
f
l
a
¨
c
h
e
=
a
2
+
2
a
⋅
1
4
a
2
+
h
2
=
a
(
a
+
2
⋅
1
4
a
2
+
h
2
)
{\displaystyle {\begin{alignedat}{2}A_{O}&=\mathrm {Grundfl{\ddot {a}}che} +4\cdot \mathrm {Seitenfl{\ddot {a}}che} \\&=a^{2}+2a\cdot {\sqrt {{\frac {1}{4}}a^{2}+h^{2}}}\\&=a\left(a+2\cdot {\sqrt {{\frac {1}{4}}a^{2}+h^{2}}}\right)\end{alignedat}}}
Volumen einer quadratischen Pyramide:
V
=
1
3
⋅
H
o
¨
h
e
⋅
G
r
u
n
d
f
l
a
¨
c
h
e
=
1
3
⋅
h
⋅
a
2
{\displaystyle {\begin{alignedat}{2}V&={\frac {1}{3}}\cdot \mathrm {H{\ddot {o}}he} \cdot \mathrm {Grundfl{\ddot {a}}che} \\&={\frac {1}{3}}\cdot h\cdot a^{2}\end{alignedat}}}
Für einen Tetraeder mit der Seitenlänge a gilt:
Grundfläche eines Tetraeders:
A
G
=
a
2
4
3
{\displaystyle A_{G}={\frac {a^{2}}{4}}{\sqrt {3}}}
Mantelfläche eines Tetraeders:
A
M
=
3
a
2
4
3
{\displaystyle A_{M}={\frac {3a^{2}}{4}}{\sqrt {3}}}
Oberfläche eines Tetraeders:
A
O
=
a
2
3
{\displaystyle A_{O}=a^{2}{\sqrt {3}}}
Volumen eines Tetraeders:
V
=
a
3
12
2
{\displaystyle V={\frac {a^{3}}{12}}{\sqrt {2}}}
Höhe eines gleichseitigen Tetraeders:
h
=
a
3
6
{\displaystyle h=\,{\frac {a}{3}}{\sqrt {6}}}
Für eine Pyramide der Höhe h mit der Grundfläche A G und der Mantelfläche A M gilt allgemein:
Oberfläche einer Pyramide:
A
O
=
A
G
+
A
M
{\displaystyle A_{O}=\,A_{G}+A_{M}}
Volumen einer Pyramide:
V
=
1
3
A
G
h
{\displaystyle V={\frac {1}{3}}A_{G}h}
Für einen Kreiszylinder mit der Höhe h und dem Radius r gilt:
Mantelfläche eines geraden Kreiszylinders:
A
M
=
Umfang
⋅
h
=
2
π
r
h
{\displaystyle A_{M}={\text{Umfang}}\cdot h=2\pi rh}
Oberfläche eines geraden Kreiszylinders:
A
O
=
A
M
+
2
r
2
π
=
2
π
r
h
+
2
π
r
2
=
2
π
r
(
h
+
r
)
{\displaystyle A_{O}=\,A_{M}+2r^{2}\pi =2\pi rh+2\pi r^{2}=2\pi r(h+r)}
Volumen eines geraden Kreiszylinders:
V
=
h
r
2
π
{\displaystyle V=hr^{2}\pi \,}
Für einen Kreiskegel der Höhe h mit dem Radius r bzw. dem Durchmesser d und der Mantellinie s gilt:
Mantelfläche eines geraden Kreiskegels
A
M
=
1
2
⋅
π
⋅
d
⋅
s
=
π
⋅
r
⋅
s
{\displaystyle {\begin{alignedat}{2}A_{M}&={\frac {1}{2}}\cdot \pi \cdot d\cdot s\\&=\pi \cdot r\cdot s\end{alignedat}}}
Oberfläche eines geraden Kreiskegels
A
O
=
1
4
⋅
π
⋅
d
⋅
(
d
+
2
⋅
s
)
=
π
⋅
r
⋅
(
r
+
s
)
{\displaystyle {\begin{alignedat}{2}A_{O}&={\frac {1}{4}}\cdot \pi \cdot d\cdot (d+2\cdot s)\\&=\pi \cdot r\cdot (r+s)\end{alignedat}}}
Volumen eines geraden Kreiskegels
V
=
1
3
⋅
G
r
u
n
d
f
l
a
¨
c
h
e
⋅
H
o
¨
h
e
=
1
3
⋅
π
⋅
r
2
⋅
h
=
1
12
⋅
π
⋅
d
2
⋅
h
{\displaystyle {\begin{alignedat}{2}V&={\frac {1}{3}}\cdot \mathrm {Grundfl{\ddot {a}}che} \cdot \mathrm {H{\ddot {o}}he} \\&={\frac {1}{3}}\cdot \pi \cdot r^{2}\cdot h\\&={\frac {1}{12}}\cdot \pi \cdot d^{2}\cdot h\end{alignedat}}}
Ein gerader Kegelstumpf ist ein parallel zur Grundfläche abgeschnittener Kegel
Mantelfläche eines geraden Kegelstumpfs
A
M
=
π
⋅
s
⋅
(
r
1
+
r
2
)
{\displaystyle A_{M}=\pi \cdot s\cdot (r_{1}+r_{2})}
Oberfläche eines geraden Kegelstumpfs
A
O
=
π
⋅
r
1
2
+
π
⋅
r
2
2
+
A
M
=
π
⋅
r
1
2
+
π
⋅
r
2
2
+
π
⋅
s
⋅
(
r
1
+
r
2
)
{\displaystyle {\begin{alignedat}{2}A_{O}&=\pi \cdot r_{1}^{2}+\pi \cdot r_{2}^{2}+A_{M}\\&=\pi \cdot r_{1}^{2}+\pi \cdot r_{2}^{2}+\pi \cdot s\cdot (r_{1}+r_{2})\end{alignedat}}}
Volumen eines geraden Kegelstumpfs
V
=
1
3
⋅
π
⋅
h
⋅
(
r
1
2
+
r
1
⋅
r
2
+
r
2
2
)
{\displaystyle V={\frac {1}{3}}\cdot \pi \cdot h\cdot \left(r_{1}^{2}+r_{1}\cdot r_{2}+r_{2}^{2}\right)}
Zinsfuß:
p
{\displaystyle p}
Zinssatz:
i
=
p
100
{\displaystyle i={\frac {p}{100}}}
Aufzinsungsfaktor:
r
=
1
+
i
{\displaystyle r=1+i}
Abzinsungsfaktor (Diskontierungsfaktor):
v
=
1
r
{\displaystyle v={\frac {1}{r}}}
Vorschüssiger Zins (Diskontrate):
d
=
1
−
v
{\displaystyle d=1-v}
Anfangskapital:
K
0
{\displaystyle K_{0}}
Endkapital (nach
n
{\displaystyle n}
K
n
{\displaystyle K_{n}}
Dekursive Zinsen:
K
n
=
K
0
⋅
r
n
{\displaystyle K_{n}=K_{0}\cdot r^{n}}
Antizipative Zinsen:
K
0
=
K
n
⋅
v
n
{\displaystyle K_{0}=K_{n}\cdot v^{n}}
Dekursive gemischte Verzinsung:
K
n
=
K
0
⋅
r
n
⋅
(
1
+
T
360
⋅
i
)
{\displaystyle K_{n}=K_{0}\cdot r^{n}\cdot \left(1+{\frac {T}{360}}\cdot i\right)}
Antizipative gemischte Verzinsung:
K
0
=
K
n
⋅
v
n
⋅
(
1
−
T
360
⋅
d
)
{\displaystyle K_{0}=K_{n}\cdot v^{n}\cdot \left(1-{\frac {T}{360}}\cdot d\right)}
Effektiver Zinssatz:
i
{\displaystyle i}
Konformer Zinssatz:
i
[
m
]
=
1
+
i
m
−
1
⟺
(
1
+
i
[
m
]
)
m
=
1
+
i
{\displaystyle i^{[m]}={\sqrt[{m}]{1+i}}-1\iff \left(1+i^{[m]}\right)^{m}=1+i}
Proportionaler Zinssatz:
i
⟨
m
⟩
=
i
m
⟺
1
+
m
⋅
i
⟨
m
⟩
=
1
+
i
{\displaystyle i^{\langle m\rangle }={\frac {i}{m}}\iff 1+m\cdot i^{\langle m\rangle }=1+i}
Nomineller Zinssatz:
i
(
m
)
=
m
⋅
i
[
m
]
⟺
(
1
+
i
(
m
)
m
)
m
=
1
+
i
{\displaystyle i^{(m)}=m\cdot i^{[m]}\iff \left(1+{\frac {i^{(m)}}{m}}\right)^{m}=1+i}
Kontinuierlicher Zinssatz:
ϱ
=
lim
m
→
∞
i
(
m
)
=
i
(
∞
)
=
log
(
1
+
i
)
=
log
(
r
)
{\displaystyle \varrho =\lim _{m\to \infty }i^{(m)}=i^{(\infty )}=\log(1+i)=\log(r)}
Hierbei gelten folgende Ungleichungen:
i
[
m
]
<
i
⟨
m
⟩
ϱ
<
i
(
m
)
<
i
{\displaystyle i^{[m]}<i^{\langle m\rangle }\qquad \varrho <i^{(m)}<i\,}
Ein Kredit
K
0
{\displaystyle K_{0}}
n
{\displaystyle n}
i
{\displaystyle i}
und durch die Annuität
A
{\displaystyle A}
K
n
{\displaystyle K_{n}}
Die Fälligkeit
F
∈
{
0
,
1
}
{\displaystyle F\in \{0,1\}}
0
{\displaystyle 0}
1
{\displaystyle 1}
Aus der Rekursion
K
m
+
1
=
K
m
⋅
r
−
A
⋅
r
F
{\displaystyle K_{m+1}=K_{m}\cdot r-A\cdot r^{F}}
K
n
=
K
0
⋅
r
n
−
A
⋅
r
n
−
1
i
⋅
r
F
{\displaystyle K_{n}=K_{0}\cdot r^{n}-A\cdot {\frac {r^{n}-1}{i}}\cdot r^{F}}
A
=
i
r
F
⋅
K
0
⋅
r
n
−
K
n
r
n
−
1
{\displaystyle A={\frac {i}{r^{F}}}\cdot {\frac {K_{0}\cdot r^{n}-K_{n}}{r^{n}-1}}}
In Excel gibt es die Funktion RMZ (Regelmäßige Zahlung)
RMZ(Zins;Zzr;Bw;Zw;F)
=
Zins
(
1
+
Zins
)
F
⋅
Bw
⋅
(
1
+
Zins
)
Zzr
−
Zw
(
1
+
Zins
)
Zzr
−
1
{\displaystyle {\text{RMZ(Zins;Zzr;Bw;Zw;F)}}={\frac {\text{Zins}}{(1+{\text{Zins}})^{\text{F}}}}\cdot {\frac {{\text{Bw}}\cdot (1+{\text{Zins}})^{\text{Zzr}}-{\text{Zw}}}{(1+{\text{Zins}})^{\text{Zzr}}-1}}}
E
n
=
R
⋅
r
n
−
1
i
{\displaystyle E_{n}=R\cdot {\frac {r^{n}-1}{i}}}
E
n
=
R
⋅
r
⋅
r
n
−
1
i
{\displaystyle E_{n}=R\cdot r\cdot {\frac {r^{n}-1}{i}}}
I
=
E
S
{\displaystyle I={\frac {E}{S}}}
E
{\displaystyle E}
S
{\displaystyle S}
x
{\displaystyle x}
ℓ
x
{\displaystyle \ell _{x}}
x
{\displaystyle x}
d
x
=
ℓ
x
−
ℓ
x
+
1
{\displaystyle d_{x}=\ell _{x}-\ell _{x+1}}
x
{\displaystyle x}
p
x
=
ℓ
x
+
1
ℓ
x
{\displaystyle p_{x}={\frac {\ell _{x+1}}{\ell _{x}}}}
n
{\displaystyle n}
x
{\displaystyle x}
n
p
x
=
p
x
⋅
p
x
+
1
⋯
p
x
+
n
−
1
=
ℓ
x
+
n
ℓ
x
{\displaystyle {}_{n}p_{x}=p_{x}\cdot p_{x+1}\dotsm p_{x+n-1}={\frac {\ell _{x+n}}{\ell _{x}}}}
x
{\displaystyle x}
q
x
=
1
−
p
x
=
d
x
ℓ
x
{\displaystyle q_{x}=1-p_{x}={\frac {d_{x}}{\ell _{x}}}}
n
{\displaystyle n}
x
{\displaystyle x}
n
q
x
=
1
−
n
p
x
{\displaystyle {}_{n}q_{x}=1-{}_{n}p_{x}}
x
{\displaystyle x}
e
x
=
ℓ
x
+
ℓ
x
+
1
+
⋯
+
ℓ
ω
ℓ
x
−
1
2
{\displaystyle e_{x}={\frac {\ell _{x}+\ell _{x+1}+\dotsb +\ell _{\omega }}{\ell _{x}}}-{\frac {1}{2}}}
n
+
k
p
x
=
k
p
x
⋅
n
p
x
+
k
{\displaystyle {}_{n+k}p_{x}={}_{k}p_{x}\cdot {}_{n}p_{x+k}}
Beweis
n
+
k
p
x
=
ℓ
x
+
n
+
k
ℓ
x
=
ℓ
x
+
k
ℓ
x
⋅
ℓ
x
+
n
+
k
ℓ
x
+
k
=
k
p
x
⋅
n
p
x
+
k
{\displaystyle {}_{n+k}p_{x}={\frac {\ell _{x+n+k}}{\ell _{x}}}={\frac {\ell _{x+k}}{\ell _{x}}}\cdot {\frac {\ell _{x+n+k}}{\ell _{x+k}}}={}_{k}p_{x}\cdot {}_{n}p_{x+k}}
q
x
mon
>
q
x
12
{\displaystyle q_{x}^{\text{mon}}>{\frac {q_{x}}{12}}}
Beweis
1
−
q
x
=
p
x
=
(
p
x
mon
)
12
=
(
1
−
q
x
mon
)
12
>
1
−
12
q
x
mon
{\displaystyle 1-q_{x}=p_{x}=\left(p_{x}^{\text{mon}}\right)^{12}=\left(1-q_{x}^{\text{mon}}\right)^{12}>1-12q_{x}^{\text{mon}}}
Bernoullische Ungleichung )
⇒
q
x
<
12
q
x
mon
⇒
q
x
mon
>
q
x
12
{\displaystyle \Rightarrow \,q_{x}<12q_{x}^{\text{mon}}\,\Rightarrow \,q_{x}^{\text{mon}}>{\frac {q_{x}}{12}}}
Diskontierte Tote:
C
x
=
d
x
⋅
v
x
+
1
{\displaystyle C_{x}=d_{x}\cdot v^{x+1}}
Diskontierte Lebende:
D
x
=
ℓ
x
⋅
v
x
{\displaystyle D_{x}=\ell _{x}\cdot v^{x}}
Aufsummierte diskontierte Tote:
M
x
=
C
x
+
C
x
+
1
+
⋯
+
C
ω
{\displaystyle M_{x}=C_{x}+C_{x+1}+\dotsb +C_{\omega }}
Aufsummierte diskontierte Lebende:
N
x
=
D
x
+
D
x
+
1
+
⋯
+
D
ω
{\displaystyle N_{x}=D_{x}+D_{x+1}+\dotsb +D_{\omega }}
Doppelt aufsummierte diskontierte Tote:
R
x
=
M
x
+
M
x
+
1
+
⋯
+
M
ω
{\displaystyle R_{x}=M_{x}+M_{x+1}+\dotsb +M_{\omega }}
Doppelt aufsummierte diskontierte Lebende:
S
x
=
N
x
+
N
x
+
1
+
⋯
+
N
ω
{\displaystyle S_{x}=N_{x}+N_{x+1}+\dotsb +N_{\omega }}
n Jahre für einen x -Jährigen[ Bearbeiten ]
n
E
x
=
n
p
x
⋅
v
n
=
D
x
+
n
D
x
{\displaystyle {}_{n}E_{x}={}_{n}p_{x}\cdot v^{n}={\frac {D_{x+n}}{D_{x}}}}
Beweis
n
E
x
=
n
p
x
⋅
v
n
=
ℓ
x
+
n
ℓ
x
⋅
v
x
+
n
v
x
=
D
x
+
n
D
x
{\displaystyle {}_{n}E_{x}={}_{n}p_{x}\cdot v^{n}={\frac {\ell _{x+n}}{\ell _{x}}}\cdot {\frac {v^{x+n}}{v^{x}}}={\frac {D_{x+n}}{D_{x}}}}
n -jährige Zeitrente mit m Jahren Aufschubzeit[ Bearbeiten ]
m
|
a
¨
n
¯
|
=
∑
k
=
0
n
−
1
v
m
+
k
=
v
m
−
v
m
+
n
d
{\displaystyle {}_{m|}{\ddot {a}}_{{\overline {n}}|}=\sum _{k=0}^{n-1}v^{m+k}={\frac {v^{m}-v^{m+n}}{d}}}
n -jährige Zeitrente mit m Jahren Aufschubzeit[ Bearbeiten ]
m
|
a
n
¯
|
=
∑
k
=
1
n
v
m
+
k
=
v
m
−
v
m
+
n
i
{\displaystyle {}_{m|}a_{{\overline {n}}|}=\sum _{k=1}^{n}v^{m+k}={\frac {v^{m}-v^{m+n}}{i}}}
n -jährige Rente für einen x -Jährigen mit m Jahren Aufschubzeit[ Bearbeiten ]
m
|
a
¨
x
,
n
¯
|
=
∑
k
=
0
n
−
1
m
+
k
p
x
⋅
v
m
+
k
=
N
x
+
m
−
N
x
+
m
+
n
D
x
{\displaystyle {}_{m|}{\ddot {a}}_{x,{\overline {n}}|}=\sum _{k=0}^{n-1}{}_{m+k}p_{x}\cdot v^{m+k}={\frac {N_{x+m}-N_{x+m+n}}{D_{x}}}}
Beweis
m
|
a
¨
x
,
n
¯
|
=
∑
k
=
0
n
−
1
m
+
k
p
x
⋅
v
m
+
k
=
∑
k
=
0
n
−
1
ℓ
x
+
m
+
k
ℓ
x
⋅
v
x
+
m
+
k
v
x
=
1
D
x
∑
k
=
0
n
−
1
D
x
+
m
+
k
=
N
x
+
m
−
N
x
+
m
+
n
D
x
{\displaystyle {}_{m|}{\ddot {a}}_{x,{\overline {n}}|}=\sum _{k=0}^{n-1}{}_{m+k}p_{x}\cdot v^{m+k}=\sum _{k=0}^{n-1}{\frac {\ell _{x+m+k}}{\ell _{x}}}\cdot {\frac {v^{x+m+k}}{v^{x}}}={\frac {1}{D_{x}}}\sum _{k=0}^{n-1}D_{x+m+k}={\frac {N_{x+m}-N_{x+m+n}}{D_{x}}}}
n -jährige Rente für einen x -Jährigen mit m Jahren Aufschubzeit[ Bearbeiten ]
m
|
a
x
,
n
¯
|
=
∑
k
=
1
n
m
+
k
p
x
⋅
v
m
+
k
=
N
x
+
m
+
1
−
N
x
+
m
+
n
+
1
D
x
{\displaystyle {}_{m|}a_{x,{\overline {n}}|}=\sum _{k=1}^{n}{}_{m+k}p_{x}\cdot v^{m+k}={\frac {N_{x+m+1}-N_{x+m+n+1}}{D_{x}}}}
Beweis
m
|
a
x
,
n
¯
|
=
∑
k
=
1
n
m
+
k
p
x
⋅
v
m
+
k
=
∑
k
=
1
n
ℓ
x
+
m
+
k
ℓ
x
⋅
v
x
+
m
+
k
v
x
=
1
D
x
∑
k
=
1
n
D
x
+
m
+
k
=
N
x
+
m
+
1
−
N
x
+
m
+
n
+
1
D
x
{\displaystyle {}_{m|}a_{x,{\overline {n}}|}=\sum _{k=1}^{n}{}_{m+k}p_{x}\cdot v^{m+k}=\sum _{k=1}^{n}{\frac {\ell _{x+m+k}}{\ell _{x}}}\cdot {\frac {v^{x+m+k}}{v^{x}}}={\frac {1}{D_{x}}}\sum _{k=1}^{n}D_{x+m+k}={\frac {N_{x+m+1}-N_{x+m+n+1}}{D_{x}}}}
n -jährige Risikolebensversicherung für einen x -Jährigen mit m Jahren Aufschubzeit[ Bearbeiten ] Gemeint ist, dass in den ersten
m
{\displaystyle m}
und nicht, dass Hinterbliebene bei Eintritt des Versicherungsfalles m Jahre auf ihre Leistung warten müssen.
m
|
n
A
x
=
∑
k
=
0
n
−
1
m
+
k
p
x
⋅
q
x
+
m
+
k
⋅
v
m
+
k
+
1
=
M
x
+
m
−
M
x
+
m
+
n
D
x
{\displaystyle {}_{m|n}A_{x}=\sum _{k=0}^{n-1}{}_{m+k}p_{x}\cdot q_{x+m+k}\cdot v^{m+k+1}={\frac {M_{x+m}-M_{x+m+n}}{D_{x}}}}
Beweis
m
|
n
A
x
=
∑
k
=
0
n
−
1
m
+
k
p
x
⋅
q
x
+
m
+
k
⋅
v
m
+
k
+
1
=
∑
k
=
0
n
−
1
ℓ
x
+
m
+
k
ℓ
x
⋅
d
x
+
m
+
k
ℓ
x
+
m
+
k
⋅
v
m
+
k
+
1
{\displaystyle {}_{m|n}A_{x}=\sum _{k=0}^{n-1}\!_{m+k}p_{x}\cdot q_{x+m+k}\cdot v^{m+k+1}=\sum _{k=0}^{n-1}{\frac {\ell _{x+m+k}}{\ell _{x}}}\cdot {\frac {d_{x+m+k}}{\ell _{x+m+k}}}\cdot v^{m+k+1}}
=
∑
k
=
0
n
−
1
d
x
+
m
+
k
ℓ
x
⋅
v
x
+
m
+
k
+
1
v
x
=
1
D
x
⋅
∑
k
=
0
n
−
1
C
x
+
m
+
k
=
M
x
+
m
−
M
x
+
m
+
n
D
x
{\displaystyle =\sum _{k=0}^{n-1}{\frac {d_{x+m+k}}{\ell _{x}}}\cdot {\frac {v^{x+m+k+1}}{v^{x}}}={\frac {1}{D_{x}}}\cdot \sum _{k=0}^{n-1}C_{x+m+k}={\frac {M_{x+m}-M_{x+m+n}}{D_{x}}}}
n -jährige gemischte Versicherung für einen x -Jährigen[ Bearbeiten ]
A
x
,
n
¯
|
=
|
n
A
x
+
n
E
x
=
M
x
−
M
x
+
n
D
x
+
D
x
+
n
D
x
=
1
−
(
1
−
v
)
⋅
a
¨
x
,
n
¯
|
{\displaystyle A_{x,{\overline {n}}|}={}_{|n}A_{x}+{}_{n}E_{x}={\frac {M_{x}-M_{x+n}}{D_{x}}}+{\frac {D_{x+n}}{D_{x}}}=1-(1-v)\cdot {\ddot {a}}_{x,{\overline {n}}|}}
Beweis
In der Formel
A
x
,
n
¯
|
=
|
n
A
x
+
n
E
x
{\displaystyle A_{x,{\overline {n}}|}={}_{|n}A_{x}+{}_{n}E_{x}}
|
n
A
x
{\displaystyle {}_{|n}A_{x}}
v
a
¨
x
,
n
¯
|
−
a
x
,
n
¯
|
{\displaystyle v\,{\ddot {a}}_{x,{\overline {n}}|}-a_{x,{\overline {n}}|}}
A
x
,
n
¯
|
=
v
a
¨
x
,
n
¯
|
−
(
a
x
,
n
¯
|
−
n
E
x
)
{\displaystyle A_{x,{\overline {n}}|}=v\,{\ddot {a}}_{x,{\overline {n}}|}-\left(a_{x,{\overline {n}}|}-{}_{n}E_{x}\right)}
1
+
a
x
,
n
¯
|
=
a
¨
x
,
n
¯
|
+
n
E
x
{\displaystyle 1+a_{x,{\overline {n}}|}={\ddot {a}}_{x,{\overline {n}}|}+{}_{n}E_{x}}
a
x
,
n
¯
|
−
n
E
x
=
a
¨
x
,
n
¯
|
−
1
{\displaystyle a_{x,{\overline {n}}|}-{}_{n}E_{x}={\ddot {a}}_{x,{\overline {n}}|}-1}
A
x
,
n
¯
|
=
v
a
¨
x
,
n
¯
|
−
(
a
¨
x
,
n
¯
|
−
1
)
=
1
−
(
1
−
v
)
⋅
a
¨
x
,
n
¯
|
{\displaystyle A_{x,{\overline {n}}|}=v\,{\ddot {a}}_{x,{\overline {n}}|}-\left({\ddot {a}}_{x,{\overline {n}}|}-1\right)=1-(1-v)\cdot {\ddot {a}}_{x,{\overline {n}}|}}
n -jährige Rente für einen x -Jährigen[ Bearbeiten ]
(
I
a
¨
)
x
,
n
¯
|
=
∑
k
=
0
n
−
1
k
p
x
⋅
(
k
+
1
)
⋅
v
k
=
S
x
−
S
x
+
n
−
n
⋅
N
x
+
n
D
x
{\displaystyle (I{\ddot {a}})_{x,{\overline {n}}|}=\sum _{k=0}^{n-1}{}_{k}p_{x}\cdot (k+1)\cdot v^{k}={\frac {S_{x}-S_{x+n}-n\cdot N_{x+n}}{D_{x}}}}
n -jährige Rente für einen x -Jährigen[ Bearbeiten ]
(
I
a
)
x
,
n
¯
|
=
∑
k
=
1
n
k
p
x
⋅
k
⋅
v
k
=
S
x
+
1
−
S
x
+
n
+
1
−
n
⋅
N
x
+
n
+
1
D
x
{\displaystyle (Ia)_{x,{\overline {n}}|}=\sum _{k=1}^{n}{}_{k}p_{x}\cdot k\cdot v^{k}={\frac {S_{x+1}-S_{x+n+1}-n\cdot N_{x+n+1}}{D_{x}}}}
n -jährige Risikolebensversicherung für einen x -Jährigen[ Bearbeiten ]
|
n
(
I
A
)
x
=
∑
k
=
0
n
−
1
k
p
x
⋅
q
x
+
k
⋅
(
k
+
1
)
⋅
v
k
+
1
=
R
x
−
R
x
+
n
−
n
⋅
M
x
+
n
D
x
{\displaystyle {}_{|n}(IA)_{x}=\sum _{k=0}^{n-1}{}_{k}p_{x}\cdot q_{x+k}\cdot (k+1)\cdot v^{k+1}={\frac {R_{x}-R_{x+n}-n\cdot M_{x+n}}{D_{x}}}}
m
V
x
(
re
)
=
m
V
x
(
pro
)
{\displaystyle {}_{m}V_{x}^{({\text{re}})}={}_{m}V_{x}^{({\text{pro}})}}
Beweis
Bei einem
n
{\displaystyle n}
k
{\displaystyle k}
k
{\displaystyle k}
B
k
{\displaystyle B_{k}}
k
{\displaystyle k}
x
+
k
−
1
{\displaystyle x+k-1}
k
{\displaystyle k}
T
k
{\displaystyle T_{k}}
k
{\displaystyle k}
(
k
+
1
)
{\displaystyle (k+1)}
E
k
{\displaystyle E_{k}}
(
m
=
0
)
{\displaystyle (m=0)}
0
B
x
(
pro
)
=
∑
k
=
0
n
−
1
k
p
x
⋅
B
k
+
1
⋅
v
k
{\displaystyle {}_{0}B_{x}^{({\text{pro}})}=\sum _{k=0}^{n-1}\,_{k}p_{x}\cdot B_{k+1}\cdot v^{k}}
0
T
x
(
pro
)
=
∑
k
=
0
n
−
1
k
p
x
⋅
q
x
+
k
⋅
T
k
+
1
⋅
v
k
+
1
{\displaystyle {}_{0}T_{x}^{({\text{pro}})}=\sum _{k=0}^{n-1}\,_{k}p_{x}\cdot q_{x+k}\cdot T_{k+1}\cdot v^{k+1}}
0
E
x
(
pro
)
=
∑
k
=
0
n
−
1
k
+
1
p
x
⋅
E
k
+
1
⋅
v
k
+
1
{\displaystyle {}_{0}E_{x}^{({\text{pro}})}=\sum _{k=0}^{n-1}{}_{k+1}p_{x}\cdot E_{k+1}\cdot v^{k+1}}
B
k
,
T
k
,
E
k
{\displaystyle B_{k},T_{k},E_{k}}
0
B
x
(
pro
)
=
0
T
x
(
pro
)
+
0
E
x
(
pro
)
{\displaystyle {}_{0}B_{x}^{({\text{pro}})}={}_{0}T_{x}^{({\text{pro}})}+{}_{0}E_{x}^{({\text{pro}})}}
m
{\displaystyle m}
m
B
x
(
pro
)
=
r
m
∑
k
=
m
n
−
1
k
p
x
⋅
B
k
+
1
⋅
v
k
=
r
m
∑
k
=
0
n
−
m
−
1
m
+
k
p
x
⋅
B
m
+
k
+
1
⋅
v
m
+
k
=
m
p
x
∑
k
=
0
n
−
m
−
1
k
p
x
+
m
⋅
B
m
+
k
+
1
⋅
v
k
{\displaystyle {}_{m}B_{x}^{({\text{pro}})}=r^{m}\sum _{k=m}^{n-1}\;_{k}p_{x}\cdot B_{k+1}\cdot v^{k}=r^{m}\sum _{k=0}^{n-m-1}{}_{m+k}p_{x}\cdot B_{m+k+1}\cdot v^{m+k}=\;_{m}p_{x}\sum _{k=0}^{n-m-1}{}_{k}p_{x+m}\cdot B_{m+k+1}\cdot v^{k}}
m
T
x
(
pro
)
=
r
m
∑
k
=
m
n
−
1
k
p
x
⋅
q
x
+
k
⋅
T
k
+
1
⋅
v
k
+
1
=
r
m
∑
k
=
0
n
−
m
−
1
m
+
k
p
x
⋅
q
m
+
k
⋅
T
m
+
k
+
1
⋅
v
m
+
k
+
1
=
m
p
x
∑
k
=
0
n
−
m
−
1
k
p
x
+
m
⋅
q
x
+
m
+
k
⋅
T
m
+
k
+
1
⋅
v
k
+
1
{\displaystyle {}_{m}T_{x}^{({\text{pro}})}=r^{m}\sum _{k=m}^{n-1}\;_{k}p_{x}\cdot q_{x+k}\cdot T_{k+1}\cdot v^{k+1}=r^{m}\sum _{k=0}^{n-m-1}{}_{m+k}p_{x}\cdot q_{m+k}\cdot T_{m+k+1}\cdot v^{m+k+1}={}_{m}p_{x}\sum _{k=0}^{n-m-1}{}_{k}p_{x+m}\cdot q_{x+m+k}\cdot T_{m+k+1}\cdot v^{k+1}}
m
E
x
(
pro
)
=
r
m
∑
k
=
m
n
−
1
k
+
1
p
x
⋅
E
k
+
1
⋅
v
k
+
1
=
r
m
∑
k
=
0
n
−
m
−
1
m
+
k
+
1
p
x
⋅
E
m
+
k
+
1
⋅
v
m
+
k
+
1
=
m
p
x
∑
k
=
0
n
−
m
−
1
k
+
1
p
x
+
m
⋅
E
m
+
k
+
1
⋅
v
k
+
1
{\displaystyle {}_{m}E_{x}^{({\text{pro}})}=r^{m}\sum _{k=m}^{n-1}{}_{k+1}p_{x}\cdot E_{k+1}\cdot v^{k+1}=r^{m}\sum _{k=0}^{n-m-1}{}_{m+k+1}p_{x}\cdot E_{m+k+1}\cdot v^{m+k+1}={}_{m}p_{x}\sum _{k=0}^{n-m-1}{}_{k+1}p_{x+m}\cdot E_{m+k+1}\cdot v^{k+1}}
m
{\displaystyle m}
m
B
x
(
re
)
=
r
m
∑
k
=
0
m
−
1
k
p
x
⋅
B
k
+
1
⋅
v
k
{\displaystyle {}_{m}B_{x}^{({\text{re}})}=r^{m}\sum _{k=0}^{m-1}{}_{k}p_{x}\cdot B_{k+1}\cdot v^{k}}
m
T
x
(
re
)
=
r
m
∑
k
=
0
m
−
1
k
p
x
⋅
q
x
+
k
⋅
T
k
+
1
⋅
v
k
+
1
{\displaystyle {}_{m}T_{x}^{({\text{re}})}=r^{m}\sum _{k=0}^{m-1}{}_{k}p_{x}\cdot q_{x+k}\cdot T_{k+1}\cdot v^{k+1}}
m
E
x
(
re
)
=
r
m
∑
k
=
0
m
−
1
k
+
1
p
x
⋅
E
k
+
1
⋅
v
k
+
1
{\displaystyle {}_{m}E_{x}^{({\text{re}})}=r^{m}\sum _{k=0}^{m-1}{}_{k+1}p_{x}\cdot E_{k+1}\cdot v^{k+1}}
m
V
x
(
pro
)
=
m
T
x
(
pro
)
+
m
E
x
(
pro
)
−
m
B
x
(
pro
)
{\displaystyle {}_{m}V_{x}^{({\text{pro}})}={}_{m}T_{x}^{({\text{pro}})}+{}_{m}E_{x}^{({\text{pro}})}-{}_{m}B_{x}^{({\text{pro}})}}
m
V
x
(
re
)
=
m
B
x
(
re
)
−
m
T
x
(
re
)
−
m
E
x
(
re
)
{\displaystyle {}_{m}V_{x}^{({\text{re}})}={}_{m}B_{x}^{({\text{re}})}-{}_{m}T_{x}^{({\text{re}})}-{}_{m}E_{x}^{({\text{re}})}}
m
B
x
(
re
)
+
m
B
x
(
pro
)
=
m
T
x
(
re
)
+
m
T
x
(
pro
)
+
m
E
x
(
re
)
+
m
E
x
(
pro
)
{\displaystyle {}_{m}B_{x}^{({\text{re}})}+{}_{m}B_{x}^{({\text{pro}})}={}_{m}T_{x}^{({\text{re}})}+{}_{m}T_{x}^{({\text{pro}})}+{}_{m}E_{x}^{({\text{re}})}+{}_{m}E_{x}^{({\text{pro}})}}
m
B
x
(
re
)
−
m
T
x
(
re
)
−
m
E
x
(
re
)
=
m
T
x
(
pro
)
+
m
E
x
(
pro
)
−
m
B
x
(
pro
)
{\displaystyle {}_{m}B_{x}^{({\text{re}})}-{}_{m}T_{x}^{({\text{re}})}-{}_{m}E_{x}^{({\text{re}})}={}_{m}T_{x}^{({\text{pro}})}+{}_{m}E_{x}^{({\text{pro}})}-{}_{m}B_{x}^{({\text{pro}})}}
m
V
x
(
re
)
=
m
V
x
(
pro
)
{\displaystyle {}_{m}V_{x}^{({\text{re}})}={}_{m}V_{x}^{({\text{pro}})}}









































































































































![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)





![{\displaystyle (a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a6969e731af335df071e247ee7fb331cd1a57ae)
































![{\displaystyle [F(x)]_{x=a}^{x=b}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7edf83c5754718a18d0fded7386fddf940e0d0c4)








}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f0b2edebc9d77489ccfbac6731378e12576d73d0)


}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8137563fb1ef2613d67016acd0ca5e9237123ac7)



































![{\displaystyle {\sqrt[{4}]{81}}=3}](https://wikimedia.org/api/rest_v1/media/math/render/svg/44d91764f62522cec7024ef6481f0b83305f17e9)
![{\displaystyle {\sqrt[{b}]{c}}=a}](https://wikimedia.org/api/rest_v1/media/math/render/svg/99de022e623f319469c66014aac012b2bab337e8)





























































































![{\displaystyle {\sqrt[{r}]{a}}:=\exp \left({\frac {\ln(a)}{r}}\right)=a^{1/r}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1f76a3addcdbfa058d6316ffa632a93e36b4c076)








![{\displaystyle ({\sqrt[{r}]{a}})^{s}={\sqrt[{r}]{a^{s}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c1c24b06c65a9774b06aa4831f41b33391650a19)
![{\displaystyle ({\sqrt[{r}]{a\,b}})^{s}={\sqrt[{r}]{a^{s}}}{\sqrt[{r}]{b^{s}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4273b95face8f760adf12555820668db736d05f9)
![{\displaystyle \left({\sqrt[{r}]{\frac {a}{b}}}\right)^{s}={\frac {\sqrt[{r}]{a^{s}}}{\sqrt[{r}]{b^{s}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/47600c8e984ce4cec9d8a92cc3f261729f42a653)
![{\displaystyle {\sqrt[{r}]{a^{s}}}=a^{s/r}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fa9452cb363d032fa2062f6bf737ca1278eabdeb)
![{\displaystyle {\sqrt[{r}]{a^{r}}}=a}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c05318f62d7868421622f5d7e7800bb67d769978)
![{\displaystyle {\sqrt[{-r}]{a}}={\frac {1}{\sqrt[{r}]{a}}}={\sqrt[{r}]{\frac {1}{a}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5dbcfda714560a1084f59d66f2d493c573d0666f)

















![{\displaystyle r\neq 0\implies \log({\sqrt[{r}]{x}})={\frac {1}{r}}\,\log(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c95b47235cd7dcd680e6e581df4bfe5e0a6594fc)
































































































































![{\displaystyle z=w^{n}\iff w={\sqrt[{n}]{|z|}}\exp {\Big (}{\frac {\mathrm {i} \varphi +2k\pi \mathrm {i} }{n}}{\Big )},\;k\in \{0,1,\ldots ,n-1\}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a3bea17a7d314afd793ddaf022d01dc78fe6ffb1)
![{\displaystyle {\sqrt[{n}]{z}}={\sqrt[{n}]{|z|}}\exp {\Big (}{\frac {\mathrm {i} \varphi }{n}}{\Big )}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/227dd560e1f2d20d6625adc5234e19d73047676e)

![{\displaystyle {\sqrt[{x}]{z}}:=\exp {\bigg (}{\frac {\ln(z)}{x}}{\bigg )}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/38a68ab832b5581a372562e9d462e18087cf1b2f)















































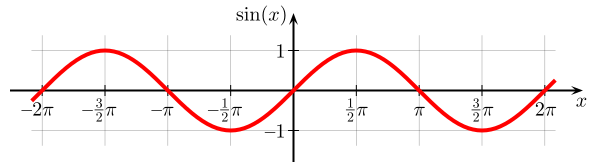
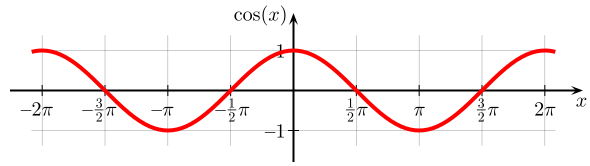

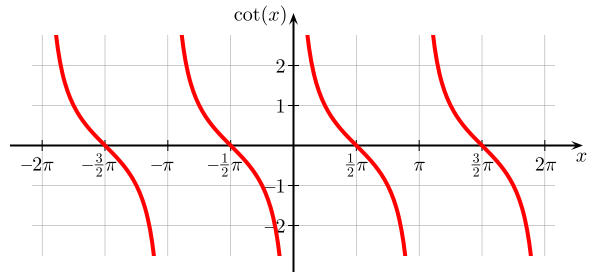



















































































































![{\displaystyle x\in [0,2\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8cedb963595290bb4f2f9e0b1e140ba8432ccd8b)

![{\displaystyle x\in [-\pi ,\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bb1d5b7c7f8c8190cb14884785f2aa663f27feff)

![{\displaystyle x\in ]-\pi ,\pi [}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a2dfb61908ceb5f8087682d464288f2f87b5ff5f)










![{\displaystyle \sin x\;\sin y\;\sin z={\frac {1}{4}}\left[\sin(x+y-z)+\sin(y+z-x)+\sin(z+x-y)-\sin(x+y+z)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/59d8ebb9b49c3d0eef86b75f53db923afd399af8)
![{\displaystyle \cos x\;\cos y\;\cos z={\frac {1}{4}}\left[\cos(x+y-z)+\cos(y+z-x)+\cos(z+x-y)+\cos(x+y+z)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2531ad917e8fd506876febc9afec3be9cfe7e685)
![{\displaystyle \sin x\;\sin y\;\cos z={\frac {1}{4}}\left[-\cos(x+y-z)+\cos(y+z-x)+\cos(z+x-y)-\cos(x+y+z)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5d89dfcd5f8887d058fc58d149fa9a3aca21a32a)
![{\displaystyle \sin x\;\cos y\;\cos z={\frac {1}{4}}\left[\sin(x+y-z)-\sin(y+z-x)+\sin(z+x-y)+\sin(x+y+z)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4742f0e8097b1d543dc9230d0244ab81b5f37888)










































![{\displaystyle \arctan(z)+\operatorname {arccot}(z)=\left\{{\begin{matrix}{\frac {\pi }{2}}&&\operatorname {Re} (z)>0&&z\in \mathrm {i} \,]-1,0]&&z\in \mathrm {i} \,]1,\infty [\\\\-{\frac {\pi }{2}}&&\operatorname {Re} (z)<0&&z\in \mathrm {i} \,]-\infty ,-1[&&z\in \mathrm {i} \,]0,1[\end{matrix}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4999e0495d3495e649c033b5e4f6d5b8978e767c)








































































![{\displaystyle \lim _{n\to \infty }{\frac {n}{\sqrt[{n}]{n!}}}=e}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9e67d9f7e2588c9b3d418f1107e9ea27b8f330ed)
![{\displaystyle {\sqrt[{n}]{a_{n}}}={\frac {{\sqrt[{n}]{n!}}\,\,e}{n\,{\sqrt[{2n}]{2\pi n}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a7f374bf6f30d710704bb55b16ce528b0d4c2de8)
![{\displaystyle \lim _{n\to \infty }{\sqrt[{2n}]{2\pi n}}=1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eb2543c120fa22ab641322f0f8509f775fba1f12)
![{\displaystyle \lim _{n\to \infty }{\frac {\sqrt[{n}]{n!}}{n}}\,e=1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4130fc79a8cd385df8bbae91ebbe54d776926203)



![{\displaystyle {\frac {e}{\sqrt[{n}]{n}}}<{\frac {n}{\sqrt[{n}]{n!}}}\,{\sqrt[{n}]{e}}<e}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b854a5418db4eae02addd58b00f820a809c75ec)

![{\displaystyle e\leq \lim _{n\to \infty }{\frac {n}{\sqrt[{n}]{n!}}}\leq e}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1950673ed0b6271e212328d47287065cc1e8d066)

![{\displaystyle \prod _{k=1}^{n}{\frac {4k^{2}-1}{4k^{2}}}=\prod _{k=1}^{n}{\frac {(2k-1)\cdot (2k+1)}{2k\cdot 2k}}={\frac {{\frac {(2n)!}{2^{n}\,n!}}\,\cdot \,{\frac {(2n)!}{2^{n}\,n!}}\,(2n+1)}{2^{n}\,n!\,\cdot \,2^{n}\,n!}}=(2n+1)\left[{\frac {(2n)!}{2^{2n}\,n!^{2}}}\right]^{2}=(2n+1)\left[{\frac {1}{2^{2n}}}{2n \choose n}\right]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/415fa17cd1528cda41c45b7f33c0732e899ff644)
![{\displaystyle \lim _{n\to \infty }(2n+1)\left[{\frac {1}{2^{2n}}}{2n \choose n}\right]^{2}=\prod _{k=1}^{\infty }{\frac {4k^{2}-1}{4k^{2}}}={\frac {2}{\pi }}\qquad {\text{(Wallis Produkt)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ca3d61110870b2c3773d0cce6e676e54f6843d0)




![{\displaystyle \lim _{n\to \infty }{\sqrt[{n}]{\frac {(\alpha n+\beta n)!}{(\alpha n)!\,(\beta n)!}}}={\frac {(\alpha +\beta )^{\alpha +\beta }}{\alpha ^{\alpha }\,\beta ^{\beta }}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/18ebd2f6c4a5d6a62ce1c79e78392309718291de)









![{\displaystyle \lim _{n\to \infty }\left[{\frac {(n+1)^{n+1}}{n^{n}}}-{\frac {n^{n}}{(n-1)^{n-1}}}\right]=e}](https://wikimedia.org/api/rest_v1/media/math/render/svg/01dafb48428a37143698050129588e4924196e9c)





























































































![{\displaystyle f:[a,b]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/b592d102ccd1ba134d401c5b3ea177baaba3ffac)





![{\displaystyle \int _{k-1}^{k}f(x)\,dx=\left[\left(x-k+{\frac {1}{2}}\right)f(x)\right]_{k-1}^{k}-\int _{k-1}^{k}\left(x-k+{\frac {1}{2}}\right)f'(x)\,dx={\frac {f(k)}{2}}+{\frac {f(k-1)}{2}}-\int _{k-1}^{k}B_{1}(x)\,f'(x)\,dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/94f13d78153c62a7794bfdd013520bca2e5a25eb)





![{\displaystyle =\left[{\frac {B_{n+1}(x)}{n+1}}\,f^{(n)}(x)\right]_{a}^{b}-\int _{a}^{b}{\frac {B_{n+1}(x)}{n+1}}\,f^{(n+1)}(x)\,dx={\frac {B_{n+1}}{n+1}}\left(f^{(n)}(b)-f^{(n)}(a)\right)-{\frac {1}{n+1}}\int _{a}^{b}B_{n+1}(x)\,f^{(n+1)}(x)\,dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/70b890900990c2fd44a105f5b8ca0600722e67fd)















































































































![{\displaystyle \varepsilon \in ]0,1[}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a7d5353c6315be28ee5c5633183b85910a6c1ccf)








![{\displaystyle \lim _{R\to \infty }\oint f\,dz=\int _{A_{\infty ,\varepsilon }}f\,dz+\int _{C_{\infty ,\varepsilon }}f\,dz=\int _{C_{\infty ,\varepsilon }}\left[f(z)-f(n+z)\right]\,dz}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b09bf9d2820c1147a5b13de7ee30f69492991b3a)

![{\displaystyle \int _{-\infty }^{\infty }\left[f{\Big (}n+(1+i)t{\Big )}-f{\Big (}(1+i)t{\Big )}\right]\,(1+i)\,dt}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6d2fe99112b0868d335ac676763d1d3271bf8ced)










![{\displaystyle \int _{i\mathbb {R} }\left[f(n+z)-f(z)\right]\,dz=\int _{-\infty }^{\infty }\left[f(n+it)-f(it)\right]\,i\,dt}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f7647ba029ebf441590a7940822f5e2fb5179b11)



















![{\displaystyle \prod _{k=0}^{n-1}\left[X+(-1)^{k}\,\sin \left({\frac {2k+1}{2n+1}}\cdot {\frac {\pi }{2}}\right)\right]={\frac {U_{n}(X)-(-1)^{n}\,U_{n-1}(X)}{2^{n}}}=:P_{n}(X)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/30c921e1d3061cc6a7289c7c00288d6f7faf7611)

![{\displaystyle P_{n}(0)=\prod _{k=0}^{n-1}\left[(-1)^{k}\,\sin \left({\frac {2k+1}{2n+1}}\cdot {\frac {\pi }{2}}\right)\right]={\frac {(-1)^{\frac {n\cdot (n-1)}{2}}}{2^{n}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6cbb94add3039937190f681032db86b94fa6a678)




![{\displaystyle \sum _{k=m}^{n}a_{k}\,\Delta b_{k}={\Big [}a_{k}\,b_{k}{\Big ]}_{m}^{n+1}-\sum _{k=m}^{n}\Delta a_{k}\,b_{k+1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/876712e5a29b0837044ea7c05cb99dad56c457a3)

![{\displaystyle \sum _{k=m}^{n}\left(a_{k}\,\Delta b_{k}+\Delta a_{k}\,b_{k+1}\right)={\Big [}a_{k}\,b_{k}{\Big ]}_{m}^{n+1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9cb6c2b808ee3cbe273c94aadc02b67c74458def)









![{\displaystyle S=\left[\sin {\frac {(2j+1)\pi }{2n}}\cdot \left\rfloor {\frac {j^{2}}{n}}\right\lfloor \,\,\,\right]_{0}^{n}-\sum _{j=0}^{n-1}\Delta \sin {\frac {(2j+1)\pi }{2n}}\cdot \left\rfloor {\frac {(j+1)^{2}}{n}}\right\lfloor }](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a5e09aeeda15109741a2c6f3292bd8966d2f416)







![{\displaystyle =\left[j\cdot \sin {\frac {(2j-1)\pi }{2n}}\right]_{0}^{n+1}-\sum _{j=0}^{n}\sin {\frac {(2j+1)\pi }{2n}}=-(n+1)\sin {\frac {\pi }{2n}}-\sum _{j=0}^{n}\sin {\frac {(2j+1)\pi }{2n}}=-n\sin {\frac {\pi }{2n}}-\sum _{j=0}^{n-1}\sin {\frac {(2j+1)\pi }{2n}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/86fb569100dfa2d68e04f14492715560c1ab926d)













![{\displaystyle F_{n}(z+1)={\frac {n^{nz}\,n^{n}\,\prod \limits _{k=0}^{n-1}\left[\left(z+{\frac {k}{n}}\right)\,\Gamma \left(z+{\frac {k}{n}}\right)\right]}{\prod \limits _{k=0}^{n-1}(nz+k)\,\Gamma (nz)}}=F_{n}(z)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7573800f412e0ecf1dc8ec6f9036ae1f57d607ef)







![{\displaystyle \psi \left(z+{\frac {k}{n}}\right)+\gamma =n\int _{0}^{1}\left[{\frac {t^{n-1}}{1-t^{n}}}-{\frac {t^{nz+k-1}}{1-t^{n}}}\right]dt}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a4dadc62847cc7b822a717e6ca0e8537661fcdc1)
![{\displaystyle \sum _{k=0}^{n-1}\psi \left(z+{\frac {k}{n}}\right)+n\gamma =n\int _{0}^{1}\left[{\frac {nt^{n-1}}{1-t^{n}}}-{\frac {t^{nz-1}}{1-t}}\right]dt}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4b9cc30d87af84720069f403f3f040ea902cfd64)

![{\displaystyle \sum _{k=0}^{n-1}\psi \left(z+{\frac {k}{n}}\right)-n\psi (nz)=n\int _{0}^{1}\left[{\frac {n\,t^{n-1}}{1-t^{n}}}-{\frac {1}{1-t}}\right]dt=n{\Big [}\log(1-t^{n})-\log(1-t){\Big ]}_{0}^{1}=-n\log n}](https://wikimedia.org/api/rest_v1/media/math/render/svg/515b6bf3078b1d722ce8cf679a9e99e3a851afc1)
















![{\displaystyle Re(z)\in [a,b],0<a}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9388a9aaa6c7142882e51450c79aaf429ed7e293)


















![{\displaystyle S^{2}=\prod _{k=1}^{n-1}\left[\Gamma \left({\frac {k}{n}}\right)\,\Gamma \left(1-{\frac {k}{n}}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c0733d92915f8f5d9840e4b7a239d9116e3fdb10)




































![{\displaystyle \prod _{k=1}^{m-1}\tan \left({\frac {k\pi }{2m}}\right)=\prod _{k=1}^{m-1}\tan \left({\frac {(m-k)\pi }{2m}}\right)=\prod _{k=1}^{m-1}\tan \left({\frac {\pi }{2}}-{\frac {k\pi }{2m}}\right)=\prod _{k=1}^{m-1}\cot \left({\frac {k\pi }{2m}}\right)=\left[\prod _{k=1}^{m-1}\tan \left({\frac {k\pi }{2m}}\right)\right]^{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eedbb97271e593e0f55ca5c0c2c6582de1fac6a3)













































![{\displaystyle G(1)=a_{0}\,\sum _{n\in \mathbb {Z} }x^{n^{2}}=\prod _{n=1}^{\infty }\left[\left(1-x^{2n}\right)\left(1+x^{2n-1}\right)^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8fb70c2d05c5c2d034f33460a0cd00d9acff1eb1)








































![{\displaystyle {\frac {e}{2}}=\left[\left({\frac {4\cdot 2}{3\cdot 3}}\right)^{\frac {1}{4}}\cdot 2^{\frac {1}{4}}\right]\cdot \left[\left({\frac {6\cdot 6\cdot 8\cdot 4}{5\cdot 5\cdot 7\cdot 7}}\right)^{\frac {1}{8}}\cdot 2^{\frac {1}{8}}\right]\cdots }](https://wikimedia.org/api/rest_v1/media/math/render/svg/1e5f789dd59e2fde949b70ec6fc5d66c9b6e8a4a)















![{\displaystyle \left[\log {\frac {\sin \pi z}{\pi z}}\right]_{0}^{x}=\sum _{n=1}^{\infty }\left[\log(n^{2}-z^{2})\right]_{0}^{x}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ffe024903981fdffaf8f7a559d8d4e373a604a36)





![{\displaystyle \prod _{k=1}^{\infty }\left(1-{\frac {z^{n}}{k^{n}}}\right)=\left[\prod _{k=0}^{n-1}\Gamma (1-\xi ^{k}z)\right]^{-1}\qquad \xi =e^{\frac {2\pi i}{n}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f76eea22b8fa96ba06a4bb045a3c5c50388fe117)

















![{\displaystyle \prod _{k=1}^{\infty }\left[{\frac {1}{\sqrt {\pi }}}\,\Gamma \left({\frac {1}{2}}+{\frac {z}{2^{k}}}\right)\right]=2^{-2z}\,\Gamma (1+z)\qquad z\notin \mathbb {Z} _{<0}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5a68e95d7d3ac8db7cdb148df7662fb7bf41f916)

![{\displaystyle \prod _{k=1}^{n}\left[{\frac {1}{\sqrt {\pi }}}\,\Gamma \left({\frac {1}{2}}+{\frac {z}{2^{k}}}\right)\right]=\prod _{k=1}^{n}2^{1-{\frac {2z}{2^{k}}}}\,\prod _{k=1}^{n}{\frac {\Gamma \left({\frac {z}{2^{k-1}}}\right)}{\Gamma \left({\frac {z}{2^{k}}}\right)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1904048fb6bdf2d9cc190841842f0ea95390a35c)

![{\displaystyle \prod _{k=0}^{\infty }\left[\left(1+{\frac {y}{k+x}}\right)e^{-{\frac {y}{k+x}}}\right]={\frac {\Gamma (x)\,e^{y\,\psi (x)}}{\Gamma (x+y)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/af5805f03b7242aa843c951a0226940d86690879)



![{\displaystyle {\frac {\Gamma (x)}{\Gamma (x+y)}}\,e^{y\,\psi (x)}=\lim _{n\to \infty }\prod _{k=0}^{n}\left[\left(1+{\frac {y}{k+x}}\right)\,e^{-{\frac {y}{k+x}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6d738154d3d0a902de716c34ad74e15fc9fb3402)























={\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{\infty }f(t)e^{-ist}\,dt}](https://wikimedia.org/api/rest_v1/media/math/render/svg/70fd2a51d505561066fdf4615660e9d5d4e46e25)
={\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{\infty }F(s)e^{ist}\,ds}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6ff64bbd8e207d95addb68792200656d17c2f29d)
={\sqrt {2\pi }}\cdot {\mathcal {F}}[f(t)](s)\cdot {\mathcal {F}}[g(t)](s)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0d8ea6a82c4d69ebe460ef86320dabe1533825c5)
={\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }f(u)\,g(t-u)\,du\,\,e^{-ist}\,dt}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c9ae92edbe45a3ec77a8dd4e97fa827e2d18bffd)


\cdot {\mathcal {F}}[g(t)](s)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0cf6036ecd6d3f8cc08a11359fa37d299f09c356)
=\int _{0}^{\infty }f(t)e^{-st}\,dt}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b5212bd9559de6c16b66aedb22b86235e084ed7a)
={\frac {1}{2\pi i}}\int _{a-i\infty }^{a+i\infty }F(s)e^{st}\,ds}](https://wikimedia.org/api/rest_v1/media/math/render/svg/59d7c3426bf3b145df9040caba1d2d3dec278751)


\right](t)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b85c35fc1464fd4daf4f38c44c2ff773adcc48db)




=F(s)\cdot G(s)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/77194f003a8ce59189215930f267bbd41175c50e)



}](https://wikimedia.org/api/rest_v1/media/math/render/svg/edc74fcf8322997a9e2ea17a609c66fb02f3edcc)
=\int _{0}^{\infty }f(t)\,t^{s-1}\,dt}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ae868bbc7da993615a78a11913a403aeb5e816f)
={\frac {1}{2\pi i}}\int _{a-i\infty }^{a+i\infty }F(s)\,t^{-s}\,ds}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c1840875a5c0a2e843fec6ce668b1a7a67709c2b)
\right](t)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c0d0ebe043820599396734e45b7768f618b8eafd)







=F(s)\cdot G(s)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7bb4149ee3c418d2d298ab09a13480ad41be8b0a)
=\int _{0}^{\infty }\int _{0}^{\infty }f\left({\frac {t}{u}}\right)g(u)\,{\frac {du}{u}}\cdot t^{s-1}\,dt}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2fe238bb4452f4176e6b2466d538749dfc0b2b84)

































![{\displaystyle =\sum _{j=0}^{m}\sum _{k=j}^{n}a_{k}\,{m \choose j}\,{\frac {k!}{(k-j)!}}\,\lambda ^{k-j}\,x^{m-j}\,e^{\lambda x}=\sum _{j=0}^{m}{m \choose j}\,\left[\sum _{k=j}^{n}a_{k}\,{\frac {k!}{(k-j)!}}\,\lambda ^{k-j}\right]\,x^{m-j}\,e^{\lambda x}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/684f1fafffe465e9c6f7f1115e68eeecfdcfcd7d)


















![{\displaystyle \left[{\begin{matrix}y'=P(x)\,y^{2}+Q(x)\,y+R(x)\\y'_{p}=P(x)\,y_{p}^{2}+Q(x)\,y_{p}+R(x)\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4919eb670d84c22876233b457831aa78934ad3ea)











































![{\displaystyle \sum _{n=1}^{\infty }{\frac {(2z)^{2n-1}}{n\,{2n \choose n}}}=\int _{0}^{\frac {\pi }{2}}{\frac {z\,\sin \theta }{1-(z\,\sin \theta )^{2}}}\,d\theta =\left[-{\frac {\arctan \left({\frac {z\,\cos \theta }{\sqrt {1-z^{2}}}}\right)}{\sqrt {1-z^{2}}}}\right]_{0}^{\frac {\pi }{2}}={\frac {\arctan \left({\frac {z}{\sqrt {1-z^{2}}}}\right)}{\sqrt {1-z^{2}}}}={\frac {\arcsin z}{\sqrt {1-z^{2}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7377795c821c4d1141592ca7e10b3746fa638a0e)





















![{\displaystyle x\in \left[-{\frac {\pi }{2}},{\frac {\pi }{2}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1456d52196a1482372d7760aa863f111d53aa824)














![{\displaystyle \arcsin ^{3}z=6\sum _{k=0}^{\infty }\left[\sum _{m=0}^{k-1}{\frac {1}{(2m+1)^{2}}}\right]\,{\frac {1}{2^{2k}}}\,{2k \choose k}\,{\frac {z^{2k+1}}{2k+1}}\qquad |z|<1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ed7ead522edb1b90bbce15416edff0f0395ab2a4)









![{\displaystyle \arcsin ^{4}z=6\sum _{k=0}^{\infty }\left[\sum _{m=1}^{k-1}{\frac {1}{(2m)^{2}}}\right]\,{\frac {(2z)^{2k}}{k^{2}\,{2k \choose k}}}\qquad |z|<1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/699d91ec8b9eacf9f2eb57edff3343e2243ae193)














![{\displaystyle =\sum _{n=2}^{N}\left(\left[{\big (}t-(n-1){\big )}\,{\frac {1}{t^{s}}}\right]_{n-1}^{n}-\int _{n-1}^{n}{\frac {1}{t^{s}}}\,dt\right)=\sum _{n=2}^{N}{\frac {1}{n^{s}}}-\int _{1}^{N}{\frac {1}{t^{s}}}\,dt}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0bdb2aab3d7d870d279b4b84a1737e3ef6dfe81d)





































































![{\displaystyle {\frac {\sin(\alpha \arcsin z)}{\alpha }}=\sum _{n=0}^{\infty }\prod _{k=1}^{n}\left[(2k-1)^{2}-\alpha ^{2}\right]{\frac {z^{2n+1}}{(2n+1)!}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5b632b917bff96eb5dda292a372ff2bfe4497c7a)
![{\displaystyle {\frac {1}{2}}\left[\left({\sqrt {1+z^{2}}}+z\right)^{2\alpha }+\left({\sqrt {1+z^{2}}}-z\right)^{2\alpha }\right]=\sum _{n=0}^{\infty }\alpha \,{\frac {(\alpha +n-1)!}{(\alpha -n)!}}\,{\frac {(2z)^{2n}}{(2n)!}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/831f1c54d2c4bf7655cbddd42eda597a7b192dfa)

![{\displaystyle {\frac {1}{2}}{\Big [}f(z)-f(-z){\Big ]}={\sqrt {1+z^{2}}}^{\,2\alpha }\sum _{k=0}^{\infty }{2\alpha \choose 2k}\,{\frac {z^{2k}}{{\sqrt {1+z^{2}}}^{\,2k}}}=\sum _{k=0}^{\infty }{2\alpha \choose 2k}\,z^{2k}\,(1+z^{2})^{\alpha -k}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/81833c75861ae0470b7f1caad9c46de64b16d122)






![{\displaystyle {\frac {1}{2}}\left[\left({\sqrt {1+z^{2}}}+z\right)^{2\alpha +1}-\left({\sqrt {1+z^{2}}}-z\right)^{2\alpha +1}\right]=\sum _{n=0}^{\infty }{\frac {2\alpha +1}{2}}\,{\frac {(\alpha +n)!}{(\alpha -n)!}}\,{\frac {(2z)^{2n+1}}{(2n+1)!}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fa2bf92ed3b45e476c35cd31b1bcd1e6d8c72821)

![{\displaystyle {\frac {1}{2}}{\Big [}f(z)-f(-z){\Big ]}={\sqrt {1+z^{2}}}^{\,2\alpha +1}\sum _{k=0}^{\infty }{2\alpha +1 \choose 2k+1}\,{\frac {z^{2k+1}}{{\sqrt {1+z^{2}}}^{\,2k+1}}}=\sum _{k=0}^{\infty }{2\alpha +1 \choose 2k+1}\,z^{2k+1}\,(1+z^{2})^{\alpha -k}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ae6007cc3d8a07f14e275a8e000809587cfa106f)





































![{\displaystyle x_{n}={\frac {1}{n!}}\,\left[{\frac {\mathrm {d} ^{n-1}}{\mathrm {d} x^{n-1}}}\left({\frac {x-x_{0}}{f(x)-f(x_{0})}}\right)^{n}\,\right]_{x\to x_{0}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2094da332f7efad084413ff3021ae87605ed16e6)
























































![{\displaystyle \underbrace {\frac {1}{{\frac {w_{1}}{x_{1}}}+...+{\frac {w_{n}}{x_{n}}}}} _{\begin{matrix}{\text{harmonisches}}\\{\text{Mittel}}\end{matrix}}\leq \underbrace {x_{1}^{w_{1}}\cdots x_{n}^{w_{n}}} _{\begin{matrix}{\text{geometrisches}}\\{\text{Mittel}}\end{matrix}}\leq \underbrace {w_{1}x_{1}+...+w_{n}x_{n}} _{\begin{matrix}{\text{arithmetisches}}\\{\text{Mittel}}\end{matrix}}\leq \underbrace {\sqrt {w_{1}x_{1}^{2}+...+w_{n}x_{n}^{2}}} _{\begin{matrix}{\text{quadratisches}}\\{\text{Mittel}}\end{matrix}}\leq \underbrace {\sqrt[{3}]{w_{1}x_{1}^{3}+...+w_{n}x_{n}^{3}}} _{\begin{matrix}{\text{kubisches}}\\{\text{Mittel}}\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f93986b5f290e21e475869fe28175294162a5337)

![{\displaystyle \underbrace {\frac {n}{{\frac {1}{x_{1}}}+...+{\frac {1}{x_{n}}}}} _{\begin{matrix}{\text{harmonisches}}\\{\text{Mittel}}\end{matrix}}\leq \underbrace {\sqrt[{n}]{x_{1}\cdots x_{n}}} _{\begin{matrix}{\text{geometrisches}}\\{\text{Mittel}}\end{matrix}}\leq \underbrace {\frac {x_{1}+...+x_{n}}{n}} _{\begin{matrix}{\text{arithmetisches}}\\{\text{Mittel}}\end{matrix}}\leq \underbrace {\sqrt {\frac {x_{1}^{2}+...+x_{n}^{2}}{n}}} _{\begin{matrix}{\text{quadratisches}}\\{\text{Mittel}}\end{matrix}}\leq \underbrace {\sqrt[{3}]{\frac {x_{1}^{3}+...+x_{n}^{3}}{n}}} _{\begin{matrix}{\text{kubisches}}\\{\text{Mittel}}\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/41bbbdb50b24eb0eff08a362f60b9361c1c3b989)



![{\displaystyle S_{1}({\boldsymbol {a}})\geq {\sqrt {S_{2}({\boldsymbol {a}})}}\geq {\sqrt[{3}]{S_{3}({\boldsymbol {a}})}}\geq ...\geq {\sqrt[{n}]{S_{n}({\boldsymbol {a}})}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d2ae825b2c3875ccd5e88e94f1b575134a8b0ecf)



![{\displaystyle b_{k}\in \,\,]a_{k},a_{k+1}[}](https://wikimedia.org/api/rest_v1/media/math/render/svg/701b0d21765fe9823a010772c793536ef33d9f61)





















![{\displaystyle {\frac {{\widehat {r_{1}}}\,r_{2}\cdots r_{m}+r_{1}\,{\widehat {r_{2}}}\cdots r_{m}+...+r_{1}\,r_{2}\cdots {\widehat {r_{m}}}}{m}}\geq {\sqrt[{m}]{\frac {(r_{1}\,r_{2}\cdots r_{m})^{m}}{r_{1}\,r_{2}\cdots r_{m}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/791ed3b21dadacef321c63f2aa3fa72137a727bc)
![{\displaystyle {\frac {m\cdot S_{m-1}({\boldsymbol {a}})}{m}}\geq {\sqrt[{m}]{S_{m}({\boldsymbol {a}})^{m-1}}}\,\Rightarrow \,{\sqrt[{m-1}]{S_{m-1}({\boldsymbol {a}})}}\geq {\sqrt[{m}]{S_{m}({\boldsymbol {a}})}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c84da0b327693a99116d5e15b02a13a6da34254)















![{\displaystyle {\sqrt[{3}]{xyz}}\leq {\sqrt {{\frac {1}{2}}\,{\frac {(x-y)(y-z)(z-x)}{(x-y)\log z+(y-z)\log x+(z-x)\log y}}}}\leq {\frac {x+y+z}{3}}\qquad x>y>z>0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a515ae9b1c92564feb5c66efd274a8a8279d1bdb)
















![{\displaystyle f:]0,e[\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/6971c8451fb787b19e241394746899568be836df)



































![{\displaystyle f,g:[0,1]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/95460500f274fab1c26d9b3eaf5e0c5eecb16ffd)






![{\displaystyle f_{1},...,f_{n}:[0,1]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/b148116cb52867b6ae9058946e17fbc96d4902f3)



![{\displaystyle f:[0,1]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/2de6d0d4c98d4ca7ad937c772dc3e3e914b062f5)











![{\displaystyle [f(x)-f(y)]\,[g(x)-g(y)]\geq 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5525b1da26f4e02103241bec813940caff8ed5b1)




![{\displaystyle \leq [\alpha f(x)+\beta f(y)]\,[\alpha g(x)+\beta g(y)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/96def5eec4f5226e94b4a4c3facd3da9d2bbc584)
![{\displaystyle \alpha ^{2}f(x)g(x)+\alpha \beta [f(x)g(y)+f(y)g(x)]+\beta ^{2}f(y)g(y)\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/92b98f4a81cafde0295bf531cc25d31a5205be8f)
![{\displaystyle \leq \alpha ^{2}f(x)g(x)+\alpha \beta [f(x)g(x)+f(y)g(y)]+\beta ^{2}f(y)g(y)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8508b93d86e112fcf04e4be2ae98e5c3be7cb75a)























![{\displaystyle \sum _{k=0}^{n}\left[{\frac {x^{k+1}}{k+1}},{\frac {x^{2k}}{(2k)!}},{\frac {x^{2k+1}}{(2k+1)!}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/45f697e2a4a7d1a9a6b7c7a7187dfb3a532b6cd8)
![{\displaystyle \left\{{\begin{matrix}>&,&n=2m\quad \;\;\,\\<&,&n=2m+1\end{matrix}}\right\}\;{\Big [}\log(1+x),\cos(x),\sin(x){\Big ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9d03326d2a732c1a13e6017aec1deedc2e7c0fe3)





![{\displaystyle \int _{1}^{n}\log(x)\,dx=\left[x\,\log(x)-x\right]_{1}^{n}=n\,\log(n)-n+1=\log \left({\frac {n^{n}}{e^{n}}}\,e\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1a1e03cd72008e48889f2d7cff696b5d93f0ed30)































![{\displaystyle \int _{0}^{\pi }f(x)\,dx=\sum _{k=1}^{\infty }a_{k}\left[{\frac {\sin kx}{k}}\right]_{0}^{\pi }=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/14eb36db0100de43544a0580caf83a2123fafb33)


















![{\displaystyle \int _{0}^{\infty }\int _{0}^{\infty }{\frac {f(x)\,g(y)}{x+y}}\,dx\,dy<{\frac {\pi }{\sin {\frac {\pi }{p}}}}\cdot \left(\int _{0}^{\infty }[f(x)]^{p}\,dx\right)^{\frac {1}{p}}\cdot \left(\int _{0}^{\infty }[g(y)]^{q}\,dy\right)^{\frac {1}{q}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/459f203c8eca754d28ac3e7bc371afe70b7c2cd0)


![{\displaystyle \int _{0}^{\infty }\left({\frac {1}{x}}\int _{0}^{x}f(t)\,dt\right)^{p}dx\leq \left({\frac {p}{p-1}}\right)^{p}\cdot \int _{0}^{\infty }[f(x)]^{p}\,dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/64106b09677e15d1795d34a001ee556874334254)


![{\displaystyle F(x)=x\cdot {\frac {p}{r}}\cdot \int _{0}^{1}f\left(x\cdot u^{\frac {p}{r}}\right)\cdot u^{{\frac {p}{r}}-1}\,du\Rightarrow [F(x)]^{p}=x^{p}\cdot \left({\frac {p}{r}}\right)^{p}\cdot \left(\int _{0}^{1}f\left(x\cdot u^{\frac {p}{r}}\right)\cdot u^{{\frac {p}{r}}-1}\,du\right)^{p}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7a9aaf66ffd11cd6c48801b49da851f628d101dc)

![{\displaystyle \left(\int _{0}^{1}f\left(x\cdot u^{\frac {p}{r}}\right)\cdot u^{{\frac {p}{r}}-1}\,du\right)^{p}\leq \int _{0}^{1}\left[f\left(x\cdot u^{\frac {p}{r}}\right)\right]^{p}\cdot u^{p\cdot \left({\frac {p}{r}}-1\right)}\cdot du}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d8c64e6c0c35c2b45d411d9d72ca60b6d2942126)


![{\displaystyle \int _{0}^{x}[f(t)]^{p}\cdot {\frac {t^{p-r}}{x^{p-r}}}\cdot {\frac {r}{p}}\cdot {\frac {t^{{\frac {r}{p}}-1}}{x^{\frac {r}{p}}}}\,dt={\frac {x^{r-{\frac {r}{p}}}}{x^{p}}}\cdot {\frac {r}{p}}\cdot \int _{0}^{x}\left[f(t)\right]^{p}\cdot t^{p-r+{\frac {r}{p}}-1}\,dt}](https://wikimedia.org/api/rest_v1/media/math/render/svg/10c2f8249594e823dcea643fe91075abfdbaa3b8)
![{\displaystyle [F(x)]^{p}\leq x^{r-{\frac {r}{p}}}\cdot \left({\frac {p}{r}}\right)^{p-1}\cdot \int _{0}^{x}[f(t)]^{p}\cdot t^{p-r+{\frac {r}{p}}-1}\,dt}](https://wikimedia.org/api/rest_v1/media/math/render/svg/638cec897dbf3a63b5a2828da34ff46c8650609e)
![{\displaystyle \int _{0}^{\infty }[F(x)]^{p}\cdot x^{-r-1}\,dx\leq \int _{0}^{\infty }x^{r-{\frac {r}{p}}}\cdot \left({\frac {p}{r}}\right)^{p-1}\cdot \int _{0}^{x}[f(t)]^{p}\cdot t^{p-r+{\frac {r}{p}}-1}\,dt\cdot x^{-r-1}\,dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/56f41ddb6e87edb7ceb9b0e0ca32c0ad7723b082)
![{\displaystyle =\left({\frac {p}{r}}\right)^{p-1}\cdot \int _{0}^{\infty }\int _{0}^{x}[f(t)]^{p}\cdot t^{p-r+{\frac {r}{p}}-1}\cdot x^{-{\frac {r}{p}}-1}\,dt\,dx=\left({\frac {p}{r}}\right)^{p-1}\cdot \int _{0}^{\infty }[f(t)]^{p}\cdot t^{p-r+{\frac {r}{p}}-1}\cdot \int _{t}^{\infty }x^{-{\frac {r}{p}}-1}\,dx\cdot dt}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4cab9a4cdbf2ef86f2e35524ed0402b789cb8846)
![{\displaystyle =\left({\frac {p}{r}}\right)^{p}\cdot \int _{0}^{\infty }[f(t)]^{p}\cdot t^{p-r-1}\,dt}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0ee3e34706a3576f5a8778a8b381541c97f92346)

![{\displaystyle \int _{0}^{\infty }\left({\frac {F(x)}{x}}\right)^{p}dx\leq \left({\frac {p}{p-1}}\right)^{p}\cdot \int _{0}^{\infty }[f(t)]^{p}\,dt}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d6693f65c78955c4cb8f97f85d16b61564e13a98)















![{\displaystyle x_{1},...,x_{n}\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5477ae6d9a99f1bbd2d6c593691828baa132ba35)








![{\displaystyle g:[a,b]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b1d5103d0e36767a27715bcfc57137119294aad)

![{\displaystyle \varphi :[0,1]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/0420aebc007dbc1c04aba32a3be90efa6353145d)










































































































































































![{\displaystyle [a_{0},a_{1},a_{2},a_{3},...]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/12b7c5cf6fb7d3b06afc3fba1f5ba472a4aff8d4)
![{\displaystyle -\left[a_{0},a_{1},a_{2},a_{3},a_{4},\ldots \right]=\left\{{\begin{matrix}\left[-(a_{0}+1),a_{2}+1,a_{3},a_{4},a_{5},\ldots \right]&,&a_{1}=1\\\\\left[-(a_{0}+1),1,a_{1}-1,a_{2},a_{3},a_{4},\ldots \right]&,&a_{1}>1\end{matrix}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c7d2d5da41fabfb8f9f3dcaff5d90899a9456291)
![{\displaystyle \left[a_{0},a_{1},a_{2},...\right]^{-1}=\left\{{\begin{matrix}\left[0,a_{0},a_{1},...\right]&,&a_{0}>0\\\\\left[a_{1},a_{2},a_{3}...\right]&,&a_{0}=0\end{matrix}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8bec999898d8f2dbda96115164b5a8d87c3683f9)
![{\displaystyle \varphi ={\frac {1+{\sqrt {5}}}{2}}=\left[{\overline {1}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f37c2cb9ccdc188570517200e9ad56c767280496)
![{\displaystyle e=\left[2,{\overline {1,2k,1}}\right]_{k\geq 1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fc2a10e969b6c51c5fe5889a3319a897f7818f28)

![{\displaystyle [a_{0};a_{1},a_{2},a_{3},...]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/68136f09b623efe5198fa8d1d1701ce9cdd33dae)


![{\displaystyle \varrho =[2;1,2,1,1,4,1,1,6,1,1,8,1,...]=\left[2,{\overline {1,2n,1}}\right]_{n\geq 1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9eb2e130fed6725582e73f5a3dbfb330bc592b40)















![{\displaystyle e^{1/n}=\left[{\overline {1,(2k-1)n-1,1}}\right]_{k\geq 1}\qquad n\in \mathbb {Z} ^{>1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/759061857f3cef4de4523271cf0a391a717f4d6b)




![{\displaystyle \varrho _{m}=[1,m-1,1,1,3m-1,1,1,5m-1,1,...]=\left[{\overline {1,(2n+1)m-1,1}}\right]_{n\geq 0}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8a71992294449d5979368ea78f70d0b78a13f86d)








![{\displaystyle e^{2}=\left[7,{\overline {3k-1,1,1,3k,6(2k+1)}}\right]_{k\geq 1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e20c47ab6412025cd2538717c77676b5e05c50ef)


![{\displaystyle \varrho =[7;2,1,1,3,18,5,1,1,6,30,8,1,1,9,42,...]=\left[7,{\overline {3n-1,1,1,3n,6(2n+1)}}\right]_{n\geq 1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/63aa1045491e622f5d7ea254d2bf8244b9427384)








![{\displaystyle e^{2/n}=\left[\,{\overline {1,{\frac {(6k-5)n-1}{2}},6(2k-1)n,{\frac {(6k-1)n-1}{2}},1}}\,\right]_{k\geq 1}\qquad n\in \mathbb {Z} ^{>1}\;\mathrm {ungerade} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/039ad8bf300b8094020ba6d12a726f991262fa16)


![{\displaystyle \varrho _{m}=\left[1,{\frac {m-1}{2}},6m,{\frac {5m-1}{2}},1,1,{\frac {7m-1}{2}},18m,{\frac {11m-1}{2}},1,...\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1b38e24888f3098f4aff88479536cae2e3d6b552)
![{\displaystyle =\left[\,{\overline {1,{\frac {(6n+1)m-1}{2}},6(2n+1)m,{\frac {(6n+5)m-1}{2}},1}}\,\right]_{n\geq 0}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5c15360801f4141f46d2ccf179e25b5ae321b839)









![{\displaystyle {\frac {e-1}{2}}=\left[0,1,{\overline {4k+2}}\right]_{k\geq 1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/89d3ad70831002418063d0952ba9bba28d4aa8b3)
![{\displaystyle {\frac {1}{{\sqrt {e}}-1}}=\left[{\overline {4k+1,1,1}}\right]_{k\geq 0}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9e7e413d7a0090b5527d4e97d326484e60d95238)
![{\displaystyle {\frac {1}{{\sqrt {e}}+1}}=\left[0,2,{\overline {4k+1,1,1}}\right]_{k\geq 0}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/16d00e40763244097d3d4a1e607feaa71716b6fb)
![{\displaystyle \tan(1)=\left[{\overline {1,2k-1}}\right]_{k\geq 1}\quad ,\quad \cot(1)=\left[0,{\overline {1,2k-1}}\right]_{k\geq 1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/674eec7c9acd4649e21d2b333e5dadc387ec33b2)
![{\displaystyle \cot \left({\frac {1}{n}}\right)=\left[n-1,{\overline {1,(2k+1)n-2}}\right]_{k\geq 1}\quad ,\quad \tan \left({\frac {1}{n}}\right)=\left[0,n-1,{\overline {1,(2k+1)n-2}}\right]_{k\geq 1}\qquad n\in \mathbb {Z} ^{>1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9f2c2c5fa3db873621df6a2bc582ceff3b82524d)
![{\displaystyle \coth \left({\frac {1}{n}}\right)=\left[{\overline {(2k-1)n}}\right]_{k\geq 1}\qquad ,\qquad \tanh \left({\frac {1}{n}}\right)=\left[0,{\overline {(2k-1)n}}\right]_{k\geq 1}\qquad n\in \mathbb {Z} ^{>0}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1192ba0b2f0d71a937d6539182e83069eb21e92a)
![{\displaystyle {\sqrt {n}}\,\tan \left({\frac {1}{\sqrt {n}}}\right)=\left[{\overline {1,(4k-1)n-2,1,4k-1}}\right]_{k\geq 1}\qquad n\in \mathbb {Z} ^{>0}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8d781e0ce8ebf9e151b126122eae29f4271d4e75)
![{\displaystyle {\sqrt {n}}\,\cot \left({\frac {1}{\sqrt {n}}}\right)=\left[n-1,{\overline {1,4k-3,1,(4k+1)n-2}}\right]_{k\geq 1}\quad n\in \mathbb {Z} ^{>0}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f481e50a683ea1cf15cdac9c0b60ced12e696b72)
![{\displaystyle {\sqrt {n}}\,\tanh \left({\frac {1}{\sqrt {n}}}\right)=\left[0,{\overline {4k-3,(4k-1)n}}\right]_{k\geq 1}\qquad n\in \mathbb {Z} ^{>0}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c4bd80850c1621ea97d61786fec811acbf6bbda2)
![{\displaystyle {\sqrt {n}}\,\coth \left({\frac {1}{\sqrt {n}}}\right)=\left[{\overline {(4k-3)n,4k-1}}\right]_{k\geq 1}\quad n\in \mathbb {Z} ^{>0}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/adf2364ee637342b43a6cc44e8748d9c277f53f4)
![{\displaystyle {\sqrt {2}}=\left[1,{\overline {2}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/841eb20230f6bb90ad17fb368e6fef35701e372f)
![{\displaystyle {\sqrt {3}}=\left[1,{\overline {1,2}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4a915069cd79df7e201ded8a9bec63fafca67f63)
![{\displaystyle {\sqrt {4}}=\left[2\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd08269665467da74507734d912a33830cb48030)
![{\displaystyle {\sqrt {5}}=\left[2,{\overline {4}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/82fa249a1a32c0aa56ba98a12cb9f904b7598608)
![{\displaystyle {\sqrt {6}}=\left[2,{\overline {2,4}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d5c2938a1584b814997fde014617e9cbe405cab0)
![{\displaystyle {\sqrt {7}}=\left[2,{\overline {1,1,1,4}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9942f2038f946e50a267fead8bfd8e2b72ab71c4)
![{\displaystyle {\sqrt {8}}=\left[2,{\overline {1,4}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fb1ec323735d78f286779bdb604ae72c8188c03b)
![{\displaystyle {\sqrt {9}}=\left[3\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1ab5cbba4b5b6cfb07e774a2da5c4d7b53203f53)
![{\displaystyle {\sqrt {10}}=\left[3,{\overline {6}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/57994e58b52ffd146a9f336ba11d00837c47a8f5)


![{\displaystyle \left[a_{0},{\overline {a_{1},...,a_{n},2a_{0}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/272cdced246bf2de47926ef7d8ea4c9dca5a99ea)
![{\displaystyle {\sqrt {a^{2}+1}}=\left[a,{\overline {2a}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e71aef90c746a5f38e85edbcf28bb4b6d70c341f)
![{\displaystyle {\sqrt {a^{2}+2}}=\left[a,{\overline {a,2a}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/26c0b4fbf8ce35d024ae6423833d7a56c19772ee)
![{\displaystyle {\sqrt {a^{2}+a}}=\left[a,{\overline {2,2a}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e6c276f77ed0e68ee9a829e370c815ff243d24e5)
![{\displaystyle {\sqrt {a^{2}+2a}}=\left[a,{\overline {1,2a}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/62fe74e5e5363082019714a11a954e8aa3a0a3a2)
![{\displaystyle {\sqrt {9a^{2}+3}}=\left[3a,{\overline {2a,6a}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a93afff390f17526e1b93dcec8d060624621c599)




![{\displaystyle \alpha =[{\overline {a_{0},...,a_{n}}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/16c63a14210bcdc33ca512d9ce7f8923eeba0131)



![{\displaystyle \beta =[{\overline {a_{n},...,a_{0}}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e14e60fcb4c089175002e5290269fb13f75f12ac)
































































![{\displaystyle \left({\frac {\sqrt {5}}{1+{\sqrt[{5}]{{\sqrt[{4}]{5}}^{\,3}\cdot {\sqrt {\frac {{\sqrt {5}}-1}{2}}}^{\,5}-1}}}}-{\frac {{\sqrt {5}}+1}{2}}\right)\,e^{2\pi /{\sqrt {5}}}={\underset {k=0}{\overset {\infty }{K}}}{\frac {e^{-2k\pi {\sqrt {5}}}}{1}}={\frac {1|}{|1}}+{\frac {e^{-2\pi {\sqrt {5}}}|}{|1}}+{\frac {e^{-4\pi {\sqrt {5}}}|}{|1}}+{\frac {e^{-6\pi {\sqrt {5}}}|}{|1}}+{\frac {e^{-8\pi {\sqrt {5}}}|}{|1}}+...}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a509259c5dc0f4dce90f391ee4b4c1b708c96c2e)















































































































































































![{\displaystyle i^{[m]}={\sqrt[{m}]{1+i}}-1\iff \left(1+i^{[m]}\right)^{m}=1+i}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e83785e686f651901ad07804ecfc4d055ba02735)

![{\displaystyle i^{(m)}=m\cdot i^{[m]}\iff \left(1+{\frac {i^{(m)}}{m}}\right)^{m}=1+i}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d0208b020f2a6165e2b7dfdf4bae67fd960d9c11)

![{\displaystyle i^{[m]}<i^{\langle m\rangle }\qquad \varrho <i^{(m)}<i\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/acc0538fb138b93df8d9095bd5041215daa151f7)





















































![{\displaystyle ={\frac {1}{D_{x}}}\left(D_{x}+2D_{x+1}+\dotsb +n\,D_{x+n-1}\right)={\frac {1}{D_{x}}}\left[(D_{x}+\dotsb +D_{x+n-1})+(D_{x+1}+\dotsb +D_{x+n-1})+\dotsb +D_{x+n-1}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7160fb8db28fc0c372a3c4d92a8d19048518fe47)
![{\displaystyle ={\frac {1}{D_{x}}}\left[(N_{x}-N_{x+n})+(N_{x+1}-N_{x+n})+\dotsb +(N_{x+n-1}-N_{x+n})\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6b75103bc223bd79e658735be396bce2c95ee608)
![{\displaystyle ={\frac {1}{D_{x}}}\left[N_{x}+N_{x+1}+\dotsb +N_{x+n-1}-n\,N_{x+n}\right]={\frac {S_{x}-S_{x+n}-n\cdot N_{x+n}}{D_{x}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a5e95da84a7ffa19efb7f279d52bcec2dafb8dc9)


![{\displaystyle ={\frac {1}{D_{x}}}\left(D_{x+1}+2D_{x+2}+\dotsb +n\,D_{x+n}\right)={\frac {1}{D_{x}}}\left[(D_{x+1}+\dotsb +D_{x+n})+(D_{x+2}+\dotsb +D_{x+n})+\dotsb +D_{x+n}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2f209fa9ef43122e76b2d89af1baa33b1ff5440c)
![{\displaystyle ={\frac {1}{D_{x}}}\left[(N_{x+1}-N_{x+n+1})+(N_{x+2}-N_{x+n+1})+\dotsb +(N_{x+n}-N_{x+n+1})\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e823ffddf6ff2a22574de13b989e41c5341e4cad)
![{\displaystyle ={\frac {1}{D_{x}}}\left[N_{x+1}+N_{x+2}+\dotsb +N_{x+n}-n\,N_{x+n+1}\right]={\frac {S_{x+1}-S_{x+n+1}-n\cdot N_{x+n+1}}{D_{x}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f164075728c85dc8c538f36ba937acd15070f5d0)


![{\displaystyle ={\frac {1}{D_{x}}}\left(C_{x}+2C_{x+1}+\dotsb +n\,C_{x+n-1}\right)={\frac {1}{D_{x}}}\left[(C_{x}+\dotsb +C_{x+n-1})+(C_{x+1}+\dotsb +C_{x+n-1})+\dotsb +C_{x+n-1}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ae2a384adf9556c1a971bfb1ffe9cc62f2b3805f)
![{\displaystyle ={\frac {1}{D_{x}}}\left[(M_{x}-M_{x+n})+(M_{x+1}-M_{x+n})+\dotsb +(M_{x+n-1}-M_{x+n})\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f1da1ee4015a30ca682eb5a37403f8771cc77efa)
![{\displaystyle ={\frac {1}{D_{x}}}\left[M_{x}+M_{x+1}+\dotsb +M_{x+n-1}-n\,M_{x+n}\right]={\frac {R_{x}-R_{x+n}-n\cdot M_{x+n}}{D_{x}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6835d1ffaae852cba2caaffd2b2bb5b33aff7267)





















