Benutzer:Dirk Hünniger/mnfana

Analysis 1

Wikibooks

Was ist Analysis?

Was ist eigentlich Analysis?

Ein Mathematikstudium beginnt normalerweise mit den beiden Grundvorlesungen Analysis und Lineare Algebra, wobei die lineare Algebra ein Teilgebiet der Algebra ist. Analysis und Algebra bilden die beiden Grundpfeiler der modernen Mathematik, die ihrerseits auf der Mengenlehre fußen. Wir werden uns also eine ganze Weile mit diesen beiden Bereichen beschäftigen. Soweit, so gut – doch worum geht es in beiden Vorlesungen überhaupt? Was tut ein Algebraiker und was ein Analytiker? Mit welchen Fragen beschäftigen sie sich? Es ist sinnvoll, zu Beginn einen kleinen Vorgeschmack zu geben, was uns in welchem Bereich erwartet, um den „roten Faden“ einer jeden Vorlesung besser sehen zu können.

Die Algebra, oder viel mehr eine Algebra, ist, ähnlich wie die rationalen oder die reellen Zahlen, eine Art „Zahlenraum“: In einer Algebra kann man addieren und multiplizieren. So beschäftigt sich die Algebra zu einem großen Teil mit Umformungen, die durch Addition oder Multiplikation entstehen, wobei auch das Wurzelziehen dazu gehört. In der Algebra möchte man unter anderem die Frage beantworten, wie man eine Gleichung umformen muss, um sie zu „lösen“ und ob eine bestimmte Gleichung überhaupt lösbar ist. Generell beschäftigt sich die Algebra häufig mit Gleichungen und eher selten mit Ungleichungen.

In der linearen Algebra treten alle beteiligten Größen einer Gleichung nur in erster Potenz (also in linearer Ordnung) auf. Eine klassische Fragestellung aus der linearen Algebra ist die, wann sich ein Gleichungssystem der folgenden Form lösen lässt:

${\begin{array}{ccccccccccc}a_{11}\cdot x_{1}&+&a_{12}\cdot x_{2}&+&a_{13}\cdot x_{3}&+&\ldots &+&a_{1n}\cdot x_{n}&=&b_{1}\\a_{21}\cdot x_{1}&+&a_{22}\cdot x_{2}&+&a_{23}\cdot x_{3}&+&\ldots &+&a_{2n}\cdot x_{n}&=&b_{2}\\\vdots &&\vdots &&\vdots &&\ddots &&\vdots &\vdots &\vdots \\a_{m1}\cdot x_{1}&+&a_{m2}\cdot x_{2}&+&a_{m3}\cdot x_{3}&+&\ldots &+&a_{mn}\cdot x_{n}&=&b_{m}\end{array}}$

Beachte, dass alle $x_{i}$ hier nur in erster Potenz, d. h. „hoch eins“ auftauchen, die wegen $x^{1}=x$ im obigen Gleichungssystem weggelassen wurde.

Die Analysis auf der anderen Seite beschäftigt sich mit der Stetigkeit von Funktionen, mit Grenzwerten, mit der Differential- und der Integralrechnung. Wenn wir eine Funktion wie zum Beispiel

$f\ :\ \mathbb {R} \rightarrow \mathbb {R} ,\quad x\mapsto f(x)={\frac {x^{2}-x+1}{x^{2}-9}}$

betrachten, so ist die Suche nach ihren Nullstellen algebraischer Natur. Wenn wir uns aber für ihr Verhalten in der Nähe ihrer Polstellen oder ihr Verhalten für $x\rightarrow \pm \infty$ interessieren, so ist das eine analytische Fragestellung. Ebenso ist die Untersuchung ihrer Steigung und ihrer Krümmung ein analytisches Vorhaben.

Eine weitere Frage der Analysis ist die, ob es Funktionen gibt, die unstetig sind, aber nirgends einen „Sprung“ machen – die Antwort hierauf lautet „ja“. Ferner können wir uns fragen, ob eine Funktion, die differenzierbar ist, eine unstetige Ableitung haben kann – auch hier ist die Antwort „ja“ – oder ob ihre Ableitung einen der eben erwähnten Sprünge aufweisen kann – diesmal lautet die Antwort „nein“. Wir folgern somit, dass eine Funktion mit Sprung niemals die Ableitung einer anderen Funktion sein kann. Sie kann aber trotzdem integrierbar sein. Die Berechnung ihres Integrals ist ebenfalls Aufgabe des Analytikers.

Die Analysis gibt uns Konzepte an die Hand, mit denen wir die aktuelle Änderung einer Funktion beschreiben können. Diese Konzepte werden in den Naturwissenschaften verwendet, um Naturgesetze oder Formeln für bestimmte Modelle aufzustellen. Dies ist auch der Grund, warum die Analysis eine so wichtige Rolle für die Naturwissenschaften spielt. Der Analytiker untersucht, wie die Veränderung eines Systems vorhergesagt werden kann, und wie exakt solche Vorhersagen sind.

Wir haben damit bereits einen kleinen Einblick in die Welt der Mathematik gewonnen und wissen zumindest grob, was uns auf welcher Seite (Algebra und Analysis) erwartet. Oft bevorzugt ein Mathematiker eine der beiden Seiten, ist also eher Algebraiker oder eher Analytiker. In Wirklichkeit kommt jedes der beiden Gebiete nicht ohne das jeweils andere aus. Es muss also nicht beim entweder – oder bleiben, denn beide Felder können gleichermaßen interessant und bereichernd sein. Zumindest in diesem Projekt werden wir uns der Analysis widmen…

Wozu Analysis studieren?

Wieso sollte ich Analysis studieren? Dies ist eine berechtigte Frage, auf die zu Beginn jeder Vorlesung und jedes Lehrbuchs zur Analysis eingegangen werden sollte. Ich möchte dir in diesem Kapitel einige der Gründe darlegen.

Analysis als Grundlage der Mathematik

Die Analysis ist eine der grundlegenden Vorlesungen der Mathematik. Viele Theorien wie die Funktionentheorie, Funktionalanalysis und die Theorie der gewöhnlichen Differentialgleichungen bauen direkt auf ihr auf. Außerdem werden zahlreiche Konzepte der Analysis in abgewandelter Form in anderen Bereichen der Mathematik verwendet.

Um Mathematik studieren zu können, ist es daher unumgänglich, sich auch mit Analysis zu befassen. Diese Theorie wird ein Schlüssel sein, um andere mathematische Teilbereiche zu verstehen. Egal für welche Gebiete in der Mathematik du dich interessierst, du wirst dafür sehr wahrscheinlich Hintergrundwissen aus der Analysis benötigen.

Das Gleiche gilt, wenn du Mathematik vor allem als Werkzeug für dein Studium oder deine Forschung verwendest. Was auch immer du aus der Mathematik brauchst, Kenntnisse in der Analysis werden dir mit hoher Wahrscheinlichkeit helfen, deine mathematischen Werkzeuge und Hilfsmittel zu verstehen.

Analysis als Sprache der Natur

Die meisten naturwissenschaftlichen Problemstellungen werden mit Hilfe von Konzepten modelliert, die du in der Analysis kennen lernen wirst: Wie lassen sich Ort und Geschwindigkeit eines sich bewegenden Objekts bestimmen und vorhersagen? Wie lässt sich das elektrische Feld eines Systems geladener Körper berechnen?

Der Anwendungsbereich der Analysis reicht von einfachen Problemen bis hin zu modernen Forschungsgebieten wie axiomatische Quantenfeldtheorien oder die quantitative Modellierung biologischer Prozesse. Eine sehr gute Kenntnis dieser Konzepte wird dir demnach helfen, die Gesetze der Natur zu verstehen und zu formulieren. Wenn du also Student einer Naturwissenschaft sein solltest oder dich generell für eine Naturwissenschaft interessierst, wird dir ein Studium der Analysis äußerst hilfreich sein.

Analysis in der Schule

Die Analysis ist eine der wenigen Vorlesungen im Mathematikstudium, die bereits in der Schule gelehrt werden. Wenn du also Mathematik auf Lehramt studierst, wirst du Kenntnisse dieser Vorlesung direkt für deinen späteren Lehrberuf verwenden können. Ein tiefgründiges Verständnis der Analysis wird dir helfen, deinen Schülern die Mathematik besser zu erklären.

Analysis als exakte mathematische Theorie

Anders als du die Analysis in der Schule kennen gelernt hast, werden wir in diesem Buch die Theorie mathematisch exakt formulieren. Das heißt, dass wir jeden Satz rigoros beweisen und jeden Begriff exakt definieren werden. Am Ende wirst du beispielsweise wissen, wieso die Ableitung von $f(x)=x^{2}$ gleich $2x$ ist und was eine „Ableitung“ überhaupt ist. Wir werden dabei jeden Begriff motivieren, damit du auch weißt, warum wir gewisse Konzepte in der Analysis einführen. Dadurch wirst du nicht nur dein Schulwissen über die Analysis vertiefen, dieses Wissen kann dir auch helfen, komplizierte Probleme der Analysis zu lösen.

Analysis als Übung für mathematisches Denken

Dass die Analysis bereits in der Schule gelehrt wurde, hat auch einen weiteren Vorteil: Der Stoff ist bereits mehr oder weniger bekannt, was uns die Chance gibt, uns mehr auf die mathematische Arbeitsweise zu konzentrieren. Das exakte und saubere mathematische Arbeiten ist nämlich ungewohnt und muss am Anfang eines Studiums erst geübt werden. Die Analysis bietet sich hierfür hervorragend an.

Auch wenn du später keine Analysis mehr brauchen solltest, ist eine erlernte mathematische Denk- und Arbeitsweise sehr nützlich für dich. Studenten der Mathematik (und auch naturwissenschaftlicher Fächer) sind gerade aufgrund dieser Fähigkeit bei Arbeitgebern beliebt. Ich bin mir sicher, dass dir die mathematische Denk- und Arbeitsweise bei deinen Projekten und Aufgaben sehr helfen wird.

Was sind reelle Zahlen?

Motivation der unterschiedlichen Zahlen Mengen. (YouTube-Video vom Kanal Quatematik)

Reelle Zahlen bilden die Grundlage für dieses Lehrbuch. Schließlich wollen wir uns mit Folgen reeller Zahlen oder mit reellwertigen Funktionen beschäftigen. Bevor wir mit dem Studium der Analysis beginnen, sollten wir uns zunächst fragen: Was sind reelle Zahlen?

Das ist gar keine einfache Frage. Schauen wir uns zunächst auf der Meta-Ebene die Möglichkeiten an, diese zu definieren.

Die Beschreibungsmöglichkeiten reeller Zahlen

Jeder von uns hat bereits eine intuitive Vorstellung, was reelle Zahlen sind, auch wenn nicht alle diese Idee in Worte fassen können. Beispielsweise kann man sich die reellen Zahlen als Punkte auf der Zahlengeraden vorstellen:

Vorstellung der reellen Zahlen als Punkte auf der Zahlengeraden

Unsere Aufgabe besteht darin, diese intuitive Idee in die exakte Sprache der Mathematik zu übersetzen. Dazu haben wir zwei Möglichkeiten: die axiomatische und die konstruktive Beschreibung.

Die axiomatische Beschreibung

In der axiomatischen Beschreibung der Analysis legen wir mit den Axiomen das Fundament, auf dem wir schrittweise die Theoreme der Analysis herleiten.

Bei der axiomatischen Beschreibung wird nicht direkt gesagt, was reelle Zahlen sind, es wird vielmehr nur erklärt, welche Eigenschaften sie haben. Bei dieser Herangehensweise sagen wir: „Die reellen Zahlen sind eine Menge von Objekten, die folgende charakteristische Eigenschaften besitzen: <Aufzählung der Eigenschaften reeller Zahlen>“. Die grundlegenden Eigenschaften werden dabei über Axiome festgelegt. Zur Erinnerung: Ein Axiom ist eine Aussage, die ohne Beweis als wahr angenommen wird. Jedes mathematische Modell, das alle genannten Eigenschaften/Axiome erfüllt, wird als Modell der reellen Zahlen angesehen. Aussagen, die auf Grundlage der Axiome bewiesen werden, werden Theoreme genannt.

Bei der Wahl der Axiome müssen wir darauf achten, dass sie widerspruchsfrei sind. Es muss also mindestens ein Modell geben, das alle Axiome erfüllt. Beispielsweise können wir nicht sagen, dass gleichzeitig $1<0$ als auch $1\geq 0$ gelten soll. Eine solche Struktur kann es nämlich nicht geben. Außerdem sollten die Axiome nachvollziehbar sein, also wirklich Eigenschaften bezeichnen, die wir auch intuitiv den reellen Zahlen zuschreiben.

Des Weiteren müssen ausreichend viele Axiome zur Charakterisierung der reellen Zahlen definiert sein. Bei zu wenigen Axiomen könnten auch Strukturen diese erfüllen, die wir intuitiv nicht als Modell reeller Zahlen ansehen. So ist es beispielsweise nicht ausreichend zu sagen, dass es für die reellen Zahlen eine Addition $+$ mit $x+y=y+x$ für alle $x$ und $y$ gibt. Allein dieses Axiom ist zu wenig, denn die natürlichen Zahlen erfüllen diese Eigenschaft auch. Sie sind für uns aber kein Modell reeller Zahlen.

Außerdem soll eine gewisse Sparsamkeit beachtet werden: Es sollten keine Axiome unnötig definiert werden. Dies bedeutet, dass keine Eigenschaften als Axiome benannt werden, die sich bereits aus anderen Axiomen herleiten lassen. Wenn also aus den Axiomen $A_{1}$ und $A_{2}$ bereits folgt, dass auch die Eigenschaft $E$ erfüllt sein muss, dann wird $E$ nicht extra als Axiom definiert.

Die konstruktive Beschreibung

Bei der konstruktiven Beschreibung werden die reellen Zahlen aus den rationalen Zahlen konstruiert. Das bedeutet, dass durch ein gewisses Verfahren aus rationalen Zahlen neue Objekte geschaffen werden, welche man danach als reelle Zahlen definiert.

Anders als bei der axiomatischen Beschreibung, welche die reellen Zahlen nur durch ihre Eigenschaften beschreibt, kann man beim konstruktiven Verfahren genau sagen, was die reellen Zahlen sind. Es sind genau die Objekte, die durch das Konstruktionsverfahren entstanden sind. Die Eigenschaften der reellen Zahlen müssen bei dieser Beschreibung auch nicht durch Axiome definiert werden, sondern ergeben sich aus den Eigenschaften der konstruierten Objekte.

Es gibt mehrere Konstruktionsverfahren der reellen Zahlen. Die dabei entstandenen Strukturen sind jedoch äquivalent in dem Sinne, dass sie dieselben Eigenschaften haben (man nennt solche Strukturen „isomorph“).

Der Zusammenhang beider Beschreibungen

Beide Vorgehensweisen liefern am Ende dieselben Ergebnisse. Wenn man für ein konstruiertes Modell alle diejenigen Eigenschaften nachweisen kann, die man als Axiome in der axiomatischen Beschreibung definiert hat, dann besitzt das Modell auch die Eigenschaften, die man aus den Axiomen hergeleitet hat. Wenn man umgekehrt in der konstruierten Beschreibung nur diejenigen Eigenschaften des Modells für spätere Argumentationen heranzieht, die man in der axiomatischen Beschreibung als Axiome definieren würde, dann kann man auch alle mit dem Modell bewiesenen Sätze in der axiomatischen Beschreibung beweisen.

Es ist also egal, welchen Weg wir wählen. Zu Beginn gehen wir den Weg der axiomatischen Beschreibung, weil er leichter zu verstehen ist (für die konstruktive Beschreibung brauchen wir Konzepte, die Studienanfänger in der Regel noch nicht oder nicht ausreichend kennen).

Zusammenfassung: Weg zur axiomatischen Beschreibung reeller Zahlen

Um die Axiome der reellen Zahlen zu finden, kann man folgendermaßen vorgehen:

1. Intuitive Idee entwickeln: Zunächst brauchen wir eine intuitive Idee der reellen Zahlen. Hierzu können wir beispielsweise auf die intuitive Idee zurückgreifen, dass reelle Zahlen Punkte auf der Zahlengeraden sind.
2. Axiome definieren: Nun müssen alle Axiome definiert werden. Dazu müssen wir folgende Punkte beachten:
   • Nachvollziehbarkeit: Die Axiome sollten sinnvoll sein. Das bedeutet, dass jedes Axiom intuitiv nachvollziehbar ist.
   • Widerspruchsfreiheit: Die Axiome müssen in sich widerspruchsfrei sein. Das kann implizit dadurch gezeigt werden, dass ein konkretes Modell der reellen Zahlen konstruiert werden kann. Damit es ein Modell der reellen Zahlen geben kann, müssen die Axiome nämlich in sich widerspruchsfrei sein.
   • Vollständigkeit: Sobald ein Modell alle Axiome erfüllt, sollte es unserer intuitiven Vorstellung von reellen Zahlen entsprechen. Alle Theoreme über reelle Zahlen müssen wir aus den Axiomen herleiten können.
   • Sparsamkeit: Kein Axiom kann aus den anderen hergeleitet werden.
3. Begriffe definieren und Theoreme beweisen: Aufbauend auf den Axiomen werden wir Grundbegriffe der Analysis einführen und die Theoreme der Analysis beweisen.

In der Analysis werden alle Theoreme mit Hilfe der Axiome reeller Zahlen bewiesen. Dabei wird es zwangsweise vorkommen, dass wir Konzepte einführen oder Sätze beweisen, die schon aus der Schule bekannt sind – wie die Gleichung $1\cdot 0=0$. Bei diesen Beweisen ist es wichtig, dass wir nur solche Eigenschaften reeller Zahlen heranziehen, die entweder in den Axiomen definiert wurden oder die wir bereits bewiesen haben. Bekannte Tatsachen aus der Schule dürfen nicht ohne weiteres verwendet werden!

Die Axiome der reellen Zahlen können in drei Gruppen aufgeteilt werden: Die Körperaxiome, die Anordnungsaxiome und das Vollständigkeitsaxiom.

Die Körperaxiome

Mit den Körperaxiomen wird die Addition und Multiplikation, also die arithmetische Struktur der reellen Zahlen, definiert. Die reellen Zahlen sind Objekte, die addiert und multipliziert werden können, wobei die grundlegenden Eigenschaften der Additionen und Multiplikationen genannt werden. Die Subtraktion und die Division werden auf die Addition beziehungsweise die Multiplikation zurückgeführt. Diese Axiomengruppe beschreibt, wie man mit reellen Zahlen rechnen kann.

Definition (Körperaxiome)

Auf der Menge der reellen Zahlen $\mathbb {R}$ sind zwei Operationen $+:\mathbb {R} \times \mathbb {R} \to \mathbb {R}$ und $\cdot :\mathbb {R} \times \mathbb {R} \to \mathbb {R}$ definiert. Diese erfüllen folgende Eigenschaften:

• Eigenschaften der Addition:
  • Assoziativgesetz der Addition: Für alle reellen Zahlen $x,y,z$ gilt $x+(y+z)=(x+y)+z$.
  • Kommutativgesetz der Addition: Für alle reellen Zahlen $x$ und $y$ gilt $x+y=y+x$.
  • Existenz der Null: Es gibt mindestens eine reelle Zahl $0\in \mathbb {R}$, für die $0+x=x$ für alle reellen Zahlen $x$ gilt.
  • Existenz des Negativen: Für jede reelle Zahl $x$ gibt es mindestens eine reelle Zahl $-x$ mit $x+(-x)=0$.
• Eigenschaften der Multiplikation:
  • Assoziativgesetz der Multiplikation: Für alle reellen Zahlen $x,y,z$ gilt $x\cdot (y\cdot z)=(x\cdot y)\cdot z$.
  • Kommutativgesetz der Multiplikation: Für alle reellen Zahlen $x$ und $y$ gilt $x\cdot y=y\cdot x$.
  • Existenz der Eins: Es gibt mindestens eine reelle Zahl $1\in \mathbb {R}$ mit $1\neq 0$, für die $1\cdot x=x$ für alle reellen Zahlen $x$ gilt.
  • Existenz des Inversen: Für jede reelle Zahl $x\neq 0$ gibt es mindestens eine reelle Zahl $x^{-1}$ mit $x\cdot x^{-1}=1$.
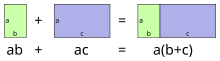
• Distributivgesetz: Für alle reellen Zahlen $x,y,z$ gilt $x\cdot (y+z)=x\cdot y+x\cdot z$.

Die Anordnungsaxiome

Die Anordnungsaxiome beschreiben die lineare Ordnung der reellen Zahlen. Die reellen Zahlen sind also Objekte, die man miteinander vergleichen kann, wobei für zwei verschiedene reelle Zahlen entweder die eine Zahl größer ist als die andere oder umgekehrt. Dadurch ergibt sich ein wesentlicher Zusammenhang der Struktur der reellen Zahlen mit der einer Geraden, da auch die Punkte einer Geraden in natürlicher Art und Weise geordnet sind. Diese Axiomengruppe ist also wesentlich für die Vorstellung der reellen Zahlen als Punkte auf einer Zahlengeraden. In dieser Axiomengruppe wird auch definiert, wie die Operationen der Addition und Multiplikation mit der Ordnungsstruktur in Verbindung stehen.

Die Ordnung der reellen Zahlen kann dadurch beschrieben werden, dass wir alle positiven Zahlen kennen. Wenn $x$ eine positive Zahl ist, schreiben wir $0<x$. Die Positivität der reellen Zahlen wird dabei über die Anordnungsaxiome definiert:

Definition (Anordnungsaxiome)

Die Anordnungsaxiome lauten

• Trichotomie der Positivität: Für alle reellen Zahlen $x$ gilt entweder $0<x$ oder $x=0$ oder $0<-x$. Mit den Abkürzungen "$\forall$" für "für alle" und "${\dot {\lor }}$" für "entweder oder" können wir dies schreiben als
  $\forall x\in \mathbb {R} :0<x\ {\dot {\lor }}\ 0=x\ {\dot {\lor }}\ 0<-x$
• Abgeschlossenheit bezüglich Addition: Für alle reellen Zahlen $a$ und $b$ gilt: Wenn $0<a$ und $0<b$ ist, dann ist auch $0<a+b$. In Zeichen:
  $\forall a,b\in \mathbb {R} :0<a\land 0<b\implies 0<a+b$
• Abgeschlossenheit bezüglich Multiplikation: Für alle reellen Zahlen $a$ und $b$ gilt: Wenn $0<a$ und $0<b$ ist, dann ist auch $0<ab$. In Zeichen:
  $\forall a,b\in \mathbb {R} :0<a\land 0<b\implies 0<ab$

Mit Hilfe der Positivitätseigenschaft $0<x$ können wir die Kleiner-Relation definieren:

Definition (Kleiner-Relation)

Die Kleiner-Relation $x<y$ ist durch folgende Äquivalenz definiert:

$x<y:\iff 0<y-x$

Es ist also genau dann $x$ kleiner als $y$, wenn die Differenz $y-x$ positiv ist. Über die Kleiner-Relation können wir alle weiteren Ordnungsrelationen definieren:

Definition (Weitere Ordnungsrelationen auf Grundlage der Kleiner-Relation)

Für die reellen Zahlen sind außerdem die Relationen $\geq$, $\leq$ und $>$ über folgende Äquivalenzen definiert:

• $x\leq y:\iff x<y\lor x=y$
• $x\geq y:\iff y<x\lor x=y$
• $x>y:\iff y<x$

Das Vollständigkeitsaxiom

Das Vollständigkeitsaxiom beschreibt den Übergang beziehungsweise den markanten Unterschied zwischen den rationalen und den reellen Zahlen. Während die obigen beiden Axiomengruppen noch durch die Menge der rationalen Zahlen erfüllt werden, gilt dies nicht mehr für das Vollständigkeitsaxiom. Der Grund dafür ist, dass es im Zahlenbereich der rationalen Zahlen „Lücken“ wie ${\sqrt {2}}$ gibt. Diese Lücken können zwar beliebig durch rationale Zahlen approximiert werden, sind aber selbst keine rationalen Zahlen mehr. Bei den reellen Zahlen gibt es solche Lücken nicht, weil das Vollständigkeitsaxiom die Existenz von Lücken ausschließt. Wenn man irgendetwas beliebig durch reelle Zahlen annähern kann, so existiert dieses „irgendetwas“ und ist wieder eine reelle Zahl.

Eine Approximation einer Zahl kann durch eine Intervallschachtelung realisiert werden. Diese ist eine Folge von Intervallen, die ineinander liegen und deren Länge gegen Null streben:

Eine Intervallschachtelung

Eine Intervallschachtelung dient als Approximation einer reellen Zahl. Jedes Intervall schränkt den Bereich ein, in dem die zu approximierende Zahl liegt und im Laufe der Intervallschachtelung wird dieser Bereich immer kleiner. Das Intervallschachtelungsprinzip garantiert, dass durch jede Intervallschachtelung mindestens eine Zahl approximiert wird:

Definition (Allgemeines Intervallschachtelungsprinzip)

Zu jeder allgemeinen Intervallschachtelung $I_{1}$, $I_{2}$, $I_{3}$... existiert eine reelle Zahl, die in allen Intervallen liegt und damit von allen Intervallen approximiert wird.

Dieses Vollständigkeitsaxiom beschreibt, dass die Menge der reellen Zahlen keine „Lücken“ besitzt. Um zu beschreiben, dass die reellen Zahlen die kleinstmögliche Erweiterung sind, um die Lücken der rationalen Zahlen zu füllen, müssen wir das Intervallschachtelungsprinzip um ein weiteres Axiom ergänzen. Hierzu müssen wir ausschließen, dass es unendlich kleine bzw. unendlich großen Zahlen gibt. Eine positive Zahl $y$ wäre im Vergleich zu einer positiven Zahl $x$ unendlich groß, wenn $y$ größer als alle Vielfachen von $x$ wäre, wenn also keine der Vielfachen $x,2x,3x,4x,\ldots$ jemals über $y$ hinauswächst. Für alle natürlichen Zahlen $n$ wäre also $nx<y$. Dies wollen wir nun ausschließen. Für je zwei positive Zahlen $x$ und $y$ soll es also mindestens eine natürliche Zahl $n$ mit $nx\geq y$ geben. Genau diese Eigenschaft beschreibt das archimedische Axiom:

Definition (Das Archimedische Axiom)

Für alle reellen Zahlen $x,y>0$ gibt es eine natürliche Zahl $n$, so dass $nx\geq y$ ist. Mit den Abkürzungen "$\forall$" für "für alle" und "$\exists$" für "es gibt" liest sich dies als

$\forall x>0,y>0\,\exists n\in \mathbb {N} :nx\geq y$

Mit Hilfe des Vollständigkeitsaxioms kann man zeigen, dass reelle Zahlen beliebig durch rationale Zahlen angenähert werden können. Diese Eigenschaft ist wesentlich, denn sie ermöglicht das Rechnen mit rationalen Zahlen anstelle von reellen Zahlen. Beispielsweise werden Computerberechnungen in der Regel nur mit rationalen Zahlen durchgeführt. Solche Rechnungen sind zwar fehleranfällig, ihre Fehler können aber in der Regel beliebig klein gemacht werden.

Die Zahlengerade

Im vorherigen Abschnitt zu den reellen Zahlen habe ich dir erklärt, dass wir im Folgenden die reellen Zahlen axiomatisch einführen wollen. Um die gewählten Axiome auch nachvollziehen zu können, ist es sehr hilfreich, eine intuitive Idee der reellen Zahlen zu haben. Damit wir auch dieselbe intuitive Idee besitzen, möchte ich an dieser Stelle die Vorstellung der reellen Zahlen als Punkte auf einer Zahlengeraden kurz wiederholen.

Reelle Zahlen als Punkte auf der Zahlengeraden

Zunächst starten wir mit einer Geraden:

unbeschriftete Zahlengerade

Auf dieser Geraden legen wir zwei Punkte für die Zahlen „0“ und „1“ fest, wobei die Eins rechts neben der Null liegen soll:

Zahlengerade mit eingezeichneten Zahlen 0 und 1

Sobald wir diese zwei Zahlen 0 und 1 auf der Zahlengeraden eingezeichnet haben, ergeben sich automatisch auch die Positionen aller anderen Zahlen. Die negativen reellen Zahlen werden dabei links und die positiven reellen Zahlen rechts von der Null eingezeichnet. Der Abstand von jeder einzelnen Zahl zur Null soll gleich dem Betrag dieser Zahl sein. Der Abstand der bereits eingetragenen Zahlen 0 und 1 ist dabei die Einheitslänge, womit wir alle weiteren Abstände auf der Zahlengeraden bestimmen können. Am Ende haben wir folgendes Bild:

Zahlengerade mit eingezeichneten Zahlen von -3 bis +3

Ordnung der reellen Zahlen

Durch die Identifizierung der reellen Zahlen mit Punkten auf der Zahlengeraden ergibt sich auf natürliche Art und Weise auch eine Ordnung. Für zwei reelle Zahlen $x$ und $y$ definiert man $x<y$ bzw. $y>x$, wenn $y$ rechts von $x$ auf der Zahlengeraden liegt:

Zahlengerade mit eingezeichneten Punkten x kleiner gleich y

Anhand dieser Vorstellung der Ordnung reeller Zahlen sind viele Eigenschaften der Ordnungsrelation direkt nachvollziehbar. So kann man sich klar machen, dass wenn $x<y$ und $y<z$ ist, automatisch auch $x<z$ ist. Wenn also $x$ links von $y$ liegt und $y$ selbst wieder links von $z$ liegt, dann liegt auch $x$ links von $z$.

Rechnen auf der Zahlengeraden

Um unsere intuitive Idee der Zahlengeraden zu vervollständigen, müssen wir noch klären, wie man mit reellen Zahlen auf der Zahlengeraden rechnen kann. Wir müssen also definieren, wie man Zahlen auf der Zahlengeraden addiert, subtrahiert, multipliziert und dividiert.

Die Addition

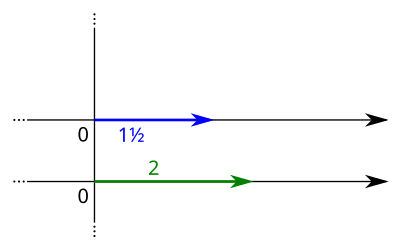
Die Addition reeller Zahlen als Vektoraddition

Um Zahlen auf der Zahlengeraden zu addieren, identifiziert man jede einzelne Zahl mit einem Vektor, der in der Null beginnt und bei der jeweiligen Zahl endet. Ein Vektor ist dabei nichts anderes als ein Pfeil, also eine gerichtete Strecke, mit klar definiertem Anfangs- und Endpunkt. Für das Beispiel der Zahlen -2 und 3 sehen die entsprechenden Vektoren so aus:

Zahlengerade mit den Zahlen -2 und 3 eingezeichnet als Vektoren

Um nun 3 plus -2 zu rechnen, nimmt man den Anfangspunkt des Vektors -2 (welcher vorher bei 0 lag) und legt ihn auf den Endpunkt des Vektors 3. Der so verschobene Endpunkt des Vektors -2 zeigt dann auf das Ergebnis der Addition $3+(-2)$, also 1:

Addition von -2 und 3 auf der Zahlengeraden

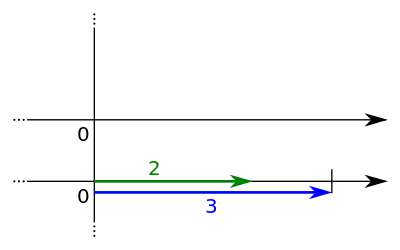
Analog erhält man 3 als die Summe von 1 und 2:

Addition von 1 und 2 auf der Zahlengeraden

Zuordnung zwischen Vektoren und Punkten auf der Zahlengeraden

Beachte, dass wir dabei das Modell der reellen Zahlen gewechselt haben: Die einzelnen Vektoren, die wir als Zwischenschritt benutzt haben, sind nämlich keine Punkte auf der Zahlengeraden mehr, sondern Pfeile, die in der Null beginnen und irgendwo auf der Zahlengeraden enden (also ganz andere Objekte). Da es aber zu jedem Punkt auf der Zahlengeraden genau einen Vektor gibt, der von der 0 zu diesem Punkt verläuft, und weil jeder Vektor eindeutig durch seinen Endpunkt beschrieben wird, gibt es eine 1-zu-1-Zurordnung zwischen Punkten auf der Zahlengeraden und ihren jeweiligen Vektoren. Somit können wir jederzeit zwischen den beiden Modellen hin- und herwechseln. Das zweite Modell entspricht im Übrigen der Vorstellung der reellen Zahlen als eindimensionaler Vektorraum, den du vielleicht schon aus der linearen Algebra kennst.

Die Addition reeller Zahlen als Translation

In der obigen Methode haben wir beide Summanden als Vektoren aufgefasst. Es ist jedoch auch möglich, sich weiterhin einen Summanden als Punkt auf der Zahlengeraden vorzustellen und nur einen Summanden als Vektor aufzufassen. Hierzu nimmt man für die Summe $a+x$ den Vektor $a$ und trägt diesen beginnend beim Punkt $x$ auf der Zahlengeraden ab. Der Endpunkt von $a$ zeigt dann auf das Ergebnis von $a+x$:

Addition a+x als Translation von x um den Vektor a

Hier entspricht die Addition einer Verschiebung des Punktes $x$ auf der Zahlengeraden um den Vektor $a$ und ist damit eine Translation. Translation ist dabei der mathematische Begriff für eine (Parallell-)Verschiebung.

Die Subtraktion

Die Subtraktion funktioniert wie die Addition, nur dass man die Richtung des Vektors ändern muss, den wir subtrahieren wollen. Wenn wir beispielsweise $3-2$ rechnen wollen, so kehren wir die Richtung des Vektors 2 um und erhalten so den Vektor -2. Am Ende wird dann $3+(-2)$ mit der obigen Methode berechnet. Diese Art und Weise der Subtraktion werden wir später auch bei der axiomatischen Einführung der reellen Zahlen nutzen.

Die Multiplikation

Dem Produkt $a\cdot b$ entspricht der Fläche eines Rechtecks mit den Seitenlängen $a$ und $b$

Die Multiplikation entspricht der Skalierung einer Zahl mit einem Skalierungsfaktor. Hier wird die Zahl $2$ um den Faktor $3$ gestreckt, wobei das Endergebnis gleich $6$ ist.

Um zu klären, was die Multiplikation ist, könnten wir definieren, dass $a\cdot b$ gleich dem Flächeninhalt eines Rechtecks mit den Seitenlängen $a$ und $b$ ist. Diese Vorgehensweise hat jedoch folgende Nachteile:

• Für uns sind Zahlen Punkte auf der Zahlengeraden. Jedoch ist ein Flächeninhalt kein solcher Punkt und wir müssten zunächst klären, wie wir einem Flächeninhalt eines Rechtecks einen Punkt auf der Zahlengeraden zuordnen. Anders als bei den Vektoren im Abschnitt zur Addition ist dies nicht trivial.
• Da $a\cdot b$ auch negativ sein kann, müssten wir zusätzlich noch definieren, welche Flächen als negativ anzusehen sind. Hier stellt sich im Gegensatz zur Zahlengeraden die Frage: „Was ist eine negative Fläche?“, was wiederum nicht aus dem Stegreif zu beantworten ist. Für Punkte auf der Zahlengeraden gibt es demgegenüber eine einfache geometrische Bedeutung der Negativität: Ein Punkt ist genau dann negativ, wenn er links von der Null liegt.

Deswegen folgen wir dem Vorschlag von René Descartes, der 1637 in seinem Werk „Géométrie“ die Multiplikation zum ersten Mal so einführte, dass das Ergebnis eines Produktes wieder eine Strecke ist. Hierzu will ich eine etwas abgewandelte Methode benutzen, und zwar folgende Vorstellung einer Multiplikation durch eine Streckung:

Stell dir vor, wir wollen das Produkt $2\cdot 1{\tfrac {1}{2}}$ berechnen. Hierzu zeichnest du zunächst zwei parallele Zahlengeraden. Auf der einen Zahlengeraden zeichnest du den Faktor 2 und auf der anderen den Faktor $1{\tfrac {1}{2}}$ ein. Die beiden Zahlengeraden verbindest du durch eine vertikale Gerade, welche durch die Null geht:

Ausgangslage zur Berechnung des Produkts 2·1½ auf der Zahlengeraden

Nun zeichnest du eine Gerade ein, welche durch den eingezeichneten Punkt 2 auf der einen Zahlengeraden und dem Punkt 1 auf der anderen Zahlengeraden geht:

Berechnung von 2·1½ auf der Zahlengeraden (Schritt 1)

Die so eingezeichnete Gerade schneidet irgendwo die vertikale Gerade. Diesen Punkt verbindet man mit dem zweiten Faktor $1{\tfrac {1}{2}}$ zu einer zweiten Hilfsgeraden. Der Punkt, in dem diese Hilfsgerade die andere Zahlengerade schneidet, entspricht dem Ergebnis des Produkts $2\cdot 1{\tfrac {1}{2}}$. In diesem Beispiel ist das Ergebnis 3:

Berechnung von 2·1½ auf der Zahlengeraden (Schritt 2)

Das Ganze funktioniert genauso, wenn einer oder beide Faktoren negativ sind:

Berechnung von -½·2 auf der Zahlengeraden

Eine Besonderheit gibt es aber: Wenn der erste Faktor 1 ist, ist nämlich die erste Hilfsgerade parallel zur vertikalen Geraden durch die Nullpunkte und schneidet dementsprechend diese Gerade nie. In diesem Fall muss auch die zweite Hilfsgerade parallel zur vertikalen Geraden eingezeichnet werden. Der zweite Faktor ändert sich dann durch die Multiplikation nicht:

Multiplikation mit 1 auf der Zahlengeraden: Der zweite Faktor wird nicht geändert

Obige Methode entspricht tatsächlich der Vorstellung der Multiplikation durch eine Streckung. Wenn man nämlich die 1 auf $a$ streckt, dann entspricht $a\cdot b$ der Streckung von $b$ um denselben Streckungsfaktor. Dass am Ende die obige Methode auch das richtige Ergebnis liefert, lässt sich durch den Strahlensatz nachvollziehen.

Die Division

Die Division kann ähnlich zur Multiplikation durchgeführt werden. Anders als bei der Multiplikation werden hier beide Zahlen, also sowohl Dividend als auch Divisor, auf derselben Zahlengeraden eingetragen. Für das Beispiel ${\tfrac {3}{2}}$ sieht die Zahlengeraden so aus:

Ausgangslage der Berechnung von 3:2 auf der Zahlengeraden

Nun verbindet man den Divisor, hier also 2, mit der Zahl 1 der anderen Zahlengeraden zu einer Hilfsgeraden:

Berechnung von 3:2 auf der Zahlengeraden (Schritt 1)

Die eben eingezeichnete Hilfsgerade schneidet die vertikale Gerade in einem Punkt, welchen man mit dem Dividenden, hier 3, zu einer zweiten Hilfsgeraden verbindet:

Berechnung von 3:2 auf der Zahlengeraden (Schritt 2)

Der Schnittpunkt der zweiten Hilfsgeraden mit der zweiten Zahlengeraden ist dann das Ergebnis der Division. Wir erhalten so das Ergebnis ${\tfrac {3}{2}}=1,5$. Auch diese Methode lässt sich mit dem Strahlensatz nachvollziehen.

Dem Quotienten ${\tfrac {a}{b}}$ entspricht also die Strecke, die man erhält, wenn man $a$ um denselben Streckungsfaktor streckt, der notwendig ist, um $b$ auf $1$ zu strecken. Hier sieht man auch, dass eine Division mit 0 nicht möglich ist, weil man 0 nicht auf 1 strecken kann (jede Streckung von 0 bleibt nämlich 0).

Vollständigkeit der Zahlengeraden

Die Zahlengerade ist vollständig in dem Sinn, dass sie keine Lücken enthält. So muss es auf der Zahlengeraden einen Punkt für ${\sqrt {2}}$ geben, weil man ${\sqrt {2}}$ durch folgende Konstruktion finden kann:

Konstruktion von Wurzel 2 auf der Zahlengeraden

Diese Eigenschaft der Zahlengeraden ist noch recht schwammig. Wie lässt sich beispielsweise mathematisch definieren, was „Lücken“ sind und dass sie nicht auf der Zahlengeraden existieren? Da wir in diesem Kapitel aber nur eine intuitive Idee der reellen Zahlen entwickeln wollen, ist es kein Problem, wenn wir hierzu intuitiv verständliche Eigenschaften heranziehen. Später im Abschnitt zur Vollständigkeit reeller Zahlen werden wir klären, wie man diese intuitive Idee der Lückenfreiheit in die strikte Sprache der Mathematik übersetzt.

Körperaxiome

Was würdest du auf folgende Frage antworten: „Was sind die reellen Zahlen?“ Manche meinen: „Reelle Zahlen sind das, mit dem man rechnen kann“. Diese Antwort kommt der tatsächlichen Definition reeller Zahlen durchaus nah. Sie muss aber noch konkretisiert werden. Was bedeutet es, dass man „mit Zahlen rechnen kann“? In diesem Kapitel erfährst du die Antwort darauf...

Einleitung

Wir beginnen die Definition der reellen Zahlen mit den sogenannten Körperaxiomen. Diese bilden neben den Anordnungsaxiomen und dem Vollständigkeitsaxiom die Basis, um die reellen Zahlen zu charakterisieren. Zur Wiederholung: Axiome sind Aussagen, die ohne Beweis als wahr angenommen werden. Die Körperaxiome beschreiben damit Eigenschaften der reellen Zahlen, die wir nicht hinterfragen. Es sind Eigenschaften, die wir als charakteristisch für die reellen Zahlen ansehen. Die Körperaxiome (und die anderen Axiome der reellen Zahlen) entsprechen damit folgender Aussagenstruktur

Reelle Zahlen sind Objekte, die folgende Eigenschaften besitzen: …

Dabei definieren die Körperaxiome die vier Grundrechenarten der reellen Zahlen: Addition, Subtraktion, Multiplikation und Division. In den Körperaxiomen selbst wird die Addition und die Multiplikation charakterisiert. Die Subtraktion und die Division werden anschließend, wie du noch sehen wirst, über gesonderte Definitionen eingeführt.

Die Körperaxiome

Die Körperaxiome lauten: Auf der Menge der reellen Zahlen $\mathbb {R}$ sind zwei (zweistellige) Verknüpfungen definiert:

• eine Verknüpfung der Addition: $+:\mathbb {R} \times \mathbb {R} \rightarrow \mathbb {R}$
• eine Verknüpfung der Multiplikation: $\cdot :\mathbb {R} \times \mathbb {R} \rightarrow \mathbb {R}$

Die Schreibweise $\mathbb {R} \times \mathbb {R} \rightarrow \mathbb {R}$ bezeichnet eine zweistellige Operation. Das bedeutet beispielsweise in der Schreibweise $+:\mathbb {R} \times \mathbb {R} \rightarrow \mathbb {R}$, dass die Addition zwei reelle Zahlen als Argumente annimmt und ihnen eine reelle Zahl als Ergebnis zuordnet. Analog macht auch die Multiplikation aus zwei reellen Zahlen als Argumente eine reelle Zahl als Ergebnis. Weiterhin fordern die Körperaxiome, dass diese Verknüpfungen folgende Eigenschaften besitzen sollen:

Definition (Körperaxiome)

Auf der Menge der reellen Zahlen $\mathbb {R}$ sind zwei Operationen $+:\mathbb {R} \times \mathbb {R} \to \mathbb {R}$ und $\cdot :\mathbb {R} \times \mathbb {R} \to \mathbb {R}$ definiert. Diese erfüllen folgende Eigenschaften:

• Eigenschaften der Addition:
  • Assoziativgesetz der Addition: Für alle reellen Zahlen $x,y,z$ gilt $x+(y+z)=(x+y)+z$.
  • Kommutativgesetz der Addition: Für alle reellen Zahlen $x$ und $y$ gilt $x+y=y+x$.
  • Existenz der Null: Es gibt mindestens eine reelle Zahl $0\in \mathbb {R}$, für die $0+x=x$ für alle reellen Zahlen $x$ gilt.
  • Existenz des Negativen: Für jede reelle Zahl $x$ gibt es mindestens eine reelle Zahl $-x$ mit $x+(-x)=0$.
• Eigenschaften der Multiplikation:
  • Assoziativgesetz der Multiplikation: Für alle reellen Zahlen $x,y,z$ gilt $x\cdot (y\cdot z)=(x\cdot y)\cdot z$.
  • Kommutativgesetz der Multiplikation: Für alle reellen Zahlen $x$ und $y$ gilt $x\cdot y=y\cdot x$.
  • Existenz der Eins: Es gibt mindestens eine reelle Zahl $1\in \mathbb {R}$ mit $1\neq 0$, für die $1\cdot x=x$ für alle reellen Zahlen $x$ gilt.
  • Existenz des Inversen: Für jede reelle Zahl $x\neq 0$ gibt es mindestens eine reelle Zahl $x^{-1}$ mit $x\cdot x^{-1}=1$.
• Distributivgesetz: Für alle reellen Zahlen $x,y,z$ gilt $x\cdot (y+z)=x\cdot y+x\cdot z$.

Definitionen im Zusammenhang mit den Körperaxiomen

Die Körperaxiome nehmen noch keinen Bezug auf die Subtraktion und Division. Diese müssen erst auf Grundlage der Körperaxiome definiert werden:

Definition (Subtraktion und Division)

Die Subtraktion wird auf eine Addition und die Division auf eine Multiplikation zurückgeführt:

${\begin{aligned}-&:\mathbb {R} \times \mathbb {R} \rightarrow \mathbb {R} &:(x,y)\mapsto x-y&:=x+(-y)\\\div &:\mathbb {R} \times \mathbb {R} \setminus \{0\}\rightarrow \mathbb {R} &:(x,y)\mapsto x\div y&:=x\cdot y^{-1}\\\end{aligned}}$

Die Subtraktion ist damit die Addition des Negativen einer Zahl und die Division die Multiplikation mit dem Inversen einer Zahl.

So entpuppt sich nach unserer Definition die Subtraktion als eine Addition und die Division als eine Multiplikation. Die Eigenschaften der Division und der Subtraktion werden damit auch durch die Körperaxiome beschrieben. In der Mathematik sagt man dementsprechend zu Differenzen oft Summen und zu Quotienten oft Produkte.

Definition weiterer Begriffe

Im Folgenden verwenden wir die aus der Schule bekannten Bezeichnungen:

$\overbrace {\underbrace {x{\underset {}{}}} _{\text{Summand}}+\underbrace {y{\underset {}{}}} _{\text{Summand}}} ^{\text{Summe}}$

$\overbrace {\underbrace {x{\underset {}{}}} _{\text{Minuend}}-\underbrace {y{\underset {}{}}} _{\text{Subtrahend}}} ^{\text{Differenz}}$

$\overbrace {\underbrace {x{\underset {}{}}} _{\text{Faktor}}\cdot \underbrace {y{\underset {}{}}} _{\text{Faktor}}} ^{\text{Produkt}}$

$\overbrace {\underbrace {x{\underset {}{}}} _{\text{Dividend}}\div \underbrace {y{\underset {}{}}} _{\text{Divisor}}} ^{\text{Quotient}}$

Weiterhin nennen wir eine Struktur, die alle Körperaxiome erfüllt, einen Körper:

Definition (Körper)

Eine Menge, die eine Addition und eine Multiplikation mit den obigen Eigenschaften besitzt, nennt man einen „Körper“.

Somit ist $\mathbb {R}$ mit der Addition und Multiplikation ein Körper. Es gibt aber auch andere Körper wie beispielsweise die Menge der rationalen Zahlen $\mathbb {Q}$. Für das Studium der reellen Analysis ist der Körperbegriff nur insofern wichtig, als dass du wissen musst, dass die reellen Zahlen alle Körperaxiome erfüllen und $\mathbb {R}$ demnach ein Körper ist. Der Körperbegriff als solcher wird in der Algebra näher untersucht.

Verständnisfrage: Kann es für die einelementige Menge $\{0\}$ eine geeignete Addition und Multiplikation geben, so dass diese Menge ein Körper ist?

Nein, denn laut Körperaxiom "Existenz der Eins" muss $1\neq 0$ sein. Jeder Körper muss also mindestens zwei Elemente, nämlich $0$ und $1$, besitzen. Somit kann $\{0\}$ als einelementige Menge kein Körper sein.

Anmerkungen zu den Körperaxiomen

• Assoziativgesetz der Addition und Multiplikation ($x+(y+z)=(x+y)+z$ bzw. $x\cdot (y\cdot z)=(x\cdot y)\cdot z$): Dank des Assoziativgesetzes ist die Reihenfolge der Ausführung einer endlichen Addition/Multiplikation egal. Dementsprechend können Klammern in endlichen Summen/Produkten weggelassen werden. (Dies gilt nicht für unendliche Summen/Produkte!)
• Kommutativgesetz der Addition und Multiplikation ($x+y=y+x$ bzw. $x\cdot y=y\cdot x$): Dank dieses Axioms ist die Reihenfolge der Terme in endlichen Summen/Produkten egal. (Dies gilt nicht für unendliche Summen/Produkte!)
• Existenz des neutralen Elements der Addition und Multiplikation ($0+x=x$ und $1\cdot x=x$): Hier wird explizit nur die Existenz, nicht die Eindeutigkeit, der Null beziehungsweise Eins definiert. Die Eindeutigkeit lässt sich aus den Körperaxiomen herleiten und damit ist es unnötig, diese Eigenschaft zu fordern. Da laut der Axiome die Zahl Eins ungleich Null ist, muss ein Körper mindestens zwei Elemente besitzen (in der Algebra wirst du lernen, dass es einen Körper mit genau zwei Elementen gibt).
• Existenz des Negativen und Inversen ($x+(-x)=0$ und $x\cdot x^{-1}=1$): Auch hier wird erst einmal nur die Existenz des Negativen und Inversen gefordert. Wir werden aber später die Eindeutigkeit des Negativen und Inversen beweisen.
• Distributivgesetz ($x\cdot (y+z)=x\cdot y+x\cdot z$): Dieses Axiom stellt eine Verbindung zwischen Addition und Multiplikation her und ist deshalb ziemlich hilfreich. Es ist auch das einzige Axiom, das einen solchen Zusammenhang herstellt. Beachte, dass $(x+y)\cdot z=x\cdot z+y\cdot z$ nicht definiert wurde und deswegen noch bewiesen werden muss.

Nachvollziehbarkeit der Körperaxiome

Die Kommutativität der Addition ist bereits aus dem Alltag bekannt.

Visualisierung des Distributivgesetzes für positive reelle Zahlen

Eines der Ziele, die ich im vorherigen Kapitel für die Axiome der reellen Zahlen formuliert habe, ist ihre Nachvollziehbarkeit. Deswegen sollten wir jetzt schauen, ob die gewählten Axiome auch wirklich unserer intuitiven Idee der reellen Zahlen entsprechen.

Man erkennt, dass die gewählten Körperaxiome aus der Schule oder aus dem Alltag bekannt sind. Einige der Axiome können wir auch mit dem Modell der reellen Zahlen als Punkte auf der Zahlengeraden verstehen. So trifft es beispielsweise zu, dass die Addition mit Null auf der Zahlengeraden den zweiten Summanden nicht ändert. Auch die Assoziativität der Addition lässt sich mit dem Zahlengeradenmodell einfach verstehen (die grünen Vektoren werden hierbei zuerst miteinander addiert):

Zeichnung zur Assoziativität der Addition reeller Zahlen

Leider können wir nicht alle Körperaxiome mit der Zahlengeraden erklären. So ist beispielsweise die Assoziativität der Multiplikation schwierig darzustellen. Jedoch entsprechen alle Körperaxiome unserer Erfahrung im Umgang mit reellen Zahlen.

Potenzen reeller Zahlen

Aus der Schule kennst du Potenzen wie $5^{3}$ als Abkürzungen für Produkte mit immer demselben Faktor. So ist $5^{3}$ die abkürzende Schreibweise für $5\cdot 5\cdot 5$. Um die Theorie der Analysis sauber aufzubauen, dürfen wir keine bekannten Sachverhalte der Schule übernehmen und müssen so auch den Begriff der Potenz neu (und sauber) einführen. Hier werden wir das Hilfsmittel der Rekursion kennen lernen, welches dir noch oft im Studium der Mathematik begegnen wird.

Intuitive Definition der Potenz

Intuitiv können wir die Potenz mit natürlichem Exponenten folgendermaßen definieren:

Definition (intuitive Definition der Potenz)

Die Potenz $x^{k}$ ist definiert über

$x^{k}=\underbrace {x\cdot x\cdot \ldots \cdot x} _{k{\text{-mal}}}$

Dies entspricht der Vorstellung der Potenz, welche wir aus der Schule haben. Doch diese Definition birgt folgende Nachteile:

• Wir wissen nicht, was $x^{0}=\underbrace {x\cdot x\cdot \ldots \cdot x} _{0{\text{-mal}}}$ sein soll. Generell überträgt sich obige Gleichung nicht auf solche $x^{k}$, für die $k$ keine natürliche Zahl ist. So sind die Ausdrücke $\underbrace {x\cdot x\cdot \ldots \cdot x} _{-1{\text{-mal}}}$ oder $\underbrace {x\cdot x\cdot \ldots \cdot x} _{{\tfrac {1}{2}}{\text{-mal}}}$ nicht sinnvoll.
• Der Ausdruck $\underbrace {\ldots } _{k{\text{-mal}}}$ ist zwar intuitiv verständlich, er ist aber nicht mathematisch definiert. Wenn man also die Theorie der Analysis exakt aufbauen möchte, dann kann man die obige Definition nicht verwenden.

Formale Definition der Potenz mit natürlichem Exponenten

Die Elemente der Potenzschreibweise: ${\text{Potenzwert}}={\text{Basis}}^{\text{Exponent}}$

Mathematisch exakt wird die Potenz rekursiv definiert:

Definition (rekursive Definition der Potenz mit natürlichem Koeffizienten)

Die Potenz ist rekursiv über die folgenden beiden Formeln für alle $x\in \mathbb {R}$ und $k\in \mathbb {N} _{0}$ definiert:

${\begin{aligned}x^{0}&:=1\\x^{k+1}&:=x\cdot x^{k}\end{aligned}}$

Insbesondere definieren wir $0^{0}=1$.

Hier werden zwei Eigenschaften der Potenz angegeben, die zusammen bereits den Wert jeder Potenz eindeutig festlegen. Die Formel

$x^{k+1}=x\cdot x^{k}$

wird Rekursionsschritt genannt. Durch sie lässt sich jede Potenz auf eine Potenz mit einem um eins verringerten Exponenten zurückführen. So ist nach dem Rekursionsschritt

$5^{3}=5\cdot 5^{2}$

Wenn wir $5^{2}$ ausgerechnet haben, können wir $5^{3}$ nach obiger Gleichung ausrechnen. $5^{2}$ selbst kann durch weitere Anwendung des Rekursionsschritts aus $5^{1}$ berechnet werden und so weiter. Irgendwann landet man so bei der Potenz $5^{0}$, die man wegen der Formel

$x^{0}=1$

gleich eins setzen kann. Die Formel $x^{0}=1$ wird Rekursionsanfang genannt und beendet die Rekursion. Insgesamt erhält man so

${\begin{array}{rll}&5^{3}&\ \left|\ {\color {Orange}{\text{Rekursionsschritt: }}5^{3}=5\cdot 5^{2}}\right.\\=\ &5\cdot 5^{2}&\ \left|\ {\color {Orange}{\text{Rekursionsschritt: }}5^{2}=5\cdot 5^{1}}\right.\\=\ &5\cdot (5\cdot 5^{1})&\ \left|\ {\color {Orange}{\text{Rekursionsschritt: }}5^{1}=5\cdot 5^{0}}\right.\\=\ &5\cdot (5\cdot (5\cdot 5^{0}))&\ \left|\ {\color {Orange}{\text{Rekursionsanfang: }}5^{0}=1}\right.\\=\ &5\cdot (5\cdot (5\cdot 1))\\=\ &5\cdot (5\cdot 5)\\=\ &5\cdot 25\\=\ &125\end{array}}$

Man sieht hier exemplarisch, wie durch Angabe von zwei Eigenschaften der Wert jeder Potenz eindeutig festgelegt ist. Diese Vorgehensweise hat folgende Vorteile:

• Wir wissen, was $x^{0}$ ist.
• Wir haben sowohl in der Angabe des Rekursionsschritts als auch bei der Angabe des Rekursionsanfangs keine Ausdrücke verwendet, die wir nicht vorher schon definiert haben.
• Die beiden Eigenschaften der Rekursion sind auch dann gültig, wenn $k$ keine natürliche Zahl ist. Diese Eigenschaften sind also insofern charakteristisch für die Potenz, als dass sie auch für den verallgemeinerten Potenzbegriff mit beliebigen Exponenten gelten.
• Die rekursive Definition zeigt einen Weg, wie Sätze über Potenzen mit Hilfe von vollständiger Induktion bewiesen werden können.

Warum ist $x^{0}=1$ definiert?

Diese Frage ist berechtigt. Schließlich hätten wir ja auch $5^{1}=5$ als Rekursionsanfang definieren können. Zwar wäre dann $5^{0}$ undefiniert gewesen, aber die Gleichung $5^{1}=5$ lässt sich mit der Intuition der Potenz als k-fache Multiplikation leicht erklären. Auch die Potenz $5^{3}$ könnten wir ohne Probleme mit dem Rekursionsanfang $5^{1}=5$ berechnen.

Der Grund liegt darin, dass für die allgemeine Potenz die Gleichung

$x^{a+b}=x^{a}\cdot x^{b}$

erfüllt sein soll. Obige Gleichung soll für alle $a,b\in \mathbb {R}$ und insbesondere auch für $b=0$ erfüllt sein. Es soll also gelten:

$x^{a+0}=x^{a}\cdot x^{0}$

Gleichzeitig ist $a+0=a$ und deswegen

$x^{a}=x^{a+0}=x^{a}\cdot x^{0}$

Damit diese Gleichung für alle $x>0$ und $a\in \mathbb {R}$ gelten kann, muss $x^{0}=1$ sein. Die Tatsache $x^{0}=1$ folgt also aus der Gleichung

$x^{a+b}=x^{a}\cdot x^{b}$

welche man als die charakteristische Gleichung der Potenz ansehen kann. Auch der Rekursionsschritt folgt aus obiger Gleichung. Damit hat die rekursive Definition den Vorteil, dass sie auf der charakteristischen Gleichung der allgemeinen Potenz beruht und mit ihr begründet werden kann.

Hinweis

Es gibt in der Literatur keine eindeutige Definition für $0^{0}$. In Analysis-Lehrbüchern wird normalerweise (wie bei uns) $0^{0}=1$ gesetzt. Dadurch bleiben so wichtige Ergebnisse wie der binomische Lehrsatz und die Geometrische Summenformel für den jeweiligen Spezialfall gültig. Manche Autoren setzen hingegen $0^{0}=0$, da $0^{a}=0$ für alle $a\in \mathbb {R} \setminus \{0\}$ ist. Manchmal wird dieser Ausdruck in der Literatur auch je nach Kontext anders definiert, und gelegentlich bleibt $0^{0}$ auch undefiniert. Genauere Erklärungen findet man im Wikipedia-Artikel „Null hoch null“.

Das Prinzip der Rekursion

Im obigen Abschnitt hast du das Definitionsschema der Rekursion kennen gelernt. Hierfür ist die Angabe des Rekursionsanfangs und des Rekursionsschritts notwendig:

• Rekursionsschritt: Durch den Rekursionsschritt kann ein Ausdruck auf einen Ausdruck „mit geringerer Ordnung“ reduziert werden. Dieser Schritt wird so lange angewandt, bis man den Rekursionsanfang verwenden kann.
• Rekursionsanfang: Beendet die Rekursion, indem definiert wird, was der Ausdruck mit der „geringsten Ordnung“ sein soll.

Durch diese beiden Angaben wird eine Art Algorithmus definiert, wie Ausdrücke ausgerechnet werden können (siehe obiges Beispiel mit der Potenz). Solltest du programmieren können, wirst du dieses Prinzip vielleicht schon von deinen Programmiertätigkeiten her kennen.

Verständnisfrage: Definiere das Produkt $k\cdot x=\underbrace {x+x+\ldots +x} _{k{\text{-mal}}}$ mit $x\in \mathbb {R}$ und $k\in \mathbb {N} _{0}$ rekursiv.

Folgende zwei Formeln definieren das Produkt $k\cdot x$ rekursiv:

${\begin{aligned}0\cdot x&=0\\(k+1)\cdot x&=x+k\cdot x\end{aligned}}$

Rechenregeln für Potenzen

Übersicht

Um uns zu überlegen, warum unsere formale Definition der Potenz Sinn ergibt, haben wir auf folgende Rechenregel für $x\in \mathbb {R}$ und $m,n\in \mathbb {N} _{0}$ zurückgegriffen:

$x^{m+n}=x^{m}\cdot x^{n}$

Diese war aber nur eine Motivation für uns, wie wir die Potenz definieren wollen. Dass unsere formale Definition einer Potenz tatsächlich diese Rechenregel erfüllt, müssen wir erst noch beweisen. Dies werden wir im Folgenden nachholen. Auch werden wir folgende Rechenregeln beweisen, die aus der Schule bekannt sind:

• $(x^{k})^{n}=x^{kn}$ für alle $x\in \mathbb {R}$ und $k,n\in \mathbb {N} _{0}$
• $(x\cdot y)^{k}=x^{k}\cdot y^{k}$ für alle $x,y\in \mathbb {R}$ und $k\in \mathbb {N} _{0}$

Produkt von Potenzen mit gleicher Basis

Satz (Produkt von Potenzen mit gleicher Basis)

Sei $x\in \mathbb {R}$ und seien $m,n\in \mathbb {N} _{0}$. Dann gilt

$x^{m}\cdot x^{n}=x^{m+n}$

Wir betrachten das Produkt $x^{m}\cdot x^{n}$ zweier Potenzen $x^{m}$ und $x^{n}$ zur selben Basis $x\in \mathbb {R}$ mit irgendwelchen Exponenten $m,n\in \mathbb {N} _{0}$. Anschaulich ist

$x^{m}=\underbrace {x\cdot x\cdot \ldots \cdot x} _{m{\text{-mal}}}$

und

$x^{n}=\underbrace {x\cdot x\cdot \ldots \cdot x} _{n{\text{-mal}}}$

Also ist

$x^{m}\cdot x^{n}=\underbrace {x\cdot x\cdot \ldots \cdot x} _{m{\text{-mal}}}\cdot \underbrace {x\cdot x\cdot \ldots \cdot x} _{n{\text{-mal}}}$

Wir multiplizieren das Produkt von $m$ vielen $x$ mit dem Produkt von $n$ vielen $x$. Das können wir zusammenfassen zu einem Produkt von insgesamt $m+n$ vielen $x$:

$\underbrace {x\cdot x\cdot \ldots \cdot x} _{m{\text{-mal}}}\cdot \underbrace {x\cdot x\cdot \ldots \cdot x} _{n{\text{-mal}}}=\underbrace {x\cdot x\cdot \ldots \cdot x} _{(m+n){\text{-mal}}}$

Das Produkt von $m+n$ vielen $x$ ist genau die Potenz $x^{m+n}$:

$\underbrace {x\cdot x\cdot \ldots \cdot x} _{(m+n){\text{-mal}}}=x^{m+n}$

So haben wir einen anschauliche Argumentation dafür gefunden, dass folgende zu zeigende Rechenregel gilt.

$x^{m}\cdot x^{n}=x^{m+n}$

Jedoch haben wir die unsaubere Notation mit $\underbrace {\ldots }$ verwendet. Es ist auch nicht klar, was in diesem „Beweis“ passiert, wenn $m=0$ oder $n=0$ ist. Wie können wir diese Regel sauber mithilfe unserer rekursiven Definition der Potenz beweisen?

Zusammenfassung des Beweises (Produkt von Potenzen mit gleicher Basis)

Um die rekursive Definition der Potenz verwenden zu können, bietet sich ein Beweis mittels Vollständiger Induktion an. Allerdings kommen in der zu zeigenden Aussage zwei Variablen $m,n\in \mathbb {N} _{0}$ vor, über die eine vollständige Induktion gemacht werden kann. Wir suchen uns einfach eine davon aus, sagen wir $n$, und lassen die andere Variable, also $m$, fest.

Beweis (Produkt von Potenzen mit gleicher Basis)

Sei $m\in \mathbb {N} _{0}$ fest. Wir beweisen die Aussage mittels vollständiger Induktion über $n\in \mathbb {N} _{0}$:

Aussageform, deren Allgemeingültigkeit für $n\in \mathbb {N} _{0}$ bewiesen werden soll:

$x^{m}\cdot x^{n}=x^{m+n}$

1. Induktionsanfang:

$x^{m}\cdot x^{0}=x^{m}\cdot 1=x^{m}=x^{m+0}$

2. Induktionsschritt:

2a. Induktionsvoraussetzung:

$x^{m}\cdot x^{n}=x^{m+n}$

2b. Induktionsbehauptung:

$x^{m}\cdot x^{n+1}=x^{m+(n+1)}$

2c. Beweis des Induktionsschritts:

${\begin{aligned}&x^{m}\cdot x^{n+1}\\[0.3em]&{\color {OliveGreen}\left\downarrow \ {\text{Definition von }}x^{n+1}\right.}\\[0.3em]=\ &x^{m}\cdot (x\cdot x^{n})\\[0.3em]&{\color {OliveGreen}\left\downarrow \ {\text{Assoziativgesetz und Kommutativgesetz in }}\mathbb {R} \right.}\\[0.3em]=\ &x\cdot (x^{m}\cdot x^{n})\\[0.3em]&{\color {OliveGreen}\left\downarrow \ {\text{Induktionsvoraussetzung }}x^{m}\cdot x^{n}=x^{m+n}\right.}\\[0.3em]=\ &x\cdot x^{m+n}\\[0.3em]&{\color {OliveGreen}\left\downarrow \ {\text{Definition von }}x^{(m+n)+1}\right.}\\[0.3em]=\ &x^{(m+n)+1}\\[0.3em]&{\color {OliveGreen}\left\downarrow \ {\text{Assoziativgesetz in }}\mathbb {N} _{0}\right.}\\[0.3em]=\ &x^{m+(n+1)}\end{aligned}}$

Zusammenfassen von mehrmaligem Potenzieren

Satz (Zusammenfassen von mehrmaligem Potenzieren)

Sei $x\in \mathbb {R}$ und seien $k,n\in \mathbb {N} _{0}$. Dann gilt

$(x^{k})^{n}=x^{kn}$

Beweis (Zusammenfassen von mehrmaligem Potenzieren)

Sei $k\in \mathbb {N} _{0}$ fest. Wir beweisen die Aussage mittels vollständiger Induktion über $n\in \mathbb {N} _{0}$:

Aussageform, deren Allgemeingültigkeit für $n\in \mathbb {N} _{0}$ bewiesen werden soll:

$(x^{k})^{n}=x^{kn}$

1. Induktionsanfang:

$(x^{k})^{0}=1=x^{0}=x^{k\cdot 0}$

2. Induktionsschritt:

2a. Induktionsvoraussetzung:

$(x^{k})^{n}=x^{kn}$

2b. Induktionsbehauptung:

$(x^{k})^{n+1}=x^{k(n+1)}$

2c. Beweis des Induktionsschritts:

${\begin{aligned}&(x^{k})^{n+1}\\[0.3em]&{\color {OliveGreen}\left\downarrow \ {\text{Definition von }}(x^{k})^{n+1}\right.}\\[0.3em]=\ &x^{k}\cdot (x^{k})^{n}\\[0.3em]&{\color {OliveGreen}\left\downarrow \ {\text{Induktionsvoraussetzung }}(x^{k})^{n}=x^{kn}\right.}\\[0.3em]=\ &x^{k}\cdot x^{kn}\\[0.3em]&{\color {OliveGreen}\left\downarrow \ {\text{Produkt von Potenzen mit gleicher Basis}}\right.}\\[0.3em]=\ &x^{k+kn}\\[0.3em]&{\color {OliveGreen}\left\downarrow \ {\text{Distributivgesetz in }}\mathbb {N} _{0}\right.}\\[0.3em]=\ &x^{k(n+1)}\end{aligned}}$

Produkt von Potenzen mit gleichem Exponenten

Satz (Produkt von Potenzen mit gleichem Exponenten)

Seien $x,y\in \mathbb {R}$ und sei $k\in \mathbb {N} _{0}$. Dann gilt

$(x\cdot y)^{k}=x^{k}\cdot y^{k}$

Beweis (Produkt von Potenzen mit gleichem Exponenten)

Wir beweisen die Aussage mittels vollständiger Induktion über $k\in \mathbb {N} _{0}$:

Aussageform, deren Allgemeingültigkeit für $k\in \mathbb {N} _{0}$ bewiesen werden soll:

$(x\cdot y)^{k}=x^{k}\cdot y^{k}$

1. Induktionsanfang:

$(x\cdot y)^{0}=1=1\cdot 1=x^{0}\cdot y^{0}$

2. Induktionsschritt:

2a. Induktionsvoraussetzung:

$(x\cdot y)^{k}=x^{k}\cdot y^{k}$

2b. Induktionsbehauptung:

$(x\cdot y)^{k+1}=x^{k+1}\cdot y^{k+1}$

2c. Beweis des Induktionsschritts:

${\begin{aligned}&(x\cdot y)^{k+1}\\[0.3em]&{\color {OliveGreen}\left\downarrow \ {\text{Definition von }}(x\cdot y)^{k+1}\right.}\\[0.3em]=\ &(x\cdot y)\cdot (x\cdot y)^{k}\\[0.3em]&{\color {OliveGreen}\left\downarrow \ {\text{Induktionsvoraussetzung }}(x\cdot y)^{k}=x^{k}\cdot y^{k}\right.}\\[0.3em]=\ &(x\cdot y)\cdot (x^{k}\cdot y^{k})\\[0.3em]&{\color {OliveGreen}\left\downarrow \ {\text{Assoziativgesetz und Kommutativgesetz in }}\mathbb {R} \right.}\\[0.3em]=\ &(x\cdot x^{k})\cdot (y\cdot y^{k})\\[0.3em]&{\color {OliveGreen}\left\downarrow \ {\text{Definition von }}x^{k+1}{\text{ und }}y^{k+1}\right.}\\[0.3em]=\ &x^{k+1}\cdot y^{k+1}\end{aligned}}$

Potenzen mit negativen Exponenten

Für eine reelle Zahl $x\in \mathbb {R}$ wollen wir die Definition der Potenz $x^{k}$ auf ganzzahlige Exponenten $k\in \mathbb {Z}$ erweitern. Die Potenz soll also auch für negative Exponenten $k$ definiert werden. Dies wird sich nämlich als praktisch erweisen.

Auf den ersten Blick macht es nicht so viel Sinn. Nach unserer intuitiven Vorstellung wäre zum Beispiel $5^{-3}$ das Produkt von „$-3$ vielen“ $5$en. Was soll das bitteschön sein? Vielleicht $-5^{3}=-125$? Wenn wir so tun, als ob alle Rechenregeln für Potenzen weiterhin gelten, wäre aber $5=5^{1}=5^{-3+4}=5^{-3}\cdot 5^{4}=-125\cdot 625$. Es macht also keinen Sinn, $5^{-3}=-5^{3}$zu definieren. Wir sollten uns erst einmal überlegen, wie eine sinnvolle Definition aussehen könnte. Im Wesentlichen gibt es zwei Anforderungen:

• Die Definition sollte anschaulich erklärbar sein.
• Alle bisherigen Rechenregeln für Potenzen sollten weiterhin gelten.

Um diesen Anforderungen gerecht zu werden betrachten wir ein einfaches Beispiel: Wir wissen, dass $x^{0}=1$ für jede reelle Zahl $x$ gilt und dass $x^{a+b}=x^{a}\cdot x^{b}$ für $a,b\in \mathbb {N} _{0}$. Zur Verallgemeinerung auf $a,b\in \mathbb {Z}$ betrachten wir zunächst $a=1$,$b=-1$ und $x\neq 0$. Wir erhalten $1=x^{0}=x^{1+(-1)}=x\cdot x^{-1}$. Da wir $x\neq 0$ fordern können wir die Gleichung umstellen zu ${\frac {1}{x}}=x^{-1}$. Intuitiv ist klar, dass wir um $x^{-1}$ zu erhalten durch $x$ teilen müssen. Den gleichen Trick können wir auch für ein allgemeines $k\in \mathbb {N}$ anwenden. Mit der Forderung $x\neq 0$ ergibt sich aus $1=x^{0}=x^{k+(-k)}=x^{k}\cdot x^{-k}$ die folgende sinnvolle Definition:

Definition (Potenz mit ganzzahligem Exponenten)

Sei $x\in \mathbb {R} \setminus \{0\}$ und $k\in \mathbb {Z}$. Für $k\geq 0$ ist $x^{k}$ bereits definiert. Für $k<0$ legen wir fest:

$x^{k}:={\frac {1}{x^{-k}}}$

Beachte, dass in dieser Definition $x^{-k}$ bereits definiert ist, da $-k>0$ für $k<0$ gilt. Und wegen $x\neq 0$ ist auch $x^{-k}\neq 0$. Wir teilen also nicht durch $0$.

Hinweis

Man könnte sich fragen, ob eine sinnvolle Definition für "$0^{-k}$" möglich ist. Da wir in der Herleitung obiger Definition sowohl durch $x$ teilen als auch $x^{0}=1$ fordern, ist dieser Weg ausgeschlossen. Außerdem ist dieser Fall von geringem praktischen Interesse, da wir ja über $0^{k}=0$ für alle $k\in \mathbb {N}$ verfügen. Somit kann "$0^{-k}$" in $\mathbb {R}$ getrost undefiniert bleiben. Im erweiterten Zahlenraum ${\bar {\mathbb {R} }}:=\mathbb {R} \cup \{\infty \}$ wäre $0^{k}=\infty$ für alle $k<0$ sinnvoll.

Übertragung der Rechenregeln auf den ganzen Zahlen

Produkt von Potenzen mit gleicher Basis

Satz (Produkt von Potenzen mit gleicher Basis)

Sei $x\in \mathbb {R} \setminus \{0\}$ und seien $m,n\in \mathbb {Z}$. Dann gilt

$x^{m}\cdot x^{n}=x^{m+n}$

Beweis (Produkt von Potenzen mit gleicher Basis)

Unsere Definition von $x^{m}$, $x^{n}$ und $x^{m+n}$ hängt davon ab, ob die Exponenten $m$, $n$ und $m+n$ negativ sind oder nicht. Wir führen also eine Fallunterscheidung durch. In den einzelnen Fällen führen wir die Rechenregel jeweils auf die bereits bewiesene Regel für nichtnegative Exponenten zurück.

Fall 1: $m\geq 0$ und $n\geq 0$

Für $m,n\in \mathbb {N} _{0}$ wurde die Rechenregel bereits bewiesen, sodass in diesem Fall nichts mehr zu tun ist.

Fall 2: $m\geq 0$, $n<0$ und $m+n\geq 0$

Sei $n=-a$ und $m+n=b$ mit $a,b\in \mathbb {N} _{0}$. Somit ist $m=-n+m+n=a+b$. Nach Definition ist $x^{n}={\frac {1}{x^{a}}}$. Für $a,b\in \mathbb {N} _{0}$ haben wir bereits gezeigt, dass

$x^{a}\cdot x^{b}=x^{a+b}$

gilt. Es folgt

${\frac {1}{x^{n}}}\cdot x^{m+n}=x^{m}$

Multiplizieren wir beide Seiten der Gleichung mit $x^{n}$, so erhalten wir die Behauptung.

Fall 3: $m\geq 0$, $n<0$ und $m+n<0$

Sei $m=a$ und $m+n=-b$ mit $a,b\in \mathbb {N} _{0}$. Somit ist $n=-m+m+n=-(a+b)$. Nach Definition ist $x^{n}={\frac {1}{x^{a+b}}}$ und $x^{m+n}={\frac {1}{x^{b}}}$. Für $a,b\in \mathbb {N} _{0}$ haben wir bereits gezeigt, dass

$x^{a}\cdot x^{b}=x^{a+b}$

gilt. Es folgt

$x^{m}\cdot {\frac {1}{x^{m+n}}}={\frac {1}{x^{n}}}$

Multiplizieren wir beide Seiten der Gleichung mit $x^{m+n}\cdot x^{n}$, so erhalten wir die Behauptung.

Fall 4: $m<0$, $n\geq 0$ und $m+n\geq 0$

Da Addition in $\mathbb {Z}$ und Multiplikation in $\mathbb {R}$ kommutativ sind, gilt $x^{m}\cdot x^{n}=x^{n}\cdot x^{m}$ sowie $x^{m+n}=x^{n+m}$. Indem wir die Variablen $m$ und $n$ vertauschen, lässt sich dieser Fall also auf Fall 2 zurückführen.

Fall 5: $m<0$, $n\geq 0$ und $m+n<0$

Da Addition in $\mathbb {Z}$ und Multiplikation in $\mathbb {R}$ kommutativ sind, gilt $x^{m}\cdot x^{n}=x^{n}\cdot x^{m}$ sowie $x^{m+n}=x^{n+m}$. Indem wir die Variablen $m$ und $n$ vertauschen, lässt sich dieser Fall also auf Fall 3 zurückführen.

Fall 6: $m<0$ und $n<0$

Sei $m=-a$ und $n=-b$ mit $a,b\in \mathbb {N} _{0}$. Somit ist $m+n=-(a+b)$. Nach Definition ist $x^{m}={\frac {1}{x^{a}}}$, $x^{n}={\frac {1}{x^{b}}}$ und $x^{m+n}={\frac {1}{x^{a+b}}}$. Für $a,b\in \mathbb {N} _{0}$ haben wir bereits gezeigt, dass

$x^{a}\cdot x^{b}=x^{a+b}$

gilt. Es folgt

${\frac {1}{x^{m}}}\cdot {\frac {1}{x^{n}}}={\frac {1}{x^{m+n}}}$

Multiplizieren wir beide Seiten der Gleichung mit $x^{m}\cdot x^{n}\cdot x^{m+n}$, so erhalten wir die Behauptung.

Zusammenfassen von mehrmaligem Potenzieren

Satz (Zusammenfassen von mehrmaligem Potenzieren)

Sei $x\in \mathbb {R} \setminus \{0\}$ und seien $k,n\in \mathbb {Z}$. Dann gilt

$(x^{k})^{n}=x^{kn}$

Beweis (Zusammenfassen von mehrmaligem Potenzieren)

Wir führen eine Fallunterscheidung durch, ob $k$ und $n$ jeweils negativ sind oder nicht. In den einzelnen Fällen führen wir die Rechenregel jeweils auf die bereits bewiesene Regel für nichtnegative Exponenten zurück.

Fall 1: $k\geq 0$ und $n\geq 0$

Für $k,n\in \mathbb {N} _{0}$ wurde die Rechenregel bereits bewiesen, sodass in diesem Fall nichts mehr zu tun ist.

Fall 2: $k<0$ und $n\geq 0$

Sei $k=-a$ mit $a\in \mathbb {N} _{0}$. Nach Definition ist $x^{k}={\frac {1}{x^{a}}}$ und $x^{kn}={\frac {1}{x^{an}}}$. Wir wissen bereits, dass $(x^{a})^{n}=x^{an}$ gilt. Somit folgt

$1=\left({\frac {1}{x^{a}}}\cdot x^{a}\right)^{n}=\left({\frac {1}{x^{a}}}\right)^{n}\cdot (x^{a})^{n}=(x^{k})^{n}\cdot x^{an}=(x^{k})^{n}\cdot {\frac {1}{x^{kn}}}$

Also gilt wie gewünscht $(x^{k})^{n}=x^{kn}$.

Fall 3: $k\geq 0$ und $n<0$

Sei $n=-b$ mit $b\in \mathbb {N} _{0}$. Nach Definition ist $(x^{k})^{n}={\frac {1}{(x^{k})^{b}}}$ und $x^{kn}={\frac {1}{x^{kb}}}$. Wir wissen bereits, dass $(x^{k})^{b}=x^{kb}$ gilt. Somit folgt wie gewünscht

$(x^{k})^{n}={\frac {1}{(x^{k})^{b}}}={\frac {1}{x^{kb}}}=x^{kn}$

Fall 4: $k<0$ und $n<0$

Seien $k=-a$ und $n=-b$ mit $a,b\in \mathbb {N} _{0}$. Nach Definition ist $x^{k}={\frac {1}{x^{a}}}$ und $(x^{k})^{n}={\frac {1}{(x^{k})^{b}}}$. Wir wissen bereits, dass $(x^{a})^{b}=x^{ab}$ gilt. Somit folgt

$1=\left({\frac {1}{x^{a}}}\cdot x^{a}\right)^{b}=\left({\frac {1}{x^{a}}}\right)^{b}\cdot (x^{a})^{b}=(x^{k})^{b}\cdot x^{ab}={\frac {1}{(x^{k})^{n}}}\cdot x^{kn}$

Also gilt wie gewünscht $(x^{k})^{n}=x^{kn}$.

Produkt von Potenzen mit gleichem Exponenten

Satz (Produkt von Potenzen mit gleichem Exponenten)

Seien $x,y\in \mathbb {R} \setminus \{0\}$ und sei $k\in \mathbb {Z}$. Dann gilt

$(x\cdot y)^{k}=x^{k}\cdot y^{k}$

Beweis (Produkt von Potenzen mit gleichem Exponenten)

Unsere Definition der $k$-ten Potenz hängt davon ab, ob $k$ negativ ist oder nicht. Für $k\geq 0$ wurde der Beweis der Gleichung $(x\cdot y)^{k}=x^{k}\cdot y^{k}$ bereits durchgeführt. Damit fehlt nur noch der Beweis für $k<0$.

Sei also $k=-a$ mit $a\in \mathbb {N} _{0}$. Nach Definition ist $(x\cdot y)^{k}={\tfrac {1}{(x\cdot y)^{a}}}$ sowie $x^{k}={\tfrac {1}{x^{a}}}$ und $y^{k}={\tfrac {1}{y^{a}}}$. Für $a\in \mathbb {N} _{0}$ haben wir bereits gezeigt, dass gilt:

$(x\cdot y)^{a}=x^{a}\cdot y^{a}$

Es folgt

${\frac {1}{(x\cdot y)^{k}}}={\frac {1}{x^{k}}}\cdot {\frac {1}{y^{k}}}$

Multiplizieren wir beide Seiten der Gleichung mit $(x\cdot y)^{k}\cdot x^{k}\cdot y^{k}$, so erhalten wir die Behauptung.

Anordnungsaxiome

Die Anordnungsaxiome beschreiben die lineare Ordnung der reellen Zahlen und den Zusammenhang dieser Ordnung mit den arithmetischen Operationen, welche durch die Körperaxiome eingeführt wurden.

Herleitung der Anordnungsaxiome

Anders als andere Mathematik-Lehrbücher möchten wir an dieser Stelle nicht einfach die Anordnungsaxiome nennen, wir möchten vielmehr dieses Kapitel mit der Skizze eines Gedankenweges beginnen, über den man auf die Formulierung der Anordnungsaxiome kommen kann.

Charakteristische Eigenschaften der Kleiner-Relation

Transitivität: Aus $a>b$ und $b>c$ folgt $a>c$.

Aus unserer intuitiven Idee der Zahlengerade wissen wir, dass die reellen Zahlen eine Ordnung haben. Diese wollen wir nun durch die Anordungsaxiome beschreiben. Dazu müssen wir angeben, wie die Relationen $\leq$, $\geq$, $<$ und $>$ für die reellen Zahlen definiert sind.

Dabei reicht es aus, nur eine der vier Relationen anzugeben (siehe Ordnungsrelation aus dem Buch „Grundlagen der Mathematik“). Die restlichen drei Ordnungsrelationen ergeben sich dann automatisch aus der bereits angegebenen Relation.

Wir wählen hierzu die Kleiner-Relation $<$. Aus dem Kapitel zur Ordnungsrelation wissen wir bereits, dass für diese Relation die folgenden beiden Eigenschaften charakteristisch sind:

• $\forall x,y:x<y\ {\dot {\lor }}\ x=y\ {\dot {\lor }}\ y<x$ (Trichotomie der Kleiner-Relation)
• $\forall x,y,z:x<y\land y<z\implies x<z$ (Transitivität der Kleiner-Relation)

Das Zeichen ${\dot {\lor }}$ steht dabei für die Kontravalenz, die Entweder-Oder-Verknüpfung zwischen Aussagen.

Nun müssen wir noch klären, wie die Kleiner-Relation mit den arithmetischen Operationen der Addition, Subtraktion, Multiplikation und Division im Zusammenhang steht. Im Kapitel zu den Körperaxiomen wurde erklärt, dass die Subtraktion als Addition und die Division als Multiplikation angesehen werden können. Insofern reicht es, nur die Zusammenhänge mit der Addition und der Multiplikation zu untersuchen.

Zusammenhang mit der Addition

Aus dem Modell der reellen Zahlen als Zahlengerade wissen wir, dass wenn wir beide Seiten der Ungleichung $x<y$ mit einer reellen Zahl $a$ addieren, die Ordnung erhalten bleibt:

Addition beider Seiten einer Ungleichung mit einer Zahl erhält die Ungleichung

Es gilt also:

$x<y\implies a+x<a+y$

Aus der obigen Zeichnung lässt sich aber auch die umgekehrte Implikationsrichtung herleiten. Es gilt also auch

$a+x<a+y\implies x<y$

Es ist also genau dann $x<y$, wenn $a+x<a+y$ ist. Dementsprechend erhalten wir insgesamt die Äquivalenz:

$x<y\iff a+x<a+y$

Zusammenhang mit der Multiplikation

Bei der Multiplikation müssen wir unterscheiden, ob mit einer negativen oder mit einer positiven Zahl multipliziert wird. Werden beide Seiten der Ungleichung $x<y$ mit einer positiven Zahl $a$ multipliziert, so bleibt die Ungleichung erhalten:

Multiplikation mit positiver Zahl erhält die Ungleichung

Ähnlich wie bei der Addition gilt für positive Zahlen $a$:

$x<y\iff ax<ay$

Bei der Multiplikation mit negativen Zahlen dreht sich die Ordnung um:

Multiplikation mit negativer Zahl dreht die Ungleichung um

Es gilt für negative Zahlen $a$:

$x<y\iff ay<ax$

Die Multiplikation beider Seiten der Ungleichung $x<y$ mit 0 ergibt immer die falsche Aussage $0<0$ und muss deswegen nicht betrachtet werden.

Zusammenfassung bisheriger Ergebnisse

Bisher haben wir Folgendes herausgefunden: Es muss nur die Kleiner-Relation $<$ definiert werden. Diese hat die charakteristischen Eigenschaften:

• $\forall x,y:x<y\ {\dot {\lor }}\ x=y\ {\dot {\lor }}\ y<x$
• $x<y\land y<z\implies x<z$
• $x<y\iff a+x<a+y$
• Für positives $a$: $x<y\iff ax<ay$
• Für negatives $a$: $x<y\iff ay<ax$

Reduzierung auf die notwendigen Axiome

Eigentlich könnten wir bereits obige Aussagen als Anordnungsaxiome definieren. Jedoch haben wir im Einführungskapitel zu den reellen Zahlen das Ziel formuliert, dass möglichst wenige und nur die wirklich notwendigen Aussagen als Axiome definiert werden. Insofern müssen wir noch schauen, ob die obigen Aussagen in ihrer Aussagekraft oder in ihrer Anzahl reduziert werden können.

Beginnen wir mit der Ungleichung

$x<y$

Wegen $x<y\iff a+x<a+y$ können wir beide Seiten mit $-x$ addieren. Wir erhalten

${\begin{aligned}{\begin{array}{rrcl}&x&<&y\\\iff \ &x+(-x)&<&y+(-x)\\\iff \ &0&<&y-x\end{array}}\end{aligned}}$

Es ist also genau dann $x<y$, wenn $0<y-x$ ist. Um die Kleiner-Relation $<$ definieren zu können, reicht es also aus zu wissen, welche Zahlen positiv sind. Eine Zahl $x$ ist nämlich genau dann kleiner als $y$, wenn die bereits in den Körperaxiomen definierte Differenz $y-x$ positiv ist. Eine zweistellige Relation $x<y$ können wir also auf die Eigenschaft der Positivität und damit auf eine einstellige Relation reduzieren (Im Abschnitt zu den Relationen haben wir geklärt, dass Eigenschaften von Objekten als einstellige Relationen definiert werden).

Aus der Äquivalenz $x<y\iff 0<y-x$ ist erkennbar, dass es auf die Differenz $y-x$ ankommt. Wenn wir die obigen Aussagen geschickt umformen, dann erhalten wir:

• $\forall x,y:0<y-x\ {\dot {\lor }}\ 0=y-x\ {\dot {\lor }}\ 0<-(y-x)$
• $0<y-x\land 0<z-y\implies 0<z-x$
• $0<y-x\iff 0<a+y-(a+x)$
• Für positives $a$: $0<y-x\iff 0<ay-ax=a(y-x)$
• Für negatives $a$: $0<y-x\iff 0<ax-ay=-a(y-x)$

In der Aussage

$\forall x,y:0<y-x\ {\dot {\lor }}\ 0=y-x\ {\dot {\lor }}\ 0<-(y-x)$

können wir $z=y-x$ setzen und erhalten

$\forall z:0<z\ {\dot {\lor }}\ 0=z\ {\dot {\lor }}\ 0<-z$

Die Aussage

$0<y-x\iff 0<a+y-(a+x)$

ist trivialerweise immer wahr, weil $a+y-(a+x)=y-x$ ist. Sie muss deswegen nicht extra als Axiom aufgenommen werden. Bei der Transitivitätsaussage

$0<y-x\land 0<z-y\implies 0<z-x$

kann man erkennen, dass $z-x=(z-y)+(y-x)$ ist. Diese Aussage könnte man also beweisen, wenn gilt

$0<y-x\land 0<z-y\implies 0<(y-x)+(z-y)$

Obige Aussage können wir vereinfachen, indem wir $a=y-x$ und $b=z-y$ setzen. Wir erhalten dann

$0<a\land 0<b\implies 0<a+b$

Diese Aussage, welche auch unserer intuitiven Idee der reellen Zahlen entspricht, nehmen wir nun in die Anordnungsaxiome auf, um später die Transitivität der Kleiner-Relation zu beweisen. Weiterhin setzen wir bei der Aussage

Für positives $a$: $0<y-x\iff 0<ay-ax=a(y-x)$

für $y-x=b$ ein und erhalten analog zur gerade gefundenen Aussage mit der Addition positiver Zahlen:

$0<a\land 0<b\implies 0<ab$

Wie wir später sehen werden, kann die Regel mit der Multiplikation mit einer negativen Zahl aus den bereits genannten Axiomen hergeleitet werden. Insofern müssen wir auch diese Aussage nicht als Axiom definieren. Insgesamt erhalten wir folgende Aussagen als Axiome für die Anordnung reeller Zahlen:

• $\forall x:0<x\ {\dot {\lor }}\ 0=x\ {\dot {\lor }}\ 0<-x$
• $\forall a,b:0<a\land 0<b\implies 0<a+b$
• $\forall a,b:0<a\land 0<b\implies 0<ab$

Fassen wir nun unsere Erkenntnisse in Definitionen zusammen.

Definitionen zu den Anordnungsaxiomen

Die Ordnung der reellen Zahlen kann dadurch beschrieben werden, dass wir alle positiven Zahlen kennen. Wenn $x$ eine positive Zahl ist, schreiben wir $0<x$. Die Positivität der reellen Zahlen wird dabei über die Anordnungsaxiome definiert:

Definition (Anordnungsaxiome)

Die Anordnungsaxiome lauten

• Trichotomie der Positivität: Für alle reellen Zahlen $x$ gilt entweder $0<x$ oder $x=0$ oder $0<-x$. Mit den Abkürzungen "$\forall$" für "für alle" und "${\dot {\lor }}$" für "entweder oder" können wir dies schreiben als
  $\forall x\in \mathbb {R} :0<x\ {\dot {\lor }}\ 0=x\ {\dot {\lor }}\ 0<-x$
• Abgeschlossenheit bezüglich Addition: Für alle reellen Zahlen $a$ und $b$ gilt: Wenn $0<a$ und $0<b$ ist, dann ist auch $0<a+b$. In Zeichen:
  $\forall a,b\in \mathbb {R} :0<a\land 0<b\implies 0<a+b$
• Abgeschlossenheit bezüglich Multiplikation: Für alle reellen Zahlen $a$ und $b$ gilt: Wenn $0<a$ und $0<b$ ist, dann ist auch $0<ab$. In Zeichen:
  $\forall a,b\in \mathbb {R} :0<a\land 0<b\implies 0<ab$

Mit Hilfe der Positivitätseigenschaft $0<x$ können wir die Kleiner-Relation definieren:

Definition (Kleiner-Relation)

Die Kleiner-Relation $x<y$ ist durch folgende Äquivalenz definiert:

$x<y:\iff 0<y-x$

Es ist also genau dann $x$ kleiner als $y$, wenn die Differenz $y-x$ positiv ist. Über die Kleiner-Relation können wir alle weiteren Ordnungsrelationen definieren:

Definition (Weitere Ordnungsrelationen auf Grundlage der Kleiner-Relation)

Für die reellen Zahlen sind außerdem die Relationen $\geq$, $\leq$ und $>$ über folgende Äquivalenzen definiert:

• $x\leq y:\iff x<y\lor x=y$
• $x\geq y:\iff y<x\lor x=y$
• $x>y:\iff y<x$

Eine Struktur wie die der reellen Zahlen, die die Körper- und Anordnungsaxiome erfüllt, wird im Übrigen angeordneter Körper genannt:

Definition (angeordneter Körper)

Ein angeordneter Körper ist ein Körper, der die Anordnungsaxiome erfüllt.

Alternative Beschreibung der Anordnungsaxiome

Die Eigenschaft für eine Zahl, positiv zu sein, ist eine einstellige Relation. Im Kapitel zu den Relationen aus dem Buch „Grundlagen der Mathematik“ haben wir gelernt, dass einstellige Relationen über Mengen modelliert werden können. Hierzu definieren wir uns eine Menge $M$, die alle Zahlen $x$ enthält, für die $0<x$ gilt und die damit positiv sind. Wenn man eine solche Menge $M$ hat, kann man anstelle von $0<x$ auch $x\in M$ schreiben. Dementsprechend können die Anordnungsaxiome auch umgeschrieben werden:

Definition (Alternative Definition der Anordnungsaxiome)

Es gibt eine Menge $M\subseteq \mathbb {R}$ mit folgenden Eigenschaften:

• Trichotomie:
  $M\ {\dot {\cup }}\ \{0\}\ {\dot {\cup }}\ \{-x:x\in M\}=\mathbb {R}$
• Abgeschlossenheit bezüglich Addition:
  $\forall a,b:a\in M\land b\in M\implies a+b\in M$
• Abgeschlossenheit bezüglich Multiplikation:
  $\forall a,b:a\in M\land b\in M\implies ab\in M$

Eine Zahl wird positiv genannt, wenn sie Element von $M$ ist. Es gilt also

$0<x:\iff x\in M$

Alle weiteren Definitionen sind nun identisch zum obigen Abschnitt. Das Zeichen ${\dot {\cup }}$ ist im Übrigen die disjunkte Vereinigung.

Zur Erklärung der alternativen Anordnungsaxiome: Die Axiome zur Abgeschlossenheit wurden direkt übernommen, wobei $0<x$ durch $x\in M$ ersetzt wurde.

Zum Axiom der Trichotomie: Weil $M\ {\dot {\cup }}\ \{0\}\ {\dot {\cup }}\ \{-x:x\in M\}$ gleich $\mathbb {R}$ ist, ist jede reelle Zahl Element der Menge $M\ {\dot {\cup }}\ \{0\}\ {\dot {\cup }}\ \{-x:x\in M\}$. Nun ist aber die Vereinigung von $M\ {\dot {\cup }}\ \{0\}\ {\dot {\cup }}\ \{-x:x\in M\}$ disjunkt und damit jede reelle Zahl Element von genau einer der drei Mengen

1. $M$
2. $\{0\}$
3. $\{-x:x\in M\}$

Im ersten Fall $x\in M$ ist $0<x$. Für $x\in \{0\}$ ist $x=0$ und für $x\in \{-x:x\in M\}$ ist $0<-x$. Die Gleichung

$M\ {\dot {\cup }}\ \{0\}\ {\dot {\cup }}\ \{-x:x\in M\}=\mathbb {R}$

ist also äquivalent zur oben eingeführten Version der Trichotomie.

Folgerungen der Anordnungsaxiome

Ähnlich wie bei den Körperaxiomen beweisen wir nun erste kleinere Sätze, die direkt auf den Anordnungsaxiomen aufbauen. Insbesondere werden wir die charakteristischen Eigenschaften der Kleiner-Relation beweisen, die wir bereits im Abschnitt „Herleitung der Anordnungsaxiome“ erwähnt haben.

Übersicht zu den Folgen der Anordnungsaxiome

In diesem Kapitel werden wir zeigen, dass folgende Aussageformen allgemeingültig in $\mathbb {R}$ sind:

• Eigenschaften der Kleiner-Relation:
  • Trichotomie: $x<y\ {\dot {\lor }}\ x=y\ {\dot {\lor }}\ x>y$
  • Transitivität: $x<y\land y<z\implies x<z$
  • Translationsinvarianz: $x<y\iff x+a<y+a$
• Addition / Negatives und Kleiner-Relation:
  • $x<y\land a<b\implies x+a<y+b$
  • $x<y\iff -y<-x$
• Multiplikation und Kleiner-Relation:
  • $0<a\land x<y\implies ax<ay$
  • $0\leq x<y\land 0\leq a<b\implies ax<by$
  • $x<y\land a<0\implies ay<ax$
  • $x<0\land y<0\implies 0<xy$
  • $x\neq 0\implies x^{2}>0$
• Inverses und Kleiner-Relation:
  • $0<x\iff 0<x^{-1}$
  • $x<0\iff x^{-1}<0$
  • $0<x<y\iff 0<y^{-1}<x^{-1}$
  • $x<y<0\iff y^{-1}<x^{-1}<0$
  • $x<0<y\iff x^{-1}<0<y^{-1}$
• Bernoulli-Ungleichung:
  • $x\geq -1\land n\in \mathbb {N} \implies (1+x)^{n}\geq 1+n\cdot x$

Die Bernoulli-Ungleichung $(1+x)^{n}\geq 1+n\cdot x$ werden wir im Kapitel zur „Bernoulli-Ungleichung“ beweisen.

Eigenschaften der Kleiner-Relation

Trichotomie

Satz (Trichotomie der Kleiner-Relation)

Für alle reellen Zahlen $x$ und $y$ ist entweder $x<y$, $x=y$ oder $y<x$. Es gilt also:

$\forall x,y\in \mathbb {R} :x<y\ {\dot {\lor }}\ x=y\ {\dot {\lor }}\ x>y$

Beweis (Trichotomie der Kleiner-Relation)

Mit Hilfe der Äquivalenz $x<y\Leftrightarrow 0<y-x$ können wir die zu beweisende Aussage

$\forall x,y:x<y\ {\dot {\lor }}\ x=y\ {\dot {\lor }}\ y<x$

umformen zu

$\forall x,y:0<y-x\ {\dot {\lor }}\ 0=y-x\ {\dot {\lor }}\ 0<x-y=-(y-x)$

Für gegebene $x$ und $y$ müssen wir also beweisen, dass $0<y-x\ {\dot {\lor }}\ 0=y-x\ {\dot {\lor }}\ 0<-(y-x)$. Durch das Setzen von $z=y-x$ erhalten wir die zu beweisende Aussage

$0<z\ {\dot {\lor }}\ 0=z\ {\dot {\lor }}\ 0<-z$

Dies ist aber gerade die Trichotomie der Positivität, welche wir in den Anordnungsaxiomen gegeben haben und damit wahr ist. Insgesamt haben wir so den Satz bewiesen.

Transitivität

Satz (Transitivität der Kleiner-Relation)

Für alle $x$, $y$ und $z$ gilt

$x<y\land y<z\Rightarrow x<z$

Die Transitivitätseigenschaft der Kleiner-Relation rechtfertigt es, Ungleichungsketten wie

$x_{1}<x_{2}<\ldots <x_{n}$

zu schreiben. Wegen der Transitivität folgt dann nämlich auch $x_{1}<x_{n}$.

Beweis (Transitivität der Kleiner-Relation)

Sei $x<y$ und $y<z$. Nach Definition der Kleiner-Relation gilt damit $0<y-x$ und $0<z-y$. Wegen der Abgeschlossenheit der Positivität bezüglich der Addition ist damit auch

$0<(y-x)+(z-y)=z-x$

Damit ist aber auch $x<z$ nach Definition der Kleiner Relation.

Translationsinvarianz

Translationsinvarianz der Kleiner-Relation.

Satz (Translationsinvarianz der Kleiner-Relation)

Für alle reellen Zahlen $x$, $y$ und $a$ ist

$x<y\iff x+a<y+a$

Beweis (Translationsinvarianz der Kleiner-Relation)

Es ist

${\begin{aligned}{\begin{array}{rrcll}&x&<&y&\left|\ {\color {Orange}x<y\iff 0<y-x}\right.\\\iff &0&<&y-x&\left|\ {\color {Orange}y-x=y-a+a-x}\right.\\\iff &0&<&y-a+a-x&\left|\ {\color {Orange}y+a-a-x=(y+a)-(x+a)}\right.\\\iff &0&<&(y+a)-(x+a)&\left|\ {\color {Orange}w<u\iff 0<u-w}\right.\\\iff &x+a&<&y+a\end{array}}\end{aligned}}$

Addition / Negatives und Kleiner-Relation

Monotonie der Addition

Satz (Monotonie der Addition)

Aus $x<y$ und $a<b$ folgt $x+a<y+b$.

Beweis (Monotonie der Addition)

Aus $x<y$ folgt wegen der Translationsinvarianz der Kleiner-Relation $x+a<y+a$. Aus $a<b$ folgt analog $y+a<y+b$. Es ist also $x+a<y+a<y+b$. Aus der Transitivität folgt nun $x+a<y+b$.

Alternativer Beweis (Monotonie der Addition)

Aus $x<y$ und $a<b$ folgt aus der Definition der Kleiner-Relation $0<y-x$ und $0<b-a$. Nun sind nach den Anordnungsaxiomen die positiven Zahlen abgeschlossen bezüglich der Addition. Aus $0<y-x$ und $0<b-a$ folgt damit $0<(y-x)+(b-a)=(y+b)-(x+a)$. Nun wenden wir nochmals (allerdings in umgekehrter Richtung) die Definition der Kleiner-Relation an, so dass aus $0<(y+b)-(x+a)$ die Ungleichung $x+a<y+b$ folgt. Damit ist der Satz bewiesen.

Spiegelung bei Bildung des Negativen

Satz (Spiegelung bei Bildung des Negativen)

Es ist genau dann $x<y$, wenn $-y<-x$ ist.

Beweis (Spiegelung bei Bildung des Negativen)

${\begin{aligned}{\begin{array}{rrcll}&x&<&y&\left|\ {\color {Orange}x<y\Leftrightarrow 0<y-x}\right.\\\Leftrightarrow \ &0&<&y-x&\left|\ {\color {Orange}y=-(-y)}\right.\\\Leftrightarrow \ &0&<&-x-(-y)&\left|\ {\color {Orange}a<b\Leftrightarrow 0<b-a}\right.\\\Leftrightarrow \ &-y&<&-x\end{array}}\end{aligned}}$

Alternativer Beweis (Spiegelung bei Bildung des Negativen)

Sei $a=-x-y$. Es ist

${\begin{aligned}{\begin{array}{lrcll}&x&<&y&\ \left|\ {\color {Orange}{\text{Translationsinvarianz der Kleiner-Relation}}}\right.\\\Leftrightarrow \ &x+a&<&y+a&\ \left|\ {\color {Orange}{\text{a = -x -y}}}\right.\\\Leftrightarrow \ &x+(-x-y)&<&y+(-x-y)&\ \left|\ {\color {Orange}{\text{Kommutativ- und Assoziativgesetz der Addition}}}\right.\\\Leftrightarrow \ &(x+(-x))-y&<&(y+(-y))-x&\ \left|\ {\color {Orange}{\text{Addition einer Zahl mit ihrem Negativen ergibt Null}}}\right.\\\Leftrightarrow \ &0-y&<&0-x&\ \left|\ {\color {Orange}{\text{Nulleigenschaft}}}\right.\\\Leftrightarrow \ &-y&<&-x\end{array}}\end{aligned}}$

Multiplikation und Kleiner-Relation

Multiplikation mit positiver Zahl

Satz (Multiplikation mit positiver Zahl)

Ist $0<a$ und $x<y$, dann ist auch $ax<ay$.

Die Multiplikation mit einer positiven Zahl erhält also die Ungleichungsrelation.

Beweis (Multiplikation mit positiver Zahl)

Aus der Definition der Kleiner-Relation folgt aus $x<y$ die Ungleichung $0<y-x$. Weil die Mulitplikation bezüglich der Positivität abgeschlossen und $0<a$ ist, ist auch $0<a\cdot (y-x)$. Also $0<ay-ax$. Daraus folgt nach der Definition der Kleiner-Relation $ax<ay$.

Monotonie der Multiplikation mit nicht-negativen Zahlen

Satz (Monotonie der Multiplikation mit nicht-negativen Zahlen)

Aus $0\leq x<y$ und $0\leq a<b$ folgt $ax<by$.

Beweis (Monotonie der Multiplikation mit nicht-negativen Zahlen)

Fall 1: $x=0$ oder $a=0$

In diesem Fall ist $ax=0$. Es muss also bewiesen werden, dass $0<by$ ist. Jedoch ist nach Voraussetzung $0<y$ und $0<b$. $0<by$ folgt nun aus der Abgeschlossenheit der Positivität bezüglich der Multiplikation, welche in den Anordnungsaxiomen definiert wurde.

Fall 2: $0<x$ und $0<a$

Wegen $0<a$ und $x<y$ ist nach dem vergangenem Satz $ax<ay$. Gleichzeitig folgt aus $0<y$ und $a<b$ analog $ay<by$. Ingesamt haben wir $ax<ay<by$ und damit insgesamt $ax<by$.

Multiplikation mit negativer Zahl

Satz (Multiplikation mit negativer Zahl)

Aus $x<y$ und $a<0$ folgt $ay<ax$.

Beweis (Multiplikation mit negativer Zahl)

Nach dem Satz über die Spiegelung folgt aus $a<0$, dass $0<-a$ ist. Nach dem Satz zur Multiplikation mit positiven Zahlen ist dann $-a\cdot x<-a\cdot y$. Nun können wir wieder den Satz zur Spiegelung anwenden und erhalten $-(-a\cdot y)<-(-a\cdot x)$ und damit $ay<ax$, weil $-(-a)=a$ ist.

Produkte mit negativen Faktoren sind positiv

Satz (Produkte mit negativen Faktoren sind positiv)

Aus $x<0$ und $y<0$ folgt $0<xy$.

Beweis (Produkte mit negativen Faktoren sind positiv)

Nach dem Satz „Multiplikation mit negativer Zahl“ folgt aus $x<0$ und $y<0$, dass $0\cdot y<x\cdot y$ ist. Es ist also $0<xy$.

Quadrate von Zahlen ungleich 0 sind positiv

Satz (Quadrate von Zahlen ungleich 0 sind positiv)

Alle Quadrate $x^{2}$ für Zahlen $x\neq 0$ sind positiv.

Zusammen mit $0^{2}=0$ folgt aus dem obigen Satz direkt, dass Quadratzahlen nicht negativ sind. Da wir im Kapitel „Folgerungen aus den Körperaxiomen“ bewiesen haben, dass ein Produkt von reellen Zahlen genau dann gleich Null ist, wenn mindestens einer der Faktoren Null ist, gilt zusätzlich die Äquivalenz $x\neq 0\iff x^{2}\neq 0$. Damit und aus dem obigen Satz folgt die Äquivalenz $x\neq 0\iff 0<x^{2}$.

Außerdem kann mit diesem Satz bewiesen werden, dass $1$ eine positive Zahl ist. Es ist nämlich $1=1\cdot 1$ und damit ist $1$ eine Quadratzahl. Nach den Körperaxiomen ist $1\neq 0$ und damit folgt aus obigem Satz, dass $1$ eine positive Zahl sein muss.

Beweis (Quadrate von Zahlen ungleich 0 sind positiv)

Fall 1: $x>0$

Aus dem Satz zur Multiplikation mit positiven Zahlen folgt aus $x>0$, dass $x\cdot x>x\cdot 0$, also $x^{2}>0$ ist.

Fall 2: $x<0$

Mit $x<0$ folgt aus dem Satz zur Multiplikation mit negativen Zahlen, dass $x\cdot x>x\cdot 0$ ist und damit $x^{2}>0$.

Inverses und Kleiner-Relation

Inverse haben gleiches Vorzeichen

Satz (Inverse positiver Zahlen sind positiv)

Es ist genau dann $0<x$, wenn $0<x^{-1}$.

Beweis (Inverse positiver Zahlen sind positiv)

Fall 1: $0<x\Rightarrow 0<x^{-1}$

Wegen $0<x$ ist $x^{-1}\neq 0$ und damit $x^{-2}:=x^{-1}\cdot x^{-1}$ positiv, weil wir bereits gezeigt haben, dass Quadrate von Zahlen ungleich 0 positiv sind. Es folgt damit nach dem Satz zur Multiplikation mit positiver Zahlen, dass $0\cdot x^{-2}<x\cdot x^{-2}$ ist. Nun ist $0\cdot x^{-2}=0$ und $x\cdot x^{-2}=x^{-1}$ und damit $0<x^{-1}$.

Fall 2: $0<x^{-1}\Rightarrow 0<x$

Aus dem ersten Fall folgt aus $0<x^{-1}$, dass $0<\left(x^{-1}\right)^{-1}$ ist. Wegen $\left(x^{-1}\right)^{-1}=x$ ist somit $0<x$.

Satz (Inverse negativer Zahlen sind negativ)

Es ist genau dann $x<0$, wenn $x^{-1}<0$ ist.

Beweis (Inverse negativer Zahlen sind negativ)

Sei $x$ eine negative Zahl, also $x<0$. Aus der eben bewiesenen Äquivalenz $0<a\Leftrightarrow 0<a^{-1}$ wissen wir, dass $x^{-1}$ nicht positiv sein kann (sonst müsste ja $x$ auch positiv sein). $x^{-1}$ ist aber auch nicht 0, weil sonst $1=x\cdot x^{-1}=x\cdot 0$ wäre. Also muss $x^{-1}$ negativ sein aufgrund der Trichotomie der Kleiner-Relation. Analog kann man von der Negativität von $x^{-1}$ auf die Negativität von $x$ schließen.

Kleiner-Relation und Inversenbildung

Satz (Kleiner-Relation und Inversenbildung)

Für alle $x,y\in \mathbb {R}$ gilt:

• $0<x<y\iff y^{-1}<x^{-1}$.
• $x<y<0\iff y^{-1}<x^{-1}$.
• $x<0<y\iff x^{-1}<0<y^{-1}$.

Beweis (Kleiner-Relation und Inversenbildung)

Beweisschritt 1: $0<x<y\implies 0<y^{-1}<x^{-1}$

Wegen $0<x<y$ gilt sowohl $0<x$ als auch $0<y$ (Transitivität der Kleiner-Relation). Da sowohl $x$ als auch $y$ positiv sind, ist auch ihr Produkt positiv (Abgeschlossenheit der Positivität bezüglich Multiplikation). Es gilt also: $0<xy$. Somit gilt aber auch:$0<(xy)^{-1}=x^{-1}y^{-1}$ (Inverse haben gleiches Vorzeichen). Aus dem Satz zur Multiplikation mit einer positiven Zahl folgt nun: $x\cdot \left(x^{-1}y^{-1}\right)<y\cdot \left(x^{-1}y^{-1}\right)$. Wegen $x\cdot \left(x^{-1}y^{-1}\right)=y^{-1}$ und $y\cdot \left(x^{-1}y^{-1}\right)=x^{-1}$ ist deshalb $y^{-1}<x^{-1}$. Da außerdem Inverse stets dieselben Vorzeichen haben (Siehe Beweis zum Satz $0<x\implies 0<x^{-1}$), ist $0<y^{-1}<x^{-1}$.

Beweisschritt 2: $0<y^{-1}<x^{-1}\implies 0<x<y$

Sei $0<y^{-1}<x^{-1}$. Nach dem ersten Beweisschritt ist damit $0<\left(x^{-1}\right)^{-1}<\left(y^{-1}\right)^{-1}$. Da $\left(x^{-1}\right)^{-1}=x$ und $\left(y^{-1}\right)^{-1}=y$ ist, ist damit $0<x<y$.

Beweisschritt 3: $x<y<0\implies y^{-1}<x^{-1}<0$

Sei $x<y<0$. Aus der Transitivität der Kleiner-Relation folgt, dass sowohl $y<0$ als auch $x<0$ ist. Aus dem Satz „Produkte mit negativen Faktoren sind positiv“ folgt, dass ihr Produkt positiv ist. Es gilt also: $0<xy$. Somit ist auch: $0<(xy)^{-1}=x^{-1}y^{-1}$ (Inverse haben gleiches Vorzeichen).

Aus dem Satz zur Multiplikation mit einer positiven Zahl folgt nun aus $x<y$ und $0<x^{-1}y^{-1}$, dass $x\cdot \left(x^{-1}y^{-1}\right)<y\cdot \left(x^{-1}y^{-1}\right)$. Wegen $x\cdot \left(x^{-1}y^{-1}\right)=y^{-1}$ und $y\cdot \left(x^{-1}y^{-1}\right)=x^{-1}$ ist deshalb $y^{-1}<x^{-1}$. Da $y^{-1}$ und $x^{-1}$ negativ sind (Inverse haben gleiches Vorzeichen), ist damit $y^{-1}<x^{-1}<0$.

Beweisschritt 4: $y^{-1}<x^{-1}<0\implies x<y<0$

Sei $y^{-1}<x^{-1}<0$. Aus dem dritten Beweisschritt folgt $\left(x^{-1}\right)^{-1}<\left(y^{-1}\right)^{-1}<0$. Mit $\left(x^{-1}\right)^{-1}=x$ und $\left(y^{-1}\right)^{-1}=y$ folgt $x<y<0$.

Beweisschritt 5: $x<0<y\implies x^{-1}<0<y^{-1}$

In diesem Fall findet hingegen keine Umkehrung der Kleiner-Relation. Der Grund dafür ist, dass $x$ und $y$ ungleiches Vorzeichen haben. $x$ wird nämlich als negativ vorausgesetzt und $y$ als positiv. Da Inverse, wie bereits bewiesen, ihr Vorzeichen beibehalten, gilt $x^{-1}<0$ und $0<y^{-1}$. Aus der Transitivität der Kleiner-Relation folgt somit, dass $x^{-1}<y^{-1}$ ist. Insgesamt folgt also: $x<0<y\implies x^{-1}<0<y^{-1}$

Beweisschritt 6: $x^{-1}<0<y^{-1}\implies x<0<y$

Dies folgt aus dem fünften Beweisschritt. Nach diesem gilt $x^{-1}<0<y^{-1}\implies \left(x^{-1}\right)^{-1}<0<\left(y^{-1}\right)^{-1}$. Mit $\left(x^{-1}\right)^{-1}=x$ und $\left(y^{-1}\right)^{-1}=y$ folgt die zu zeigende Aussage.

Betragsfunktion, Maximum und Minimum

Nachdem wir in den vergangenen Kapiteln die Anordnungsaxiome eingeführt haben, führen wir nun die ersten Begriffe ein, die direkt auf der Ordnung der reellen Zahlen aufbauen.

Maximum und Minimum

Definition

Das Maximum zweier Zahlen gibt die größere der beiden Zahlen zurück, während das Minimum die kleinere Zahl zurückgibt. Beide Funktionen sind folgendermaßen definiert:

Definition (Maximum)

$\max(x,y)={\begin{cases}x&;\,x\geq y\\y&;\,{\text{sonst}}\end{cases}}$

Definition (Minimum)

$\min(x,y)={\begin{cases}x&;\,x\leq y\\y&;\,{\text{sonst}}\end{cases}}$

Es ist genauso möglich, das Maximum und Minimum von endlich vielen Zahlen anzugeben. Hierzu definieren wir

$\max(\{x_{1},x_{2},\ldots x_{n}\})=\max(x_{1},\max(x_{2},\ldots \max(x_{n-1},x_{n})))$

und

$\min(\{x_{1},x_{2},\ldots x_{n}\})=\min(x_{1},\min(x_{2},\ldots \min(x_{n-1},x_{n})))$

Beachte, dass es nur möglich ist, das Maximum und Minimum von endlichen Mengen auszurechnen. Für eine Verallgemeinerung des Maximums und Minimums auf unendliche Mengen werden wir später die Begriffe vom „Supremum“ und vom „Infimum“ einführen.

Charakteristische Eigenschaften von Minimum und Maximum

Das Maximum und das Minimum erfüllen folgende Eigenschaften für beliebige reelle Zahlen $x$, $y$ und $z$, welche für diese Funktionen charakteristisch sind:

Satz (Maximum und Minimum sind genauso groß, wie die größte, bzw. kleinste Zahl die sie enthalten.)

Jede reelle Zahl, die größer ist als das Maximum zweier beliebiger reellen Zahlen $x$ und $y$, ist auch größer als beide Zahlen. Umgekehrt gilt auch: Jede reelle Zahl, die kleiner ist als das Minimum zweier beliebiger reellen Zahlen $x$ und $y$ ist auch kleiner als beide Zahlen.

${\begin{aligned}\max(x,y)\leq z&\iff x\leq z\land y\leq z\\z\leq \min(x,y)&\iff z\leq x\land z\leq y\end{aligned}}$

Beweis (Maximum und Minimum sind genauso groß, wie die größte, bzw. kleinste Zahl die sie enthalten.)

Beweisschritt: $\max(x,y)\leq z\Rightarrow x\leq z\land y\leq z$

Nach der Definition des Maximums gilt $\max(x,y)={\begin{cases}x&;\,x\geq y\\y&;\,{\text{sonst}}\end{cases}}$. Hier müssen wir also zwei Fälle untersuchen: $x\geq y$ und den umkehrten Fall. Durch die Trichotomie muss hier gelten $x<y$, da $x=y$ und $x>y$ bereits im ersten Fall betrachtet werden.

Fall 1: $x\geq y$

Da nun nach Definition des Maximums $\max(x,y)=x$ gilt können wir $x$ einsetzen und erhalten damit die immer wahre Aussage $x\leq z\Rightarrow x\leq z$. Daher wissen wir nun durch die Trichotomie $y\leq x\leq z$ und können über die Transitivität $y\leq z$ folgern. (Beachte, das nach Definition $x\leq y$ und $y\geq x$ äquivalent sind.)

Fall 2: $x<y$ ("sonst")

Im zweiten Fall können wir $\max(x,y)=y$ setzen und wir wissen bereits, dass $x<y$ sein muss. Also können wir schreiben $x<y\leq z\Rightarrow x\leq z\land y\leq z$. Die Transitivität sagt uns, dass wir diesen Ausdruck auch als $x<z\land y\leq z\Rightarrow x\leq z\land y\leq z$ schreiben können. Der Ausdruck $x<z\Rightarrow x\leq z$ ist aber nach der Definition von $\leq$ immer Wahr.

Beweisschritt: $x\leq z\land y\leq z\Rightarrow max(x,y)\leq z$

Analog zur obigen Fallunterscheidung sollten wir auch hier untersuchen, wie sich welcher Fall auswirkt. Setzt man die jeweilige Bedingung für das Maximum ein, ergibt sich eine wahre Aussage für beide Fälle:

Fall 1: $x\geq y$

$x\leq z\land y\leq z\Rightarrow x\leq z$

Fall 2: $x<y$ ("sonst")

$x\leq z\land y\leq z\Rightarrow y\leq z$

Beweisschritt: $z\leq min(x,y)\Rightarrow z\leq x\land z\leq y$

Betrachten wir zunächst wieder die Definition des Minimums $\min(x,y)={\begin{cases}x&;\,x\leq y\\y&;\,{\text{sonst}}\end{cases}}$ so fällt auf, dass wir wieder zwei Fälle beachten müssen: $x\leq y$ und das "sonst". Im Sinne der Trichotomie muss hier gelten $y<x$ da $y=x$ und $y>x$ durch den ersten Fall ausgeschlossen werden.

Fall 1: $x\leq y$

Nach Definition des Minimums können wir in diesem Fall $min(x,y)=x$ einsetzen. Da wir außerdem noch wissen, dass $x\leq y$ gelten muss, erhalten wir $z\leq x\leq y$ und durch die Transitivität $z\leq x\land z\leq y$.

Fall 2: $y<x$ ("sonst")

Ähnlich dem ersten Fall können wir $y$ und das Minimum gleichsetzen ($min(x,y)=y$), was nach der Definition des Minimums gelten muss. Daher muss $z\leq y<x$ gelten. Durch die Transitivität der Relation können wir das zu $z\leq y\land z<x$ auseinander ziehen. Auch der Ausdruck $z<x\Rightarrow z\leq x$ ist immer wahr, da $z\leq x$ immer dann wahr ist, wenn auch $z<x$ wahr ist (Siehe Definition von $\leq$).

Beweisschritt: $z\leq x\land z\leq y\Rightarrow z\leq min(x,y)$

Setzt man die jeweilige Bedingung für $min(x,y)$ in den zu zeigenden Ausdruck ein, so erhalten wir für die beiden möglichen Fälle immer eine wahre Aussage.

Fall 1: $x\leq y$

$z\leq x\land z\leq y\Rightarrow z\leq x$

Fall 2: $y<x$ ("sonst")

$z\leq x\land z\leq y\Rightarrow z\leq y$

Diese Eigenschaften werden in der Analysis genutzt, um obere bzw. untere Schranken auszurechnen. Wenn beispielsweise eine Variable $n$ gleichzeitig größer oder gleich $N_{1}$ und größer oder gleich $N_{2}$ sein soll, so definieren wir $n\geq \max(N_{1},N_{2})$. Dann ist nämlich garantiert, dass $n\geq N_{1}$ und $n\geq N_{2}$.

To-Do:

Abschnitt muss ausgebaut werden:

• Frage muss beantwortet werden: Warum sind die obigen Äquivalenzen charakteristisch für das Maximum und das Minimum?

Betrag

Definition

Erklärung des Betrags. (YouTube-Video vom Kanal Quatematik)

Verlauf der Betragsfunktion.

Der Betrag (auch Betragsfunktion oder Absolutbetrag genannt) gibt den Abstand einer Zahl zur Null zurück. Er ist definiert über:

Definition (Betrag)

Der Betrag $|x|$ einer reellen Zahl $x$ ist definiert durch

$|x|=\max(x,-x)={\begin{cases}x&;\,x\geq 0\\-x&;\,x<0\end{cases}}$

$|x-y|$ ist der Abstand zwischen $x$ und $y$.

In der Analysis werden wir den Betrag vor allem in der Form $|x-y|$ kennen lernen. Dieser Term gibt den Abstand der Zahlen $x$ und $y$ und damit eine Art „Fehler“ zwischen $x$ und $y$ wieder. In der Analysis werden wir diesen Abstand verwenden, um das Konzept des Grenzwertes zu beschreiben.

Verständnisfrage: Warum ist $\max(x,-x)={\begin{cases}x&;\,x\geq 0\\-x&;\,x<0\end{cases}}$?

Wegen Trichotomie ist entweder $x>0$, $x=0$ oder $x<0$.

Fall 1: $x>0$

Aus $x>0$ folgt $-x<0$, also $x>0>-x$ und damit $x>-x$. Es ist dann

$\max(x,-x)=x={\begin{cases}x&;\,x\geq 0\\-x&;\,x<0\end{cases}}$

Fall 2: $x=0$

Ist $x=0$, dann ist auch $-x=0$, weil Null ihr eigenes Negative ist. Entsprechend ist

$\max(x,-x)=0={\begin{cases}x&;\,x\geq 0\\-x&;\,x<0\end{cases}}$

Fall 3: $x<0$

Aus $x<0$ folgt $-x>0$, also $x<0<-x$ und damit $x<-x$. Es ist dann

$\max(x,-x)=-x={\begin{cases}x&;\,x\geq 0\\-x&;\,x<0\end{cases}}$

Charakteristische Eigenschaft

Für das Maximum und Minimum haben wir folgende charakteristische Eigenschaft kennen gelernt:

${\begin{aligned}\max(x,y)\leq z&\iff x\leq z\land y\leq z\\z\leq \min(x,y)&\iff z\leq x\land z\leq y\end{aligned}}$

Aus dieser können wir eine für Beweise nützliche Eigenschaft für Beträge ableiten. Ersetzt man nämlich $y$ durch $-x$, ergibt sich:

${\begin{aligned}\max(x,-x)\leq z&\iff x\leq z\land -x\leq z\\z\leq \min(x,-x)&\iff z\leq x\land z\leq -x\end{aligned}}$

Daraus folgt:

${\begin{aligned}|x|\leq z&\iff x\leq z\land -x\leq z\\z\leq -|x|&\iff z\leq x\land z\leq -x\end{aligned}}$

Es ist also genau dann $|x|\leq z$, wenn $x\leq z$ und $-x\leq z$ ist. Analog ist genau dann $z\leq -|x|$, wenn $z\leq x$ und $z\leq -x$.

Eigenschaften (Übersicht)

Es folgt eine Zusammenfassung aller wichtigen Eigenschaften des Betrags. Dabei habe ich auch die Form aufgeführt, die dir in den Beweisen der Analysis oft begegnen wird:

Eigenschaft des Betrags	Eigenschaft für den Abstand $|x-y|$
$|x|=0\Leftrightarrow x=0$	$|x-y|=0\Leftrightarrow x=y$
$|x\cdot y|=|x|\cdot |y|$	$|\lambda \cdot (x-y)|=|\lambda |\cdot |x-y|$
$|x+y|\leq |x|+|y|$	$|x-y|\leq |x-z|+|z-y|$
$|x-y|\geq ||x|-|y||$	$|x-y|\geq ||x|-|y||$
$\left|{\tfrac {x}{y}}\right|={\tfrac {|x|}{|y|}}$	$\left|{\tfrac {x-y}{\lambda }}\right|={\tfrac {|x-y|}{|\lambda |}}$

Beweise der Betragseigenschaften

Die Null ist die einzige Zahl mit Betrag null

Satz (Die Null ist die einzige Zahl mit Betrag null)

Es ist genau dann der Betrag einer Zahl 0, wenn die Zahl selbst 0 ist. Es gilt also

$|x|=0\Leftrightarrow x=0$

Beweis (Die Null ist die einzige Zahl mit Betrag null)

Beweisschritt: $x=0\Rightarrow |x|=0$

Für $x=0$ ist $|x|=\max(0,-0)=\max(0,0)=0$.

Beweisschritt: $|x|=0\Rightarrow x=0$

Nach der Definition des Betrags folgt aus $|x|=0$, dass $\max(x,-x)=0$ ist. Nun impliziert $\max(a,b)=c$ die beiden Ungleichungen $a\leq c$ und $b\leq c$. Damit folgen aus $\max(x,-x)=0$ die beiden Ungleichungen $x\leq 0$ und $-x\leq 0$. Nach Multiplikation von der Ungleichung $-x\leq 0$ mit $-1$ erhalten wir $0\leq x$. Damit haben wir die beiden Bedingungen $x\leq 0$ und $0\leq x$. Mit der Antisymmetrie der Kleiner-Gleich-Relation („Aus $a\leq b$ und $b\leq a$ folgt $a=b$“) erhalten wir $x=0$.

Alternativer Beweis (Die Null ist die einzige Zahl mit Betrag null)

Beweisschritt: $x=0\Rightarrow |x|=0$

Für $x=0$ ist $|x|=\max(0,-0)=\max(0,0)=0$.

Beweisschritt: $|x|=0\Rightarrow x=0$

Gegeben sei $|x|=0$. Nach der Definition des Betrags ist $\max(x,-x)=0$. Somit ist $0=x$ oder $0=-x$. Für $0=x$ bzw. $x=0$ gibt es nichts mehr zu beweisen. Andererseits folgt aus $0=-x$ bzw. $-x=0$, dass $x=-0$ ist (Spiegelung bei Bildung des Negativen). Da aber das Negative der Null die Null selbst ist, folgt aus $x=-0$, dass $x=0$ ist. In beiden Fällen $0=x$ oder $0=-x$ folgt also $x=0$, womit dieser Beweisschritt gezeigt ist.

Multiplizität

Satz (Multiplizität)

Es ist $|xy|=|x|\cdot |y|$.

Beweis (Multiplizität)

Fall 1: $x=0$ und $y$ beliebig

Es ist $|xy|=|0\cdot y|=|0|=0=0\cdot |y|=|0|\cdot |y|=|x|\cdot |y|$.

Fall 2: $x$ beliebig und $y=0$

Es ist $|xy|=|x\cdot 0|=|0|=0=|x|\cdot 0=|x|\cdot |0|=|x|\cdot |y|$.

Fall 3: $x>0$ und $y>0$

Es folgt $xy>0$ und damit $|xy|=xy=|x|\cdot |y|$.

Fall 4: $x<0$ und $y>0$

Es folgt $xy<0$ und damit $|xy|=-xy$. Wegen $x<0$ ist $|x|=-x$. Somit haben wir $|xy|=-xy=(-x)\cdot y=|x|\cdot |y|$.

Fall 5: $x>0$ und $y<0$

Es folgt $xy<0$ und damit $|xy|=-xy$. Wegen $y<0$ ist $|y|=-y$. Somit haben wir $|xy|=-xy=x\cdot (-y)=|x|\cdot |y|$.

Fall 6: $x<0$ und $y<0$

Es folgt $xy>0$ und damit $|xy|=xy=(-x)\cdot (-y)=|x|\cdot |y|$.

Dreiecksungleichung

Satz (Dreiecksungleichung)

Für alle reellen Zahlen $x$ und $y$ ist $|x+y|\leq |x|+|y|$.

Beweis (Dreiecksungleichung)

Aus $x\leq |x|$ und $y\leq |y|$ folgt $x+y\leq |x|+|y|$ („Monotonie der Addition“). Analog folgt aus $-x\leq |x|$ und $-y\leq |y|$, dass $-x+(-y)\leq |x|+|y|$, also $-(x+y)\leq |x|+|y|$ ist (wiederum „Monotonie der Addition“). Da $|x+y|$ entweder $x+y$ oder $-(x+y)$ ist, ist auch $|x+y|\leq |x|+|y|$.

Die Dreiecksungleichung werden wir vor allem nutzen, um Abstände $|x-y|$ nach oben abzuschätzen. In die Differenz kann nämlich ein Term $z-z$ eingeschoben werden, also

$|x-y|=|(x-z)+(z-y)|\leq |x-z|+|z-y|$

Der Abstand $|x-y|$ kann also über die Abstände $|x-z|$ und $|z-y|$ nach oben abgeschätzt werden. Der obige Trick wird in der Analysis häufig verwendet.

Abschätzung des Abstands nach unten

Satz (Abschätzung des Abstands nach unten)

Es ist $|x-y|\geq {\big |}|x|-|y|{\big |}$.

Beweis (Abschätzung des Abstands nach unten)

Es ist

$|x|=|(x-y)+y|\leq |x-y|+|y|$

und damit nach Umformung der Ungleichung

$|x|-|y|\leq |x-y|$

Analog folgt aus

$|y|=|(y-x)+x|\leq |y-x|+|x|$

die Ungleichung

$|y|-|x|\leq |y-x|=|x-y|$

Insgesamt ist also sowohl $|x|-|y|$ als auch $|y|-|x|=-(|x|-|y|)$ kleiner als $|x-y|$. Damit ist

${\big |}|x|-|y|{\big |}=\max(|x|-|y|,|y|-|x|)\leq |x-y|$

Betrag des Quotienten

Satz (Betrag des Quotienten)

Für Quotienten ${\tfrac {x}{y}}$ ist

$\left|{\frac {x}{y}}\right|={\frac {|x|}{|y|}}$

Beweis (Betrag des Quotienten)

Es ist wegen der Multiplizität des Betrags:

$|x|=\left|y\cdot {\tfrac {x}{y}}\right|=|y|\cdot \left|{\tfrac {x}{y}}\right|$

Durch Multiplikation von $|y|^{-1}$ auf beiden Seiten der Gleichung erhalten wir die zu beweisende Gleichung.

Alternativer Beweis (Betrag des Quotienten)

Gegeben sei $\left|{\tfrac {x}{y}}\right|$. Wegen der Multiplizität des Betrags gilt: $\left|{\tfrac {x}{y}}\right|\cdot |y|=\left|{\tfrac {x}{y}}\cdot y\right|=|x|$. Wir haben somit: $\left|{\tfrac {x}{y}}\right|\cdot |y|=|x|$. Durch Multiplikation von $|y|^{-1}$ auf beiden Seiten der Gleichung erhalten wir die zu beweisende Gleichung.

Beweise der Abstandseigenschaften

Abstand mit Betrag Null

Satz (Abstand mit Betrag null)

Der Abstand zwischen $x$ und $y$ ist genau dann null, wenn $x$ und $y$ identisch sind. Es gilt also

$|x-y|=0\iff x=y$

Beweis (Abstand mit Betrag null)

Gegeben sei $|x-y|=0$. Sei nun $z=x-y$, so dass $|x-y|=|z|=0$ ist. Da die Null die einzige Zahl mit dem Betrag null ist, gilt:

$|z|=0\iff z=0$

Durch Rücksubstitution ergibt sich:

$|x-y|=0\iff x-y=0$

bzw.

$|x-y|=0\iff x=y$

Multiplizität des Abstands

Satz (Multiplizität des Abstands)

Es ist $|\lambda \cdot (x-y)|=|\lambda |\cdot |x-y|$.

Beweis (Multiplizität des Abstands)

Gegeben sei $|\lambda \cdot (x-y)|$. Sei nun $z=x-y$, so dass $|\lambda \cdot (x-y)|=|\lambda \cdot z|$. Daraus folgt (Multiplizität des Betrags und Rücksubstitution):

$|\lambda \cdot (x-y)|=|\lambda \cdot z|=|\lambda |\cdot |z|=|\lambda |\cdot |x-y|$

Dreiecksungleichung für den Abstand

Satz (Dreiecksungleichung für den Abstand)

Für alle reellen Zahlen $x$ und $y$ ist $|x-y|\leq |x-z|+|z-y|$.

Beweis (Dreiecksungleichung für den Abstand)

Gegeben seien $|x-z|$ und $|z-y|$. Sei nun $a=x-z$ und $b=z-y$, so dass $|x-z|+|z-y|=|a|+|b|$. Wegen der Dreiecksungleichung gilt nun: $|a+b|\leq |a|+|b|$. Durch Rücksubstitution erhalten wir: $|(x-z)+(z-y)|\leq |x-z|+|z-y|$ bzw. $|x-y|\leq |x-z|+|z-y|$.

Abschätzung des Abstands nach unten

Satz (Abschätzung des Abstands nach unten)

Es ist $|x-y|\geq {\big |}|x|-|y|{\big |}$.

Beweis (Abschätzung des Abstands nach unten)

Es ist

$|x|=|(x-y)+y|\leq |x-y|+|y|$

und damit nach Umformung der Ungleichung

$|x|-|y|\leq |x-y|$

Analog folgt aus

$|y|=|(y-x)+x|\leq |y-x|+|x|$

die Ungleichung

$|y|-|x|\leq |y-x|=|x-y|$

Insgesamt ist also sowohl $|x|-|y|$ als auch $|y|-|x|=-(|x|-|y|)$ kleiner als $|x-y|$. Damit ist

${\big |}|x|-|y|{\big |}=\max(|x|-|y|,|y|-|x|)\leq |x-y|$

Betrag des Quotienten

Satz (Betrag des Quotienten)

Für Quotienten ${\tfrac {x-y}{\lambda }}$ ist

$\left|{\tfrac {x-y}{\lambda }}\right|={\tfrac {|x-y|}{|\lambda |}}$

Beweis (Betrag des Quotienten)

Gegeben sei $\left|{\tfrac {x-y}{\lambda }}\right|$. Sei $z=x-y$, so dass $\left|{\tfrac {x-y}{\lambda }}\right|=\left|{\tfrac {z}{\lambda }}\right|$. Nun aber gilt (Betrag des Quotienten): $\left|{\tfrac {z}{\lambda }}\right|={\tfrac {|z|}{|\lambda |}}$. Daraus folgt (durch Rücksubstitution), dass $\left|{\tfrac {x-y}{\lambda }}\right|={\tfrac {|x-y|}{|\lambda |}}$.

Intervalle

Nachdem wir in den vergangenen Kapiteln die Anordnungsaxiome eingeführt haben, können wir jetzt auch den Begriff des Intervalls definieren.

Überblick zu den Intervallen

Begriff	Schreibweise	Definition	Bild
(ab)geschlossenes Intervall oder kompaktes Intervall	$[a,b]$	$\{x\in \mathbb {R} :a\leq x\leq b\}$
offenes Intervall	$(a,b)$ oder $]a,b[$	$\{x\in \mathbb {R} :a<x<b\}$
halboffenes (genauer: rechtsoffenes) Intervall	$[a,b)$ oder $[a,b[$	$\{x\in \mathbb {R} :a\leq x<b\}$
halboffenes (genauer: linksoffenes) Intervall	$(a,b]$ oder $]a,b]$	$\{x\in \mathbb {R} :a<x\leq b\}$

Eine runde Klammer beziehungsweise eine nach außen stehende eckige Klammer zeigt an, dass dieser Randpunkt nicht Element des Intervalls ist. Bei einer nach innen zeigenden eckigen Klammer ist der Randpunkt Teil des Intervalls:

Beispiel (Intervalle)

• ${\color {Red}[}1,2{\color {Red}]}=\{x\in \mathbb {R} :1\,{\color {Red}\leq }\,x\,{\color {Red}\leq }\,2\}$
• ${\color {Red}[}1,2{\color {OliveGreen})}=\{x\in \mathbb {R} :1\,{\color {Red}\leq }\,x\,{\color {OliveGreen}<}\,2\}$
• ${\color {OliveGreen}]}1,2{\color {Red}]}=\{x\in \mathbb {R} :1\,{\color {OliveGreen}<}\,x\,{\color {Red}\leq }\,2\}$
• ${\color {OliveGreen}]}1,2{\color {OliveGreen}[}=\{x\in \mathbb {R} :1\,{\color {OliveGreen}<}\,x\,{\color {OliveGreen}<}\,2\}$

Dir ist dabei freigestellt, welche der beiden Schreibweisen du benutzt. Die Schreibweise $(a,b)$ hat den Nachteil, dass das Intervall mit dem geordneten Paar $(a,b)$ verwechselt werden kann, ist aber weiter verbreitet und die traditionelle Schreibweise des offenen Intervalls (vor allem im englischsprachigen Kulturraum wird diese Schreibweise eingesetzt).

Demgegenüber besteht bei der Notation $]a,b[$ keine Verwechslungsgefahr mit dem geordneten Paar. Diese Notation wurde im Übrigen von Nicolas Bourbaki eingeführt, einem französischen Autorenkollektiv, das Anfang des 20. Jahrhunderts in vier Lehrbüchern das bestehende mathematische Wissen stringent zusammenfasste.

Zur Unterscheidung zwischen offenen und abgeschlossenen Intervallen

Ein offenes Intervall $(a,b)$ und ein abgeschlossenes Intervall $[a,b]$ unterscheiden sich dahingehend, dass bei dem offenen Intervall $(a,b)$ die Randpunkte $a$ und $b$ keine Elemente des Intervalls sind, während dies beim abgeschlossenen Intervall $[a,b]$ schon der Fall ist. Dies ist auch der wesentliche Unterschied zwischen beiden Intervalltypen, der alle weiteren Unterschiede erklärt.

Dieser Unterschied begründet auch die Benennung der einzelnen Intervalle. In der Topologie heißt nämlich eine Menge genau dann offen, wenn keiner ihrer Randpunkte ein Element von der Menge ist. Weiterhin ist eine Menge abgeschlossen, wenn sie alle ihre Randpunkte enthält. Offene und abgeschlossene Mengen werden in der Topologie genauer studiert.

Uneigentliche Intervalle

Es ist auch möglich, dass ein Intervall nur zu einer Seite hin begrenzt ist. Ein solches Intervall wird dann uneigentliches Intervall genannt:

Schreibweise	Definition	Bild
$(-\infty ,a]$ oder $]-\infty ,a]$	$\{x\in \mathbb {R} :x\leq a\}$
$(-\infty ,a)$ oder $]-\infty ,a[$	$\{x\in \mathbb {R} :x<a\}$
$[a,\infty )$ oder $[a,\infty [$	$\{x\in \mathbb {R} :x\geq a\}$
$(a,\infty )$ oder $]a,\infty [$	$\{x\in \mathbb {R} :x>a\}$

Hinweis

Beachte bitte, dass hier das Zeichen $\infty$ in einem ganz genau definierten Kontext steht (keine untere bzw. obere Grenze für $x$). Man kann mit diesem Zeichen nicht wie mit normalen reellen Zahlen rechnen!

Intervallschachtelung mit rationaler Genauigkeit

Nach den Körper- und Anordungsaxiomen möchte ich nun die Vollständigkeit der reellen Zahlen beschreiben.

Wieso brauchen wir ein Vollständigkeitsaxiom?

Den Grund finden wir, indem wir uns zunächst eine andere Frage stellen: Können wir mit den bisher vorgestellten Axiomen bereits die Existenz von ${\sqrt {2}}$ beweisen? Die Antwortet lautet: „Nein“. Wenn wir nämlich die Existenz von ${\sqrt {2}}$ beweisen könnten, so würde jedes Modell der bisherigen Axiome auch die Zahl ${\sqrt {2}}$ enthalten. Nun sind aber die rationalen Zahlen ein solches Modell, weil sie alle Körper- und Anordnungsaxiome erfüllen. Jedoch ist ${\sqrt {2}}$ bekanntlich keine rationale Zahl (siehe Wikipedia-Artikel „Beweis der Irrationalität der Wurzel aus 2 bei Euklid“). Es folgt, dass die Existenz von ${\sqrt {2}}$ mit den Körper- und Anordnungsaxiomen unbeweisbar ist, weil wir sonst einen Widerspruch hätten. Analog ist auch die Existenz der Kreiszahl $\pi$ oder der eulerschen Zahl $e$ nicht beweisbar, da auch sie irrational sind. Wir brauchen also zusätzliche Axiome, um diese Lücken zu schließen.

Ist die Existenz rationaler Zahlen gesichert?

Wie sieht es nun mit der Existenz rationaler Zahlen aus? Können wir wenigstens diese beweisen, wenn wir schon nicht die Existenz irrationaler Zahlen annehmen können? Hier lautet die Antwort: „Ja“.

Die Körperaxiome sichern uns die Existenz der Zahlen $0$ und $1$. Hier wurde nämlich direkt in den Axiomen definiert, dass $0$ und $1$ existieren. Da $1$ existiert, existiert auch jede Summe $1+1+\ldots +1$. Im Abschnitt zu den Anordnungsaxiomen haben wir bereits bewiesen, dass $0<1$ ist. Damit folgt

$0<1<1+1<1+1+1<1+1+1+1<\ldots$

Jede Summe von Einsern ist also positiv und paarweise unterschiedlich. Damit können wir die natürlichen Zahlen über

$n=\underbrace {1+1+\ldots +1} _{n{\text{-mal}}}$

einführen. Weil nun auch jede reelle Zahl ein Negatives hat, muss es zu jeder natürlichen Zahl $n$ auch ihr Negatives $-n$ geben. Damit ist die Existenz ganzer Zahlen gewährleistet. Weil wir nach den Körperaxiomen auch beliebig dividieren können, folgt die Existenz von Brüchen ${\tfrac {a}{b}}$ mit ganzen Zahlen $a$ und $b$, wobei $b\neq 0$ ist. Insgesamt folgt so aus den Anordnungs- und Körperaxiomen die Existenz rationaler Zahlen.

Hinweis

Der obige Abschnitt ist kein Beweis im strengen mathematischen Sinn, sondern vielmehr eine Skizze, wie die rationalen Zahlen in jedem angeordneten Körper gefunden werden können. Damit dieses Kapitel nicht zu lang wird, möchte ich aber an dieser Stelle auf einen ausführlichen Beweis verzichten.

Die Körper- und Anordnungsaxiome garantieren uns also die Existenz rationaler Zahlen. Was fehlt, ist, durch zusätzliche Axiome die Lücken zwischen den rationalen Zahlen zu schließen.

Wie kann die Lückenfreiheit reeller Zahlen beschrieben werden?

Sackgasse: Weg über den Begriff „Lücke“

Wie können wir die Lücken schließen? Eine Möglichkeit wäre es zu sagen, dass die reellen Zahlen lückenfrei sein sollen. Hier haben wir aber das Problem, dass wir den Begriff „Lücke“ bisher noch nicht definiert haben. Diesen Begriff haben wir nur intuitiv verwendet. Eine Definition des Konzepts „Lücke“ ist aber schwierig, denn dieses Konzept beschreibt etwas, das selbst nicht existiert. Ich möchte deswegen diesen Weg vermeiden.

Sackgasse: Weg über den Konstruktionsbegriff

Eine weitere Möglichkeit wäre es zu sagen, dass alles, was irgendwie konstruiert werden kann, auch existiert. Beispielsweise ist ${\sqrt {2}}$ gleich der Länge der Diagonalen eines Quadrates mit der Seitenlänge Eins und kann so mit Lineal und Zirkel auf der Zahlengeraden eingezeichnet werden:

Konstruktion von Wurzel 2 auf der Zahlengeraden

Hier haben wir aber das Problem, den Begriff der Konstruktion richtig zu definieren. Dieser Begriff müsste nämlich mächtig genug sein, um alle reellen Zahlen konstruieren zu können (in der Algebra wirst du sehen, dass es reelle Zahlen wie $\pi$ gibt, die nicht mit Zirkel und Lineal auf der Zahlengeraden eingetragen werden können). Gleichzeitig müsste der Konstruktionsbegriff auch einfach in seiner Handhabung sein. Dieser Weg scheint zu schwierig zu sein.

Lösung: Weg über Approximationen

$\pi$ kann approximiert werden, indem man einen Kreis mit Polygonen mit immer größerer Seitenanzahl umschließt und die Umfänge der Polygone bestimmt

Wir können aber auch die Tatsache verwenden, dass die bereits formulierten Axiome uns die Existenz der rationalen Zahlen garantieren. Jede reelle Zahl kann nämlich beliebig durch rationale Zahlen angenähert werden. Nimm zum Beispiel die Zahl ${\sqrt {2}}$. Aus der Schule weißt du, dass es für diese Zahl eine Darstellung als unendlichen Dezimalbruch gibt:

${\sqrt {2}}=1{,}414213562373\ldots$

Dabei musst du dir anstatt der Pünktchen die fehlende unendliche Folge von Ziffern vorstellen. Wenn du nun von dieser unendlichen Dezimalbruchdarstellung einen endlichen Dezimalbruch nimmst, erhältst du eine rationale Zahl, die den unendlichen Dezimalbruch approximiert. So ist $1{,}414={\tfrac {1414}{1000}}$ eine rationale Zahl, deren Abstand zu ${\sqrt {2}}$ kleiner gleich ${\tfrac {1}{1000}}$ ist. Je mehr Nachkommastellen du in den endlichen Dezimalbruch aufnimmst, um so genauer ist deine Approximation. Wenn du allgemein von einem unendlichen Dezimalbruch den endlichen Dezimalbruch mit $n$ Nachkommastellen wählst, erhältst du eine rationale Zahl, deren Abstand vom unendlichen Dezimalbruch kleiner gleich $10^{-n}={\tfrac {1}{10^{n}}}$ ist. Damit ist jeder unendliche Dezimalbruch durch rationale Zahlen approximierbar. Weil nun jede reelle Zahl eine unendliche Dezimalbruchdarstellung besitzt, ist auch jede reelle Zahl durch rationale Zahlen annäherbar.

Gleichzeitig ist jede Zahl, die durch rationale Zahlen angenähert wurde, selbst wieder reell. Dies kannst du dir aus der intuitiven Idee der Zahlengeraden erklären. Alle rationalen Zahlen liegen nämlich auf der Zahlengeraden, und wenn etwas mit Punkten auf der Zahlengeraden approximiert wird, dann liegt dieser approximierte Punkt wieder auf der Zahlengeraden (und ist damit eine reelle Zahl). Damit könnte das Vollständigkeitsaxiom vom Schema her folgendermaßen aussehen:

„Alles, was mit rationalen Zahlen approximiert werden kann, muss existieren.“

Mit diesem Axiom wäre die Existenz jeder reellen Zahl gewährleistet. Wir müssen nun noch eine mathematische Definition für das intuitive Konzept der Approximation finden.

Intervallschachtelungen mit rationaler Genauigkeit

Definition

Die ersten vier Intervalle einer Intervallschachtelung.

Um das Konzept der Approximation mathematisch zu definieren, wähle ich den Weg über Intervallschachtelungen. Eine Intervallschachtelung ist eine spezielle Folge von Intervallen $I_{1}$, $I_{2}$, $I_{3}$ usw. Jedes dieser Intervalle $I_{n}=[a_{n},b_{n}]$ ist eine konkrete Approximation. Die Angabe des Intervalls $[a_{n},b_{n}]$ bedeutet dabei, dass die zu approximierende Zahl $x$ im Intervall $[a_{n},b_{n}]$ liegt, dass also $a_{n}\leq x\leq b_{n}$ ist. Die zu einem Intervall gehörenden Zahlen $a_{n}$ und $b_{n}$ stellen also jeweils eine untere beziehungsweise eine obere Schranke für die zu approximierende Zahl dar. Die Angabe dieser beiden Zahlen hat folgenden Vorteil: Der Fehler der Approximation ist direkt ersichtlich. Wenn man nämlich in jedem Schritt nur eine Zahl als Approximation angeben würde, wüsste man nicht, wie gut diese Approximation ist. Dieses Problem hat man bei Intervallen nicht. Die Breite eines Intervalls ist ein gutes Maß für die Qualität der Approximation.

Nun soll die Approximation mit jedem angegebenen Intervall immer genauer werden. Wenn wir bereits wissen, dass die approximierte Zahl im Intervall $I_{N}$ liegt, dann wollen wir dieses Wissen auch in den folgenden Schritten nutzen. Wir fordern deshalb

$I_{N+1}\subseteq I_{N}$

Es soll also gelten

$I_{1}\supseteq I_{2}\supseteq I_{3}\supseteq I_{4}\ldots$

Auch müssen wir garantieren, dass die Approximation beliebig genau wird. Deswegen soll auch folgende Anforderung erfüllt sein:

„Für alle positiven rationalen Zahlen $q$ gibt es mindestens ein Intervall $I_{N}$ mit der Breite kleiner gleich $q$.“

Wir wollen nämlich durch eine Approximation genau eine reelle Zahl beschreiben. Deswegen müssen wir verhindern, dass alle Intervalle eine Mindestbreite haben, weil es sonst mehrere reelle Zahlen geben würde, die in allen Intervallen liegen. Damit würden mehrere Zahlen durch die Intervallfolge gleichermaßen approximiert, was wir nicht wollen.

In den meisten Beispielen für Intervallschachtelungen können wir nur garantieren, dass die Intervalle kleiner als jede positive rationale Zahl werden. Deswegen haben wir in der obigen Eigenschaft auch nur rationale Zahlen $q>0$ und nicht beliebige reelle Zahlen $\epsilon >0$ gewählt. Wie wir im nächsten Kapitel sehen werden, werden so auch infinitesimale, also unendlich kleine Zahlen ausgeschlossen. So sparen wir uns im Vergleich zu anderen Lehrbüchern ein Axiom.

Eine Folge von Intervallen mit den obigen Eigenschaften nennt man Intervallschachtelung mit rationaler Genauigkeit:

Definition (Intervallschachtelung mit rationaler Genauigkeit)

Eine Intervallschachtelung mit rationaler Genauigkeit ist eine Folge von abgeschlossenen Intervallen $I_{1}=[a_{1},b_{1}]$, $I_{2}=[a_{2},b_{2}]$, $I_{3}=[a_{3},b_{3}]$... mit folgenden Eigenschaften

• Alle Intervalle sind Teilmengen ihres Vorgängers:
  $\forall n\in \mathbb {N} :I_{n+1}\subseteq I_{n}$
• Für jede rationale Zahl $q>0$ gibt es ein Intervall $I_{N}$ mit der Breite kleiner $q$:
  $\forall q\in \mathbb {Q} ^{+}\exists N\in \mathbb {N} :b_{N}-a_{N}<q$

Hinweis

In vielen anderen Lehrbüchern wirst du einen anderen Begriff der Intervallschachtelung finden. Dort werden die Intervalle kleiner als jede positive reelle Zahl und nicht nur kleiner als jede positive rationale Zahl. Diese Art der Intervallschachtelung werde ich in einem späteren Kapitel erläutern. Zur besseren Unterscheidung werde ich für diese Intervallschachtelung immer den Begriff „Intervallschachtelung mit rationaler Genauigkeit“ verwenden (es sei denn, die gemeinte Art der Intervallschachtelung erschließt sich aus dem Kontext). Die andere Art der Intervallschachtelung werde ich „Allgemeine Intervallschachtelung“ nennen.

Beachte, dass die Grenzen der Intervalle, also die Zahlen $a_{n}$ und $b_{n}$, durchaus irrational sein können. Wir haben nämlich in der obigen Definition keine Einschränkungen für die Zahlen $a_{n}$ und $b_{n}$ getroffen. Zwar wissen wir aktuell noch nicht, ob es irrationale Zahlen wie ${\sqrt {2}}$ oder $\pi$ gibt, wenn wir aber durch geeignete Approximationen deren Existenz bewiesen haben, dann können wir diese Zahlen nutzen, um weitere reelle Zahlen zu approximieren. Diese Entscheidung wurde auch getroffen, um Beweise im späteren Kapitel zur „allgemeinen Intervallschachtelung“ zu vereinfachen.

Verständnisfrage: Warum folgt aus der obigen Definition, dass wenn ein Intervall $I_{N}$ eine Breite kleiner $q$ hat, auch alle nachfolgenden Intervalle eine Breite kleiner $q$ haben?

Weil alle nachfolgenden Intervalle Teilmengen von $I_{N}$ sind und damit eine Breite kleiner gleich $I_{N}$ haben.

Verständnisaufgabe: Sei $q$ eine beliebige rationale Zahl. Finde eine Intervallschachtelung mit rationaler Genauigkeit für $q$.

Eine einfache Möglichkeit ist die Folge $I_{n}=[q,q]$, wo jedes Intervall gleich dem einelementigen Intervall $[q,q]=\{q\}$ ist. Beachte, dass diese Intervallschachtelung nur deswegen möglich ist, weil wir in der Definition abgeschlossene und keine offenen Intervalle gefordert haben. Deswegen ist es auch die Wahl von abgeschlossenen Intervallen in der Definition sinnvoll.

Eine andere Möglichkeit ist die Intervallschachtelung $I_{n}=\left[q-{\tfrac {1}{n}},q+{\tfrac {1}{n}}\right]$. Dies zeigt, dass es für eine Zahl mehrere mögliche Intervallschachtelungen rationaler Genauigkeit geben kann.

Intervallschachtelung aus unendlichem Dezimalbruch

Im obigen Abschnitt habe ich bereits dargelegt, dass aus jedem unendlichen Dezimalbruch eine Approximierbarkeit der durch den Dezimalbruch dargestellten Zahl folgt. Nimm beispielsweise wieder die Zahl ${\sqrt {2}}$. Diese besitzt die Dezimalbruchdarstellung

${\sqrt {2}}=1{,}414213562373\ldots$

Ich habe bereits erwähnt, dass wenn man einen endlichen Dezimalbruch mit $n$ Nachkommastellen wählt, dieser endliche Dezimalbruch ${\sqrt {2}}$ mit einem Fehler von maximal $10^{-n}$ approximiert. Genauer: Wenn $r$ der endliche Dezimalbruch mit $n$ Nachkommastellen ist, dann liegt ${\sqrt {2}}$ zwischen $r$ und $r+10^{-n}$. Es gilt

${\begin{aligned}1{,}4\leq &{\sqrt {2}}\leq 1{,}5\\1{,}41\leq &{\sqrt {2}}\leq 1{,}42\\1{,}414\leq &{\sqrt {2}}\leq 1{,}415\\&\ \vdots \end{aligned}}$

Damit ist

${\begin{aligned}I_{1}&=[{\tfrac {14}{10}},{\tfrac {15}{10}}]\\I_{2}&=[{\tfrac {141}{100}},{\tfrac {142}{100}}]\\I_{3}&=[{\tfrac {1414}{1000}},{\tfrac {1415}{1000}}]\\&\ \vdots \end{aligned}}$

eine Folge von Intervallen, die ${\sqrt {2}}$ approximieren. Jedes Intervall ist dabei Teilmenge des Vorgängers, und da beim $n$-ten Intervall die Breite des Intervalls gleich $10^{-n}$ ist, werden die Breiten der Intervalle kleiner als jede positive rationale Zahl. Damit ist obige Folge von Intervallen eine Intervallschachtelung mit rationaler Genauigkeit. Analog kann man aus jedem unendlichen Dezimalbruch eine Intervallschachtelung mit rationaler Genauigkeit für die durch den Dezimalbruch dargestellte Zahl gewinnen.

Alternative Intervallschachtelung für Wurzel 2

Alternativ kann auch eine Intervallschachtelung über eine Art Algorithmus gewonnen werden. Ich möchte dir an dieser Stelle einen solchen Algorithmus vorstellen, weil dir diese Methode in der Analysis häufiger begegnen wird. Stelle dir also vor, dass wir wieder ${\sqrt {2}}$ approximieren wollen. Zunächst wissen wir, dass $1\leq {\sqrt {2}}\leq 2$ ist, denn es ist

$\underbrace {1^{2}} _{=\ 1}\leq 2\leq \underbrace {2^{2}} _{=\ 4}$

Damit muss ${\sqrt {2}}$ im Intervall $[1,2]$ liegen. Nun nehmen wir die Mitte ${\tfrac {3}{2}}$ des Intervalls $[1,2]$ und schauen, ob sie kleiner oder größer als ${\sqrt {2}}$ sein muss. Dies tun wir, indem wir ${\tfrac {3}{2}}$ quadrieren und schauen, ob das größer oder kleiner 2 ist. Da $\left({\tfrac {3}{2}}\right)^{2}={\tfrac {9}{4}}$ größer als 2 ist, muss auch ${\tfrac {3}{2}}$ größer als ${\sqrt {2}}$ sein. Es gilt also $1\leq {\sqrt {2}}\leq {\tfrac {3}{2}}$ und somit erhalten wir $\left[1,{\tfrac {3}{2}}\right]$ als zweites Intervall der Intervallschachtelung.

Dieses Verfahren können wir nun beliebig wiederholen. Jedes Mal teilen wir das aktuelle Intervall in zwei Hälften und schauen, in welcher der beiden Hälften sich die Zahl ${\sqrt {2}}$ befinden muss. Diese Intervallhälfte wählen wir als neues Intervall der Intervallschachtelung.

Jedes Intervall ist Teilmenge des Vorgängerintervalls, und weil in jedem Schritt die Breite des Intervalls halbiert wird, wird die Intervallbreite kleiner als jede positive rationale Zahl. Damit gewinnen wir durch den Algorithmus eine Intervallschachtelung mit rationaler Genauigkeit für ${\sqrt {2}}$.

Intervallschachtelungsprinzip mit rationaler Genauigkeit

Nun sind wir soweit, die Vollständigkeit von $\mathbb {R}$ als Axiom zu definieren. In unserer Vorstellung soll jede Intervallschachtelung mit rationaler Genauigkeit genau eine reelle Zahl approximieren. Deswegen fordern wir, dass genau eine reelle Zahl durch alle Intervalle der Intervallschachtelung approximiert wird, dass also genau eine reelle Zahl in allen Intervallen liegt. Diese Forderung nennen wir „Intervallschachtelungsprinzip mit rationaler Genauigkeit“:

Definition (Intervallschachtelungsprinzip mit rationaler Genauigkeit)

Für jede Intervallschachtelung mit rationaler Genauigkeit gibt es genau eine reelle Zahl, die in allen Intervallen liegt.

Dieses Axiom beschreibt die minimale Vervollständigung der rationalen zu den reellen Zahlen. Um das zu sehen, können wir den Satzteil „es existiert genau eine reelle Zahl“ aufsplitten in „es existiert mindestens eine reelle Zahl“ und „es existiert höchstens eine reelle Zahl“. Der erste Aspekt beschreibt die Vollständigkeit der reellen Zahlen und der zweite Aspekt die Minimalität dieser Vervollständigung:

• Die reellen Zahlen sind vollständig: „Zu jeder Intervallschachtelung mit rationaler Genauigkeit existiert mindestens eine reelle Zahl, die in allen Intervallen liegt.“
• Die Vervollständigung ist minimal: „Zu jeder Intervallschachtelung mit rationaler Genauigkeit existiert höchstens eine reelle Zahl, die in allen Intervallen liegt.“

Insgesamt beschreibt also das Intervallschachtelungsprinzip mit rationaler Genauigkeit die minimale Vervollständigung der rationalen zu den reellen Zahlen.

Alternative Beschreibung der Vollständigkeit

In vielen Lehrbüchern wirst du zwei Axiome anstatt eines zur Beschreibung der Vollständigkeit finden. Die Vollständigkeit selbst wird dabei meistens durch das allgemeine Intervallschachtelungsprinzip (nicht zu verwechseln mit dem hier vorgestellten Axiom!) oder über das so genannte Konvergenzkriterium von Cauchy beschrieben. Die Minimalität der Vervollständigung wird über das archimedische Axiom definiert. Diese Axiome werde ich in den kommenden Kapiteln behandeln.

Beachte aber, dass für uns diese Axiome Theoreme sein werden, da wir bereits ein Axiom zur Vollständigkeit haben. Darauf solltest du vor allem beim archimedischen Axiom achten, weil bereits in dessen Namen das Wort „Axiom“ vorkommt.

Das archimedische Axiom

Das archimedische Axiom

Veranschaulichung des archimedischen Axioms: Egal wie klein die Strecke A ist, wenn man diese Strecke nur hinreichend oft aneinander legt, wird die Gesamtlänge größer als bei der Strecke B

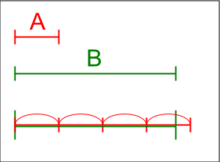
Beginnen wir das Kapitel mit dem archimedischen Axiom:

Satz (Das Archimedische Axiom)

Zu jedem $x>0$ und zu jedem $y>0$ gibt es eine natürliche Zahl $n$, so dass $nx\geq y$ ist. In Quantorenschreibweise:

$\forall x>0,y>0\,\exists n\in \mathbb {N} :nx\geq y$

Beachte, dass für uns das archimedische Axiom kein Axiom ist, sondern ein Theorem. Denn im letzten Kapitel zur Vollständigkeit der reellen Zahlen haben wir bereits ein Axiom definiert, aus dem das archimedische Axiom folgt. Da aber die meisten Lehrbücher den obigen Satz als eines der Axiome für reelle Zahlen benutzen und es somit als „archimedisches Axiom“ bezeichnen, werde ich dies auch in diesem Lehrbuch machen.

Bedeutung des archimedischen Axioms

Archimedisches Axiom (Youtube-Video vom Youtube-Kanal Quatematik)

Die Bedeutung des archimedischen Axioms wird klar, wenn wir seine Aussage negieren. Aus

$\forall x>0,y>0\,\exists n\in \mathbb {N} :nx\geq y$

wird durch Negation

$\exists x>0,y>0\,\forall n\in \mathbb {N} :nx<y$

Es gibt also positive Zahlen $x$ und $y$, so dass jedes Vielfache von $x$ kleiner als $y$ ist. Damit wäre $y$ eine in Relation zu $x$ unendlich große Zahl. Wir können also sagen

Das archimedische Axiom lautet: „Es gibt keine zwei Zahlen $x$ und $y$, so dass $y$ in Relation zu $x$ unendlich groß ist.”

Wenn $y$ bezüglich $x$ unendlich groß ist, dann ist ${\tfrac {y}{x}}$ eine unendlich große Zahl, also eine Zahl, welche größer als jede natürliche Zahl ist. Analog ist ${\tfrac {x}{y}}$ eine unendlich kleine Zahl, welche kleiner als jede positive rationale Zahl ist. Da es aber nach dem archimedischen Axiom keine solche Zahlen $x$ und $y$ geben kann, schließt es auch die Existenz unendlich kleiner oder unendlich großer Zahlen aus. Man kann also auch sagen:

Das archimedische Axiom lautet: „Es gibt keine positiven unendlich kleinen oder unendlich großen reellen Zahlen.“

Alternative Formulierung des archimedischen Axioms

Das Inverse einer unendlich kleinen Zahl ist unendlich groß und umgekehrt. Damit bedingen sich unendlich kleine und unendlich große Zahlen gegenseitig. Es reicht also aus, nur die Existenz der unendlich kleinen oder die Existenz der unendlich großen Zahlen auszuschließen, um eine Aussage äquivalent zum archimedischen Axiom zu erhalten.

Eine unendlich große Zahl ist eine Zahl $x$, die größer als jede natürliche Zahl $N$ ist. Die Existenz einer unendlich großen Zahl wird also durch folgende Aussage beschrieben:

$\exists x>0\,\forall N\in \mathbb {N} :x>N$

Die Negation dieser Aussage schließt damit die Existenz unendlich großer Zahlen aus. Sie lautet:

$\forall x>0\,\exists N\in \mathbb {N} :x\leq N$

Analog kann auch die Existenz unendlich kleiner Zahlen ausgeschlossen werden. Eine unendlich kleine Zahl ist eine Zahl, die kleiner als jeder Quotient ${\tfrac {1}{N}}$ mit einer natürlichen Zahl $N$ ist. Wenn es also unendlich kleine Zahlen geben würde, würde gelten:

$\exists x>0\,\forall N\in \mathbb {N} :{\tfrac {1}{N}}>x$

Die Aussage, die die Existenz unendlich kleiner Zahlen ausschließt, lautet damit:

$\forall x>0\,\exists N\in \mathbb {N} :{\tfrac {1}{N}}\leq x$

Damit haben wir zwei Alternativformulierungen für das archimedische Axiom gefunden. Dass die beiden Aussagen auch wirklich alternative Formulierungen des archimedischen Axioms sind, können wir dadurch zeigen, dass sie äquivalent zum archimedischen Axiom sind:

Satz (Alternative Formulierungen des archimedischen Axioms)

Folgende Aussagen sind äquivalent zum archimedischen Axiom:

• $\forall x>0\,\exists N\in \mathbb {N} :x\leq N$
• $\forall x>0\,\exists N\in \mathbb {N} :{\tfrac {1}{N}}\leq x$

Beweis (Alternative Formulierungen des archimedischen Axioms)

Obigen Satz können wir beweisen, indem wir folgende Implikationskette zeigen

${\begin{aligned}{\text{Archimedisches Axiom }}&\Rightarrow \forall x>0\,\exists N\in \mathbb {N} :x\leq N\\&\Rightarrow \forall x>0\,\exists N\in \mathbb {N} :{\tfrac {1}{N}}\leq x\\&\Rightarrow {\text{Archimedisches Axiom}}\end{aligned}}$

Beweisschritt: ${\text{Archimedisches Axiom }}\Rightarrow \forall x>0\,\exists N\in \mathbb {N} :x\leq N$

Diese Implikation kann direkt gezeigt werden. Hierzu setzt man im archimedischen Axiom

$\forall x>0,y>0\,\exists n\in \mathbb {N} :nx\geq y$

für $y=x$ und für $x=1$ ein. Man erhält dann die Aussage

$\forall x>0\,\exists N\in \mathbb {N} :x\leq N$

.

Beweisschritt: $\forall x>0\,\exists N\in \mathbb {N} :x\leq N\Rightarrow \forall x>0\,\exists N\in \mathbb {N} :{\tfrac {1}{N}}\leq x$

Sei $x>0$ beliebig. Wir müssen nun zeigen, dass es eine natürliche Zahl $N$ gibt, so dass ${\tfrac {1}{N}}\leq x$ ist. Nun ist aber auch ${\tfrac {1}{x}}$ größer 0 und damit gibt es eine natürliche Zahl $N$ mit ${\tfrac {1}{x}}\leq N$. Daraus folgt aber ${\tfrac {1}{N}}\leq x$, was zu beweisen war.

Beweisschritt: $\forall x>0\,\exists N\in \mathbb {N} :{\tfrac {1}{N}}\leq x\Rightarrow {\text{Archimedisches Axiom}}$

Seien $x$ und $y$ beliebige positive reelle Zahlen. Nun ist auch ${\tfrac {x}{y}}>0$ und es gibt damit eine natürliche Zahl $n$ mit ${\tfrac {x}{y}}\geq {\tfrac {1}{n}}$. Wenn wir diese Ungleichung umstellen, kommen wir auf $nx\geq y$, was zu zeigen war. Somit ist der Beweis der Implikationskette abgeschlossen.

Beweis des archimedischen Axioms

Wie oben bereits erwähnt, ist für uns das archimedische Axiom kein Axiom, sondern ein Satz, den wir dementsprechend auch beweisen müssen. Dies wollen wir nun tun:

Wie kommt man auf den Beweis? (Das archimedische Axiom)

Es ist egal, welche der drei vorgestellten Varianten des archimedischen Axioms wir beweisen, da sie alle äquivalent zueinander sind. Ich wähle zum Beweis die Aussage

$\forall x>0\,\exists N\in \mathbb {N} :{\tfrac {1}{N}}\leq x$

welche die Nicht-Existenz unendlich kleiner positiver Zahlen beschreibt. Um eine Idee für einen Beweis zu bekommen, gehen wir einmal vom Gegenteil aus und nehmen an, dass es eine unendlich kleine Zahl $x$ gibt. Dies bedeutet aber, dass wir $x$ nicht von $0$ durch jede Intervallschachtelung mit rationaler Genauigkeit unterscheiden können, da der Abstand zwischen $x$ und $0$ kleiner als jede rationale Zahl ist. Jedoch haben wir im Intervallschachtelungsprinzip mit rationaler Genauigkeit definiert, dass jede solche Intervallschachtelung maximal eine Zahl approximiert.

Wir müssen also eine Intervallschachtelung mit rationaler Genauigkeit so geschickt wählen, dass wir bei der Existenz einer unendlich kleinen Zahl $x$ einen Widerspruch erhalten. Mit etwas Nachdenken kommt man hier auf die Intervallschachtelung $I_{n}=[0,{\tfrac {1}{n}}]$.

Beweis (Das archimedische Axiom)

Wir beweisen die Aussage

$\forall x>0\,\exists N\in \mathbb {N} :{\tfrac {1}{N}}\leq x$

Sei also $x>0$ beliebig. Betrachte nun die Intervallfolge $I_{n}=[0,{\tfrac {1}{n}}]$, also die Folge

${\begin{aligned}I_{1}&=[0,1]\\I_{2}&=\left[0,{\tfrac {1}{2}}\right]\\I_{3}&=\left[0,{\tfrac {1}{3}}\right]\\&\ \vdots \end{aligned}}$

Diese Folge ist eine Intervallschachtelung mit rationaler Genauigkeit und damit existiert maximal eine reelle Zahl, die in allen Intervallen liegt. Nun liegt bereits $0$ in allen Intervallen, womit $x$ nicht in allen Intervallen $I_{n}$ liegen kann. Es gibt also ein $N\in \mathbb {N}$ mit $x\notin I_{N}=\left[0,{\tfrac {1}{N}}\right]$. Wegen $x>0$ muss $x>{\tfrac {1}{N}}$ sein. Es gilt also ${\tfrac {1}{N}}\leq x$, was zu beweisen war.

Bernoullische Ungleichung

Die Bernoulli-Ungleichung ist eine wichtige Ungleichung der Analysis. Mit ihr können nämlich Ungleichungen mit Potenzen gelöst werden, für die man normalerweise den Logarithmus verwendet, welcher aber am Anfang einer Analysis-Vorlesung noch nicht zur Verfügung steht. Zunächst werde ich dir die Bernoulli-Ungleichung vorstellen. Später werde ich dir dann zeigen, wie man mit ihr Ungleichungen mit Potenzen beweist, ohne dass man dazu den Logarithmus zur Hilfe nehmen muss.

Die Bernoulli-Ungleichung

Formulierung

Satz (Bernoullische Ungleichung)

Für alle reellen Zahlen $x\geq -1$ und alle natürlichen Zahlen $n$ gilt:

$(1+x)^{n}\geq 1+n\cdot x$

Die Bernoulli-Ungleichung geht dabei auf den Schweizer Mathematiker Jacob Bernoulli zurück, der sie 1689 in seiner Arbeit „Positiones Arithmeticae de Seriebus Infinitis“ veröffentlichte und dort auch häufig anwendete.

Veranschaulichung

Folgendes Diagramm veranschaulicht die Bernoulli-Ungleichung. Hier sind die beiden Funktionen $f(x)=(1+x)^{n}$ (roter Graph) und $g(x)=1+n\cdot x$ (blauer Graph) für den konkreten Wert $n=3$ eingetragen:

Veranschaulichung der Bernoulli-Ungleichung

Du siehst, dass für alle $x\geq -1$ der rote Graph niemals unter dem blauen Graph liegt. Dies zeigt, dass im betrachteten Bereich $(1+x)^{3}\geq 1+3\cdot x$ ist (beachte, dass im obigen Graph der konkrete Wert $n=3$ genutzt wurde).

Die Bernoulli-Ungleichung ist für große $x$ außerdem eine sehr starke Abschätzung nach unten – für große $x$ ist $(1+x)^{n}$ um ein Vielfaches größer als $1+n\cdot x$. Dies kannst du nachvollziehen, indem du dir die Fortsetzung des obigen Diagramms für große $x$ vorstellst. Für viele Anwendungen der Bernoulli-Ungleichungen ist es aber egal, dass die Abschätzung nach unten sehr stark ist.

Beweis

Beweis der Bernoulli Ungleichung über vollständige Induktion (Youtube-Video von Franziska Egbers)

Wie kommt man auf den Beweis?

Die Ungleichung zeigen wir durch vollständige Induktion nach $n$. Der Induktionsanfang lässt sich durch direktes Nachrechnen zeigen. Im Induktionsschritt müssen wir zeigen, dass

$(1+x)^{n+1}\geq 1+(n+1)\cdot x$

ist. Als Induktionsvoraussetzung haben wir $(1+x)^{n}\geq 1+n\cdot x$ gegeben. Um diese verwenden zu können, teilen wir zunächst die Potenz $(1+x)^{n+1}$ geschickt auf:

$(1+x)^{n+1}=(1+x)^{n}\cdot (1+x)$

Für $(1+x)^{n}$ können wir die Induktionsvoraussetzung $(1+x)^{n}\geq 1+n\cdot x$ benutzen. Außerdem wissen wir, dass $x\geq -1$ und somit $1+x\geq 0$ ist. Damit erhalten wir:

${\begin{aligned}&&(1+x)^{n}&\geq 1+n\cdot x\\[0.5em]&&&{\color {OliveGreen}\left\downarrow \ 1+x\geq 0\right.}\\[0.5em]&\Rightarrow \ &(1+x)^{n}\cdot (1+x)&\geq (1+nx)\cdot (1+x)\end{aligned}}$

Nun können wir das rechtsstehende Produkt ausmultiplizieren:

$(1+nx)\cdot (1+x)=1+n\cdot x+x+n\cdot x^{2}=1+(n+1)\cdot x+n\cdot x^{2}$

Wir haben also fast den rechten Term der Zielungleichung, nur der Summand $n\cdot x^{2}$ ist noch zuviel. Da aber $x^{2}\geq 0$ und $n\geq 1$ ist, ist auch $n\cdot x^{2}\geq 0$ und wir können diesen Term für die Abschätzung nach unten weglassen:

$1+(n+1)\cdot x+n\cdot x^{2}\geq 1+(n+1)\cdot x$

Wir haben damit einen Beweis für die bernoullische Ungleichung gefunden, der nun nur noch schön aufgeschrieben werden muss.

Beweis

Wir führen den Beweis über vollständige Induktion:

Aussageform, deren Allgemeingültigkeit für $n\in \mathbb {N}$ bewiesen werden soll:

$(1+x)^{n}\geq 1+n\cdot x$

1. Induktionsanfang:

$(1+x)^{1}=1+x=1+1\cdot x$

2. Induktionsschritt:

2a. Induktionsvoraussetzung:

$(1+x)^{n}\geq 1+n\cdot x$

2b. Induktionsbehauptung:

$(1+x)^{n+1}\geq 1+(n+1)\cdot x$

2c. Beweis des Induktionsschritts:

${\begin{aligned}(1+x)^{n+1}&={\color {OliveGreen}(1+x)^{n}}\cdot (1+x)\\[0.5em]&\qquad {\color {OliveGreen}\left\downarrow \ {\text{Induktionsvoraussetzung und }}(1+x)\geq 0\right.}\\[0.5em]&\geq {\color {OliveGreen}(1+n\cdot x)}\cdot (1+x)\\&=1+(n+1)\cdot x+n\cdot x^{2}\\&\qquad \left\downarrow \ n\cdot x^{2}\geq 0\right.\\&\geq 1+(n+1)\cdot x\end{aligned}}$

Was kann man mit der Bernoulli-Ungleichung machen?

Beweise von Ungleichungen mit Potenzen mit Hilfe der Bernoulli-Ungleichung (Potenz soll der größere der beiden Terme sein).

Potenzen nach unten abschätzen

Ich möchte dir nun an einem Beispiel kurz erläutern, wie man Ungleichungen mit Potenzen mit der Bernoulli-Ungleichung lösen kann. Stelle dir hierzu vor, dass wir ein $n\in \mathbb {N}$ finden müssen, so dass $2^{n}\geq M$ ist, wobei $M$ irgendeine vorgegebene reelle (positive) Zahl ist. Normalerweise würden wir hier den Logarithmus verwenden, um die Gleichung nach $n$ umzustellen:

${\begin{array}{lrl}&2^{n}&\geq M\\[0.5em]&&{\color {OliveGreen}\left\downarrow \ \log(\cdot ){\text{ ist streng monoton steigend. }}\right.}\\[0.5em]\iff \ &\log \left(2^{n}\right)&\geq \log(M)\\[0.5em]&&{\color {OliveGreen}\left\downarrow \ \log \left(a^{b}\right)=b\log(a)\right.}\\[0.5em]\iff \ &n\cdot \log(2)&\geq \log(M)\\[0.5em]\iff \ &n&\geq {\frac {\log(M)}{\log(2)}}\\\end{array}}$

$n$ muss also irgendeine natürliche Zahl größer gleich ${\tfrac {\log(M)}{\log(2)}}$ sein. Wir haben an dieser Stelle nur ein Problem: Wir können den Logarithmus nicht verwenden, weil wir ihn noch nicht mathematisch exakt eingeführt haben. Es ist auch nicht trivial, den Logarithmus mathematisch exakt einzuführen, weil wir hierzu Konzepte der Analysis benötigen, die wir erst später kennenlernen werden. Jetzt kommt uns die Bernoulli-Ungleichung gelegen. Wir können nämlich $2$ zu $1+1$ umschreiben und erhalten damit:

${\begin{aligned}2^{n}&=(1+1)^{n}\\&{\color {OliveGreen}\left\downarrow \ {\text{Bernoulli-Ungleichung}}\right.}\\&\geq 1+n\cdot 1\\&=n+1\end{aligned}}$

Wir wissen also dank der Bernoulli-Ungleichung, dass stets $2^{n}\geq n+1$ ist. Wenn also $n+1\geq M$ ist, dann muss automatisch auch $2^{n}\geq M$ sein. Somit können wir alternativ ein $n$ finden, so dass $n+1\geq M$ ist. Die letzte Ungleichung lässt sich einfach umformen:

${\begin{array}{lrl}&n+1&\geq M\\\iff \ &n&\geq M-1\end{array}}$

Für jede natürliche Zahl $n$ größer gleich $M-1$ ist somit $2^{n}\geq M$. Durch die Bernoulli-Ungleichung können wir die Zweierpotenzen so nach unten abschätzen, dass sich die Zielungleichung leicht ergibt. Eine solche Argumentation wird dir noch öfters in der Analysis-Vorlesung begegnen.

Potenzen nach oben abschätzen

Beweise von Ungleichungen mit Potenzen mit Hilfe der Bernoulli-Ungleichung (Potenz soll der größere der beiden Terme sein).

Beachte, dass du die Bernoulli-Ungleichung nur bei solchen Ausdrücken verwenden kannst, die nach unten abgeschätzt werden sollen. Wenn dem nicht so ist, dann musst du deine Zielungleichung so geschickt durch Äquivalenzumformungen umbauen, dass du die Bernoulli-Ungleichung verwenden kannst.

Stelle dir hierzu vor, wir wollen ein $n\in \mathbb {N}$ finden, so dass ${\tfrac {1}{2^{n}}}\leq a$ für irgendeine positive Zahl $a$ ist. Hier bringt uns die Bernoulli-Ungleichung nichts, denn durch sie können wir die Potenz ${\tfrac {1}{2^{n}}}$ nur nach unten und nicht wie gefordert nach oben abschätzen. Doch wir können unsere Zielungleichung geschickt umformen:

${\begin{array}{lrl}&{\frac {1}{2^{n}}}&\leq a\\\iff \ &1&\leq a2^{n}\\\iff \ &{\frac {1}{a}}&\leq 2^{n}\end{array}}$

Anstelle der Ungleichung ${\tfrac {1}{2^{n}}}\leq a$ können wir auch $2^{n}\geq {\tfrac {1}{a}}$ beweisen. Die zweite Ungleichung kann nun so ähnlich mit der bernoullischen Ungleichung bewiesen werden, wie wir es bereits im obigen Abschnitt gesehen haben.

Beachte, dass wir nur Äquivalenzumformungen verwendet haben, um die neue Zielgleichung $2^{n}\geq {\tfrac {1}{a}}$ zu gewinnen. Durch die Äquivalenzumformungen ist nämlich gewährleistet, dass bei Erfüllung von ${\tfrac {1}{a}}\leq 2^{n}$ die eigentliche Zielungleichung ${\tfrac {1}{2^{n}}}\leq a$ erfüllt sein muss.

Unbeschränktheit von Potenzfunktionen zeigen

Mit Hilfe der Bernoulli-Ungleichung kann auch gezeigt werden, dass die Potenzfunktion der Form $f(x)=x^{n}$ für $n\geq 1$ nach oben unbeschränkt ist, ohne dafür die Wurzel verwenden zu müssen. Hierfür müssen wir zeigen, dass es für alle $y\in \mathbb {R}$ ein $x\in \mathbb {R}$ mit $x^{n}\geq y$ gibt.

Normalerweise würden wir $x$ finden, indem wir auf beide Seiten der Ungleichung $x^{n}\geq y$ die Wurzel ziehen. Hier müssten wir jedoch auch unterscheiden, ob $n$ gerade oder ungerade ist. Bei geradem $n$ lautet unsere Rechnung:

${\begin{array}{lrl}&x^{n}&\geq y\\\iff &{\sqrt[{n}]{x^{n}}}&\geq {\sqrt[{n}]{y}}\\\iff &x&\geq {\sqrt[{n}]{y}}\end{array}}$

Bei ungeradem $n$ müssen wir beachten, dass es für negative $y$ keine $n$-te Wurzel gibt. Dies ist aber kein Problem, da wir uns auf $y\geq 0$ beschränken können. Wenn nämlich $x^{n}$ größer als jede positive Zahl wird, dann wird es auch größer als jede negative Zahl. Auch ist bei geradem $n$ nicht ${\sqrt[{n}]{x^{n}}}=x$, sondern ${\sqrt[{n}]{x^{n}}}=|x|$. Deswegen haben wir bei geradem $n$ (unter der Einschränkung, dass $y\geq 0$ ist):

${\begin{array}{lrl}&x^{n}&\geq y\\\iff &{\sqrt[{n}]{x^{n}}}&\geq {\sqrt[{n}]{y}}\\\iff &|x|&\geq {\sqrt[{n}]{y}}\end{array}}$

Nun wollen wir aber die Unbeschränktheit nach oben nicht mit Hilfe der Wurzel beweisen (weil wir beispielsweise die Wurzel noch nicht definiert haben und diese nicht extra einführen möchten). Hier können wir zunächst wie oben vorgehen: Zunächst schreiben wir $x$ in $1+s$ um. Wir definieren also $x=1+s$ und erhalten:

$x^{n}=(1+s)^{n}\geq 1+n\cdot s$

Die letzte Ungleichung gilt, solange $s\geq -1$ ist. Wenn wir also ein $s$ finden, so dass $1+n\cdot s\geq y$ ist, dann muss auch $x^{n}\geq y$ sein. Die Ungleichung $1+n\cdot s\geq y$ besitzt keine nervigen Potenzen mehr, weswegen wir direkt umstellen können:

${\begin{array}{lrl}&1+n\cdot s&\geq y\\\iff &n\cdot s&\geq y-1\\\iff &s\geq {\frac {y-1}{n}}\end{array}}$

Wenn also $s\geq {\tfrac {y-1}{n}}$ und $s\geq -1$ ist, dann muss nach der Bernoulli-Ungleichung $x^{n}=(1+s)^{n}\geq y$ sein. Wir wählen also $s=\max \left\{{\tfrac {y-1}{n}},-1\right\}$ und damit

${\begin{aligned}x&=1+\max \left\{{\tfrac {y-1}{n}},-1\right\}\\&=\max \left\{1+{\tfrac {y-1}{n}},1-1\right\}\\&=\max \left\{1+{\tfrac {y-1}{n}},0\right\}\end{aligned}}$

Dieses $x$ erfüllt die Eigenschaft, dass $x^{n}\geq y$. Man beachte, dass wir $x$ finden können, ohne die Wurzel zu verwenden und ohne eine Fallunterscheidung in gerade und ungerade $n$ machen zu müssen. Zwar ist unsere Wahl von $x$ nicht optimal im Sinne, dass es das kleinste $x$ mit $x^{n}\geq y$ ist. Das ist aber egal, um zu zeigen, dass Potenzfunktionen nach oben unbeschränkt sind.

Folgerungen aus der Bernoulli-Ungleichung

Aus der Bernoulli-Ungleichung kann zusammen mit dem archimedischen Axiom Abschätzungen für Potenzen hergeleitet werden, die für die Grenzwertberechnung wichtig sind.

Beliebig wachsende Potenzen

Lösungsweg und Beweis dafür, dass Potenzen mit Basis größer als 1 beliebig groß werden.

Satz (Beliebig wachsende Potenzen)

Für jede Zahl $p>1$ und jede Zahl $M\in \mathbb {R}$ gibt es ein $n\in \mathbb {N}$, so dass $p^{n}>M$ ist.

Wie kommt man auf den Beweis? (Beliebig wachsende Potenzen)

Obigen Satz können wir über die Bernoulli-Ungleichung herleiten. Diese lautet

$(1+x)^{n}\geq 1+nx$

für alle $x\geq -1$. Nun haben wir $p^{n}>\ldots$ zu beweisen und dementsprechend setzen wir $p=1+x$, also $x=p-1$. Auf der rechten Seite des Ausdrucks steht das Produkt $nx$, welches wir bereits vom archimedischen Axiom kennen.

Insgesamt wollen wir $p^{n}>M$ beweisen. Wegen $p^{n}\geq 1+nx$ reicht es also, $1+nx>M$ zu beweisen. Nun können wir wegen des archimedischen Axioms $nx$ beliebig groß werden lassen – unter anderem so groß, dass es größer $M-1$ ist, was unsere Ungleichung beweist.

Um aber das archimedische Axiom hier anwenden zu können, muss $x>0$ sein. Wegen $x=p-1$ folgt dies aber aus $p>1$.

Beweis (Beliebig wachsende Potenzen)

Sei $p>1$ und $M\in \mathbb {R}$ beliebig. Setze $x=p-1$. Wegen $p>1$ ist $x>0$ und damit gibt es nach dem archimedischen Axiom ein $n\in \mathbb {N}$ mit $nx\geq M$. Nun gilt nach der Bernoulli-Ungleichung

$p^{n}=(x+1)^{n}\geq 1+nx\geq 1+M>M$

Beliebig fallende Potenzen

Lösungsweg und Beweis dafür, dass Potenzen mit Basis kleiner 1 beliebig klein werden.

Satz (Beliebig fallende Potenzen)

Zu jedem $0\leq q<1$ und zu jedem $\epsilon >0$ gibt es ein $n\in \mathbb {N}$ mit $q^{n}<\epsilon$.

Wie kommt man auf den Beweis? (Beliebig fallende Potenzen)

Zunächst ist der Satz für $q=0$ trivial, weil dann immer $q^{n}=0<\epsilon$ ist. Wir können uns im Folgenden also auf den Fall $0<q<1$ beschränken. Wir haben zu zeigen:

$q^{n}<\epsilon$

Nun können wir anders als im obigen Satz die Bernoulli-Ungleichung nicht direkt anwenden. Der Grund dafür ist, dass wir hier eine Abschätzung nach oben für die Potenz brauchen, wir aber mit der Bernoulli-Ungleichung nur eine Abschätzung nach unten bekommen. Wir können aber die Zielgleichung durch geschickte Äquivalenzumformungen so umschreiben, dass der obige Satz anwendbar ist:

${\begin{aligned}q^{n}&<\epsilon \\{\frac {1}{\epsilon }}&<{\frac {1}{q^{n}}}\\{\frac {1}{\epsilon }}&<\left({\frac {1}{q}}\right)^{n}\end{aligned}}$

Weil nun ${\tfrac {1}{q}}>1$ und ${\tfrac {1}{\epsilon }}>0$ ist, kann die letzte Ungleichung mit obigem Satz bewiesen werden.

Beweis (Beliebig fallende Potenzen)

Sei $0\leq q<1$ und $\epsilon >0$ beliebig.

Fall 1: $q=0$

Ist $q=0$, dann ist stets $q^{n}=0<\epsilon$.

Fall 2: $q\neq 0$

Sei $0<q<1$. Es ist dann ${\tfrac {1}{q}}>1$ und ${\tfrac {1}{\epsilon }}>0$. Nach obigen Satz gibt es ein $n\in \mathbb {N}$ mit

$\left({\tfrac {1}{q}}\right)^{n}>{\tfrac {1}{\epsilon }}$

Damit gilt aber nach Umstellung dieser Ungleichung:

$q^{n}<\epsilon$

Allgemeine Intervallschachtelungen

Allgemeine Intervallschachtelung

In diesem Kapitel werde ich die Art der Intervallschachtelung beschreiben, welche du in den meisten Lehrbüchern findest. Hier wird die Breite der Intervalle kleiner als jede positive reelle Zahl und nicht nur kleiner als jede positive rationale Zahl. Für diese Art der Intervallschachtelung werde ich den Begriff „allgemeine Intervallschachtelung“ verwenden. Die Definition lautet:

Definition (Allgemeine Intervallschachtelung)

Eine allgemeine Intervallschachtelung ist eine Folge von abgeschlossenen Intervallen $I_{1}=[a_{1},b_{1}]$, $I_{2}=[a_{2},b_{2}]$, $I_{3}=[a_{3},b_{3}]$... mit den Eigenschaften

• Alle Intervalle sind Teilmengen ihres Vorgängers:
  $\forall n\in \mathbb {N} :I_{n+1}\subseteq I_{n}$
• Für jede reelle Zahl $\epsilon >0$ gibt es ein Intervall $I_{N}$ mit der Breite kleiner $\epsilon$:
  $\forall \epsilon \in \mathbb {R} ^{+}:\exists N\in \mathbb {N} :b_{N}-a_{N}<\epsilon$

Wenn du noch nicht den Abschnitt mit der Definition zur Intervallschachtelung mit rationaler Genauigkeit gelesen haben solltest, dann empfehle ich dir, dies nun nachzuholen. Du wirst dann auch obige Definition besser verstehen.

Allgemeines Intervallschachtelungsprinzip

Definition

Auch zur obigen Art der Intervallschachtelung gibt es ein Intervallschachtelungsprinzip. Dieses lautet:

Satz (Allgemeines Intervallschachtelungsprinzip)

Zu jeder allgemeinen Intervallschachtelung $I_{1}$, $I_{2}$, $I_{3}$... existiert eine reelle Zahl, die in allen Intervallen liegt und damit von allen Intervallen approximiert wird.

Wie auch beim archimedischen Axiom ist dieses Intervallschachtelungsprinzip für uns ein zu beweisender Satz, während es in anderen Lehrbücher als Axiom eingeführt wird. Wir werden obigen Satz später aus dem Intervallschachtelungsprinzip mit rationaler Genauigkeit beweisen.

Eindeutigkeit der Approximation

Du wirst vielleicht schon festgestellt haben, dass im Gegensatz zum Intervallschachtelungsprinzip mit rationaler Genauigkeit im obigen Satz nur die Existenz, aber nicht die Eindeutigkeit einer reellen Zahl gefordert wird, die von allen Intervallen approximiert wird. Der Grund ist, dass bereits aus der Definition der allgemeinen Intervallschachtelung folgt, dass es maximal eine reelle Zahl geben kann, die in allen Intervallen liegt.

Satz (Eindeutigkeit der Approximation)

Es gibt maximal eine reelle Zahl, die in allen Intervallen einer allgemeinen Intervallschachtelung liegt.

Wie kommt man auf den Beweis? (Eindeutigkeit der Approximation)

Ein Satz zur Eindeutigkeit eines Objektes mit bestimmten Eigenschaften wird oft dadurch bewiesen, dass die Annahme von zwei verschiedenen solchen Objekten zum Widerspruch geführt wird. Nehmen wir also an, es gäbe zwei Objekte $x$ und $y$, die in allen Intervallen $I_{1}$, $I_{2}$ usw. einer allgemeinen Intervallschachtelung liegen. Nun müssen wir daraus einen Widerspruch ableiten.

Frage: Wie kann ein Widerspruch hergeleitet werden?

Nehmen wir den Abstand $|x-y|$ zwischen $x$ und $y$. Da $x$ ungleich $y$ ist, ist $|x-y|>0$. Nun wird aber die Breite der Intervalle $I_{n}$ kleiner als jede positive reelle Zahl, also auch kleiner als $|x-y|$. Ein Intervall mit der Breite kleiner $|x-y|$ kann aber nicht beide Zahlen $x$ und $y$ enthalten, womit wir den gewünschten Widerspruch haben.

Beweis (Eindeutigkeit der Approximation)

Sei $I_{1}$, $I_{2}$ usw. eine allgemeine Intervallschachtelung. Seien außerdem $x$ und $y$ reelle Zahlen, die in allen Intervallen $I_{1}$, $I_{2}$ usw. liegen.

Da $x$ und $y$ verschieden sind, ist $|x-y|>0$ und damit gibt es ein Intervall $I_{N}$ mit einer Breite kleiner als $|x-y|$. Damit können aber nicht gleichzeitig $x$ und $y$ in $I_{N}$ liegen. Widerspruch ↯.

Mit dieser Erkenntnis können wir obiges Intervallschachtelungsprinzip verbessern:

Satz (Verbesserte Variante des allgemeinen Intervallschachtelungsprinzips)

Zu jeder allgemeinen Intervallschachtelung $I_{1}$, $I_{2}$, $I_{3}$... existiert genau eine reelle Zahl, die in allen Intervallen liegt und damit von allen Intervallen approximiert wird.

Unterschiede zwischen den Intervallschachtelungen

Mit der allgemeinen Intervallschachtelung und der Intervallschachtelung mit rationaler Genauigkeit haben wir zwei verschiedene Arten der Intervallschachtelung kennen gelernt. Im obigen Abschnitt haben wir gesehen, dass die allgemeine Intervallschachtelung bereits aus ihrer Definition heraus impliziert, dass jede durch sie approximierte reelle Zahl eindeutig ist. Dies ist bei Intervallschachtelungen mit rationaler Genauigkeit nicht der Fall. Bei diesen Intervallschachtelungen wissen wir nämlich nur, dass die Breite der Intervalle kleiner als jede positive rationale Zahl wird, aber nicht, ob sie kleiner als jede positive reelle Zahl wird. Wenn es nun zwei Zahlen mit unendlich kleinem Abstand zueinander gäbe, dann gäbe es auch eine Intervallschachtelung mit rationaler Genauigkeit, die beide Zahlen gleichermaßen approximieren.

Deswegen mussten wir per Axiom festlegen, dass auch Intervallschachtelungen mit rationaler Genauigkeit maximal eine Zahl approximieren. Der Vorteil hier ist aber, dass wir dadurch das archimedische Axiom geschenkt bekommen und es nicht mehr extra als Axiom formulieren müssen. Aus dem allgemeinen Intervallschachtelungsprinzip ist demgegenüber das archimedische Axiom nicht ableitbar. Denn es ist nicht ohne Weiteres klar, ob die Folge der Intervalle $[0,1]$, $\left[0,{\tfrac {1}{2}}\right]$, $\left[0,{\tfrac {1}{3}}\right]$ usw. wirklich eine allgemeine Intervallschachtelung ist oder nicht. Hierzu benötigen wir nämlich das archimedische Axiom als extra formuliertes Axiom.

Beweis des allgemeinen Intervallschachtelungsprinzip

Wir müssen nun das allgemeine Intervallschachtelungsprinzip beweisen:

Beweis (Allgemeines Intervallschachtelungsprinzip)

Jede allgemeine Intervallschachtelung ist auch eine Intervallschachtelung mit rationaler Genauigkeit, denn wenn die Breite der Intervalle kleiner als jede positive reelle Zahl wird, wird sie insbesondere auch kleiner als jede positive rationale Zahl. Aus dem Intervallschachtelungsprinzip mit rationaler Genauigkeit folgt damit, dass auch jede allgemeine Intervallschachtelung mindestens eine reelle Zahl approximiert. Damit ist das allgemeine Intervallschachtelungsprinzip bewiesen.

Alternative Formulierung der Vollständigkeit

Viele andere Lehrbücher gehen einen anderen Weg, die Vollständigkeit der reellen Zahlen zu beschreiben. Einige dieser Lehrbücher nutzen dazu das allgemeine Intervallschachtelungsprinzip in Kombination mit dem archimedischen Axiom. Ich habe bereits gezeigt, dass aus dem Intervallschachtelungsprinzip mit rationaler Genauigkeit das archimedische Axiom und die allgemeine Intervallschachtelung folgen. Jetzt muss nur noch bewiesen werden, dass das archimedische Axiom zusammen mit der allgemeinen Intervallschachtelung auch das Intervallschachtelungsprinzip mit rationaler Genauigkeit impliziert. Damit zeigen wir nämlich, dass beide Beschreibungsmöglichkeiten für die Vollständigkeit der reellen Zahlen äquivalent sind. Es ist also egal, welche Beschreibungsmöglichkeit man wählt. Weitere Möglichkeiten, die Vollständigkeit zu charakterisieren, werden wir dir in späteren Kapiteln vorstellen. Jetzt aber zeigen wir:

Satz (Alternative Formulierung der Vollständigkeit)

Aus dem archimedischen Axiom und dem allgemeinen Intervallschachtelungsprinzip folgt das Intervallschachtelungsprinzip mit rationaler Genauigkeit.

Wie kommt man auf den Beweis? (Alternative Formulierung der Vollständigkeit)

Um das Intervallschachtelungsprinzip mit rationaler Genauigkeit zu beweisen, müssen wir zeigen, dass jede Intervallschachtelung mit rationaler Genauigkeit genau eine reelle Zahl approximiert, dass es also genau eine reelle Zahl gibt, die in allen Intervallen der Intervallschachtelung liegt. Einen solchen Existenz- und Eindeutigkeitssatz beweisen wir am besten, indem wir die Beweise für die Existenz und die Eindeutigkeit getrennt behandeln.

Sei im folgenden $I_{1}$, $I_{2}$, $I_{3}$ usw. eine Intervallschachtelung mit rationaler Genauigkeit.

Beweisschritt: Es gibt eine reelle Zahl $x$, die in allen Intervallen $I_{1}$, $I_{2}$ usw. liegt.

Es liegt nahe, das allgemeine Intervallschachtelungsprinzip zu benutzen, um die Existenz von $x$ zu beweisen. Hierzu müsste aber die gegebene Intervallschachtelung $I_{1}$, $I_{2}$ usw. eine allgemeine Intervallschachtelung sein, weil dann das allgemeine Intervallschachtelungsprinzip direkt die Existenz der gewünschten Zahl $x$ vorhersagt. Die Breite der Intervalle müsste also kleiner als jede gegebene positive reelle Zahl werden. Jedoch wissen wir nur, dass die Breite der Intervalle kleiner als jede vorgegebene positive rationale Zahl wird.

Frage: Wie kann man zeigen, dass die Breite der Intervalle kleiner wird als jede reelle Zahl?

Den Beweis können wir mit dem archimedischen Axiom führen. Denn dieses garantiert uns, dass es für jede reelle Zahl $\epsilon >0$ eine rationale Zahl ${\tfrac {1}{N}}$ gibt mit ${\tfrac {1}{N}}\leq \epsilon$.

Wenn also ein beliebiges $\epsilon >0$ vorgegeben ist, so finden wir ein $N\in \mathbb {N}$ mit ${\tfrac {1}{N}}\leq \epsilon$ und weiter ein Intervall $I_{K}$ mit Breite kleiner ${\tfrac {1}{N}}$. Wegen ${\tfrac {1}{N}}\leq \epsilon$ hat dieses Intervall eine Breite kleiner $\epsilon$. So haben wir wie gewünscht bewiesen, dass es für jedes $\epsilon >0$ ein Intervall mit einer Breite kleiner $\epsilon$ gibt.

Beweisschritt: Es kann keine zwei reelle Zahlen $x$ und $y$ geben, die in allen Intervallen $I_{1}$, $I_{2}$ usw. liegen.

Hier können wir analog zum Beweis vorgehen, wo wir die Eindeutigkeit der Approximation einer allgemeinen Intervallschachtelung bewiesen haben. Damals haben wir gezeigt, dass es ein Intervall mit Breite kleiner $|x-y|$ gibt. Dann können nämlich nicht $x$ und $y$ gleichzeitig in diesem Intervall liegen und wir haben einen Widerspruch. Hierzu können wir ausnutzen, dass die Breite der Intervalle kleiner als jede positive rationale Zahl wird. Jedoch wissen wir nur, dass $|x-y|>0$ ist.

Frage: Wie kann man zeigen, dass es ein Intervall mit einer Breite kleiner $|x-y|$ gibt?

Auch dies können wir mit dem archimedischen Axiom beweisen. Aus diesem wissen wir, dass es eine natürliche Zahl $N$ mit ${\tfrac {1}{N}}\leq |x-y|$ gibt. Da ${\tfrac {1}{N}}$ rational ist, gibt es damit auch ein Intervall $I_{K}$ mit einer Breite kleiner ${\tfrac {1}{N}}$, also mit einer Breite kleiner $|x-y|$.

Beweis (Alternative Formulierung der Vollständigkeit)

Sei $I_{1}$, $I_{2}$ usw. eine Intervallschachtelung mit rationaler Genauigkeit.

Beweisschritt: $I_{1}$, $I_{2}$ usw. ist eine allgemeine Intervallschachtelung.

Wir müssen nur noch zeigen, dass die Breite der Intervalle kleiner als jede positive reelle Zahl wird. Sei also $\epsilon >0$ vorgegeben. Nach dem archimedischen Axiom gibt es eine natürliche Zahl $N$ mit ${\tfrac {1}{N}}\leq \epsilon$. Da ${\tfrac {1}{N}}$ eine rationale Zahl ist, gibt es ein Intervall $I_{K}$ mit einer Breite kleiner ${\tfrac {1}{N}}$. Wegen ${\tfrac {1}{N}}\leq \epsilon$ ist auch die Breite von $I_{K}$ kleiner als $\epsilon$. $I_{1}$, $I_{2}$ usw. ist damit eine allgemeine Intervallschachtelung.

Beweisschritt: Es gibt eine reelle Zahl $x$, die in allen Intervallen $I_{1}$, $I_{2}$ usw. liegt.

Da, wie gerade bewiesen, $I_{1}$, $I_{2}$ usw. eine allgemeine Intervallschachtelung ist, folgt aus dem allgemeinen Intervallschachtelungsprinzip, dass es eine reelle Zahl $x$ gibt, die in allen Intervallen der Intervallschachtelung liegt.

Beweisschritt: Es kann keine zwei reelle Zahlen $x$ und $y$ geben, die in allen Intervallen $I_{1}$, $I_{2}$ usw. liegen.

Seien $x$ und $y$ zwei verschiedene Zahlen, die in allen Intervallen $I_{1}$, $I_{2}$ usw. liegen. Wegen $x\neq y$ ist $|x-y|>0$ und damit gibt es nach dem archimedischen Axiom ein $N\in \mathbb {N}$ mit ${\tfrac {1}{N}}\leq |x-y|$. Weil ${\tfrac {1}{N}}$ eine rationale Zahl ist, gibt es ein Intervall $I_{K}$ mit einer Breite kleiner ${\tfrac {1}{N}}$. Nun ist ${\tfrac {1}{N}}\leq |x-y|$ und damit ist die Breite von $I_{K}$ auch kleiner als der Abstand $|x-y|$ zwischen $x$ und $y$. Dann können aber $x$ und $y$ nicht gleichzeitig in $I_{K}$ liegen. Widerspruch ↯.

Supremum und Infimum

Einleitung

Supremum (aus dem Lateinischen von „supremum“ = „das Höchste/das Oberste“) klingt, als ob es „das Maximum“ (also das größte Element der Menge) wäre. Im Laufe dieses Artikels werden wir allerdings sehen, dass das Supremum das Maximum verallgemeinert. Merken wir uns zu Beginn:

Jedes Maximum ist ein Supremum, aber nicht jedes Supremum ist ein Maximum.

Während nämlich das Maximum ein Element der betrachteten Menge sein muss, muss das nicht für das Supremum gelten. Deshalb sollten wir „Supremum“ treffender mit „die unmittelbar nach oben beschränkende Zahl“ übersetzen. Es ist „nach oben beschränkend“, weil es wie das Maximum größer oder gleich jeder Zahl der Menge ist. Und es ist „unmittelbar“, weil es die kleinste aller „nach oben beschränkenden“ Zahlen ist.

Analog ist das Infimum eine Verallgemeinerung des Minimums. Es ist die „unmittelbar nach unten beschränkende Zahl“, also die größte aller „nach unten beschränkenden“ Zahlen einer Menge. Konkrete Beispiele werden wir in den kommenden Abschnitten kennenlernen.

Für uns ist der Begriff des Supremums wichtig, weil mit ihm die Vollständigkeit der reellen Zahlen alternativ beschrieben werden kann. Außerdem ist das Supremum ein nützliches Hilfsmittel in Beweisen oder zur Definition neuer Begriffe.

Erklärung des Supremums

Um das Supremum zu erklären, werden wir untersuchen, wie man zu dessen genauer Definition kommt. Hierzu werden wir feststellen, wie das Supremum aus dem Maximum verallgemeinert werden kann. Zur Erinnerung: Das Maximum einer Menge ist ihr größtes Element. Das Maximum $m$ einer Menge $M$ hat also folgende Eigenschaften:

• $m$ ist Element von $M$.
• Für jedes $y\in M$ ist $y\leq m$.

In der zweiten Eigenschaft steht deshalb ein Kleiner-Gleich- und kein Kleiner-Zeichen, weil in der Aussage auch $y$ gleich $m$ sein könnte. Bei endlichen Mengen ist das Maximum stets definiert, jedoch ist dies bei unendlichen Mengen nicht unbedingt der Fall.

Zunächst können wir auf das Problem stoßen, dass die betrachtete Menge nach oben unbeschränkt ist. Nimm zum Beispiel die Menge $\mathbb {R} ^{+}=\{x\in \mathbb {R} :x>0\}$. Diese Menge kann kein Maximum oder ähnliches besitzen, da es für jede reelle Zahl eine größere Zahl aus $\mathbb {R} ^{+}$ gibt. Diese Menge kann also kein größtes Element besitzen. Es gibt auch kein Element, das „unmittelbar das größte“ Element sein könnte. Demnach ist eine Frage danach bei dieser Menge schlicht nicht sinnvoll.

Für die Übertragung des Maximumbegriffs auf unendliche Mengen muss also die Menge nach oben beschränkt sein. Es muss also eine Zahl $b$ geben, welche größer gleich jedem Element der Menge ist. Dabei muss $b$ nicht zwangsläufig Element der Menge sein.

Doch auch dann kann es zu Problemen kommen. Nehmen wir zum Beispiel die Menge $M=\{x\in \mathbb {R} :x<1\}$. Diese Menge ist nach oben beschränkt, weil man für $b$ jede Zahl größer gleich $1$ wählen kann.

Hat die Menge $M$ ein Maximum? Leider nein. Für jedes $x\in M$ ist ${\tfrac {x+1}{2}}$ eine weitere Zahl aus $M$ mit der Eigenschaft $x<{\tfrac {x+1}{2}}$ (die Zahl ${\tfrac {x+1}{2}}$ liegt in der Mitte zwischen $x$ und $1$). So kann aber $M$ kein maximales Element besitzen, weil es zu jeder Zahl aus $M$ mindestens eine größere Zahl aus $M$ gibt.

Bei der Betrachtung unendlicher Mengen büßt das Maximum also eine Eigenschaft ein. Nämlich, dass es Element der Menge ist:

• m ist Element von M.
• Für jedes $y\in M$ ist $y\leq m$.

Eine Menge mit eingezeichneten oberen und unteren Schranken

Es bleibt also erst einmal nur die Eigenschaft, dass die gesuchte Zahl größer als jedes Element der Menge ist. Eine solche Zahl wird „obere Schranke“ der Menge genannt:

Definition (obere Schranke)

Sei $M$ eine Teilmenge von $\mathbb {R}$. Dann nennt man eine Zahl $u$, die größer gleich jedem Element von $M$ ist, eine obere Schranke. Es ist also $x\leq u$ für alle $x\in M$.

Analog ist eine untere Schranke eine Zahl, die eine Menge nach unten beschränkt:

Definition (untere Schranke)

Sei $M$ eine Teilmenge von $\mathbb {R}$. Dann nennt man eine Zahl ${\tilde {u}}$, die kleiner gleich jedem Element von $M$ ist, eine untere Schranke. Es ist also $x\geq {\tilde {u}}$ für alle $x\in M$.

Wenn wir unsere neue Definition betrachten, stellen wir zwei Dinge fest. Erstens: Obere und untere Schranken müssen keine Elemente der betrachteten Menge sein, weil dies nicht von der Definition gefordert wird. Und zweitens: Die Definition sagt nichts über eine etwaige Eindeutigkeit der Schranken aus.

Betrachten wir zum Beispiel die Menge $M=\{x\in \mathbb {R} :x<1\}$. Hier fällt uns sicherlich zuerst $1$ als obere Schranke ein. Jedoch ist $17$ ebenfalls eine obere Schranke und erfüllt die Forderungen der Definition. Abgesehen davon, dass $17$ weit oberhalb unserer Beispielmenge liegt, sind beide Zahlen keine Elemente der Menge. Dieses Beispiel zeigt, dass es mehr als eine obere Schranke geben kann. Es wird aber noch beunruhigender: Eine beschränkte Teilmenge der reellen Zahlen hat immer unendlich viele obere Schranken. Wenn $u$ eine obere Schranke von $M$ ist, so ist auch jede größere Zahl, also $u+a$ für alle $a>0$, eine obere Schranke.

Bei genauerer Betrachtung sind die Begriffe von oberer bzw. unterer Schranke nicht sehr treffend. Sie leisten viel weniger als ein Maximumbegriff. Das Maximum ist nämlich immer eindeutig: Es kann höchstens eins davon geben. Mit der oberen Schranke verhält es sich nicht so. Deshalb wollen wir versuchen, den Begriff zu verbessern.

Betrachten wir als Beispiel wieder die Menge $M=\{x\in \mathbb {R} :x<1\}$. Welche Zahl könnte man als Verallgemeinerung des Maximums für $M$ wählen? Intuitiv fällt uns die Zahl $1$ ein. Doch warum sollte man diese Zahl wählen?

Wir wollen einen allgemein gültigen Begriff, der auch dann funktioniert, wenn die Menge nicht mehr so anschaulich ist. Deswegen kommen zunächst alle oberen Schranken von $M$, also alle Zahlen größer gleich $1$, in Frage. Nun sollte unsere Zahl optimal in dem Sinne sein, dass sie möglichst klein ist. So kommen wir auf die Zahl $1$. Sie ist nicht nur eine obere Schranke, sie ist auch die kleinste obere Schranke von $M$. Wir haben ja bereits gesehen, dass es für jedes $x<1$ eine andere Zahl $y<1$ mit $x<y$ gibt (nämlich $y={\tfrac {x+1}{2}}$). Damit kann keine Zahl kleiner $1$ eine obere Schranke von $M$ sein. $1$ ist also das, was wir als „unmittelbar darüberliegende“ Zahl von $\{x\in \mathbb {R} :x<1\}$ ansehen.

Frage: Wie könnte eine Menge aussehen, bei der nicht intuitiv „klar“ ist, welche Zahl das Supremum sein könnte?

Betrachten wir kurz eine sehr schöne Zahlenmenge: Die Mandelbrotmenge. Man erhält sie, wenn man alle Punkte in einem zweidimensionalen Koordinatensystem in eine bestimmte Funktion $f$ steckt. Sie nimmt einen Koordinatenpunkt $(x,y)$ und macht daraus einen anderen Koordinatenpunkt $(x',y')$. Dieses Ergebnis steckt man wieder in diese Funktion und dann wieder und wieder und wieder… Die Koordinaten, die man bei jedem Schritt erhält, werden für manche Startpunkte sehr schnell riesig groß, für andere bleiben sie klein. Wenn sich die Koordinaten erst einmal weit genug von ihrem Anfangspunkt entfernt haben (eine Grenze $g$ überschritten haben), kommen sie nie wieder zurück und „hauen ab“. Bleibt ein Punkt für den Startwert $(x,y)$ für immer unterhalb von $g$, so gehört der Punkt $(x,y)$ zur Menge und wird schwarz eingefärbt. Überschreitet er $g$, so erhält er eine bestimmte Farbe, je nachdem, wann er $g$ überschritten hat. Was wir rechts sehen, ist das dabei entstehende Bild.

Die Mandelbrotmenge liegt nun in der Ebene, ihre Punkte haben $x$- und $y$-Koordinaten, darum ist sie für unseren Supremumsbegriff zunächst nicht geeignet. Wir können aber einfach „die Menge aller $y$-Koordinaten der Mandelbrotmenge“ betrachten und versuchen, ihr Supremum zu finden. Anschaulicher gesagt: Wir wüssten gern, wie weit nach oben die schwarzen Punkte in dem Bild reichen und suchen dafür die kleinste obere Schranke. Welchen Wert diese aber genau hat, ist beim ersten (und auch beim zweiten) Hinsehen völlig unklar.

Die kleinste obere Schranke $s$ wird durch folgende zwei Eigenschaften charakterisiert:

• $s$ ist obere Schranke von $M$: Für jedes $y\in M$ ist $y\leq s$.
• Jede obere Schranke $u$ von $M$ ist mindestens so groß wie $s$: Gilt $y\leq u$ für alle $y\in M$, so gilt auch $s\leq u$. Anders formuliert: Für jedes $u<s$ gibt es mindestens eine Zahl $y\in M$ mit $u<y$.

Das können wir als Definition des Supremums verwenden, da es offenbar die kleinste obere Schranke charakterisiert. Das Infimum wird analog als die größte untere Schranke definiert.

Definition des Supremums und Infimums

Das Supremum ist die kleinste obere Schranke einer Menge.

Die Definition des Supremums und des Infimums lautet:

Definition (Supremum)

Sei $M$ eine Teilmenge von $\mathbb {R}$. Das Supremum $s$ einer Menge $M$ ist die kleinste obere Schranke von $M$. Das Supremum wird charakterisiert über die beiden Eigenschaften:

• Für jedes $y\in M$ ist $y\leq s$.
• Keine Zahl $x$ kleiner als $s$ ist obere Schranke von $M$: Für alle $x<s$ gibt es mindestens eine Zahl $y\in M$ mit $x<y$.

Definition (Infimum)

Sei $M$ eine Teilmenge von $\mathbb {R}$. Das Infimum ${\tilde {s}}$ einer Menge $M$ ist die größte untere Schranke von $M$. Das Infimum wird charakterisiert über die beiden Eigenschaften:

• Für jedes $y\in M$ ist $y\geq {\tilde {s}}$.
• Keine Zahl $x$ größer als ${\tilde {s}}$ ist untere Schranke von $M$: Für alle $x>{\tilde {s}}$ gibt es mindestens eine Zahl $y\in M$ mit $x>y$.

Die Epsilon-Definition

In der zweiten Eigenschaft der Definition des Supremums $s$ als Teil einer Menge $M$ steht:

„Jede Zahl $x$ kleiner als $s$ ist keine obere Schranke von $M$: Für alle $x<s$ gibt es mindestens eine Zahl $y\in M$ mit $x<y$.“

Hier ist es in einigen Lehrbüchern auch üblich, $x=s-\epsilon$ mit $\epsilon >0$ zu setzen. Dadurch erhält man folgende Aussage, die man auch als zweite Eigenschaft des Supremums nutzen kann:

„Für alle $\epsilon >0$ gibt es ein $y\in M$ mit $s-\epsilon <y$.“

Bei Beweisen dürfen wir frei entscheiden, welche der beiden Aussagen wir heranziehen wollen. Da beide Aussagen zueinander äquivalent sind, ist es egal, welche davon bewiesen wird.

Frage: Wie lautet die Epsilon-Definition des Infimums?

${\tilde {s}}$ ist ein Infimum von $M$, wenn ${\tilde {s}}$ eine untere Schranke von $M$ ist und wenn es für alle $\epsilon >0$ ein $y\in M$ gibt, so dass ${\tilde {s}}+\epsilon >y$ ist.

Maximum und Minimum

Für das Maximum und Minimum haben wir bekanntlich folgende Definitionen:

Definition (Maximum)

Das Maximum $m$ einer Menge $M$ ist eine Zahl mit den folgenden zwei Eigenschaften:

• $m\in M$.
• Für alle $y\in M$ ist $y\leq m$.

Definition (Minimum)

Das Minimum ${\tilde {m}}$ einer Menge $M$ ist eine Zahl mit den folgenden zwei Eigenschaften:

• ${\tilde {m}}\in M$.
• Für alle $y\in M$ ist $y\geq {\tilde {m}}$.

Das Maximum ist stets Supremum der Menge. Sei nämlich $m$ Maximum einer Menge $M$. Zum einen ist $m$ per Definition obere Schranke von $M$. Zum anderen gibt es für alle $x$ mit $x<m$ ein $y\in M$ mit $x<y$, nämlich $y=m$. Umgekehrt ist nicht jedes Supremum Maximum, wie wir oben an der Menge $\{x\in \mathbb {R} :x<1\}$ gesehen haben. Die Zahl $1$ ist zwar Supremum dieser Menge, aber kein Maximum. Analoges gilt für Minimum und Infimum.

Schreibweisen

Schreibweise	Bedeutung
$\sup M$	Supremum von $M$
$\sup _{x\in D}f(x)$	Supremum von $\{f(x):x\in D\}$
$\inf M$	Infimum von $M$
$\inf _{x\in D}f(x)$	Infimum von $\{f(x):x\in D\}$
$\max M$	Maximum von $M$
$\min M$	Minimum von $M$

Das Dualitätsprinzip

Wir haben bereits in den Definitionen und in der obigen Erklärung gesehen, dass die Begriffe des Supremums und des Infimums analog zueinander betrachtet werden können. Der Grund liegt darin, dass bei Umkehrung der Ordnung auf den reellen Zahlen das Supremum zum Infimum wird und umgekehrt. Wir können nämlich eine neue Ordnung $\leq _{\text{neu}}$ dadurch einführen, dass $x\leq _{\text{neu}}y$ genau dann ist, wenn $x\geq y$ ist (wir spiegeln hier die reelle Zahlengerade an der Null). Bei dieser neuen Ordnung verhält sich das ursprüngliche Supremum wie ein Infimum und umgekehrt. Beide Ordnungen $\leq _{\text{neu}}$ und $\leq$ haben dieselben ordnungstheoretischen Eigenschaften. Sie sind daher isomorph zueinander. Deshalb müssen auch die Eigenschaften von Supremum und Infimum bei umgekehrter Ordnung dieselben sein. Alles was wir in Zukunft für Suprema sagen, gilt in ähnlicher Weise auch für Infima und umgekehrt. Das Gleiche gilt folglich auch für Maximum und Minimum.

Beispiel (Dualitätsprinzip)

Für alle $x\in M$ ist $x\leq \sup M$. Analog ist für alle $x\in M$ die Ungleichung $x\geq \inf M$ erfüllt.

Existenz und Eindeutigkeit

Wir haben bisher ganz selbstverständlich von dem Supremum gesprochen. Das klingt so, als ob es immer eines gäbe und als ob es immer eindeutig wäre. Der Verdacht liegt auch nahe: Wozu sollten wir uns die Mühe machen, den Begriff „Supremum“ überhaupt zu definieren, wenn er das Grundproblem des Maximums (nämlich oftmals gar nicht zu existieren) gar nicht lösen könnte? Was wäre der Vorteil des Supremums gegenüber dem Begriff der „oberen Schranke“, wenn auch das Supremum nicht eindeutig wäre? Intuitiv ist irgendwie klar, dass es unter allen oberen Schranken genau eine kleinste geben muss, aber bis jetzt haben wir das noch nicht streng mathematisch bewiesen.

Im folgenden Satz werden wir die Eindeutigkeit des Infimums und Supremums beweisen, also dass eine Menge höchstens ein Supremum und Infimum besitzen kann:

Satz (Eindeutigkeit des Supremums und Infimums)

Eine Menge kann höchstens ein Supremum und höchstens ein Infimum besitzen.

Beweis (Eindeutigkeit des Supremums und Infimums)

Wir können die Standardbeweismethode für Eindeutigkeit nutzen: Zunächst nehmen wir eine Menge $M$ an, die zwei Suprema $s_{1}$ und $s_{2}$ besitzt, und zeigen dann, dass $s_{1}=s_{2}$ ist. Die beiden Suprema haben folgende Eigenschaften:

• $s_{1}$ und $s_{2}$ sind obere Schranken von $M$.
• Keine Zahl kleiner als $s_{1}$ und $s_{2}$ ist eine obere Schranke von $M$.

Keine Zahl kleiner als $s_{1}$ ist obere Schranke von $M$. Da $s_{2}$ eine obere Schranke von $M$ ist, kann $s_{2}$ nicht kleiner als $s_{1}$ sein und muss damit größer gleich $s_{1}$ sein. Analog ist $s_{1}\geq s_{2}$. Aus $s_{2}\geq s_{1}$ und $s_{1}\geq s_{2}$ folgt $s_{1}=s_{2}$. Der Beweis für die Eindeutigkeit des Infimums ist analog.

Mit dem Vollständigkeitsaxiom kann auch die Existenz des Supremums einer nach oben beschränkten nicht-leeren Teilmenge der reellen Zahlen bewiesen werden. Dies werden wir in diesem Kapitel jedoch nicht behandeln. Analog besitzt eine nach unten beschränkte nicht-leere Teilmenge der reellen Zahlen stets ein Infimum. Somit ist es tatsächlich so, dass Supremum und Infimum einer nach oben beschränkten und nicht-leeren Teilmenge der reellen Zahlen immer existieren und immer eindeutig sind. Deswegen dürfen wir beruhigt von dem Supremum sprechen.

Ausblick: Suprema und Infima in Halbordnungen

Obige Definition für Suprema und Infima haben wir speziell für Mengen von reellen Zahlen eingeführt. Für eine „Analysis 1“-Vorlesung reicht diese Definition aus, weil wir hier nur Teilmengen von $\mathbb {R}$ betrachten. Für spätere Vorlesungen, in denen wir uns auch mit echten Halbordnungen befassen werden, ist unsere bisherige Definition allerdings nicht ausreichend. Zur Erinnerung: Halbordnungen sind Ordnungsstrukturen, bei denen wir nicht zwangsweise zwei Paare von Objekten miteinander vergleichen können. In solchen Halbordnungen wird obige Definition von Supremum und Infimum nicht verwendet, weil mit ihr Suprema nicht eindeutig sind. Um weiterhin einen eindeutigen Supremumbegriff zu haben, wird für Halbordnungen definiert:

Definition (Supremum in Halbordnungen)

In halbgeordneten Mengen $(A,\leq )$ ist ein Element $s\in A$ Supremum einer Menge $M\subseteq A$, wenn gilt:

• $s$ ist obere Schranke von $M$: Für jedes $y\in M$ ist $y\leq s$.
• Für jede andere obere Schranke $t$ von $M$ gilt: $s\leq t$

Um zu zeigen, dass diese Definition eine sinnvolle Verallgemeinerung des Supremums auf Halbordnungen ist, müssen wir zeigen, dass beide Definitionen auf Teilmengen der reellen Zahlen übereinstimmen:

Satz (Äquivalente Definition des Supremums)

Sei $M\subseteq \mathbb {R}$ beliebig. Unsere Definition des Supremums $s$ lautet:

• Für jedes $y\in M$ ist $y\leq s$.
• Jede Zahl $x$ kleiner als $s$ ist keine obere Schranke von $M$: Für alle $x<s$ gibt es mindestens eine Zahl $y\in M$ mit $x<y$.

Diese Definition ist äquivalent zur Definition des Supremums in Halbordnungen:

• $s$ ist obere Schranke von $M$: Für jedes $y\in M$ ist $y\leq s$.
• Für jede andere obere Schranke $t$ von $M$ gilt: $s\leq t$

Beweis (Äquivalente Definition des Supremums)

Sei $M\subseteq \mathbb {R}$ beliebig. Da die jeweils ersten beiden Eigenschaften identisch sind, muss nur noch die Äquivalenz der folgenden beiden Aussagen bewiesen werden:

• Jede Zahl $x$ kleiner als $s$ ist keine obere Schranke von $M$: Für alle $x<s$ gibt es mindestens eine Zahl $y\in M$ mit $x<y$.
• Für jede andere obere Schranke $t$ von $M$ gilt $s\leq t$.

Beide Aussagen formalisiert lauten:

• $t<s\Rightarrow \exists y\in M\colon t<y$
• $(\forall y\in M\colon y\leq t)\Rightarrow s\leq t$

Die Äquivalenz beider Aussagen können wir folgendermaßen zeigen:

${\begin{array}{l}t<s\Rightarrow \exists y\in M\colon t<y\\[0.5em]\quad {\color {Gray}\left\Updownarrow \ {\text{In Totalordnung wie }}\mathbb {R} {\text{ ist }}a<b\Leftrightarrow b\not \leq a\right.}\\[0.5em]s\not \leq t\Rightarrow \exists y\in M\colon y\not \leq t\\[0.5em]\quad {\color {Gray}\left\Updownarrow \ {\text{Kontraposition: }}(A\Rightarrow B)\iff (\neg B\Rightarrow \neg A)\right.}\\[0.5em]\neg (\exists y\in M\colon y\not \leq t)\Rightarrow \neg (s\not \leq t)\\[0.5em]\quad {\color {Gray}\left\Updownarrow \ {\text{Teilaussagen negieren}}\right.}\\[0.5em](\forall y\in M\colon y\leq t)\Rightarrow s\leq t\end{array}}$

Uneigentliches Supremum und Infimum

Damit eine Menge ein Supremum besitzen kann, muss sie nach oben beschränkt sein. In diesem Kapitel untersuchen wir den Fall unbeschränkter Mengen bzw. den Fall der leeren Menge.

Uneigentliche Suprema und Infima für unbeschränkte Mengen

Eine Menge $M$ ist nach oben unbeschränkt, wenn $M$ keine obere Schranke besitzt. Für alle $S\in \mathbb {R}$ gibt es also ein $x\in M$ mit $x>S$. Dies ist dann auch die Definition der Unbeschränktheit nach oben:

Definition (nach oben unbeschränkte Menge)

Eine Menge $M$ ist nach oben unbeschränkt, wenn sie keine obere Schranke besitzt, wenn also

$\forall S\in \mathbb {R} \,\exists x\in M:S<x$

Wenn $M$ nach oben unbeschränkt ist, schreiben wir nun

$\sup M=\infty$

Intuitiv lässt sich die Schreibweise gut erklären: „unendlich“ ist größer als jedes Element aus $M$ und gleichzeitig kann es keine obere Schranke kleiner „unendlich“ geben, weil $M$ nach oben unbeschränkt ist. Also ist es sinnvoll, „unendlich“ als Supremum einer nach oben unbeschränkten Menge anzusehen.

Aber Vorsicht! Das Symbol $\infty$ ist keine reelle Zahl und damit bedeutet $\sup M=\infty$ auch nicht, dass $\infty$ Supremum von $M$ wäre, weil Suprema per Definition immer reell sein müssen. Es gibt auch kein Objekt $\infty$ in unserer Theorie, weil die von uns in den ersten Kapiteln formulierten Axiome kein Objekt $\infty$ zulassen. Deshalb müsste eine Schreibweise wie $\sup M=\infty$ von uns abgelehnt werden.

Um diese Widersprüche aufzulösen, sehen wir $\sup M=\infty$ nur als Kurzschreibweise für den Fakt an, dass $M$ nach oben unbeschränkt ist, und nennen $\infty$ das uneigentliche Supremum von $M$:

Definition (uneigentliches Supremum)

Ist eine Menge $M$ nach oben unbeschränkt, so nennen wir $\infty$ das uneigentliche Supremum von $M$ und schreiben

$\sup M=\infty$

Warnung

Das Adjektiv „uneigentlich“ ist hier sehr wichtig. Achte darauf, dass du es immer verwendest. $\infty$ ist nämlich keine reelle Zahl und kann deswegen kein Supremum sein. Es verhält sich nur in mancher Hinsicht wie ein Supremum. Kurz: Auch wenn man $\sup M=\infty$ schreibt, dann besitzt $M$ trotzdem kein Supremum!

Analog gilt für nach unten unbeschränkte Mengen:

Definition (uneigentliches Infimum)

Eine Menge $M$ ist nach unten unbeschränkt, wenn es für alle $S\in \mathbb {R}$ ein $x\in M$ mit $x<S$ gibt. In diesem Fall schreibt man

$\inf M=-\infty$

Uneigentliches Supremum und Infimum der leeren Menge

Ein weiterer Sonderfall ist die leere Menge. Hier ist nämlich nicht das Problem, dass es keine oberen beziehungsweise unteren Schranken gibt, sondern zu viele obere und untere Schranken existieren. In den Lehrbüchern findest du dafür folgende Definitionen:

Definition (Uneigentliches Supremum und Infimum der leeren Menge)

Für die leere Menge $\emptyset$ gilt

${\begin{aligned}\sup \emptyset &=-\infty \\\inf \emptyset &=\infty \end{aligned}}$

Auch hier handelt es sich um uneigentliche und damit um keine echten Suprema und Infima. Doch wieso ergibt obige Festlegung Sinn?

Gehen wir schrittweise vor: Per Definition ist das Supremum die kleinste obere Schranke einer Menge. Was sind also die oberen Schranken der leeren Menge? Eine Zahl $S$ ist per Definition eine obere Schranke von $\emptyset$, wenn

$\forall x\in \emptyset :x\leq S$

Frage: Was sind die oberen Schranken von $\emptyset$?

Allaussagen über die leere Menge wie die obige sind immer wahr (es gibt nämlich kein $x$ in $\emptyset$, für welches man die Bedingung $x\leq S$ überprüfen müsste). Damit ist jede reelle Zahl eine obere Schranke der leeren Menge. Als Bezeichnung für die kleinste all dieser oberen Schranken von $\emptyset$ kann man also $-\infty$ verwenden. Jedoch ist $-\infty$ keine reelle Zahl und daher auch kein Supremum im eigentlichen Sinne.

Verständnisfrage: Wieso ergibt $\inf \emptyset =\infty$ Sinn?

Eine Zahl $S$ ist untere Schranke der leeren Menge, wenn $\forall x\in \emptyset :x\geq S$. Diese Allaussage ist stets wahr und damit ist jede reelle Zahl eine untere Schranke von $\emptyset$. Als Bezeichnung für die größte all dieser unteren Schranken von $\emptyset$ kann man also $\infty$ verwenden. Jedoch ist $\infty$ keine reelle Zahl und daher auch kein Infimum im eigentlichen Sinne.

Supremum und Infimum bestimmen und beweisen

Allgemeine Vorgehensweise

Um das Supremum oder Infimum einer Menge zu finden, kannst du folgendermaßen vorgehen:

1. Menge veranschaulichen: Überlege dir, wie die Menge aussieht. Hierzu kannst du Skizzen anfertigen oder ggf. auch Computerprogramme verwenden.
2. Hypothese über Supremum und Infimum anstellen: Ist die Menge nach oben beschränkt? Wenn ja, dann überlege dir, welche Zahl das Supremum sein kann. Wenn nein, dann besitzt die Menge kein Supremum. Analog schaue, ob die Menge nach unten beschränkt ist oder nicht, und überlege dir gegebenenfalls, welche Zahl das Infimum sein könnte.
3. Beweise für Supremum und Infimum finden: Überlege dir auf einem Schmierblatt den Beweis dafür, dass die gefundene Zahl ein Supremum oder ein Infimum ist. Die notwendige Beweisstruktur findest du im nächsten Abschnitt.
4. Beweis ins Reine schreiben: Zum Schluss musst du den Beweis aufschreiben. Dabei kannst du dich an der im nächsten Abschnitt folgenden Beweisstruktur für Supremum und Infimum orientieren.

Allgemeine Beweisstrukturen

Die hier aufgelisteten Beweisstrukturen sollten dir helfen, deine Beweise richtig und sauber aufzuschreiben. Sie zeigen dir aber auch, worauf du in der Beweisfindung achten musst.

Supremum: Beweisstruktur

Um zu zeigen, dass eine Zahl $s$ Supremum einer Menge $M$ ist, kannst du folgendermaßen vorgehen:

1. Beweise, dass $s$ eine obere Schranke von $M$ ist: Zeige hierzu, dass $y\leq s$ für alle $y\in M$ ist.
2. Beweise, dass keine Zahl $x<s$ obere Schranke von $M$ ist: Nimm hierzu ein beliebiges $x<s$ und zeige, dass es ein $y\in M$ gibt mit $y>x$.

Infimum: Beweisstruktur

Beweise, dass ${\tilde {s}}$ Infimum einer Menge $M$ ist, können so aussehen:

1. Beweise, dass ${\tilde {s}}$ eine untere Schranke von $M$ ist: Zeige hierzu, dass $y\geq {\tilde {s}}$ für alle $y\in M$ ist.
2. Beweise, dass keine Zahl $x>{\tilde {s}}$ untere Schranke von $M$ ist: Nimm hierzu ein beliebiges $x>{\tilde {s}}$ und zeige, dass es ein $y\in M$ gibt mit $y<x$.

Maximum: Beweisstruktur

Hier kann man direkt der Definition des Maximums folgen:

1. Beweise, dass $m$ eine obere Schranke von $M$ ist: Zeige hierzu, dass $y\leq m$ für alle $y\in M$ ist.
2. Zeige, dass $m\in M$ ist.

Minimum: Beweisstruktur

Um zu zeigen, dass ${\tilde {m}}$ Minimum der Menge $M$ ist, kann man analog zum Maximum vorgehen:

1. Beweise, dass ${\tilde {m}}$ eine untere Schranke von $M$ ist: Zeige hierzu, dass $y\geq {\tilde {m}}$ für alle $y\in M$ ist.
2. Zeige, dass ${\tilde {m}}\in M$ ist.

Beispielaufgaben für Supremum und Infimum

Endliche Mengen

Bei endlichen Mengen reeller Zahlen ist die Bestimmung des Infimums und Supremums einfach. Diese Mengen müssen nämlich immer ein Maximum und ein Minimum besitzen. Das Maximum der Menge ist automatisch Supremum und das Minimum ist automatisch Infimum der Menge.

Beispiel (Supremum und Infimum einer endlichen Menge)

Gegeben sei die Menge $M=\{23,\,42,\,-1,\,5\}$. Das Maximum der Menge ist $42$ und das Minimum ist $-1$. Es ist nämlich $42$ Teil der Menge und gleichzeitig ist $42$ größer gleich jedem anderen Element der Menge (Analoges gilt für das Minimum $-1$).

Damit ist $42$ Supremum der Menge $M$ (weil es dessen Maximum ist). Analog ist $-1$ Infimum der Menge.

Verständnisaufgabe: Bestimme das Supremum und das Infimum der folgenden Mengen:

1. $M_{1}=\{4,\,72,\,-5,\,99,\,42\}$
2. $M_{2}=\{(-1)^{k}\cdot 2^{-k}:1\leq k\leq 5\land k\in \mathbb {N} \}$
3. $M_{3}=\{\pi ,\,{\sqrt {2}},\,1\}\cap \{{\sqrt {2}},\,-1,\,4\}$

Lösung:

1. Das Supremum von $M_{1}$ ist $99$ und das Infimum dieser Menge ist $-5$.
2. Es ist $\{(-1)^{k}\cdot 2^{-k}:1\leq k\leq 5\land k\in \mathbb {N} \}=\left\{-{\tfrac {1}{2}},\,{\tfrac {1}{4}},-{\tfrac {1}{8}},{\tfrac {1}{16}},-{\tfrac {1}{32}}\right\}$. Damit ist das Supremum dieser Menge gleich ${\tfrac {1}{4}}$ und das Infimum ist $-{\tfrac {1}{2}}$.
3. Es ist $\{\pi ,\,{\sqrt {2}},\,1\}\cap \{{\sqrt {2}},\,-1,\,4\}=\{{\sqrt {2}}\}$. Also ist das Supremum und das Infimum von $M_{3}$ gleich ${\sqrt {2}}$.

Intervalle

Die Bestimmung des Infimums und Supremums bei Intervallen ist recht einfach, da der untere Randpunkt stets das Infimum und der obere Randpunkt stets das Supremum ist:

Satz (Supremum und Infimum von Intervallen)

Sei $I$ ein Intervall. Es gibt also $a,b\in \mathbb {R}$ mit $a<b$, so dass $I$ eine der folgenden Formen besitzt:

1. $I=[a,b]$
2. $I=(a,b]$
3. $I=[a,b)$
4. $I=(a,b)$

Es ist dann $a$ das Infimum und $b$ das Supremum des Intervalls.

Wie kommt man auf den Beweis? (Supremum und Infimum von Intervallen)

Die obigen Intervalle unterscheiden sich darin, ob die Endpunkte $a$, $b$ enthalten sind oder nicht. In jedem Fall wissen wir, dass für jedes $x\in I$ gilt: $a\leq x\leq b$. Wir wissen also, dass $a$ eine untere Schranke ist und $b$ eine obere. Damit ist $a\leq \inf I$, $b\geq \sup I$ und wir müssen noch zeigen, dass $a$ die größte untere Schranke und $b$ die kleinste obere Schranke ist.

Dazu nehmen wir also an, es gäbe ein ${\tilde {a}}>a$, so dass ${\tilde {a}}$ auch eine untere Schranke ist, und führen dies zu einem Widerspruch.

Um zu zeigen, dass ${\tilde {a}}$ keine untere Schranke sein kann, finden wir ein $x\in I$, so dass $x<{\tilde {a}}$. Um so ein $x$ zu konstruieren, bilden wir den Mittelwert zwischen $a$ und ${\tilde {a}}$, der nach Definition größer als $a$ ist. Es könnte passieren, dass ${\tilde {a}}$ so groß ist, dass der Mittelwert größer als $b$ wird. Hier bietet sich eine Fallunterscheidung an. Wenn ${\tilde {a}}$ so groß ist, dann liegt das komplette Intervall zwischen $a$ und ${\tilde {a}}$ und wir können einen beliebigen Punkt des Intervalls für $x$ nutzen. So können wir den Mittelwert von $a$ und $b$ für $x$ wählen. Analog verfährt man dann mit der oberen Schranke $b$.

Beweis (Supremum und Infimum von Intervallen)

Sei $I$ ein Intervall. Wir legen uns nicht fest, ob die Randpunkte in $I$ enthalten sind. Damit decken wir alle Intervalltypen auf einmal ab. Für jedes solche Intervall gilt: $a\leq x$. Also ist $a$ eine untere Schranke. Wir zeigen nun durch Widerspruch, dass $a$ die größte untere Schranke ist.

Sei also ${\tilde {a}}>a$. Angenommen ${\tilde {a}}$ wäre eine untere Schranke von $I$. Dann existiert kein $x\in I$, so dass $x<{\tilde {a}}$. Wir machen nun eine Fallunterscheidung:

Fall 1: ${\tilde {a}}>b$

Sei $x:={\tfrac {a+b}{2}}$. Mit unseren Voraussetzungen können wir abschätzen

${\begin{aligned}&a={\frac {a+a}{2}}\\[0.3em]&{\color {OliveGreen}\left\downarrow \ a<b\right.}\\[0.3em]<&{\frac {a+b}{2}}=x\\[0.3em]&{\color {OliveGreen}\left\downarrow \ a<b\right.}\\[0.3em]<&{\frac {b+b}{2}}=b\end{aligned}}.$

Folglich gilt $a<x<b$ und damit $x\in I$. Aus ${\tilde {a}}>b$ folgt

$x={\frac {a+b}{2}}<b<{\tilde {a}}.$

Das ist aber ein Widerspruch zu unserer Annahme, dass ${\tilde {a}}$ eine untere Schranke von $I$ ist.

Fall 2: ${\tilde {a}}\leq b$

Wir betrachten $x:={\tfrac {a+{\tilde {a}}}{2}}$. Aus unseren Annahmen folgt

${\begin{aligned}&a={\frac {a+a}{2}}\\[0.3em]&{\color {OliveGreen}\left\downarrow \ a<{\tilde {a}}\right.}\\[0.3em]<&{\frac {a+{\tilde {a}}}{2}}=x\\[0.3em]&{\color {OliveGreen}\left\downarrow \ a<{\tilde {a}}\leq b\right.}\\[0.3em]<&{\frac {b+b}{2}}=b\end{aligned}}.$

Also gilt $a<x<b$. Daraus folgt $x\in I$.

Weil $a<{\tilde {a}}$ gilt, folgt $x={\tfrac {a+{\tilde {a}}}{2}}<{\tfrac {{\tilde {a}}+{\tilde {a}}}{2}}={\tilde {a}}$. Das ist aber wieder ein Widerspruch zu ${\tilde {a}}$ ist eine untere Schranke von $I$.

To-Do:

Skizze, um die Lage von x im Intervall zu veranschaulichen, für die beiden Fälle.

In beiden Fällen haben wir ein Widerspruch dazu, dass ${\tilde {a}}$ eine untere Schranke von $I$ ist. Also ist $a$ das Infimum des Intervalls $I$.

Um zu zeigen, dass $b$ das Supremum ist, kann man analog vorgehen. Ist ${\tilde {b}}$ eine kleinere obere Schranke von $I$, betrachtet man $x:={\tfrac {a+b}{2}}$ für den Fall ${\tilde {b}}<a$ und $x:={\tfrac {b+{\tilde {b}}}{2}}$ für den Fall ${\tilde {b}}\geq a$.

Alternativ kann man auch mit den Rechenregeln für Supremum und Infiumum folgenden Trick benutzen: Benutzen wir $\sup(I)=-\inf(-I)$, können wir den obigen Beweis auf das Intervall $-I=[-b,-a]$ anwenden.

Verständnisaufgabe: Bestimmen Sie das Supremum und das Infimum der folgenden Mengen:

1. $M_{1}=(-1,3]$
2. $M_{2}=\{x\in \mathbb {R} :2\leq 2x\leq 8\}$
3. $M_{3}=\{x\in \mathbb {R} :|x-1|<4\}$
4. $M_{4}=\{\sin(x):x\in \mathbb {R} \}$ (bei dieser Aufgabe darfst du dein Schulwissen zum Sinus verwenden  )

1. Das Supremum ist $3$ und das Infimum ist $-1$.
2. Wegen $2\leq 2x\leq 8\iff 1\leq x\leq 4$ entspricht $M_{2}$ dem Intervall $[1,4]$. Damit ist das Infimum gleich 1 und das Supremum gleich 4.
3. $M_{3}$ entspricht der Menge aller $x$ deren Abstand zu $1$ kleiner als $4$ ist. Damit entspricht diese Menge dem offenen Intervall $(1-4,1+4)=(-3,5)$. Das Infimum ist also $-3$ und das Supremum ist $5$.
4. $M_{4}$ ist die Menge aller reellen Zahlen, die durch die Sinus-Funktion getroffen werden. Damit ist $M_{4}$ gleich $[-1,1]$. Das Infimum von $M_{4}$ ist damit $-1$ und das Supremum ist $1$.

Intervalle in den ganzen Zahlen

Verständnisaufgabe: Obiger Satz ist eine Besonderheit der reellen Zahlen. Es sei $a,b\in \mathbb {Z}$ mit $a<b$. Unter welchen Bedingungen existieren Suprema beziehungsweise Infima folgender Intervalle? Welchen Wert haben sie?

1. $[a,b]\cap \mathbb {Z}$
2. $(a,b]\cap \mathbb {Z}$
3. $[a,b)\cap \mathbb {Z}$
4. $(a,b)\cap \mathbb {Z}$

Es handelt sich in allen Fällen um endliche Mengen. Es ist nämlich:

1. $[a,b]\cap \mathbb {Z} =\{x\in \mathbb {Z} :a\leq x\leq b\}=\{a,a+1,a+2,\ldots ,b-1,b\}$
2. $(a,b]\cap \mathbb {Z} =\{x\in \mathbb {Z} :a<x\leq b\}=\{a+1,a+2,\ldots ,b-1,b\}$
3. $[a,b)\cap \mathbb {Z} =\{x\in \mathbb {Z} :a\leq x<b\}=\{a,a+1,a+2,\ldots ,b-2,b-1\}$
4. $(a,b)\cap \mathbb {Z} =\{x\in \mathbb {Z} :a<x<b\}=\{a+1,a+2,\ldots ,b-1\}$

In den ersten 3 Fällen ist wegen $a<b$ die Menge nicht leer, und damit ist

1. $\sup([a,b]\cap \mathbb {Z} )=b$ und $\inf([a,b]\cap \mathbb {Z} )=a$
2. $\sup((a,b]\cap \mathbb {Z} )=b$ und $\inf((a,b]\cap \mathbb {Z} )=a+1$
3. $\sup([a,b)\cap \mathbb {Z} )=b-1$ und $\inf([a,b)\cap \mathbb {Z} )=a$

Im vierten Fall kann es passieren, dass $(a,b)\cap \mathbb {Z}$ leer ist. Das ist genau dann der Fall, wenn $a+1=b$. In diesem Fall existiert weder ein Supremum noch ein Infimum der Menge. Die leere Menge hat zwar das uneigentliche Supremum $\sup \emptyset =-\infty$ und das uneigentliche Infimum $\inf \emptyset =\infty$. Diese sind aber keine reellen Zahlen und damit keine Suprem / Infimum nach der Definition. Ist aber $a+1\neq b$, dann ist im vierten Fall das Supremum gleich $b-1$ und das Infimum gleich $a+1$.

Menge von Folgengliedern

Die Menge $M=\left\{5+{\tfrac {2}{n}}:n\in \mathbb {N} \right\}$.

Wir werden nun folgende Aufgabe beweisen:

Aufgabe (Menge von Folgengliedern)

Bestimme das Supremum und das Infimum der Menge $M=\left\{5+{\tfrac {2}{n}}:n\in \mathbb {N} \right\}$. Handelt es sich bei dem Supremum um ein Maximum und beim Infimum um ein Minimum? Beweise deine Behauptungen!

Wie kommt man auf den Beweis? (Menge von Folgengliedern)

Wir gehen nun schrittweise nach dem obigen Beweisverfahren vor:

Beweisschritt: Veranschauliche die Menge $M$.

Die ersten Elemente der Menge $M$ lauten:

1. $5+{\tfrac {2}{1}}=7\implies 7\in M$
2. $5+{\tfrac {2}{2}}=6\implies 6\in M$
3. $5+{\tfrac {2}{3}}=5{\tfrac {2}{3}}\implies 5{\tfrac {2}{3}}\in M$
4. $5+{\tfrac {2}{4}}=5{\tfrac {1}{2}}\implies 5{\tfrac {1}{2}}\in M$
5. ⋮

Die Menge $M$ hat also die Gestalt $M=\left\{7,6,5{\tfrac {2}{3}},5{\tfrac {1}{2}},5{\tfrac {2}{5}},\dots \right\}$, wobei sich die fehlenden Elemente immer mehr der $5$ annähern.

Beweisschritt: Stelle eine Hypothese an, welche Zahlen Supremum bzw. Infimum der Menge sind.

Wir sehen, dass die Menge nach oben durch $7$ beschränkt ist. Gleichzeitig ist $7$ ein Element der Menge, womit $7$ Maximum der Menge sein muss. Außerdem ist die Menge nach unten durch $5$ beschränkt. Da sich die Elemente der Menge immer mehr der $5$ annähern, kann es keine untere Schranke größer als $5$ geben. Es folgt, dass $5$ wahrscheinlich das Infimum der Menge ist. Beachte, dass wir hier nur Vermutungen anstellen, weil wir intuitiv argumentieren. Es fehlt noch der handfeste Beweis.

Beweisschritt: Finde einen Beweis für das Supremum / Maximum.

Wir haben bereits festgestellt, dass $7$ wahrscheinlich das Maximum der Menge ist. Wir müssen also zwei Dinge zeigen:

• $7\in M$
• $7\geq x$ für alle $x\in M$

Wir haben bereits im ersten Schritt gesehen, dass $7$ Element von $M$ ist, denn für $n=1$ ist $5+{\tfrac {2}{n}}=7$. Um zu zeigen, dass $7$ eine obere Schranke von $M$ ist, müssen wir zeigen, dass $7\geq 5+{\tfrac {2}{n}}$. Stellen wir diese Ungleichung schrittweise um:

${\begin{aligned}7&\geq 5+{\tfrac {2}{n}}\\2&\geq {\tfrac {2}{n}}\\2n&\geq 2\\n&\geq 1\end{aligned}}$

Nun ist $n\geq 1$ eine für natürliche Zahlen offensichtliche Aussage. Im Beweis müssen wir aber den umgekehrten Weg gehen: Da wir die Ungleichung $7\geq 5+{\tfrac {2}{n}}$ zeigen wollen, müssen wir bei $n\geq 1$ anfangen und diese Ungleichung schrittweise in $7\geq 5+{\tfrac {2}{n}}$ umformen. Dies können wir machen, weil wir oben nur Äquivalenzumformungen verwendet haben.

Im letzten Kapitel haben wir gesehen, dass jedes Maximum einer Menge automatisch auch das Supremum der Menge ist (nur umgekehrt ist es nicht immer der Fall). Daraus folgt, dass $7$ Supremum von $M$ ist.

Beweisschritt: Finde einen Beweis für das Infimum / Minimum.

Um zu zeigen, dass $5$ Infimum ist, müssen wir zeigen:

• $5\leq x$ für alle $x\in M$
• Für alle $y>5$ gibt es ein $x\in M$ mit $x<y$

Um auch zu zeigen, dass $5$ kein Minimum ist, haben wir außerdem zu beweisen, dass $5\notin M$. Zunächst muss ein Beweis für $5\leq 5+{\tfrac {2}{n}}$ für alle $n\in \mathbb {N}$ gefunden werden:

${\begin{aligned}5&\leq 5+{\tfrac {2}{n}}\\0&\leq {\tfrac {2}{n}}\end{aligned}}$

Nun ist $0\leq {\tfrac {2}{n}}$ eine offensichtlich wahre Aussage, da ${\tfrac {2}{n}}$ positiv ist. Im späteren Beweis können wir also aus $0\leq {\tfrac {2}{n}}$ die Ungleichung $5\leq 5+{\tfrac {2}{n}}$ beweisen, indem wir obige Umformung rückwärts durchführen (also zu beiden Seiten $5$ addieren).

Sei nun weiterhin $y>5$ beliebig. Wir müssen nun ein $x$ mit $x=5+{\tfrac {2}{N}}$ mit $N\in \mathbb {N}$ finden, so dass $y>x=5+{\tfrac {2}{N}}$ ist. Wir wählen hier die Variable $N$ und nicht $n$, weil wir ein konkretes Element der Menge $M$ finden wollen (in der Mathematik wird oft $N$ verwendet, wenn man ein konkretes $n$ sucht). Formen wir diese Ungleichung nach $N$ um, um so ein passendes $N\in \mathbb {N}$ zu finden:

${\begin{aligned}y&>5+{\tfrac {2}{N}}\\y-5&>{\tfrac {2}{N}}\\{\tfrac {y-5}{2}}&>{\tfrac {1}{N}}\end{aligned}}$

Wegen $y>5$ ist $y-5>0$, also auch ${\tfrac {y-5}{2}}>0$. Das archimedische Axiom garantiert uns nun, dass wir ein passendes $N$ finden, da nach dem archimedischen Axiom der Bruch ${\tfrac {1}{N}}$ kleiner wird als jede positive reelle Zahl.

Als Letztes fehlt noch die Beweisidee dafür, dass $5\notin M$ ist. Hier müssen wir zeigen, dass $5\neq 5+{\tfrac {2}{n}}$ für alle $n\in \mathbb {N}$ gilt. Doch wegen ${\tfrac {2}{n}}>0$ ist $5+{\tfrac {2}{n}}>5$ und somit $5\neq 5+{\tfrac {2}{n}}$.

Beweis (Menge von Folgengliedern)

Es ist $7$ Maximum (und damit Supremum) der Menge $M$ und $5$ ist Infimum, aber kein Minimum der Menge $M$.

Beweisschritt: $7$ ist Maximum der Menge $M$

Beweisschritt: $7$ ist Element der Menge $M$

Für $n=1$ ist $5+{\tfrac {2}{n}}=7$. Damit ist $7\in M$.

Beweisschritt: $7$ ist eine obere Schranke der Menge $M$

Für alle $n\in \mathbb {N}$ gilt

${\begin{aligned}&&n&\geq 1\\&\implies &2n&\geq 2\\&\implies &2&\geq {\tfrac {2}{n}}\\&\implies &7&\geq 5+{\tfrac {2}{n}}\end{aligned}}$

Damit ist $7$ größer gleich jedem Element von $M$.

Beweisschritt: $5$ ist Infimum der Menge $M$

Beweisschritt: $5$ ist untere Schranke der Menge $M$

Für alle $n\in \mathbb {N}$ gilt

${\begin{aligned}&&0&\leq {\tfrac {2}{n}}\\&\implies &5&\leq 5+{\tfrac {2}{n}}\end{aligned}}$

Damit ist $5$ kleiner gleich jedem Element von $M$.

Beweisschritt: Keine Zahl größer $5$ ist untere Schranke der Menge $M$

Sei $y>5$ beliebig. Es ist damit ${\tfrac {y-5}{2}}>0$ und somit gibt es nach dem archimedischen Axiom ein $N\in \mathbb {N}$ mit ${\tfrac {y-5}{2}}>{\tfrac {1}{N}}$. Es ist

${\begin{aligned}&&{\tfrac {y-5}{2}}&>{\tfrac {1}{N}}\\&\implies &y-5&>{\tfrac {2}{N}}\\&\implies &y&>5+{\tfrac {2}{N}}\end{aligned}}$

Weil $5+{\tfrac {2}{N}}\in M$ ist, gibt es damit ein Element aus $M$, welches kleiner als $y$ ist. Somit ist $y$ keine untere Schranke von $M$.

Beweisschritt: $5$ ist kein Minimum von $M$

Es ist ${\tfrac {2}{n}}>0$ und damit ${\tfrac {2}{n}}+5>5$. Somit ist $5$ kein Element und damit auch kein Minimum von $M$.

Menge von Funktionswerten

Supremum beweisen - Vorgehen anhand eines Beispiels erklärt (Youtube-Video vom Youtube-Kanal „MJ Education“)

Aufgabe

Bestimmen Sie Supremum und Infimum der Menge

$M=\left\{{\frac {1}{1+x^{2}}}:x\in \mathbb {R} \right\}$

Wie kommt man auf den Beweis?

Sei im Folgenden $f:\mathbb {R} \rightarrow \mathbb {R} :x\mapsto {\tfrac {1}{1+x^{2}}}$. Gehen wir nun schrittweise vor:

Schritt 1: Veranschauliche die Menge $M$.

Die Funktion $f(x)={\tfrac {1}{1+x^{2}}}$ hat den Graphen:

Der Graph der Funktion f(x)=1/(1+x²)

Die Menge $M$ ist nun die Menge aller tatsächlich durch $f$ getroffenen Werte, also das Bild der Funktion $f$.

Schritt 2: Stelle eine Hypothese an, welche Zahlen Supremum bzw. Infimum der Menge sind.

Wir können vermuten, dass $1$ das Supremum von $M$ ist. Weil $f(0)={\tfrac {1}{1+0^{2}}}=1$ ist, wird $1$ auch durch die Funktion $f$ getroffen. Damit liegt diese Zahl in $M$ und müsste demnach Maximum dieser Menge sein.

Außerdem liegt die Vermutung nahe, dass $0$ das Infimum von $M$ ist. Die Funktion scheint immer positiv, also größer gleich null zu sein. Je größer bzw. je kleiner $x$, desto näher gehen die Funktionswerte gegen null (so sieht es zumindest auf den ersten Blick aus). Es sollte also insgesamt $0$ Infimum der Menge $M$ sein, wobei es nicht direkt in $M$ liegt und somit kein Minimum sein sollte.

Schritt 3: Finde einen Beweis für das Supremum / Maximum.

Wir vermuten, dass $1$ das Maximum der Menge $M$ ist. Weil ${\tfrac {1}{1+0^{2}}}=1$ ist, können wir beweisen, dass $1\in M$ sein muss. Es fehlt jetzt nur noch der Beweis, dass $1$ eine obere Schranke der Menge $M$ ist. Hierzu müssen wir beweisen, dass für alle reellen Zahlen $x$ wir folgende Ungleichung haben:

${\frac {1}{1+x^{2}}}\leq 1$

Formen wir diese Ungleichung durch Äquivalenzumformungen um:

${\begin{array}{lrl}&{\frac {1}{1+x^{2}}}&\leq 1\\[0.3em]\iff \ &1&\leq 1+x^{2}\\[0.3em]\iff \ &0&\leq x^{2}\end{array}}$

Wir wissen bereits, dass die letzte Ungleichung für alle $x\in \mathbb {R}$ erfüllt ist. Da wir nur Äquivalenzumformungen verwendet haben, können wir aus dieser später die Ungleichung ${\frac {1}{1+x^{2}}}\leq 1$ wieder herleiten.

Schritt 4: Finde einen Beweis für das Infimum / Minimum.

Hier müssen wir zunächst zeigen, dass alle Elemente aus $M$ größer gleich null sind. Jedoch ist ${\tfrac {1}{1+x^{2}}}$ der Quotient von zwei positiven Zahlen, welches damit wieder positiv ist. Alle Elemente aus $M$ sind somit positiv und damit insbesondere größer gleich $0$.

Fehlt noch der Beweis, dass $0$ auch die größte untere Schranke von $M$ ist. Sei hierzu $y>0$ beliebig. Wir müssen nun ein Element aus $M$ finden, welches kleiner als $y$ ist. Es muss also ein $x\in \mathbb {R}$ geben, so dass

${\frac {1}{1+x^{2}}}<y$

ist. Formen wir diese Ungleichung durch Äquivalenzumformungen um:

${\begin{array}{lrl}&{\frac {1}{1+x^{2}}}&<y\\\iff \ &1&<y\cdot (1+x^{2})\\\iff \ &1&<y+y\cdot x^{2}\\\iff \ &1-y&<y\cdot x^{2}\\[0.5em]&&{\color {OliveGreen}\left\downarrow \ y{\text{ ist positiv}}\right.}\\[0.5em]\iff \ &{\frac {1-y}{y}}&<x^{2}\\\end{array}}$

Um die Wurzel ziehen zu können, muss ${\tfrac {1-y}{y}}\geq 0$ also $y\leq 1$ sein. Für die weitere Beweisfindung ist es aber kein Problem $0<y\leq 1$ anzunehmen, denn für $y>1$ ist die letzte Ungleichung immer erfüllt. Die Quadratzahl $x^{2}$ ist dann nämlich immer größer als die negative Zahl ${\tfrac {1-y}{y}}$.

Sei also $0<y\leq 1$. Wir erhalten weiter:

${\begin{array}{lrl}&{\frac {1-y}{y}}&<x^{2}\\\iff &{\sqrt {\frac {1-y}{y}}}&<|x|\\\end{array}}$

Für $0<y\leq 1$ müssen wir also nur ein $x\in \mathbb {R}$ mit $|x|>{\sqrt {\frac {1-y}{y}}}$ wählen. Dieses $x$ erfüllt dann automatisch

${\frac {1}{1+x^{2}}}<y$

was zeigt, dass $y$ keine untere Schranke von $M$ ist.

Beweis

$1$ ist Maximum (und damit Supremum) der Menge $M$ und $0$ ist Infimum, aber kein Minimum der Menge $M$.

Beweisschritt: $1$ ist Maximum der Menge $M$

Beweisschritt: $1$ ist Element der Menge $M$

Für $x=0$ ist ${\tfrac {1}{1+x^{2}}}=1$. Damit ist $1\in M$.

Beweisschritt: $1$ ist eine obere Schranke der Menge $M$

Es ist

${\begin{array}{lrl}&0&\leq x^{2}\\\implies \ &1&\leq 1+x^{2}\\\implies \ &{\frac {1}{1+x^{2}}}&\leq 1\\\end{array}}$

Damit ist $1$ eine obere Schranke von $M$.

Beweisschritt: $0$ ist Infimum der Menge $M$

Beweisschritt: $0$ ist untere Schranke der Menge $M$

Es ist für alle $x\in \mathbb {R}$:

${\begin{array}{lrl}&x^{2}&\geq 0\\\implies \ &1+x^{2}&>0\\\implies \ &{\frac {1}{1+x^{2}}}&>0\\\end{array}}$

Damit ist null eine untere Schranke von $M$.

Beweisschritt: Keine Zahl größer $0$ ist untere Schranke der Menge $M$

Sei $y>0$ beliebig. Für $y>1$ ist

${\frac {1-y}{y}}<x^{2}$

für jedes reelle $x$, weil $1-y$ dann negativ ist. Für $0<y\leq 1$ wähle $x$ so, dass $|x|>{\sqrt {\tfrac {1-y}{y}}}$ ist. Dann ist nämlich auch obige Ungleichung erfüllt.

Für jedes $y>0$ gibt es also mindestens eine reelle Zahl $x$ mit $x^{2}>{\tfrac {1-y}{y}}$. Für diese reelle Zahlen haben wir

${\begin{array}{lrl}&{\frac {1-y}{y}}&<x^{2}\\\implies \ &1-y&<y\cdot x^{2}\\\implies \ &1&<y+y\cdot x^{2}\\\implies \ &1&<y\cdot (1+x^{2})\\&{\frac {1}{1+x^{2}}}&<y\\\end{array}}$

Damit kann aber $y$ keine untere Schranke von $M$ sein, was beweist, dass $0$ die größte untere Schranke von $M$ ist.

Eigenschaften Supremum und Infimum

Da das Supremum auf Mengen angewandt wird, ist eine sehr naheliegende Frage: Was passiert mit dem Supremum, wenn wir die Menge verändern? Wenn wir sie mit einer anderen Menge beispielsweise schneiden oder vereinigen, wenn wir sie größer oder kleiner machen? Hier werden wir einige Regeln kennen lernen, die dir helfen werden, mit dem Supremum zu arbeiten.

Übersicht der Regeln zum Supremum und Infimum

Wir definieren zuerst einige Kurzschreibweisen.

Definition

Für alle Mengen $A,B\subseteq \mathbb {R}$ und alle $\lambda \in \mathbb {R}$ definieren wir:

• $-A:=\{-x:x\in A\}$
• $\lambda A:=\{\lambda x:x\in A\}$
• $A+B:=\{a+b:a\in A,b\in B\}$
• $A\cdot B:=\{a\cdot b:a\in A,b\in B\}$

Für das Supremum und Infimum gelten folgende Regeln. Dabei ist $A,B,D\subseteq \mathbb {R}$ und $f,g:D\rightarrow \mathbb {R}$ sowie $\lambda \in \mathbb {R}$. Im Folgenden wird immer angenommen, dass das Supremum beziehungsweise das Infimum existiert.

Regeln für das Supremum

• $\sup A\geq \inf A$
• $A\subseteq B\Rightarrow \sup A\leq \sup B$

• $\sup(A\cup B)=\max\{\sup A,\sup B\}$
• $\sup(A\cap B)\leq \min\{\sup A,\sup B\}$
• $\sup(-A)=\sup(\{-x:x\in A\})=-\inf(A)$
• $\sup(\{x^{-1}:x\in A\})=(\inf(A))^{-1}$, falls $\inf(A)>0$ ist.
• $\sup(\lambda A)=\sup(\{\lambda x:x\in A\})=\lambda \cdot \sup(A)$ für $\lambda \geq 0$
• $\sup(A+B)=\sup(\{x+y:x\in A\land y\in B\})=\sup(A)+\sup(B)$
• $\sup(A\cdot B)=\sup(\{x\cdot y:x\in A\land y\in B\})=\sup(A)\cdot \sup(B)$, falls $A$ und $B$ nur nichtnegative Elemente enthalten.
• $\sup(f+g)(D)\leq \sup f(D)+\sup g(D)$
• Es gibt eine Folge $(a_{n})_{n\in \mathbb {N} }$ aus $A$ mit $\lim _{n\rightarrow \infty }a_{n}=\sup A$.

Frage: Warum gilt nicht $\sup A\leq \sup B\Rightarrow A\subseteq B$? Finde ein Gegenbeispiel!

Ein Gegenbeispiel hierfür ist $A:=\{1\},B:=\{2\}$.

Frage: Warum gilt nicht $\sup(A\cap B)=\min\{\sup A,\sup B\}$? Finde ein Gegenbeispiel!

Sei $A=\{1,2\}$ und $B=\{1,3\}$. Dann gilt $A\cap B=\{1\}$ und also $\sup A\cap B=1$, aber $\sup A=2$ und $\sup B=3$, also $\min\{\sup A,\sup B\}=2$.

Das Supremum der Summe zweier Funktionen kann kleiner als die Summe ihrer Suprema sein.

Frage: Warum gilt nicht $\sup(f+g)(D)=\sup f(D)+\sup g(D)$? Finde ein Gegenbeispiel!

Wir setzen $D:=[0,1]$. Als Funktionen wählen wir $f:D\to \mathbb {R} ,x\mapsto x$ und $g:D\to \mathbb {R} ,x\mapsto 1-x$. Also ist $(f+g):D\to \mathbb {R} ,x\mapsto 1$. Es gilt

$\sup(f+g)(D)=1<1+1=\sup f(D)+\sup g(D)$

Regeln für das Infimum

• $\inf A\leq \sup A$
• $A\subseteq B\Rightarrow \inf A\geq \inf B$
• $\inf(A\cup B)=\min\{\inf A,\inf B\}$
• $\inf(A\cap B)\geq \max\{\inf A,\inf B\}$
• $\inf(-A)=\inf(\{-x:x\in A\})=-\sup(A)$
• $\inf(\lambda A)=\inf(\{\lambda x:x\in A\})=\lambda \cdot \inf(A)$ für $\lambda \geq 0$
• $\inf(A+B)=\inf(\{x+y:x\in A\land y\in B\})=\inf(A)+\inf(B)$
• $\inf(A\cdot B)=\inf(\{x\cdot y:x\in A\land y\in B\})=\inf(A)\cdot \inf(B)$, falls $A$ und $B$ nur nichtnegative Elemente enthalten.
• $\inf(f+g)(D)\geq \inf f(D)+\inf g(D)$
• Es gibt eine Folge $(a_{n})_{n\in \mathbb {N} }$ aus $A$ mit $\lim _{n\rightarrow \infty }a_{n}=\inf A$.

Beweis der Regeln

In den folgenden Abschnitten werde ich die obigen Eigenschaften nur für das Supremum beweisen.

Supremum ist größer gleich dem Infimum

Satz

Sei $A$ eine nicht leere, beschränkte Menge. Es ist dann $\sup A\geq \inf A$.

Wie kommt man auf den Beweis?

Die Aussage bedeutet anschaulich gesprochen, dass die kleinste obere Schranke einer Menge größer oder gleich als die größte untere Schranke ist. Dies ist sinnvoll, da eine obere Schranke einer Menge immer größer oder gleich als eine untere Schranke sein sollte. Die einzige Schwierigkeit besteht nun darin, dies formal zu beweisen. Hier hilft die Anschauung, dass eine nichtleere Menge mindestens ein Element hat, welches dann zwischen Supremum und Infimum "eingequetscht" ist. Auf dem Zahlenstrahl ist die Reihenfolge auch klar, nämlich drückt das Infimum von unten, während das Supremum oben aufsitzt. Wir nehmen also das garantierte Element und "quetschen" es in eine Ungleichungskette, starten links beim Infimum und enden rechts beim Supremum. Dann haben wir aber Supremum und Infimum so getrennt, wie es der Satz will.

Beweis

Als nicht leere Menge besitzt $A$ mindestens ein Element $x$. Da $\sup A$ eine obere Schranke ist, ist $x\leq \sup A$. Analog gilt $\inf A\leq x$. Insgesamt ist $\inf A\leq x\leq \sup A$ und damit auch $\inf A\leq \sup A$.

Abschätzung des Supremums bei Teilmengen

Satz

Ist $A\subseteq B$, dann ist $\sup A\leq \sup B$.

Beweis

Nach der ersten Supremumsbedingung ist $\sup B$ eine obere Schranke von $B$, also wegen $A\subseteq B$ insbesondere auch von $A$, d.h. für alle $x\in A$ gilt $x\leq \sup B$. Das Supremum von $A$ ist aber gerade charakterisiert als die kleinste obere Schranke von $A$, es muss also insbesondere kleiner oder gleich $\sup B$ sein.

Supremum bei der Vereinigung

Satz

Es ist

$\sup(A\cup B)=\max\{\sup A,\sup B\}$

Beweis

Ist $x\in A\cup B$, so ist $x\in A$ oder $x\in B$. Nach der ersten Supremumsbedingung gilt somit $x\leq \sup A$ oder $x\leq \sup B$. Also insbesondere $x\leq \max\{\sup A,\sup B\}$. Damit ist $\max\{\sup A,\sup B\}$ eine obere Schranke von $A\cup B$.

Den zweiten Teil erhalten wir wie folgt: Es gilt immer $\sup A\leq \sup B$ oder $\sup B\leq \sup A$. Gehen wir vom ersten Fall aus (falls wir nicht im ersten Fall sind, benennen wir unsere Mengen einfach um): Dann gilt für alle $x\in A$ wegen der ersten Supremumsbedingung $x\leq \sup A$, aber wegen $\sup A\leq \sup B$ auch $x\leq \sup B$ und $\sup B$ ist eine obere Schranke von $A$ und nach Definition auch von $B$, also von $A\cup B$. Dass es auch die kleinste obere Schranke ist, folgt aus der zweiten Supremumsbedingung: Jede kleinere Zahl ist keine obere Schranke mehr von $B$, also auch nicht von $A\cup B$.

Supremum beim Schnitt

Satz

Es ist

$\sup(A\cap B)\leq \min\{\sup A,\sup B\}$

Beweis

Dieser Teil folgt direkt aus 1. und der Tatsache, dass $A\cap B\subseteq A$ und $A\cap B\subseteq B$ gilt: $\sup(A\cap B)\leq \sup A$ und $\sup(A\cap B)\leq \sup B$, also $\sup A\cap B\leq \min\{\sup A,\sup B\}$. Theoretisch sind wir damit mit dem Beweis fertig, aber es ist sicherlich illustrativ, so zu überlegen, warum hier im Allgemeinen eine Ungleichheit steht.

Supremum und Multiplikation mit $-1$

Satz

Es ist

$\sup(-A)=\sup(\{-x:x\in A\})=-\inf(A)$

Beweis

Für alle $x\in A$ gilt $\inf(A)\leq x$. Multiplikation der Ungleichung mit $-1$ ergibt gerade $-x\leq -\inf(A)$. Da aber alle Elemente von $-A$ von dieser Form sind, ist $-\inf(A)$ eine obere Schranke für $-A$. Da jedoch das Supremum von $-A$ die kleinste aller oberen Schranken ist, folgt $\sup(-A)\leq -\inf(A)$.

Sei nun $\varepsilon >0$ gegeben. Nach der Definition des Infimums ist $\inf(A)+\varepsilon$ dann keine untere Schranke von $A$. Das bedeutet, dass ein $x\in A$ existiert, sodass $x<\inf(A)+\varepsilon$. Multipliziert man diese Ungleichung mit $-1$ so erhält man $-x>-\inf(A)-\varepsilon$. Es ist aber $-x$ ein Element in $-A$, also kann $-\inf(A)-\varepsilon$ keine obere Schranke von $-A$ sein. Da unser $\varepsilon$ beliebig gewählt war, folgt die gewünschte Gleichheit $\sup(-A)=-\inf(A)$.

Hinweis

Aus dieser Regel erhalten wir zwischen Supremum und Infimum die Zusammenhänge $\sup(A)=\sup(-(-A))=-\inf(-A)$ und $\inf(A)=-(-\inf(A))=-\sup(-A)$.

Supremum und Multiplikation mit einem nicht negativen Skalar

Satz

Für $\lambda \geq 0$ gilt

$\sup(\lambda A)=\sup(\{\lambda x:x\in A\})=\lambda \sup(A)$

Beweis

Ist $\lambda =0$, so gibt es nicht viel zu zeigen, denn $\lambda \cdot A=0\cdot A=\{0\}$ und $\sup(\{0\})=0=0\sup(A)$.

Wir können also im Weiteren $\lambda >0$ voraussetzen. Für alle $x\in A$ gilt $x\leq \sup(A)$. Multiplikation der Ungleichung mit $\lambda$ ergibt gerade $\lambda x\leq \lambda \sup(A)$. Da aber alle Elemente von $\lambda \cdot A$ von dieser Form sind, ist $\lambda \sup(A)$ eine obere Schranke für $\lambda \cdot A$. Da jedoch das Supremum von $\lambda \cdot A$ die kleinste aller oberen Schranken ist, folgt $\sup(\lambda \cdot A)\leq \lambda \sup(A)$.

Sei nun $\varepsilon >0$ gegeben und wir definieren $\varepsilon ':={\frac {\varepsilon }{\lambda }}$. Dies ist erlaubt, da wir $\lambda >0$ voraussetzen. Nach der Definition des Supremums ist $\sup(A)-\varepsilon '$ dann keine obere Schranke von $A$. Das bedeutet, dass ein $x\in A$ existiert, sodass $x>\sup(A)-\varepsilon '$. Multipliziert man diese Ungleichung mit $\lambda$ so erhält man

$\lambda x>\lambda \sup(A)-\lambda \varepsilon '=\lambda \sup(A)-\lambda {\frac {\varepsilon }{\lambda }}=\lambda \sup(A)-\varepsilon$

Es ist aber $\lambda x$ ein Element in $\lambda \cdot A$, also kann $\lambda \sup(A)-\varepsilon$ keine obere Schranke von $\lambda \cdot A$ sein. Da unser $\varepsilon$ beliebig gewählt war, folgt die gewünschte Gleichheit $\sup(\lambda \cdot A)=\lambda \sup(A)$.

Supremum und Summen

Satz

Es ist

$\sup(A+B)=\sup(\{x+y:x\in A\land y\in B\})=\sup(A)+\sup(B)$

Beweis

Jedes Element $z\in A+B$ besitzt die Form $z=x+y$ für ein $x\in A$ und ein $y\in B$. Nach der Definition des Supremums gilt $x\leq \sup(A)$ und $y\leq \sup(B)$. Addition der beiden Ungleichungen ergibt $z=x+y\leq \sup(A)+\sup(B)$. Also ist $\sup(A)+\sup(B)$ eine obere Schranke für $A+B$. Da jedoch das Supremum von $A+B$ die kleinste aller oberen Schranken ist, folgt $\sup(A+B)\leq \sup(A)+\sup(B)$.

Sei nun $\varepsilon >0$ gegeben und wir definieren $\varepsilon ':={\frac {\varepsilon }{2}}$. Nach der Definition des Supremums ist $\sup(A)-\varepsilon '$ dann keine obere Schranke von $A$ und $\sup(B)-\varepsilon '$ keine obere Schranke von $B$. Das bedeutet, dass ein $x\in A$ und ein $y\in B$ existieren, sodass $x>\sup(A)-\varepsilon '$ und $y>\sup(B)-\varepsilon '$. Durch Addition beider Ungleichungen erhält man

$x+y>\sup(A)+\sup(B)-2\varepsilon '=\sup(A)+\sup(B)-2{\frac {\varepsilon }{2}}=\sup(A)+\sup(B)-\varepsilon$

Es ist aber $x+y$ ein Element in $A+B$, also kann $\sup(A)+\sup(B)-\varepsilon$ keine obere Schranke von $A+B$ sein. Da unser $\varepsilon$ beliebig gewählt war, folgt die gewünschte Gleichheit $\sup(A+B)=\sup(A)+\sup(B)$.

Supremum und Produkte

Satz

Falls $A$ und $B$ nur nicht negative Elemente enthalten, ist

$\sup(A\cdot B)=\sup(\{x\cdot y:x\in A\land y\in B\})=\sup(A)\cdot \sup(B)$

Beweis

Jedes Element $z\in A\cdot B$ besitzt die Form $z=x\cdot y$ für ein $x\in A$ und ein $y\in B$. Nach der Definition des Supremums gilt $x\leq \sup(A)$ und $y\leq \sup(B)$. Multiplikation der beiden Ungleichungen ergibt $z=x\cdot y\leq \sup(A)\cdot \sup(B)$. Also ist $\sup(A)\cdot \sup(B)$ eine obere Schranke für $A\cdot B$. Da jedoch das Supremum von $A\cdot B$ die kleinste aller oberen Schranken ist, folgt $\sup(A\cdot B)\leq \sup(A)\cdot \sup(B)$.

Ist $\sup(A)=0$ oder $\sup(B)=0$, so folgt $A=\{0\}$ oder $B=\{0\}$, denn es wurden alle Elemente aus $A$ und $B$ als nicht negativ also größer oder gleich Null vorausgesetzt. Damit folgt sofort $\sup(A\cdot B)=0$.

Im Folgenden kann man also $\sup(A)>0$ und $\sup(B)>0$ voraussetzen. Sei nun $\varepsilon >0$ gegeben. Dann können wir nach dem vorangehenden Satz ohne Probleme $\varepsilon _{A}:={\frac {\varepsilon }{2\sup(B)}}$ und $\varepsilon _{B}:={\frac {\varepsilon }{2\sup(A)}}$ definieren.

Nach der Definition des Supremums ist $\sup(A)-\varepsilon _{A}$ dann keine obere Schranke von $A$ und $\sup(B)-\varepsilon _{B}$ keine obere Schranke von $B$. Das bedeutet, dass ein $x\in A$ und ein $y\in B$ existieren, sodass $x>\sup(A)-\varepsilon _{A}$ und $y>\sup(B)-\varepsilon _{B}$. Durch Produktbildung beider Ungleichungen erhält man

$x\cdot y>(\sup(A)-\varepsilon _{A})\cdot (\sup(B)-\varepsilon _{B})=\sup(A)\cdot \sup(B)-{\frac {\varepsilon }{2\sup(B)}}\cdot \sup(B)-{\frac {\varepsilon }{2\sup(A)}}\cdot \sup(A)+\varepsilon _{A}\cdot \varepsilon _{B}=\sup(A)\cdot \sup(B)-{\frac {\varepsilon }{2}}-{\frac {\varepsilon }{2}}+\varepsilon _{A}\cdot \varepsilon _{B}=\sup(A)\cdot \sup(B)-\varepsilon +\varepsilon _{A}\cdot \varepsilon _{B}>\sup(A)\cdot \sup(B)-\varepsilon$

Man beachte das $>$-Zeichen im letzten Schritt. Hierbei wurde $\varepsilon _{A}\cdot \varepsilon _{B}>0$ verwendet. Nun ist $x\cdot y$ ein Element in $A\cdot B$, also kann $\sup(A)\cdot \sup(B)-\varepsilon$ keine obere Schranke von $A\cdot B$ sein. Da unser $\varepsilon$ beliebig gewählt war, folgt die gewünschte Gleichheit $\sup(A\cdot B)=\sup(A)\cdot \sup(B)$.

Supremum der Summe zweier Funktionen kleiner gleich der Summe der Suprema dieser Funktionen

Satz

Es gilt $\sup(f+g)(D)=\sup(\{f(t)+g(t):t\in D\})\leq \sup f(D)+\sup g(D)$

Beweis

Es gilt

${\begin{aligned}&\sup(f+g)(D)\\[0.3em]=\ &\sup(\{f(t)+g(t):t\in D\})\\[0.3em]&{\color {OliveGreen}\left\downarrow \ \sup A\leq \sup B{\text{ für }}A\subseteq B\right.}\\[0.3em]\leq \ &\sup(\{f(t)+g(s):t,s\in D\})\\[0.3em]=\ &\sup(\{a+b:a\in f(D),b\in g(D)\})\\[0.3em]&{\color {OliveGreen}\left\downarrow \ \sup(A+B)=\sup A+\sup B\right.}\\[0.3em]=\ &\sup f(D)+\sup g(D)\end{aligned}}$

Existenz einer Folge $(a_{n})_{n\in \mathbb {N} }$ in $A$ mit $\lim _{n\to \infty }a_{n}=\sup A$

Satz

Wenn $\sup A$ existiert, dann gibt es eine Folge $(a_{n})_{n\in \mathbb {N} }$ in $A$ mit $\lim _{n\to \infty }a_{n}=\sup A$.

Beweis

Wir erinnern und an den zweiten Teil der Definition des Supremums, die Epsilon-Definition: Für alle $\epsilon >0$ gibt es ein $a\in A$ mit $a+\epsilon >\sup A$.

Folglich gibt es für alle $n\in \mathbb {N}$ ein $a_{n}\in A$ mit $a_{n}+{\tfrac {1}{n}}>\sup A$. Da alle $a_{n}$ aus $A$ sind, gilt auch $a_{n}\leq \sup A$. Damit ergibt sich für alle $n\in \mathbb {N}$:

${\frac {1}{n}}>\sup A-a_{n}\geq 0$

Nach dem Sandwichtheorem gilt also $\lim _{n\to \infty }a_{n}=\sup A$.

Wurzel reeller Zahlen

Mathe für Nicht-Freaks: Wurzel

Lösungen von Potenzgleichungen

Mathe für Nicht-Freaks: Potenzgleichungen

Rechenregeln der Wurzel

Mathe für Nicht-Freaks: Rechenregeln der Wurzel

Verallgemeinerte Potenzen

Mathe für Nicht-Freaks: Potenzen mit rationalem Exponenten

Aufgaben zu Wurzeln

Mathe für Nicht-Freaks: Aufgaben zu Wurzeln

Definition der Folgen

Mathe für Nicht-Freaks: Folge

Explizite und rekursive Bildungsgesetze der Folgen

Mathe für Nicht-Freaks: Explizite und rekursive Bildungsgesetze für Folgen

Beispiele und Eigenschaften für und von Folgen

Mathe für Nicht-Freaks: Beispiele und Eigenschaften von Folgen

Aufgaben zu Folgen

Mathe für Nicht-Freaks: Aufgaben zu Folgen

Definition Grenzwert

Mathe für Nicht-Freaks: Grenzwert: Konvergenz und Divergenz

Konvergenz und Divergenz beweisen

Mathe für Nicht-Freaks: Konvergenz und Divergenz beweisen

Beispiele für Grenzwerte

Mathe für Nicht-Freaks: Grenzwert: Beispiele

Unbeschränkte Folgen divergieren

Mathe für Nicht-Freaks: Unbeschränkte Folgen divergieren

Grenzwertsätze

Mathe für Nicht-Freaks: Grenzwertsätze: Grenzwert von Folgen berechnen

Der Sandwichsatz

Mathe für Nicht-Freaks: Sandwichsatz

Monotoniekriterium

Mathe für Nicht-Freaks: Monotoniekriterium für Folgen

Konvergenzbeweise rekursiver Folgen

Mathe für Nicht-Freaks: Konvergenz rekursiver Folgen beweisen

Aufgaben zur Konvergenz und Divergenz

Mathe für Nicht-Freaks: Aufgaben zur Konvergenz und Divergenz

Teilfolgen

Mathe für Nicht-Freaks: Teilfolge

Häufungspunkte von Folgen

Mathe für Nicht-Freaks: Häufungspunkt einer Folge

Häufungs- und Berührpunkte von Mengen

Mathe für Nicht-Freaks: Häufungspunkt und Berührpunkt einer Menge

Satz von Bolzano-Weierstraß

Mathe für Nicht-Freaks: Satz von Bolzano-Weierstraß

Bestimmte Divergenz

Mathe für Nicht-Freaks: Bestimmte Divergenz, uneigentliche Konvergenz

Bestimmte Divergenz: Regeln

Mathe für Nicht-Freaks: Rechenregeln der bestimmten Divergenz

Lim sup und Lim inf

Mathe für Nicht-Freaks: Lim sup und Lim inf

Cauchy-Folgen

Mathe für Nicht-Freaks: Cauchy-Folgen und das Cauchy-Kriterium

Aufgaben zu Teilfolgen, Häufungspunkte und Cauchy-Folgen

Mathe für Nicht-Freaks: Aufgaben zu Teilfolgen, Häufungspunkte und Cauchy-Folgen

Begriff der Reihe

Mathe für Nicht-Freaks: Reihe

Rechenregeln für Reihen

Mathe für Nicht-Freaks: Rechenregeln für Reihen

Teleskopsumme und Teleskopreihe

Mathe für Nicht-Freaks: Teleskopsumme und Teleskopreihe

Geometrische Reihe

Mathe für Nicht-Freaks: Geometrische Reihe

Harmonische Reihe

Mathe für Nicht-Freaks: Harmonische Reihe

e-Reihe

Mathe für Nicht-Freaks: e-Reihe

Absolute Konvergenz einer Reihe

Mathe für Nicht-Freaks: Absolute Konvergenz einer Reihe

Umordnungssatz für Reihen

Mathe für Nicht-Freaks: Umordnungssatz für Reihen

Aufgaben zu Reihen

Mathe für Nicht-Freaks: Aufgaben zu Reihen

Übersicht Konvergenzkriterien für Reihen

Mathe für Nicht-Freaks: Konvergenz und Divergenz einer Reihe beweisen: Konvergenzkriterien

Cauchy-Kriterium

Mathe für Nicht-Freaks: Cauchy-Kriterium für Reihen

Trivialkriterium

Mathe für Nicht-Freaks: Trivialkriterium, Nullfolgenkriterium, Divergenzkriterium

Beschränkte Reihen und Konvergenz

Mathe für Nicht-Freaks: Beschränkte Reihen und Konvergenz

Majoranten- und Minorantenkriterium

Mathe für Nicht-Freaks: Majorantenkriterium und Minorantenkriterium

Wurzelkriterium

Mathe für Nicht-Freaks: Wurzelkriterium

Quotientenkriterium

Mathe für Nicht-Freaks: Quotientenkriterium

Leibniz-Kriterium

Mathe für Nicht-Freaks: Leibniz-Kriterium

Verdichtungskriterium

Mathe für Nicht-Freaks: Cauchysches Verdichtungskriterium

Anwendung der Konvergenzkriterien

Mathe für Nicht-Freaks: Anwendung der Konvergenzkriterien bei Reihen

Aufgaben zu Konvergenzkriterien für Reihe

Mathe für Nicht-Freaks: Aufgaben zu Konvergenzkriterien für Reihen

Herleitung und Definition der Exponentialfunktion

Mathe für Nicht-Freaks: Herleitung und Definition der Exponentialfunktion

Stetigkeit von Funktionen

Mathe für Nicht-Freaks: Stetigkeit von Funktionen

Folgenkriterium der Stetigkeit

Mathe für Nicht-Freaks: Folgenkriterium der Stetigkeit

Epsilon-Delta-Definition der Stetigkeit

Mathe für Nicht-Freaks: Epsilon-Delta-Definition der Stetigkeit

Grenzwert von Funktionen

Mathe für Nicht-Freaks: Grenzwert von Funktionen

Stetigkeit beweisen

Mathe für Nicht-Freaks: Stetigkeit beweisen

Komposition stetiger Funktionen

Mathe für Nicht-Freaks: Komposition stetiger Funktionen

Zwischenwertsatz

Mathe für Nicht-Freaks: Zwischenwertsatz

Satz vom Minimum und Maximum

Mathe für Nicht-Freaks: Satz vom Minimum und Maximum

Stetigkeit der Umkehrfunktion

Mathe für Nicht-Freaks: Stetigkeit der Umkehrfunktion

Gleichmäßige Stetigkeit

Mathe für Nicht-Freaks: Gleichmäßige Stetigkeit

Lipschitz-Stetigkeit

Mathe für Nicht-Freaks: Lipschitz-Stetigkeit

Aufgaben zur Stetigkeit

Mathe für Nicht-Freaks: Aufgaben zur Stetigkeit]

Ableitung und Differenzierbarkeit

Mathe für Nicht-Freaks: Ableitung und Differenzierbarkeit

Rechengesetze für die Ableitung

Mathe für Nicht-Freaks: Rechengesetze für die Ableitung

Ableitung der Umkehrfunktion

Mathe für Nicht-Freaks: Ableitung der Umkehrfunktion

Beispiele für Ableitungen

Mathe für Nicht-Freaks: Beispiele für Ableitungen

Ableitung höherer Ordnung

Mathe für Nicht-Freaks: Ableitung höherer Ordnung

Satz von Rolle

Mathe für Nicht-Freaks: Satz von Rolle

Mittelwertsatz

Mathe für Nicht-Freaks: Mittelwertsatz

Kriterium für Konstanz und Monotoniekriterium

Mathe für Nicht-Freaks: Kriterium für Konstanz und Monotoniekriterium

Ableitung und lokale Extrema

Mathe für Nicht-Freaks: Ableitung und lokale Extrema

Regel von L'Hospital

Mathe für Nicht-Freaks: Regel von L'Hospita

Aufgaben zur Ableitung 1

Mathe für Nicht-Freaks: Aufgaben zur Ableitung 1

Aufgaben zur Ableitung 2

Mathe für Nicht-Freaks: Aufgaben zur Ableitung 2

Aufgaben zur Ableitung 3

Mathe für Nicht-Freaks: Aufgaben zur Ableitung 3

Aufgaben zur Ableitung 4

Mathe für Nicht-Freaks: Aufgaben zur Ableitung 4

Das Integral

Mathe für Nicht-Freaks: Integral einer Funktion

Riemann-Integral

Mathe für Nicht-Freaks: Riemann-Integral

Eigenschaften des Riemann-Integrals

Mathe für Nicht-Freaks: Eigenschaften des Riemann-Integrals

Regelintegral

Mathe für Nicht-Freaks: Regelintegral

Hauptsatz der Differential- und Integralrechnung

Mathe für Nicht-Freaks: Hauptsatz der Differential- und Integralrechnung

Substitutionsregel

Mathe für Nicht-Freaks: Substitutionsregel für Integrale

Partielle Integration

Mathe für Nicht-Freaks: Partielle Integration